数据库系统基础教程

合集下载

数据库系统基础教程第六章答案

Solutions Chapter 6Attributes must be separated by commas. Thus here B is an alias of A.6.1.2a)SELECT address AS Studio_AddressFROM StudioWHERE NAME = 'MGM';b)SELECT birthdate AS Star_BirthdateFROM MovieStarWHERE name = 'Sandra Bullock';c)SELECT starNameFROM StarsInWHERE movieYear = 1980OR movieTitle LIKE '%Love%';However, above query will also return words that have the substring Love e.g. Lover. Below query will only return movies that have title containing the word Love.SELECT starNameFROM StarsInWHERE movieYear = 1980OR movieTitle LIKE 'Love %'OR movieTitle LIKE '% Love %'OR movieTitle LIKE '% Love'OR movieTitle = 'Love';d)SELECT name AS Exec_NameFROM MovieExecWHERE netWorth >= 10000000;e)SELECT name AS Star_NameFROM movieStarWHERE gender = 'M'OR address LIKE '% Malibu %';a)SELECT model,speed,hdFROM PCWHERE price < 1000 ;MODEL SPEED HD----- ---------- ------1002 2.10 2501003 1.42 801004 2.80 2501005 3.20 2501007 2.20 2001008 2.20 2501009 2.00 2501010 2.80 3001011 1.86 1601012 2.80 1601013 3.06 8011 record(s) selected.b)SELECT model ,speed AS gigahertz,hd AS gigabytesFROM PCWHERE price < 1000 ;MODEL GIGAHERTZ GIGABYTES ----- ---------- ---------1002 2.10 2501003 1.42 801004 2.80 2501005 3.20 2501007 2.20 2001008 2.20 2501009 2.00 2501010 2.80 3001011 1.86 1601012 2.80 1601013 3.06 8011 record(s) selected.c)SELECT makerFROM ProductWHERE TYPE = 'printer' ; MAKER-----DDEEEHH7 record(s) selected.d)SELECT model,ram ,screenFROM LaptopWHERE price > 1500 ; MODEL RAM SCREEN ----- ------ -------2001 2048 20.12005 1024 17.02006 2048 15.42010 2048 15.44 record(s) selected.e)SELECT *FROM PrinterWHERE color ;MODEL CASE TYPE PRICE----- ----- -------- ------3001 TRUE ink-jet 993003 TRUE laser 9993004 TRUE ink-jet 1203006 TRUE ink-jet 1003007 TRUE laser 2005 record(s) selected.Note: Implementation of Boolean type is optional in SQL standard (feature IDT031). PostgreSQL has implementation similar to above example. Other DBMS provide equivalent support. E.g. In DB2 the column type can be declare as SMALLINT with CONSTRAINT that the value can be 0 or 1. The result can be returned as Boolean type CHAR using CASE.CREATE TABLE Printer(model CHAR(4) UNIQUE NOT NULL,color SMALLINT ,type VARCHAR(8) ,price SMALLINT ,CONSTRAINT Printer_ISCOLOR CHECK(color IN(0,1)));SELECT model,CASE colorWHEN 1THEN 'TRUE'WHEN 0THEN 'FALSE'ELSE 'ERROR'END CASE ,type,priceFROM PrinterWHERE color = 1;f)SELECT model,hdFROM PCWHERE speed = 3.2AND price < 2000;MODEL HD----- ------1005 2501006 3202 record(s) selected.6.1.4a)SELECT class,countryFROM ClassesWHERE numGuns >= 10 ; CLASS COUNTRY------------------ ------------ Tennessee USA1 record(s) selected.b)SELECT name AS shipName FROM ShipsWHERE launched < 1918 ; SHIPNAME------------------HarunaHieiKirishimaKongoRamilliesRenownRepulseResolutionRevengeRoyal OakRoyal Sovereign11 record(s) selected.c)SELECT ship AS shipName, battleFROM OutcomesWHERE result = 'sunk' ; SHIPNAME BATTLE------------------ ------------------ Arizona Pearl Harbor Bismark Denmark Strait Fuso Surigao Strait Hood Denmark Strait Kirishima Guadalcanal Scharnhorst North Cape Yamashiro Surigao Strait 7 record(s) selected.d)SELECT name AS shipNameFROM ShipsWHERE name = class ;SHIPNAME------------------IowaKongoNorth CarolinaRenownRevengeYamato6 record(s) selected.e)SELECT name AS shipNameFROM ShipsWHERE name LIKE 'R%';SHIPNAME------------------RamilliesRenownRepulseResolutionRevengeRoyal OakRoyal Sovereign7 record(s) selected.Note: As mentioned in exercise 2.4.3, there are some dangling pointers and to retrieve all ships a UNION of Ships and Outcomes is required.Below query returns 8 rows including ship named Rodney.SELECT name AS shipNameFROM ShipsWHERE name LIKE 'R%'UNIONSELECT ship AS shipNameFROM OutcomesWHERE ship LIKE 'R%';f) Only using a filter like '% % %' will incorrectly match name such as ' a b ' since % can match any sequence of 0 or more characters.SELECT name AS shipNameFROM ShipsWHERE name LIKE '_% _% _%' ;SHIPNAME------------------0 record(s) selected.Note: As in (e), UNION with results from Outcomes.SELECT name AS shipNameFROM ShipsWHERE name LIKE '_% _% _%'UNIONSELECT ship AS shipNameFROM OutcomesWHERE ship LIKE '_% _% _%' ;SHIPNAME------------------Duke of YorkKing George VPrince of Wales3 record(s) selected.6.1.5a)The resulting expression is false when neither of (a=10) or (b=20) is TRUE.a = 10b = 20 a = 10 OR b = 20NULL TRUE TRUETRUE NULL TRUEFALSE TRUE TRUETRUE FALSE TRUETRUE TRUE TRUEb)The resulting expression is only TRUE when both (a=10) and (b=20) are TRUE.a = 10b = 20 a = 10 AND b = 20TRUE TRUE TRUEThe expression is always TRUE unless a is NULL.a < 10 a >= 10 a = 10 ANDb = 20TRUE FALSE TRUEFALSE TRUE TRUEd)The expression is TRUE when a=b except when the values are NULL.a b a = bNOT NULL NOT NULL TRUE when a=b; else FALSEe)Like in (d), the expression is TRUE when a<=b except when the values are NULL.a b a <= bNOT NULL NOT NULL TRUE when a<=b; else FALSE6.1.6SELECT *FROM MoviesWHERE LENGTH IS NOT NULL;6.2.1a)SELECT AS starNameFROM MovieStar M,StarsIn SWHERE = S.starNameAND S.movieTitle = 'Titanic'AND M.gender = 'M';b)SELECT S.starNameFROM Movies M ,StarsIn S,Studios TWHERE ='MGM'AND M.year = 1995AND M.title = S.movieTitleAND M.studioName = ;SELECT AS presidentName FROM MovieExec X,Studio TWHERE X.cert# = T.presC#AND = 'MGM';d)SELECT M1.titleFROM Movies M1,Movies M2WHERE M1.length > M2.lengthAND M2.title ='Gone With the Wind' ;e)SELECT AS execNameFROM MovieExec X1,MovieExec X2WHERE Worth > WorthAND = 'Merv Griffin' ;6.2.2a)SELECT R.maker AS manufacturer,L.speed AS gigahertzFROM Product R,Laptop LWHERE L.hd >= 30AND R.model = L.model ; MANUFACTURER GIGAHERTZ------------ ----------A 2.00A 2.16A 2.00B 1.83E 2.00E 1.73E 1.80F 1.60F 1.60G 2.0010 record(s) selected.SELECT R.model,P.priceFROM Product R,PC PWHERE R.maker = 'B'AND R.model = P.model UNIONSELECT R.model,L.priceFROM Product R,Laptop LWHERE R.maker = 'B'AND R.model = L.model UNIONSELECT R.model,T.priceFROM Product R,Printer TWHERE R.maker = 'B'AND R.model = T.model ; MODEL PRICE----- ------1004 6491005 6301006 10492007 14294 record(s) selected.c)SELECT R.makerFROM Product R,Laptop LWHERE R.model = L.model EXCEPTSELECT R.makerFROM Product R,PC PWHERE R.model = P.model ; MAKER-----FG2 record(s) selected.SELECT DISTINCT P1.hd FROM PC P1,PC P2WHERE P1.hd =P2.hdAND P1.model > P2.model ; Alternate Answer:SELECT DISTINCT P.hdFROM PC PGROUP BY P.hdHAVING COUNT(P.model) >= 2 ;e)SELECT P1.model,P2.modelFROM PC P1,PC P2WHERE P1.speed = P2.speed AND P1.ram = P2.ramAND P1.model < P2.model ; MODEL MODEL----- -----1004 10121 record(s) selected.f)SELECT M.makerFROM(SELECT maker,R.modelFROM PC P,Product RWHERE SPEED >= 3.0AND P.model=R.modelUNIONSELECT maker,R.modelFROM Laptop L,Product RWHERE speed >= 3.0AND L.model=R.model) MGROUP BY M.makerHAVING COUNT(M.model) >= 2 ; MAKER-----B1 record(s) selected.6.2.3a)SELECT FROM Ships S,Classes CWHERE S.class = C.classAND C.displacement > 35000;NAME------------------IowaMissouriMusashiNew JerseyNorth CarolinaWashingtonWisconsinYamato8 record(s) selected.b)SELECT ,C.displacement,C.numGunsFROM Ships S ,Outcomes O,Classes CWHERE = O.shipAND S.class = C.classAND O.battle = 'Guadalcanal' ;NAME DISPLACEMENT NUMGUNS------------------ ------------ -------Kirishima 32000 8Washington 37000 92 record(s) selected.Note:South Dakota was also engaged in battle of Guadalcanal but not chosen since it is not in Ships table(Hence, no information regarding it's Class isavailable).SELECT name shipName FROM ShipsUNIONSELECT ship shipName FROM Outcomes ; SHIPNAME------------------ArizonaBismarkCaliforniaDuke of YorkFusoHarunaHieiHoodIowaKing George VKirishimaKongoMissouriMusashiNew JerseyNorth CarolinaPrince of Wales RamilliesRenownRepulseResolutionRevengeRodneyRoyal OakRoyal Sovereign ScharnhorstSouth DakotaTenneseeTennesseeWashingtonWest VirginiaWisconsinYamashiroYamato34 record(s) selected.SELECT C1.countryFROM Classes C1,Classes C2WHERE C1.country = C2.country AND C1.type = 'bb'AND C2.type = 'bc' ; COUNTRY------------Gt. BritainJapan2 record(s) selected.e)SELECT O1.shipFROM Outcomes O1,Battles B1WHERE O1.battle = AND O1.result = 'damaged'AND EXISTS(SELECT B2.dateFROM Outcomes O2,Battles B2WHERE O2.battle= AND O1.ship = O2.shipAND B1.date < B2.date) ;SHIP------------------0 record(s) selected.f)SELECT O.battleFROM Outcomes O,Ships S ,Classes CWHERE O.ship = AND S.class = C.class GROUP BY C.country,O.battleHAVING COUNT(O.ship) > 3; SELECT O.battleFROM Ships S ,Classes C,Outcomes OWHERE C.Class = S.classAND O.ship = GROUP BY C.country,O.battleHAVING COUNT(O.ship) >= 3;6.2.4Since tuple variables are not guaranteed to be unique, every relation Ri should be renamed using an alias. Every tuple variable should be qualified with the alias. Tuple variables for repeating relations will also be distinctlyidentified this way.Thus the query will be likeSELECT A1.COLL1,A1.COLL2,A2.COLL1,…FROM R1 A1,R2 A2,…,Rn AnWH ERE A1.COLL1=A2.COLC2,…6.2.5Again, create a tuple variable for every Ri, i=1,2,...,nThat is, the FROM clause isFROM R1 A1, R2 A2,...,Rn An.Now, build the WHERE clause from C by replacing every reference to some attribute COL1 of Ri by Ai.COL1. In addition apply Natural Join i.e. add condition to check equality of common attribute names between Ri and Ri+1 for all i from 0 to n-1. Also, build the SELECT clause from list of attributes L by replacing every attribute COLj of Ri by Ai.COLj.6.3.1a)SELECT DISTINCT makerFROM ProductWHERE model IN(SELECT modelFROM PCWHERE speed >= 3.0);SELECT DISTINCT R.makerFROM Product RWHERE EXISTS(SELECT P.modelFROM PC PWHERE P.speed >= 3.0AND P.model =R.model);SELECT P1.modelFROM Printer P1WHERE P1.price >= ALL(SELECT P2.priceFROM Printer P2) ;SELECT P1.modelFROM Printer P1WHERE P1.price IN(SELECT MAX(P2.price)FROM Printer P2) ;c)SELECT L.modelFROM Laptop LWHERE L.speed < ANY(SELECT P.speedFROM PC P) ;SELECT L.modelFROM Laptop LWHERE EXISTS(SELECT P.speedFROM PC PWHERE P.speed >= L.speed ) ;SELECT modelFROM(SELECT model,priceFROM PCUNIONSELECT model,priceFROM LaptopUNIONSELECT model,priceFROM Printer) M1WHERE M1.price >= ALL (SELECT priceFROM PCUNIONSELECT priceFROM LaptopUNIONSELECT priceFROM Printer) ;(d) – contd --SELECT modelFROM(SELECT model,priceFROM PCUNIONSELECT model,priceFROM LaptopUNIONSELECT model,priceFROM Printer) M1WHERE M1.price IN(SELECT MAX(price)FROM(SELECT priceFROM PCUNIONSELECT priceFROM LaptopUNIONSELECT priceFROM Printer) M2) ;e)SELECT R.makerFROM Product R,Printer TWHERE R.model =T.model AND T.price <= ALL(SELECT MIN(price)FROM Printer);SELECT R.makerFROM Product R,Printer T1WHERE R.model =T1.model AND T1.price IN(SELECT MIN(T2.price) FROM Printer T2);f)SELECT R1.makerFROM Product R1,PC P1WHERE R1.model=P1.modelAND P1.ram IN(SELECT MIN(ram)FROM PC)AND P1.speed >= ALL(SELECT P1.speedFROM Product R1,PC P1WHERE R1.model=P1.model AND P1.ram IN(SELECT MIN(ram)FROM PC));SELECT R1.makerFROM Product R1,PC P1WHERE R1.model=P1.modelAND P1.ram =(SELECT MIN(ram)FROM PC)AND P1.speed IN(SELECT MAX(P1.speed)FROM Product R1,PC P1WHERE R1.model=P1.model AND P1.ram IN(SELECT MIN(ram)FROM PC));6.3.2a)SELECT C.countryFROM Classes CWHERE numGuns IN(SELECT MAX(numGuns)FROM Classes);SELECT C.countryFROM Classes CWHERE numGuns >= ALL(SELECT numGunsFROM Classes);b)SELECT DISTINCT C.class FROM Classes C,Ships SWHERE C.class = S.classAND EXISTS(SELECT shipFROM Outcomes OWHERE O.result='sunk' AND O.ship = ) ;SELECT DISTINCT C.class FROM Classes C,Ships SWHERE C.class = S.classAND IN(SELECT shipFROM Outcomes OWHERE O.result='sunk' ) ;c)SELECT FROM Ships SWHERE S.class IN(SELECT classFROM Classes CWHERE bore=16) ;SELECT FROM Ships SWHERE EXISTS(SELECT classFROM Classes CWHERE bore =16AND C.class = S.class );SELECT O.battleFROM Outcomes OWHERE O.ship IN(SELECT nameFROM Ships SWHERE S.Class ='Kongo' );SELECT O.battleFROM Outcomes OWHERE EXISTS(SELECT nameFROM Ships SWHERE S.Class ='Kongo' AND = O.ship );SELECT FROM Ships S,Classes CWHERE S.Class = C.ClassAND numGuns >= ALL(SELECT numGunsFROM Ships S2,Classes C2WHERE S2.Class = C2.Class AND C2.bore = C.bore) ;SELECT FROM Ships S,Classes CWHERE S.Class = C.ClassAND numGuns IN(SELECT MAX(numGuns)FROM Ships S2,Classes C2WHERE S2.Class = C2.Class AND C2.bore = C.bore) ;Better answer;SELECT FROM Ships S,Classes CWHERE S.Class = C.ClassAND numGuns >= ALL(SELECT numGunsFROM Classes C2WHERE C2.bore = C.bore) ;SELECT FROM Ships S,Classes CWHERE S.Class = C.ClassAND numGuns IN(SELECT MAX(numGuns)FROM Classes C2WHERE C2.bore = C.bore) ;6.3.3SELECT titleFROM MoviesGROUP BY titleHAVING COUNT(title) > 1 ;6.3.4SELECT FROM Ships S,Classes CWHERE S.Class = C.Class ;Assumption: In R1 join R2, the rows of R2 are unique on the joining columns. SELECT COLL12,COLL13,COLL14FROM R1WHERE COLL12 IN(SELECT COL22FROM R2)AND COLL13 IN(SELECT COL33FROM R3)AND COLL14 IN(SELECT COL44FROM R4) ...6.3.5(a)SELECT ,S.addressFROM MovieStar S,MovieExec EWHERE S.gender ='F'AND Worth > 10000000AND = AND S.address = E.address ;Note: As mentioned previously in the book, the names of stars are unique. However no such restriction exists for executives. Thus, both name and address are required as join columns.Alternate solution:SELECT name,addressFROM MovieStarWHERE gender = 'F'AND (name, address) IN(SELECT name,addressFROM MovieExecWHERE netWorth > 10000000) ;(b)SELECT name,addressFROM MovieStarWHERE (name,address) NOT IN(SELECT name addressFROM MovieExec) ;6.3.6By replacing the column in subquery with a constant and using IN subquery forthe constant, statement equivalent to EXISTS can be found.i.e. replace "WHERE EXISTS (SELECT C1 FROM R1..)" by "WHERE 1 IN (SELECT 1 FROM R1...)"Example:SELECT DISTINCT R.makerFROM Product RWHERE EXISTS(SELECT P.modelFROM PC PWHERE P.speed >= 3.0AND P.model =R.model) ;Above statement can be transformed to below statement.SELECT DISTINCT R.makerFROM Product RWHERE 1 IN(SELECT 1FROM PC PWHERE P.speed >= 3.0AND P.model =R.model) ;6.3.7(a)n*m tuples are returned where there are n studios and m executives. Each studiowill appear m times; once for every exec.(b)There are no common attributes between StarsIn and MovieStar; hence no tuplesare returned.(c)There will be at least one tuple corresponding to each star in MovieStar. Theunemployed stars will appear once with null values for StarsIn. All employedstars will appear as many times as the number of movies they are working in. Inother words, for each tuple in StarsIn(starName), the correspoding tuple fromMovieStar(name)) is joined and returned. For tuples in MovieStar that do nothave a corresponding entry in StarsIn, the MovieStar tuple is returned with nullvalues for StarsIn columns.6.3.8Since model numbers are unique, a full natural outer join of PC, Laptop andPrinter will return one row for each model. We want all information about PCs,Laptops and Printers even if the model does not appear in Product but vice versais not true. Thus a left natural outer join between Product and result above isrequired. The type attribute from Product must be renamed since Printer has atype attribute as well and the two attributes are different.(SELECT maker,model,type AS productTypeFROM Product) RIGHT NATURAL OUTER JOIN ((PC FULL NATURAL OUTER JOIN Laptop) FULL NATURAL OUTER JOIN Printer);Alternately, the Product relation can be joined individually with each ofPC,Laptop and Printer and the three results can be Unioned together. Forattributes that do not exist in one relation, a constant such as 'NA' or 0.0 canbe used. Below is an example of this approach using PC and Laptop.SELECT R.MAKER ,R.MODEL ,R.TYPE ,P.SPEED ,P.RAM ,P.HD ,0.0 AS SCREEN,P.PRICEFROM PRODUCT R,PC PWHERE R.MODEL = P.MODELUNIONSELECT R.MAKER ,R.MODEL ,R.TYPE ,L.SPEED ,L.RAM ,L.HD ,L.SCREEN,L.PRICEFROM PRODUCT R,LAPTOP LWHERE R.MODEL = L.MODEL;6.3.9SELECT *FROM Classes RIGHT NATURALOUTER JOIN Ships ;6.3.10SELECT *FROM Classes RIGHT NATURALOUTER JOIN ShipsUNION(SELECT C2.class ,C2.type ,C2.country ,C2.numguns ,C2.bore ,C2.displacement,C2.class NAME ,FROM Classes C2,Ships S2WHERE C2.Class NOT IN(SELECT ClassFROM Ships)) ;6.3.11(a)SELECT *FROM R,S ;(b)Let Attr consist ofAttrR = attributes unique to RAttrS = attributes unique to SAttrU = attributes common to R and SThus in Attr, attributes common to R and S are not repeated. SELECT AttrFROM R,SWHERE R.AttrU1 = S.AttrU1AND R.AttrU2 = S.AttrU2 ...AND R.AttrUi = S.AttrUi ;(c)SELECT *FROM R,SWHERE C ;6.4.1(a)DISTINCT keyword is not required here since each model only occurs once in PC relation.SELECT modelFROM PCWHERE speed >= 3.0 ;(b)SELECT DISTINCT R.makerFROM Product R,Laptop LWHERE R.model = L.modelAND L.hd > 100 ;(c)SELECT R.model,P.priceFROM Product R,PC PWHERE R.model = P.modelAND R.maker = 'B'UNIONSELECT R.model,L.priceFROM Product R,Laptop LWHERE R.model = L.modelAND R.maker = 'B'UNIONSELECT R.model,T.priceFROM Product R,Printer TWHERE R.model = T.modelAND R.maker = 'B' ;SELECT modelFROM PrinterWHERE color=TRUEAND type ='laser' ;(e)SELECT DISTINCT R.makerFROM Product R,Laptop LWHERE R.model = L.modelAND R.maker NOT IN(SELECT R1.makerFROM Product R1,PC PWHERE R1.model = P.model) ;better:SELECT DISTINCT R.makerFROM Product RWHERE R.type = 'laptop'AND R.maker NOT IN(SELECT R.makerFROM Product RWHERE R.type = 'pc') ;(f)With GROUP BY hd, DISTINCT keyword is not required. SELECT hdFROM PCGROUP BY hdHAVING COUNT(hd) > 1 ;(g)SELECT P1.model,P2.modelFROM PC P1,PC P2WHERE P1.speed = P2.speedAND P1.ram = P2.ramAND P1.model < P2.model ;SELECT R.makerFROM Product RWHERE R.model IN(SELECT P.modelFROM PC PWHERE P.speed >= 2.8)OR R.model IN(SELECT L.modelFROM Laptop LWHERE L.speed >= 2.8)GROUP BY R.makerHAVING COUNT(R.model) > 1 ;(i)After finding the maximum speed, an IN subquery can provide the manufacturer name.SELECT MAX(M.speed)FROM(SELECT speedFROM PCUNIONSELECT speedFROM Laptop) M ;SELECT R.makerFROM Product R,PC PWHERE R.model = P.modelAND P.speed IN(SELECT MAX(M.speed)FROM(SELECT speedFROM PCUNIONSELECT speedFROM Laptop) M)UNIONSELECT R2.makerFROM Product R2,Laptop LWHERE R2.model = L.modelAND L.speed IN(SELECT MAX(N.speed)FROM(SELECT speedFROM PCUNIONSELECT speedFROM Laptop) N) ;Alternately,SELECT COALESCE(MAX(P2.speed),MAX(L2.speed),0) SPEED FROM PC P2FULL OUTER JOIN Laptop L2ON P2.speed = L2.speed ;SELECT R.makerFROM Product R,PC PWHERE R.model = P.modelAND P.speed IN(SELECT COALESCE(MAX(P2.speed),MAX(L2.speed),0) SPEED FROM PC P2FULL OUTER JOIN Laptop L2ON P2.speed = L2.speed)UNIONSELECT R2.makerFROM Product R2,Laptop LWHERE R2.model = L.modelAND L.speed IN(SELECT COALESCE(MAX(P2.speed),MAX(L2.speed),0) SPEED FROM PC P2FULL OUTER JOIN Laptop L2ON P2.speed = L2.speed)SELECT R.makerFROM Product R,PC PWHERE R.model = P.modelGROUP BY R.makerHAVING COUNT(DISTINCT speed) >= 3 ;(k)SELECT R.makerFROM Product R,PC PWHERE R.model = P.modelGROUP BY R.makerHAVING COUNT(R.model) = 3 ;better;SELECT R.makerFROM Product RWHERE R.type='pc'GROUP BY R.makerHAVING COUNT(R.model) = 3 ;6.4.2(a)We can assume that class is unique in Classes and DISTINCT keyword is not required.SELECT class,countryFROM ClassesWHERE bore >= 16 ;(b)Ship names are not unique (In absence of hull codes, year of launch can help distinguish ships).SELECT DISTINCT name AS Ship_NameFROM ShipsWHERE launched < 1921 ;(c)SELECT DISTINCT ship AS Ship_NameFROM OutcomesWHERE battle = 'Denmark Strait'AND result = 'sunk' ;(d)SELECT DISTINCT AS Ship_NameFROM Ships S,Classes CWHERE S.class = C.classAND C.displacement > 35000 ;SELECT DISTINCT O.ship AS Ship_Name,C.displacement ,C.numGunsFROM Classes C ,Outcomes O,Ships SWHERE C.class = S.classAND = O.shipAND O.battle = 'Guadalcanal' ;SHIP_NAME DISPLACEMENT NUMGUNS------------------ ------------ -------Kirishima 32000 8Washington 37000 92 record(s) selected.Note: South Dakota was also in Guadalcanal but its class information is not available. Below query will return name of all ships that were in Guadalcanal even if no other information is available (shown as NULL). The above query is modified from INNER joins to LEFT OUTER joins.SELECT DISTINCT O.ship AS Ship_Name,C.displacement ,C.numGunsFROM Outcomes OLEFT JOIN Ships SON = O.shipLEFT JOIN Classes CON C.class = S.classWHERE O.battle = 'Guadalcanal' ;SHIP_NAME DISPLACEMENT NUMGUNS------------------ ------------ -------Kirishima 32000 8South Dakota - -Washington 37000 93 record(s) selected.(f)The Set opearator UNION guarantees unique results.SELECT ship AS Ship_NameFROM OutcomesUNIONSELECT name AS Ship_NameFROM Ships ;(g)SELECT C.classFROM Classes C,Ships SWHERE C.class = S.classGROUP BY C.classHAVING COUNT() = 1 ;better:SELECT S.classFROM Ships SGROUP BY S.classHAVING COUNT() = 1 ;(h)The Set opearator INTERSECT guarantees unique results.SELECT C.countryFROM Classes CWHERE C.type='bb'INTERSECTSELECT C2.countryFROM Classes C2WHERE C2.type='bc' ;However, above query does not account for classes without any ships belonging to them.SELECT C.countryFROM Classes C,Ships SWHERE C.class = S.classAND C.type ='bb'INTERSECTSELECT C2.countryFROM Classes C2,Ships S2WHERE C2.class = S2.classAND C2.type ='bc' ;SELECT O2.ship AS Ship_Name FROM Outcomes O2,Battles B2WHERE O2.battle = AND B2.date > ANY(SELECT B.dateFROM Outcomes O,Battles BWHERE O.battle = AND O.result ='damaged' AND O.ship = O2.ship);6.4.3a)SELECT DISTINCT R.maker FROM Product R,PC PWHERE R.model = P.modelAND P.speed >= 3.0;b)Models are unique.SELECT P1.modelFROM Printer P1LEFT OUTER JOIN Printer P2 ON (P1.price < P2.price) WHERE P2.model IS NULL ;c)SELECT DISTINCT L.model FROM Laptop L,PC PWHERE L.speed < P.speed ;Due to set operator UNION, unique results are returned.It is difficult to completely avoid a subquery here. One option is to use Views. CREATE VIEW AllProduct ASSELECT model,priceFROM PCUNIONSELECT model,priceFROM LaptopUNIONSELECT model,priceFROM Printer ;SELECT A1.modelFROM AllProduct A1LEFT OUTER JOIN AllProduct A2ON (A1.price < A2.price)WHERE A2.model IS NULL ;But if we replace the View, the query contains a FROM subquery. SELECT A1.modelFROM(SELECT model,priceFROM PCUNIONSELECT model,priceFROM LaptopUNIONSELECT model,priceFROM Printer) A1LEFT OUTER JOIN(SELECT model,priceFROM PCUNIONSELECT model,priceFROM LaptopUNIONSELECT model,priceFROM Printer) A2ON (A1.price < A2.price) WHERE A2.model IS NULL ;e)SELECT DISTINCT R.makerFROM Product R,Printer TWHERE R.model =T.modelAND T.price <= ALL(SELECT MIN(price)FROM Printer);f)SELECT DISTINCT R1.makerFROM Product R1,PC P1WHERE R1.model=P1.modelAND P1.ram IN(SELECT MIN(ram)FROM PC)AND P1.speed >= ALL(SELECT P1.speedFROM Product R1,PC P1WHERE R1.model=P1.modelAND P1.ram IN(SELECT MIN(ram)FROM PC));6.4.4a)SELECT DISTINCT C1.countryFROM Classes C1LEFT OUTER JOIN Classes C2 ON (C1.numGuns < C2.numGuns) WHERE C2.country IS NULL ;。

数据库系统基础教程(第二版)课后习题答案2

Database Systems: The Complete BookSolutions for Chapter 2Solutions for Section 2.1Exercise 2.1.1The E/R Diagram.Exercise 2.1.8(a)The E/R DiagramKobvxybzSolutions for Section 2.2Exercise 2.2.1The Addresses entity set is nothing but a single address, so we would prefer to make address an attribute of Customers. Were the bank to record several addresses for a customer, then it might make sense to have an Addresses entity set and make Lives-at a many-many relationship.The Acct-Sets entity set is useless. Each customer has a unique account set containing his or her accounts. However, relating customers directly to their accounts in a many-many relationship conveys the same information and eliminates the account-set concept altogether.Solutions for Section 2.3Exercise 2.3.1(a)Keys ssNo and number are appropriate for Customers and Accounts, respectively. Also, we think it does not make sense for an account to be related to zero customers, so we should round the edge connecting Owns to Customers. It does not seem inappropriate to have a customer with 0 accounts;they might be a borrower, for example, so we put no constraint on the connection from Owns to Accounts. Here is the The E/R Diagram，showing underlined keys andthe numerocity constraint.Exercise 2.3.2(b)If R is many-one from E1 to E2, then two tuples (e1,e2) and (f1,f2) of the relationship set for R must be the same if they agree on the key attributes for E1. To see why, surely e1 and f1 are the same. Because R is many-one from E1 to E2, e2 and f2 must also be the same. Thus, the pairs are the same.Solutions for Section 2.4Exercise 2.4.1Here is the The E/R Diagram.We have omitted attributes other than our choice for the key attributes of Students and Courses. Also omitted are names for the relationships. Attribute grade is not part of the key for Enrollments. The key for Enrollements is studID from Students and dept and number from Courses.Exercise 2.4.4bHere is the The E/R Diagram Again, we have omitted relationship names and attributes other than our choice for the key attributes. The key for Leagues is its own name; this entity set is not weak. The key for Teams is its own name plus the name of the league of which the team is a part, e.g., (Rangers, MLB) or (Rangers, NHL). The key for Players consists of the player's number and the key for the team on which he or she plays. Since the latter key is itself a pair consisting of team and league names, the key for players is the triple (number, teamName, leagueName). e.g., JeffGarcia is (5, 49ers, NFL).Database Systems: The Complete BookSolutions for Chapter 3Solutions for Section 3.1Exercise 3.1.2(a)We can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Solutions for Section 3.2Exercise 3.2.1Customers(ssNo, name, address, phone)Flights(number, day, aircraft)Bookings(ssNo, number, day, row, seat)Being a weak entity set, Bookings' relation has the keys for Customers and Flights and Bookings' own attributes.Notice that the relations obtained from the toCust and toFlt relationships are unnecessary. They are:toCust(ssNo, ssNo1, number, day)toFlt(ssNo, number, day, number1, day1)That is, for toCust, the key of Customers is paired with the key for Bookings. Since both include ssNo, this attribute is repeated with two different names, ssNo and ssNo1. A similar situation exists for toFlt.Exercise 3.2.3Ships(name, yearLaunched)SisterOf(name, sisterName)Solutions for Section 3.3Exercise 3.3.1Since Courses is weak, its key is number and the name of its department. We do not have arelation for GivenBy. In part (a), there is a relation for Courses and a relation for LabCourses that has only the key and the computer-allocation attribute. It looks like:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, allocation)For part (b), LabCourses gets all the attributes of Courses, as:Depts(name, chair)Courses(number, deptName, room)LabCourses(number, deptName, room, allocation)And for (c), Courses and LabCourses are combined, as:Depts(name, chair)Courses(number, deptName, room, allocation)Exercise 3.3.4(a)There is one relation for each entity set, so the number of relations is e. The relation for the root entity set has a attributes, while the other relations, which must include the key attributes, have a+k attributes.Solutions for Section 3.4Exercise 3.4.2Surely ID is a key by itself. However, we think that the attributes x, y, and z together form another key. The reason is that at no time can two molecules occupy the same point.Exercise 3.4.4The key attributes are indicated by capitalization in the schema below:Customers(SSNO, name, address, phone)Flights(NUMBER, DAY, aircraft)Bookings(SSNO, NUMBER, DAY, row, seat)Exercise 3.4.6(a)The superkeys are any subset that contains A1. Thus, there are 2^{n-1} such subsets, since each of the n-1 attributes A2 through An may independently be chosen in or out.Solutions for Section 3.5Exercise 3.5.1(a)We could try inference rules to deduce new dependencies until we are satisfied we have them all.A more systematic way is to consider the closures of all 15 nonempty sets of attributes.For the single attributes we have A+ = A, B+ = B, C+ = ACD, and D+ = AD. Thus, the only new dependency we get with a single attribute on the left is C->A.Now consider pairs of attributes:AB+ = ABCD, so we get new dependency AB->D. AC+ = ACD, and AC->D is nontrivial. AD+ = AD, so nothing new. BC+ = ABCD, so we get BC->A, and BC->D. BD+ = ABCD, giving usBD->A and BD->C. CD+ = ACD, giving CD->A.For the triples of attributes, ACD+ = ACD, but the closures of the other sets are each ABCD. Thus, we get new dependencies ABC->D, ABD->C, and BCD->A.Since ABCD+ = ABCD, we get no new dependencies.The collection of 11 new dependencies mentioned above is: C->A, AB->D, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.Exercise 3.5.1(b)From the analysis of closures above, we find that AB, BC, and BD are keys. All other sets either do not have ABCD as the closure or contain one of these three sets.Exercise 3.5.1(c)The superkeys are all those that contain one of those three keys. That is, a superkey that is not a key must contain B and more than one of A, C, and D. Thus, the (proper) superkeys are ABC, ABD, BCD, and ABCD.Exercise 3.5.3(a)We must compute the closure of A1A2...AnC. Since A1A2...An->B is a dependency, surely B is in this set, proving A1A2...AnC->B.Exercise 3.5.4(a)Consider the relationThis relation satisfies A->B but does not satisfy B->A.Exercise 3.5.8(a)If all sets of attributes are closed, then there cannot be any nontrivial functional dependenc ies. For suppose A1A2...An->B is a nontrivial dependency. Then A1A2...An+ contains B and thus A1A2...An is not closed.Exercise 3.5.10(a)We need to compute the closures of all subsets of {ABC}, although there is no need to think about the empty set or the set of all three attributes. Here are the calculations for the remaining six sets: A+ = AB+ = BC+ = ACEAB+ = ABCDEAC+ = ACEBC+ = ABCDEWe ignore D and E, so a basis for the resulting functional dependencies for ABC are: C->A and AB->C. Note that BC->A is true, but follows logically from C->A, and therefore may be omitted from our list.Solutions for Section 3.6Exercise 3.6.1(a)In the solution to Exercise 3.5.1 we found that there are 14 nontrivial dependencies, including the three given ones and 11 derived dependencies. These are: C->A, C->D, D->A, AB->D, AB-> C, AC->D, BC->A, BC->D, BD->A, BD->C, CD->A, ABC->D, ABD->C, and BCD->A.We also learned that the three keys were AB, BC, and BD. Thus, any dependency above that does not have one of these pairs on the left is a BCNF violation. These are: C->A, C->D, D->A, AC->D, and CD->A.One choice is to decompose using C->D. That gives us ABC and CD as decomposed relations. CD is surely in BCNF, since any two-attribute relation is. ABC is not in BCNF, since AB and BC are its only keys, but C->A is a dependency that holds in ABCD and therefore holds in ABC. We must further decompose ABC into AC and BC. Thus, the three relations of the decomposition are AC, BC, and CD.Since all attributes are in at least one key of ABCD, that relation is already in 3NF, and no decomposition is necessary.Exercise 3.6.1(b)(Revised 1/19/02) The only key is AB. Thus, B->C and B->D are both BCNF violations. The derived FD's BD->C and BC->D are also BCNF violations. However, any other nontrivial, derived FD will have A and B on the left, and therefore will contain a key.One possible BCNF decomposition is AB and BCD. It is obtained starting with any of the four violations mentioned above. AB is the only key for AB, and B is the only key for BCD.Since there is only one key for ABCD, the 3NF violations are the same, and so is the decomposition.Solutions for Section 3.7Exercise 3.7.1Since A->->B, and all the tuples have the same value for attribute A, we can pair the B-value from any tuple with the value of the remaining attribute C from any other tuple. Thus, we know that R must have at least the nine tuples of the form (a,b,c), where b is any of b1, b2, or b3, and c is any of c1, c2, or c3. That is, we can derive, using the definition of a multivalued dependency, that each of the tuples (a,b1,c2), (a,b1,c3), (a,b2,c1), (a,b2,c3), (a,b3,c1), and (a,b3,c2) are also in R.Exercise 3.7.2(a)First, people have unique Social Security numbers and unique birthdates. Thus, we expect the functional dependencies ssNo->name and ssNo->birthdate hold. The same applies to children, so we expect childSSNo->childname and childSSNo->childBirthdate. Finally, an automobile has a unique brand, so we expect autoSerialNo->autoMake.There are two multivalued dependencies that do not follow from these functional dependencies. First, the information about one child of a person is independent of other information about that person. That is, if a person with social security number s has a tuple with cn,cs,cb, then if there isany other tuple t for the same person, there will also be another tuple that agrees with t except that it has cn,cs,cb in its components for the child name, Social Security number, and birthdate. That is the multivalued dependencyssNo->->childSSNo childName childBirthdateSimilarly, an automobile serial number and make are independent of any of the other attributes, so we expect the multivalued dependencyssNo->->autoSerialNo autoMakeThe dependencies are summarized below:ssNo -> name birthdatechildSSNo -> childName childBirthdateautoSerialNo -> autoMakessNo ->-> childSSNo childName childBirthdatessNo ->-> autoSerialNo autoMakeExercise 3.7.2(b)We suggest the relation schemas{ssNo, name, birthdate}{ssNo, childSSNo}{childSSNo, childName childBirthdate}{ssNo, autoSerialNo}{autoSerialNo, autoMake}An initial decomposition based on the two multivalued dependencies would give us {ssNo, name, birthDate}{ssNo, childSSNo, childName, childBirthdate}{ssNo, autoSerialNo, autoMake}Functional dependencies force us to decompose the second and third of these.Exercise 3.7.3(a)Since there are no functional dependencies, the only key is all four attributes, ABCD. Thus, each of the nontrvial multivalued dependencies A->->B and A->->C violate 4NF. We must separate out the attributes of these dependencies, first decomposing into AB and ACD, and then decomposing the latter into AC and AD because A->->C is still a 4NF violation for ACD. The final set of relations are AB, AC, and AD.Exercise 3.7.7(a)Let W be the set of attributes not in X, Y, or Z. Consider two tuples xyzw and xy'z'w' in the relation R in question. Because X ->-> Y, we can swap the y's, so xy'zw and xyz'w' are in R. Because X ->-> Z, we can take the pair of tuples xyzw and xyz'w' and swap Z's to get xyz'w and xyzw'. Similarly, we can take the pair xy'z'w' and xy'zw and swap Z's to get xy'zw' and xy'z'w.In conclusion, we started with tuples xyzw and xy'z'w' and showed that xyzw' and xy'z'w must also be in the relation. That is exactly the statement of the MVD X ->-> Y-union-Z. Note that the above statements all make sense even if there are attributes in common among X, Y, and Z.Exercise 3.7.8(a)Consider a relation R with schema ABCD and the instance with four tuples abcd, abcd', ab'c'd, and ab'c'd'. This instance satisfies the MVD A->-> BC. However, it does not satisfy A->-> B. For example, if it did satisfy A->-> B, then because the instance contains the tuples abcd and ab'c'd, we would expect it to contain abc'd and ab'cd, neither of which is in the instance.Database Systems: The Complete BookSolutions for Chapter 4Solutions for Section 4.2Exercise 4.2.1class Customer {attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account {attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Exercise 4.2.4class Person {attribute string name;relationship Person motherOfinverse Person::childrenOfFemalerelationship Person fatherOfinverse Person::childrenOfMalerelationship Set<Person> childreninverse Person::parentsOfrelationship Set<Person> childrenOfFemaleinverse Person::motherOfrelationship Set<Person> childrenOfMaleinverse Person::fatherOfrelationship Set<Person> parentsOfinverse Person::children}Notice that there are six different relationships here. For example, the inverse of the relationship that connects a person to their (unique) mother is a relationship that connects a mother (i.e., a female person) to the set of her children. That relationship, which we call childrenOfFemale, is different from the children relationship, which connects anyone -- male or female -- to their children.Exercise 4.2.7A relationship R is its own inverse if and only if for every pair (a,b) in R, the pair (b,a) is also in R. In the terminology of set theory, the relation R is ``symmetric.''Solutions for Section 4.3Exercise 4.3.1We think that Social Security number should me the key for Customer, and account number should be the key for Account. Here is the ODL solution with key and extent declarations.class Customer(extent Customers key ssNo){attribute string name;attribute string addr;attribute string phone;attribute integer ssNo;relationship Set<Account> ownsAcctsinverse Account::ownedBy;}class Account(extent Accounts key number){attribute integer number;attribute string type;attribute real balance;relationship Set<Customer> ownedByinverse Customer::ownsAccts}Solutions for Section 4.4Exercise 4.4.1(a)Since the relationship between customers and accounts is many-many, we should create a separate relation from that relationship-pair.Customers(ssNo, name, address, phone)Accounts(number, type, balance)CustAcct(ssNo, number)Exercise 4.4.1(d)Ther is only one attribute, but three pairs of relationships from Person to itself. Since motherOf and fatherOf are many-one, we can store their inverses in the relation for Person. That is, for each person, childrenOfMale and childrenOfFemale will indicate that persons's father and mother. The children relationship is many-many, and requires its own relation. This relation actually turns out to be redundant, in the sense that its tuples can be deduced from the relationships stored with Person. The schema:Persons(name, childrenOfFemale, childrenOfMale)Parent-Child(parent, child)Exercise 4.4.4Y ou get a schema like:Studios(name, address, ownedMovie)Since name -> address is the only FD, the key is {name, ownedMovie}, and the FD has a left side that is not a superkey.Exercise 4.4.5(a,b,c)(a) Struct Card { string rank, string suit };(b) class Hand {attribute Set theHand;};For part (c) we have:Hands(handId, rank, suit)Notice that the class Hand has no key, so we need to create one: handID. Each hand has, in the relation Hands, one tuple for each card in the hand.Exercise 4.4.5(e)Struct PlayerHand { string Player, Hand theHand };class Deal {attribute Set theDeal;}Alternatively, PlayerHand can be defined directly within the declaration of attribute theDeal. Exercise 4.4.5(h)Since keys for Hand and Deal are lacking, a mechanical way to design the database schema is to have one relation connecting deals and player-hand pairs, and another to specify the contents of hands. That is:Deals(dealID, player, handID)Hands(handID, rank, suit)However, if we think about it, we can get rid of handID and connect the deal and the player directly to the player's cards, as:Deals(dealID, player, rank, suit)Exercise 4.4.5(i)First, card is really a pair consisting of a suit and a rank, so we need two attributes in a relation schema to represent cards. However, much more important is the fact that the proposed schema does not distinguish which card is in which hand. Thus, we need another attribute that indicates which hand within the deal a card belongs to, something like:Deals(dealID, handID, rank, suit)Exercise 4.4.6(c)Attribute b is really a bag of (f,g) pairs. Thus, associated with each a-value will be zero or more (f,g) pairs, each of which can occur several times. We shall use an attribute count to indicate the number of occurrences, although if relations allow duplicate tuples we could simply allow duplicate (a,f,g) triples in the relation. The proposed schema is:C(a, f, g, count)Solutions for Section 4.5Exercise 4.5.1(b)Studios(name, address, movies{(title, year, inColor, length,stars{(name, address, birthdate)})})Since the information about a star is repeated once for each of their movies, there is redundancy. To eliminate it, we have to use a separate relation for stars and use pointers from studios. That is: Stars(name, address, birthdate)Studios(name, address, movies{(title, year, inColor, length,stars{*Stars})})Since each movie is owned by one studio, the information about a movie appears in only one tuple of Studios, and there is no redundancy.Exercise 4.5.2Customers(name, address, phone, ssNo, accts{*Accounts})Accounts(number, type, balance, owners{*Customers})Solutions for Section 4.6Exercise 4.6.1(a)We need to add new nodes labeled George Lucas and Gary Kurtz. Then, from the node sw (which represents the movie Star Wars), we add arcs to these two new nodes, labeled direc tedBy and producedBy, respectively.Exercise 4.6.2Create nodes for each account and each customer. From each customer node is an arc to a node representing the attributes of the customer, e.g., an arc labeled name to the customer's name. Likewise, there is an arc from each account node to each attribute of that account, e.g., an arc labeled balance to the value of the balance.To represent ownership of accounts by customers, we place an arc labeled owns from each customer node to the node of each account that customer holds (possibly jointly). Also, we placean arc labeled ownedBy from each account node to the customer node for each owner of that account.Exercise 4.6.5In the semistructured model, nodes represent data elements, i.e., entities rather than entity sets. In the E/R model, nodes of all types represent schema elements, and the data is not represented at all. Solutions for Section 4.7Exercise 4.7.1(a)<STARS-MOVIES><STAR starId = "cf" starredIn = "sw, esb, rj"><NAME>Carrie Fisher</NAME><ADDRESS><STREET>123 Maple St.</STREET><CITY>Hollywood</CITY></ADDRESS><ADDRESS><STREET>5 Locust Ln.</STREET><CITY>Malibu</CITY></ADDRESS></STAR><STAR starId = "mh" starredIn = "sw, esb, rj"><NAME>Mark Hamill</NAME><ADDRESS><STREET>456 Oak Rd.<STREET><CITY>Brentwood</CITY></ADDRESS></STAR><STAR starId = "hf" starredIn = "sw, esb, rj, wit"><NAME>Harrison Ford</NAME><ADDRESS><STREET>whatever</STREET><CITY>whatever</CITY></ADDRESS></STAR><MOVIE movieId = "sw" starsOf = "cf, mh"><TITLE>Star Wars</TITLE><YEAR>1977</YEAR></MOVIE><MOVIE movieId = "esb" starsOf = "cf, mh"><TITLE>Empire Strikes Back</TITLE><YEAR>1980</YEAR></MOVIE><MOVIE movieId = "rj" starsOf = "cf, mh"><TITLE>Return of the Jedi</TITLE><YEAR>1983</YEAR></MOVIE><MOVIE movieID = "wit" starsOf = "hf"><TITLE>Witness</TITLE><YEAR>1985</YEAR></MOVIE></STARS-MOVIES>Exercise 4.7.2<!DOCTYPE Bank [<!ELEMENT BANK (CUSTOMER* ACCOUNT*)><!ELEMENT CUSTOMER (NAME, ADDRESS, PHONE, SSNO)> <!A TTLIST CUSTOMERcustId IDowns IDREFS><!ELEMENT NAME (#PCDA TA)><!ELEMENT ADDRESS (#PCDA TA)><!ELEMENT PHONE (#PCDA TA)><!ELEMENT SSNO (#PCDA TA)><!ELEMENT ACCOUNT (NUMBER, TYPE, BALANCE)><!A TTLIST ACCOUNTacctId IDownedBy IDREFS><!ELEMENT NUMBER (#PCDA TA)><!ELEMENT TYPE (#PCDA TA)><!ELEMENT BALANCE (#PCDA TA)>]>Database Systems: The CompleteBookSolutions for Chapter 5Solutions for Section 5.2Exercise 5.2.1(a)PI_model( SIGMA_{speed >= 1000} ) (PC)Exercise 5.2.1(f)The trick is to theta-join PC with itself on the condition that the hard disk sizes are equal. That gives us tuples that have two PC model numbers with the same value of hd. However, these two PC's could in fact be the same, so we must also require in the theta-join that the model numbers be unequal. Finally, we want the hard disk sizes, so we project onto hd.The expression is easiest to see if we write it using some temporary values. We start by renaming PC twice so we can talk about two occurrences of the same attributes.R1 = RHO_{PC1} (PC)R2 = RHO_{PC2} (PC)R3 = R1 JOIN_{PC1.hd = PC2.hd AND PC1.model <> PC2.model} R2R4 = PI_{PC1.hd} (R3)Exercise 5.2.1(h)First, we find R1, the model-speed pairs from both PC and Laptop. Then, we find from R1 those computers that are ``fast,'' at least 133Mh. At the same time, we join R1 with Product to connect model numbers to their manufacturers and we project out the speed to get R2. Then we join R2 with itself (after renaming) to find pairs of different models by the same maker. Finally, we get our answer, R5, by projecting onto one of the maker attributes. A sequence of steps giving the desired expression is: R1 = PI_{model,speed} (PC) UNION PI_{model,speed} (Laptop)R2 = PI_{maker,model} (SIGMA_{speed>=700} (R1) JOIN Product)R3 = RHO_{T(maker2, model2)} (R2)R4 = R2 JOIN_{maker = maker2 AND model <> model2} (R3)R5 = PI_{maker} (R4)Exercise 5.2.2Here are figures for the expression trees of Exercise 5.2.1 Part (a)Part (f)Part (h). Note that the third figure is not really a tree, since it uses a common subexpression. We could duplicate the nodes to make it a tree, but using common subexpressions is a valuable form of query optimization. One of the benefits one gets from constructing ``trees'' for queries is the ability to combine nodes that represent common subexpressions.Exercise 5.2.7The relation that results from the natural join has only one attribute from each pair of equated attributes. The theta-join has attributes for both, and their columns are identical.Exercise 5.2.9(a)If all the tuples of R and S are different, then the union has n+m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Surely the union has at least as many tuples as the larger of R and that is, max(n,m) tuples. However, it is possible for every tuple of the smaller to appear in the other, so it is possible that there are as few as max(n,m) tuples in the union.Exercise 5.2.10In the following we use the name of a relation both as its instance (set of tuples) and as its schema (set of attributes). The context determines uniquely which is meant.PI_R(R JOIN S) Note, however, that this expression works only for sets; it does not preserve the multipicity of tuples in R. The next two expressions work for bags.R JOIN DELTA(PI_{R INTERSECT S}(S)) In this expression, each projection of a tuple from S onto the attributes that are also in R appears exactly once in the second argument of the join, so it preserves multiplicity of tuples in R, except for those thatdo not join with S, which disappear. The DELTA operator removes duplicates, as described in Section 5.4.R - [R - PI_R(R JOIN S)] Here, the strategy is to find the dangling tuples of R and remove them.Solutions for Section 5.3Exercise 5.3.1As a bag, the value is {700, 1500, 866, 866, 1000, 1300, 1400, 700, 1200, 750, 1100, 350, 733}. The order is unimportant, of course. The average is 959.As a set, the value is {700, 1500, 866, 1000, 1300, 1400, 1200, 750, 1100, 350, 733}, and the average is 967. H3>Exercise 5.3.4(a)As sets, an element x is in the left-side expression(R UNION S) UNION Tif and only if it is in at least one of R, S, and T. Likewise, it is in the right-side expressionR UNION (S UNION T)under exactly the same conditions. Thus, the two expressions have exactly the same members, and the sets are equal.As bags, an element x is in the left-side expression as many times as the sum of the number of times it is in R, S, and T. The same holds for the right side. Thus, as bags the expressions also have the same value.Exercise 5.3.4(h)As sets, element x is in the left sideR UNION (S INTERSECT T)if and only if x is either in R or in both S and T. Element x is in the right side(R UNION S) INTERSECT (R UNION T)if and only if it is in both R UNION S and R UNION T. If x is in R, then it is in both unions. If x is in both S and T, then it is in both union. However, if x is neither in R nor in both of S and T, then it cannot be in both unions. For example, suppose x is not in R and not in S. Then x is not in R UNION S. Thus, the statement of when x is in the right side is exactly the same as when it is in the left side: x is either in R or in both of S and T.Now, consider the expression for bags. Element x is in the left side the sum of the number of times it is in R plus the smaller of the number of times x is in S and the number of times x is in T. Likewise, the number of times x is in the right side is the smaller ofThe sum of the number of times x is in R and in S.The sum of the number of times x is in R and in T.A moment's reflection tells us that this minimum is the sum of the number of times x is in R plus the smaller of the number of times x is in S and in T, exactly as for the left side.Exercise 5.3.5(a)For sets, we observe that element x is in the left side(R INTERSECT S) - T。

数据库系统基础教程课后答案第五章

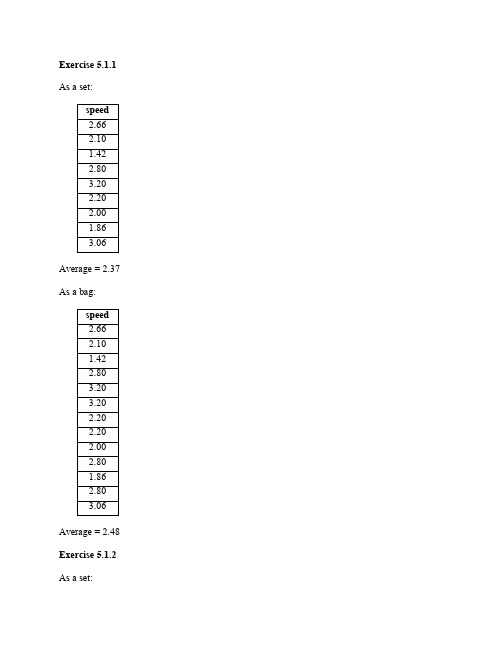
Exercise 5.1.1 As a set:Average = 2.37 As a bag:Average = 2.48 Exercise 5.1.2 As a set:Average = 218 As a bag:Average = 215 Exercise 5.1.3a As a set:As a bag:Exercise 5.1.3bπbore(Ships Classes)Exercise 5.1.4aFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the union of bags R and S will have tuple t appear n + m times. The further union of bag T with the tuple t appearing o times will have tuple t appear n + m + o times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively, the union of bags R and S will have tuple t appear m + o times. The further union of bag R with the tuple t appearing n times will have tuple t appear m + o + n times in the final result.For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result. Since we cannot have duplicates, the result only has at most one copy of the tuple t.Exercise 5.1.4bFor bags:On the left-hand side:Given bags R and S where a tuple t appears n and m times respectively, the intersectionof bags R and S will have tuple t appear min( n, m ) times. The further intersection of bag T with the tuple t appearing o times will produce tuple t min( o, min( n, m ) ) times in the final result.On the right-hand side:Given bags S and T where a tuple t appears m and o times respectively, the intersection of bags R and S will have tuple t appear min( m, o ) times. The further intersection of bag R with the tuple t appearing n times will produce tuple t min( n, min( m, o ) ) times in thefinal result.The intersection of bags R,S and T will yield a result where tuple t appears min( n,m,o ) times. For sets:This is a similar case when dealing with bags except the tuple t can only appear at most once in each set. The tuple t only appears in the result if all the sets have the tuple t. Otherwise, the tuple t will not appear in the result.Exercise 5.1.4cFor bags:On the left-hand side:Given that tuple r in R, which appears m times, can successfully join with tuple s in S,which appears n times, we expect the result to contain mn copies. Also given that tuple tin T, which appears o times, can successfully join with the joined tuples of r and s, weexpect the final result to have mno copies.On the right-hand side:Given that tuple s in S, which appears n times, can successfully join with tuple t in T,which appears o times, we expect the result to contain no copies. Also given that tuple rin R, which appears m times, can successfully join with the joined tuples of s and t, weexpect the final result to have nom copies.The order in which we perform the natural join does not matter for bags.For sets:This is a similar case when dealing with bags except the joined tuples can only appear at most once in each result. If there are tuples r,s,t in relations R,S,T that can successfully join, then the result will contain a tuple with the schema of their joined attributes.Exercise 5.1.4dFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the union of these two bags R ⋃ S, tuple t would appear n + m times. Likewise, in the union of these two bags S ⋃ R, tuple t would appear m + n times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in both sets R and S will the union R ⋃ S have the tuple t. The same reasoning holds when we take the union S ⋃ R.Therefore the commutative law for union holds.Exercise 5.1.4eFor bags:Suppose a tuple t occurs n and m times in bags R and S respectively. In the intersection of these two bags R ∩ S, tuple t would appear min( n,m ) times. Likewise in the intersection of these two bags S ∩ R, tuple t would appear min( m,n ) times. Both sides of the relation yield the same result.For sets:A tuple t can only appear at most one time. Tuple t might appear each in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t appears in at least one of the sets R and S will the intersection R ∩ S have the tuple t. The same reasoning holds when we take the intersection S ∩ R.Therefore the commutative law for intersection holds.Exercise 5.1.4fFor bags:Suppose a tuple t occurs n times in bag R and tuple u occurs m times in bag S. Suppose also that the two tuples t,u can successfully join. Then in the natural join of these two bags R S, the joined tuple would appear nm times. Likewise in the natural join of these two bags S R, the joined tuple would appear mn times. Both sides of the relation yield the same result.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuples u,v might appear respectively in sets R and S one or zero times. The combinations of number of occurrences for tuples u,v in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple u exists in Rand tuple v exists in S will the natural join R S have the joined tuple. The same reasoning holds when we take the natural join S R.Therefore the commutative law for natural join holds.Exercise 5.1.4gFor bags:Suppose tuple t appears m times in R and n times in S. If we take the union of R and S first, we will get a relation where tuple t appears m + n times. Taking the projection of a list of attributes L will yield a resulting relation where the projected attributes from tuple t appear m + n times. If we take the projection of the attributes in list L first, then the projected attributes from tuple t would appear m times from R and n times from S. The union of these resulting relations would have the projected attributes of tuple t appear m + n times.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple t might appear in sets R and S one or zero times. The combinations of number of occurrences for tuple t in R and S respectively are (0,0), (0,1), (1,0), and (1,1). Only when tuple t exists in R or S (or both R and S) will the projected attributes of tuple t appear in the result.Therefore the law holds.Exercise 5.1.4hFor bags:Suppose tuple t appears u times in R, v times in S and w times in T. On the left hand side, the intersection of S and T would produce a result where tuple t would appear min(v , w) times. With the addition of the union of R, the overall result would have u + min(v , w) copies of tuple t. On the right hand side, we would get a result of min(u + v, u + w) copies of tuple t. The expressions on both the left and right sides are equivalent.For sets:An arbitrary tuple t can only appear at most one time in any set. Tuple t might appear in sets R,S and T one or zero times. The combinations of number of occurrences for tuple t in R, S and T respectively are (0,0,0), (0,0,1), (0,1,0), (0,1,1), (1,0,0), (1,0,1), (1,1,0) and (1,1,1). Only when tuple t appears in R or in both S and T will the result have tuple t.Therefore the distributive law of union over intersection holds.Exercise 5.1.4iSuppose that in relation R, u tuples satisfy condition C and v tuples satisfy condition D. Suppose also that w tuples satisfy both conditions C and D where w≤ min(v , w). Then the left hand side will return those w tuples. On the right hand side, σC(R) produces u tuples and σD(R) produces v tuples. However, we know the intersection will produce the same w tuples in the result.When considering bags and sets, the only difference is bags allow duplicate tuples while sets only allow one copy of the tuple. The example above applies to both cases.Therefore the law holds.Exercise 5.1.5aFor sets, an arbitrary tuple t appears on the left hand side if it appears in both R,S and not in T. The same is true for the right hand side.As an example for bags, suppose that tuple t appears one time each in both R,T and two times in S. The result of the left hand side would have zero copies of tuple t while the right hand side would have one copy of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5bFor sets, an arbitrary tuple t appears on the left hand side if it appears in R and either S or T. This is equivalent to saying tuple t only appears when it is in at least R and S or in R and T. The equivalence is exactly the right side’s expression.As an example for bags, suppose that tuple t appears one time in R and two times each in S and T. Then the left hand side would have one copy of tuple t in the result while the right hand side would have two copies of tuple t.Therefore the law holds for sets but not for bags.Exercise 5.1.5cFor sets, an arbitrary tuple t appears on the left hand side if it satisfies condition C, condition Dor both condition C and D. On the right hand side, σC(R) selects those tuples that satisfy condition C while σD(R) selects those tuples that satisfy condition D. However, the union operator will eliminate duplicate tuples, namely those tuples that satisfy both condition C and D. Thus we are ensured that both sides are equivalent.As an example for bags, we only need to look at the union operator. If there are indeed tuples that satisfy both conditions C and D, then the right hand side will contain duplicate copies of those tuples. The left hand side, however, will only have one copy for each tuple of the original set of tuples.Exercise 5.2.1bExercise 5.2.1cExercise 5.2.1dExercise 5.2.1fExercise 5.2.1gExercise 5.2.1hExercise 5.2.1iExercise 5.2.1jExercise 5.2.1kExercise 5.2.1lExercise 5.2.1mExercise 5.2.1nExercise 5.2.2aApplying the δ operator on a relation with no duplicates will yield the same relation. Thus δ is idempotent.Exercise 5.2.2bThe result of πL is a relation over the list of attributes L. Performing the projection again will return the same relation because the relation only contains the list of attributes L. Thus πL is idempotent.Exercise 5.2.2cThe result of σC is a relation where condition C is satisfied by every tuple. Performing the selection again will return the same relation because the relation only contains tuples that satisfy the condition C. Thus σC is idempotent.Exercise 5.2.2dThe result of γL is a relation whose schema consists of the grouping attributes and the aggregated attributes. If we perform the same grouping operation, there is no guarantee that the expression would make sense. The grouping attributes will still appear in the new result. However, the aggregated attributes may or may not appear correctly. If the aggregated attribute is given a different name than the original attribute, then performing γL would not make sense because it contains an aggregation for an attribute name that does not exist. In this case, the resultingrelation would, according to the definition, only contain the grouping attributes. Thus, γL is not idempotent.Exercise 5.2.2eThe result of τ is a sorted list of tuples based on some attributes L. If L is not the entire schema of relation R, then there are attributes that are not sorted on. If in relation R there are two tuples that agree in all attributes L and disagree in some of the remaining attributes not in L, then it is arbitrary as to which order these two tuples appear in the result. Thus, performing the operation τ multiple times can yield a different relation where these two tuples are swapped. Thus, τ is not idempotent.Exercise 5.2.3If we only consider sets, then it is possible. We can take πA(R) and do a product with itself. From this product, we take the tuples where the two columns are equal to each other.If we consider bags as well, then it is not possible. Take the case where we have the two tuples (1,0) and (1,0). We wish to produce a relation that contains tuples (1,1) and (1,1). If we use the classical operations of relational algebra, we can either get a result where there are no tuples or four copies of the tuple (1,1). It is not possible to get the desired relation because no operation can distinguish between the original tuples and the duplicated tuples. Thus it is not possible to get the relation with the two tuples (1,1) and (1,1).Exercise 5.3.1a)Answer(model) ← PC(model,speed,_,_,_) AND speed ≥ 3.00b)Answer(maker) ← Laptop(model,_,_,hd,_,_) AND Product(maker,model,_) AND hd ≥100c)Answer(model,price) ← PC(model,_,_,_,price) AND Product(maker,model,_) ANDmaker=’B’Answer(model,price) ← Laptop(mode l,_,_,_,_,price) AND Product(maker,model,_)AND maker=’B’Answer(model,price) ← Printer(model,_,_,price) AND Product(maker,model,_) ANDmaker=’B’d)Answer(model) ← Printer(model,color,type,_) AND color=’true’ AND type=’laser’e)PCMaker(maker) ← Product(maker,_,type) AND type=’pc’LaptopMaker(maker) ← Product(maker,_,type) AND type=’laptop’Answer(maker) ← LaptopMaker(maker) AND NOT PCMaker(maker)f)Answer(hd) ← PC(model1,_,_,hd,_) AND PC(model2,_,_,hd,_) AND model1 <>model2g)Answer(model1,model2) ← PC(model1,speed, ram,_,_) ANDPC(model2,_speed,ram,_,_) AND model1 < model2h)FastComputer(model) ← PC(model,speed,_,_,_) AND speed ≥ 2.80FastComputer(model) ← Laptop(model,speed,_,_,_,_) AND speed ≥ 2.80Answer(maker) ← Product(maker,model1,_) AND Product(maker,mod el2,_) ANDFastComputer(model1) AND FastComputer(model2) AND model1 <> model2i)Computers(model,speed) ← PC(model,speed,_,_,_)Computers(model,speed) ← Laptop(model,speed,_,_,_,_)SlowComputers(model) ← Computers(model,speed) AND Computers(model1,speed1)AND speed < speed1FastestComputers(model) ← Computers(model,_) AND NOT SlowComputers(model)Answer(maker) ← Fast estComputers(model) AND Product(maker,model,_)j)PCs(maker,speed) ← PC(model,speed,_,_,_) AND Product(maker,model,_) Answer(maker) ← PCs(maker,spe ed) AND PCs(maker,speed1) AND PCs(maker,speed2) AND speed <> speed1 AND speed <> speed2 AND speed1 <> speed2k)PCs(maker,model) ← Product(maker,model,type) AND type=’pc’Answer(maker) ← PCs(maker,model) AND PCs(maker,model1) ANDPCs(maker,model2) AND PCs(maker,model3) AND model <> model1 AND model <>model2 AND model1 <> model2 AND (model3 = model OR model3 = model1 ORmodel3 = model2)Exercise 5.3.2a)Answer(class,country) ← Classes(class,_,country,_,bore,_) AND bore ≥ 16b)Answer(name) ← Ships(name,_,launch ed) AND launched < 1921c)Answer(ship) ← Outcomes(ship,battle,result) AND battle=’Denmark Strait’ AND result= ‘sunk’d)Answer(name) ← Classes(class,_,_,_,_,displacement) AND Ships(name,class,launched)AND displacement > 35000 AND launched > 1921e)Answer(nam e,displacement,numGuns) ← Classes(class,_,_,numGuns,_,displacement)AND Ships(name,class,_) AND Outcomes (ship,battle,_) AND battle=’Guadalcanal’AND ship=namef)Answer(name) ← Ships(name,_,_)Answer(name) ← Outcomes(name,_,_) AND NOT Answer(name)g)MoreThan One(class) ← Ships(name,class,_) AND Ships(name1,class,_) AND name <>name1Answer(class) ← Classes(class,_,_,_,_,_) AND NOT MoreThanOne(class)h)Battleship(country) ← Classes(_,type,country,_,_,_) AND type=’bb’Battlecruiser(country) ← Classes(_,type,country,_,_,_) AND type=’bc’Answer(country) ← Battleship(country) AND Battlecruiser(country)i)Results(ship,result,date) ← Battles(name,date) AND Outcomes(ship,battle,result) ANDbattle=nameAnswer(ship) ← Results(ship,result,date) AND Results(ship,_,date1) ANDresult=’damaged’ AND date < date1Exercise 5.3.3A nswer(x,y) ← R(x,y) AND z = zExercise 5.4.1aAnswer(a,b,c) ← R(a,b,c)Answer(a,b,c) ← S(a,b,c)Exercise 5.4.1bAnswer(a,b,c) ← R(a,b,c) AND S(a,b,c)Exercise 5.4.1cAnswer(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)Exercise 5.4.1dUnion(a,b,c) ← R(a,b,c)Union(a,b,c) ← S(a,b,c)Answer(a,b,c) ← Union(a,b,c) AND NOT T(a,b,c)Exercise 5.4.1eJ(a,b,c) ← R(a,b,c) AND NOT S(a,b,c)K(a,b,c) ← R(,a,b,c) AND NOT T(a,b,c)Answer(a,b,c) ← J(a,b,c) AND K(a,b,c)Exercise 5.4.1fAnswer(a,b) ← R(a,b,_)Exercise 5.4.1gJ(a,b) ← R(a,b,_)K(a,b) ← S(_,a,b)Answer(a,b) ← J(a,b) AND K(a,b)Exercise 5.4.2aAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2bAnswer(x,y,z) ← R(x,y,z) AND x < y AND y < z Exercise 5.4.2cAnswer(x,y,z) ← R(x,y,z) AND x < yAnswer(x,y,z) ← R(x,y,z) AND y < zExercise 5.4.2dChange: NOT(x < y OR x > y)To: x ≥ y AND x ≤ yThe above simplifies to x = yAnswer(x,y,z) ← R(x,y,z) AND x = yExercise 5.4.2eChange: NOT((x < y OR x > y) AND y < z)NOT(x < y OR x > y) OR y ≥ z(x ≥ y AND x ≤ y) OR y ≥ zTo: x = y OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x = yAnswer(x,y,z) ← R(x,y,z) AND y ≥ zExercise 5.4.2fChange: NOT((x < y OR x < z) AND y < z)NOT(x < y OR x < z) OR y ≥ z To: (x ≥ y AND x ≥ z) OR y ≥ zAnswer(x,y,z) ← R(x,y,z) AND x ≥ y AND x ≥ zAnswer(x,y,z) ← R(x,y,z) AND y ≥zExercise 5.4.3aAnswer(a,b,c,d) ← R(a,b,c) AND S(b,c,d)Exercise 5.4.3bAnswer(b,c,d,e) ← S(b,c,d) AND T(d,e)Exercise 5.4.3cAnswer(a,b,c,d,e) ← R(a,b,c) AND S(b,c,d) AND T(d,e)Exercise 5.4.4a)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syb)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < sy AND ry < szc)Answer(rx,ry,rz,sx,sy,s z) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx < syAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry < szd)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = sye)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx = syAnswe r(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szf)Answer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND rx ≥ sy AND rx ≥ szAnswer(rx,ry,rz,sx,sy,sz) ← R(rx,ry,rz) AND S(sx,sy,sz) AND ry ≥ szExercise 5.4.5aR1 := πx,y(Q R)Exercise 5.4.5bR1 := ρR1(x,z)(Q)R2 := ρR2(z,y)(Q)R3 := πx,y(R1 (R1.z = R2.z) R2)Exercise 5.4.5cR1 := πx,y(Q R)R2 := σx < y(R1)。

(完整版)数据库系统基础教程第二章答案解析

For relation Accounts, the attributes are:acctNo, type, balanceFor relation Customers, the attributes are:firstName, lastName, idNo, accountExercise 2.2.1bFor relation Accounts, the tuples are:(12345, savings, 12000),(23456, checking, 1000),(34567, savings, 25)For relation Customers, the tuples are:(Robbie, Banks, 901-222, 12345),(Lena, Hand, 805-333, 12345),(Lena, Hand, 805-333, 23456)Exercise 2.2.1cFor relation Accounts and the first tuple, the components are:123456 → acctNosavings → type12000 → balanceFor relation Customers and the first tuple, the components are:Robbie → firstNameBanks → lastName901-222 → idNo12345 → accountExercise 2.2.1dFor relation Accounts, a relation schema is:Accounts(acctNo, type, balance)For relation Customers, a relation schema is:Customers(firstName, lastName, idNo, account) Exercise 2.2.1eAn example database schema is:Accounts (acctNo,type,balance)Customers (firstName,lastName,idNo,account)A suitable domain for each attribute:acctNo → Integertype → Stringbalance → IntegerfirstName → StringlastName → StringidNo → String (because there is a hyphen we cannot use Integer)account → IntegerExercise 2.2.1gAnother equivalent way to present the Account relation:Another equivalent way to present the Customers relation:Exercise 2.2.2Examples of attributes that are created for primarily serving as keys in a relation:Universal Product Code (UPC) used widely in United States and Canada to track products in stores.Serial Numbers on a wide variety of products to allow the manufacturer to individually track each product.Vehicle Identification Numbers (VIN), a unique serial number used by the automotive industry to identify vehicles.Exercise 2.2.3aWe can order the three tuples in any of 3! = 6 ways. Also, the columns can be ordered in any of 3! = 6 ways. Thus, the number of presentations is 6*6 = 36.Exercise 2.2.3bWe can order the three tuples in any of 5! = 120 ways. Also, the columns can be ordered in any of 4! = 24 ways. Thus, the number of presentations is 120*24 = 2880Exercise 2.2.3cWe can order the three tuples in any of m! ways. Also, the columns can be ordered in any of n! ways. Thus, the number of presentations is n!m!Exercise 2.3.1aCREATE TABLE Product (maker CHAR(30),model CHAR(10) PRIMARY KEY,type CHAR(15));CREATE TABLE PC (model CHAR(30),speed DECIMAL(4,2),ram INTEGER,hd INTEGER,price DECIMAL(7,2));Exercise 2.3.1cCREATE TABLE Laptop (model CHAR(30),speed DECIMAL(4,2),ram INTEGER,hd INTEGER,screen DECIMAL(3,1),price DECIMAL(7,2));Exercise 2.3.1dCREATE TABLE Printer (model CHAR(30),color BOOLEAN,type CHAR (10),price DECIMAL(7,2));Exercise 2.3.1eALTER TABLE Printer DROP color;Exercise 2.3.1fALTER TABLE Laptop ADD od CHAR (10) DEFAULT ‘none’; Exercise 2.3.2aCREATE TABLE Classes (class CHAR(20),type CHAR(5),country CHAR(20),numGuns INTEGER,bore DECIMAL(3,1),displacement INTEGER);Exercise 2.3.2bCREATE TABLE Ships (name CHAR(30),class CHAR(20),launched INTEGER);Exercise 2.3.2cCREATE TABLE Battles (name CHAR(30),date DATE);Exercise 2.3.2dCREATE TABLE Outcomes (ship CHAR(30),battle CHAR(30),result CHAR(10));Exercise 2.3.2eALTER TABLE Classes DROP bore;Exercise 2.3.2fALTER TABLE Ships ADD yard CHAR(30); Exercise 2.4.1aR1 := σspeed ≥ 3.00 (PC)R2 := πmodel(R1)model100510061013Exercise 2.4.1bR1 := σhd ≥ 100 (Laptop)R2 := Product (R1)R3 := πmaker (R2)makerEABFGExercise 2.4.1cR1 := σmaker=B (Product PC)R2 := σmaker=B (Product Laptop)R3 := σmaker=B (Product Printer)R4 := πmodel,price (R1)R5 := πmodel,price (R2)R6: = πmodel,price (R3)R7 := R4 R5 R6model price1004 6491005 6301006 10492007 1429Exercise 2.4.1dR1 := σcolor = true AND type = laser (Printer)R2 := πmodel (R1)model30033007Exercise 2.4.1eR1 := σtype=laptop (Product)R2 := σtype=PC(Product)R3 := πmaker(R1)R4 := πmaker(R2)R5 := R3 – R4Exercise 2.4.1fR1 := ρPC1(PC)R2 := ρPC2(PC)R3 := R1 (PC1.hd = PC2.hd AND PC1.model <> PC2.model) R2R4 := πhd(R3)Exercise 2.4.1gR1 := ρPC1(PC)R2 := ρPC2(PC)R3 := R1 (PC1.speed = PC2.speed AND PC1.ram = PC2.ram AND PC1.model < PC2.model) R2R4 := πPC1.model,PC2.model(R3)Exercise 2.4.1hR1 := πmodel(σspeed ≥ 2.80(PC)) πmodel(σspeed ≥ 2.80(Laptop))R2 := πmaker,model(R1 Product)R3 := ρR3(maker2,model2)(R2)R4 := R2 (maker = maker2 AND model <> model2) R3R5 := πmaker(R4)Exercise 2.4.1iR1 := πmodel,speed(PC)R2 := πmodel,speed(Laptop)R3 := R1 R2R4 := ρR4(model2,speed2)(R3)R5 := πmodel,speed (R3 (speed < speed2 ) R4)R6 := R3 – R5makerBExercise 2.4.1jR1 := πmaker,speed(Product PC)R2 := ρR2(maker2,speed2)(R1)R3 := ρR3(maker3,speed3)(R1)R4 := R1 (maker = maker2 AND speed <> speed2) R2R5 := R4 (maker3 = maker AND speed3 <> speed2 AND speed3 <> speed) R3R6 := πmaker(R5)makerFGhd25080160PC1.model PC2.model1004 1012makerBEmakerADEExercise 2.4.1kR1 := πmaker,model(Product PC)R2 := ρR2(maker2,model2)(R1)R3 := ρR3(maker3,model3)(R1)R4 := ρR4(maker4,model4)(R1)R5 := R1 (maker = maker2 AND model <> model2) R2R6 := R3 (maker3 = maker AND model3 <> model2 AND model3 <> model) R5R7 := R4 (maker4 = maker AND (model4=model OR model4=model2 OR model4=model3)) R6R8 := πmaker(R7)makerABDEExercise 2.4.2aπmodelσspeed≥3.00PCExercise 2.4.2bπmakerσhd ≥ 100 ProductLaptopExercise 2.4.2cσmaker=B πmodel,priceσmaker=B πmodel,price σmaker=Bπmodel,priceProduct PC Laptop Printer ProductProductExercise 2.4.2dPrinter σcolor = true AND type = laserπmodelExercise 2.4.2e σtype=laptop σtype=PC πmakerπmaker –Product ProductExercise 2.4.2fρPC1ρPC2 (PC1.hd = PC2.hd AND PC1.model <> PC2.model)πhdPC PCExercise 2.4.2gρPC1ρPC2PC PC(PC1.speed = PC2.speed AND PC1.ram = PC2.ram AND PC1.model < PC2.model)πPC1.model,PC2.modelExercise 2.4.2hPC Laptop σspeed ≥ 2.80σspeed ≥ 2.80πmodelπmodel πmaker,modelρR3(maker2,model2)(maker = maker2 AND model <> model2)makerExercise 2.4.2iPCLaptopProductπmodel,speed πmodel,speed ρR4(model2,speed2)πmodel,speed(speed < speed2 )–makerExercise 2.4.2jProduct PC πmaker,speed ρR3(maker3,speed3)ρR2(maker2,speed2)(maker = maker2 AND speed <> speed2)(maker3 = maker AND speed3 <> speed2 AND speed3 <> speed)πmakerExercise 2.4.2kπmaker(maker4 = maker AND (model4=model OR model4=model2 OR model4=model3)) (maker3 = maker AND model3 <> model2 AND model3 <> model)(maker = maker2 AND model <> model2)ρR2(maker2,model2)ρR3(maker3,model3)ρR4(maker4,model4)πmaker,modelProduct PCExercise 2.4.3aR1 := σbore ≥ 16 (Classes)R2 := πclass,country (R1)Exercise 2.4.3bR1 := σlaunched < 1921 (Ships)R2 := πname (R1)KirishimaKongoRamilliesRenownRepulseResolutionRevengeRoyal OakRoyal SovereignTennesseeExercise 2.4.3cR1 := σbattle=Denmark Strait AND result=sunk(Outcomes)R2 := πship (R1)shipBismarckHoodExercise 2.4.3dR1 := Classes ShipsR2 := σlaunched > 1921 AND displacement > 35000 (R1)R3 := πname (R2)nameIowaMissouriMusashiNew JerseyNorth CarolinaWashingtonWisconsinYamatoExercise 2.4.3eR1 := σbattle=Guadalcanal(Outcomes)R2 := Ships (ship=name) R1R3 := Classes R2R4 := πname,displacement,numGuns(R3)name displacement numGuns Kirishima 32000 8Washington 37000 9Exercise 2.4.3fR1 := πname(Ships)R2 := πship(Outcomes)R3 := ρR3(name)(R2)R4 := R1 R3nameCaliforniaHarunaHieiIowaKirishimaKongoMissouriMusashiNew JerseyExercise 2.4.3gFrom 2.3.2, assuming that every class has one ship named after the class.R1 := πclass (Classes) R2 := πclass (σname <> class (Ships)) R3 := R1 – R2Exercise 2.4.3hR1 := πcountry (σtype=bb (Classes)) R2 := πcountry (σtype=bc (Classes)) R3 := R1 ∩ R2Exercise 2.4.3iR1 := πship,result,date (Battles (battle=name) Outcomes)R2 := ρR2(ship2,result2,date2)(R1)R3 := R1 (ship=ship2 AND result=damaged AND date < date2) R2R4 := πship (R3)No results from sample data.Exercise 2.4.4aσbore ≥ 16πclass,countryClassesExercise 2.4.4bNorth Carolina Ramillies Renown Repulse Resolution Revenge Royal Oak Royal Sovereign Tennessee Washington Wisconsin Yamato Arizona Bismarck Duke of York Fuso Hood King George V Prince of Wales Rodney Scharnhorst South Dakota West Virginia Yamashiro class Bismarck country Japan Gt. Britainπnameσlaunched < 1921ShipsExercise 2.4.4cπshipσbattle=Denmark Strait AND result=sunkOutcomesExercise 2.4.4dπnameσlaunched > 1921 AND displacement > 35000Classes Ships Exercise 2.4.4eσbattle=Guadalcanal Outcomes Ships(ship=name)πname,displacement,numGunsExercise 2.4.4f Ships Outcomesπnameπship ρR3(name)Exercise 2.4.4g Classes Shipsπclass σname <> class πclass–Exercise 2.4.4hClasses Classesσtype=bb σtype=bcπcountry πcountry∩Exercise 2.4.4iBattles Outcomes (battle=name)πship,result,dateρR2(ship2,result2,date2)(ship=ship2 AND result=damaged AND date < date2)πshipExercise 2.4.5The result of the natural join has only one attribute from each pair of equated attributes. On the other hand, the result of the theta-join has both columns of the attributes and their values are identical.Exercise 2.4.6UnionIf we add a tuple to the arguments of the union operator, we will get all of the tuples of the original result and maybe the added tuple. If the added tuple is a duplicate tuple, then the set behavior will eliminate that tuple.Thus the union operator is monotone.IntersectionIf we add a tuple to the arguments of the intersection operator, we will get all of the tuples of the originalresult and maybe the added tuple. If the added tuple does not exist in the relation that it is added but does exist in the other relation, then the result set will include the added tuple. Thus the intersection operator is monotone.DifferenceIf we add a tuple to the arguments of the difference operator, we may not get all of the tuples of the originalresult. Suppose we have relations R and S and we are computing R – S. Suppose also that tuple t is in R but not in S. The result of R – S would include tuple t. However, if we add tuple t to S, then the new result will not have tuple t. Thus the difference operator is not monotone.ProjectionIf we add a tuple to the arguments of the projection operator, we will get all of the tuples of the original result and the projection of the added tuple. The projection operator only selects columns from the relation and does not affect the rows that are selected. Thus the projection operator is monotone.SelectionIf we add a tuple to the arguments of the selection operator, we will get all of the tuples of the original result and maybe the added tuple. If the added tuple satisfies the select condition, then it will be added to the newresult. The original tuples are included in the new result because they still satisfy the select condition. Thusthe selection operator is monotone.Cartesian ProductIf we add a tuple to the arguments of the Cartesian product operator, we will get all of the tuples of the original result and possibly additional tuples. The Cartesian product pairs the tuples of one relation with the tuples ofanother relation. Suppose that we are calculating R x S where R has m tuples and S has n tuples. If we add a tuple to R that is not already in R, then we expect the result of R x S to have (m + 1) * n tuples. Thus the Cartesianproduct operator is monotone.Natural JoinsIf we add a tuple to the arguments of a natural join operator, we will get all of the tuples of the original result and possibly additional tuples. The new tuple can only create additional successful joins, not less. If, however, the added tuple cannot successfully join with any of the existing tuples, then we will have zero additionalsuccessful joins. Thus the natural join operator is monotone.Theta JoinsIf we add a tuple to the arguments of a theta join operator, we will get all of the tuples of the original result and possibly additional tuples. The theta join can be modeled by a Cartesian product followed by a selection onsome condition. The new tuple can only create additional tuples in the result, not less. If, however, the addedtuple does not satisfy the select condition, then no additional tuples will be added to the result. Thus the theta join operator is monotone.RenamingIf we add a tuple to the arguments of a renaming operator, we will get all of the tuples of the original result and the added tuple. The renaming operator does not have any effect on whether a tuple is selected or not. In fact, the renaming operator will always return as many tuples as its argument. Thus the renaming operator is monotone.Exercise 2.4.7aIf all the tuples of R and S are different, then the union has n + m tuples, and this number is the maximum possible.The minimum number of tuples that can appear in the result occurs if every tuple of one relation also appears in the other. Then the union has max(m , n) tuples.Exercise 2.4.7bIf all the tuples in one relation can pair successfully with all the tuples in the other relation, then the natural join has n * m tuples. This number would be the maximum possible.The minimum number of tuples that can appear in the result occurs if none of the tuples of one relation can pairsuccessfully with all the tuples in the other relation. Then the natural join has zero tuples.Exercise 2.4.7cIf the condition C brings back all the tuples of R, then the cross product will contain n * m tuples. This number would be the maximum possible.The minimum number of tuples that can appear in the result occurs if the condition C brings back none of the tuples of R. Then the cross product has zero tuples.Exercise 2.4.7dAssuming that the list of attributes L makes the resulting relation πL(R) and relation S schema compatible, then the maximum possible tuples is n. This happens when all of the tuples of πL(R) are not in S.The minimum number of tuples that can appear in the result occurs when all of the tuples in πL(R) appear in S. Then the difference has max(n–m , 0) tuples.Exercise 2.4.8Defining r as the schema of R and s as the schema of S:1.πr(R S)2.R δ(πr∩s(S)) where δ is the duplicate-elimination operator in Section 5.2 pg. 2133.R – (R –πr(R S))Exercise 2.4.9Defining r as the schema of R1.R - πr(R S)Exercise 2.4.10πA1,A2…An(R S)Exercise 2.5.1aσspeed < 2.00 AND price > 500(PC) = øModel 1011 violates this constraint.Exercise 2.5.1bσscreen < 15.4 AND hd < 100 AND price ≥ 1000(Laptop) = øModel 2004 violates the constraint.Exercise 2.5.1cπmaker(σtype = laptop(Product)) ∩ πmaker(σtype = pc(Product)) = øManufacturers A,B,E violate the constraint.Exercise 2.5.1dThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R4 that stand for nodes of expression trees. Here is the sequence:R1(maker, model, speed) := πmaker,model,speed(Product PC)R2(maker, speed) := πmaker,speed(Product Laptop)R3(model) := πmodel(R1 R1.maker = R2.maker AND R1.speed ≤ R2.speed R2)R4(model) := πmodel(PC)The constraint is R4 ⊆ R3Manufacturers B,C,D violate the constraint.Exercise 2.5.1eπmodel(σLaptop.ram > PC.ram AND Laptop.price ≤ PC.price(PC × Laptop)) = øModels 2002,2006,2008 violate the constraint.Exercise 2.5.2aπclass(σbore > 16(Classes)) = øThe Yamato class violates the constraint.Exercise 2.5.2bπclass(σnumGuns > 9 AND bore > 14(Classes)) = øNo violations to the constraint.Exercise 2.5.2cThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R5 that stand for nodes of expression trees. Here is the sequence:R1(class,name) := πclass,name(Classes Ships)R2(class2,name2) := ρR2(class2,name2)(R1)R3(class3,name3) := ρR3(class3,name3)(R1)R4(class,name,class2,name2) := R1 (class = class2 AND name <> name2) R2R5(class,name,class2,name2,class3,name3) := R4 (class=class3 AND name <> name3 AND name2 <> name3) R3The constraint is R5 = øThe Kongo, Iowa and Revenge classes violate the constraint.Exercise 2.5.2dπcountry(σtype = bb(Classes)) ∩ πcountry(σtype = bc(Classes)) = øJapan and Gt. Britain violate the constraint.Exercise 2.5.2eThis complex expression is best seen as a sequence of steps in which we define temporary relations R1 through R5 that stand for nodes of expression trees. Here is the sequence:R1(ship,bat tle,result,class) := πship,battle,result,class(Outcomes (ship = name) Ships)R2(ship,battle,result,numGuns) := πship,battle,result,numGuns(R1 Classes)R3(ship,battle) := πship,battle(σnumGuns < 9 AND result = sunk (R2))R4(ship2,battle2) := ρR4(ship2,battle2)(πship,battle(σnumGuns > 9(R2)))R5(ship2) := πship2(R3 (battle = battle2) R4)The constraint is R5 = øNo violations to the constraint. Since there are some ships in the Outcomes table that are not in the Ships table, we are unable to determine the number of guns on that ship.Exercise 2.5.3Defining r as the schema A1,A2,…,A n and s as the schema B1,B2,…,B n:πr(R) πs(S) = øwhere is the antisemijoinExercise 2.5.4The form of a constraint as E1 = E2 can be expressed as the other two constraints.Using the “equating an expression to the empty set” method, we can simply say:E1– E2 = øAs a containment, we can simply say:E1⊆ E2 AND E2⊆ E1Thus, the form E1 = E2 of a constraint cannot express more than the two other forms discussed in this section.。

南京理工大学《数据库系统基础教程》试题和标准答案

一、选择题60(选择一个最合适的答案，在答题纸上涂黑)１.一个事务中的一组更新操作是一个整体,要么全部执行,要么全部不执行。

这是事务的：A．原子性B.一致性 C.隔离性 D.持久性２．在数据库的三级模式结构中,描述一个数据库中全体数据的全局逻辑结构和特性的是：Ａ．外模式 B．内模式 C.存储模式D．模式3．关于联系的多重性,下面哪种说法不正确？A.一个多对多的联系中允许多对一的情形。

B.一个多对多的联系中允许一对一的情形。

C．一个多对一的联系中允许一对一的情形。

Ｄ．一个多对一的联系中允许多对多的情形。

4.考虑学校里的"学生"和"课程＂之间的联系，该联系的多重性应该是:A. 一对一 B．多对一 C．一对多 D. 多对多5．下面哪种约束要求一组属性在同一实体集任意两个不同实体上的取值不同。

A. 键(key）约束。

Ｂ．单值约束。

C．参照完整性。

D．域(domａin)约束6．关系模型要求各元组的每个分量的值必须是原子性的。

对原子性,下面哪种解释不正确: A.每个属性都没有内部结构。

ﻩＢ.每个属性都不可再分解。

Ｃ.各属性值应属于某种基本数据类型。

ﻩD.属性值不允许为ＮUＬL。

７．对于一个关系的属性(列)集合和元组（行）集合，下面哪种说法不正确:A.改变属性的排列次序不影响该关系。

B．改变元组的排列次序不影响该关系。

C.改变元组的排列次序会改变该关系。

D.关系的模式包括其名称及其属性集合。

８．若Ｒ是实体集R1与R２间的一个多对多联系,将其转换为关系R'，哪种说法不正确：Ａ.R'属性应包括R１与R2的所有属性。

B.R'属性应包括R1与R2的键属性。

C.R1与R２的键属性共同构成R'的键。

D.R'的属性应包括R自身定义的属性。

9.关于函数依赖的判断,下面哪种说法不正确？A.若任意两元组在属性A上一致，在Ｂ上也一致，则有A →B成立。

B.若任意两元组在属性A上一致,在B上不一致,则A → B不成立。

Access数据库入门教程

性和方法。
利用VBA扩展Access功能
第一季度
第二季度
第三季度
第四季度
自定义函数
通过VBA编写自定义函数，可以实现Access 内置函数无法实现的功能。例如，可以编写一个函数来计算特定条件下的数据总和或平均值。
数据处理自动化
利用VBA编程，可以实现数据处理的自动化。例如，可以编写代码来自动导入、导出数据，或者对数据进行清洗、
启动Access
双击桌面上的Access图标，或者在开始菜单中找到Access并单击启动。
创建新数据库及表结构定义
创建新数据库
在Access启动界面选择“新建”，然后选择“数据库”并按照向导指引完成数据库的创建。
定义表结构
在数据库中创建新表，定义字段名称、数据类型、字段大小等属性，以构建合适的表结构。
模块（Modules）
用于编写和存储VBA代码，实现复杂的数据处理功能。
Access应用领域举例
01
02
03
04
企业数据管理
Access可用于创建企业级的数据库管理系统，实现数据的
集中存储、查询和分析。
网站后台数据库
Access可以作为网站后台的数据库支持，存储网站内容、
用户信息等数据。
科研数据管理
Access数据库入门教程
目录
• 数据库基础知识 • Access数据库概述 • 创建与管理Access数据库 • 表单设计与应用 • 报表设计与应用 • 宏与VBA编程在Access中应用 • 数据安全与优化策略
01 数据库基础知识
数据库概念及作用
数据库（Database）是按照数据结构来组织、存储和管理数据的仓库。

初学者必读的SQL数据库基础教程

初学者必读的SQL数据库基础教程SQL数据库是一种常用的数据库管理系统，广泛应用于各种软件开发和数据管理领域。

对于初学者来说，掌握SQL数据库的基础知识是非常重要的。

本文将从数据定义语言、数据操作语言、数据查询语言和数据控制语言等方面，为初学者提供一份必读的SQL数据库基础教程。

第一章数据定义语言（DDL）数据定义语言（DDL）是SQL数据库中用来定义数据库结构的语言。

它包括创建、修改和删除数据库、表、列以及其他对象的操作。

在SQL中，创建数据库使用CREATE DATABASE语句，创建表使用CREATE TABLE语句，修改表结构使用ALTER TABLE语句，删除表使用DROP TABLE语句等。

初学者在学习时应该了解这些常用的DDL语句，并能够正确地使用它们。

第二章数据操作语言（DML）数据操作语言（DML）是SQL数据库中用来对数据库中的数据进行操作的语言。

它包括插入、更新和删除数据的操作。

在SQL中，插入数据使用INSERT INTO语句，更新数据使用UPDATE语句，删除数据使用DELETE FROM语句等。

初学者需要熟悉这些基本的DML语句，并能够通过它们来操作数据库中的数据。

第三章数据查询语言（DQL）数据查询语言（DQL）是SQL数据库中用来查询数据库中的数据的语言。

它包括SELECT语句和一些用于过滤、排序和聚合数据的函数。

初学者需要掌握SELECT语句的基本用法，了解如何使用WHERE子句进行条件过滤，如何使用ORDER BY子句进行排序，以及如何使用GROUP BY子句进行数据聚合。

第四章数据控制语言（DCL）数据控制语言（DCL）是SQL数据库中用来控制数据库访问权限和事务处理的语言。

它包括GRANT和REVOKE语句用于授权和撤销权限，以及BEGIN TRANSACTION、COMMIT和ROLLBACK语句用于管理事务。

初学者需要了解如何使用DCL语句来管理数据库的安全性和事务一致性。

数据库系统基础教程_[全文]

第一章数据库系统的世界The Worlds of Database Systems数据库系统的发展数据库管理系统的结构未来的数据库系统*§1.1 数据库系统的发展c一、术语1.数据库是长期储存在计算机内的、有组织的、可共享的数据的集合。

*2.数据库管理系统数据库系统基础教程A First Course in Database SystemsDBMS - DataBase Management System是处理数据库访问的软件。

提供数据库的用户接口。

DBMS的目的：提供一个可以方便地、有效地存取数据库信息的环境*3.数据库系统是指在计算机系统中引入数据库后的系统*数据库最终用户应用系统应用开发工具DBMS操作系统数据库管理员DBA数据库系统构成应用程序员*保存信息的两种不同方法：永久性的系统文件、数据库系统。

文件方式的问题：数据的冗余和不一致数据访问困难数据孤立完整性问题原子性问题并发访问异常安全性问题二、文件系统与数据库系统*数据库方法能较好地解决以上的问题数据的独立性有效地访问数据减少应用程序的开发时间数据的一致性和安全性统一的数据管理并发的数据访问三、为什么用数据库*几种模型：基于树的层次模型基于图的网状模型物理相关、无高级查询语言基于表的关系模型物理无关、支持高级查询语言，基于对象的面向对象模型OOOR四、数据库模型的发展定长记录*关系数据库系统属性元组*关查询语言SQL语言SELECT balanceFROM AccountsWHERE accountNO = 67890;关系数据库系统*DBMS的组成数据、元数据存储管理程序事务管理程序查询处理程序§1.2 数据库管理系统的结构数据元数据存储管理程序查询处理程序事务管理程序模式更新更新查询*数据、元数据关于数据结构的信息（关于数据的数据）索引（INDEX）DBMS的组成*存储管理程序文件管理程序缓冲区管理查程序DBMS的组成*查询处理程序查询优化磁盘访问，是查询的主要代价；索引是查询优化的利器DBMS的组成*事务管理程序事务：是用户定义的一个数据库操作序列事务的四个特性原子性A一致性C隔离性I持久性DDBMS的组成*客户-服务器程序体系结构浏览器-服务器体系结构DBMS的组成*客户-服务器程序体系结构浏览器-服务器体系结构§1.3 未来的数据库系统第二章数据库建模Database Modeling*数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构设计物理结构物理实现*数据库的设计步骤需求收集和分析用户关心什么用户要什么结果设计概念结构设计逻辑结构设计物理结构物理实现*数据库的设计步骤需求收集和分析设计概念结构存什么关系（联系）如何ODL或E/R图，是各种数据模型的共同基础设计逻辑结构设计物理结构物理实现*数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构用什么数据模型数据库的模式（database schema）用户子模式设计物理结构物理实现*数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构设计物理结构数据怎么存根据DBMS产品、环境特点物理实现*数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构设计物理结构物理实现运行DDL装入测试数据应用程序*数据库的设计步骤想法需求ODLE / R关系RDBMSOODBMS*§2.1 ODL对象定义语言Object Definition Language以面向对象的观点、方法，说明数据库的概念结构可方便地直接转换成OODBMS 的说明经过努力，可以转换成RDBMS 的说明*面向对象的设计对象标识—OID对象与对象的区别类具有相同特性的对象归为一类对象的归并必须有意义属于同一类的对象其特性必须相同*面向对象的设计对象的三个特性属性：特性联系：引用方法：函数接口说明interface < 名字> {< 特性表>}*属性对象某方面的特征，属性就是数据只由基本数据类型构成属性的类型，不能是类、也不能从类中构造Interface Movie { //Movie Class 的ODL说明attribute string title;attribute integer year;attribute integer length;attribute enum Film { color, blackAndWhite } filmType;};*Interface Star {attribute string name;attribute Struct Addr{ string street,string city } address;};记录结构类型*联系对象的引用对象的关联对象集合的引用（1:N）Relationship Set < Star > stars;单一对象集合的引用（1:1）Relationship Star starOf;*反向联系ODL要求显式表示存在的反向联系Interface Movie { //Movie Class 的ODL说明attribute string title;attribute integer year;attribute integer length;attribute enum Film { color, blackAndWhite } filmType;relationship Set < Star > starsinverse Star :: starredIn; //Star与Movie的联系};联系的多重性N:N在联系中，每个C都和D的集合有关，而在反向联系中，每个D都和C的集合有关N:1在联系中，每个C都和唯一的D有关，而在反向联系中，每个D都和C的集合有关1:1在联系中，每个C都和唯一的D有关，而在反向联系中，每个D都和唯一的C有关*Interface Moive{……relationship Set <Star> starsinverse Star :: staredIn;relationship Studio ownedByinverse Studio :: owns;};Interface Star{……relationship Set <Moive> staredIninverse Moive :: stars;};Interface Studio{……relationship Set <Moive> ownsinverse Moive :: ownedBy;};NNN1*ODL中的类型基本类型原子类型接口类型结构类型，可由以下类型组合而成集合无重复，次序无关包可重复，次序无关列表可重复，次序相关数组结构*§2.2 实体联系图（E/R）用图形的方法，描述实体及实体间的联系世界由一组称作实体的基本对象及这些对象间的联系组成元素实体（Entity）客观存在并可相互区别的事件或物体对应于ODL中的对象实体集（Entity Set）同类（具有相同类型、相同性质）实体的集合对应于ODL中的类用矩形表示*§2.2 实体联系图（E/R）元素属性（Attribute）实体所具有的某一特性用与实体集相连的椭圆表示联系（Relationship）实体集之间的关联可涉及多个实体集可表示双向的联系用与相应的实体集相连的菱形表示*MoviesStarsStars-inlenghtfilmTypetitleyearnameaddress*E/R联系的多重性N与1的表示MoviesStarsStars-inStudiosPresidentsRunsMoviesStudiosOwns*联系的多向性E/R图能方便地描述两个以上实体集间的联系StarsMoviesContractsStudios一个制片公司与一位特定的影星签约来演一部特定的电影*联系中的角色实体集在联系中的作用参与联系的实体集互异只标注联系名同一实体集在一个联系中多次出现标注联系名及角色名Sequel-ofMoviesOriginalSequelStarsMoviesContractsStudiosStudio of starProducing studio*联系中的属性联系中可以包含属性由联系而产生的属性可为由联系产生的属性建立实体集StarsMoviesContractsStudiossalary*将多向联系转换成二元联系新增连接实体集引入连接实体集至原实体集的多对一的联系*§2.3 设计原则真实性设计应当忠于规范存什么避免冗余任何事物只表达一次避免引入过多的元素选择合适的元素类型属性？类/实体集？联系集？*§2.4 子类特殊化与概括子类与超类属性的继承*ODL中的子类子类继承其超类的所有特性属性联系Interface Cartoon : Movie {relationship set < Star > voices;}*ODL中的多重继承类的层次一个类可以有多个超类Interface MurderMystery : Movie{attribute string weapon;}Interface Cartoon-MurderMystery : Cartoon,MurderMystery { }*E/R中的子类IsaE/R中的继承*§2.5 对约束的建模建模包含对现实世界的对象及联系的描述，也包含对它们的一些约束键码单值约束参照完整性约束域的约束一般约束*键码在类的范围内唯一标识一个对象（或者在实体集的范围内唯一标识一个实体）的属性或属性集一个类中的两个对象（或一个实体集中的两个实体）在构成键码的属性集上取值不能相同ODL中键码的表示interface Movie( key (title,year) ) {……}*超码一个或多个属性的集合，能在一个实体集中唯一地标识一个实体一个类（或实体集）中可能有多个超码候选码其任意真子集都不为超码的超码一个类（或实体集）中可能有多个候选码主码从候选码中选取的一个，一个类（实体集）中只有一个主码E / R图中只能表示主码：主码属性名加上下划线*单值约束要求某个角色的值是唯一的，如键码当一个属性为单值时可以要求该属性值存在（not null）可以允许该属性值任选（null）构成键码的属性，必须有值存在（not null）*参照完整性约束要求由某个对象引用的值在数据库中确实存在参照与被参照、引用与被引用参照完整性约束的操作（各产品不同）禁止删除被引用的对象级联删除/ 修改E/R图中参照完整性的表示MoviesStudiosOwns*§2.6 弱实体集弱实体集的属性不足以形成主码有主码的实体集称为强实体集弱实体集只有作为一对多联系的一部分（多）才有意义弱实体集与其拥有者之间的联系是标识性联系CrewsUnit-ofStudiosnumbernameaddr*§2.7 关于联系集联系集的成份参加联系的实体集的主码联系集的属性联系中属性的决策(二元联系)1:1 联系集的属性：放到任意一端1:N 联系集的属性：放到N 端N:M联系集的属性：只能留在联系集中*联系集的取舍（二元联系）1:1联系：将一端的主码作为另一端的属性1:N联系：将一端的主码作为N 端的属性N:M联系：必须保留联系集联系集的键码（二元联系）1:1联系：任意一端的主码1:N联系：N端的主码N:M联系：参加联系的所有实体集的主码*ODL、E/R建模关心：存什么数据、关系如何不关心：用什么数学模型、DBMS产品透过E/R图，便于与用户交流*作业思考所有带*的练习，并上网查阅解答练习2.1.7 / 2.2.8 / 2.3.2 / 2.5.3 / 2.5.4 /2.6.4(a) 第三章关系数据模型The Relational Data Model*ODL、E/R到关系模型的转换关系模型的设计理论*§3.1 关系模型的基本概念逻辑数据模型是用户从数据库所看到的数据模型与DBMS有关层次、网状、关系、面向对象关系数据模型数据结构两维的扁平表数据操作关系代数关系演算数据的完整性实体完整性参照完整性用户定义的完整性*现实世界的实体以及实体间的各种联系均用关系表示关系数据库系统是建立在关系模型上的数据库系统关系数据库是表的集合*模型和模式数据模型是描述数据的手段数据模式是用给定的数据模型对具体数据的描述属性元组域型值联系关系的联系是通过关联属性的值连接的*SnoSnameSsexSagesdept95001张三男25CS95002李四女24CS96101王五23MA96001赵六男23CS关系( 表)属性(列、字段)元组(行、记录)域(string,{男，女})Student ( sno, sname, ssex, sage, sdept )*关系实例关系→实体集、类关系的实例→元组的集合元组→实体、对象数据库实例→给定时刻数据库中数据的一个快照*§3.2 从ODL设计到关系设计ODL设计是概念设计的产物( Using OO )ODL描述→关系模式→实现*ODL属性→关系属性原子属性类→关系属性→属性非原子属性（复杂数据类型）必须转换成原子属性记录结构结构的每个item对应一个属性多值集合针对每个值建立一个元组会产生冗余→需规范化*ODL属性→关系属性（续）其他类型属性（包、数组、列表）针对每个元素建立一个元组增加一个记数属性，表示包的成员号定长数组扩展为多个属性*ODL联系→关系描述单值联系联系的类型为一个类增加一个（组）属性，存放相关类的键码属性（组）将类之间的联系→关系之间的联系*ODL联系→关系描述（续）多值联系联系的类型为某个类的集合类型1 : N、N : M增加一个键码属性为集合的每个成员建立一个元组其他原始属性重复多次（与集合成员的个数相等）导致大量的冗余，需要规范化*键码是必需的选择合适的属性（组）作为键码学号、工号、身份证号…...增加计数属性联系与反向联系在联系的双方均有联系的描述→冗余ODL：双向描述E/R：相关的键码值进行连接*§3.3 从E/R图到关系的设计E/R与ODL描述的差异联系作为独立的概念←→联系嵌套在类定义中结构化数据←→允许使用集合、聚集类型联系可以有属性←→联系无属性E/R →关系模式→实现*实体集到关系的转换非弱实体集实体集名→关系名属性→属性弱实体集为弱实体集建立关系属性：弱实体集的属性+ 辅助实体集的键码*E/R联系到关系的转换用关系表示联系联系名→关系名属性→属性+ 相关实体集的键码属性（集）多向联系的转换注意，属性的命名*§3.4 子类结构到关系的转换ODL中的子类一个对象完全属于一个类子类继承其超类的特性E/R中的子类分层结构通过与ISA联系有关的实体集进行扩展*用关系表示ODL子类每个子类都有自己的关系包含该子类的所有特性（含继承特性）在一个关系中含有所有属性Movie(title,year,length,filmType,studioName,starName)Cartoon(title,year,length,filmType,studioName,starName,voice) MurderMystery(title,year,length,filmType,studioName,starName,weapon)Cartoon- MurderMystery(title,year,length,filmType,studioName,starName,voice, weapon)*在关系模型中表示isa 联系子类的信息被分散到上层的几个关系中与ISA联系有关的实体集拥有相同的键码Movie(title,year,length,filmType)Cartoon(title,year)MurderMystery(title,year, weapon)Voice(title,year,name)*使用NULL值合并关系将关系描述成一个‘全集’属性：所有可能的属性描述：允许Null值层次越高，取Null值的属性越多Movie (title,year,length,filmType,studioName,starName,voice, weapon) 只是一种方法而已*作业思考所有带*的练习，并上网查询解答练习3.2.3 / 3.3.1 / 3.4.1 / 3.5.3 /*§3.5 函数依赖数据依赖函数依赖多值依赖数据依赖是针对数据模式，而不是特定的实例*函数依赖（FD）属性之间的联系假设给定X 属性的值，就知道Y的值，那么X 函数决定Y如果R的两个元组在属性A1,A2,…,An上一致，则它们在另一个属性B上也一致，那么A1,A2,…,An函数决定B，记作A1A2…An→Bif A1A2…An→B1 thenA1A2…An→B2 A1A2…An→B1 B2 ... Bm……A1A2…An→Bm*关系的键码如果一个或多个属性的集合{A1A2…An}满足如下条件，则该集合为关系R的键码：1.这些属性函数决定该关系的所有其他属性2. {A1A2…An}的任何真子集都不能函数决定R的所有其他属性*超键码包含键码的属性集称为超键码*寻找关系的键码（来自E/R）来自实体集的关系的键码就是该实体集的键码属性对于二元联系R：N：M，相关两个实体的键码都是R的键码属性N：1，多端实体集的键码是R的加码属性1：1，任意一端实体集的键码是R的键码对于多向联系R：如果多向联系R有一个箭头指向实体集E，则响应的关系中，除了E的键码以外，至少还存在一个键码。

数据库基础教程(完整版)

数据库基础教程（完整版）第一部分：认识数据库数据库，顾名思义，就是一个用来存储、管理数据的仓库。

在这个信息爆炸的时代，数据已经成为了企业的核心资产，而数据库就是管理这些资产的重要工具。

无论是电商平台、社交媒体，还是企业内部的管理系统，都离不开数据库的支持。

一、数据库的分类1. 关系型数据库：以表的形式组织数据，每个表由行和列组成，行代表记录，列代表字段。

常见的有MySQL、Oracle、SQL Server等。

2. 非关系型数据库：与关系型数据库不同，非关系型数据库的数据结构更加灵活，常见的有MongoDB、Redis、Cassandra等。

3. NoSQL数据库：NoSQL是Not Only SQL的缩写，表示不仅仅是SQL，它包含了非关系型数据库以及一些新型的数据库技术，如NewSQL 等。

二、数据库的组成1. 数据库管理系统（DBMS）：负责管理和维护数据库的软件系统，如MySQL、Oracle等。

2. 数据库：存储数据的仓库，由多个表组成。

3. 表：数据库中的基本单位，由行和列组成，行代表记录，列代表字段。

4. 记录：表中的一行数据，代表一个完整的信息。

5. 字段：表中的一列数据，代表记录中的一个属性。

三、数据库的作用1. 数据存储：将数据存储在数据库中，方便管理和查询。

2. 数据管理：通过数据库管理系统，可以对数据进行增删改查等操作。

3. 数据安全：数据库管理系统提供了数据备份、恢复、权限控制等功能，保障数据的安全。

4. 数据共享：多个用户可以同时访问数据库，实现数据共享。

5. 数据分析：通过数据库管理系统，可以对数据进行统计、分析等操作，为企业决策提供依据。

四、学习数据库的必要性1. 提高工作效率：掌握数据库技术，可以快速地处理大量数据，提高工作效率。

2. 适应市场需求：随着互联网的发展，数据库技术已经成为IT 行业的必备技能。

3. 拓展职业发展：学习数据库技术，可以为职业发展打下坚实的基础。

数据库系统基础教程第三版

数据库系统基础教程第三版1 数据库系统基础教程第三版介绍数据库系统是现代信息化建设中最重要的核心基础设施之一，也是各类信息系统实现高效、可靠、安全管理的保障。

《数据库系统基础教程》是一本通俗易懂、基础全面、逐步深入的数据库系统学习教材。

本书在第三版中对数据库系统的各个方面进行了深入的剖析和介绍，为读者提供了全面系统的数据库系统学习和实践指导。

2 数据库系统的基本概念数据库是按照特定数据模型组织、管理、存储和维护数据的集合，具有以下特点：- 一致性：数据库中存储的各个数据之间应该相互协调、不冲突；- 持久性：数据库应该能够长期保存存储的数据；- 可共享：数据库中的数据应该能够供多个应用程序共同访问；- 独立性：数据库中的数据应该与具体的应用程序和物理存储设备无关。

3 数据库系统的组成数据库系统是由数据库、数据库管理系统（DBMS）、应用程序和数据库管理员等部分组成的。

其中，DBMS是数据库管理的核心部分，主要用于数据的创建、存储、查询、更新和删除等操作。

应用程序则是数据库系统的最终使用者，通过应用程序可以实现对数据库的访问与操作。

数据库管理员则是负责数据库的管理与维护，包括数据库的安装、配置、备份、恢复等工作。

4 数据库设计数据库设计是指按照特定的设计方法和原则，对数据库进行逻辑和物理上的设计，包括数据建模、数据规范化、索引设计、安全性设计等。

数据库设计应该能够满足用户对数据的操作需求，同时也应该考虑系统的性能和可维护性等因素。

5 数据库管理数据库管理主要包括数据库的创建与删除、数据备份与恢复、数据安全与权限管理等。

数据库管理需要依据具体的业务需求和实际情况，制定合理的管理策略和方案，确保数据库的安全、可靠和高效管理。

6 数据库应用数据库应用主要包括数据管理应用、数据分析应用和数据挖掘应用等。

数据管理应用是指基于数据库系统进行数据的存储、查询、更新和删除等操作；数据分析应用则是基于数据库系统中存储的数据进行分析和处理，得出各种统计分析结果；数据挖掘应用则是通过对数据库系统中的大量数据进行挖掘和分析，提取出隐藏在数据中的有价值的信息。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

28
面向对象的设计
对象的三个特性属性：特性联系：引用方法：函数接口说明 interface < 名字 > { < 特性表 > } 29
属性对象某方面的特征，属性就是数据只由基本数据类型构成属性的类型，不能是类、也不能从类中构造 Interface Movie { //Movie Class 的ODL 说明 attribute string title; attribute integer year; attribute integer length; attribute enum Film { color, blackAndWhite } filmType; }; 30
§2.2 实体联系图（E/R）元素属性（Attribute）实体所具有的某一特性用与实体集相连的椭圆表示联系（Relationship）实体集之间的关联可涉及多个实体集可表示双向的联系用与相应的实体集相连的菱形表示
38
title Movies lenght
year
第一章数据库系统的世界 The Worlds of Database Systems 数据库系统的发展数据库管理系统的结构未来的数据库系统
§1.1 数据库系统的发展c 一、术语 1.数据库是长期储存在计算机内的、有组织的、可共享的数据的集合。
2
2.数据库管理系统
3
数
A
据
将多向联系转换成二元联系新增连接实体集引入连接实体集至原实体集的多对一的联系
44
§2.3 设计原则真实性设计应当忠于规范存什么避免冗余任何事物只表达一次避免引入过多的元素选择合适的元素类型属性？类/实体集？联系集？
45
§2.4 子类特殊化与概括子类与超类属性的继承
超码一个或多个属性的集合，能在一个实体集中唯一地标识一个实体一个类（或实体集）中可能有多个超码候选码其任意真子集都不为超码的超码一个类（或实体集）中可能有多个候选码主码从候选码中选取的一个，一个类（实体集）中只有一个主码 E / R图中只能表示主码：主码属性名加上下划线 52
E/R中的子类 Isa E/R中的继承
49
§2.5 对约束的建模建模包含对现实世界的对象及联系的描述，也包含对它们的一些约束键码单值约束参照完整性约束域的约束一般约束
50
键码在类的范围内唯一标识一个对象（或者在实体集的范围内唯一标识一个实体）的属性或属性集一个类中的两个对象（或一个实体集中的两个实体）在构成键码的属性集上取值不能相同 ODL中键码的表示 interface Movie ( key (title,year) ) { …… } 51
Movies
Contracts
Sequel Studio of star
Studios
42 Producing studio
联系中的属性联系中可以包含属性由联系而产生的属性可为由联系产生的属性建立实体集 salary Stars Contracts Studi os 43 Movie s
17
§1.3 未来的数据库系统
客户-服务器程序体系结构浏览器-服务器体系结构
18
第二章数据库建模 Database Modeling
数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构设计物理结构物理实现
20
数据库的设计步骤需求收集和分析用户关心什么用户要什么结果设计概念结构设计逻辑结构设计物理结构物理实现 21
Stars Contracts Movies
Studios
一个制片公司与一位特定的影星签约来演一部特定的电影
41
联系中的角色实体集在联系中的作用参与联系的实体集互异只标注联系名同一实体集在一个联系中多次出现标注联系名及角色名
Original Stars Movies
Sequel-of
32
反向联系 ODL要求显式表示存在的反向联系
Interface Movie { //Movie Class 的ODL 说明 attribute string title; attribute integer year; attribute integer length; attribute enum Film { color, blackAndWhite } filmType; relationship Set < Star > stars 33 inverse Star :: starredIn; //Star
35
ODL中的类型基本类型原子类型接口类型结构类型，可由以下类型组合而成集合 •无重复，次序无关包 •可重复，次序无关列表 •可重复，次序相关数组
36
§2.2 实体联系图（E/R）用图形的方法，描述实体及实体间的联系世界由一组称作实体的基本对象及这些对象间的联系组成元素实体（Entity）客观存在并可相互区别的事件或物体对应于ODL中的对象实体集（Entity Set）同类（具有相同类型、相同性质）实体的集合 37
46
ODL中的子类子类继承其超类的所有特性属性联系 Interface Cartoon : Movie { relationship set < Star > voices; }
47
ODL中的多重继承类的层次一个类可以有多个超类 Interface MurderMystery : Movie{ attribute string weapon; } Interface Cartoon-MurderMystery : Cartoon,MurderMystery { } 48
name Stars-in
address Stars
filmType
39
E/R联系的多重性 N与1的表示 Movies Stars-in Stars
Studios
Runs
Presidents
Movies
Owns
Studio s
40
联系的多向性 E/R图能方便地描述两个以上实体集间的联系
Interface Star { attribute string name; attribute Struct Addr { string street,string city } address; };
记录结构类型
31
联系对象的引用对象的关联对象集合的引用（1:N） Relationship Set < Star > stars; 单一对象集合的引用（1:1） Relationship Star starOf;
5
最终用户
应用系统应用开发工具应用程序员
数据库系统构成
DBMS
操作系统数据库管理员 DBA
数据库
6
二、文件系统与数据库系统
保存信息的两种不同方法：永久性的系统文件、数据库系统。文件方式的问题：数据的冗余和不一致数据访问困难数据孤立完整性问题原子性问题并发访问异常安全性问题
9
关系数据库系统
accountNO 12345 67890 …
Balance
Type
1000.00 Savings 2846.92 Checking … …
属性
元组
10
关系数据库系统关查询语言 SQL语言 SELECT balance FROM Accounts WHERE accountNO = 67890;
数据库的设计步骤
需求收集和分析设计概念结构存什么关系（联系）如何 ODL或E/R图，是各种数据模型的共同基础
设计逻辑结构设计物理结构物理实现 22
数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构用什么数据模型数据库的模式（database schema）用户子模式设计物理结构物理实现 23
数据库的设计步骤需求收集和分析设计概念结构设计逻辑结构设计物理结构数据怎么存根据DBMS产品、环境特点物理实现 24
数据库的设计步骤
需求收集和分析设计概念结构设计逻辑结构设计物理结构物理实现运行DDL 装入测试数据应用程序
25
数据库的设计步骤11ຫໍສະໝຸດ §1.2 数据库管理系统的结构
模式更新查询 DBMS的组成数据、元数据存储管理程序查询处理程序事务管理程序查询处理程序存储更新
事务管理程序
管理程序
数据元数据
12
DBMS的组成数据、元数据关于数据结构的信息（关于数据的数据）索引（INDEX）
13
DBMS的组成存储管理程序文件管理程序缓冲区管理查程序
联系的多重性 N:N 在联系中，每个C都和D的集合有关，而在反向联系中，每个D都和C的集合有关 N:1 在联系中，每个C都和唯一的D有关，而在反向联系中，每个D都和C的集合有关 1:1 在联系中，每个C都和唯一的D有关，而在反向联系中，每个D都和唯一的C有关
34
Interface Moive{ …… N relationship Set <Star> stars inverse Star :: staredIn; relationship Studio ownedBy N inverse Studio :: owns; }; Interface Star{ N …… relationship Set <Moive> staredIn inverse Moive :: stars; }; 1 Interface Studio{ …… relationship Set <Moive> owns
14
DBMS的组成查询处理程序查询优化磁盘访问，是查询的主要代价；索引是查询优化的利器