2015年普通高等学校自出卷子A4竖开
2015年普通高等学校招生全国统一考试语文试题(四川卷,无答案)不分版本

2015年普通高等学校招生全国统一考试语文试题(四川卷,无答案)不分版本2015年普通高等学校招生全国统一考试〔四川卷〕语文本试卷分第I卷〔单项选择题〕和第II卷〔非单项选择题〕。
第I卷1至3页,第II卷4至6页,共6页。
总分值150分。
考试时间150分钟。
考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效。
考试结束后,将本试题卷和答题卡一并交回。
第I卷〔单项选择题共27分〕考前须知:必须用2B铅笔在答题卡上将所选答案对应的标号涂黑。
第I卷共3大题,9小题。
每题3分。
一、〔12分,每题3分〕1.以下词语中加点字的读音,全部正确的一项为哪一项A. 暂.时zàn 埋.怨 mái 谆.谆告诫 zhūn 引吭.高歌 hángB. 豆豉.chǐ踝.骨 huái 踉踉跄.跄 cāng 按图索骥. jìC. 梗.概gěn 删.改 shān 炊烟袅.袅niǎo 明眸.皓齿 móuD. 搁.浅gē解剖.pōu 鬼鬼祟.祟 suì不屑.一顾 xiè2.以下词语中,没有错别字的一项为哪一项A. 阻碍功夫片钟灵毓秀管中窥豹,可见一斑B. 梳妆吊胃口瞠目结舌文武之道,一张一驰C. 辐射入场券循章摘句风声鹤唳,草木皆兵D. 蜚然直辖市秘而不宣城门失火,殃及池鱼3.以下各句中加点词语的使用,不恰当的一项为哪一项A.“2015年度文化跨界论坛〞日前在北京举行,届时..来自世界各国的艺术家、企业家和媒体人围绕当前文化创意产业开展中的热点进行了交流。
B. 对于那些熟稔..互联网的人来说,进行“互联网+〞创业,最难的可能并不是“互联网〞这一局部,而是“+〞什么以及怎么“+〞的问题。
C. 这家民用小型无人机公司一年前还寂寂无闻,一年后却声名鹊起....,其系列产品先后被评为“十大科技产品〞“2014年接触高科技产品〞。
D. 近年来,广袤蜀地的新村建设全面推进,大巴山区漂亮民居星罗棋布,大凉山上彝家新寨鳞次栉比....,西部高原羌寨碉楼拔地而起。
新课标(I,II)2015年普通高等学校招生全国统一考试试卷(附答案)word版

绝密★启用前试卷类型:A2015年普通高等学校招生全国统一考试语文试题(全国卷1)注意事项:1.本试题分第I卷(阅渎题)和第Ⅱ卷(表达题)两部分。
答卷前,考生务必将自己的姓名、准考证号填写在答题卡相应的位臵。
2.作答时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
第Ⅰ卷阅读题甲必考题一、现代文阅读(9分,每小题3分)阅读下面的文字,完成1-3题。
宋代的农业、手工业、商业在唐代的基础上又有了新的发展,特别是商品经济出现了空前的繁荣。
在此背景下,宋代的货币流通和信用进入迅速发展时期,出现了古代金融的新篇章。
宋代在信用形式和信用工具方面都呈现出新的特点。
信用形式有借贷、质、押、典、赊买赊卖等多种形式。
借贷分为政府借贷和私人借贷。
政府借贷主要表现为赈贷的形式,在紧急情况下通过贷给百姓粮食或种子的方式,帮助他们度过困境。
私人借贷多为高利贷,它可以解决社会的分化和“钱荒”的带来的平民百姓资金严重不足的问题,满足特殊支付和燃眉之急的需要。
质、押是借贷担保的形式,由质库、解库库等机构经营。
质属于动产担保,它必须转移动产的占有;押属于不动产担保,通常将抵押物的契约交付债权人即可。
债务人违约时,债权人可用变卖价款优先受偿。
典作为不动产转移的一种形式是在宋代形成和发展起来的。
其特点是典权人向出典人支付典价后,在典期内就占有了出典人典产的使用权和收益支配权,出典人也不必向典权人支付利息。
宋代的商业贸易非常发达,但存在着通货紧缩现象,故赊买赊卖行为也很普遍,几乎生产、流通、消费领域的所有物品都能进行赊买赊卖。
从实际效果看,它解决了军需、加强了流通,更重要的一点,它对束缚生产流通扩大和发展的高利贷构成了冲击。
随着社会经济的发展,宋代商业贸易的发展对货币的要求越来越高,但是社会中货币供给和流通状况不尽理想,表现为货币流通区域的割据性、货币供给数量的有限性以及大量流通的铜铁钱细碎和不便携带的特性,其结果是抑制了经济发展。
2015年普通高等学校招生全国统一考试语文试题(湖北卷含解析).docx

2015 年普通高等学校招生全国统一考试语文试题(湖北卷,含解析)本试题卷共8 页,六大题23 小题。
全卷满分150 分。
考试用时150 分钟。
★祝考试顺利★注意事项:1.答卷前,先将自己的姓名、准考证号填写在试题卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置。
用2B 铅笔将答题卡上试卷类型 A 后的方框涂黑。
2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
3.非选择题的作答:用签字笔直接答在答题卡上对应的答题区域内。
写在试题卷、草稿纸和答题卡上的非答题区域均无效。
4.考试结束后,请将本试题卷和答题卡一并上交。
一、语文基础知识(共 15 分,共 5 小题,每小题 3 分)1.下列各组词语中,加点字的注音全都正确的一组是A.缜(shèn)密感喟(kuì)..B.镶(xi ānɡ)嵌驰骋(chěnɡ)..(chu án)飞紫蔷薇( wēi).暗香盈( yínɡ)袖.栀( zhī)子花逸兴遄..C.热忱( ch én)别( bi é)扭康乃馨(xīn)积微成著....(zhù)D.菜肴( yáo)酣( hān)畅蒲( pú)公英春风拂(f ó)面....【答案】 B【考点定位】识记现代汉语普通话常用字的字音。
能力层级为识记A。
2.下列各组词语中,没有错别字的一组是A.商埠绰约扣人心弦扶老携幼B.博奕翘楚以逸待劳固若金汤C.笃信聪慧日臻成熟灸手可热D.溃乏矫情所向披靡汗流浃背【答案】 A【解析】试题分析:本题选 A 项。
B 项中,“博奕”错误,本意是下棋的意思。
所以应为“博弈”。
C 项中,“灸手可热”错误,应为“炙手可热”。
D 项中,“溃乏”错误,应该是“匮乏”。
【考点定位】识记并正确书写现代常用规范汉字。
能力层级为识记A。
(精校版)福建地区2015年度高等考试理数卷2015年度普通高等学校招生统一考试
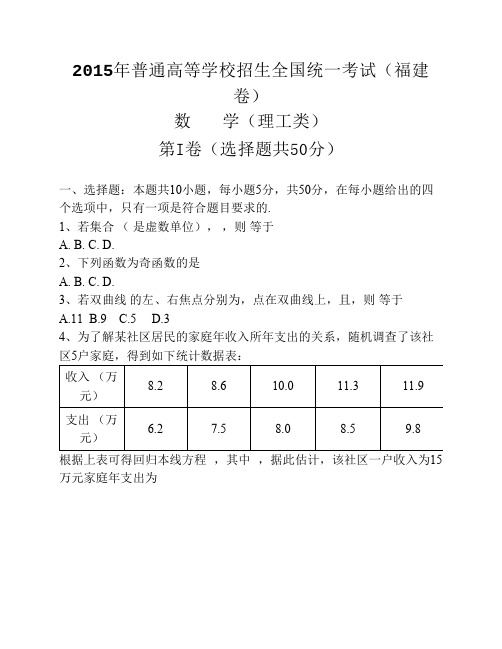
20.本小题主要考查导数及其应用等基础知识,考查推理论证能力、运 算求解能力、创新意识,考查函数与方程思想、化归与转化思想、分类 与整合思想、有限与无限思想、数形结合思想.满分14分. 解法一:(1)令则有 当 ,所以在上单调递减, 故当. (2)令则有 当 ,所以在上单调递增, 故对任意正实数均满足题意. 当. 取,所以在上单调递增, ,即. 综上,当时,总存在,使得对任意的. (3)当时,由(1)知,对于, , 令,则有 故当时,,在上单调递增,故,即,所以满足题意的t不存在. 当时,由(2)知存在,使得对任意的. 此时, 令,则有 故当时,,在上单调递增,故,即,记与中较小的为, 则当,故满足题意的t不存在. 当,由(1)知,, 令,则有 当时,,所以在上单调递减,故, 故当时,恒有,此时,任意实数t满足题意. 综上,. 解法二:(1)(2)同解法一. (3)当时,由(1)知,对于,
.
14、若函数 ( 且 )的值域是 ,则实数 的取值范围是
.
15、一个二元码是由0和1组成的数字串 ,其中 称为第 位码元,二元码
是通信中常用的码,但在通信过程中有时会发生码元错误(即码元由0
变为1,或者由1变为0)
已知某种二元码 的码元满足如下校验方程组:
其中运算 定义为: .
现已知一个这种二元码在通信过程中仅在第 位发生码元错误后变成了
(12)设圆心C到直线l的距离等于2,求m的值.
选修4-5:不等式选讲 已知函数的最小值为4.
2015年普通高等学校招生全国统一考试.doc

2018年普通高等学校招生全国统一考试理科数学(友情提醒,本卷答案非官方,仅供参考)注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至3页,第Ⅱ卷3至5页。
2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置。
3.全部答案在答题卡上完成,答在本试题上无效。
4.考试结束后,将本试题和答题卡一并交回。
第Ⅰ卷一.选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)设复数z满足=i,则|z|=(A) 1 (B)(C)(D)2【参考答案】A第1题:ABCD(2)sin20°cos10°-con160°sin10°=(A)(B)(C)(D)【参考答案】D第2题:ABCD(3)设命题P:nN,>,则P为(A)nN,>(B)nN, ≤(C)nN,≤(D)nN, =【参考答案】C第3题:ABCD(4)投篮测试中,每人投3次,至少投中2次才能通过测试。
已知某同学每次投篮投中的概率为0.6,且各次投篮是否投中相互独立,则该同学通过测试的概率为(A)0.648 (B)0.432 (C)0.36 (D)0.312【参考答案】A第4题:ABCD(5)已知M(x0,y0)是双曲线C:上的一点,F1、F2是C上的两个焦点,若<0,则y0的取值范围是(A)(-,)(B)(-,)(C)(,)(D)(,)【参考答案】A第5题:ABCD(6)《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺。
问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有(A)14斛(B)22斛(C)36斛(D)66斛【参考答案】B第6题:ABCD(7)设D为ABC所在平面内一点,则(A) (B)(C) (D) 【参考答案】A第7题:ABCD(8)函数f(x)=的部分图像如图所示,则f(x)的单调递减区间为(A)(),k(B)(),k(C)(),k(D)(),k【参考答案】B第8题:ABCD(9)执行右面的程序框图,如果输入的t=0.01,则输出的n=(A)5 (B)6 (C)7 (D)8【参考答案】C第9题:ABCD(10)(10)的展开式中,的系数为(A)10 (B)20 (C) 30 (D)60【参考答案】C第10题:ABCD(11)圆柱被一个平面截去一部分后与半球(半径为r)组成一个几何体,该几何体三视图中的正视图和俯视图如图所示。
2015年普通高等学校招生全国统一考试数学试卷(文科)(新课标I卷)

2015年普通高等学校招生全国统一考试数学试卷(文科)(新课标I 卷) 本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分。
满分150分,考试时间120分钟。
第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 已知集合{}|32,A x x n n N ==+∈,{}6,8,10,12,14B =,则集合A B 中元素的个数为( )A. 5B. 4C. 3D. 22. 已知点A (0,1),B (3,2),向量(4,3)AC =-- ,则向量BC = ( )A. (-7,-4)B. (7,4)C. (-1,4)D. (1,4)3. 已知复数z 满足(1)1z i i -=+,则z=( )A. 2i --B. 2i -+C. 2i -D. 2i +4. 如果3个正整数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( ) A. 310 B. 15 C. 110 D. 1205. 已知椭圆E 的中心在坐标原点,离心率为12,E 的右焦点与抛物线2:8C y x =的焦点重合,A ,B 是C 的准线与E 的两个交点,则AB =( )A. 3B. 6C. 9D. 126. 《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺,问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度长为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米约有( )A. 14斛B. 22斛C. 36斛D. 66斛7. 已知{}n a 是公差为1的等差数列,n S 为{}n a 的前n 项和,若844S S =,则10a =( ) A. 172 B. 192 C. 10 D. 128. 函数()cos()f x x ωϕ=+的部分图象如图所示,则f (x )的单调递减区间为( )A. 13,),44k k k Z ππ-+∈( B. 13,2),44k k k Z ππ-+∈(2 C. 13,),44k k k Z -+∈( D. 13,2),44k k k Z -+∈(29. 执行如图所示的程序框图,如果输入的t=0.01,则输出的n=( )A. 5B. 6C. 7D. 810. 已知函数1222,1()log (1),1x x f x x x -⎧-≤=⎨-+>⎩且()3f a =-,则(6)f a -=()A. 74-B. 54-C. 34-D. 14- 11. 圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体三视图中的正视图和俯视图如图所示,若该几何体的表面积为,则r=( ) A. 1 B. 2 C. 4D. 812. 设函数()y f x =的图象与2x a y +=的图象关于直线y x =-对称,且(2)(4)f f -+-=,则a=( )A. -1B. 1C. 2D. 4第II 卷注意事项:本卷包括必考题和选考题两部分。
2015年普通高等学校招生全国统一考试数学文试题(福建卷,含解析)
通项公式,根据通项公式的不同特点,选择相应的求和方法,本题 bn 2n n ,故可采取分组求和法求其
前 10 项和.
试题解析:(I)设等差数列an 的公差为 d .
由已知得
a1 d
a1 3d
4
a1
6d
15
,
解得
ad1
3 1
.
所以 an a1 n 1 d n 2 .
考点:1、等差数列通项公式;2、分组求和法. 18.(本题满分 12 分) 全网传播的融合指数是衡量电视媒体在中国网民中影响了的综合指标.根据相关报道提供的全网传播 2015 年某全国性大型活动的“省级卫视新闻台”融合指数的数据,对名列前 20 名的“省级卫视新闻台”的融合 指数进行分组统计,结果如表所示.
二、填空题:本大题共 4 小题,每小题 4 分,共 16 分.把答案填在答题卡的相应位置.
13.某校高一年级有 900 名学生,其中女生 400 名,按男女比例用分层抽样的方法,从该年级学生中抽取
一个容量为 45 的样本,则应抽取的男生人数为_______.
【答案】 25
【解析】
试题分析:由题意得抽样比例为 45 1 ,故应抽取的男生人数为 500 1 25.
考点:集合的运算. 3.下列函数为奇函数的是( )
A. y x B. y ex C. y cos x D. y ex ex
【答案】D 【解析】
试题分析:函数 y x 和 y ex 是非奇非偶函数; y cos x 是偶函数; y ex ex 是奇函数,故选 D.
考点:函数的奇偶性.
2
4
2
4
【答案】A
考点:1、椭圆的定义和简单几何性质;2、点到直线距离公式.
2015年普通高等学校招生全国统一考试数学试卷(文科)(四川卷)
2015年普通高等学校招生全国统一考试数学试卷(文科)(四川卷)第I 卷 (选择题 共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一个是符合题目要求的。
1. 设集合A ={x|-1<x <2},集合B ={x|1<x <3},则A ∪B = A. {x|-1<x <3}B. {x|-1<x <1}C. {x|1<x <2}D. {x|2<x <3}2. 设向量a =(2,4)与向量b =(x,6)共线,则实数x =A. 2B. 3C. 4D. 63. 某学校为了了解三年级、六年级、九年级这三个年级之间的学生视力是否存在显著差异,拟从这三个年级中按人数比例抽取部分学生进行调查,则最合理的抽 样方法是A. 抽签法B. 系统抽样法C. 分层抽样法D. 随机数法 4. 设a,b 为正实数,则“a >b >1”是“log 2a >log 2b >0”的A. 充要条件B. 充分不必要条件C. 必要不充分条件D. 既不充分也不必要条件 5. 下列函数中,最小正周期为π的奇函数是 A. y =sin (2x +2π) B . y =cos (2x +2π) C. y =sin2x +cos2x D. y =sinx +cosx 6. 执行如图所示的程序框图,输出S 的值为A.-2B.2C. -12D.127. 过双曲线2213yx-=的右焦点且与x轴垂直的直线交该双曲线的两条渐近线于A、B两点,则|AB|=A.C. 68. 某食品的保鲜时间y(单位:小时)与储藏温度x(单位:℃)满足函数关系y=e kx+b(e =2.718…为自然对数的底数,k,b为常数)。
若该食品在0℃的保鲜时间是192小时,在22℃的保鲜时间是48小时,则该食品在33℃的保鲜时间是A. 16小时B. 20小时C. 24小时D. 28小时9. 设实数x,y满足2102146x yx yx y+≤⎧⎪+≤⎨⎪+≥⎩,则xy的最大值为A. 252B.492C. 12D. 1410. 设直线l与抛物线y2=4x相交于A,B两点,与圆(x-5)2+y2=r2(r>0)相切于点M,且M为线段AB中点,若这样的直线l恰有4条,则r的取值范围是A. (1,3)B. (1,4)C. (2,3)D. (2,4)第II 卷 (非选择题 共100分)二、填空题:本大题共5小题,每小题5分,共25分。
2015年普通高等学校招生全国统一考试理科数学(四川卷) (2)
2015年普通高等学校招生全国统一考试(四川卷)数学(理工类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷1至2页,第Ⅱ卷3至4页,共4页.满分150分.考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 第Ⅰ卷共10小题.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一个是符合题目要求的. 1.(2015四川,理1)设集合A={x|(x+1)(x-2)<0},集合B={x|1<x<3},则A ∪B=( ) A.{x|-1<x<3} B.{x|-1<x<1} C.{x|1<x<2} D.{x|2<x<3} 答案:A解析:由题意,得A={x|-1<x<2},B={x|1<x<3},所以A ∪B={x|-1<x<3},故选A . 2.(2015四川,理2)设i 是虚数单位,则复数i 3-2i=( )A.-iB.-3iC.iD.3i答案:C解析:i 3-2i=i 2·i -2ii2=-i +2i =i,故选C .3.(2015四川,理3)执行如图所示的程序框图,输出S 的值为( )A.-√32B.√32C.-12D.12答案:D解析:由程序框图,可知当k=5时,循环结束,所以S=sin 5π6=12,故选D .4.(2015四川,理4)下列函数中,最小正周期为π且图象关于原点对称的函数是( )A.y=cos (2x +π2)B.y=sin (2x +π2)C.y=sin2x+cos 2xD.y=sin x+cos x答案:A解析:因为y=cos (2x +π2)=-sin 2x ,故T=2π2=π.又因为-sin (-2x )=sin 2x ,所以函数y=-sin 2x 为奇函数,其图象关于原点对称,故选A .5.(2015四川,理5)过双曲线x 2-y 23=1的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则|AB|=( ) A.4√33B.2√3C.6D.4√3答案:D解析:双曲线x 2-y 23=1的两条渐近线方程为y=±√3x ,右焦点为F (2,0)如图所示.根据题意,由{y =√3x ,x =2,得A (2,2√3).同理可得B (2,-2√3). 所以|AB|=4√3,故选D .6.(2015四川,理6)用数字0,1,2,3,4,5组成没有重复数字的五位数,其中比40 000大的偶数共有( ) A.144个 B.120个 C.96个 D.72个 答案:B解析:当首位数字为4,个位数字为0或2时,满足条件的五位数有C 21A 43个;当首位数字为5,个位数字为0或2或4时,满足条件的五位数有C 31A 43个.故满足条件的五位数共有C 21A 43+C 31A 43=(2+3)A 43=5×4×3×2×1=120个.故选B .7.(2015四川,理7)设四边形ABCD 为平行四边形,|AB ⃗⃗⃗⃗⃗ |=6,|AD ⃗⃗⃗⃗⃗ |=4.若点M ,N 满足BM ⃗⃗⃗⃗⃗⃗ =3MC ⃗⃗⃗⃗⃗⃗ ,DN ⃗⃗⃗⃗⃗⃗ =2NC ⃗⃗⃗⃗⃗ ,则AM ⃗⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗⃗ =( ) A.20 B.15 C.9 D.6 答案:C解析:如图所示,在▱ABCD 中,|AB⃗⃗⃗⃗⃗ |=6,|AD ⃗⃗⃗⃗⃗ |=4.∵AD ⃗⃗⃗⃗⃗ =BC ⃗⃗⃗⃗⃗ ,BM ⃗⃗⃗⃗⃗⃗ =3MC ⃗⃗⃗⃗⃗⃗ ,∴BM⃗⃗⃗⃗⃗⃗ =34AD ⃗⃗⃗⃗⃗ ,CM ⃗⃗⃗⃗⃗⃗ =-14AD ⃗⃗⃗⃗⃗ . 又AB ⃗⃗⃗⃗⃗ =DC ⃗⃗⃗⃗⃗ ,DN ⃗⃗⃗⃗⃗⃗ =2NC ⃗⃗⃗⃗⃗ , ∴NC ⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ .又NM ⃗⃗⃗⃗⃗⃗⃗ =NC ⃗⃗⃗⃗⃗ +CM ⃗⃗⃗⃗⃗⃗ =13AB ⃗⃗⃗⃗⃗ −14AD ,AM⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +BM ⃗⃗⃗⃗⃗⃗ =AB ⃗⃗⃗⃗⃗ +34AD ⃗⃗⃗⃗⃗ , ∴AM ⃗⃗⃗⃗⃗⃗ ·NM ⃗⃗⃗⃗⃗⃗⃗ =(AB ⃗⃗⃗⃗⃗ +34AD ⃗⃗⃗⃗⃗ )·(13AB ⃗⃗⃗⃗⃗ -14AD ⃗⃗⃗⃗⃗ )=13|AB ⃗⃗⃗⃗⃗ |2-14AB ⃗⃗⃗⃗⃗ ·AD ⃗⃗⃗⃗⃗ +34×13AD ⃗⃗⃗⃗⃗ ·AB ⃗⃗⃗⃗⃗ −34×14|AD ⃗⃗⃗⃗⃗ |2 =13|AB ⃗⃗⃗⃗⃗ |2-316|AD ⃗⃗⃗⃗⃗ |2=13×62-316×42=12-3=9.故选C . 8.(2015四川,理8)设a ,b 都是不等于1的正数,则“3a >3b >3”是“log a 3<log b 3”的( ) A.充要条件 B.充分不必要条件 C.必要不充分条件 D.既不充分也不必要条件 答案:B解析:∵3a >3b >3,∴a>b>1.∴log 3a>log 3b>0.∴1log3a<1log 3b,即log a 3<log b 3.∴3a >3b >3是log a 3<log b 3的充分条件.当0<a<1,b>1时,满足log a 3<log b 3,而由3a >3b >3,得a>b>1,所以由log a 3<log b 3不能推出3a >3b >3,所以3a >3b >3不是log a 3<log b 3的必要条件. 所以3a >3b >3是log a 3<log b 3的充分不必要条件,故选B .9.(2015四川,理9)如果函数f (x )=12(m-2)x 2+(n-8)x+1(m ≥0,n ≥0)在区间[12,2]上单调递减,那么mn 的最大值为( )A.16B.18C.25D.812答案:B解析:f'(x )=(m-2)x+(n-8),由于f (x )在[12,2]上单调递减,所以f'(x )≤0在[12,2]上恒成立,即(m-2)x+(n-8)≤0在[12,2]上恒成立, 于是{(m -2)·12+n -8≤0,(m -2)·2+n -8≤0,即{m +2n ≤18,2m +n ≤12.又m ≥0,n ≥0,所以{m +2n ≤18,2m +n ≤12,m ≥0,n ≥0.画出满足上述不等式组的点(m ,n )所对应的平面区域(如图).得B (0,9),C (6,0),由{m +2n =18,2m +n =12,可得A (2,8).当0≤m ≤2时,mn ≤m (18-m 2)=-12m 2+9m=-12(m-9)2+812,当m=2时,mn 取最大值16;当2<m ≤6时,mn ≤m (12-2m )=-2m 2+12m=-2(m-3)2+18,当m=3时,mn 取最大值18.故mn 的最大值为18. 10.(2015四川,理10)设直线l 与抛物线y 2=4x 相交于A ,B 两点,与圆(x-5)2+y 2=r 2(r>0)相切于点M ,且M 为线段AB 的中点.若这样的直线l 恰有4条,则r 的取值范围是( ) A.(1,3) B.(1,4) C.(2,3) D.(2,4) 答案:D解析:如图所示,设A (x 1,y 1),B (x 2,y 2),M (x 0,y 0),则{y 12=4x 1,y 22=4x 2,两式相减,得(y 1+y 2)(y 1-y 2)=4(x 1-x 2).当l 的斜率不存在,即x 1=x 2时,符合条件的直线l 必有两条. 当l 的斜率k 存在,即x 1≠x 2时,有2y 0(y 1-y 2)=4(x 1-x 2),即k=2y 0. 由CM ⊥AB ,得k CM =y 0x 0-5=-y02,即x 0=3.因为点M 在抛物线内部,所以y 02<4x 0=12, 又x 1≠x 2,所以y 1+y 2≠0,即0<y 02<12.因为点M 在圆上,所以(x 0-5)2+y 02=r 2,即r 2=y 02+4.所以4<r 2<16,即2<r<4,故选D .第Ⅱ卷(非选择题 共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷、草稿纸上无效.第Ⅱ卷共11小题.二、填空题:本大题共5小题,每小题5分,共25分.11.(2015四川,理11)在(2x-1)5的展开式中,含x 2的项的系数是 (用数字填写答案). 答案:-40解析:(2x-1)5的展开式的通项为T r+1=C 5r (2x )5-r (-1)r =(-1)r C 5r 25-r x 5-r.根据题意,得5-r=2,解得r=3.所以含x 2项的系数为(-1)3C 5325-3=-22C 52=-40. 12.(2015四川,理12)sin 15°+sin 75°的值是 .答案:√62解析:sin 15°+sin 75°=sin (45°-30°)+sin (45°+30°)=sin 45°cos 30°-cos 45°sin 30°+sin 45°cos 30°+cos 45°sin 30°=2sin 45°cos 30°=2×√22×√32=√62.13.(2015四川,理13)某食品的保鲜时间y (单位:小时)与储藏温度x (单位:℃)满足函数关系y=e kx+b (e =2.718…为自然对数的底数,k ,b 为常数).若该食品在0 ℃的保鲜时间是192小时,在22 ℃的保鲜时间是48小时,则该食品在33 ℃的保鲜时间是 小时. 答案:24解析:由题意,得{192=e b ,48=e 22k+b ,①②②①得e 22k =48192,即(e k )22=14, 所以(e k )11=12.当x=33 ℃时,y=e 33k+b =(e k )33·e b =(e 11k )3·e b =(12)3×192=24(小时).所以该食品在33 ℃的保鲜时间是24小时.14.(2015四川,理14)如图,四边形ABCD 和ADPQ 均为正方形,它们所在的平面互相垂直,动点M 在线段PQ 上,E ,F 分别为AB ,BC 的中点.设异面直线EM 与AF 所成的角为θ,则cos θ的最大值为 . 答案:25解析:以A 为坐标原点,射线AB ,AD ,AQ 分别为x ,y ,z 轴的正半轴,建立如图所示的空间直角坐标系.设正方形ABCD 和ADPQ 的边长为2,则E (1,0,0),F (2,1,0),M (0,y ,2)(0≤y ≤2).所以AF⃗⃗⃗⃗⃗ =(2,1,0),EM ⃗⃗⃗⃗⃗⃗ =(-1,y ,2). 所以AF ⃗⃗⃗⃗⃗ ·EM ⃗⃗⃗⃗⃗⃗ =-2+y ,|AF ⃗⃗⃗⃗⃗ |=√5,|EM ⃗⃗⃗⃗⃗⃗ |=√5+y 2. 所以cos θ=|AF ⃗⃗⃗⃗⃗⃗ ·EM ⃗⃗⃗⃗⃗⃗⃗ ||AF ⃗⃗⃗⃗⃗⃗||EM ⃗⃗⃗⃗⃗⃗⃗ |=√5·√5+y =√5·√5+y .令2-y=t ,则y=2-t ,且t ∈[0,2].所以cos θ=√5·√5+(2-t )2=t√5·9-4t+t .当t=0时,cos θ=0. 当t ≠0时,cos θ=1√5·√9t 2-4t+1=√5·√9(1t -29)+59,由t ∈[0,2],得1t∈[12,+∞),所以√9(1t -29)2+59≥√9×(12-29)2+59=√52.所以cos θ≤25,即cos θ的最大值为25.15.(2015四川,理15)已知函数f (x )=2x ,g (x )=x 2+ax (其中a ∈R ). 对于不相等的实数x 1,x 2,设m=f (x 1)-f (x 2)x 1-x 2,n=g (x 1)-g (x 2)x 1-x 2. 现有如下命题:①对于任意不相等的实数x 1,x 2,都有m>0;②对于任意的a 及任意不相等的实数x 1,x 2,都有n>0; ③对于任意的a ,存在不相等的实数x 1,x 2,使得m=n ; ④对于任意的a ,存在不相等的实数x 1,x 2,使得m=-n. 其中的真命题有 (写出所有真命题的序号). 答案:①④解析:对于①,因为函数f (x )=2x 单调递增,所以m=f (x 1)-f (x 2)x 1-x 2>0,故该命题正确; 对于②,函数g (x )=x 2+ax 的对称轴为x=-a2,故函数在(-∞,-a 2)上单调递减,在(-a 2,+∞)上单调递增. 所以当x 1,x 2∈(-∞,-a 2)时,n=g (x 1)-g (x 2)x 1-x 2<0.所以该命题错误.对于③,若存在不相等的实数x 1,x 2,使得m=n ,即f (x 1)-f (x 2)x 1-x 2=g (x 1)-g (x 2)x 1-x 2, 整理得f (x 1)-g (x 1)=f (x 2)-g (x 2), 设函数h (x )=f (x )-g (x ),则h (x )=f (x )-g (x )=2x -x 2-ax 的图象与平行于x 轴的直线可能有两个交点. h'(x )=2x ln 2-2x-a ,记p (x )=h'(x ),则p'(x )=2x (ln 2)2-2, 令p'(x )=0,解得2x =2(ln2)2,故x=log 22(ln2)2=1-2log 2(ln 2),记为x 0.当x ∈(-∞,x 0)时,p'(x )<0,函数单调递减;当x ∈(x 0,+∞)时,p'(x )>0,函数单调递增,所以p (x )≥p (x 0).显然当p (x 0)≥0时,h'(x )≥p (x 0)≥0,此时函数h (x )在R 上单调,函数h (x )=f (x )-g (x )=2x -x 2-ax 的图象与平行于x 轴的直线只有一个交点,即此时h (x )的图象与平行于x 轴的直线不可能有两个交点.所以该命题错误.对于④,若存在不相等的实数x 1,x 2,使得m=-n ,即f (x 1)-f (x 2)x 1-x 2=-g (x 1)-g (x 2)x 1-x 2,整理得f (x 1)+g (x 1)=f (x 2)+g (x 2),设函数h (x )=f (x )+g (x ),则q (x )=f (x )+g (x )=2x +x 2+ax 的图象与平行于x 轴的直线可能有两个交点.q'(x )=2x ln 2+2x+a ,显然q'(x )在R 上单调,设q'(x )=0的解为t ,则当x ∈(-∞,t )时,q'(x )<0,函数q (x )单调递减,x ∈(t ,+∞)时,q'(x )>0,函数q (x )单调递增.所以函数q (x )=2x +x 2+ax 的图象与平行于x 轴的直线可能有两个交点.所以该命题正确. 综上,正确的命题为①④.三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)(2015四川,理16)设数列{a n }(n=1,2,3,…)的前n 项和S n 满足S n =2a n -a 1,且a 1,a 2+1,a 3成等差数列.(1)求数列{a n }的通项公式;(2)记数列{1a n}的前n 项和为T n ,求使得|T n -1|<11 000成立的n 的最小值.解:(1)由已知S n =2a n -a 1,有a n =S n -S n-1=2a n -2a n-1(n ≥2), 即a n =2a n-1(n ≥2).从而a 2=2a 1,a 3=2a 2=4a 1.又因为a 1,a 2+1,a 3成等差数列, 即a 1+a 3=2(a 2+1).所以a 1+4a 1=2(2a 1+1),解得a 1=2.所以,数列{a n }是首项为2,公比为2的等比数列. 故a n =2n .(2)由(1)得1a n=12n. 所以T n =12+122+…+12n =12[1-(12)n]1-12=1-12n . 由|T n -1|<11 000,得|1-12n -1|<11 000,即2n >1 000.因为29=512<1 000<1 024=210, 所以n ≥10. 于是,使|T n -1|<11 000成立的n 的最小值为10.17.(本小题满分12分)(2015四川,理17)某市A ,B 两所中学的学生组队参加辩论赛,A 中学推荐了3名男生、2名女生,B 中学推荐了3名男生、4名女生,两校所推荐的学生一起参加集训.由于集训后队员水平相当,从参加集训的男生中随机抽取3人、女生中随机抽取3人组成代表队. (1)求A 中学至少有1名学生入选代表队的概率;(2)某场比赛前,从代表队的6名队员中随机抽取4人参赛.设X 表示参赛的男生人数,求X 的分布列和数学期望. 解:(1)由题意知,参加集训的男、女生各有6名.参赛学生全从B 中学抽取(等价于A 中学没有学生入选代表队)的概率为C 33C 43C 63C 63=1100. 因此,A 中学至少有1名学生入选代表队的概率为1-1100=99100. (2)根据题意,X 的可能取值为1,2,3. P (X=1)=C 31C 33C 64=15, P (X=2)=C 32C 32C 64=35, P (X=3)=C 33C 31C 64=15.所以X 的分布列为因此,X 的数学期望为E (X )=1×P (X=1)+2×P (X=2)+3×P (X=3)=1×15+2×35+3×15=2.18.(本小题满分12分)(2015四川,理18)一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC 的中点为M ,GH 的中点为N.(1)请将字母F ,G ,H 标记在正方体相应的顶点处(不需说明理由); (2)证明:直线MN ∥平面BDH ; (3)求二面角A-EG-M 的余弦值.(1)解:点F ,G ,H 的位置如图所示. (2)证明:连接BD ,设O 为BD 的中点.因为M ,N 分别是BC ,GH 的中点,所以OM ∥CD ,且OM=12CD , HN ∥CD ,且HN=12CD.所以OM ∥HN ,OM=HN.所以MNHO 是平行四边形,从而MN ∥OH. 又MN ⊄平面BDH ,OH ⊂平面BDH , 所以MN ∥平面BDH. (3)解法一:连接AC ,过M 作MP ⊥AC 于P. 在正方体ABCD-EFGH 中,AC ∥EG , 所以MP ⊥EG.过P 作PK ⊥EG 于K ,连接KM ,所以EG ⊥平面PKM ,从而KM ⊥EG. 所以∠PKM 是二面角A-EG-M 的平面角. 设AD=2,则CM=1,PK=2.在Rt △CMP 中,PM=CM sin 45°=√22.在Rt △PKM 中,KM=√PK 2+PM 2=3√22. 所以cos ∠PKM=PKKM=2√23.即二面角A-EG-M 的余弦值为2√23.解法二:如图,以D 为坐标原点,分别以DA⃗⃗⃗⃗⃗ ,DC ⃗⃗⃗⃗⃗ ,DH ⃗⃗⃗⃗⃗⃗ 方向为x ,y ,z 轴的正方向,建立空间直角坐标系Dxyz. 设AD=2,则M (1,2,0),G (0,2,2),E (2,0,2),O (1,1,0),所以,GE ⃗⃗⃗⃗⃗ =(2,-2,0),MG ⃗⃗⃗⃗⃗⃗ =(-1,0,2).设平面EGM 的一个法向量为n 1=(x ,y ,z ),由{n 1·GE ⃗⃗⃗⃗⃗ =0,n 1·MG ⃗⃗⃗⃗⃗⃗ =0,得{2x -2y =0,-x +2z =0,取x=2,得n 1=(2,2,1).在正方体ABCD-EFGH 中,DO ⊥平面AEGC ,则可取平面AEG 的一个法向量为n 2=DO⃗⃗⃗⃗⃗⃗ =(1,1,0), 所以cos <n 1,n 2>=n 1·n2|n 1|·|n 2|=√4+4+1·√1+1+0=2√23, 故二面角A-EG-M 的余弦值为2√23.19.(本小题满分12分)(2015四川,理19)如图,A ,B ,C ,D 为平面四边形ABCD 的四个内角. (1)证明:tan A 2=1-cosAsinA ; (2)若A+C=180°,AB=6,BC=3,CD=4,AD=5,求tan A 2+tan B 2+tan C 2+tan D 2的值.(1)证明:tanA2=sin A2cos A2=2sin 2A22sin A 2cos A 2=1-cosAsinA. (2)解:由A+C=180°,得C=180°-A ,D=180°-B.由(1),有tan A 2+tan B 2+tan C 2+tan D2=1-cosA sinA +1-cosB sinB +1-cos (180°-A )sin (180°-A )+1-cos (180°-B )sin (180°-B )=2sinA +2sinB. 连接BD.在△ABD 中,有BD 2=AB 2+AD 2-2AB ·AD cos A ,在△BCD 中,有BD 2=BC 2+CD 2-2BC ·CD cos C ,所以AB 2+AD 2-2AB ·AD cos A=BC 2+CD 2+2BC ·CD cos A ,则cos A=AB 2+AD 2-BC 2-CD 22(AB ·AD+BC ·CD )=62+52-32-422(6×5+3×4)=37. 于是sin A=√1-cos 2A =√1-(37)2=2√107. 连接AC.同理可得cos B=AB 2+BC 2-AD 2-CD 22(AB ·BC+AD ·CD )=62+32-52-422(6×3+5×4)=119, 于是sin B=√1-cos 2B =√1-(119)2=6√1019. 所以,tan A 2+tan B 2+tan C 2+tan D 2=2sinA +2sinB =2√106√10 =4√103.20.(本小题满分13分)(2015四川,理20)如图,椭圆E :x 2a2+y 2b2=1(a>b>0)的离心率是√22,过点P (0,1)的动直线l 与椭圆相交于A ,B 两点.当直线l 平行于x 轴时,直线l 被椭圆E 截得的线段长为2√2. (1)求椭圆E 的方程;(2)在平面直角坐标系xOy 中,是否存在与点P 不同的定点Q ,使得|QA ||QB |=|PA ||PB |恒成立?若存在,求出点Q 的坐标;若不存在,请说明理由.解:(1)由已知,点(√2,1)在椭圆E 上.因此,{ 2a 2+1b 2=1,a 2-b 2=c 2,c a=√22.解得a=2,b=√2. 所以椭圆E 方程为x 24+y 22=1. (2)当直线l 与x 轴平行时,设直线l 与椭圆相交于C ,D 两点. 如果存在定点Q 满足条件,则有|QC ||QD |=|PC ||PD |=1,即|QC|=|QD|. 所以Q 点在y 轴上,可设Q 点的坐标为(0,y 0).当直线l 与x 轴垂直时,设直线l 与椭圆相交于M ,N 两点, 则M ,N 的坐标分别为(0,√2),(0,-√2). 由|QM ||QN |=|PM ||PN |,有0√2||y 0+√2|=√2-√2+1,解得y 0=1,或y 0=2. 所以,若存在不同于点P 的定点Q 满足条件,则Q 点坐标只可能为(0,2). 下面证明:对任意直线l ,均有|QA ||QB |=|PA ||PB |. 当直线l 的斜率不存在时,由上可知,结论成立.当直线l 的斜率存在时,可设直线l 的方程为y=kx+1,A ,B 的坐标分别为(x 1,y 1),(x 2,y 2).联立{x 24+y 22=1,y =kx +1,得(2k 2+1)x 2+4kx-2=0.其判别式Δ=(4k )2+8(2k 2+1)>0, 所以,x 1+x 2=-4k2k 2+1,x 1x 2=-22k 2+1.因此1x 1+1x 2=x 1+x 2x 1x 2=2k. 易知,点B 关于y 轴对称的点B'的坐标为(-x 2,y 2).又k QA =y 1-2x 1=kx 1-1x 1=k-1x 1,k QB'=y 2-2-x 2=kx 2-1-x 2=-k+1x 2=k-1x 1,所以k QA =k QB',即Q ,A ,B'三点共线. 所以|QA ||QB |=|QA ||QB '|=|x 1||x 2|=|PA ||PB |. 故存在与P 不同的定点Q (0,2),使得|QA ||QB |=|PA ||PB |恒成立. 21.(本小题满分14分)(2015四川,理21)已知函数f (x )=-2(x+a )ln x+x 2-2ax-2a 2+a ,其中a>0. (1)设g (x )是f (x )的导函数,讨论g (x )的单调性;(2)证明:存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解. (1)解:由已知,函数f (x )的定义域为(0,+∞),g (x )=f'(x )=2(x-a )-2ln x-2(1+ax),所以g'(x )=2-2x +2ax 2=2(x -12)2+2(a -14)x 2.当0<a<14时,g (x )在区间(0,1-√1-4a 2),(1+√1-4a2,+∞)上单调递增,在区间(1-√1-4a 2,1+√1-4a2)上单调递减;当a ≥14时,g (x )在区间(0,+∞)上单调递增.(2)证明:由f'(x )=2(x-a )-2ln x-2(1+a x )=0,解得a=x -1-lnx1+x -1.令φ(x )=-2(x +x -1-lnx 1+x -1)ln x+x 2-2(x -1-lnx 1+x -1)x-2(x -1-lnx 1+x -1)2+x -1-lnx 1+x -1. 则φ(1)=1>0,φ(e)=-e (e -2)1+e -1-2(e -21+e-1)2<0.故存在x 0∈(1,e),使得φ(x 0)=0. 令a 0=x 0-1-ln x 01+x 0-1,u (x )=x-1-ln x (x ≥1). 由u'(x )=1-1x ≥0知,函数u (x )在区间(1,+∞)上单调递增.所以0=u (1)1+1<u (x 0)1+x 0-1=a 0<u (e )1+e -1=e -21+e -1<1. 即a 0∈(0,1).当a=a 0时,有f'(x 0)=0,f (x 0)=φ(x 0)=0. 由(1)知,f'(x )在区间(1,+∞)上单调递增, 故当x ∈(1,x 0)时,f'(x )<0,从而f (x )>f (x 0)=0; 当x ∈(x 0,+∞)时,f'(x )>0,从而f (x )>f (x 0)=0. 所以,当x ∈(1,+∞)时,f (x )≥0.综上所述,存在a ∈(0,1),使得f (x )≥0在区间(1,+∞)内恒成立,且f (x )=0在区间(1,+∞)内有唯一解.。
2015年普通高等学校招生全国统一考试(湖北卷)数学试题 (理科)解析版
()
A. sgn[g(x)] sgn x
B. sgn[g(x)] sgn x
C. sgn[g(x)] sgn[ f (x)]
D. sgn[g(x)] sgn[ f (x)]
【答案】B
【解析】
试题分析:因为 f (x) 是 R 上的增函数,令 f (x) x ,所以 g(x) (1 a)x ,因为 a 1 ,
x,
y
,记
p1 为事件“
x
y
1 2
”的概率,p2
为事件“ |
x
y
|
1 2
”
的概率,
p3
为事件“
xy
1 2
”的概率,则
(
A. p1 p2 p3
B. p2 p3 p1
【答案】B
) C. p3 p1 p2
D. p3 p2 p1
(1)
(2)
考点:几何概型.
(3)
8.将离心率为 e1 的双曲线 C1 的实半轴长 a 和虚半轴长 b (a b) 同时增加 m (m 0) 个单位长
度,得到离心率为 e2 的双曲线 C2 ,则( )
A.对任意的 a, b , e1 e2
B.当 a b 时, e1 e2 ;当 a b 时, e1 e2
C.对任意的 a, b , e1 e2
D.当 a b 时, e1 e2 ;当 a b 时, e1 e2
【答案】D
3
考点:1.双曲线的性质,2.离心率.
9.已知集合 A {(x, y) x2 y2 1, x, y Z}, B {(x, y) | x | 2 , | y | 2, x, y Z},定义集合
A B {(x1 x2 , y1 y2 ) (x1, y1) A, (x2 , y2 ) B} ,则 A B 中元素的个数为( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015年普通高等学校招生全国统一考试(课程标准卷Ⅰ) 数学(理科) 姓名:________ 日期:_________
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、已知集合{}2|30A x x x =-
,{|B y y ==,则A B 为( )
A.[)0,3
B.()0,3
C. {}0
D.∅
2、用0,1,…,9十个数字,可以组成有重复数字的三位数的个数为( )
A.243
B.252
C.261
D.279 3、已知i 是虚数单位,若
31i i z
+=-,则z 的共轭复数为( ) A.12i - B.24i - C.12i + D.24i +
4、命题:p 实数x 满足12123x ---,:q 实数x 满足222(1)0x x m -+-, (0)m >若p 是q 的必要不充分条件,则实数m 的取值范围( )
A.9m
B.9m <
C.210m -
D.910m
5、如果变量,x y 满足条件22020210x y x y y -+⎧⎪+-⎨⎪-⎩
,则z x y =-的最小值为( )
A.2
B.54
- C.1 D.2- 6、阅读右边的程序框图,运行相应的程序则输出i 的值为( )
A.3
B.4
C.5
D.6
7、如图,已知棱长为1的正方体容器1111ABCD A B C D -,
在棱AB ,1BB 及对角线1BC 的中点各有一个小孔,,E F G ,
若此容器可以任意放置,则该容器可装水的最大容积是( )
A.12
B.78
C.1112
D. 4748
8、已知函数1ƒ()cos cos 22x x x x =+,若将其图像向右平移 (0)ϕϕ>个单位后所得的图像关于原点对称,则ϕ的最小值为( )
A.6
π B.56π C.12π D. 512π 9、函数2sin(2)6y x π=-[](0,)x π∈为增函数的区间是( ) A.0,
3π⎡⎤⎢⎥⎣⎦ B.7,1212ππ⎡⎤⎢⎥⎣⎦ C.5,36ππ⎡⎤⎢⎥⎣⎦ D. 5,6ππ⎡⎤⎢⎥⎣⎦
10、已知双曲线22
221x y a b
-=的焦点到其渐近线的距离等于2,抛物线22y px =的焦点为双曲线的右焦点,双曲线截抛物线的准线所得的线段长为4,则抛物线方程为( )
A.24y x =
B.2y =
C.2y =
D. 28y x =
11、已知椭圆2
2110
x y +=的中心为坐标原点O ,点F 是其右焦点,点A 是其短轴的一个端点,过点F 的直线l 与该椭圆交于M ,N 两点,与OA 所在直线交于点E ,若1EM MF λ=,2EN NF λ=,则1λ+2λ=( )
A.20
B.20-
C.10
D.-10
12、设函数ƒ()x 是定义在(),0-∞上的可导函数,其导函数为ƒ'()x ,且有xf′(x )>x 2+2f (x ),则不等式9f (x +2015)−(x +2015)2f (−3)>0的解集为( )
A.(),2011-∞-
B.(),2018-∞-
C.()2015,0-
D. ()2016,0-
第Ⅱ卷(非选择题 共90分)
二、填空题:本大题共4小题,每小题5分,共20分。
把答案填在题中的横线上。
13、已知22n
x ⎫⎪⎭的展开式中所有的二项式系数之和为1024,则展开式中的所有项的系数和是___________. 14、已知数列{}n a 中,11a =,2n n a n a =-,211n n a a +=+,则12349a a a a ++++=…__________. 15、已知一条双曲线的渐近线方程可以写成34
x y =±
,那么这条双曲线的离心率为__________.
16、在锐角ABC Δ中,角,,A B C 所对边分别为,,a b c ,且tan 21tan C a B b +=,若c =a b +的取值范围 为________.
三、解答题:本大题共6小题,共70分,解答应写出必要的文字说明、证明过程或演算步骤。
17、(本小题满分12分)
已知数列{}n a 满足11a =,131n n a a +=+.
()I 证明{}
12n a +是等比数列,并求{}n a 的通项公式 ()II 证明:1231112
n a a a ++<…+.
18、(本小题满分12分)
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点. (Ⅰ)证明:PB∥平面AEC;
(Ⅱ)设二面角D-AE-C为60°,AP=1,E-ACB的体积.
某电视台举行电视奥运知识大奖赛,比赛分初赛和决赛两部分.为了增加节目的趣味性,初赛采用选手选一题答一题的方式进行,每位选手最多有5次选题答题的机会,选手累计答对3题或答错3题即终止其初赛的比赛,答对3
题者直接进入决赛,答错3题者则被淘汰.已知选手甲答题的正确率为2 3
(Ⅰ)求选手甲可进入决赛的概率;
(Ⅱ)设选手甲在初赛中答题的个数为ξ,试写出ξ的分布列,并求ξ的数学期望
如图,焦点在x 轴的椭圆C:22
21(0)8x y b b
+=>,点G (2,0),点P 在椭圆上,且PG x ⊥轴,连接OP 交直线x=4于点M ,连接MG 交椭圆于A 、B.
()I 若G 为椭圆右焦点,求OM
()II 记直线PA ,PB 的斜率为12,k k ,求12k k +的取值范围
()I 当0x >时,证明:
(1)x 1x ln +x x
<<+ ()II 设0c >,1111n a n c n c n n c =+++++++…+,求证:2121n n c n c ln a ln n c n c +++<<+-+
22.(本小题满分10)选修4—1:几何证明选讲
如图,P 是O 外一点,PA 是切线,A 为切点,割线PBC 与
O 相交于点B ,C ,PC=2PA ,D 为PC 的中点,AD 的延长线交O 于点E.证明:
(Ⅰ)BE=EC ;
(Ⅱ)AD ⋅DE=22PB
23. (本小题满分10)选修4-4:坐标系与参数方程 在直角坐标系xoy 中,以坐标原点为极点,x 轴为极轴建立极坐标系,半圆C 的极坐标方程为2cos ρθ=,
0,2πθ⎡⎤∈⎢⎥⎣⎦
.zxxk (Ⅰ)求C 的参数方程;
(Ⅱ)设点D 在C 上,C 在D 处的切线与直线:2l y =+垂直,根据(Ⅰ)中你得到的参数方程,确定D 的坐标.
24. (本小题满分10)选修4-5:不等式选讲
设函数()f x =1(0)x x a a a
++-> (Ⅰ)证明:()f x ≥2;
(Ⅱ)若()35f <,求a 的取值范围.
选题______。
