高考数学常见题型解法归纳反馈训练第63讲根据频率分布直方图求中位数众数和平均数
利用频率分布直方图计算中位数-频率图中位数计算方法

利用频次分散曲圆图预计中位数之阳早格格创做从下列频次分散曲圆图中预计所有中位数取寡数之战为()元.
问案:7400
怎么样用频次分散曲圆图供圆好,中位数,仄衡数,寡数已知一组数据的频次分散曲圆图如图所示.供寡数、中位数、仄衡数.
如图所示是一般原的频次分散曲圆图,则由图形中的数据,不妨预计寡数取中位数)分别是( )
A.12.5 12.5 B.12.5 13 C.13 12.5 D.13 13
寡数是频次分散曲圆图中最下矩形的底边中面的横坐标,∴中间的一个矩形最下,故10取15的中面是12.5,寡数是12.5
而中位数是把频次分散曲圆图分成二个里积相等部分的仄止于Y轴的曲线横坐标第一个矩形的里积是0.2,第三个矩形的里积是0.3,故将第二个矩形分成3:2即可∴中位数是13故选B.
为了相识某校1000名初中死左眼眼光情况,随机对于50名教死左眼眼光举止了查看,画造了如下统计表战频次分
散曲圆图.
请解问下列问题:(1)补齐统计表战频次分散曲圆图;(2)挖空:正在那个问题中,样原是50名教死左眼眼光,正在那个样原中,眼光的中位数是1,眼光的寡数降正在频次分散曲圆图(从左至左依次是第一、二、三、四、五小组)的第四小组内;(3)如果左眼眼光正在0.6及0.6以下的必须矫正,试预计该校左眼眼光必须矫正的教死约有几人?。
直方图众数、中位数、平均数、回归方程
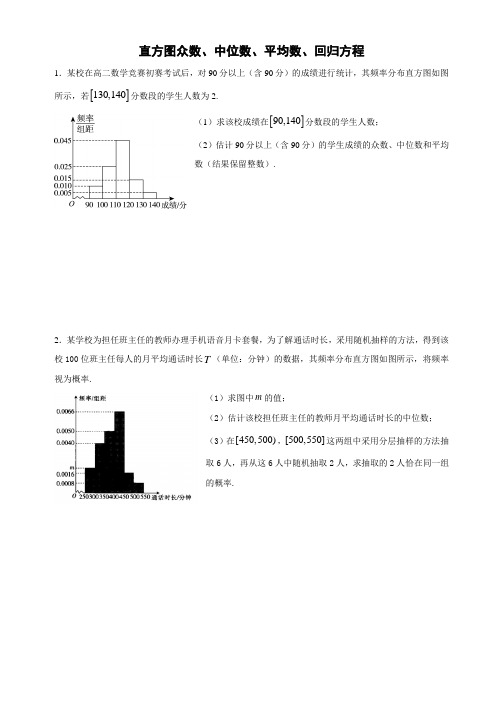
直方图众数、中位数、平均数、回归方程1.某校在高二数学竞赛初赛考试后,对90分以上(含90分)的成绩进行统计,其频率分布直方图如图130,140分数段的学生人数为2.所示,若[]90,140分数段的学生人数;(1)求该校成绩在[](2)估计90分以上(含90分)的学生成绩的众数、中位数和平均数(结果保留整数).2.某学校为担任班主任的教师办理手机语音月卡套餐,为了解通话时长,采用随机抽样的方法,得到该校100位班主任每人的月平均通话时长T(单位:分钟)的数据,其频率分布直方图如图所示,将频率视为概率.(1)求图中m的值;(2)估计该校担任班主任的教师月平均通话时长的中位数;(3)在[450,500),[500,550]这两组中采用分层抽样的方法抽取6人,再从这6人中随机抽取2人,求抽取的2人恰在同一组的概率.3.随机观测生产某种零件的某工厂25名工人的日加工零件数(单位:件),获得数据如下:30,42,41,36,44,40,37,37,25,45,29,43,31,36,49,34,33,43,38,42,32,34,46,39,36.根据上述数据得到样本的频率分布表如右:(1)确定样本频率分布表中n 1,n 2,f 1和f 2的值; (2)根据上述频率分布表,画出样本频率分布直方图;4.某校从参加高一年级期末考试的学生中抽出40名学生,将其成绩(均为整数)分成六段[)40,50,[)50,60…[]90,100后画出如下部分频率分布直方图,观察图形的信息,回答下列问题:(1)求第四小组的频率,并补全频率分布直方图;(2)根据频率分布直方图估计这次考试的及格率(60分及以上为及格)和平均分.5.随着移动互联网的发展,与餐饮美食相关的手机APP 软件层出不穷,现从某市使用A 和B 两款订餐软件的商家中分别随机抽取100个商家,对它们的“平均送达时间”进行统计,得到频率分布直方图如下:(1)使用A 订餐软件的商家中“平均送达时间”不超过30分钟的商家有多少个? (2)试估计该市使用A 款订餐软件的商家的“平均送达时间”的众数及中位数;(3)如果以“平均送达时间”的平均数作为决策依据,从A 和B 两款订餐软件中选择一款订餐,你会选择哪款?6.某市十所重点中学进行高三联考,共有5000名考生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在这次测试中的数学成绩,制成如下频率分布表:(1)根据上面频率分布表,推出①,②,③,④处的数值分别为 , , , ;(2)在所给的坐标系中画出区间[80,150]上的频率分布直方图; (3)根据题中信息估计总体: (i )120分及以上的学生数; (ii )成绩落在[126,150]中的概率.7.为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有900名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频数分布直方图,解答下列问题: (1)填充频率分布表的空格(将答案直接填在表格内); (2)补全频数分布直方图;(3)若成绩在75.5~85的学生为二等奖,问获得二等奖的学生约为多少人?8.为了研究某种细菌在特定条件下随时间变化的繁殖情况,得到如下所示实验数据,若t 与y 线性相关.(1)求y 关于x 的回归直线方程; (2)预测8t =时细菌繁殖的个数.(参考公式:1221ni ii nii x y nx yb xnx==-=-∑∑,ˆˆˆˆˆ,ay bx y bx a =-=+)答案1.(1)40;(2)众数115、中位数113,平均数113. 【解析】 【分析】(1)先求得成绩在[]130,140内的频率,结合[]130,140分数段的人数即可求得成绩在[]90,140分数段的学生人数;(2)根据频率分布直方图中最高矩形,即可得众数;从左至右,将小矩形面积求和,至面积和为0.5时,对应底边的数值即为中位数;将各小矩形面积乘以对应底边的中点值,求和即为平均数的估计值. 【详解】(1)∵[]130,140分数段的频率为0.005100.05⨯=, 又[]130,140分数段的人数为2,∴[]90,140分数段的参赛学生人数为20.0540÷=.(2)根据频率分布直方图,最高小矩形底面中点值为115,所以90分以上(含90分)的学生成绩的众数的估计值为115,从左依次计算各小矩形的面积为0.10.250.450.5++>,因而中位数的估计值为0.50.10.25340101101130.453--⨯+=≈,平均数的估计值为950.11050.251150.451250.151350.05113⨯+⨯+⨯+⨯+⨯=. 【点睛】本题考查了频率分布直方图的简单应用,由频率分布直方图估计众数、中位数与平均数,属于基础题. 2.(1) 0.0020m = (2)390分钟. (3) 715P = 【解析】 【分析】(1)根据频率分布直方图中所有矩形的面积和为1,列出方程,即可求解;(2)设该校担任班主任的教师月平均通话时长的中位数为t ,根据频率分布直方图的中位数的计算方法,即可求解.(3)根据分层抽样,可得在[450,500)内抽取4人,分别记为a b c d ,,,,在[500,550]内抽取2人,记为,e f ,利用古典概型及其概率的计算公式,即可求解. 【详解】(1)依题意,根据频率分布直方图的性质,可得:50(0.00400.00500.00660.00160.0008)1m ⨯+++++=,解得0.0020m =.(2)设该校担任班主任的教师月平均通话时长的中位数为t . 因为前2组的频率之和为(0.00200.0040)500.30.5+⨯=<, 前3组的频率之和为(0.00200.00400.0050)500.550.5++⨯=>, 所以350400t <<,由0.30.0050(350)0.5t +⨯-=,得390t =. 所以该校担任班主任的教师月平均通话时长的中位数为390分钟. (3)由题意,可得在[450,500)内抽取0.0016640.00160.0008⨯=+人,分别记为a b c d ,,,,在[500,550]内抽取2人,记为,e f ,则6人中抽取2人的取法有:{,}a b ,{,}a c ,{,}a d ,{,}a e ,{,}a f ,{,}b c ,{,}b d ,{,}b e ,{,}b f ,{,}c d ,{,}c e ,{,}c f ,{,}d e ,{,}d f ,{,}e f ,共15种等可能的取法.其中抽取的2人恰在同一组的有{,}a b ,{,}a c ,{,}a d ,{,}b c ,{,}b d ,{,}c d ,{,}e f ,共7种取法, 所以从这6人中随机抽取的2人恰在同一组的概率715P =. 【点睛】本题主要考查了频率分布直方图的应用,以及古典概型及其概率的计算,其中解答中熟记频率分布直方图的相关性质,合理利用古典概型及其概率的计算公式,准确计算是解答的关键,着重考查了分析问题和解答问题的能力,属于基础题. 3. 【解】(1)(40,45]的频数n 1=7,频率f 1=0.28;(45,50]的频数n 2=2,频率f 2=0.08; (2)绘制频率分布直方图如图所示:4.(1)0.3,直方图见解析;(2)及格率为0.75,平均分为71【解析】【分析】(1)根据频率分布直方图可得除第四小组外各小组频率,再根据所有频率和为1求第4小组的频率,计算第4小组的对应的矩形的高,补全频率分布直方图;(2)计算60分及以上各小组对应频率和即得及格率,利用组中值计算平均分.【详解】解(1)由频率分布直方图可知第1、2、3、5、6小组的频率分别为:0.1、0.15、0.15、0.25、0.05,所以第4小组的频率为:10.10.150.150.250.050.3-----=.∴在频率分布直方图中第4小组的对应的矩形的高为0.30.0310=,对应图形如图所示:(2)考试的及格率即60分及以上的频率∴及格率为0.150.30.250.050.75+++=又由频率分布直方图有平均分为:0.1450.15550.15650.3750.25850.059571⨯+⨯+⨯+⨯+⨯+⨯=.【点睛】本题考查频率分布直方图及其应用,考查基本分析求解能力,属基础题. 5.(1)40个(2)55;1383(3)B 款 【解析】 【分析】(1)根据频率分布直方图计算出概率即可求出频数.(2)利用频率分布直方图能求出使用A 款订餐软件的商家中“平均送达时间”的众数,中位数. (3)使用B 款订餐软件的商家中“平均送达时间”的平均数为35,小于A 款订餐软件的商家中“平均送达时间”的平均数40,以“平均送达时间”的平均数作为决策依据,从A 和B 两款订餐软件中选择B 款订餐. 【详解】解:(1)使用A 款订餐软件的商家中“平均送达时间”不超过30分钟的商家共有100(0.0060.034)1040⨯+⨯=个.(2)依题意可得,使用A 款订餐软件的商家中“平均送达时间”的众数为55, 由频率分布直方图可判断中位数位于[)30,40设中位数为x ,则()()0.0060.03410300.0120.5x +⨯+-⨯=,解得1383x =. (3)使用款A 订餐软件的商家中“平均送达时间”的平均数为150.06250.34350.12450.04550.4650.0440⨯+⨯++⨯+⨯+⨯=使用B 款订餐软件的商家中“平均送达时间”的平均数为150.04250.2350.56450.14550.04650.023540⨯+⨯+⨯+⨯+⨯+⨯=<所以选B 款订餐软件. 【点睛】本题考查频率分布直方图的应用,考查概率的求法,众数、中位数、平均数的求法,考查运算求解能力,考查数形结合思想,是基础题6.(1)3,0.025,0.100,1;(2)直方图见解析;(3)(i )2125;(ii )117.5;(iii )0.260. 【解析】【分析】(1)根据[110,120)的频数和频率可求③,根据频率之和为1可得④和②,然后可求①;(2)求出各组的频率/组距,作图可得频率分布直方图;(3)(i)根据120分及以上的频率可求120分及以上的学生数;(ii)利用每个区间中点值及频率之积可求平均分;(iii)求出[126,150]之间的频率即可得成绩落在[126,150]中的概率.【详解】(1)由[110,120)之间的频率为0.300,频数为36,所以当频数为12时,频率为0.100,即③处的数值为0.100,;由于频率之和为1,所以④处的数值为1,②处的数值为0.025,频数为3,所以①,②,③,④处的数值分别为:3,0.025,0.100,1.(2)频率分布直方图如图所示(3)(i)120分及以上的学生数为:(0.275+0.100+0.050)×5000=2125;(ii)成绩落在[126,150]中的概率为:40.2750.100.0500.26010P=⨯++=.【点睛】本题主要考查频率分布直方图,利用频率分布直方图求解平均数注意利用区间中点值进行求解,侧重考查数据分析的核心素养.7.【分析】(1)计算第二组的频数为8,第三组的频率为0.20,第四组的频数为:12,频率为:0.24,得到答案. (2)根据表格补全频数分布直方图得到答案.(3)计算成绩在75.5~85的学生频率为0.26,得到答案.【详解】(1)由已知样本容量为50,故第二组的频数为0.16508⨯=,第三组的频率为010500.2=, 第四组的频数为:()5048101612-+++=,频率为:120.2450=, 故频率分布表为:(2)如图:(3)成绩在75.5~80的学生占70.5~80的学生的510,因为成绩在70.5~80的学生频率为0.2,所以成绩在75.5~80的学生频率为0.1.成绩在80.5~85的学生占80.5~90的学生的510,因为成绩在80.5~90的学生频率为0.32,所以成绩在80.5~85的学生频率为0.16所以成绩在75.5~85的学生频率为0.26,由于有900名学生参加了这次竞赛, 所以该校获得二等奖的学生约为0.26900234⨯=(人). 【点睛】本题考查了频数分布直方图,根据样本估计总体,意在考查学生的计算能力和应用能力.。
频率分布直方图中的基本计算问题

所以该样本的中位数为2.02
3.由频率分布直方图估计样本平均数公式:
每个小矩形底边中点的横坐标与对应矩形面积的 乘积之和
平均数
a1
2
b1
•
S1
a2
2
b2
•
S2
a3
2
b3
•
S3...
an
2
bn
•
Sn
(S为区间a, b对应矩形的面积)
0.4
0.04
0.03 0.3
0.2
0.02
0.1
0.01
各小组内频率的大小。
(2)小矩形面积之和为1
(3)频率
频数 样本容量
频数 频率 样本容量
样本容量
频数 频率
1.求某一小矩形的高:利用所有小矩形面积之和为1
2.求众数:最高矩形底边中点的横坐标
3.求平均数:每个小矩形底边中点的横坐标与对应矩形面 积的乘积之和
4.求中位数:线段之比=面积之比(或面积之和为0.5)
O
取一人,估计其上学路上所需
时间超过60分钟的概率。
时间
10 20 30 40 50 60 70 80 90 100 110
O 0.5
1
1.5 2
2.5 3 3.5 4 4.5
月平均用水量(t)
例题分析:月均用水量的众数是2.25t.如图所示:(2+2.5)/2=2.25
2、从频率分布直方图中估计中位数(中位数左边立方图的小矩形 面积为0.5)
频率/组距
0.404.50
0.40 0.30
0.16 0.20 0.08 0.10
5.求样本数据在某一区间内的频数:样本容量X该区间小 矩形的面积总和
频率分布直方图的平均数

频率分布直方图的平均数
频率分布直方图是用来描述一组数据的分布情况的图表。
它将数据的取值范围划分成一些区间,统计每个区间内数据出现的次数,然后将这些次数用纵向的条形图表示出来。
频率分布直方图的平均数是指所有数据的平均数。
如果数据有n个,则平均数计算公式为:
平均数= Σ(数据值× 频率) / Σ频率
其中,Σ(数据值× 频率)表示所有数据值乘以对应的频率的总和,Σ频率表示所有数据的频率的总和。
例如,对于如下的频率分布直方图:
数据值频率
0-10 3
10-20 5
20-30 2
30-40 4
40-50 1
则平均数计算如下:
平均数= (0 × 3 + 10 × 5 + 20 × 2 + 30 × 4 + 40 × 1) / (3 + 5 + 2 + 4 + 1)
= 270 / 15
= 18
频率分布直方图的平均数可以反映出数据的中位数,即大多数数据取值的中间值。
高二数学频率分布直方图练习题

高二数学频率分布直方图练习题在高二数学学习中,频率分布直方图是一个重要的概念和工具。
它能够帮助我们直观地了解数据的分布情况,并能够进行一些有关数据分析的操作。
下面是一些高二数学频率分布直方图练习题,希望能对同学们的学习有所帮助。
1. 一家超市通过调查了解到顾客每天购买的饮料数量,数据如下:2, 3, 2, 4, 1, 2, 4, 2, 3, 2, 1, 3, 2, 1, 2, 4, 2, 3, 2, 1根据以上数据绘制频率分布直方图,并确定众数、中位数、均值。
2. 某班级同学们的体重数据如下:52, 55, 53, 57, 54, 56, 55, 51, 58, 60, 59, 62, 63, 64, 61, 56, 55, 54, 57, 59根据以上数据绘制频率分布直方图,并确定众数、中位数、均值。
3. 某城市某月份的降水量数据如下:20, 15, 18, 22, 17, 19, 23, 16, 21, 20, 15, 20, 19, 23, 20, 18, 16, 22, 19, 17根据以上数据绘制频率分布直方图,并确定众数、中位数、均值。
4. 下面是一组学生在一次月考中的数学成绩数据:90, 85, 78, 92, 88, 79, 81, 85, 86, 90, 84, 88, 92, 89, 77, 82, 84, 87, 91, 83根据以上数据绘制频率分布直方图,并确定众数、中位数、均值。
5. 某工厂生产了一批产品,产品的重量数据如下:2.5, 2.7, 2.8, 2.6, 2.9, 2.7, 2.6, 2.8, 2.7, 2.6, 2.8, 2.7, 2.5, 2.8, 2.6, 2.9根据以上数据绘制频率分布直方图,并确定众数、中位数、均值。
以上是几道关于频率分布直方图的练习题。
通过解决这些题目,我们可以巩固对频率分布直方图的理解和应用,提高数据分析的能力。
在实际问题中,频率分布直方图也可以用来对比不同数据集的分布情况,帮助我们做出更好的决策。
2020版高中数学(理)一轮复习:第11章 第62讲 用样本估计总体

的频率分布直方图,则由图形中的数据,可知其中位数为( B )
A. 12.5B.Fra bibliotek13C. 13.5
D. 14
【解析】 中位数是把频率分布直方图分成两个面积相等部分的平行于纵轴的直
线的横坐标,第一个矩形的面积是 0.2,第二个矩形的面积是 0.5,第三个矩形的面积
是 0.3,故将第二个矩形分成 3∶2 即可,所以中位数是 13.故选 B.
(1)
A. 5
B. 6
C. 7
D. 8
【思维引导】(1)根据茎叶图提供的数据,以及已知的样本平均数计算即得;(2) 依据中位数和众数的概念得出.
【解析】 由题知 177=17×(180+181+170+173+170+x+178+179),解得 x =8,故选 D.
(2)(2017·菏泽模拟)如图(2)所示的茎叶图表示连续多天同一路口同一时段通过车 辆的数目,则这些车辆数的中位数和众数分别是( C )
频率分布直方图估计电子元件的平均寿命为:150×0.1+250×0.15+350×0.45+
450×0.15+550×0.15;④寿命超过 400 h 的频率为 0.3.
A. ①
B. ②
C. ③
D. ④
【解析】 若①正确,则 300~400 对应的频率为 0.45,则 400~500 对应的频率 为 0.15,则②错误;电子元件的平均寿命为 150×0.1+250×0.15+350×0.45+ 450×0.15+550×0.15,则③正确;寿命超过 400 h 的频率为 0.15+0.15=0.3,则④ 正确,故不符合题意.若②正确,则 300~400 对应的频率为 0.4,则①错误;电子元 件的平均寿命为 150×0.1+250×0.15+350×0.4+450×0.2+550×0.15,则③错误; 寿命超过 400 h 的频率为 0.2+0.15=0.35,则④错误,故符合题意.故选 B.
利用频率分布直方图计算中位数知识分享.doc

利用频率分布直方图计算中位数从下列频率分布直方图中估计所有中位数与众数之和为(答案:7400如何用频率分布直方图求方差,屮位数,平均数,众数平均数则是每组频率的中间值乘频数再相加 平均数二4 <3^0,02^7*0.08+11*0 09+17*0 03) =8 48方差二 1 何0848广2十(7-848广2"11-8 48广2斗15-848广2十(19-848汽]二先 3504 中位数就是频率分布直方圏面积的1半所对应的值 即左右面积和为0 5就行了。
设中位数为9杈则? <OJ2+O.08^)=O.5x=OB25所以中位数为9.(]质 k 数就是频率最高的中间值 就是11 您的满意是我维续的动力!)元。
0.0005 t 频率戲距0.0002 0.0001]月收\(元!1000 1500 2000 2500 3090 3500 40000.0004 卜 0.0^03己知一组数据的频率分布直方图如图所示•求众数、中位数、平均数•封仙在换專号布必芳開中,金敷是很•检卜衣芳那諂庭边巧中克極主林的值9 □俭蛙昙血苛卜七方尼的如:刈黑的竹屛蛭「军口业昙笆小萩方葩竝比甲I 点的嵐坐标与对应權牢的舉的和-宙此求岀即h,irffi 单:胸饗军分滞直再13町ML自[Q*atn+6・mO"ILG扁碳而从響零的介界銓& BT护ttffc物册.平场變肖56 « Q. 3*66 *0. 4*?5 «U.】5+盹"0・"肪虫0・占译I *題可用预不和帝頁产89・第看了牢險悔的心皆,中值歎和F垢或•蔚胆劃・簞閉幻应杞毘处帥.申伦鱼塩购釦更*・骨网岸出畠「h•眄如图所示是一样本的频率分布直方图,则由图形屮的数据,可以估计众数与中位数)分别是0.1 0.04jjL ■ ■ ■01 5 10 15 20 数众数是频率分布直方图中最高矩形的底边中点的横坐标,•••中间的一个矩形最高,故10与15的中点是12.5 ,众数是12.5而中位数是把频率分布直方图分成两个面积相等部分的平行于第一个矩形的面积是0・2 ,第三个矩形的面积是0・3 ,故将第二个矩形分成3: 2即可•••中位数是13故选B・为了了解某校1000名初中生右眼视力情况,随机对50名学生右眼视力进行了检查,绘制了如下统计表和频率分布直方图.|视力| 0.1 || 0.2 | 1 0.3 I I 0.4 I| 0.5 || 0.6 || 0.7 || 0.8 ||1人数「II X 1 1 3 || 2|| 3 || 4|| 2 || IA •12.5 12.5B •12.5 13C . 13 12.5 D. 13 13Y轴的直线横坐标请解 答下列问题:(1)补全统计表和频率分布直方图:(2 )填空:在这个问题中,样本是血•名学牛右眼视力,在这个样本中,视力的中血数是1 ,视力的众 数落在频率分布直方图(从左至右依次是第一、二、三、四丄五小组)的第四小组内;(3 )如果右眼视力在0.6及0.6以下的必须娇正,试估计该校右眼视力必须娇正的学生约有多少人?组和第三组的频率,接着得到其他小组的频率,然后利用这些已知条件可以求出观力为 。
2023年高考数学复习----《统计图表》规律方法与典型例题讲解

2023年高考数学复习----《统计图表》规律方法与典型例题讲解【规律方法】1、制作频率分布直方图的步骤.第一步:求极差,决定组数和组距,组距=极差组数第二步:分组,通常对组内数值所在区间取左闭右开区间,最后一组取闭区间;第三步:登记频数,计算频率,列出频率分布表;第四步:画频率分布直方图.2、解决频率分布直方图问题时要抓住3个要点.(1)直方图中各小矩形的面积之和为1;(2)直方图中纵轴表示频率组距,故每组样本的频率为组距⨯频率组距(3)直方图中每组样本的频数为频率⨯总体个数.3、用频率分布直方图估计众数、中位数、平均数的方法.(1)众数为频率分布直方图中最高矩形底边中点的横坐标;(2)中位数为平分频率分布直方图面积且垂直于横轴的直线与横轴交点的横坐标;(3)平均数等于每个小矩形面积与小矩形底边中点横坐标之积的和.【典型例题】例1.(2022·云南昆明·昆明一中模拟预测)为了响应教育部门疫情期间“停课不停学”的号召,某校实施网络授课,为了检验学生上网课的效果,在高三年级进行了一次网络模拟考试,从中抽取了100人的数学成绩,绘制成频率分布直方图(如下图所示),其中数学成绩落在区间[110,120),[120,130),[130,140]的频率之比为4:2:1.(1)根据频率分布直方图求学生成绩在区间[110,120)的频率,并求抽取的这100名同学数学成绩的中位数(2)若将频率视为概率,从全校高三年级学生中随机抽取3个人,记抽取的3人成绩在[100,130)内的学生人数为X ,求X 的分布列与数学期望.【解析】(1)由直方图可知,数学成绩落在区间[70,110)内的频率为(0.0040.0120.0190.030)10+++⨯=0.65,所以数学成绩落在区间[110,140]内的频率为10.650.35−=,因为数学成绩落在区间[110,120),[120,130),[130,140]的频率之比为4:2:1,所以数学成绩落在区间[110,120)的频率为40.35421⨯++0.2=, 数学成绩落在区间[70,100)的频率为(0.0040.0120.019)100.35++⨯=, 所以中位数落在区间[100,110)内,设中位数为x ,则(100)0.0300.50.35x −⨯=−,解得105x =, 所以抽取的这100名同学数学成绩的中位数为105.(2)由(1)知,数学成绩落在区间[100,130)内的频率为0.0310⨯+0.2+20.35421⨯++0.6=,由题意可知,3~(3,)5X B ,X 的所有可能取值为0,1,2,3,033338(0)C ()(1)55125P X ==⋅−=,12333(1)C (1)55P X ==⋅⋅−36125=, 22333(2)C ()(1)55P X ==⋅⋅−54125=,330333(3)C ()(1)55P X ==⋅−27125=,所以X 的分布列为:所以数学期望8365427()0123125125125125E X =⨯+⨯+⨯+⨯95=.例2.(2022·贵州贵阳·贵阳六中校考一模)某校组织1000名学生进行科学探索知识竞赛,成绩分成5组:[)50,60,[)60,70,[)70,80,[)80,90,[]90,100,得到如图所示的频率分布直方图.若图中未知的数据a ,b ,c 成等差数列,成绩落在区间[)60,70内的人数为400.(1)求出直方图中a ,b ,c 的值;(2)估计中位数(精确到0.1)和平均数(同一组中的数据用该组区间的中点值代替); (3)若用频率估计概率,设从这1000人中抽取的6人,得分在区间[]90,100内的学生人数为X ,求X 的数学期望.【解析】(1)依题意可得:4001000100.04a =÷÷=,又a ,b ,c 成等差数列,所以2b a c =+且(0.0050.005)101a b c ++++⨯=,解得:0.02,0.03c b == 所以0.04,0.03,0.02a b c ===.(2)因为(0.0050.04)100.450.5+⨯=<,设中位数为x , 则[70,80)x ∈,所以()()0.0050.0410700.030.5x +⨯+−⨯=,解得:71.7x ≈,即中位数约为71.7,平均数为(550.005650.04750.03850.02950.005)1073⨯+⨯+⨯+⨯+⨯⨯=. (3)由题意可知:得分在区间[]90,100内概率为10.0051020⨯=, 根据条件可知:X 的所有可能值为0,1,2,3,4,5,6,且1(6,)20X ,所以1()60.320E X np ==⨯=.例3.(2022·全国·高三专题练习)为丰富学生课外生活,某市组织了高中生钢笔书法比赛,比赛分两个阶段进行:第一阶段由评委为所有参赛作品评分,并确定优胜者;第二阶段为附加赛,参赛人员由组委会按规则另行确定.数据统计员对第一阶段的分数进行了统计分析,这些分数X 都在[75,100)内,再以5为组距画分数的频率分布直方图(设“Y=频率组距”)时,发现Y 满足:7,15,15019,16,30011,16,1520n Y n k n n ⎧=⎪⎪⎪==⎨⎪⎪−⋅>⎪−⎩,55(1)n N n X n *∈≤<+. (1)试确定n 的所有取值,并求k ;(2)组委会确定:在第一阶段比赛中低于85分的同学无缘获奖也不能参加附加赛;分数在[95,100)内的同学评为一等奖;分数在[90,95)内的同学评为二等奖,但通过附加赛有111的概率提升为一等奖;分数在[85,90)内的同学评为三等奖,但通过附加赛有17的概率提升为二等奖(所有参加附加赛的获奖人员均不降低获奖等级,且附加赛获奖等级在第一阶段获奖等级基础上,最多升高一级).已知学生A 和B 均参加了本次比赛,且学生A 在第一阶段获得二等奖.①求学生B 最终获奖等级不低于学生A 最终获奖等级的概率;②已知学生A 和B 都获奖,记A ,B 两位同学最终获得一等奖的人数为ξ,求ξ的分布列和数学期望.【解析】(1)根据题意,X 在[75,100)内,按5为组距可分成5个小区间, 分别是[75,80),[80,85),[85,90),[90,95),[95,100),因为75100X ≤<,由55(1)n X n ≤<+,n N *∈,所以15,16,17,18,19n =.每个小区间的频率值分别是7,15,30195,1660115,17,18,19320n P Y n k n n ⎧=⎪⎪⎪===⎨⎪⎪−⋅=⎪−⎩由719111511306032k ⎛⎫++−++= ⎪⎝⎭,解得350k =. (2)①由于参赛学生很多,可以把频率视为概率.由(1)知,学生B 的分数属于区间[75,80),[80,85),[85,90),[90,95),[95,100)的概率分别是:730,1960,1460,1160,260.我们用符号ijA (或ijB )表示学生A (或B )在第一轮获奖等级为i ,通过附加赛最终获奖等级为j ,其中(,1,2,3)j i i j ≤=记“学生B 最终获奖等级不低于学生A 的最终获奖等级”为事件W , 则()12122223222()P W P B B B A B A =+++()()()()()()12122223222P B P B P B P A P B P A =+++2111111010141105160601160111160711220=+⋅+⋅⋅+⋅⋅=.②学生A 最终获得一等奖的概率是111A P =,学生B 最终获得一等奖的概率是21112116060272711272796060B P =+⋅=+=,1180(0)1111999P ξ⎛⎫⎛⎫==−−= ⎪⎪⎝⎭⎝⎭,111118(1)1111911999P ξ⎛⎫⎛⎫==⋅−+−⋅=⎪ ⎪⎝⎭⎝⎭, 111(2)11999P ξ==⋅=.所以ξ的分布列为:801812001299999999E ξ=⋅+⋅+⋅=.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第63讲 根据频率分布直方图求中位数众数和平均数
【知识要点】
一、用样本估计总体的两个手段(用样本的频率分布估计总体的分布;用样本的数字特征估计总体的数字
特征),需要从总体中抽取一个质量较高的样本,才能不会产生较大的估计偏差,且样本容量越大,估计
的结果也就越精确,分析数据的一种基本方法是用图将它们画出来,或者用紧凑的表格改变数据的排列方
式,作图可以达到两个目的,一是从数据中提取信息,二是利用图形传递信息.
二、频率分布是指一个样本数据在各个小范围内所占比例的大小.一般是用频率分布直方图反映样本频率
分布.
三、样本的数字特征
众数:就是数据中出现次数最多的那个,比其他的都多,如果几个数据出现的次数都是最多,则它们
都是众数;每个数据都只有一次,那么数据没有众数.所以众数可以不止一个或者没有.
中位数:就是这些数据排列好了以后中间的那个数字,那么如果有偶数个数据,那么就是中间两个数
字的平均数,如果有奇数个数据,则中间那个就是数据的中位数.所以数据的中位数不一定在数据中.
平均数:这个就是把所有数据相加,除以个数,就是数据的平均数.
平均数:
方差:
标准差:
四、茎叶图
茎叶图又称“枝叶图”,它的思路是将数组中的数按位数进行比较,将数的大小基本不变或变化
不大的位作为一个主干(茎),将变化大的位的数作为分枝(叶),列在主干的后面,这样就可以清
楚地看到每个主干后面的几个数,每个数具体是多少.
当数据是两位有效数字时,用中间的数字表示十位数,即第一个有效数字,两边的数字表示个位
数,即第二个有效数字,它的中间部分像植物的茎,两边部分像植物茎上长出的叶子,因此通常把这
样的图叫做茎叶图.
【方法讲评】
题型一 求众数
解题步骤
一般先计算出频率分布直方图中的每个小矩形的面积,找到面积最大的那个矩形,取
该矩形的横边中点对应的数为众数.
【例1】 对某小区100户居民的月均用水量进行统计,得到样本的频率分布直方图如图,则估计此样
本的众数、中位数分别为( )
A. , B., C., D.,
【点评】(1)求频率分布图中的众数,一般先计算出频率分布直方图中的每个小矩形的面积,找到
面积最大的那个矩形,取该矩形的横边中点对应的数为众数.(2)求众数也可以直接找最高矩形的横边的
中点.
【反馈检测1】某学校900名学生在一次百米测试中,成绩全部介于13秒与18秒之间,抽取其中50
个样本,将测试结果按如下方式分成五组:第一组[13,14],第二组[14,15),…,第五组[17,18],
如图是按上述分组方法得到的频率分布直方图.
(1)若成绩小于14秒认为优秀,求该样本在这次百米测试中成绩优秀的人数;
(2)请估计学校900名学生中,成绩属于第四组的人数;
(3)请根据频率分布直方图,求样本数据的众数和中位数.
3 / 7
题型二 求中位数
解题步骤
先计算出每个小矩形的面积,通过解方程找到左边面积为0.5的点P,点P对应的数就
是中位数.
【例2】高二某班50名学生在一次百米测试中,成绩全部都介于13秒到18秒之间,将测试结果按如
下方式分成五组,第一组[13,14),第二组[14,15)…第五组[17,18],如图是按上述分组方法得到的
频率分布直方图.
(1)若成绩大于等于14秒且小于16秒规定为良好,求该班在这次百米测试中成绩为良好的人数.
(2)请根据频率分布直方图,估计样本数据的众数和中位数(精确到0.01).
(3)设表示该班两个学生的百米测试成绩,已知,求事件的概率.
4 / 7
事件由6个基本事件组成.
所以.
【点评】求频率分布直方图中的中位数,一般先计算出每个小矩形的面积,通过解方程找到左边面积
为0.5的点,点对应的数就是中位数.
【反馈检测2】某公路段在某一时刻内监测到的车速频率分布直方图如图所示.
(Ⅰ)求纵坐标中参数的值及第三个小长方形的面积;
(Ⅱ)求车速的众数,中位数的估计值;
(Ⅲ)求平均车速的估计值.
题型三 求平均数
解题步骤
一般利用平均数的公式计算.其中代表第个矩形的横边
的中点对应的数,代表第个矩形的面积.
【例3】 某校从参加考试的学生中抽出60名学生,将其成绩(均为整数)分成六组[40,50),[50,
60) ...[90,100]后画出如下部分频率分布直方图.观察图形的信息,回答下列问题:
(Ⅰ)求成绩落在[70,80)上的频率,并补全这个频率分布直方图;
(Ⅱ) 估计这次考试的及格率(60分及以上为及格)和平均分;
(Ⅲ) 从成绩是70分以上(包括70分)的学生中选两人,求他们在同一分数段的概率.
【解析】(Ⅰ)成绩落在[70,80)上的频率是0.3,频率分布直方图如下图.
(Ⅲ) 成绩是70分以上(包括70分)的学生人数为(0.03+0.025+0.005)×10×60=36
所以所求的概率为
【点评】求频率分布直方图中的平均数,一般利用平均数的公式计算.其中
代表第个矩形的横边的中点对应的数,代表第个矩形的面积.
【反馈检测3】某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间
是:[50,60),[60,70),[70,80),[80,90),[90,100].
(1)求图中的值;
(2)根据频率分布直方图,估计这100名学生语文成绩的平均分;
(3)若这100名学生语文成绩某些分数段的人数()与数学成绩相应分数段的人数()之比如下
表所示,求数学成绩在[50,90)之外的人数.
分数段 [50,60) [60,70) [70,80) [80,90)
x:y 1:1 2:1 3:4 4:5
高中数学常见题型解法归纳及反馈检测第63讲:
根据频率分布直方图求中位数众数和平均数参考答案
【反馈检测1答案】(1)3;(2)288;(3),.
【反馈检测2答案】(1),第三个小长方形的面积为;(2);(3)
.
【反馈检测2详细解析】(Ⅰ)∵所有小长形面积之和为1,∴10+10×3+10×4+10×2=1,
解得=0.01, ∴第三个小长方形的面积为:10×4=10×0.04=0.4.
(Ⅱ)车速的众数==65,车速的中位数是两边直方图的面积相等,
于是得:10×0.01+10×0.03+(﹣60)×0.04=0.5,解得=62.5.
(Ⅲ)平均车速=0.01×10×45+0.03×10×55+0.04×10×65+0.02×10×75=62.
【反馈检测3答案】(1);(2)73;(3)10.
【反馈检测3详细解析】(1)依题意得,,解得
(2)这100名学生语文成绩的平均分为:
(3)数学成绩在[50,60)的人数为:100×0.05=5
数学成绩在[60,70)的人数为:,数学成绩在[70,80)的人数为:.
数学成绩在[80,90)的人数为:
所以数学成绩在[50,90)之外的人数为:
