时序逻辑电路的分析(精)
第6章-时序逻辑电路
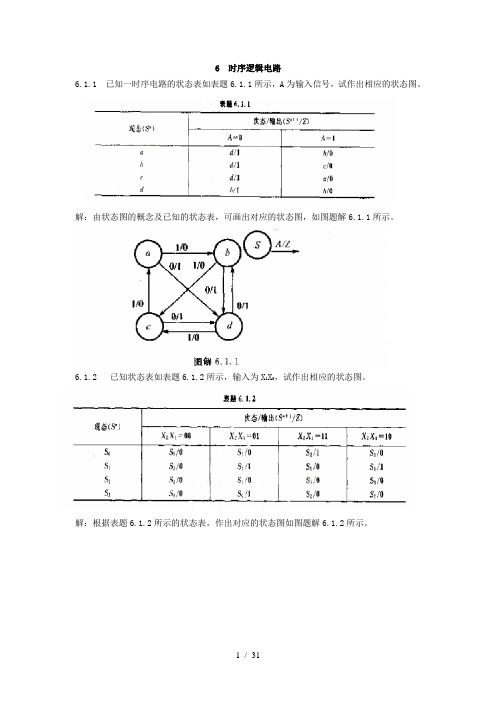
6 时序逻辑电路6.1.1 已知一时序电路的状态表如表题6.1.1所示,A为输入信号,试作出相应的状态图。
解:由状态图的概念及已知的状态表,可画出对应的状态图,如图题解6.1.1所示。
6.1.2已知状态表如表题6.1.2所示,输入为X1X0,试作出相应的状态图。
解:根据表题6.1.2所示的状态表,作出对应的状态图如图题解6.1.2所示。
6.1.3已知状态图如图题6.1.3所示,试列出它的状态表。
解:按图题6.1.3列出的状态表如表题解6.1.3所示。
6.1.5 图题6.1.5所示是某时序电路的状态图,设电路的初始状态为01,当序列A=100110(自左至右输入)时,求该电路输出Z的序列。
解:由图题6.1.5所示的状态图可知,当初态为01,输入信号的序列A=100110时,该时序电路将按图题解6.1.5所示的顺序改变状态,因而对应的输出序列为Z=011010。
6.1.6已知某时序电路的状态表如表题6.1.6所示,输入A,试画出它的状态图。
如果电路的初始状态在b,输入信号A一次是0、1、0、1、1、1、1,试求出其相应的输出。
解:根据表题6.1.6所示的状态表,可直接画出与其对应的状态图,如图题解6.1.6(a)当从初态b开始,依次输入0、1、0、1、1、1、1信号时,该时序电路将按图题解6.1.6(b)所示的顺序改变状态,因而其对应的输出为1、0、1、0、1、0、1。
6.2 同步时序逻辑电路的分析6.2.1 试分析图题6.2.1(a)所示时序电路,画出其状态表和状态图。
设电路的初始状态为0,试画出6.2.1(b)所示波形作用下,Q和Z的波形图。
解:由所给电路图可写出该电路的状态方程和输出方程,分别为1n nQ A QZAQ+=⊕=其状态表如表题解6.2.1所示,状态图如图题解6.2.1(a)所示,Q和Z的波形图如图题解6.2.1(b)所示。
6.2.2 试分析图题6.2.2(a)所示时序电路,画出其状态表和状态图。
同步时序和异步时序电路

5 . 1 异步时序逻辑电路模型(一)异步时序逻辑电路的分类异步时序电路可以从不同的角度进行分类。
1•冲异步时序电路和电平异步时序电路输入信号有脉冲信号和电平信号两种。
所谓电平信号是以电平的高低来表示信号;而脉冲信号是以脉冲的有无来表示信号。
根据输入信号的不同,异步时序电路又分脉脉冲时序电路和电平异步时序电路两种。
如果加到异步时序电路的输入为脉冲,则称为脉冲异步时序电路;反之,如果输入信号为电平.则称为电平异步时序电路。
2.米勒电路和莫尔电路根据输出与输入的不同关系,异步时序电路有米勒电路和莫尔电路两种类型。
假如电路的输出状态不仅与输入状态有关,还与二次状态有关,这样的异步时序电路称米勒电路;如果电路的输出状态仅与二次状态有关,而与输入状态无关,这样的异步时序电路称为莫尔电路。
(二)异步时序逻辑电路的一般结构异步时序电路由组合电路和存储电路两部分组成。
脉冲异步时序电路的存储电路常采用触发器,它可以是时钟控制触发器,也可以是基本R-S触发器。
在使用时钟控制触发器时,触发器不被统一的时钟脉冲同步,每个触发器的时钟端作为一个独立的输入端。
电平异步时序电路的存储电路采用延迟元件,它可以是外加的延迟元件,也可以利用反馈回路的附加延迟。
脉冲异步时序电路与同步时序电路的主要差别是电路的状态改变方式不同,前者在输入信号的控制下改变状态,而后者却在同一时钟脉冲控制下改变状态。
这一差别导致了脉冲异步时序电路和同步时序电路在分析和设计方法上都有若干差别。
一、5 . 2 脉冲异步时序逻辑电路脉冲异步时序电路状态的改变直接依赖于输入脉冲,即每来一个输入脉冲,电路状态发生一次变化。
由于触发器没有公共的时钟脉冲来同步,电路状态的转换将不可预测。
为了使脉冲异步时序电路可靠工作,对脉冲异步时序电路的输入信号应作如下规定:(1)不允许在两个(或两个以上)输入端同时加输入脉冲;(2)第二个输入脉冲的到来,必须在第一个输入脉冲所引起的整个电路的响应完全结束之后。
时序逻辑电路的分析方法

序逻辑电路则把 CP 信号作为一个变量来处理。 3.用已有的数器。当 M 》N 时,用 1 片 M 进制计数器采取反馈清零法或反馈置数法跳过 M-N 个 状态,而得到 N 进制计数器。当 M 《N 时,用多片 M 进制计数器组合起 来,构成 N 进制计数器,各级之间的连接方式可分为并行进位、串行进位、 整体反馈清零和整体反馈置数等几种方式。
时序逻辑电路的分析方法
时序逻辑电路基本分析步骤: 1、写方程式 (1)输出方程。时序逻辑电路的输出逻辑表达式,它通常为现态的 函数。 (2)驱动方程。各触发器输入端的逻辑表达式。 (3)状态方程。将驱动方程代入相应触发器的特性方程中,便得到 该触发器的次态方程。时序逻辑电路的状态方程由各触发器次态的逻辑表达 式组成。 2、列状态转换真值表 将外输入信号和现态作为输入,次态和输出作为输出,列出状态转换 真值表。
3、逻辑功能的说明 根据状态转换真值表来说明电路的逻辑功能。 4、画状态转换图和时序图 状态转换图:电路由现态转换到次态的示意图。 时序图:在时钟脉冲 CP 作用下,各触发器状态变化的波形图。 时序逻辑电路的设计: 1.时序电路的设计是根据要求实现其逻辑功能,先作出原始状态图或 原始状态表,然后进行状态化简(状态合并)和状态编码(状态分配),再求 出所选触发器的驱动方程、时序电路的状态方程和输出方程,最后画出设计 好的逻辑电路图。 2.在设计同步时序逻辑电路时,把 CP 信号作逻辑 1 处理,对异步时
时序逻辑电路的分析方法(新)

J1 = Q3Q2 ; J2 = Q1 ;
J3 = Q2Q1 ;
K1 = 1 K2 = Q3 Q1 K3 = Q2
Q1n+1 = J1Q1+K1Q1 =Q3Q2 Q1 =(Q3+Q2 ) Q1
3) 状态方程 Q2n+1 = J2Q2+K2Q2 =Q2Q1+Q3Q2Q1
Q3n+1 = J3Q3+K3Q3 =Q3Q2Q1+Q3Q2
置入
(Q3Q2Q1Q0 / Y)
(检查自启动情况略)
(二)M >N 的情况(用多片N进制计数器组合构成)
例1 试用两片74LS160构成百进制计数器。
1、连接线路
P.264.
图 5.3.39
Y
C Q3 Q2 Q1 Q0 EP
LD 74LS160(2)ET
RD D3 D2 D1 D0 CP
2、连接方式与特点
Q3 Q2 Q1 Q0 CP0 74LS290 CP1
R01R02 S91S92
三、任意进制计数器的构成方法
用 N 进制计数器,构成 M 进制计数器 (一) M<N 的情况
1、复位法(即清零法) 利用第M+1个状态译码, 使 RD=0 , 不等下一个CP到来,电路立即回到0000状态。 第M+1个状态为暂态,不等稳定,就已消失。 电路输出 M个稳定状态, 是M进制计数器。
5-3-2 计数器
计数器
同步
二进制 十进制 任意进制
异步
二进制 十进制 任意进制
加法,减法,可逆 加法,减法,可逆
加法计数器:随cp的输入,电路递增计数 减法计数器:随cp的输入,电路递减计数 可逆计数器:随cp的输入,电路可增可减计数
第六章 时序电路

二、时序逻辑电路的分类:
按 动 作 特 点 可 分 为
同步时序逻辑电路
所有触发器状态的变化都是在 同一时钟信号操作下同时发生。
异步时序逻辑电路
触发器状态的变化不是同时发生。
按 输 出 特 点 可 分 为
米利型时序逻辑电路(Mealy)
输出不仅取决于存储电路的状态,而且还 决定于电路当前的输入。
Q2 Q1 Q0
/Y
/0 /0 000→001→011 /1↑ ↓/0
CP Q0 010 Q1 Q2 Y
/0 101 /1 (b) 无效循环
100←110←111 /0 /0 (a) 有效循环
有效循环的6个状态分别是0~5这6个十进制数
字的格雷码,并且在时钟脉冲CP的作用下,这6个
状态是按递增规律变化的,即: 000→001→011→111→110→100→000→… 所以这是一个用格雷码表示的六进制同步加法 计数器。当对第6个脉冲计数时,计数器又重新从 000开始计数,并产生输出Y
Q=0时
LED亮
RD Q0 Q1 D1 Q2 D2 D3 Q3 S1
DIR D0 D1D2D3S0 DIL CLK +5V
74LS194
DIR D0
S0 DIL CLK +5V
清0按键 1秒
S1=0,S0=1
CLK 右移控制
本节小结:
寄存器是用来存放二进制数据或代
码的电路,是一种基本时序电路。任何
画状态转换图
Q3Q2Q1 /Y
000
/1 /1 111
/0
001
/0
010
/0
011 /0
数电第六章时序逻辑电路

• 根据简化的状态转换图,对状态进行编码,画出编码形式 的状态图或状态表
• 选择触发器的类型和个数 • 求电路的输出方程及各触发器的驱动方程 • 画逻辑电路图,并检查电路的自启动能力 EWB
典型时序逻辑集成电路
• 寄存器和移位寄存器 – 寄存器 – 移位寄存器 –集成移位寄存器及其应用 • 计数器 – 计数器的定义和分类 – 常用集成计数器 • 74LVC161 • 74HC/HCT390 • 74HC/HCT4017 – 应用 • 计数器的级联 • 组成任意进制计数器 • 组成分频器 • 组成序列信号发生器和脉冲分配器
– 各触发器的特性方程组:Q n1 J Q n KQ n CP
2. 将驱动方程组代入相应触发器的特性方程,求出各触发器 的次态方程,即时序电路的状态方程组
n n FF0:Q0 1 Q 0 CP n n n FF1:Q1 1 A Q0 Q1 CP
同步时序逻辑电路分析举例(例6.2.2C)
分析时序逻辑电路的一般步骤
• 根据给定的时序电路图写方程式 – 各触发器的时钟信号CP的逻辑表达式(同步、异步之分) – 时序电路的输出方程组 – 各触发器的驱动(激励)方程组 • 将驱动方程组代入相应触发器的特性方程,求出各触发器 的次态方程,即时序电路的状态方程组 • 根据状态方程组和输出方程组,列出该时序电路的状态 表,画状态图或时序图 • 判断、总结该时序电路的逻辑功能
• 电路中存在反馈
驱动方程、激励方程: E F2 ( I , Q )
状态方程 : Q n1 F3 ( E , Q n ) • 电路状态由当前输入信号和前一时刻的状态共同决定
• 分为同步时序电路和异步时序电路两大类
什么是组合逻辑电路?
第六章时序逻辑电路
CLK异0为步计计数数输器入与端、同Q步0为计输数出器端比,二,进具制有计如数下器 特点: CLK* 1电为计路数简输单入;端、Q3为输出端,五进制计数器 CLK* 1速与Q度0慢相连;、CLK0为输入端、Q3为输出端,十进制计数器
四、任意进制计数器的构成方法 设已知计数器的进制为N,要构成的任意进制计数
圆圈表示电路的各个状态,箭头表示状态表示的方向, 箭头旁注明转换前的输入变量取值和输出值
三、状态机流程图(SM图) 采用类似于编写计算机程序时使用的程序流程图的形
式,表示在一系列时钟脉冲作用下时序电路状态的流程以及 每个状态下的输入和输出。
四、时序图 在输入信号和时钟脉冲序列作用下,电路状态、
输出状态随时间变化的波形图。
电路在某一给定时刻的输出
取决于该时刻电路由的触输发入器保存 还取决于前一时刻电路的状态
时序电路: 组合电路 + 触发器
电路的状态与时间顺序有关
例:串行加法器电路
利用D触发器 把本位相加后 的进位结果保 存下来
时序电路在结构上的特点:
(1)包含组合电路和存储电路两个组成部分
(2)存储输出状态必须反馈到组合电路的输入端,与输入 信号共同决定组合逻辑电路的输出
串行进位方式以低位片的进位输出信号作为高位片的时 钟输入信号;
并行进位方式以低位片的进位输出信号作为高位片的 工作状态控制信号(计数的使能信号),两片的CLK同时接 计数输入信号。
二、异步计数器
B、减法计数器
二、异步计数器
B、减法计数器
根据T触发器的翻转规律即可画出在一系列CLK0脉冲信号 作用下输出的电压波形。
2、异步十进制计数器
J K端悬空相当于接逻辑1电平 将4位二进制计数器在计数过程中跳过从1010到1111这6个状态。
第5章 时序逻辑电路
第5章 时序逻辑电路 ①时钟方程:
CP0=CP
n Z Q1n Q0
CP1=Q0
②输出方程:
③各触发器的驱动方程:
n D0 Q0
D1 Q1n
(2)将各驱动方程代入D触发器的特性方程,得各触发器的次态 方程:
Q0
Q1
现 0 1 1 0 态 0 1 0 1
n 1
n D0 Q0
(CP由0→1时此式有效) (Q0由0→1时此式有效)
/0
001
/0 010 /0
011 /0
/Y
6) 时序图
CP Q1 Q2 Q3 1 2
/1 110 /0 101 /0 100
7、分析电路的功能 t
0 0
t
1 0
1 0
t
t t
随CP的输入,电路循 环输出七个稳定状态, 所以是七进制计数器。 Y端的输出是此七进制 计数器的进位脉冲。
8、检查自启动 由状态转换表知,此 电路能自启动。
的输入端。
Q0 串行 输出 D0 FF0 1D
∧
并
行 Q1
输 Q2
出 Q3 DI 串行 输入 Q
FF1 Q D1 1D
∧
FF2 Q D2 1D
∧
FF3 Q D3 1D
∧
C1
C1
C1
C1
R CP CR
R
R
R
2 .双向移位寄存器 将右移寄存器和左移寄存器组合起来,并引入一控制 端S便构成既可左移又可右移的双向移位寄存器。
Vcc Q0 Q1 Q2 Q3 CP
16 15 14 13 12 11
S1 S0
10 9
CP
Q 0Q 1 Q 2Q 3 74194 D 0 D 1 D2 D 3 S0 S1 DSL
数字电子技术基础6时序逻辑电路
Q1 Q3 * Q2 * Q1 * Y
输 出 方 程
Y Q2Q3
Q1 Y
CLK Q3 Q2
0 0 0 0 1 1 1 1
0 0 1 1 0 0 1 1
0 1 0 1 0 1 0 1
0 0 0 1 1 1 0 0
0 1 1 0 0 1 0 0
1 0 1 0 1 0 0 0
DI 串行 输入
D Q3 Q D Q2 Q D Q1 D Q0 Q
0 0 0 0 0 0 1 1
0 0 0 0 0 1 0 1 0 缺少111为 0 1 1 初态的情况 1 0 0 1 0 1 1 1 0 1 1 1
0 0 0 0 0 0 1 1
7进制计数器
其中Q3Q2Q1为计数状态,Y为进位
我们可以把状态转换表表示为状态转换图的形式
/Y /0 /0
CLK Q3 0 1 0 0
*
Q
* 3
Q Q Q (Q )
1 2 3 0
C Q0Q3
设初态为0000
作状态转换图
可以看出这是一个异步十进制加法计数器! 3. 检验其能否自动启动 ?
什么叫 “自动启动” ? 四个触发器本应有十六个稳定状态 ,可 上图电路的状态图中只有十个状态。如果由 于某种原因进入了其余的六个状态当中的任 一个状态,若电路能够自动返回到计数链 ( 即有效循环 ) ,人们就称其为能自动启动。
*6.2.3
异步时序逻辑电路的分析方法
例6.2.4 分析图6.2.10所示电路的逻辑功能。
1、写三大方程
驱 动 方 程 状 Q0 Q 0 cp0 Q 0 (cp0 ) * 态 Q1 Q 3 Q 1 (cp1 ) Q 3 Q 1 (Q0 ) * 方 Q2 Q 2 (cp2 ) Q 2 (Q1 ) 程 *
时序逻辑电路
第6章 时序逻辑电路
20
2)列出电路的状态方程
J1 Q3 K1 1 CP CP 1 J 2 K 2 1 CP2 Q1 J 3 Q1Q2 K 3 1 CP3 CP
Q
n 1
J Q KQ
n
n
Q1n 1 Q1 Q3 n 1 Q2 Q2 n 1 Q3 Q1Q2 Q3
第6章 时序逻辑电路 46
(3)减法计数器 由此得出规律,若用T触发
74LS194
CR DSR D0 D1 D2 D3 DSLGND
5V 1
第6章 时序逻辑电路
SB
清零
34
6.3.2 计数器
计数器是数字系统中使用最多的时序电路。
功能:计算输入脉冲CP的个数;
应用:计数、分频、定时、产生脉冲序列及节拍
脉冲,进行数字运算等。
第6章 时序逻辑电路
35
计数器分类 按计数增减分为
40
第6章 时序逻辑电路
3
6.1 概述
时序逻辑电路的特点:
由组合逻辑电路和存储电路构成,它在某一时
刻的输入状态不仅与该时刻输入信号有关,还
与电路原来的输出状态有关。
第6章 时序逻辑电路
4
时序逻辑电路结构上的特点
1、 包含组合电路和存储电路两部分
2、存储电路的输出反馈到组合电路的输入端。
第6章 时序逻辑电路
6.2.1 同步时序逻辑电路分析方法 时序电路的分析:
找出电路的状态和输出状态在输入变量和时钟 信号的作用下的变化规律,即已知逻辑图说明 其逻辑功能。
步骤 : 1、写方程:根据逻辑电路图写出各触发器的
时钟方程、驱动方程、输出方程
