2004年7月新教材高中毕业会考数...(389K)
2004年云南省高中(中专)招生统一考试数学试卷(含答案)

云南省2004年高中(中专)招生统一考试数学试题一、填空题(每小题3分,共1 8分)1. 71-的相反数是 .2.把a 2-b 2+a-b 分解因式结果为 .3.如图,AB∥CD,直线EF 分别交AB 、CD 于点E .F ,FH 平分∠EFD ,若∠1=110°,则∠24.在扇形面积公式S=21 lR 中,已知S 、l ,且S≠0,则R= 5.已知一次函数y=kx+b 的图象经过点(1.3)、(-2,一3),则这个一次函数的解析式为6.延长线段AB 到点c ,使BC=31AB ,D 为AC 的中点,且DC=6cm ,则AB 的长是 cm . 二、选择题(每小题只有一个正确选项.每小题4分,共32分)7.下列计算正确的是 ( )A .43169±= B .(-5)0=-1 C .2 +32 =42 D . (一x)2·x 6=一x 8 8.银原予的直径为0.0003微米,用科学记数法可表示为 ( )A .3×l04微米B .3×10-4微米C .3×l0-3微米D .0.3×10-3微米9.函数y=352-x 中,自变量x 的取值范围是 ( ) A .x>53 B .x≥53 C .x≠-53 D .x≠53 l 0.已知一个等腰三角形的一边长为5,另一边长为7,则这个等腰三角形的周长为( )A .1 2B .1 7C .1 7或1 9D .1 911.用配方法解一元二次方程x 2+8x+7=O ,则方程可变形为 ( )A .(x-4)2=9B .(x+4)2=9C .(x-8)2=16 D.(x+8)2=571 2.已知:如图,在△ABC 中、DE∥BC,AD/DB=1/3,则DE/BC ( )A .1/2B .1/3C .1/4 D.1/51 3.已知:如图,∠CAB=∠DBA ,AC=BD ,则下列结论中不正确的是( )A .BC=ADB .CO=ODC .∠C=∠DD .∠AOB=∠C+∠D14.已知点P(a ,b)是平面直角坐标系中第二象限的点,则化简|a-b|+|b-a|的结果是( )A .-2a+2bB .2aC .2a-2 bD .0三、解答题(本大题共7个小题,共70分)l 5.(6分)解不等式组⎩⎨⎧>+≥465x 42)-3(x -x . 1 6.(7分)已知:关于x 的一元二次方程x 2+(2k-1)x+k 2=0有两个不相等的实数根,且方程的两根之和比两根之积小7,求k 的值.1 7.(6分)某中学初三年级共有学生350名,为了解这些学生在一次考试中的数学成绩状况,随机抽取了20名学生的试卷进行分析,这20名学生的数学成绩(单位:分)分别为:87,85,68,72,58,100,93,97,96,83,51,84,92,62,83,79,74,72,65,79.[注:这份试卷满分为1 00分,60分(含60分)以上者为合格](1)求这20名学生的平均成绩;(2)试估计该校初三年级此次数学考试的合格率为多少?合格人数约为多少?18.(本小题共15分,其中(1)小题5分;(2)小题4分;(3)小题6分)花圃设计、公式证明与问题解决(1)现需要将形如△ABC 的空地(如图l 所示)平均分成面积相等的4块,然后在上面分别种上红、黄、蓝、紫4种不同颜色的花(要求分出的同一块地种相同颜色的花).请设计出一种平分办法,并在划分出的空地上标出红、黄、蓝、紫字样,分别表示所种不同颜色的花,简要说明你的设计方案.(2)已知:如图2,在△ABC 中,∠A 、∠B 、∠C 所对的边分别为a 、b 、c .求证:S △ABC =21absinC=21bcsinA=21casinB . (3)已知:如图3所示,在等边△ABC 中,边BC=10厘米,点P 1、P 2分别从B 、A 同时出发,以1厘米/秒的速度沿线段BA 、AC 移动.问:当移动时间t 为何值时△AP 1P 2的面积最大? 并求出最大面积S 的值.19.(14分)水是重要的资源,节约用水是每个公民应尽的职责.我省某地为加强城市用水管理,增强居民节约用水意识,缓解用水紧张状况,决定在一段时间内将每户居民每月的用水基数(15立方米)进行下调,超过部分的自来水水费将加价收费.具体规定如下:每户居民每月实际用水量不超过10立方米的,按现行水价收费,即每立方米收费1.80元(含污水处理费);用水量1l 至l 5立方米的部分加价50%;16至20立方米的部分加价100%;21立方米以上的部分加价150%.(说明:统计每月用水量时只取整数部分,小数部分留作下月统问:(1)水价调整后污水处理价格每立方米是——元;(2)在表中标有①、②、③的横线上填上所缺的数字,使表完整;(3)小王家水价调整前平均每月水费为25.20元,调整后第一个月的水费为22.90元.求小王家水价调整后每一个月用水量为多少立方米.20.(10分)如图,在平面直角坐标系中,四边形ABCO是正方形,C点的坐标是(4,0).(1)写出A、B两点的坐标;(2)若E是线段BC上一点,且∠AEB=60°,沿AE折叠正方形ABCO,折叠后B点落在平面内F点处.请画出F点并求出它的坐标;(3)若E是直线BC上任意一点,问是否存在这样的E点使正方形ABCO沿AE折叠后,B点恰好落在x轴上的某一点P处?若存在,请写出此时P点和E点的坐标.若不存在,请说明理由.21.(12分)已知:如图,⊙O1的半径r l=6,⊙O2的半径r2=2,且两圆外切,AB和AC是两圆的外公切线,点B、C、D、E分别是切点.(1)求∠BAC的度数;(2)在线段O2A上存在以点O3为圆心、半径为r3的圆.若⊙O3与⊙O2相外切且AB、AC是它们的外公切线,则称⊙O3为点O3圆.请求出点O3圆的半径r3;(3)同上,设在线段O3A上的点O4圆的半径为r4,线段O4A上的点O5圆的半径为r5,…,线段O n—1A上的点O n圆的半径为r n,求r n(用含n的代数式表示r n).云南省2004年高中(中专)招生统一考试数学试题答案一、1.1/7 2.(a-b)(a+b+1) 3.35° 4.2S/l 5.y=2x+l 6.9二、7.C 8.B 9.D 10.C 1 1.B 1 2.C l 3.D 14.A三、l5. 原不等式组的解集为-6<x≤<1l6.解:∵ △=(2k -1)2-4k 2>0 即-4k+1>0∴ k<1/4 ∵ -(2k-1)=k 2-7∴ k 2+2 k-8=0得k 1=-4,k 2=2(舍去)∴ k=-4为所求的值l7.解:(1)20名学生的平均成绩:79(分)(2)样本的合格率=90%∴该校初三年级此次数学考试的合格率约为90%合格人数约为:350 x 90%=315(人)l8.(1)解:如图,分别取△ABC 三边的中点D 、E 、F ,连结DE 、EF 、FD则S △ADF =S △DBE =S △DEF =S △FEC各块空地所种花如图所示(说明:本题解法、答案不唯一,请参照给分)(2)证明:过A 作AD⊥BC 于D则AD=bsin C...S △ABC =21BC ·AD ∴S △ABC =21ab sin c 同理可证:S △ABC =21 acsinB S △ABC =21bc sinA ∴s △AB C =21ab sin c=21 bcsinA=21sinB (3)解:经过t 秒P l 、P 2位置如图所示, △AP l P 2的面积为:.s△AP 1P 2=21AP 1·AP 2sinA=21(10一t)·t·sin60°=一43(t 2一10t) =一43 (t-5)2+4325 (0<t<0) ∴ 当t=5秒时.△AP 1P 2的面积最大且S=4325平方厘米1 9.解:(1)0.50(2)①1.80②3.10③3.25(3) ∵调整后.10立方米水费为18元,l 5立方米水费为30.25元,而调整后小王家第一个月水费为22.90元∴ 小王家水价调整后第一个月用水超过10立方米,但少于15立方米∵超过10立方米的用水量为(22.90一l 8)÷2.45=2(立方米)∴ 小王家水价调整后第一个月用水量为l 2立方米答:小王家水价调整后第一个月用水量为12立方米20.解:(1)A、B两点的坐标分别为A(0,4)、B(4.4)(2)以AE为对称轴作B点的对称点F,则点F为所要画的点连结AF、EF,过F作FM⊥x轴、FH⊥y轴,垂足分别为M、H在Rt△AHF中,AF=AB=4,∠HAF=30°∴HF=AF·sin30°=2AH=AF·cos30°=23∴ OH==4—23∴ F点的坐标为(2,4—23 )(3)存在当E点与C点重合时,正方形沿AE折叠后B点落在x轴上,且B点与O点重合.∴ 此时折叠后B点对应点P的坐标为P(0,0),E点坐标为(4,O)21.解:(1)连结BO1、EO2,过O2作O2F⊥O1B,垂足为F。
2004年普通高等学校招生全国统一考试数学试卷(全国卷Ⅲ.文)

web试卷生成系统谢谢使用一、填空题(每空?分,共?分)1、函数的定义域是.2、用平面α截半径为R的球,如果球心到平面α的距离为,那么截得小圆的面积与球的表面积的比值为.二、选择题(每空?分,共?分)3、函数的最小正周期是A. B.C. D.4、设数列是等差数列,且,是数列的前项和,则A.B. =C.D.5、函数的定义域为A. B. C. D.6、设双曲线的焦点在轴上,两条渐近线为,则该双曲线的离心率A. B. C. D.7、不等式的解集为A. B. C. D.8、在△ABC中,AB=3,BC=,AC=4,则边AC上的高为A.B. C.D.9、设函数,则使得的自变量的取值范围为A. B.C. D.10、将4名教师分配到3所中学任教,每所中学至少1名,则不同的分配方案共有A.12种B.24种C.36种D.48种三、计算题(每空?分,共?分)11、解方程12、某村计划建造一个室内面积为800m2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧内墙各保留1m宽的通道,沿前侧内墙保留3m宽的空地。
当矩形温室的边长各为多少时,蔬菜的种植面积最大?最大种植面积是多少?13、设椭圆的两个焦点是与,且椭圆上存在点P,使得直线PF2与直线PF2垂直.(1)求实数m的取值范围;(2)设L是相应于焦点F2的准线,直线PF2与L相交于点Q. 若,求直线PF2的方程.14、如图,直三棱柱ABC―A1B1C1中,∠ACB=90°,AC=1,CB =,侧棱AA1=1,侧面AA1B1B的两条对角线交点为D,B1C1的中点为M.(Ⅰ)求证CD⊥平面BDM;(Ⅱ)求面B1BD与面CBD所成二面角的大小.15、已知数列的前项和满足.(Ⅰ)写出数列的前三项;(Ⅱ)求数列的通项公式;(Ⅲ)证明:对任意的整数,有 .参考答案一、填空题1、2、二、选择题3、C4、B5、A6、C7、D8、B9、A10、C三、计算题11、解:(无解).所以12、解:设矩形温室的左侧边长为a m,后侧边长为b m ,则蔬菜的种植面积所以当答:当矩形温室的左侧边长为40m,后侧边长为20m时,蔬菜的种植面积最大,最大种植面积为648m2.13、解:(1)由题设有设点P的坐标为(),由,得,化简得①将①与联立,解得由所以m的取值范围是.(2)准线L的方程为设点Q的坐标为,则②将代入②,化简得由题设,得,无解. 将代入②,化简得由题设,得解得m=2.从而得到PF2的方程14、本小题主要考查线面关系和直棱柱等基础知识,同时考查空间想象能力和推理运算能力.解法一:(Ⅰ)如图,连结CA1、AC1、CM,则CA1=.∵CB=CA1=,∴△CBA1为等腰三角形,又知D为其底边A1B的中点,∴CD⊥A1B.∵A1C1=1,C1B1=,∴A1B1=,又BB1=1,∴A1B=2.∵△A1CB为直角三角形,D为A1B的中点,∴CD =A1B=1,CD=CC1.又DM =AC1=,DM=C1M,∴△CDM≌△CC1M, ∠CDM=∠CC1M=90°,即CD⊥DM.因为A1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM. (Ⅱ)设F、G分别为BC、BD的中点,连结B1G、FG、B1F,则FG∥CD,FG =CD.∴FG =,FG⊥BD.由侧面矩形BB1A1A的对角线的交点为D,知BD=B1D =A1B=1,所以△BB1D是边长为1的正三角形,于是B1G⊥BD,B1G =∴∠B1GF是所求二面角的平面角.又B1F2=B1B2+BF2=1+()2=∴cos B1GF ==.即所求二面角的大小为π-arccos解法二:如图,以C为原点建立坐标系.(Ⅱ)B (,0,0),B1(,1,0),A1(0,1,1),D (,,),M (,1,0),=(,,),=(,-1,-1),=(0,,-),则・=0,・=0,∴CD⊥A1B,CD⊥DM.因为A1B、DM为平面BDM内两条相交直线,所以CD⊥平面BDM.(Ⅱ)设BD中点为G,连结B1G,则G(,,),=(-,,), =(-,-,),∴・=0.∴BD⊥B1G. 又CD⊥BD,∴与的夹角θ等于所求二面角的平面角. cosθ==-.所以所求二面角的大小等于π-arccos.15、(Ⅰ)解:由由由(Ⅱ)解:当时,有……所以经验证a1也满足上式,所以(Ⅲ)证明:由通项公式得当且n为奇数时,当为偶数时,当为奇数时,所以对任意整数m>4,有。
2004年高考数学试题(全国4理)及答案

2004年高考试题全国卷Ⅳ理科数学(必修+选修Ⅱ)第I 卷参考公式: 如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么 n 次独立重复试验中恰好发生k 次的概率P n (k)=C k nP k (1-P)n -k一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项是符合题目要求的 1.已知集合},2|{},2,1,0{M a a x x N M ∈===,则集合N M ⋂= ( )A .{0}B .{0,1}C .{1,2}D .{0,2} 2.函数)(2R x e y x ∈=的反函数为( )A .)0(ln 2>=x x yB .)0)(2ln(>=x x yC .)0(ln 21>=x x y D .)0(2ln 21>=x x y 3.过点(-1,3)且垂直于直线032=+-y x 的直线方程为( )A .012=-+y xB .052=-+y xC .052=-+y xD .072=+-y x 4.)1)31(2ii +-=( )A .i +3B .i --3C .i -3D .i +-3 5.不等式03)2(<-+x x x 的解集为( )A .}30,2|{<<-<x x x 或B .}3,22|{><<-x x x 或C .}0,2|{>-<x x x 或D .}3,0|{<<x x x 或6.等差数列}{n a 中,78,24201918321=++-=++a a a a a a ,则此数列前20项和等于 ( )A .160B .180C .200D .220 7.对于直线m 、n 和平面α,下面命题中的真命题是( )A .如果m n m ,,αα⊄⊂、n 是异面直线,那么α//n ;B .如果m n m ,,αα⊄⊂、n 是异面直线,那么α与n 相交C .如果m n m ,//,αα⊂、n 共面,那么n m //;D .如果m n m ,//,//αα、n 共面,那么n m //球的表面积公式S=42R π其中R 表示球的半径, 球的体积公式V=334R π其中R 表示球的半径8.已知椭圆的中心在原点,离心率21=e ,且它的一个焦点与抛物线x y 42-=的焦点重合, 则此椭圆方程为( )A .13422=+y x B .16822=+y x C .1222=+y x D .1422=+y x 9.从5位男教师和4位女教师中选出3位教师,派到3个班担任班主任(每班1位班主任),要求这3位班主任中男、女教师都要有,则不同的选派方案共有( )A .210种B .420种C .630种D .840种10.已知球的表面积为20π,球面上有A 、B 、C 三点.如果AB=AC=2,BC=32,则球心 到平面ABC 的距离为( )A .1B .2C .3D .211.△ABC 中,a 、b 、c 分别为∠A 、∠B 、∠C 的对边.如果a 、b 、c 成等差数列,∠B=30°,△ABC 的面积为23,那么b = ( )A .231+ B .31+C .232+ D .32+12.设函数))((R x x f ∈为奇函数,),2()()2(,21)1(f x f x f f +=+=则=)5(f ( )A .0B .1C .25 D .5第Ⅱ卷二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 13.8)1(xx -展开式中5x 的系数为 .14.向量a 、b 满足(a -b )·(2a +b )=-4,且|a |=2,|b |=4,则a 与b夹角的余弦值等于 .15.函数)(2cos 21cos )(R x x x x f ∈-=的最大值等于 . 16.设y x ,满足约束条件:⎪⎩⎪⎨⎧≥≤≤+,0,,1y x y y x 则y x z +=2的最大值是 .三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)C已知α为第二象限角,且 sin α=,415求12cos 2sin )4sin(+++ααπα的值. 18.(本小题满分12分)求函数241)1ln()(x x x f -+=在[0,2]上的最大值和最小值. 19.(本小题满分12分) 某同学参加科普知识竞赛,需回答三个问题.竞赛规则规定:每题回答正确得100分,回答不正确得-100分.假设这名同学每题回答正确的概率均为0.8,且各题回答正确与否相互之间没有影响. (Ⅰ)求这名同学回答这三个问题的总得分ξ的概率分布和数学期望; (Ⅱ)求这名同学总得分不为负分(即ξ≥0)的概率. 20.(本小题满分12分)如图,四棱锥P —ABCD 中,底面ABCD 为矩形,AB=8,AD=43,侧面PAD 为等边三角形,并且与底面所成二面角为60°.(Ⅰ)求四棱锥P —ABCD 的体积; (Ⅱ)证明PA ⊥BD. 21.(本小题满分12分)双曲线)0,1(12222>>=-b a by a x 的焦点距为2c ,直线l 过点(a ,0)和(0,b ),且点(1,0)到直线l 的距离与点(-1,0)到直线l 的距离之和.54c s ≥求双曲线的离心率e 的取值范围. 22.(本小题满分14分)已知函数0)(),sin (cos )(='+=-x f x x e x f x将满足的所有正数x 从小到大排成数列}.{n x(Ⅰ)证明数列{}{n x f }为等比数列;(Ⅱ)记n S 是数列{}{n n x f x }的前n 项和,求.lim 21nS S S nn +++∞→2004年高考试题全国卷4理科数学(必修+选修Ⅱ)参考答案一、选择题1—12 D C A D A B C A B A B C二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 13.28 14.21-15.4316.2三、解答题17.本小题主要考查同角三角函数的基本关系式,二倍角公式以及三角函数式的恒等变形等 基础知识和基本技能.满分12分.解:αααααααπα2cos 2cos sin 2)cos (sin 2212cos 2sin )4sin(++=+++.)cos (sin cos 4)cos (sin 2ααααα++= 当α为第二象限角,且415sin =α时41cos ,0cos sin -=≠+ααα,所以12cos 2sin )4sin(+++ααπα=.2cos 42-=α18.本小题主要考查函数的导数计算,利用导数讨论函数的性质,判断函数的最大值、最小 值以及综合运算能力.满分12分. 解:,2111)(x x x f -+=' 令,02111=-+x x 化简为,022=-+x x 解得.1),(221=-=x x 舍去 当)(,0)(,10x f x f x >'<≤时单调增加; 当)(,0)(,21x f x f x <'≤<时单调减少. 所以412ln )1(-=f 为函数)(x f 的极大值. 又因为 ),2()1(,013ln )2(,0)0(f f f f >>-==所以 0)0(=f 为函数)(x f 在[0,2]上的最小值,412ln )1(-=f 为函数)(x f图2Cy图1在[0,2]上的最大值.19.本小题主要考查离散型随机变量的分布列、数学期望等概念,以及运用概率统计知识解 决实际问题的能力.满分12分. 解:(Ⅰ)ξ的可能值为-300,-100,100,300.P (ξ=-300)=0.23=0.008, P (ξ=-100)=3×0.22×0.8=0.096, P (ξ=100)=3×0.2×0.82=0.384, P (ξ=300)=0.83=0.512, 所以ξ的概率分布为根据ξ的概率分布,可得ξ的期望E ξ=(-300)×0.08+(-100)×0.096+100×0.384+300×0.512=180.(Ⅱ)这名同学总得分不为负分的概率为P (ξ≥0)=0.384+0.512=0.896.20.本小题主要考查棱锥的体积、二面角、异面直线所成的角等知识和空间想象能力、分析 问题能力.满分12分. 解:(Ⅰ)如图1,取AD 的中点E ,连结PE ,则PE ⊥AD.作PO ⊥平面在ABCD ,垂足为O ,连结OE. 根据三垂线定理的逆定理得OE ⊥AD , 所以∠PEO 为侧面PAD 与底面所成的二面角的平面角, 由已知条件可知∠PEO=60°,PE=6, 所以PO=33,四棱锥P —ABCD 的体积 V P —ABCD =.963334831=⨯⨯⨯ (Ⅱ)解法一:如图1,以O 为原点建立空间直角坐标系.通过计算可得P (0,0,33),A (23,-3,0),B (23,5,0),D (-23,-3,0) 所以).0,8,34(),33,3,32(--=--= 因为,002424=++-=⋅BD PA 所以PA ⊥BD.解法二:如图2,连结AO ,延长AO 交BD 于点F.通过计算可得EO=3,AE=23知AD=43,AB=8,得.ABADAE EO = 所以 Rt △AEO ∽Rt △BAD. 得∠EAO=∠ABD.所以∠EAO+∠ADF=90° 所以 AF ⊥BD.因为 直线AF 为直线PA 在平面ABCD 内的身影,所以PA ⊥BD.21.本小题主要考查点到直线距离公式,双曲线的基本性质以及综合运算能力.满分12分. 解:直线l 的方程为1=+bya x ,即 .0=-+ab ay bx 由点到直线的距离公式,且1>a ,得到点(1,0)到直线l 的距离221)1(ba ab d +-=,同理得到点(-1,0)到直线l 的距离222)1(ba ab d ++=.222221cabb a ab d d s =+=+= 由,542,54c c ab c s ≥≥得 即 .25222c a c a ≥- 于是得 .025254,2152422≤+-≥-e e e e 即解不等式,得.5452≤≤e 由于,01>>e 所以e 的取值范围是.525≤≤e 22.本小题主要考查函数的导数,三角函数的性质,等差数列与等比数列的概念和性质,以及综合运用的能力.满分14分. (Ⅰ)证明:.sin 2)cos sin ()sin (cos )(x ex x e x x e x f xx x ----=+-++-='由,0)(='x f 得.0sin 2=--x ex解出n n x ,π=为整数,从而,3,2,1,==n n x n π .)1()(πn n n e x f --=.)()(1π-+-=e x f x f n n所以数列)}({n x f 是公比π--=eq 的等比数列,且首项.)(1q x f =(Ⅱ)解:)()()(2211n n n x f x x f x x f x S +++= ),21(1-+++=n nqq q π),11()21(),2(122n nnn n n n n nq qq q nq qq q qS S nq q q q qS ---=-+++=-+++=-πππ 而).11(1n nn nq qq q q S ----=πnS S S n+++ 21.)1()1()1(2)1()11()1(11)1()1()21()1()1()1()1(2232222222121222q q q q n q q qnq q q q n q q q q n q q q nq q q n q qq q n q q qn nnn n n n -+----=----------=+++--+++---=+--πππππππππ因为0lim .1||=<=∞→-n n q eq π,所以.)1()1(lim 2221+-=-=+++∞→ππππe e q q n S S S n n。
澳门(新版)2024高考数学人教版考试(综合卷)完整试卷

澳门(新版)2024高考数学人教版考试(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题椭圆与双曲线焦点相同,、分别为左焦点和右焦点,椭圆与双曲线在第一象限交点为,且,则当这两条曲线的离心率之积为时,双曲线的渐近线斜率是A.B.C.D.第(2)题函数的图像大致为()A.B.C.D.第(3)题口袋中共有2个白球2个黑球,从中随机取出两个球,则两个球颜色不同的概率为()A.B.C.D.第(4)题设集合,则()A.B.C.D.第(5)题班级举行知识竞猜闯关活动,设置了三个问题.答题者可自行决定答三题顺序.甲有的可能答对问题,的可能答对问题,的可能答对问题.记答题者连续答对两题的概率为,要使得最大,他应该先回答()A.问题B.问题C.问题和都可以D.问题第(6)题函数的反函数()A.B.C.D.第(7)题已知集合,,则的子集个数为()A.1B.2C.4D.8第(8)题已知集合,,,则()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题在的展开式中()A.二项式系数之和为B.第项的系数最大C.所有项系数之和为D.不含常数项第(2)题以下条件能够判断平面与平面平行的是()A.平面内有两条直线与平面平行B.两不同平面,平行于同一个平面C.平面内的任意一条直线与平面无公共点D.夹在平面与平面间的两条平行线段相等第(3)题十七世纪法国数学家费马在《平面与立体轨迹引论》中证明,方程表示椭圆,费马所依据的是椭圆的重要性质:若从椭圆上任意一点P(异于A,B两点)向长轴AB引垂线,垂足为Q,记.下列说法正确的是()A.M的值与Р点在椭圆上的位置有关B.M的值与Р点在椭圆上的位置无关C.M的值越大,椭圆的离心率越大D.M的值越大,椭圆的离心率越小三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题设点,若直线关于对称的直线与圆有公共点,则a的取值范围是________.第(2)题将指定的6名学生随机分配到3个不同的校办公室打扫卫生,要求每个办公室分配2人,则恰好甲、乙两人打扫同一个办公室的概率为______.第(3)题已知,函数,若存在,使得,则实数的最大值是____.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题在平面直角坐标系中,已知椭圆:的左、右焦点分别为,,为椭圆上一点,线段与圆相切于该线段的中点,且的面积为2.(Ⅰ)求椭圆的方程;(Ⅱ)过点的直线与椭圆交于,两点,且,求的面积.第(2)题已知函数,曲线在点处的切线与直线垂直(其中为自然对数的底数).(I)求的解析式及单调递减区间;(II)是否存在常数,使得对于定义域内的任意恒成立?若存在,求出的值;若不存在,请说明理由.第(3)题设函数.已知曲线在点处的切线与直线垂直.(1)求的值;(2)求函数的极值点;(3)若对于任意,总存在,使得成立,求实数的取值范围.第(4)题国际比赛赛制常见的有两种,一种是单败制,一种是双败制.单败制即每场比赛的失败者直接淘汰,常见的有等等.表示双方进行一局比赛,获胜者晋级.表示双方最多进行三局比赛,若连胜两局,则直接晋级;若前两局两人各胜一局,则需要进行第三局决胜负.现在四人进行乒乓球比赛,比赛赛制采用单败制,A与B一组,C与D一组,第一轮两组分别进行,胜者晋级,败者淘汰;第二轮由上轮的胜者进行,胜者为冠军.已知A与比赛,A的胜率分别为;B与比赛,B的胜率分别;C与D比赛,C的胜率为.任意两局比赛之间均相互独立.(1)在C进入第二轮的前提下,求A最终获得冠军的概率;(2)记A参加比赛获胜的局数为X,求X的分布列与数学期望.第(5)题“熵”常用来判断系统中信息含量的多少,也用来判断概率分布中随机变量的不确定性大小,一般熵越大表示随机变量的不确定性越明显.定义:随机变量对应取值的概率为,其单位为bit的熵为,且.(当,规定.)(1)若抛掷一枚硬币1次,正面向上的概率为,正面向上的次数为,分别比较与时对应的大小,并根据你的理解说明结论的实际含义;(2)若拋掷一枚质地均匀的硬币次,设表示正面向上的总次数,表示第次反面向上的次数(0或1).表示正面向上次且第次反面向上次的概率,如时,.对于两个离散的随机变量,其单位为bit的联合熵记为,且.(ⅰ)当时,求的值;(ⅱ)求证:.。
2004年上海市中等学校高中阶段招生文化考试数学试卷

G图1E2004年上海市中等学校高中阶段招生文化考试数学试卷(满分120分,考试时间120分钟)一、 填空题:(本大题共14题,每题2分,共28分) 1.计算:(2)(2)__________a b a b -+=.2.不等式组230320x x -<⎧⎨+>⎩的整数解是______________.3.函数y =__________________. 41x =-的根是________________. 5.用换元法解22114x x x x +++=,可设1y x x=+,则原方程可化为关于y 的方程是______________.6.一个射箭运动员连续射靶5次,所得的环数分别是8,6,10,7,9,则这个运动员所得环数的标准差为__________. 7.已知0a b <<,则点A (,)a b b -在第________象限. 8.正六边形是轴对称图形,它有_______条对称轴.9.在△ABC 中,点D 、E 分别在边AB 、AC 上,DE ∥BC ,AD=1,BD =2,:ADE ABC S S ∆∆=__________.10.在△ABC 中,∠A =90°,设∠B =θ,AC =b ,则AB =______(用b 和θ的三角比表示). 11.某山路坡面坡度i =沿此山路向上前进200米,升高了__________米. 12.在△ABC 中,点G 是重心,若BC 边上的高为6,则点G 到BC 的距离为______________.13.直角三角形的两条边长分别为6和8,那么这个三角形的外接圆的半径等于__________. 14.如图1,边长为3的正方形ABCD 绕点C 按顺时针方向旋转30°后得到的正方形EFCG ,EF 交AD 与点H ,那么DH 的长为___________. 二、 多项选择题:(本大题共4题,每题3分,共12分)【每题列出的四个答案中,至少有一个是正确的,把所有正确答案的代号填入括号内,错选或不选得0分,否则每漏选一个扣一分,直至扣完为止】15.下列运算,计算结果正确的是( )(A )437a a a =;(B )632a a a ÷=;(C )325()a a =;(D )333()a b a b =.16.如图2,在△ABC 中,AB=AC ,∠A =36°,BD 平分∠ABC ,DE ∥BC , 那么在下列三角形中,与相似的三角形是( )(A ) △DBE ; (B ) △ADE ; (C ) △ABD ; (D ) △BDC . 17.下列命题中,正确的是…………………………( ) (A )一个点到圆心的距离大于这个圆的半径,这个点在圆外; (B )一条直线垂直于圆的半径,这条直线一定是圆的切线;(C )两个圆的圆心距等于它们的半径之和,这两个圆有三条公切线;(D )圆心到一条直线的距离小于这个圆的半径,这条直线与圆有两个交点. 18.在函数(0)ky k x=>的图像上有三点111(,)A x y 、222(,)A x y 、333(,)A x y ,已知1230x x x <<<,则下列各式中,正确的是…………………………( )(A ) 130y y <<;(B ) 310y y <<;(C ) 213y y y <<;(D ) 312y y y <<. 三、(本大题共4题,每题7分,共28分) 19-20.关于x 的一元二次方程2(31)210mx m x m --+-=,其根的判别式的值为1,求m 的值及该方程的根.21.如图3,等腰梯形ABCD 中,AD ∥BC ,∠DBC =45°,翻折梯形ABCD ,使点B 重合于点D ,折痕分别交AB 、BC 于点F 、E .若AD=2,BC =8,求:(1)BE 的长; (2)∠CDE 的正切值.22.某区从参加数学质量检测的8000名学生中,随机抽取了部分学生的成绩作为样本,为了节省时间,先将样本分成甲、乙两组,分别进行分析,得表一;随后汇总成样本数据,得到部分结果,如表二.请根据表一、表二所示的信息回答下列问题:(1)样本中,学生的数学成绩的平均分数约为_________分(结果精确到0.1分); (2)样本中,数学成绩在[)84,96分数段的频数________,等第为A 的人数占抽样学生总数的百分比为_________,中位数所在的分数段为______________;(3)估计这8000名学生成绩的平均分数约为__________分(结果精确到0.1分). 四、(本大题共4题,每题10分,共40分) 23.在平面直角坐标系中,点O 是坐标原点,二次函数)4()5(2+--+=k x k x y 的图像交x 轴于A )0,(1x 、B )0,(2x ,且8)1)(1(21-=++x x .(1)求二次函数的解析式; (2)将上述二次函数的图像沿x 轴向右平移2个单位,设平移后的图像与y 轴的交点为C ,顶点为P ,求△POC 的面积.图424.如图4,在△ABC 中,∠BAC =90°,延长BA 到点D ,使AD =21AB ,点E 、F 分别为边BC 、AC 的中点.(1)求证:DF=BE ;(2)过点A 作AG ∥BC ,交DF 于点G ,求证:25.为加强防汛工作,市工程队准备对苏州河一段长为2240米的河堤进行加固.由于采用新的加固模式,现在计划每天加固的长度比原计划增加了20米,因而完成此段加固工程所需天数将比原计划缩短2天.为进一步缩短该段加固工程的时间,如果要求每天加固224米,那么在现在计划的基础上,每天加固的长度还要再增加多少米?A B C图526.在△ABC 中,∠BAC =90°,AB=AC=22,⊙A 的半径为1,如图5所示.若点O 在BC 上运动(与点B 、C 不重合),设BO =x ,△AOC 的面积为y (1)求关于的函数解析式,并写出函数的定义域;(2)以点O 为圆心,BO 长为半径作⊙O ,求当⊙O 与⊙A 相切时,△AOC 的面积.如图6,在平面直角坐标系中,O 为坐标原点,A 点的坐标为(1,0),点B 在x 轴上,且在点A 的右侧,AB=OA ,过点A 和B 作x 轴的垂线,分别交二次函数2x y =的图像于点C 和D ,直线OC 交BD 于点M ,直线CD 交y 轴于点H ,记点C 、D 的的横坐标分别为C x 、D x ,点H 的纵坐标为H y .五、(本大题只有1题,满分12分,(1)小题满分6分,(2)(3)小题满分均为3分)27.数学课上,老师出示图6和下面框中的条件.同学发现两个结论:①3:2:A BM C =梯形S S CMD ∆ ②数值相等关系:H D C y x x -=∙ (1)请你验证结论①和结论②成立;(2)请你研究:如果上述框中的条件“A 的坐标(1,0)”改为“A 的坐标(t ,0) (t>0)”,其他条件不变,结论①是否仍成立?(请说明理由)(3)进一步研究:如果上述框中的条件“A 的坐标(1,0)”改为“A 的坐标(t ,0) (t>0)”,又将条件“2x y =”改为“)0(2>=a ax y ”, 其他条件不变,那么C x 、D x 与H y 有怎样的数值关系?写出结果并说明由)1MO DCBA y。
2004年河南省高级中等学校招生统一考试数学试卷(含课改区)
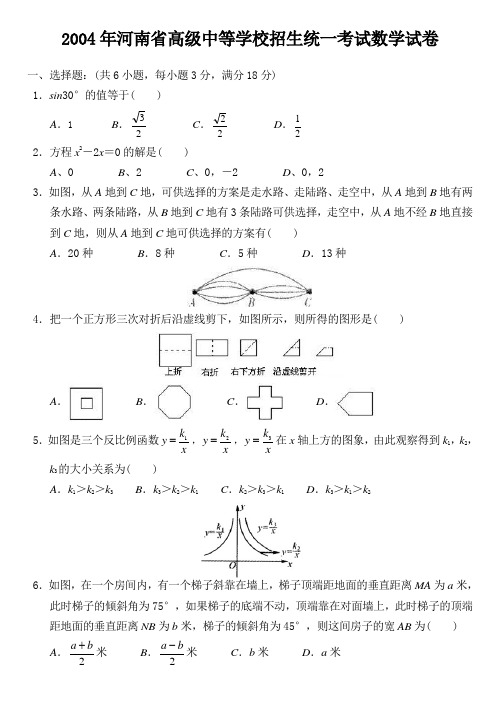
2004年河南省高级中等学校招生统一考试数学试卷一、选择题:(共6小题,每小题3分,满分18分) 1.sin 30°的值等于( ) A .1 B .23C .22 D .212.方程x 2-2x =0的解是( )A 、0B 、2C 、0,-2D 、0,23.如图,从A 地到C 地,可供选择的方案是走水路、走陆路、走空中,从A 地到B 地有两条水路、两条陆路,从B 地到C 地有3条陆路可供选择,走空中,从A 地不经B 地直接到C 地,则从A 地到C 地可供选择的方案有( )A .20种B .8种C .5种D .13种4.把一个正方形三次对折后沿虚线剪下,如图所示,则所得的图形是( )A .B .C .D .5.如图是三个反比例函数x k y 1=,x k y 2=,xky 3=在x 轴上方的图象,由此观察得到k 1,k 2,k 3的大小关系为( )A .k 1>k 2>k 3B .k 3>k 2>k 1C .k 2>k 3>k 1D .k 3>k 1>k 26.如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA 为a 米,此时梯子的倾斜角为75°,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距地面的垂直距离NB 为b 米,梯子的倾斜角为45°,则这间房子的宽AB 为( ) A .2b a +米 B .2ba -米 C .b 米 D .a 米二、填空题:(共11小题,每小题2分,满分22分) 7.-|-2|= . 8.函数12-+=x x y 中,自变量x 的取值范围是 . 9.如果两圆半径恰好是方程x 2-6x +1=0的两个根,圆心距d =2,则两圆的公切线的条数是 .10.如果点P (2,k )在直线y =2x +2上,那么点P 到x 轴的距离为 . 11.到一个三角形三条边所在直线等距离的点有 个.12.如图,在长方形ABCD 中,AB =3,BC =2,E 为BC 的中点,F 在AB 上,且BF =2AF ,则四边形AFEC 的面积为 .13.若|a -b +1|与42++b a 互为相反数,则(a +b )2004= .14.如图,在正方体ABCD -A 1B 1C 1D 1中,连接AB 1、AC 、B 1C ,则△AB 1C 的形状是 .15.观察下列等式:71=7,72=49,73=343,74=2401,…由此可判断7100的个位数字是 .16.如图,直线l 是四边形ABCD 的对称轴,若AB =CD ,有下面的结论:①AB //CD ;②AC⊥BD ;③AO =OC ;④AB ⊥BC .其中正确的结论有 .17.小王同学想利用树影测量校园内的树高.他在某一时刻测得小树高为1.5米时,其影长为1.2米,当他测量教学楼旁的一棵大树的影长时,因大树靠近教学楼,有一部分影子在墙上.经测量,地面部分影长为6.4米,墙上影长为1.4米,那么这棵大树高约为米.三、(每小题6分,共18分)18.一次函数y=x+b,与x轴、y轴的交点分别为A、B,若△OAB的周长为2+2(O为坐标原点),求b的值.19.如图,AB为半圆O的直径,在AB的同侧作AC、BD切半圆O于A、B,CD切半圆O 于E.请分别写出两个角相等、两条边相等、两个三角形全等、两个三角形相似等四个正确的结论.20.已知a>2,b>2,试判断关于x的方程x2-(a+b)x+ab=0与x2-abx+(a+b)=0有没有公共根.请说明理由.四、(本大题共两小题,每小题7分,共14分)21.如图,边长为3的正△ABC中,M、N分别位于AC、BC上,且AM=1,BN=2.过C、M、N三点的圆交△ABC的一条对称轴于另一点O.求证:点O是正△ABC的中心.22.某水果店一周内甲、乙两种水果每天销售情况统计如下(单位:千克):(1)(2)甲、乙两种水果哪个销售更稳定?五、(本题满分9分)23.如图,边长为2的正方形ABCD中,顶点A的坐标是(0,2),一次函数y=x+t的图象l随t的不同取值变化时,位于l的右下方由l和正方形的边围成的图形面积为S(阴影部分).(1)当t何值时,S=3;(2)在平面直角坐标系下,画出S与t的函数图象.六、(本题满分10分)24.如图,∠BAC=90°,AC=AB,直线l与以AB为直径的圆相切于点B,点E是圆上异于A、B的任意一点.直线AE与l相交于点D.(1)如果AD=10,BD=6,求DE的长;(2)连接CE,过E作CE的垂线交直线AB于F.当点E在什么位置时,相应的F位于线段AB上、位于BA的延长线上、位于AB的延长线上(写出结果,不要求证明).无论点E如何变化,总有BD=BF.请你就上述三种情况任选一种说明理由.七、(本题满分9分)25.某市近年来经济发展速度很快,根据统计:该市国内生产总值1990年为8.6亿元人民币,1995年为10.4亿元人民币,2000年为12.9亿元人民币.经论证,上述数据适合一个二次函数关系.请你根据这个函数关系,预测2005年该市国内生产总值将达到多少?。
2004年高考数学真题
2004年普通高等学校招生全国统一考试理科数学(必修+选修Ⅱ)本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分. 考试时间120分钟.第I 卷(选择题 共60分)参考公式:如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B ) 如果事件A 在一次试验中发生的概率是P ,那么n 次独立重复试验中恰好发生k 次的概率P n (k)=C kn P k (1-P)n -k一、选择题 :本大题共12小题,每小题6分,共60。
1.(1-i)2·i=( )A .2-2iB .2+2iC .-2D .22.已知函数=-=+-=)(.)(.11lg)(a f b a f x xx f 则若( )A .bB .-bC .b 1D .-b 13.已知a 、b 均为单位向量,它们的夹角为60°,那么|a +3b |= ( )A .7B .10C .13D .4 4.函数)1(11≥+-=x x y 的反函数是( ) A .y=x 2-2x +2(x <1) B .y=x 2-2x +2(x ≥1)C .y=x 2-2x (x <1)D .y=x 2-2x (x ≥1)5.73)12(x x -的展开式中常数项是( )A .14B .-14C .42D .-426.设A 、B 、I 均为非空集合,且满足A ⊆B ⊆I ,则下列各式中错误的是 ( )A .( I A)∪B=IB .( I A)∪( I B)=IC .A ∩( I B)=φD .( I A)∪( I B)= I B7.椭圆1422=+y x 的两个焦点为F 1、F 2,过F 1作垂直于x 轴的直线与椭圆相交,一个交点为P ,则||2PF =( )球的表面积公式S=42R π其中R 表示球的半径, 球的体积公式V=334R π,其中R 表示球的半径A .23B .3C .27D .48.设抛物线y 2=8x 的准线与x 轴交于点Q ,若过点Q 的直线l 与抛物线有公共点,则直线l 的斜率的取值范围是( )A .[-21,21]B .[-2,2]C .[-1,1]D .[-4,4]9.为了得到函数)62sin(π-=x y 的图象,可以将函数x y 2cos =的图象( )A .向右平移6π个单位长度 B .向右平移3π个单位长度C .向左平移6π个单位长度D .向左平移3π个单位长度10.已知正四面体ABCD 的表面积为S ,其四个面的中心分别为E 、F 、G 、H.设四面体EFGH的表面积为T ,则S T等于 ( )A .91B .94C .41D .3111.从数字1,2,3,4,5,中,随机抽取3个数字(允许重复)组成一个三位数,其各位数字之和等于9的概率为( )A .12513B .12516C .12518D .1251912.ca bc ab a c c b b a ++=+=+=+则,2,2,1222222的最小值为( )A .3-21B .21-3 C .-21-3 D .21+3第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上. 13.不等式|x +2|≥|x |的解集是 .14.由动点P 向圆x 2+y 2=1引两条切线PA 、PB ,切点分别为A 、B ,∠APB=60°,则动点P 的轨迹方程为 .15.已知数列{a n },满足a 1=1,a n =a 1+2a 2+3a 3+…+(n -1)a n -1(n ≥2),则{a n }的通项 1, n=1, a n =,n ≥2.16.已知a 、b 为不垂直的异面直线,α是一个平面,则a 、b 在α上的射影有可能是 .①两条平行直线 ②两条互相垂直的直线 ③同一条直线④一条直线及其外一点在一面结论中,正确结论的编号是 (写出所有正确结论的编号).三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)求函数x xx x x x f 2sin 2cos sin cos sin )(2244-++=的最小正周期、最大值和最小值.18.(本小题满分12分)一接待中心有A 、B 、C 、D 四部热线电话,已知某一时刻电话A 、B 占线的概率均为0.5,电话C 、D 占线的概率均为0.4,各部电话是否占线相互之间没有影响.假设该时刻有ξ部电话占线.试求随机变量ξ的概率分布和它的期望. 19.(本小题满分12分)已知,R a ∈求函数axe x xf 2)(=的单调区间.20.(本小题满分12分)如图,已知四棱锥 P —ABCD ,PB ⊥AD 侧面PAD 为边长等于2的正三角形,底面ABCD 为菱形,侧面PAD 与底面ABCD 所成的二面角为120°.(I )求点P 到平面ABCD 的距离,(II )求面APB 与面CPB 所成二面角的大小.21.(本小题满分12分)设双曲线C :1:)0(1222=+>=-y x l a y a x 与直线相交于两个不同的点A 、B.(I)求双曲线C的离心率e的取值范围:(II)设直线l与y轴的交点为P,且.125PBPA=求a的值.22.(本小题满分14分)已知数列1}{1=aan中,且a2k=a2k-1+(-1)K,a2k+1=a2k+3k,其中k=1,2,3,…….(I)求a3, a5;(II)求{ a n}的通项公式.2004年普通高等学校招生全国统一考试理科数学(必修+选修I )参考答案一、选择题DBCBABCCBADB二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.13.{x |x ≥-1} 14.x 2+y 2=4 15.2!n 16.①②④三、解答题 17.本小题主要考查三角函数基本公式和简单的变形,以及三角函娄的有关性质.满分12分.解:x x xx x x x f cos sin 22cos sin )cos (sin )(22222--+=212sin 41)cos sin 1(21)cos sin 1(2cos sin 122+=+=--=x x x x x xx所以函数f (x )的最小正周期是π,最大值是43,最小值是41.18.本小题主要考查离散型随机变量分布列和数学期望等概念.考查运用概率知识解决实际问题的能力.满分12分. 解:P(ξ=0)=0.52×0.62=0.09.P(ξ=1)=12C ×0.52×0.62+12C ×0.52×0.4×0.6=0.3P(ξ=2)= 22C ×0.52×0.62+12C 12C ×0.52×0.4×0.6+22C ×0.52×0.42=0.37. P(ξ=3)= 22C 12C ×0.52×0.4×0.6+12C 22C ×0.52×0.42=0.2 P(ξ=4)= 0.52×0.42=0.04于是得到随机变量ξ的概率分布列为:ξ0 1 2 3 4P 0.09 0.3 0.37 0.2 0.04所以E ξ=0×0.09+1×0.3+2×0.37+3×0.2+4×0.04=1.8.19.本小题主要考查导数的概率和计算,应用导数研究函数性质的方法,考查分类讨论的数学思想.满分12分. 解:函数f (x )的导数:.)2(2)(22ax ax ax e ax x e ax xe x f ++=+='(I )当a =0时,若x <0,则)(x f '<0,若x >0,则)(x f '>0.所以当a =0时,函数f (x )在区间(-∞,0)内为减函数,在区间(0,+∞)内为增函数.(II )当,02,02,02>-<>+>x a x ax x a 或解得由时由.02,022<<-<+x a ax x 解得所以,当a >0时,函数f (x )在区间(-∞,-a 2)内为增函数,在区间(-a 2,0)内为减函数,在区间(0,+∞)内为增函数;(III )当a <0时,由2x +ax 2>0,解得0<x <-a 2,由2x +ax 2<0,解得x <0或x >-a 2.所以当a <0时,函数f (x )在区间(-∞,0)内为减函数,在区间(0,-a 2)内为增函数,在区间(-a 2,+∞)内为减函数.20.本小题主要考查棱锥,二面角和线面关系等基本知识,同时考查空间想象能力和推理、运算能力.满分12分.(I )解:如图,作PO ⊥平面ABCD ,垂足为点O.连结OB 、OA 、OD 、OB 与AD 交于点E ,连结PE.∵AD ⊥PB ,∴AD ⊥OB , ∵PA=PD ,∴OA=OD ,于是OB 平分AD ,点E 为AD 的中点,所以PE ⊥AD.由此知∠PEB 为面PAD 与面ABCD 所成二面角的平面角, ∴∠PEB=120°,∠PEO=60° 由已知可求得PE=3∴PO=PE ·sin60°=23233=⨯, 即点P 到平面ABCD 的距离为23.(II )解法一:如图建立直角坐标系,其中O 为坐标原点,x 轴平行于DA.)43,433,0(),0,233,0(),23,0,0(的坐标为中点G PB B P .连结AG .又知).0,233,2(),0,23,1(-C A 由此得到:,0).0,0,2(),23,233,0(),43,43,1(=⋅=⋅-=-=--=PB BC PB GA BC PB GA 于是有所以θ的夹角BCGA PB BC PB GA ,.⊥⋅⊥ 等于所求二面角的平面角,于是,772||||cos -=⋅⋅=BC GA BCGA θ 所以所求二面角的大小为772arccos-π .解法二:如图,取PB 的中点G ,PC 的中点F ,连结EG 、AG 、GF ,则AG ⊥PB ,FG//BC ,FG=21BC.∵AD ⊥PB ,∴BC ⊥PB ,FG ⊥PB , ∴∠AGF 是所求二面角的平面角. ∵AD ⊥面POB ,∴AD ⊥EG .又∵PE=BE ,∴EG ⊥PB ,且∠PEG=60°.在Rt △PEG 中,EG=PE ·cos60°=23.在Rt △PEG 中,EG=21AD=1. 于是tan ∠GAE=AE EG =23,又∠AGF=π-∠GAE.所以所求二面角的大小为π-arctan 23.21.(本小题主要考查直线和双曲线的概念和性质,平面向量的运算等解析几何的基本思想和综合解题能力.满分12分. 解:(I )由C 与t 相交于两个不同的点,故知方程组⎪⎩⎪⎨⎧=+=-.1,1222y x y ax有两个不同的实数解.消去y 并整理得(1-a 2)x 2+2a 2x -2a 2=0. ①.120.0)1(84.012242≠<<⎪⎩⎪⎨⎧>-+≠-a a a a a a 且解得所以双曲线的离心率).,2()2,26(226,120.11122+∞≠>∴≠<<+=+= 的取值范围为即离心率且且e e e a a a aa e(II )设)1,0(),,(),,(2211P y x B y x A .125).1,(125)1,(,125212211x x y x y x PB PA =-=-∴=由此得由于x 1+x 2都是方程①的根,且1-a 2≠0,1317,06028912,,.12125.1212172222222222=>=----=--=a a a a x a a x a a x 所以由得消去所以22.本小题主要考查数列,等比数列的概念和基本知识,考查运算能力以及分析、归纳和推理能力.满分14分. 解:(I )a 2=a 1+(-1)1=0, a 3=a 2+31=3. a 4=a 3+(-1)2=4, a 5=a 4+32=13, 所以,a 3=3,a 5=13. (II) a 2k+1=a 2k +3k= a 2k -1+(-1)k +3k , 所以a 2k+1-a 2k -1=3k +(-1)k ,同理a 2k -1-a 2k -3=3k -1+(-1)k -1, ……a 3-a 1=3+(-1).所以(a 2k+1-a 2k -1)+(a 2k -1-a 2k -3)+…+(a 3-a 1)=(3k +3k -1+…+3)+[(-1)k +(-1)k -1+…+(-1)],由此得a 2k+1-a 1=23(3k -1)+21[(-1)k -1],于是a 2k+1=.1)1(21231--++k ka 2k = a 2k -1+(-1)k=2123+k (-1)k -1-1+(-1)k =2123+k (-1)k =1. {a n }的通项公式为:当n 为奇数时,a n =;121)1(232121-⨯-+-+n n当n 为偶数时,.121)1(2322-⨯-+=nn n a。
2004年高考数学(理科)真题及答案[全国卷I]
2004年全国统一考试理科数学本试卷分第I 卷(选择题)和第II 卷(非选择题)两部分. 共150分. 考试时间120分钟.第I 卷参考公式: 如果事件A 、B 互斥,那么P (A+B )=P (A )+P (B ) 如果事件A 、B 相互独立,那么P (A ·B )=P (A )·P (B )如果事件A 在一次试验中发生的概率是P ,那么 n 次独立重复试验中恰好发生k 次的概率 P n (k)=C k n P k(1-P)n -k一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.已知集合=⋂<--=<=N M x x x N x x M 则集合},032|{},4|{22 ( )A .{2|-<x x }B .{3|>x x }C .{21|<<-x x }D . {32|<<x x }2.=-+-+→542lim 22x x x x n x ( )A .21B .1C .52 D .41 3.设复数ωω++-=1,2321则i =( )A .ω-B .2ωC .ω1-D .21ω 4.已知圆C 与圆1)1(22=+-y x 关于直线x y -=对称,则圆C 的方程为( )A .1)1(22=++y xB .122=+y xC .1)1(22=++y xD .1)1(22=-+y x球的表面积公式S=42R π其中R 表示球的半径, 球的体积公式V=334R π,其中R 表示球的半径5.已知函数)2tan(ϕ+=x y 的图象过点)0,12(π,则ϕ可以是( )A .6π-B .6πC .12π-D .12π 6.函数x e y -=的图象( )A .与x e y =的图象关于y 轴对称B .与x e y =的图象关于坐标原点对称C .与x e y -=的图象关于y 轴对称D .与x e y -=的图象关于坐标原点对称7.已知球O 的半径为1,A 、B 、C 三点都在球面上,且每两点间的球面距离均为2π,则 球心O 到平面ABC 的距离为( )A .31 B .33 C .32 D .36 8.在坐标平面内,与点A (1,2)距离为1,且与点B (3,1)距离为2的直线共有( ) A .1条 B .2条 C .3条 D .4条 9.已知平面上直线l 的方向向量e =),53,54(-点O (0,0)和A (1,-2)在l 上的射影分别是O ′和A ′,则λ=''A O e ,其中λ= ( )A .511 B .511-C .2D .-2 10.函数x x x y sin cos -=在下面哪个区间内是增函数( )A .)23,2(ππB .)2,(ππC .)25,23(ππ D .)3,2(ππ 11.函数x x y 24cos sin +=的最小正周期为 ( )A .4π B .2π C .πD .2π12.在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521 的数共有 ( ) A .56个 B .57个 C .58个 D .60个第Ⅱ卷二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.13.从装有3个红球,2个白球的袋中随机取出2个球,设其中有ξ个红球,则随机变量ξ的概率分布为14.设y x ,满足约束条件:⎪⎩⎪⎨⎧≤-≥≥,12,,0y x y x x则y x z 23+=的最大值是 .15.设中心在原点的椭圆与双曲线2222y x -=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 . 16.下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱 ③若四个侧面两两全等,则该四棱柱为直四棱柱 ④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱其中,真命题的编号是 (写出所有正确结论的编号).三、解答题:本大题共6小题,共74分.解答应写出文字说明,证明过程或演算步骤. 17.(本小题满分12分)已知锐角三角形ABC 中,.51)sin(,53)sin(=-=+B A B A (Ⅰ)求证:B A tan 2tan =;(Ⅱ)设AB=3,求AB 边上的高. 18.(本小题满分12分) 已知8支球队中有3支弱队,以抽签方式将这8支球队分为A 、B 两组,每组4支.求:(Ⅰ)A 、B 两组中有一组恰有两支弱队的概率; (Ⅱ)A 组中至少有两支弱队的概率. 19.(本小题满分12分)数列}{n a 的前n 项和记为S n ,已知).3,2,1(2,111 =+==+n S nn a a n n 证明: (Ⅰ)数列}{nS n是等比数列; (Ⅱ).41n n a S =+ 20.(本小题满分12分)如图,直三棱柱ABC —A 1B 1C 1中,∠ACB=90°,AC=1,CB=2,侧棱AA 1=1,侧面AA 1B 1B的两条对角线交点为D ,B 1C 1的中点为M.(Ⅰ)求证CD ⊥平面BDM ;(Ⅱ)求面B 1BD 与面CBD 所成二面角的大小.21.(本小题满分12分)给定抛物线C :y 2=4x ,F 是C 的焦点,过点F 的直线l 与C 相交于A 、B 两点。
教育最新2004年普通高等学校招生全国统一考试文科(广西卷)数学
2004年普通高等学校招生全国统一考试(广西卷)数学(文史类)(老课程)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
第Ⅰ卷1至2页,第Ⅱ卷3至10页。
考试结束后,将本试卷和答题卡一并交回。
第I 卷 参考公式:三角函数的和差化积公式)]sin()[sin(21cos sin βαβαβα-++= )]sin()[sin(21sin cos βαβαβα--+= )]cos()[cos(21cos cos βαβαβα-++= )]cos()[cos(21sin sin βαβαβα--+-= 一、选择题 (1)设集合(){}22,1,,M x y xy x R y R =+=∈∈,(){}2,0,,N x y xy x R y R =-=∈∈,则集合M N 中元素的个数为( )A .1B .2C .3D .4(2)函数sin2xy =的最小正周期是( ) A .2πB .πC .2πD .4π(3) 记函数13xy -=+的反函数为()y g x =,则(10)g =( )A . 2B . 2-C . 3D . 1-等比数列{}n a 中,29,a = 5243a =,则{}n a 的前4项和为( ) A . 81B . 120C .168D . 192(5) 圆2240x y x +-=在点(P 处的切线方程是( )A .20x -= B .40x -= C .40x +=D .20x +=(6) 61x ⎫⎪⎭展开式中的常数项为( )A . 15B . 15-C . 20D . 20-正棱台、圆台的侧面积公式 l c c S )(21+'=台侧其中c ′、c 分别表示上、下底面周长,l 表示 斜高或母线长台体的体积公式 334R V π=球其中R 表示球的半径(7) 设复数z 的幅角的主值为23π2z =( )A . 2--B . 2i -C . 2+D . 2i (8) 设双曲线的焦点在x 轴上,两条渐近线为12y x =±,则双曲线的离心率e =( )A . 5B .C .D . 54(9) 不等式113x <+<的解集为( ) A . ()0,2 B . ()()2,02,4- C . ()4,0- D . ()()4,20,2--(10) 正三棱锥的底面边长为2,侧面均为直角三角形,则此三棱锥的体积为( )A .B .C .3D .(11) 在ABC 中,3,4AB BC AC ===,则边AC 上的高为( )A .B .. 32D .(12) 4名教师分配到3所中学任教,每所中学至少1名教师,则不同的分配方案共有( ) A . 12 种 B . 24 种 C 36 种 D . 48 种 第Ⅱ卷二、填空题:本大题共4小题,每小题4分,共16分. 把答案填在题中横线上. (13) 函数)1(log 21-=x y 的定义域是 .(14) 用平面α截半径为R 的球,如果球心到平面α的距离为2R,那么截得小圆的面积与球 的表面积的比值为 . (15) 函数)(cos 21sin R x x x y ∈-=的最大值为 . (16) 设P 为圆122=+y x 上的动点,则点P 到直线01043=--y x 的距离的最小值为 .三、解答题:本大题共6小题,共74分. 解答应写出文字说明,证明过程或演算步骤. (17)(本小题满分12分) 解方程.012242=--+x x(18) (本小题满分12分) 已知α为锐角,且αααααα2cos 2sin sin cos 2sin ,21tan -=求的值.(19) (本上题满分12分)设数列}{n a 是公差不为零的等差数列,S n 是数列}{n a 的前n 项和,且,9221S S =244S S =,求数列}{n a 的通项公式.20.(本小题满分12分)某村计划建造一个室内面积为800m 2的矩形蔬菜温室,在温室内,沿左、右两侧与后侧 内墙各保留1m 宽的通道,沿前侧内墙保留3m 宽的空地。
2004年高考--数学(全国二)
2004年高考试题全国卷Ⅱ理科数学(必修+选修Ⅱ)一、选择题:本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一个选项是符合题目要求的. (1)已知集合M ={x |x 2<4},N ={x |x 2-2x -3<0},则集合M ∩N =(A ){x |x <-2} (B ){x |x >3} (C ){x |-1<x <2} (D ){x |2<x <3}(2)542lim 221-+-+→x x x x n =(A )21 (B )1 (C )52 (D )41 (3)设复数ω=-21+23i ,则1+ω=(A )–ω (B )ω2 (C )ω1-(D )21ω(4)已知圆C 与圆(x -1)2+y 2=1关于直线y =-x 对称,则圆C 的方程为(A )(x +1)2+y 2=1 (B )x 2+y 2=1 (C )x 2+(y +1)2=1 (D )x 2+(y -1)2=1 (5)已知函数y =tan(2x +φ)的图象过点(12π,0),则φ可以是 (A )-6π (B )6π (C )-12π (D )12π(6)函数y =-e x 的图象(A )与y =e x 的图象关于y 轴对称 (B )与y =e x 的图象关于坐标原点对称(C )与y =e -x 的图象关于y 轴对称 (D )与y =e -x 的图象关于坐标原点对称 (7)已知球O 的半径为1,A 、B 、C 三点都在球面上,且每两点间的球面距离为2π,则球心O 到平面ABC 的距离为 (A )31 (B )33 (C )32 (D )36(8)在坐标平面内,与点A (1,2)距离为1,且与点B (3,1)距离为2的直线共有(A )1条 (B )2条 (C )3条 (D )4条 (9)已知平面上直线l 的方向向量)53,54(-=e,点O (0,0)和A (1,-2)在l 上的射影分别是O 1和A 1,则11A O =λe ,其中λ= (A )511 (B )-511 (C )2 (D )-2 (10)函数y =x cos x -sin x 在下面哪个区间内是增函数(A )(2π,23π) (B )(π,2π) (C )(23π,25π) (D )(2π,3π)(11)函数y =sin 4x +cos 2x 的最小正周期为(A )4π (B )2π(C )π (D )2π (12)在由数字1,2,3,4,5组成的所有没有重复数字的5位数中,大于23145且小于43521的数共有(A )56个 (B )57个 (C )58个 (D )60个二、填空题:本大题共4小题,每小题4分,共16分.把答案填在题中横线上.(13)从装有3个红球,2个白球的袋中随机取出2个球,设其中有ξ个红球,则随机变量ξ的概率分布为ξ0 1 2 P(14)设x ,y 满足约束条件⎪⎩⎪⎨⎧≤-≥≥,y x y ,x ,x 120则z =3x +2y 的最大值是 .(15)设中心在原点的椭圆与双曲线2x 2-2y 2=1有公共的焦点,且它们的离心率互为倒数,则该椭圆的方程是 .(16)下面是关于四棱柱的四个命题:①若有两个侧面垂直于底面,则该四棱柱为直四棱柱;②若两个过相对侧棱的截面都垂直于底面,则该四棱柱为直四棱柱;③若四个侧面两两全等,则该四棱柱为直四棱柱;④若四棱柱的四条对角线两两相等,则该四棱柱为直四棱柱,其中,真命题的编号是 (写出所有真命题的编号). 三、解答题:本大题共6个小题,共74分.解答应写出文字说明,证明过程或演算步骤. (17) (本小题满分12分)已知锐角三角形ABC 中,sin(A +B )=53,sin(A -B )=51. (Ⅰ)求证:tan A =2tan B ;(Ⅱ)设AB =3,求AB 边上的高. (18)(本小题满分12分)已知8个球队中有3个弱队,以抽签方式将这8个球队分为A 、B 两组,每组4个.求 (Ⅰ)A 、B 两组中有一组恰有两个弱队的概率; (Ⅱ)A 组中至少有两个弱队的概率. (19)(本小题满分12分)数列{a n }的前n 项和记为S n ,已知a 1=1,a n +1=nn 2+S n (n =1,2,3,…).证明: (Ⅰ)数列{nS n}是等比数列; (Ⅱ)S n +1=4a n .(20)(本小题满分12分) .如图,直三棱柱ABC -A 1B 1C 1中,∠ACB =90o ,AC =1,CB =2,侧棱AA 1=1,侧面AA 1B 1B 的两条对角线交点为D ,B 1C 1的中点为M . (Ⅰ)求证:CD ⊥平面BDM ;(Ⅱ)求面B 1BD 与面CBD 所成二面角的大小.(21)(本小题满分12分) 给定抛物线C :y 2=4x ,F 是C 的焦点,过点F 的直线l 与C 相交于A 、B 两点.(Ⅰ)设l 的斜率为1,求与夹角的大小;(Ⅱ)设=AF λ,若λ∈[4,9],求l 在y 轴上截距的变化范围. (22)(本小题满分14分)已知函数f (x )=ln(1+x )-x ,g (x )=x ln x .(1)求函数f (x )的最大值;(2)设0<a <b ,证明:0<g (a )+g (b )-2g (2ba +)<(b -a )ln2.2004年高考试题全国卷2 理科数学(必修+选修Ⅱ)答案:一、选择题:本大题共12小题,每小题5分,共60分.(1)C (2)A (3)C (4)C (5)A (6)D (7)B (8)B (9)D (10)B (11)B (12)C 二、填空题:本大题共4小题,每小题4分,共16分. (13)0.1,0.6,0.3 (14)5 (15)21x 2+y 2=1 (16)②④ 17.(I)证明:∵sin(A+B)=53,sin(A-B)=51∴⎪⎪⎩⎪⎪⎨⎧=-=+51sin cos cos sin 53sin cos cos sin B A B A B A B A ⎪⎪⎩⎪⎪⎨⎧==⇒51sin cos 52cos sin B A B A ⇒2tan tan =B A ,∴B A tan 2tan =. (II)解:∵2π<A+B<π, 53)sin(=+B A , ∴54)cos(-=+B A , 43)tan(-=+B A即43tan tan 1tan tan -=-+B A B A ,将B A tan 2tan =代入上式并整理得01tan 4tan 22=--B B 解得262tan ±=B ,因为B 为锐角,所以262tan +=B ,∴B A tan 2tan = 设AB 上的高为CD ,则AB=AD+DB=623tan tan +=+CDB CD A CD ,由AB=3得CD=2+6 故AB 边上的高为2+618.(I) 解:有一组恰有两支弱队的概率72482523=C C C (II)解:A 组中至少有两支弱队的概率21481533482523=+C C C C C C 19.(I )证: 由a 1=1,a n+1=nn 2+S n (n=1,2,3,…), 知a 2=112+S 1=3a 1,224212==a S , 111=S ,∴21212=S S又a n+1=S n+1-S n (n=1,2,3,…),则S n+1-S n =nn 2+S n (n=1,2,3,…),∴nS n+1=2(n+1)S n , 211=++nS n S n n (n=1,2,3,…).故数列{nSn }是首项为1,公比为2的等比数列 (II )解:由(I )知,)2(14111≥-∙=+-+n n Sn S n n ,于是S n+1=4(n+1)·11--n S n =4a n (n 2≥)又a 2=3S 1=3,则S 2=a 1+a 2=4=4a 1,因此对于任意正整数n ≥1都有S n+1=4a n .20.解法一:(I)如图,连结CA 1、AC 1、CM ,则CA 1=2, ∵CB=CA 1=2,∴△CBA 1为等腰三角形, 又知D 为其底边A 1B 的中点,∴CD ⊥A 1B ,BA'C'∵A 1C 1=1,C 1B 1=2,∴A 1B 1=3, 又BB 1=1,∴A 1B=2,∵△A 1CB 为直角三角形,D 为A 1B 的中点,CD=21A 1B=1,CD=CC 1又DM=21AC 1=22,DM=C 1M ,∴△CDN ≌△CC 1M ,∠CDM=∠CC 1M=90°,即CD ⊥DM , 因为A 1B 、DM 为平面BDM 内两条相交直线,所以CD ⊥平面BDM(II)设F 、G 分别为BC 、BD 的中点,连结B 1G 、FG 、B 1F , 则FG ∥CD ,FG=21CD ∴FG=21,FG ⊥BD.由侧面矩形BB 1A 1A 的对角线的交点为D,知BD=B 1D=21A 1B=1, 所以△BB 1D 是边长为1的正三角形,于是B 1G ⊥BD ,B 1G=23, ∴∠B 1GF 是所求二面角的平面角又B 1F 2=B 1B 2+BF 2=1+(22)2=23.∴cos ∠B 1GF=2123223)21()23(222121221=∙∙-+=∙-+FGG B F B FG G B 即所求二面角的大小为π解法二:如图以C 为原点建立坐标系(I):B(2,0,0),B 1(2,1,0),A 1(0,1,1),D(22,21,21), M(22,1,0),=CD (22,21,21),=B A 1(2,-1,-1), =DM (0,21,-21),,0,01=∙=∙DM CD B A CD∴CD ⊥A 1B,CD ⊥DM.因为A 1B 、DM 为平面BDM 内两条相交直线, 所以CD ⊥平面BDM(II):设BD 中点为G ,连结B 1G ,则G ),41,41,423(=(-22,21,21),=G B 1),41,43,42(--∴01=∙G B BD ,∴BD ⊥B 1G ,又CD ⊥BD ,∴与G B 1的夹角θ等于所求二面角的平面角,cos .3311-==θ 所以所求二面角的大小为π21.解:(I )C 的焦点为F(1,0),直线l 的斜率为1,所以l 的方程为y=x-1. 将y=x-1代入方程y 2=4x ,并整理得x 2-6x+1=0.设A(x 1,y 1),B(x 2,y 2),则有x 1+x 2=6,x 1x 2=1,OB OA ∙=(x 1,y 1)·(x 2,y 2)=x 1x 2+y 1y 2=2x 1x 2-(x 1+x 2)+1=-3. 41]16)(4[||||21212122222121=+++=+∙+=∙x x x x x x y x y x OB OAcos<OB OA ,.41413-= 所以OA 与OB 夹角的大小为π-arccos41413. 解:(II)由题设知AF FB λ=得:(x 2-1,y 2)=λ(1-x 1,-y 1),即⎩⎨⎧-=-=-)2()1()1(11212 y y x x λλ由 (2)得y 22=λ2y 12, ∵y 12=4x 1,y 22=4x 2,∴x 2=λ2x 1(3) 联立(1)(3)解得x 2=λ.依题意有λ>0. ∴B(λ,2λ)或B(λ,-2λ),又F(1,0),得直线l 的方程为(λ-1)y=2λ(x-1)或(λ-1)y=-2λ(x-1)当λ∈[4,9]时,l 在y 轴上的截距为12-λλ或由12-λλ=1212-++λλ,可知12-λλ在[4,9]上是递减的, ∴≤4312-λλ34≤,-≤34-12-λλ4≤直线l 在y 轴上截距的变化范围是]34,43[]43,34[ --22.(I)解:函数f(x)的定义域是(-1,∞),'f (x)=111-+x.令'f (x)=0,解得x=0,当-1<x<0时, 'f (x)>0,当x>0时,'f (x)<0,又f(0)=0,故当且仅当x=0时,f(x)取得最大值,最大值是0(II)证法一:g(a)+g(b)-2g(2b a +)=alna+blnb-(a+b)ln 2b a +=a ba bb b a a +++2ln 2ln . 由(I)的结论知ln(1+x)-x<0(x>-1,且x ≠0),由题设0<a<b,得021,02<-<->-bba a ab ,因此a a b a a b b a a 2)21l n (2ln-->-+-=+,bba b b a b a b 2)21ln(2ln -->-+-=+. 所以a b a b b b a a +++2ln 2ln >-022=---ba ab .又,22b b a b a a +<+ a b a b b b a a +++2ln 2ln <a .2ln )(2ln )(2ln 2ln a b ba b a b b a b b b b a -<+-=+++ 综上0<g(a)+g(b)-2g(2ba +)<(b-a)ln2.(II)证法二:g(x)=xlnx,1ln )('+=x x g ,设F(x)= g(a)+g(x)-2g(2xa +),则.2ln ln )]'2([2)(')('xa x x a g x g x F +==+-=当0<x<a 时,0)('<x F 因此F(x)在(0,a)内为减函数当x>a 时,0)('>x F 因此F(x)在(a,+∞)上为增函数从而,当x=a 时,F(x)有极小值F(a)因为F(a)=0,b>a,所以F(b)>0,即0<g(a)+g(b)-2g(2ba +).设G(x)=F(x)-(x-a)ln2,则).ln(ln 2ln 2ln ln )('x a x xa x x G +-=-+-=当x>0时,0)('<x G ,因此G(x)在(0,+∞)上为减函数,因为G(a)=0,b>a,所以G(b)<0.即g(a)+g(b)-2g(2ba +)<(b-a)ln2.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
新教材高中毕业会考数学模拟试题(二) 一、选择题(本大题共30个小题,每小题1.5分,共45分。在每小题给出的四个选项中,只有一个选项是符合题目要求的。) 1.把―411表示成2kπ+θ(k∈Z)的形式,使|θ|最小的θ值是 (A)―43 (B)―4 (C)45 (D)43 2.设集合A=R,,集合B=R,则从集合A到集合B的映射f只可能是 (A) xy=|x| (B) xy=x (C) xy=2x (D) xy=log2(x2+1) 3.不等式2≥|3-x|的解集是 (A){x|x≤1或x≥5} (B){x|1≤x≤5} (C){x|―5≤x≤―1} (D){x|―1≤x≤5} 4.sin2=53,则cosα= (A)―257 (B)257 (C)53 (D)54 5.若不等式的x2+ax+b>0的解集为{x|x<―1或x>2},则a+b= (A)3 (B)1 (C)―1 (D)―3 6.设非空集合A、B、C,若“a∈A”的充要条件是“a∈B且a∈C”,则“a∈B”是“a∈A”的 (A)充分不必要条件 (B)必要不充分条件 (C)充要条件 (D)既不充分又不必要条件 7.有下列四个命题 (1)“若xy=1,则x、y互为倒数”的逆命题。 (2)“面积相等的三角形全等”的否命题 。 (3)“若m≤1,则x2―2x+m=0有实根”的逆否命题。 (4)“若A∩B=B,则AB”的逆否命题。 其中真命题的是 (A) (1)(2) (B) (2) (3) (C) (1) (2) (3) (D) (3) (4) 8.已知直线a、b和平面、,下列命题中正确的是 (A)aa∥ (B)aa (C)baba∥ (D)aba∥b 9.若loga2<logb2<0,则 (A)0<a<b<1 (B)0<b<a<1 (C)a>b>1 (D)b>a>1
10.若a=0.88.0,b=0.89.0,c=1.28.0,则a、b、c的大小关系是 (A)a>b>c (B)c>b>a (C)c>a>b (D)a>c>b 11.定义在R上的奇函数f(x)是减函数,设a+b≤0,给出下列不等式:(1)f(a)f(―a)≤0 (2)f(b)f(―b)≥0 (3)f(a)+f(b)≤f(―a)+f(―b) (4)f(a) +f(b)≥f(―a)+f(―b) 其中成立的是 (A) (1)(3) (B) (2)(3) (C) (1)(4) (D) (2)(4) 12.若指数函数y=f(x)的反函数的图象经过(2,―1),则此指数函数是
(A)y=(21)x (B)y=2x (C)y=3x (D)y=(31)x
13.函数y=sin(2x+3)在区间[0,π]内的一个单调递减区间是 (A) [0,125] (B) [12,32] (C) [125,1211] (D) [6,2] 14.如果函数f(x)=x2+bx+c对任意实数t都有f(2+t)=f(2-t),那么 (A) f(2)<f(1)<f(4) (B) f(1)<f(2)<f(4) (C) f(2)<f(4)<f(1) (D) f(4)<f(2)<f(1)
15.函数y=―2sin2x―3cos2x+1的最小正周期与最大值分别是
(A)π,7+1 (B)2,7+1 (C)π,3 (D)π,8 16.如果直线2x―y+a=0和直线x―21y+b=0平行,则 (A) a=0,b=1 (B) a=2b (C) a=0,b=0 (D) a≠2b 17.△ABC中,已知b=40,c=20,C=60°,则此三角形解的情况 (A)有一解 (B)有二解 (C)无解 (D)有解但解数不定 18.要保持直线y=kx―1始终与线段y=1(―1≤x≤1)相交,那么实数k的取值范围是 (A) [—2,2] (B) (—2,2)
(C)2,∪,2 (D)2,∪,2
19.方程x2+y2+Dx+Ey+F=0(D2+E2—4F>0)所表示的曲线关于y=x对称,那么 (A) D=E (B) D=F (C) E=F (D) D=E=F
20.已知a=(cosα,sinα),b=(cosβ,sinβ),则 (A)a⊥b (B)a∥b (C) (a+b)⊥(a―b) (D)a与b的夹角为α+β 21.若{an}为等差数列,且a2+a5+a8=39,则a1+a2+„+a9的值为 (A)117 (B)114 (C)111 (D)108
22.若正数等比数列{an}的公比q≠1,且a3、a5、a6成等差数列,则6453aaaa=
(A)215 (B)215 (C)21 (D)1 23.若a<b<0,则下列结论中正确的是 (A)不等式a1>b1和||1a>||1b均不能成立。
(B)不等式ba1>a1和||1a>||1b均不能成立。 (C)不等式ba1>a1和(a+b1)2>(b+a1)2均不能成立。 (D)不等式||1a>||1b和(a+b1)2>(b+a1)2均不能成立。 24.双曲线2mx2―my2=2的一条准线是y=1,则m为 (A)―31 (B)―34 (C)31 (D)55 25.假设在200件产品中有3件是次品,现在从中任意抽5件,其中至少有2件是次品的抽法有 (A)C23C2197种 (B)C23C3197+C33C2197种
(C)C5200―C5197种 (D)C5200―C13C4197种
26.已知双曲线22ax―22by=1(a>0,b>0)与x轴正半轴交于A点,F是它的左焦点,设B点坐标 为(0,b),且AB⊥BF,则双曲线的离心率为
(A)231 (B)251 (C)462 (D) 452 27.由(3x+32)100展开式所得的x的多项式中系数为有理数的共有 (A)50项 (B)17项 (C) 16项 (D) 15项 28.点P在边长为1的正方形的边上运动,设M是CD边上的中点,则当点P沿A—B—C—M运 动时,以点P经过的路程x为自变量,三角形APM的面积为y的函数y=f(x)的表达式为
(A)y=0.5(01)0.5(12)2.5(22.5)xxxxx (B)y=0.5(01)0.250.75(12)0.51.25(22.5)xxxxxx
(C)y=0.5(02)2.5(22.5)xxxx (D)y=2(1.25)0.5x(02.5)x 29.计算机是将信息换成二位制进行处理的二进制,即“逢二进一”。如(1101)2表示二进位制,将 它转换成十进制形式是1×23+1×22+0×21+1×20=13,那么将二进制数162111转换 成十进制形式是 (A)217―2 (B)216―2 (C)216―1 (D)215―1 30.已知奇函数f(x)在[―1,0]上为单调递减函数,又α、β为锐角三角形两内角,则 (A) f(cosα)>f(cosβ) (B) f(sinα)>f(sinβ) (C) f(sinα)>f(cosβ) (D) f(sinα)<f(cosβ) 二、填空题(本大题共10小题,每小题1分,共10分。请把答案填在题中的横线上。)
31.lg25+lg2lg50+(lg2)2= 。
32.设A={x | |x―a|<2},B={x |212xx<1},若AB,则a的取值范围是 。 33.已知点(1,3)按向量a平移后得点(4,1),那么(2,1)按向量a平移后所得点的坐标为 。 34.函数y=log31(5―4x―x2)的单调递增区间为 。
35.已知y=f(x)是定义在R上的奇函数,当x≥0时,f(x)=x2―2x,则x<0时,f(x)= 。 36.若三点P1、P2和P在一条直线上,点P1和P2在直角坐标系坐标分别为(0,―6)和(3,0), 且P点分21PP的比为―21,则P点坐标为 。 37.有红、黄、蓝三种颜色旗各3面,在每种颜色的3面旗上分别标上号码1、2和3,现任取出 3面,它们的颜色与号码不相同的概率为 。 38.在球面上有四个点P、A、B、C,如果PA、PB、PC两两互相垂直,且PA=PB=PC=a,则 球的表面积是 。
39.商店某种货物的进价下降了8%,但销售价没变,于是这种货物的销售利润(进价进价销售价) ×100%由原来的r%增加到(r+10)%,那么r= 。 40.设计一条单向行驶的公路隧道,需保证装有集装箱的汽车能够通过,隧道的横断面由抛物线 和矩形ABCD的三边组成,隧道的总高为5米,矩形的一边BC长为2米,装有集装箱的汽 车高为4米,宽为3米,那么如果不考虑其他因素,隧道的底部宽度AB应至少设计为 米(精确到0.1米)。 三、解答题(本大题共10小题,共45分。解答应写出文字说明和演算步骤。) 41.(本小题共3分) 已知直角三角形ABC的内切圆O的半径为r,AD是斜边BC上的高,连接OA。 (1)设∠OAD=x,将AD表示为自变量x的函数; (2)求AD长的最大值。 42.(本小题共3分) 解不等式xalog4>logax―1(0<a<1) 43.(本小题共4分) 已知α、β为锐角,tanα=71,sinβ=1010,求α+2β的值。 44.(本小题共4分) 北京某公司计划今年内同时出售新型的电子琴和洗衣机,由于这种产品的市场需求量非常大, 供不应求,因此该公司要根据实际情况(资金、劳动力)确定产品的月供应量,以使得利润 达到最大。已知对这两种产品有直接限制的因素是资金和劳力(工资),通过调查得到关于两 种产品有关数据如下表:
试问:怎样确定两种货的月供应量才能使总利润最大?最大利润是多少? 45.(本小题共5分) 在直三棱柱ABC—A1B1C1中,AA1=4,AC=BC=2,∠ACB=90°。
(1)求点B到面AB1C的距离; (2)求直线B1B与面AB1C所成角的正切值; (3)求以AB1C与AB1B为半平面的二面角的正切值。
资金 单位产品所需资金(百元) 月资金供应量 电子琴 洗衣机
成本 30 20 300 劳动力(工资) 5 10 110 单位利润 6 8
