2020年中考数学二轮复习--几何图像问题专题(图片版有答案)
2020中考数学 二轮专题复习 圆的综合题(含答案)

2020中考数学二轮专题复习圆的综合题(含答案)1.如图,∠OP A=12∠APB,∠O与P A相切于点C.(1)求证:直线PB与∠O相切.(2)PO的延长线与∠O相交于点E,若∠O的半径为3,PC=4,求CE的长.第1题图(1)证明:如解图,连接OC,作OD∠PB于D点.∠∠O与P A相切于点C,∠OC∠P A.∠点O在∠APB的平分线上,OC∠P A,OD∠PB,∠OD=OC,即OD为∠O的半径,∠直线PB与∠O相切;第1题解图(2)解:如解图,设PO交∠O于F,连接CF.∠OC=3,PC=4,∠PO=5,PE=8.∠∠O与P A相切于点C,∠∠PCF+∠FCO=∠FCO+∠OCE,又∠∠E=∠OCE,∠∠PCF=∠E.又∠∠CPF=∠EPC,∠∠PCF ∠∠PEC ,∠CF ∠EC =PC ∠PE =4∠8=1∠2.∠EF 是直径,∠∠ECF =90°.设CF =x ,则EC =2x ,则x 2+(2x )2=62,解得x =655, 则CE =2x =1255.2、如图,已知AO 为Rt∠ABC 的角平分线,∠ACB =90°,AC BC =43,以O 为圆心,OC 为半径的圆分别交AO ,BC 于点D ,E ,连接ED 并延长交AC 于点F .(1)求证:AB 是∠O 的切线;(2)求tan∠CAO 的值;(3)求CFAD 的值.第2题图(1)证明:作OG ∠AB 于点G ,如解图.∠在∠OGA 和∠OCA 中,⎩⎨⎧∠OGA =∠OCA∠GAO =∠CAO AO =AO,∠∠OGA ∠∠OCA (AAS),∠OG =OC ,∠OG 为∠O 的半径,∠OG ∠AB ,∠AB 是∠O 的切线;(2) 解:设AC =4x ,BC =3x ,∠O 半径为r ,则AB=5x ,由切线长定理知,AC =AG =4x ,故 BG =x .∠tan∠B =OG ∠BG =AC ∠BC =4∠3,∠OG =43BG =43x , ∠tan∠CAO =tan∠GAO =43x 4x =13; (3)解:在Rt∠OCA 中,AO =OC 2+AC 2=4103 x , ∠AD =OA -OD =43(10-1) x . 如解图,连接CD ,则∠DCF +∠ECD =∠ECD +∠CEF ,∠∠DCF =∠CEF ,又∠CEF =∠EDO =∠FDA ,∠∠DCF =∠ADF ,又∠∠F AD =∠DAC , 第2题解图∠∠DF A ∠∠CDA ,∠DA ∠AC =AF ∠AD ,即 43 (10-1)x ∠4x =AF ∠43(10-1)x , ∠AF =49(11-210)x ,∠CF =8(10-1)x 9, ∠AD CF =32. 3、如图, AB 是∠O 的直径,点D 是弧AE 上的一点,且∠BDE =∠CBE ,BD 与AE 交于点F .(1)求证:BC 是∠O 的切线;(2)若BD 平分∠ABE ,延长ED 、BA 交于点P ,若P A =AO ,DE =2,求PD 的长.第3题图(1)证明:∠AB 是∠O 的直径,∠∠AEB =90°,∠∠EAB +∠EBA =90°,∠∠BDE =∠EAB ,∠BDE =∠CBE ,∠∠EAB =∠CBE ,∠∠ABE +∠CBE =90°,∠CB ∠AB ,∠AB 是∠O 的直径,∠BC 是∠O 的切线;(2)解:∠BD 平分∠ABE ,∠∠ABD =∠DBE ,如解图,连接DO ,∠OD =OB ,∠∠ODB =∠OBD ,∠∠EBD=∠ODB , 第3题解图∠OD ∠BE ,∠PD PE =PO PB , ∠P A =AO ,∠P A =AO =OB ,∠PO PB =23,∠PD PE =23, ∠PD PD +DE =23, ∠DE =2,∠PD =4.4、如图,CD 是∠O 的直径,点B 在∠O 上,连接BC 、BD ,直线AB 与CD 的延长线相交于点A ,AB 2=AD ·AC ,OE ∠BD 交直线AB 于点E ,OE 与BC 相交于点F ,(1)求证:直线AE 是∠O 的切线;(2)若∠O 的半径为3,cos A =54,求OF 的长.第4题图(1)证明:如解图,连接OB ,∠AB 2=AD ·AC ,∠AB AD =AC AB, ∠∠A 为公共角,∠∠ABD ∠∠ACB ,∠∠ABD =∠ACB ,在∠O 中,OB =OC ,∠∠OBC =∠OCB ,∠∠OBC =∠ABD ,∠CD 是∠O 的直径,∠∠CBD =90°,∠∠OBC +∠OBD =90°,∠∠OBD +∠ABD =90°,即∠OBA =90°,∠点B 为AE 上一点,且OB 为∠O 的半径,∠AE 是∠O 的切线;第4题解图(2)解:在Rt∠ABO 中,OB =3,cos A =AB OA =45, ∠设AB =4k ,OA =5k (k > 0),又OA 2=AB 2+OB 2,∠(5k )2=(4k )2+32,∠k 2=1(k >0),∠k =1,即AB =4,OA =5,∠OD =3,∠AD =OA -OD =2,∠OE ∠BD ,∠AD OD =AB BE ,即23=4BE, ∠BE =6.在Rt∠OBE 中,OE =BE 2+OB 2=62+32=35, ∠∠CBD =90°,BD ∠OE ,∠∠EFB =90°,∠S ∠OBE =12OB ·BE =12OE ·BF , ∠BF =OB ·BE OE =3×635=655, 在Rt∠OBF 中,由勾股定理可知,55355632242=⎪⎪⎭⎫ ⎝⎛-=-=BF BO OF . 5、如图,在∠ABD 中,AB =AD ,以AB 为直径的∠F 交BD 于点C ,交AD 于点E ,CG ∠AD 于点G .(1)求证:GC 是∠F 的切线;(2)若∠BCF 的面积为15,求∠BDA 的面积;第5题图(1)证明:∠AB =AD ,FB =FC ,∠∠B =∠D ,∠B =∠BCF ,∠∠D =∠BCF ,∠CF ∠AD ,∠CG ∠AD ,∠CG ∠CF ,又∠FC 为∠F 的半径,∠GC 是∠F 的切线;(2)解:由(1)得:CF ∠AD ,∠∠BCF ∠∠BDA ,∠BF BA =12,∠S ∠BCF ∠S ∠BDA =1∠4, ∠S ∠BDA =4S ∠BCF =4×15=60.6、如图,四边形ABCD 内接于∠O ,AB 是∠O 的直径,点P 在CA 的延长线上,∠CAD =45°.(1)若AB =4,求CD ︵的长;(2)若BC ︵=AD ︵,AD =AP ,求证:PD 是∠O 的切线.第6题图(1)解:如解图,连接OC 、OD ,∠∠CAD =45°,∠∠COD =2∠CAD =90°,∠AB =4,∠OC =12AB =2. ∠CD ︵的长为90180×π×2=π;第6题解图(2)证明:∠BC ︵=AD ︵,∠∠BOC =∠AOD .∠∠COD =90°,∠∠AOD =180°-∠COD 2=45°. ∠OA =OD ,∠∠ODA =∠OAD .∠∠AOD +∠ODA +∠OAD =180°,∠∠ODA =180°-∠AOD 2=67.5°. ∠AD =AP ,∠∠ADP =∠APD .∠∠CAD =∠ADP +∠APD =45°,∠∠ADP =12∠CAD =22.5°. ∠∠ODP =∠ODA +∠ADP =90°.又∠OD 是∠O 的半径,∠PD 是∠O 的切线.7.如图,AB 为∠O 的直径,D 、T 是圆上的两点,且AT 平分∠BAD ,过点T 作AD 延长线的垂线PQ ,垂足为C .(1)求证:PQ是∠O的切线;(2)已知∠O的半径为2,若过点O作OE∠AD,垂足为E,OE=3,求弦AD的长.第7题图(1)证明:连接OT,如解图∠所示,∠OA=OT,∠∠OAT=∠OTA,∠AT平分∠BAD,∠∠OAT=∠CAT,第7题解图∠∠∠OTA=∠CAT,∠OT∠AC,∠PQ∠AC,∠PQ∠OT,∠OT是∠O的半径,∠PQ是∠O的切线;(2)解:如解图∠所示,∠OE∠AD,∠AE=DE,∠AEO=90°,∠AE=OA2-OE2=22-(3)2=1,第7题解图∠∠AD=2AE=2.8. 如图所示, 直线DP和☉O相切于点C,交直径AE的延长线于点P, 过点C作AE的垂线, 交AE于点F, 交☉O于点B,作平行四边形ABCD,连接BE, DO,CO.(1)求证:DA=DC ;(2)求∠P及∠AEB的大小.第8题图(1)证明:∠在平行四边形ABCD中,AD∠BC,CB∠AE,∠AD∠AE,∠∠DAO=90°,又∠直线DP 和☉O 相切于点C ,∠DC ∠OC ,∠∠DCO =90°,∠在Rt∠DAO 和Rt∠DCO 中,⎩⎨⎧DO =DO AO =CO , ∠Rt∠DAO ∠Rt∠DCO (HL),∠DA =DC ;(2)解:∠CB ∠AE ,AE 是∠O 的直径,∠CF =FB =12BC , 又∠四边形ABCD 是平行四边形,∠AD =BC ,∠CF =12AD , 又∠CF ∠DA ,∠∠PCF ∠∠PDA ,∠PC PD =DC PD =12,即PC =12PD ,DC =12PD . 由 (1) 知DA =DC ,∠DA =12PD , ∠在Rt∠DAP 中,∠P =30°.∠DP ∠AB ,∠∠F AB =∠P =30°,又∠∠ABE =90°,∠∠AEB =90°-30°=60°.9. 如图,AB 是⊙O 的直径,点C 、E 是⊙O 上的点,且AC ︵=EC ︵,连接AC 、BE ,并延长交于点D ,已知AB =2AC =6.第9题图(1)求DC 的长;(2)求EC ︵的长.解:(1)如解图,连接BC ,第9题解图∵ AB 是⊙O 的直径,∴∠ACB =90°,CB ⊥AD ,∵AC ︵=EC ︵,∴∠ABC =∠DBC ,∴△ABD 为等腰三角形,∵AB =2AC =6,∴DC =AC =3;(2)如解图,连接OC 、OE ,∵AB =2AC =6,∠ACB =90°,∴∠ABC =30°,OC =OE =3,∴∠DBC =∠ABC =30°∴∠COE =2∠DBC =60°,∴l EC ︵=60×π×3180=π. 10. 如图,AB 为圆O 的直径,CD ⊥AB 于点E ,交圆O 于点D ,OF ⊥AC 于点F .(1)求证:OF =12BD ; (2)当∠D =30°,BC =1时,求圆中阴影部分的面积.第19题图 (1)证明:如解图,连接OC ,第10题解图 ∵OF ⊥AC ,OA =OC ,∴AF =FC ,∵OA =OB ,∴OF 是△ABC 的中位线,∴OF =12BC ,∵AB ⊥CD ,∴BC ︵=BD ︵,∴BC =BD ,∴OF =12BD ; (2)解:∵∠D =30°,∴∠A =∠D =30°,∴∠COB =2∠A =60°,∴∠AOC =120°,∵AB 为⊙O 的直径,∴∠ACB =90°,在Rt △ABC 中,BC =1,∴AB =2,AC =3,由(1)可知OF =12BC =12, ∵∠COB =60°,OB =OC ,∴△BOC 是等边三角形,∴OA =OB =BC =1,∴S △AOC =12AC ·OF =12×3×12=34,S 扇形AOC =120πOA 2360=π3, ∴S 阴影=S 扇形AOC -S △AOC =π3-34. 11.如图,在∠O 中,直径CD ∠弦AB 于点E ,AM ∠BC 于点M ,交CD 于点N ,连接AD .(1)求证:AD =AN ;(2)若AB =42,ON =1,求∠O 的半径.第11题图(1)证明:∠∠BAD 与∠BCD 是同弧所对的圆周角,∠∠BAD =∠BCD ,∠AE ∠CD ,AM ∠BC ,∠∠AEN =∠AMC =90°,∠∠ANE =∠CNM ,∠∠BAM =∠BCD ,∠∠BAM =∠BAD ,在△ANE 与△ADE 中,⎩⎨⎧∠BAM =∠BADAE =AE∠AEN =∠AED, ∠△ANE ≌△ADE (ASA),∠AN =AD ;(2)解:∠AB =42,AE ∠CD ,∠AE =12AB =22, 又∠ON =1,∠设NE =x ,则OE =x -1,NE =ED =x ,OD =OE +ED =2x -1,如解图,连接AO ,则AO =OD =2x -1,第11题解图∠△AOE 是直角三角形,AE =22,OE =x -1,AO =2x -1, ∠(22)2+(x -1)2=(2x -1)2,解得x 1=2,x 2=-43(舍), ∠AO =2x -1=3,即∠O 的半径为3.12.如图,在△ABC 中,∠C =90°,D 是BC 边上一点,以DB 为直径的∠O 经过AB 的中点E ,交AD 的延长线于点F,连接EF.(1)求证:∠1=∠F;,EF=25,求CD的长.(2)若sin B=55第12题图(1)证明:如解图,连接DE.∠BD是∠O的直径,∠∠DEB=90°.∠E是AB的中点,∠DA=DB,∠∠1=∠B.∠∠B=∠F,∠∠1=∠F;第12题解图(2)解:∠∠1=∠F,∠AE=EF=25,∠AB=2AE=4 5.在Rt△ABC中,AC=AB·sin B=4,∠BC=AB2-AC2=8.设CD=x,则AD=BD=8-x.在Rt△ACD中,由勾股定理得AC2+CD2=AD2,即42+x2=(8-x)2,解得x=3,∠CD=3.13.如图,在△ABC中,AB=BC,D是AC中点,BE平分∠ABD交AC于点E,点O是AB上一点,⊙O过B、E两点,交BD于点G,交AB于点F.(1)判断直线AC与⊙O的位置关系,并说明理由;(2)当BD=6,AB=10时,求⊙O的半径.第13题图解:(1)AC与⊙O相切.理由如下:连接OE.如解图,∵BE平分∠ABD.∴∠OBE=∠DBE,∵OE=OB,∴∠OBE=∠OEB,∴∠OEB=∠DBE,∴OE∥BD,∵AB=BC,D是AC中点,∴BD⊥AC,∴OE⊥AC,∴AC与⊙O相切;第13题解图(2)设⊙O 半径为r .则AO =10-r , 由(1)知,OE ∥BD ,∴△AOE ∽△ABD ,∴AO AB =OE BD ,即61010r r =-, ∴r =154,即⊙O 半径是154.。
2020年中考数学二轮复习压轴专题:圆(题目版)
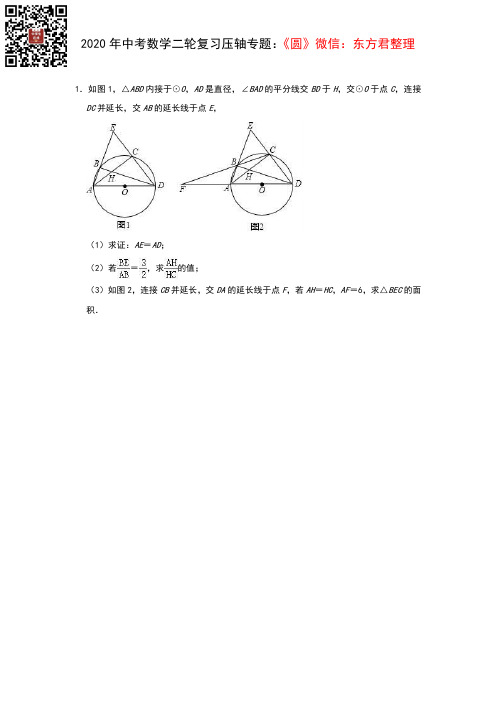
1.如图1,△ABD内接于⊙O,AD是直径,∠BAD的平分线交BD于H,交⊙O于点C,连接DC并延长,交AB的延长线于点E,(1)求证:AE=AD;(2)若=,求的值;(3)如图2,连接CB并延长,交DA的延长线于点F,若AH=HC,AF=6,求△BEC的面积.2.如图,AB是⊙O的直径,M是OA的中点,弦CD⊥AB于点M,过点D作DE⊥CA交CA的延长线于点E.(1)连接AD,求∠OAD;(2)点F在上,∠CDF=45°,DF交AB于点N.若DE=,求FN的长.3.如图1,锐角△ABC,AB=AC,⊙O是△ABC的外接圆,连接BO并延长交AC于点D,(1)若∠BDC=30°,求∠BAC的度数;(2)如图2,当0°<∠BAC<60°时,作点C关于BD的对称点E,连接AE、DE,DE交AB于F.①点E在⊙O上(选填“内”、“上”、“外”);②证明:∠AEF=∠EAB;③若△BDC为等腰三角形,AD=2,求AE的长.4.如图,AB是⊙O的直径,点C、D在⊙O上,AD与BC相交于点E.连接BD,作∠BDF=∠BAD,DF与AB的延长线相交于点F.(1)求证:DF是⊙O的切线;(2)若DF∥BC,求证:AD平分∠BAC;(3)在(2)的条件下,若AB=10,BD=6,求CE的长.5.如图1,在平面直角坐标系中,⊙O1点,且BC=8,连接AB.(1)求证:∠ABO=∠ABO;1(2)求AB的长;(3)如图2,⊙O经过A、B两点,与y2B的延长线交轴的正半轴交于点M,与O1于点N,求出BM﹣BN的值.6.如图,P是直径AB上的一点,AB=6,CP⊥AB交半圆于点C,以BC为直角边构造等腰Rt△BCD,∠BCD=90°,连接OD.小明根据学习函数的经验,对线段AP,BC,OD的长度之间的关系进行了探究.下面是小明的探究过程,请补充完整:(1)对于点P在AB上的不同位置,画图、测量,得到了线段AP,BC,OD的长度的几组值,如下表:位置1位置2位置3位置4位置5位置6位置…AP0.00 1.00 2.00 3.00 4.00 5.00…BC 6.00 5.48 4.90 4.24 3.46 2.45…OD 6.717.247.07 6.71 6.16 5.33…在AP,BC,OD的长度这三个量中确定的长度是自变量,的长度和的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合函数图象,推断:当OD=2BC时,线段AP的长度约为.7.如图,以△ABC的BC边上一点O为圆心的圆,经过A、B两点,且与BC边交于点E,D 为BE的下半圆弧的中点,连接AD交BC于F,若AC=FC.(1)求证:AC是⊙O的切线;(2)若BF=8,DF=,求⊙O的半径.(3)过点B作⊙O的切线交CA的延长线于G,如果连接AE,将线段AC以直线AE为对称轴作对称线段AH,点H正好落在⊙O上,连接BH,求证:四边形AHBG为菱形.8.已知:△ABC是⊙O的内接三角形,AB为直径,AC=BC,D、E是⊙O上两点,连接AD、DE、AE.(1)如图1,求证:∠AED﹣∠CAD=45°;(2)如图2,若DE⊥AB于点H,过点D作DG⊥AC于点G,过点E作EK⊥AD于点K,交AC于点F,求证:AF=2DG;(3)如图3,在(2)的条件下,连接DF、CD,若∠CDF=∠GAD,DK=3,求⊙O的半径.9.如图,在▱ABCD中,AB=4,BC=8,∠ABC=60°.点P是边BC上一动点,作△PAB的外接圆⊙O交BD于E.(1)如图1,当PB=3时,求PA的长以及⊙O的半径;(2)如图2,当∠APB=2∠PBE时,求证:AE平分∠PAD;(3)当AE与△ABD的某一条边垂直时,求所有满足条件的⊙O的半径.10.已知:四边形ABCD内接于⊙O,连接AC,AB=AD(1)如图1,求证:CA平分∠BCD;(2)如图2,连接BD交AC于点E,若BD为⊙O直径,求证:tan∠CAD=;(3)如图3,在(2)的条件下,点F为BC中点,连接AF并延长交⊙O于G,若FG=2,tan∠GAD=,求DE的长.11.已知:AB、AC是⊙O中的两条弦,连接OC交AB于点D,点E在AC上,连接OE,∠AEO =∠BDO.(1)如图1,若∠CAD=∠COE,求证:=;(2)如图2,连接OA,若∠OAB=∠COE,求证:AE=CD;(3)如图3,在第(2)问的条件下,延长AO交⊙O于点F,点G在AB上,连接GF,若∠ADC=2∠BGF,AE=5,DG=1,求线段BG的长.12.已知四边形ABCD为⊙O的内接四边形,直径AC与对角线BD相交于点E,作CH⊥BD于H,CH与过A点的直线相交于点F,∠FAD=∠ABD.(1)求证:AF为⊙O的切线;(2)若BD平分∠ABC,求证:DA=DC;(3)在(2)的条件下,N为AF的中点,连接EN,若∠AED+∠AEN=135°,⊙O的半径为2,求EN的长.13.MN是⊙O上的一条不经过圆心的弦,MN=4,在劣弧MN和优弧MN上分别有点A,B(不与M,N重合),且,连接AM,BM.(1)如图1,AB是直径,AB交MN于点C,∠ABM=30°,求∠CMO的度数;(2)如图2,连接OM,AB,过点O作OD∥AB交MN于点D,求证:∠MOD+2∠DMO=90°;(3)如图3,连接AN,BN,试猜想AM•MB+AN•NB的值是否为定值,若是,请求出这个值;若不是,请说明理由.14.已知,在△PAB中,PA=PB,经过A、B作⊙O.(1)如图1,连接PO,求证:PO平分∠APB;(2)如图2,点P在⊙O上,PA:AB=:2,E是⊙O上一点,连接AE、BE.求tan ∠AEB的值;(3)如图3,在(2)的条件下,AE经过圆心O,AE交PB于点F,过F作FG⊥BE于点G,EF+BG=14,求线段OF的长度.15.如图1,在⊙O中,点A为的中点,点D在⊙O上.(1)求证:∠BAC+2∠ADB=180°;(2)如图2,点G为⊙O上一点,DG与B C的延长线交于点K,若∠CBD=2∠ABC,BC=CK,求证:BG=KG;(3)如图3,在(2)的条件下,AC与BG的延长线交于点E,CE=3AC=15,BE=10,求线段BD的长.。
2020年中考数学2轮专题复习课件-第34讲图形面积问题PPT课件

B.2π D.6π
类型二:不规则几何图形的面积求法(1)
方法点拨:和差法,所求图形是不规则图形,可通 过转化成规则图形的面积的和或差.
2.如图,在 Rt△ ABC 中,∠ACB=90°,AC=2 3, 以点 B 为圆心,BC 的长为半径作弧,交 AB 于点 D,若 D 为 AB 的中点,43π
B.4 3-23π D.23π
3.如图,矩形 ABCD 的边 AB=1,BE 平分∠ABC,
交 AD 于点 E.若 E 是 AD 的中点,以点 B 为圆心,BE 长
为半径画弧,交 BC 于点 F,则图中阴影部分的面积是
(B )
A.2-π4
B.32-π4
C.2-π2
6.如图,三个小正方形的边长都为 1,则图中阴影
3π 部分面积的和是___8_____(结果保留 π).
7.(2018·四川巴中)如图,以六边形的每个顶点为圆 心,1 为半径画圆,则图中阴影部分的面积为___2_π____.
8.如图,在矩形 ABCD 中,BC=4,CD=2,以 AD 为直径的半圆 O 与 BC 相切于点 E,连接 BD,则阴影部 分的面积为__π______(结果保留 π).
2020年中考数学专题复习 1-3轮复习课件
第34讲 图形面积问题
类型一:规则几何图形的面积
方法点拨:公式法,所求图形是规则图形,如扇形、 特殊四边形等,可直接利用公式计算.
1.(2018·四川成都)如图,在▱ ABCD 中,∠B=60°,
⊙C 的半径为 3,则图中阴影部分的面积是( C )
A.π C.3π
方法点拨:等积变换法,直接求面积较麻烦或根本 求不出时,通过对图形的平移、旋转、割补等,为公式 法或和差法创造条件.
2020年中考数学二轮专题——二次函数与几何图形综合(压轴)题型(含详细解答)

2020年中考数学二轮专题——二次函数与几何图形综合(压轴)题型一、基础过关1. (2019宿迁)如图,抛物线y=x2+bx+c交x轴于A、B两点,其中点A坐标为(1,0),与y轴交于点C(0,-3).(1)求抛物线的函数表达式;(2)如图①,连接AC,点P在抛物线上,且满足∠P AB=2∠ACO.求点P的坐标;(3)如图②,点Q为x轴下方抛物线上任意一点,点D是抛物线对称轴与x轴的交点,直线AQ、BQ分别交抛物线的对称轴于点M、N.请问DM+DN是否为定值?如果是,请求出这个定值;如果不是,请说明理由.第1题图2. (2019贺州)如图,在平面直角坐标系中,已知点B的坐标为(-1,0),且OA=OC=4OB,抛物线y =ax2+bx+c(a≠0)图象经过A,B,C三点.(1)求A,C两点的坐标;(2)求抛物线的解析式;(3)若点P是直线AC下方的抛物线上的一个动点,作PD⊥AC于点D,当PD的值最大时,求此时点P 的坐标及PD的最大值.第2题图二、能力提升1. (2019菏泽)如图,抛物线与x 轴交于A ,B 两点,与y 轴交于点C (0,-2),点A 的坐标是(2,0),P 为抛物线上的一个动点,过点P 作PD ⊥x 轴于点D ,交直线BC 于点E ,抛物线的对称轴是直线x =-1.(1)求抛物线的函数表达式;(2)若点P 在第二象限内,且PE =14OD ,求△PBE 的面积;(3)在(2)的条件下,若M 为直线BC 上一点,在x 轴的上方,是否存在点M ,使△BDM 是以BD 为腰的等腰三角形?若存在,求出点M 的坐标;若不存在,请说明理由.第1题图三、满分冲关1. (2019襄阳)如图,在直角坐标系中,直线y =-12x +3与x 轴,y 轴分别交于点B ,点C ,对称轴为x=1的抛物线过B , C 两点,且交x 轴于另一点A ,连接A C.(1)直接写出点A ,点B ,点C 的坐标和抛物线的解析式;(2)已知点P 为第一象限内抛物线上一点,当点P 到直线BC 的距离最大时,求点P 的坐标; (3)抛物线上是否存在一点Q (点C 除外),使以点Q ,A ,B 为顶点的三角形与△ABC 相似?若存在,求出点Q 的坐标;若不存在,请说明理由.第1题图2、(2019滨州)如图①,抛物线y =-18x 2+12x +4与y 轴交于点A ,与x 轴交于点B ,C ,将直线AB 绕点A 逆时针旋转90°,所得直线与x 轴交于点D .(1)求直线AD 的函数解析式;(2)如图②,若点P 是直线AD 上方抛物线上的一个动点. ①当点P 到直线AD 的距离最大时,求点P 的坐标和最大距离; ②当点P 到直线AD 的距离为524时,求sin ∠P AD 的值.3、(2019金牛区一诊)如图,在平面直角坐标系中,抛物线y =ax 2+bx +c (a ≠0)与x 轴的两个交点分别为A (-3,0)、B (1,0),与y 轴交于点D (0,3),过顶点C 作CH ⊥x 轴于点H .(1)求抛物线的解析式和顶点C 的坐标;(2)连接AD 、CD ,若点E 为抛物线上一动点(点E 与顶点C 不重合),当△ADE 与△ACD 面积相等时,求点E 的坐标;(3)若点P 为抛物线上一动点(点P 与顶点C 不重合),过点P 向CD 所在的直线作垂线,垂足为点Q ,以P 、C 、Q 为顶点的三角形与△ACH 相似时,求点P 的坐标.第1题图备用图参考答案一、基础过关1. 解:(1)把A (1,0),C (0,-3)代入y =x 2+bx +c 得,⎩⎪⎨⎪⎧1+b +c =0c =-3,解得⎩⎪⎨⎪⎧b =2c =-3, ∴抛物线的函数表达式为y =x 2+2x -3;(2)如解图,作点A 关于y 轴的对称点A ′,连接A ′C ,作AD ⊥A ′C 于点D , ∴点A ′的坐标为(-1,0), 则AA ′=2,OC =3,A ′C =10, ∵S △A ′AC =12AA ′·OC =12A ′C ·AD ,∴AD =AA ′·OC A ′C =3105,在Rt △A ′AD 中,∵A ′D 2+AD 2=A ′A 2, ∴A ′D 2+(3105)2=22.解得A ′D =105(负值已舍去), ∴DC =4105,∴tan ∠ACA ′=AD DC =34. 由对称可得∠ACD =2∠ACO ,则∠P AB =∠ACA ′, 设P (a ,a 2+2a -3),①如解图,当点P 在x 轴的上方时,作P 1H 1⊥x 轴于点H 1, ∴tan ∠P 1AB =P 1H 1AH 1=a 2+2a -31-a =34,解得a 1=1(舍),a 2=-154,把a =-154代入得P (-154,5716);②如解图,当点P 在x 轴的下方时,作P 2H 2⊥x 轴于点H 2, ∴tan ∠P 2AB =P 2H 2AH 2=-a 2-2a +31-a =34,解得a 3=1(舍),a 4=-94,把a =-94代入得P (-94,-3916),综上所述,点P 的坐标为(-154,5716)或(-94,-3916);第1题解图(3)是.设Q (m ,m 2+2m -3),则-3<m <1. 设直线AQ 的解析式为y =k 1x +b 1,把A (1,0),Q (m ,m 2+2m -3),代入解析式解得⎩⎪⎨⎪⎧k 1=m +3b 1=m -3, ∴y =(m +3)x -m -3, 当x =-1时,y =-2m -6, 设直线BQ 的解析式为y =k 2x +b 2,把B (-3,0),Q (m ,m 2+2m -3)代入y =k 2x +b 2,解得⎩⎪⎨⎪⎧k 2=m -1b 2=3m -3,∴y =(m -1)x +3m -3, 当x =-1时,y =2m -2, ∴DM =2m +6,DN =-2m +2, ∴DM +DN =2m +6-2m +2=8. 2. 解:(1)∵B (-1,0), ∴OB =1.又∵OA =OC =4OB , ∴OA =OC =4, ∴A (4,0),C (0,-4);(2)将A 、B 、C 三点坐标代入y =ax 2+bx +c 得,⎩⎪⎨⎪⎧16a +4b +c =0a -b +c =0c =-4,解得⎩⎪⎨⎪⎧a =1b =-3c =-4, ∴抛物线的解析式为y =x 2-3x -4;(3)如解图,过点P 作PE ⊥x 轴交AC 于点E , ∴PE ∥y 轴. ∵OA =OC ,∴∠PED =∠OCA =45°, ∴△DEP 为等腰直角三角形, ∴PD =22PE , ∴当PE 取得最大值时,PD 取得最大值, 易得直线AC 的解析式为y =x -4, 设P (x ,x 2-3x -4),则E (x ,x -4),则PE =(x -4)-(x 2-3x -4)=-x 2+4x =-(x -2)2+4, ∵0<x <4,∴当x =2时,PE 取得最大值,最大值为4, 此时PD 取得最大值,最大值为4×22=22,∴点P 的坐标为(2,-6).第2题解图二、能力提升1. 解:(1)∵抛物线与x 轴交于A ,B 两点,点A 的坐标为(2,0),抛物线的对称轴为直线x =-1, ∴点B 的坐标为(-4,0).∴设抛物线的函数表达式为y =a (x +4)(x -2),将点C (0,-2)代入得-8a =-2,解得a =14.∴抛物线的函数表达式为y =14(x +4)(x -2)=14x 2+12x -2;(2)设点P 的坐标为(x ,14x 2+12x -2),则点D 的坐标为(x ,0),设BC 所在直线的表达式为y =kx +b , 将B (-4,0),C (0,-2)代入得,⎩⎪⎨⎪⎧-4k +b =0b =-2,解得⎩⎪⎨⎪⎧k =-12b =-2, ∴BC 所在直线的表达式为y =-12x -2.∴点E 的坐标为(x ,-12x -2).∴PE =14x 2+x .∵PE =14OD ,∴14x 2+x =-14x ,即14x 2+54x =0, 解得x =-5或x =0(舍). ∴PE =54,BD =1,∴S △PBE =12PE ·BD =12×54×1=58;(3)存在.①当DM =DB =1时,如解图①,过点M 作MF ⊥x 轴于点F , 设M (m ,-12m -2),则MF =-12m -2,DF =-m -5,∵MF 2+DF 2=DM 2,∴(-12m -2)2+(-m -5)2=1,解得m =-285或m =-4(舍去).∴点M 的坐标为(-285,45);第1题解图①②当BD =BM =1时,如解图②,过点M 作x 轴的垂线,垂足为N , ∵DE ⊥x 轴, ∴DE ∥MN ,∴BN ∶BD =BM ∶BE ,∴BN ∶1=1∶BE . ∵E (-5,12),∴DE =12,∴BE =52, ∴BN ∶1=1∶52,解得BN =255. ∴点M 的横坐标为-4-255,将x =-4-255代入y =-12x -2,得y =55,即点M 的坐标为(-4-255,55).综上所述,点M 的坐标为(-285,45)或(-4-255,55).第1题解图②三、满分冲关1. 解:(1)A (-4,0),B (6,0),C (0,3),抛物线的解析式为y =-18x 2+14x +3;【解法提示】令y =-12x +3=0,解得x =6,令x =0,得y =3,∴B (6,0),C (0,3).∵抛物线的对称轴为x =1,且过点B 、A ,∴抛物线与x 轴的另一交点A 坐标为(-4,0),设抛物线的解析式为y =a (x +4)(x -6),将点C (0,3)代入得-24a =3,解得a =-18.∴y =-18(x +4)(x -6)=-18x 2+14x +3(2)如解图①,过点P 作PG ⊥x 轴于点G ,交BC 于点Q ,过点P 作PH ⊥BC 于点H . ∵OC =3,OB =6, ∴BC =OC 2+OB 2=3 5. 又∵∠HQP =∠GQB , ∴∠HPQ =∠CBO , ∴sin ∠HPQ =sin ∠CBO =55. 故点P 到直线BC 的距离最大,即PQ 最大. 设P (m ,-18m 2+14m +3),Q (m ,-12m +3),∴PQ =-18m 2+14m +3-(-12m +3)=-18(m -3)2+98.∵-18<0,∴当m =3时,PQ 有最大值为98.∴P (3,218);第1题解图①(3)存在.由(1)得A (-4,0)、B (6,0)、C (0,3), ∴AB =10,AC =32+42=5. 分为两种情况分类讨论:①当△ABC ∽△AQB 时,如解图②所示. ∴AC AB =ABAQ,∠CAB =∠BAQ . ∴AQ =AB 2AC =1025=20,过点Q 作QD ⊥x 轴,垂足为点D , ∴QD =AQ ·sin ∠BAQ =20×35=12,AD =AQ ·cos ∠BAQ =20×45=16.∴Q (12,-12).第1题解图②②当△ABC ∽△BQA 时,如解图③所示, ∴AB BQ =ACAB,∠CAB =∠ABQ . ∴BQ =AB 2AC=20,过点Q 作QE ⊥x 轴,垂足为E ,同理可得QE =BQ ·sin ∠ABQ =20×35=12,BE =BQ ·cos ∠ABQ =20×45=16, ∴Q (-10,-12).综上所述,点Q 的坐标是(12,-12)或(-10,-12).第1题解图③2、解:(1)抛物线y =-18x 2+12x +4, 令x =0,可得A 点的坐标为(0,4),令y =0,可得B 点的坐标为(-4,0),C 点的坐标为(8,0).易得直线AB 的函数解析式为y =x +4,∵OA =OB ,∴∠BAO =45°.又∵直线AD 由直线AB 逆时针旋转90°而来,∴∠BAD =90°,∴∠OAD =45°,△OAD 为等腰直角三角形,∴OD =OA =4,D (4,0),易得直线AD 的函数解析式为y =-x +4;(2)①如解图①,过点P 作PE ⊥x 轴交AD 于点E ,PF ⊥AD 于点F ,第1题解图①易得△PEF 为等腰直角三角形,∴PF =22PE , ∴当PE 取得最大值时,PF 取得最大值,设P (x ,-18x 2+12x +4), 则E (x ,-x +4),∴PE =-18x 2+12x +4-(-x +4)=-18x 2+32x =-18(x -6)2+92, ∴当x =6时,PE 有最大值92, 此时PF 有最大值924, ∴当x =6时,-18x 2+12x +4=52, ∴当点P 到直线AD 的距离最大时,点P 的坐标为(6,52),最大距离为924; ②如解图②,连接AP ,过点P 作PE ⊥x 轴,交AD 于点E ,PF ⊥AD 于点F ,当点P 到AD 的距离为524时,PF =524, 则此时PE =2PF =52, 将PE =52代入PE =-18(x -6)2+92中, 解得x 1=10,x 2=2,∴此时点P 的坐标为(10,-72)或(2,92), 当点P 的坐标为(2,92)时,AP =22+(92-4)2=172, ∴sin ∠P AD =524172=53434; 当点P 的坐标为(10,-72)时, AP =102+(-72-4)2=252, ∴sin ∠P AD =PF AP =524252=210. 综上,sin ∠P AD 的值是53434或210.3、1. 解:(1)把点A 、B 、D 的坐标分别代入抛物线的解析式中得:⎩⎪⎨⎪⎧a +b +c =09a -3b +c =0c =3,解得⎩⎪⎨⎪⎧a =-1b =-2c =3,∴抛物线的解析式为y =-x 2-2x +3,∴抛物线的对称轴为直线x =-b 2a=-1, ∴点C 的坐标为(-1,4);(2)如解图①,过点C 作CE ∥AD 交抛物线于点E ,交y 轴于点T ,则△ADE 与△ACD 面积相等,直线AD 过点D ,设其解析式为y =mx +3,将点A 的坐标代入得:0=-3m +3,解得m =1,则直线AD 的解析式为y =x +3,∵CE ∥AD ,设直线CE 的解析式为y =x +n ,将点C 的坐标代入上式得:4=-1+n ,解得n =5,则直线CE 的解析式为y =x +5,则点T 的坐标为(0,5),联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +5, 解得x =-1或x =-2(x =-1为点C 的横坐标),即点E 的坐标为(-2,3);在y 轴取一点H ′,使DT =DH ′=2,过点H ′作直线E ′E ″∥AD ,则△ADE ′和△ADE ″都与△ACD 面积相等,同理可得直线E ′E ″的解析式为y =x +1,联立⎩⎪⎨⎪⎧y =-x 2-2x +3y =x +1, 解得x =-3±172, ∴点E ″、E ′的坐标分别为(-3+172,-1+172)、(-3-172,-1-172), 综上,满足要求的点E 的坐标为(-2,3)或(-3+172,-1+172)或(-3-172,-1-172);第1题解图①(3)如解图②,设点P 的坐标为(m ,n ),则n =-m 2-2m +3,把点C 、D 的坐标代入一次函数的解析式y =kx +b 得:⎩⎪⎨⎪⎧4=-k +b b =3, 解得⎩⎪⎨⎪⎧k =-1b =3, 即直线CD 的解析式为y =-x +3,由(1)得,直线AD 的解析式为y =x +3,∴AD ⊥CD ,而直线PQ ⊥CD ,故直线PQ 的解析式中的k 值与直线AD 的解析式中的k 值相同, 同理可得直线PQ 的解析式为y =x +(n -m ),联立⎩⎪⎨⎪⎧y =-x +3y =x +(n -m ), 解得x =3+m -n 2,即点Q 的坐标为(3+m -n 2,3-m +n 2), 则PQ 2=(m -3+m -n 2)2+(n -3-m +n 2)2=(m +n -3)22=12(m +1)2·m 2, 同理可得:PC 2=(m +1)2[1+(m +1)2],AH =2,CH =4,则AC =25,当△ACH ∽△CPQ 时,PC PQ =AC CH =52, 即4PC 2=5PQ 2,整理得3m 2+16m +16=0,解得m =-4或m =-43, ∴点P 的坐标为(-4,-5)或(-43,359); 当△ACH ∽△PCQ 时,同理可得,点P 的坐标为(-23,359)或(2,-5), 综上所述,点P 的坐标为(-4,-5)或(-43,359)或(-23,359)或(2,-5).第1题解图②。
2020年九年级数学中考几何图形综合题专题训练(含答案)

2020年九年级数学中考几何图形综合题专题训练1、如图,在▱ABCD 中,点E 在边BC 上,点F 在边AD 的延长线上,且DF=BE ,BE 与CD 交于点G(1)求证:BD ∥EF ;(2)若=,BE=4,求EC 的长.2、如图,在Rt △ABC 中,∠C =90°,AC =6,∠BAC =60°,AD 平分∠BAC 交BC 于点D ,过点D 作DE ∥AC 交AB 于点E .点M 是线段AD 上的动点,连接BM 并延长分别交DE ,AC 于点F ,G .(1)求CD 的长;(2)若点M 是线段AD 的中点,求EF DF的值;(3)请问当DM 的长满足什么条件时,在线段DE 上恰好只有一点P ,使得∠CPG =60°?3、如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.(1)求证:△AC D∽△BFD;(2)当tan∠ABD=1,AC=3时,求BF的长.4、如图,▱ABCD的对角线AC、BD交于点O,EF过点O且与BC、AD分别交于点E、F.试猜想线段AE、CF的关系,并说明理由.5、如图,平行四边形ABCD的对角线AC、BD相交于点O,E,F分别是OA,OC的中点,连接BE,DF(1)根据题意,补全原形;(2)求证:BE=DF.6、如图,在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD的内部,延长AF交CD于点G.(1)猜想并证明线段FG与CG的数量关系;(2)若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段FG与CG之间的数量关系是否改变?请证明你的结论;(3)若将图①中的正方形改成平行四边形,其他条件不变,如图③,那么线段FG与CG 之间的数量关系是否会改变?请证明你的结论.7、如图,四边形ABCD是菱形,CE⊥AB交AB的延长线于点E,CF⊥AD交AD的延长线于点F,求证:DF=BE.8、如图,□A BCD中,BD是它的一条对角线,过A、C两点作AE⊥BD,CF⊥BD,垂足分别为E、F,延长AE、CF分别交CD、AB于M、N。
2020年中考二轮复习 27道经典几何难题
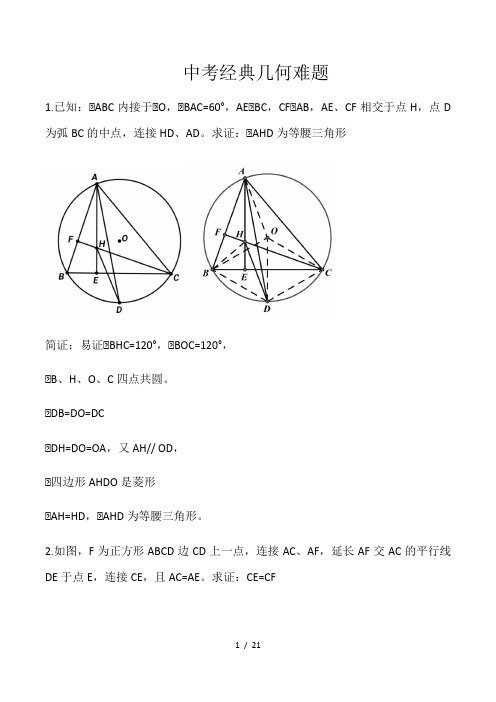
中考经典几何难题1.已知:△ABC内接于△O,△BAC=60°,AE△BC,CF△AB,AE、CF相交于点H,点D 为弧BC的中点,连接HD、AD。
求证:△AHD为等腰三角形简证:易证△BHC=120°,△BOC=120°,△B、H、O、C四点共圆。
△DB=DO=DC△DH=DO=OA,又AH// OD,△四边形AHDO是菱形△AH=HD,△AHD为等腰三角形。
2.如图,F为正方形ABCD边CD上一点,连接AC、AF,延长AF交AC的平行线DE于点E,连接CE,且AC=AE。
求证:CE=CF简证:作点E关于AD对称点G,则DE△DG△△CDG△△ADE,△ACG是等边三角形。
△△GAC=60°,△DAF=15°,△CEF=75°,△CFE=75°,△△CEF是等腰三角形。
△CE=CF。
3. 己知:△ABC中,AB=AC,△BAC=20°,△BDC=30°。
求证:AD=BC 简证:以AD为边作正三角形ADE(如图),易知△ABC△△CEA△AD=BC=AE。
4.已知:△ABC中,D为AC边的中点,△A=3△C,△ADB=45°。
求证:AB△BC简证:过点D作DE△AC交BC于E,由已知得AE=EC,△EAD=△C又△△A=3△C,△△BAE=△BEA,BA=BE,由△ADB=45°,得△EDB=45°△A、D、E、B四点共圆,△ABE=△ADE=90°,即AB△BC。
5.如图,四边形ABCD的两条对角线AC、BD交于点E,△BAC=50°,△ABD=60°,△CBD=20°,△CAD=30°,△ADB=40°。
求△ACD的度数。
解:设AD、BC交于点F,过D作DG//AB交BF于点G,AG交BD于H。
则△ABF是等腰三角形,A、B、G、D四点共圆。
2020年中考数学二轮专题——尺规作图(含详细解答)
2020年中考数学二轮专题——尺规作图基础过关1. 如图,观察图中的尺规作图痕迹,下列说法错误的是( )第1题图A. ∠DAE =∠EACB. ∠C =∠EACC. AE ∥BCD. ∠DAE =∠B2. (2019宜昌)通过如下尺规作图,能确定点D 是BC 边中点的是( )3. (2019海南)如图,直线l 1∥l 2,点A 在直线l 1上,以点A 为圆心,适当长度为半径画弧,分别交直线l 1、l 2于B 、C 两点,连接AC 、B C.若∠ABC =70°,则∠1的大小为( )A. 20°B. 35°C. 40°D. 70°第3题图4. (2019长沙)如图,Rt △ABC 中,∠C =90°,∠B =30°,分别以点A 和点B 为圆心,大于12AB 的长为半径作弧,两弧相交于M ,N 两点,作直线MN ,交BC 于点D ,连接AD ,则∠CAD 的度数是( )A. 20°B. 30°C. 45°D. 60°第4题图 5. (2019成都黑白卷)如图,在平行四边形ABCD 中,按以下步骤作图:①在直线BC 下方取一点P ;②以点A 为圆心,AP 长为半径画弧,交BC 于点M 、N ;③分别以M 、N 为圆心,大于12MN 长为半径画弧,交P 同侧于点Q ;⑤作射线AQ 交BC 于点E .若AE =BE =2,CE =4,则平行四边形ABCD 的面积为______.第5题图6. (2019高新区二诊)如图,在▱ABCD 中,以点A 为圆心,AB 长为半径作弧交AD 于点F ,分别以点B 、F 为圆心,同样长度m 为半径作弧,交于点G ,连接AG 并延长交BC 于点E .若BF =6,AB =4,则AE 的长为________.第6题图7. (2019金牛区二诊)如图,在矩形ABCD 中,AB =3BC ,以点A 为圆心,AD 为半径画弧交AB 于点E ,连接CE ,作线段CE 的中垂线交AB 于点F ,连接CF ,则sin ∠CFB =________.第7题图 能力提升1. (2019成华区二诊)如图,在平行四边形ABCD 中,AB =4,BC =7,以点B 为圆心,适当长为半径画弧,交BA 于点E ,交BC 于点F ,再分别以点E 、F 为圆心,大于12EF 的长为半径画弧,两弧相交于点G ,射线BG 交AD 于点I ,交CD 的延长线于点H ,则DH 的长是________.第1题图2. (2019葫芦岛)如图,BD 是▱ABCD 的对角线,按以下步骤作图:①分别以点B 和点D 为圆心,大于12BD 的长为半径作弧,两弧相交于E ,F 两点;②作直线EF ,分别交AD ,BC 于点M ,N ,连接BM ,DN .若BD =8,MN =6,则▱ABCD 的边BC 上的高为______.第2题图满分冲关1. (2019绍兴)如图,在直线AP上方有一个正方形ABCD,∠P AD=30°,以点B为圆心,AB长为半径作弧,与AP交于点A,M,分别以点A,M为圆心,AM长为半径作弧,两弧交于点E,连接ED,则∠ADE 的度数为________.第1题图参考答案基础过关1. A【解析】根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确,∴∠EAC=∠C,故B选项正确,∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B大小关系不确定,∴∠DAE 与∠EAC大小关系不确定,故A选项错误.2. A【解析】观察四个选项中的尺规作图可知,选项A中所作是边BC的垂直平分线,选项B中所作是边AB的垂直平分线,选项C中所作是∠BAC的平分线,选项D中所作是过点A作边BC的垂线,故选A.3. C【解析】∵由作图可知,AB=AC,∴∠ABC=∠ACB=70°,∵l1∥l2,∴∠1=∠CAB=180°-70°-70°,∴∠1=40°.4. B【解析】由题意可知,MN为AB的垂直平分线,∴∠DAB=∠B=30°.∵∠C=90°,∠B=30°,∴∠CAB=90°-∠B=60°.∴∠CAD=∠CAB-∠DAB=60°-30°=30°.5. 12【解析】由作图步骤可知AE⊥BC,即线段AE是平行四边形ABCD中BC边上的高线,∵AE=BE=2,CE=4,∴BC=6,∴S▱ABCD=BC×AE=12.6. 27 【解析】由题意可得:AB=AF=4,∠BAE=∠F AE,∴AE垂直平分BF,如解图,设AE与BF相交于点M,∴BM=MF.∵AD∥BC,∴AM=ME.∴BM=3,在Rt△AMB中,AM=42-32=7,∴AE =2AM=27.第6题解图7. 45【解析】∵AB=3BC,∴设BC=a,则AB=3a,根据题意可得:AD=AE=a,∴BE=2a,∵F在线段CE的垂直平分线上,∴设EF=CF=x,则BF=2a-x,在Rt△CFB中,x2-(2a-x)2=a2,解得x=54a,∴sin∠CFB=BCCF=a54a=45.能力提升1. 3【解析】由作图可知:BH是∠ABC的平分线,∴∠ABG=∠GBC,∵四边形ABCD是平行四边形,∴AD∥BC,∴∠AIB=∠IBC,∴∠ABI=∠AIB,∴AI=AB=4,∴ID=AD-AI=7-4=3,∵AB∥CD,∴∠H=∠ABH=∠AIB,∵∠AIB=∠HID,∴∠H=∠HID,∴DH=ID=3.2. 245 【解析】由作图方法可知MN 为BD 的垂直平分线,∵四边形ABCD 为平行四边形,∴四边形MBND 为菱形.如解图,设BD 与MN 交点为点O ,过点M 作MG ⊥BC 于点G ,∵BD =8,MN =6,∴OB =4,OM =3.∴MB =BN =5.∵S菱形MBND =12BD ·MN =BN ·MG ,∴12×8×6=5MG ,解得MG =245.即▱ABCD 的边BC 上的高为245.第2题解图满分冲关1. 15°或45° 【解析】当分别以点A ,M 为圆心,AM 长为半径画弧时,两弧的交点有两种情况,如解图中点E 与点E ′所示,当点E 在P A 下方时,∵四边形ABCD 为正方形,∠P AD =30°,∴∠DAB =90°,∴∠BAM =60°,∵AB =BM ,∴△ABM 为等边三角形,∵AM =AE =ME ,∴△AME 也是等边三角形,∴∠MAE =60°,∴∠P AE =180°-∠MAE =120°,∴∠DAE =∠P AD +∠P AE =150°,又∵AD =AE . ∴∠1=12×(180°-150°)=15°;当点E 在P A 上方与点B 重合时,∵AD =AB ,∠DAB =90°,∴∠AE ′D =∠2=45°.综上所述,∠ADE 的度数为15°或45°.第1题解图。
2020年中考数学二轮专题——矩形、菱形、正方形(含详细解答)
2020年中考数学二轮专题——矩形、菱形、正方形基础过关1. (2019无锡)下列结论中,矩形具有而菱形不一定具有的性质是()A. 内角和为360°B. 对角线相互平分C. 对角线相等D. 对角线互相垂直2. (2019娄底)顺次连接菱形四边中点得到的四边形是()A. 平行四边形B. 菱形C. 矩形D. 正方形3. (2019重庆A卷)下列命题正确的是()A.有一个角是直角的平行四边形是矩形B.四条边相等的四边形是矩形C.有一组邻边相等的平行四边形是矩形D.对角线相等的四边形是矩形4. (2019青羊区二诊)在菱形ABCD中,对角线AC、BD交于点O,下列说法错误的是()A.AB∥DC B.OC=OBC.AC⊥BD D.OA=OC5. (2019毕节)如图,点E在正方形ABCD的边AB上,若EB=1,EC=2,那么正方形ABCD的面积为()A. 3B. 3C. 5D. 5第5题图6. (2019天津)如图,四边形ABCD为菱形,A,B两点的坐标分别是(2,0),(0,1),点C,D在坐标轴上,则菱形ABCD的周长等于()A. 5B. 4 3C. 4 5D. 20第6题图7. (2019呼和浩特)已知菱形的边长为3,较短的一条对角线的长为2,则该菱形较长的一条对角线的长为()A. 2 2B. 2 5C. 4 2D. 2108. (2019临沂)如图,在▱ABCD中,M,N是BD上的两点,BM=DN,连接AM,MC,CN,N A.添加一个条件,使四边形AMCN 是矩形,这个条件是( )A. OM =12ACB. MB =MOC. BD ⊥ACD. ∠AMB =∠CND第8题图9. 如图,在正方形ABCD 外侧,作等边△ADE ,AC ,BE 相交于点F ,则∠BFC 为( ) A. 75°B. 60°C. 55°D. 45°第9题图10. 如图,在矩形ABCD 中,点E 在BC 上,AE =AD ,DF ⊥AE ,垂足为F ,若∠FDC =30°,且AB =3,则AD 的长为( )A .3B .4C .5D .6第10题图11. (2019贵阳)如图,菱形ABCD 的周长是4 cm ,∠ABC =60°,那么这个菱形的对角线AC 的长是( ) A. 1 cmB. 2 cmC. 3 cmD. 4 cm第11题图12. (2019德阳)已知▱ABCD 的对角线AC 、BD 相交于点O ,△AOD 是等边三角形,且AD =4,则AB 等于( )A. 2B. 4C. 2 3D. 4 313. (2019河池)如图,在正方形ABCD 中,点E ,F 分别在BC ,CD 上,BE =CF ,则图中与∠AEB 相等的角的个数是( )A. 1B. 2C. 3D. 4第13题图14. 如图,在矩形ABCD 中,AB =12,BC =16,点E 是BC 的中点,点F 是边CD 上的任意一点,则AF +EF 的最小值为( )A .12B .14C .12 5D .14 5第14题图15. (2019兰州)如图,边长为2的正方形ABCD 的对角线AC 与BD 交于点O ,将正方形ABCD 沿直线DF 折叠,点C 落在对角线BD 上的点E 处,折痕DF 交AC 于点M ,则OM =( )A.12B.22C.3-1D.2-1第15题图16. (2019金华)如图,矩形ABCD 的对角线交于点O ,已知AB =m ,∠BAC =∠α,则下列结论错误..的是( )A. ∠BDC =∠αB. BC =m ·tan αC. AO =m 2sin αD. BD =m cos α第16题图17. (2019台州)如图,有两张矩形纸片ABCD 和EFGH ,AB =EF =2 cm ,BC =FG =8 cm.把纸片ABCD 交叉叠放在纸片EFGH 上,使重叠部分为平行四边形,且点D 与点G 重合,当两张纸片交叉所成的角α最小时,tan α等于( )A. 14B. 12C. 817D. 815第17题图18.(2019绍兴)正方形ABCD的边AB上有一动点E,以EC为边作矩形ECFG,且边FG过点D,在点E从点A移动到点B的过程中,矩形ECFG的面积()A. 先变大后变小B. 先变小后变大C. 一直变大D. 保持不变第18题图19. (2019双流区一诊)一个菱形的周长为20 cm,一条对角线长为6 cm,则这个菱形的面积是______cm2.20. (2019扬州)如图,已知点E在正方形ABCD的边AB上,以BE为边向正方形ABCD外部作正方形BEFG,连接DF,M、N分别是DC、DF的中点,连接MN.若AB=7,BE=5,则MN=________.第20题图21.(2019徐州)如图,矩形ABCD中,AC、BD交于点O、M、N分别为BC、OC的中点.若MN=4,则AC的长为________.第21题图22. (2019菏泽)如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是________.第22题图23.如图,在矩形ABCD中,AB=6,BC=8,过对角线交点O作EF⊥AC交AD于点E,交BC于点F,则DE 的长是________.第23题图24. (2019北京)如图,在菱形ABCD 中,AC 为对角线,点E ,F 分别在AB ,AD 上,BE =DF ,连接EF . (1)求证:AC ⊥EF ;(2)延长EF 交CD 的延长线于点G ,连接BD 交AC 于点O .若BD =4,tan G =12,求AO 的长.第24题图25. (2019云南)如图,四边形ABCD 中,对角线AC 、BD 相交于点O ,AO =OC ,BO =OD ,且∠AOB =2∠OA D.(1)求证:四边形ABCD 是矩形;(2)若∠AOB ∶∠ODC =4∶3,求∠ADO 的度数.第25题图能力提升1. (2019烟台)如图,面积为24的▱ABCD中,对角线BD平分∠ABC,过点D作DE⊥BD交BC的延长线于点E,DE=6,则sin∠DCE的值为()A. 2425 B.45 C.34 D.1225第1题图2. (2019安徽)如图,在正方形ABCD中,点E,F将对角线AC三等分,且AC=12.点P在正方形的边上,则满足PE+PF=9的点P的个数是()A. 0B. 4C. 6D. 8第2题图3. (2019黄石)如图,矩形ABCD中,AC与BD相交于点E,AD∶AB=3∶1,将△ABD沿BD折叠,点A的对应点为F,连接AF交BC于点G,且BG=2,在AD边上有一点H,使得BH+EH的值最小,此时BHCF=()A.32 B.233 C.62 D.32第3题图4.(2019遵义)如图,平行四边形纸片ABCD的边AB,BC的长分别是10 cm和7.5 cm,将其四个角向内对折后,点B与点C重合于点C′,点A与点D重合于点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD的四条边上,则EF=________cm.第4题图5. (2019海南)如图,在边长为1的正方形ABCD中,E是边CD的中点,点P是边AD上一点(与点A、D不重合),射线PE与BC的延长线交于点Q.(1)求证:△PDE≌△QCE;(2)过点E作EF∥BC交PB于点F,连接AF,当PB=PQ时.①求证:四边形AFEP是平行四边形;②请判断四边形AFEP是否为菱形,并说明理由.第5题图6. (2019双流区一诊)如图①,菱形ABCD中,点P是CD的中点,∠BCD=60°,射线AP交BC的延长线于点E,射线BP交DE于点K,点O是线段BK的中点.(1)求证:△ADP≌△ECP;(2)若BP=n·PK,试求出n的值;(3)作BM⊥AE于点M,作KN⊥AE于点N,连接MO、NO,如图②,请证明△MON是等腰三角形,并求出∠MON的度数.第6题图满分冲关1. (2019新都区一诊)如图,直线l 经过正方形ABCD 的顶点A ,先分别过此正方形的顶点B 、D 作BE ⊥l 于点E 、DF ⊥l 于点F ,然后再以正方形的对角线的交点O 为端点,引两条相互垂直的射线分别与AD 、CD 交于点G 、H 两点.若EF =25,S △ABE =2,则线段GH 长度的最小值是______.第1题图2. (2018本溪)在菱形ABCD 中,∠BAD =120°,点O 为射线CA 上的动点,作射线OM 与直线BC 相交于点E ,将射线OM 绕点O 逆时针旋转60°,得到射线ON ,射线ON 与直线CD 相交于点F .(1)如图①,点O 与点A 重合时,点E ,F 分别在线段BC ,CD 上,请直接写出CE ,CF ,CA 三条线段之间的数量关系;(2)如图②,点O 在CA 的延长线上,且OA =13AC ,E ,F 分别在线段BC 的延长线和线段CD 的延长线上,请写出CE ,CF ,CA 三条线段之间的数量关系,并说明理由;(3)点O 在线段AC 上,若AB =6,BO =27,当CF =1时,请直接写出BE 的长.参考答案基础过关1. C2. C 【解析】顺次连接任意四边形的四边中点,得到四边形一定是平行四边形,如果原四边形的对角线相等,则可得中点四边形的邻边相等,即是菱形;如果原四边形的对角线互相垂直,则可得中点四边形的邻边垂直,即是矩形.因为菱形的对角线互相垂直,所以它的中点四边形是矩形.3.A 【解析】根据矩形的判定定理可知,有一个角是直角的平行四边形是矩形,故A 正确;四条边相等的四边形是菱形,不是矩形,故B 错误;有一组邻边相等的平行四边形是菱形,不是矩形,故C 错误;对角线相等的平行四边形是矩形,故D 错误.4. B 【解析】∵四边形ABCD 是菱形,∴AB ∥CD ,AC ⊥BD ,OA =OC ,故A ,C ,D 正确.5. B 【解析】在Rt △BCE 中,BC =22-12=3,∴正方形ABCD 的面积为(3)2=3.6. C 【解析】∵A (2,0),B (0,1),∴OA =2,OB =1,在Rt △AOB 中,由勾股定理得AB =22+12=5,∵四边形ABCD 为菱形,∴菱形ABCD 的周长为4AB =4 5.7. C 【解析】菱形对角线相互垂直且平分,因此另一条对角线长为2×32-1=4 2.8. A 【解析】∵四边形ABCD 是平行四边形,∴OB =OD ,OA =OC .∵BM =DN ,∴OM =ON ,∴四边形AMCN 是平行四边形.当OM =12AC 时,MN =AC ,∴四边形AMCN 是矩形.9. B 【解析】∵四边形ABCD 是正方形,∴∠BAD =90°,AB =AD ,∠BAF =45°,∵△ADE 是等边三角形,∴∠DAE =60°,AD =AE ,∴∠BAE =90°+60°=150°,AB =AE ,∴∠ABE =∠AEB =12(180°-150°)=15°,∴∠BFC =∠BAF +∠ABE =45°+15°=60°,故选B .10. D 【解析】∵四边形ABCD 是矩形,∴AD ∥BC ,∴∠AEB =∠DAF ,又∵DF ⊥AE ,∴∠DF A =∠B ,又∵AE =AD ,∴△ADF ≌△EAB ,∴DF =AB .∵∠ADF +∠FDC =90°,∠DAF +∠ADF =90°,∴∠FDC =∠DAF =30°,∴AD =2DF =2AB =6.11. A 【解析】∵菱形ABCD 的周长是4 cm ,∴AB =BC =CD =DA =1 cm ,又∵∠ABC =60°,∴△ABC 是等边三角形,∴AC =AB =BC =1 cm .12.D 【解析】在平行四边形ABCD 中,∵△AOD 为等边三角形,即OA =OD =AD =4,∴AC =BD =8,∴平行四边形ABCD 是矩形,∴由勾股定理得AB =4 3.13. C 【解析】四边形ABCD 是正方形,∴AD ∥BC ,∴∠DAE =∠AEB .∵BE =CF ,∠ABE =∠BCF ,AB =BC ∴△ABE ≌△BCF (SAS),∴∠BFC =∠AEB .∵AB ∥CD ,∴∠ABF =∠BFC =∠AEB .∴与∠AEB 相等的角有3个.14.C 【解析】如解图,作点E 关于直线CD 的对称点E ′,连接AE ′交CD 于点F ,此时AF +EF 的最小值为AE ′的长.∵在矩形ABCD 中,AB =12,BC =16,E 是BC 的中点,∴BE =CE =CE ′=8,∴BE ′=24,∴AE ′=AB 2+BE ′2=122+242=12 5.第14题解图15. D 【解析】∵四边形ABCD 是正方形,∴∠CBE =∠DCM =45°,BC =CD = 2.∴AC =BD =2.∴OC =1.由折叠的性质知,DE =CD =2,CF =EF ,∴BE =2-2,∠DFC =90°.∴∠CDM +∠DCE =90°.又∠BCE +∠DCE =90°,∴∠BCE =∠CDM . ∴△BCE ≌△CDM .∴CM =BE =2- 2.∴OM =OC -CM =1-(2-2)=2-1.16. C 【解析】∵四边形ABCD 是矩形,∴AC =BD ,且OD =OC ,∠ABC =90°,∴∠BDC =∠OCD =∠BAO =∠α,tan α=BC AB =BC m ,sin α=BC AC =BC 2AO ,cos α=AB AC =m AC ,∴BC =m ·tan α,AO =BC 2sin α,AC =m cos α,而BD =AC ,BC ≠m ,∴BD =m cos α,AO ≠m2sin α∴A 、B 、D 正确,C 错误.17.D 【解析】如解图,当B 、E 重合时, α最小,∵在△BMF 和△DMC 中,⎩⎪⎨⎪⎧∠BMF =∠DMC ∠F =∠C BF =DC ,∴△BMF ≌△DMC (AAS),∴BM =DM ,设FM =x ,则DM =BM =8-x ,在Rt △BFM 中,由勾股定理得22+x 2=(8-x )2,解得x =154,∴tan α=BF FM =2154=815.第17题解图18. D 【解析】如解图,连接DE ,∵在正方形ABCD 中,S △DEC =12AD ·CD =12S 正方形ABCD ,在长方形ECFG 中,S △DEC =12×EC ·GE =12S 矩形ECFG ,而点E 从点A 移动到点B 的过程中,三角形DEC 的面积保持不变,∴矩形ECFG 的面积保持不变.第18题解图19. 24 【解析】如解图,在菱形ABCD 中,BD =6.∵菱形的周长为20,BD =6,∴AB =5,BO =3,∴AO =52-32=4,AC =8.∴S 菱形ABCD =12×6×8=24.第19题解图20.132 【解析】 如解图,连接FC ,则MN =12CF ,在Rt △CFG 中,FG =5,CG =5+7=12,∴FC =52+122=13,∴MN =132.第20题解图21. 16 【解析】在△OBC 中,根据三角形中位线等于它所对的第三边的一半,得到OB =2MN =8,又根据矩形的性质:对角线相等且互相平分,得到AC =BD =2OB =16.22. 85 【解析】如解图,连接BD 交AC 于点O ,∵四边形ABCD 是正方形,AC 是对角线,∴CD =AD ,∠DAE =∠DCF =45°,BD ⊥AC . ∵AE =CF , ∴△DAE ≌△DCF (SAS), ∴DE =DF ,同理可证:DE =BE ,BE =BF ,∴四边形BEDF 是菱形,∵AC =8,AO =OD ,AE =2,∴OE =2,OD =4,∴DE =OD 2+OE 2=42+22=2 5.∴四边形BEDF 的周长为4DE =8 5.第22题解图23. 74 【解析】如解图,连接EC ,∵OA =OC ,EF ⊥AC ,∴EC =AE ,设DE =x ,则EC =AE =8-x ,根据勾股定理可得(8-x )2=x 2+62,解得x =74.∴DE 的长为74.第23题解图24. (1)证明:∵四边形ABCD 是菱形, ∴AB =AD ,∴∠BAC =∠DAC . ∵AB =AD ,BE =DF ,∴AB -BE =AD -DF ,即AE =AF . ∴△AEF 是等腰三角形. 又∵∠BAC =∠DAC , ∴AC ⊥EF ;(2)解:由题意作解图如下, ∵四边形ABCD 是菱形,∴AC ⊥BD ,AB ∥CD ,OB =12BD =12×4=2.∴∠G =∠AEG .由(1)知EF ⊥AC .又∵BD ⊥AC . ∴EF ∥BD .∴∠AEG =∠ABO . ∴∠G =∠ABO .∵tan G =12,∴tan ∠ABO =AO OB =12.∴AO =OB ·tan ∠ABO =2×12=1.第24题解图25. (1)证明:∵AO =OC ,BO =OD , ∴四边形ABCD 是平行四边形.又∵∠AOB =2∠OAD ,∠AOB 是△AOD 的外角, ∴∠AOB =∠OAD +∠ADO . ∴∠OAD =∠ADO . ∴AO =OD .又∵AC =AO +OC =2AO ,BD =BO +OD =2OD , ∴AC =BD .∴四边形ABCD 是矩形;(2)解:设∠AOB =∠DOC =4x ,∠ODC =3x ,则∠ODC =∠OCD =3x . 在△ODC 中,∠DOC +∠OCD +∠CDO =180°, ∴4x +3x +3x =180°, 解得x =18°.∴∠ODC =3×18°=54°.∴∠ADO =90°-∠ODC =90°-54°=36°.能力提升1. A 【解析】如解图,连接AC 交BD 于点O ,过点D 作DF ⊥BE 于点F .∵BD 平分∠ABC ,∴∠ABD =∠CBD .∵四边形ABCD 是平行四边形,∴BC ∥AD . ∴∠ADB =∠CBD .∴∠ABD =∠ADB .∴AB =AD . ∴▱ABCD 是菱形. ∴AO 垂直平分BD . ∵DE ⊥BD ,∴OC ∥DE .∴OC =12DE =12×6=3.∵菱形ABCD 的面积为24,∴BD =8. ∴BO =4. ∴BC =DC =5.∵DF ·BC =24,∴DF =245. ∴sin ∠DCE =DF DC =2425.第1题解图2. D 【解析】如解图,∵点E ,F 将对角线AC 三等分,且AC =12,∴AE =EF =FC =4,当P 点在AD 上时,作E 点关于AD 的对称点E ′,连接E ′F ,则AE ′=AE =4,当P 点运动至E ′F 和AD 交点时,PE +PF 具有最小值,由对称性可知∠E ′AF =90°,此时E ′F =(AE ′)2+AF 2=42+82=45<9,当P 点和A 点重合时,过点E 作EG ⊥AD ,垂足为G ,PE +PF =AE +AF =12,当P 点和D 点重合时,连接DF ,∵AD =CD ,∠DAE =∠DCF ,AE =CF ,∴△AED ≌△CFD (SAS),∴DE =DF ,∴PE +PF =2DE =2EG 2+DG 2=2×(22)2+(42)2=410.∵45<9<12,45<9<410,∴在AD 上有两个位置存在PE +PF =9,同理在其余三边上各有两种情况,故正方形四条边上共存在8个位置使得PE +PF =9,∴满足条件的P 点有8个.第2题解图3. B 【解析】∵矩形ABCD 中,AD ∶AB =3∶1,∴∠ADB =30°,又△ABD 沿BD 折叠,点A 的对应点为F ,∴∠ADB =∠BDF =30°,∠ABD =∠DBF =60°,AD =FD ,AB =BF ,∴∠CDF =30°,△ADF 为等边三角形,DF =AF ,∴∠BAF =12(180°-∠ABD -∠DBF )=30°=∠CDF ,又DC =AB ,∴△ABF ≌△DCF ,∴CF =BF ,在Rt △ABG 中,ABG =90°,∠BAG =30°,BG =2,∴AB =23,∴CF =23,如解图,延长BA 到B ′使AB ′=AB ,连接EB ′交AD 于H ,根据对称性可知此时点H 即为满足BH +EH 的值最小的H 点.∵∠ADB =30°,∴AB =BE =ED ,又∵AB ′=AB =BE =AE ,∴△BB ′E 为直角三角形,在Rt △BEH 和Rt △BAH 中,BH =BH ,BE =BA ,∴Rt △BEH ≌Rt △BAH ,∴∠ABH =30°,∴BH =AB cos ∠ABH=4,∴BH CF =423=233.第3题解图4. 10 【解析】根据折叠的性质可得△CFH ≌△C ′FH ,△DFG ≌△A ′FG ,△AEG ≌△A ′EG ,△HBE ≌△HC ′E ,∵四边形HFGE 是矩形,∴HF =EG ,FG =HE ,∴△CFH ≌△C ′FH ≌△AEG ≌△A ′EG ,△DFG ≌△A ′FG ≌△HBE ≌△HC ′E ,∴EF =A ′F + A ′E =FD +AE = FD +CF =CD =AB =10 cm .5. (1)证明:∵四边形ABCD 是正方形, ∴∠D =∠BCD =90°. ∴∠ECQ =90°=∠D . ∵E 是CD 的中点, ∴DE =CE .又∵∠DEP =∠CEQ , ∴△PDE ≌△QCE (ASA);(2)①证明:如解图,由(1)可知△PDE ≌△QCE , ∴PE =QE =12PQ .又∵EF ∥BC , ∴PF =FB =12PB .∵PB =PQ , ∴PF =PE . ∴∠1=∠2.∵四边形ABCD 是正方形, ∴∠BAD =90°.在Rt △ABP 中,∵F 是PB 的中点, ∴AF =12BP =FP .∴∠3=∠4.又∵AD ∥BC ,EF ∥BC , ∴AD ∥EF . ∴∠1=∠4.∴∠2=∠3. 又∵PF =FP ,∴△APF ≌△EFP (AAS). ∴AP =EF . 又∵AP ∥EF ,∴四边形AFEP 是平行四边形;第5题解图②解:四边形AFEP 不是菱形,理由如下: 设PD =x ,则AP =1-x . 由(1)可知△PDE ≌△QCE . ∴CQ =PD =x . ∴BQ =BC +CQ =1+x .∵点E ,F 分别是PQ ,PB 的中点, ∵EF 是△PBQ 的中位线. ∴EF =12BQ =1+x 2.由①可知AP =EF . 即1-x =1+x 2,解得x =13.∴PD =13,AP =23.在Rt △PDE 中,∵DE =12,∴PE =PD 2+DE 2=136. ∵AP ≠PE .∴四边形AFEP 不是菱形.6. (1)证明:∵四边形ABCD 为菱形, ∴AD ∥BC ,∴∠DAP =∠CEP ,∠ADP =∠ECP , 在△ADP 和△ECP 中,⎩⎪⎨⎪⎧∠DAP =∠CEP ∠ADP =∠ECP DP =CP, ∴△ADP ≌△ECP (AAS);(2)解:如解图①,过点P 作PI ∥CE 交DE 于点I , 则PI CE =DPDC ,又点P 是CD 的中点, ∴PI CE =12, ∵△ADP ≌△ECP , ∴AD =CE , ∴KP KB =PI BE =14, ∴BP =3PK , ∴n =3;第6题解图①(3)解:如解图②,过点O 作OG ⊥AE 于点G , ∵BM ⊥AE 于点M ,KN ⊥AE 于点N , ∴BM ∥OG ∥KN , ∵点O 是线段BK 的中点, ∴MG =NG ,又∵OG ⊥MN , ∴OM =ON ,即△MON 是等腰三角形,由题意得,△BPC ,△AMB ,△ABP 为直角三角形, 设BC =2,则CP =1,由勾股定理得,BP =3, 则AP =7,根据三角形面积公式,BM =2217, ∴MP =377.易得PB =3PO ,∴OG =13BM =22121,MG =23MP =277,tan ∠MOG =MGOG =3,∴∠MOG =60°,∴∠MON 的度数为120°.第6题解图②满分冲关1. 6 【解析】由题易证△ABE ≌△DAF .∵GO ⊥HO ,易得△AGO ≌△DHO ,∴GO =HO .∴△GHO 为等腰直角三角形.∴当GO 最小时,GH 取得最小值.令AF =a ,AE =b ,则BE =a ,DF =b ,∴a +b =25,12a ·b =2,∴AB 2=a 2+b 2=12.∴AB =23.∴当GO ⊥AD 时,GO 有最小值,此时OG ∥AB ,∵O 为BD 中点,∴OG 为△ABD 的中位线,∴GO =12AB =3,∴GO 的最小值为3,∴GH 最小值为 6.2. 解:(1)CA =CE +CF ;【解法提示】∵在菱形ABCD 中,∠BAD =120°, ∴∠DAC =∠ACB =∠D =60°. 又∵∠EAF =60°, ∴∠DAF =∠CAE . ∵AD =CD 且∠D =60°,∴△ACD 是等边三角形,AD =AC , ∴△ADF ≌△ACE , ∴DF =CE .又∵CA =CD =DF +CF , ∴CA =CE +CF . (2)CF -CE =43CA ,理由:如解图①,过点O 作OG ∥AD ,交CF 于点G , ∵四边形ABCD 是菱形, ∴AB =BC =CD =DA . ∵∠BAD =120°, ∴∠B =∠ADC =60°,∴△ABC 和△ADC 都为等边三角形. ∵OG ∥AD ,∴∠OGC =∠ADC =∠ACD =60°, ∴△OGC 为等边三角形,∴OC =OG ,∠OCE =∠OGF =180°-60°=120°. ∵∠COE =∠GOF =60°-∠EOG ,∴△OCE ≌△OFG , ∴FG =CE . ∵CF =GF +CG , ∴CF -CE =CO . ∵AO =13CA ,∴OC =43CA ,∴CF -CE =43CA ;第2题解图①(3)BE 的长为1或3或5.【解法提示】连接BD 交AC 于点I ,①如解图②,当点O 在AI 上时,过点O 作OP ⊥BC 于点P ,作OQ ⊥CD 于点Q , 又∵菱形ABCD 中,AC 平分∠BCD , ∴OP =OQ .∵∠POQ =360°-120°-90°×2=60°, ∴∠EOF =∠POQ , ∴∠EOP =∠FOQ . 又∵∠OPE =OQF =90°, ∴△EOP ≌△FOQ , ∴EP =FQ .在Rt △AIB 中,AB =6,∠BAI =60°, ∴BI =AB ·sin60°=3 3. 在Rt △BIO 中, BO =27,BI =33, ∴OI =OB 2-BI 2=1. 又∵CI =12AC =3,∴OC =3+1=4, ∴CP =CQ =12OC =2.又∵CF =1,∴EP =FQ =1,∴BE =BC -CP -EP =6-2-1=3;第2题解图②②如解图③,当点O 在AI 上,点F 在线段DC 的延长线上时,过点O 作OP ⊥BC 于点P ,过点O 作OQ ⊥CD 于点Q ,同理可得EP =QF ,OC =4,CQ =CP =2, ∵CF =1,∴QF =CQ +CF =3,∴BE =CB -CP -PE =6-2-3=1;第2题解图③③如解图④,当点O 在IC 上时,由①知OC =3-1=2, 又∵CF =1,∠ACD =60°, ∴OF ⊥CD ,∴∠OEC =360°-60°-120°-90°=90°, ∴EC =12OC =1,∴BE =6-1=5;第2题解图④④如解图⑤,当点O 在IC 上,点F 在线段DC 的延长线上时,过点O 作OP ⊥BC 于点P ,过点O 作OQ ⊥CD 于点Q ,同理可得QF =PE ,OC =2,CP =CQ =1,QF =CQ +CF =2,∴BE =BC -EP -CP =6-2-1=3; 综上所述,BE 的长为1或3或5.第2题解图⑤。
2020年无锡中考初三数学第二轮专题复习:仅用无刻度直尺作图 1
无锡市**实验学校初三数学(2017级) 日期:2020−5−21 讲义编号: < >初三数学第二轮专题复习:仅用无刻度直尺作图1班级:________ 学生:______________姓名:______________一、格点作图例1:如图1是边长为1的小正方形网格,请用无刻度的直尺在图中作图:(1)画线段AB =17,使得点A ,B 均落在格点上; (2)在线段AB 上画出点P ,使AP =2173,并说明理由.CBA练一练:如图2是边长为1的小正方形网格,请用无刻度的直尺在图中画线段AP =5267.(1)过点C 画直线CD ,使CD ∥AB ,过点C 画直线CF ,使CF ⊥AB ; (2)画线段AB 的垂直平分线MN .例3:如图4,A ,O ,B 均为格点,请用无刻度的直尺作出∠CAB 的平分线。
CBACB ACBA图4 图5 图6练一练:在6×6的正方形网格中,点A 、B 、C 均在格点上,请仅用无刻度的直尺画图: (1)在图5中找出∆ABC 的重心G .(2)在图6中找出∆ABC 的外心O .练一练:如图7,A 、B 、C 、D 均在正方形网格的格点上,D 是边AB 上一点,请用无刻度的直尺在△ABC 的边BC 上找一点E ,使得△BDE ∽△BAC 相似。
图7D CBA思考题:如图8,A、B、C均在正方形网格的格点上,用无刻度的直尺,在线段AC上找一点D,使得AB2=AD•AC。
OA图8 图9例4:如图9,点A、B、O均为6×6的正方形格点图中的格点.(1)tan∠AOB=;(2)请用无刻度的直尺画出∠COB,使得tan∠COB=23.例5:如图10,在10×10的正方形格点图中,点A、B、C均在格点上,请仅用无刻度的直尺:(1)画出∆ABD,使得∆ABD与∆ABC关于AB对称;(2)画出∆ACE,使得∆ACE与∆ACB关于AC对称;图10 图11 图12 练一练:如图11,点A,B,C是边长为1的正方形网格中的格点,点P,Q分别为线段AB,AC上的动点.请仅用无刻度的直尺,画出当PC+PQ取得最小值时的线段PC、PQ.例6:如图12,点A、B、C均为6×8的正方形格点图中的格点.请用无刻度的直尺,画出一个以AB为一边的矩形ABMN,使矩形ABMN的面积等于△ABC的面积.练一练:如图13,点A、B、C均为8×9的正方形格点图中的格点.请用无刻度的直尺,在△ABC的内部有一点P,满足S△P AB:S△PBC:S△PCA=1:2:3,并简要说明点P的位置是如何找到的(不要求证明).- 2 -- 2 -。
2020年中考数学二轮专项复习——四边形、动点、最值问题 压轴题型(含详细解答)
2020年中考数学二轮专项复习——四边形、动点、最值问题压轴题型1、如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是。
解:【分析】连接CP,当点E,P,C在同一直线上时,AP+PE的最小值为CE长,依据△ABF≌△CDE,即可得到AP+EP最小值等于线段AF的长.如图,连接CP,由AD=CD,∠ADP=∠CDP=45°,DP=DP,可得△ADP≌△CDP,∴AP=CP,∴AP+PE=CP+PE,∴当点E,P,C在同一直线上时,AP+PE的最小值为CE长,此时,由AB=CD,∠ABF=∠CDE,BF=DE,可得△ABF≌△CDE,∴AF=CE,∴AP+EP最小值等于线段AF的长,【点评】本题考查的是轴对称,最短路线问题,根据题意作出A关于BD的对称点C是解答此题的关键.2、【猜想】如图1,在平行四边形ABCD中,点O是对角线AC的中点,过点O的直线分别交AD.BC于点E.F.若平行四边形ABCD的面积是8,则四边形CDEF的面积是.【探究】如图2,在菱形ABCD中,对角线相交于点O,过点O的直线分别交AD,BC于点E,F,若AC=5,BD=10,求四边形ABFE的面积.【应用】如图3,在Rt△ABC中,∠BAC=90°,延长BC到点D,使DC=BC,连结AD,若AC=3,AD=2,则△ABD的面积是.解:猜想:∵四边形ABCD是平行四边形,∴AD∥BC,OA=OC.∴∠EAO=∠FCO,∠AEO=∠CFO,在△AOE和△COF中,,∴△AEO≌△CFO(AAS),∴四边形CDEF的面积=S△ACD=▱ABCD的面积=4;故答案为:4;探究:∵四边形ABCD是菱形,∴AD∥BC,AO=CO AC=2.5,BO=BD=5,∠AOD=90°,∴AB=AC=,∠OAE=∠OCF,∠OEA=∠OFC,在△AOE于△COF中,,∴△AOE≌△COF(AAS),∵AC⊥BD,∴S四边形ABFE=S△ABC=AC•BO=××5=.应用:延长AC到E使CE=AC=3,在△ABC与△CDE中,,∴△ABC≌△CDE(SAS),∴∠E=∠BAC=90°,∴DE=,∴S△ABD=S△ADE=AE•DE=×6×2=6.故答案为:63、如图,正方形ABCD的边长是2,点E是CD边的中点,点F是边BC上不与点B,C重合的一个动点,把∠C 沿直线EF折叠,使点C落在点C′处.当△ADC′为等腰三角形时,FC的长为.【分析】首先证明DC′≠DA,只要分两种情形讨论即可:①如图1中,当AD=AC′=2时,连接AE.构建方程即可;②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件;【解答】解:由题意DE=EC=EC′=1,∴DC′<1+1∴DC′≠DA,只要分两种情形讨论即可:①如图1中,当AD=AC′=2时,连接AE.∵AE=AE,AD=AC′,DE=DC′,∴△ADE≌△AC′E,∴∠ADE=∠AC′E=90°,∵∠C=∠FC′E=90°,∴∠AC′E+∠FC′E=180°,∴A、C′、F共线,设CF=x,则BF=2﹣x,AF=2+x,在Rt△ABF中,22+(2﹣x)2=(2+x)2,解得x=.②如图2中,当点F在BC中点时,易证AC′=DC′,满足条件,此时CF=1.综上所述,满足条件的CF的长为或1.故答案为或1.【点评】本题考查翻折变换、正方形的性质、全等三角形的判定和性质、等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的首先思考问题,属于中考填空题中的压轴题.4、如图1,在平面直角坐标系中,一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,过点A作AB ⊥x轴,垂足为点A,过点C作CB⊥y轴,垂足为点C,两条垂线相交于点B.(1)线段AB,BC,AC的长分别为AB=,BC=,AC=;(2)折叠图1中的△ABC,使点A与点C重合,再将折叠后的图形展开,折痕DE交AB于点D,交AC于点E,连接CD,如图2.请从下列A、B两题中任选一题作答,我选择题.A:①求线段AD的长;②在y轴上,是否存在点P,使得△APD为等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.B:①求线段DE的长;②在坐标平面内,是否存在点P(除点B外),使得以点A,P,C为顶点的三角形与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.解:(1)∵一次函数y=﹣2x+8的图象与x轴,y轴分别交于点A,点C,∴A(4,0),C(0,8),∴OA=4,OC=8,∵AB⊥x轴,CB⊥y轴,∠AOC=90°,∴四边形OABC是矩形,∴AB=OC=8,BC=OA=4,在Rt△ABC中,根据勾股定理得,AC==4,故答案为:8,4,4;(2)A、①由(1)知,BC=4,AB=8,由折叠知,CD=AD,在Rt△BCD中,BD=AB﹣AD=8﹣AD,根据勾股定理得,CD2=BC2+BD2,即:AD2=16+(8﹣AD)2,∴AD=5,②由①知,D(4,5),设P(0,y),∵A(4,0),∴AP2=16+y2,DP2=16+(y﹣5)2,∵△APD为等腰三角形,∴Ⅰ、AP=AD,∴16+y2=25,∴y=±3,∴P(0,3)或(0,﹣3)Ⅱ、AP=DP,∴16+y2=16+(y﹣5)2,∴y=,∴P(0,),Ⅲ、AD=DP,25=16+(y﹣5)2,∴y=2或8,∴P(0,2)或(0,8).B、①、由A①知,AD=5,由折叠知,AE=AC=2,DE⊥AC于E,在Rt△ADE中,DE==,②、∵以点A,P,C为顶点的三角形与△ABC全等,∴△APC≌△ABC,或△CPA≌△ABC,∴∠APC=∠ABC=90°,∵四边形OABC是矩形,∴△ACO≌△CAB,此时,符合条件,点P和点O重合,即:P(0,0),如图3,过点O作ON⊥AC于N,易证,△AON∽△ACO,∴,∴,∴AN=,过点N作NH⊥OA,∴NH∥OA,∴△ANH∽△ACO,∴,∴,∴NH=,AH=,∴OH=,∴N(,),而点P2与点O关于AC对称,∴P2(,),同理:点B关于AC的对称点P1,同上的方法得,P1(﹣,),即:满足条件的点P的坐标为:(0,0),(,),(﹣,).5、如图,在平面直角坐标系中,以坐标原点O为圆心,2为半径画圆,P是⊙O上一动点且在第一象限内,过点P作⊙O的切线,与x、y轴分别交于点A、B.(1)求证:△OBP与△OPA相似;(2)当点P为AB中点时,求出P点坐标;(3)在⊙O上是否存在一点Q,使得以Q,O,A、P为顶点的四边形是平行四边形.若存在,试求出Q点坐标;若不存在,请说明理由.解:(1)证明:∵AB是过点P的切线,∴AB⊥OP,∴∠OPB=∠OPA=90°;(1分)∴在Rt△OPB中,∠1+∠3=90°,又∵∠BOA=90°∴∠1+∠2=90°,∴∠2=∠3;(1分)在△OPB中△APO中,∴△OPB∽△APO.(2分)(2)∵OP⊥AB,且PA=PB,∴OA=OB,∴△AOB是等腰三角形,∴OP是∠AOB的平分线,∴点P到x、y轴的距离相等;(1分)又∵点P在第一象限,∴设点P(x,x)(x>0),∵圆的半径为2,∴OP=,解得x=或x=﹣(舍去),(2分)∴P点坐标是(,).(1分)(3)存在;①如图设OAPQ为平行四边形,∴PQ∥OA,OQ∥PA;∵AB⊥OP,∴OQ⊥OP,PQ⊥OB,∴∠POQ=90°,∵OP=OQ,∴△POQ是等腰直角三角形,∴OB是∠POQ的平分线且是边PQ上的中垂线,∴∠BOQ=∠BOP=45°,∴∠AOP=45°,设P(x,x)、Q(﹣x,x)(x>0),(2分)∵OP=2代入得,解得x=,∴Q点坐标是(﹣,);(1分)②如图示OPAQ为平行四边形,同理可得Q点坐标是(,﹣).(1分)6、如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连结AD,以AD为一边且在D的右侧作正方形ADEF,解答下列问题:(1)如果AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),如图2,线段CF,BD之间的位置关系为,数量关系为;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,为什么?(2)如果AB≠AC,∠BAC≠90°,点D在线段BC上运动(如图4)当∠ACB=时,CF⊥BC(点C,F 重合除外)?(3)若AC=4,BC=3.在(2)的条件下,设正方形ADEF的边DE与线段CF相交于点P,求线段CP长的最大值.解:(1)CF⊥BD,CF=BD,理由如下:∵四边形ADEF是正方形,∴∠DAF=90°,AD=AF,∵AB=AC,∠BAC=90°,∴∠BAD+∠DAC=∠CAF+∠DAC=90°,∴∠BAD=∠CAF,在△BAD和△CAF中,,∴△BAD≌△CAF(SAS),∴CF=BD,∴∠B=∠ACF,∴∠B+∠BCA=90°,∴∠BCA+∠ACF=90°,即CF⊥BD;故答案为:CF⊥BD,CF=BD;②当点D在BC的延长线上时,①的结论仍成立.如图2,由正方形ADEF得:AD=AF,∠DAF=90°.∵∠BAC=90°,∴∠DAF=∠BAC.∴∠DAB=∠FAC.又∵AB=AC,∴△DAB≌△FAC(SAS).∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°.∴∠BCF=∠ACB+∠ACF=90°,∴CF⊥BD;(2)当∠BCA=45°时,CF⊥BD;理由如下:如图3,过点A作AC的垂线与CB所在直线交于G,∵∠ACB=45°,∴△AGC等腰直角三角形,∴AG=AC,∠AGC=∠ACG=45°,∵AG=AC,AD=AF,∵∠GAD=∠GAC﹣∠DAC=90°﹣∠DAC,∠FAC=∠FAD﹣∠DAC=90°﹣∠DAC,∴∠GAD=∠FAC,∴△GAD≌△CAF(SAS),∴∠ACF=∠AGD=45°,∴∠GCF=∠GCA+∠ACF=90°,∴CF⊥BC;故答案为:45°;(3)过点A作AQ⊥BC交CB的延长线于点Q,如图4所示:∵DE与CF交于点P时,此时点D位于线段CQ上,∵∠BCA=45°,AC=4,∴△ACQ是等腰直角三角形,∴AQ=CQ=4.设CD=x,则DQ=4﹣x,∵∠ADB+∠ADE+∠PDC=180°且∠ADE=90°,∴∠ADQ+∠PDC=90°,又∵在直角△PCD中,∠PDC+∠DPC=90°∴∠ADQ=∠DPC,∵∠AQD=∠DCP=90°∴△AQD∽△DCP,∴=,即=.解得:CP=﹣x2+x=﹣(x﹣1)2+1.∵0<x≤3,∴当x=1时,CP有最大值1,即线段CP长的最大值为1.7、如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(与点O不重合),作AF⊥BE,垂足为G,交BC于F,交BO于H,连接OG,CG.(1)求证:AH=BE;(2)试探究:∠AGO的度数是否为定值?请说明理由;(3)若OG⊥CG,BG=2,求S△OGC的值.解析:(1)证明:∵四边形ABCD是正方形,∴OA=OB,∠AOB=∠BOE=90°,∵AF⊥BE,∴∠GAE+∠AEG=∠OBE+∠AEG=90°.∴∠GAE=∠OBE,在△AOH和△BOE中,,∴△AOH≌△BOE(ASA),∴AH=BE.(2)解:∠AGO的度数为定值,理由如下:∵∠AOH=∠BGH=90°,∠AHO=∠BHG,∴△AOH∽△BGH,∴=,∴=,∵∠OHG=∠AHB,∴△OHG∽△AHB,∴∠AGO=∠ABO=45°,即∠AGO的度数为定值.(3)解:∵∠ABC=90°,AF⊥BE,∴∠BAG=∠FBG,∠AGB=∠BGF=90°,∴△ABG∽△BFG,∴=,∴AG•GF=BG2=20,∵△AHB∽△OHG,∴∠BAH=∠GOH=∠GBF.∵∠AOB=∠BGF=90°,∴∠AOG=∠GFC,∵∠AGO=45°,CG⊥GO,∴∠AGO=∠FGC=45°.∴△AGO∽△CGF,∴=,∴GO•CG=AG•GF=20.∴S△OGC=CG•GO=10.8、已知,如图,在长方形ABCD中,AB=4,AD=6.延长BC到点E,使CE=3,连接DE.(1)DE的长为.(2)动点P从点B出发,以每秒1个单位的速度沿BC﹣CD﹣DA向终点A运动,设点P运动的时间为t秒,求当t为何值时,△ABP和△DCE全等?(3)若动点P从点B出发,以每秒1个单位的速度仅沿着BE向终点E运动,连接DP.设点P运动的时间为t秒,是否存在t,使△PDE为等腰三角形?若存在,请直接写出t的值;否则,说明理由.解:(1)∵四边形ABCD是矩形∴AB=CD=4,AD=BC=6,CD⊥BC在Rt△DCE中,DE===5 故答案为5.(2)若△ABP与△DCE全等∴BP=CE或AP=CE当BP=CE=3时,则t==3秒当AP=CE=3时,则t==13秒∴求当t为3秒或13秒时,△ABP和△DCE全等.(3)若△PDE为等腰三角形则PD=DE或PE=DE或PD=PE当PD=DE时,∵PD=DE,DC⊥BE∴PC=CE=3∵BP=BC﹣CP=3∴t==3当PE=DE=5时,∵BP=BE﹣PE∴BP=9﹣5=4∴t==4当PD=PE时,∴PE=PC+CE=3+PC∴PD=3+PC在Rt△PDC中,DP2=CD2+PC2.∴(3+PC)2=16+PC2∴PC=∵BP=BC﹣PC∴BP=∴t==综上所述:当t=3秒或4秒或秒时,△PDE为等腰三角形.9、在平面直角坐标系中,BC∥OA,BC=3,OA=6,AB=3(1)直接写出点B的坐标;(2)已知D、E分别为线段OC、OB上的点,OD=5,OE=2BE,直线DE交x轴于点F,求直线DE的解析式;(3)在(2)的条件下,点M是直线DE上的一点,在x轴上方是否存在另一个点N,使以O、D、M、N为顶点的四边形是菱形?若存在,请直接写出点N的坐标;若不存在,请说明理由.【分析】(1)过B作BG⊥OA于点G,在Rt△ABG中,利用勾股定理可求得BG的长,则可求得B点坐标;(2)由条件可求得E点坐标,利用待定系数法可求得直线DE的解析式;(3)当OD为边时,则MO=OD=5或MD=OD=5,可求得M点坐标,由MN∥OD,且MN=OD可求得N点坐标;当OD为对角线时,则MN垂直平分OD,则可求得M、N的纵坐标,则可求得M的坐标,利用对称性可求得N点坐标.【解答】解:(1)如图1,过B作BG⊥OA于点G,∵BC=3,OA=6,∴AG=OA﹣OG=OA﹣BC=6﹣3=3,在Rt△ABG中,由勾股定理可得AB2=AG2+BG2,即(3)2=32+BG2,解得BG=6,∴OC=6,∴B(3,6);(2)由OD=5可知D(0,5),∵B(3,6),OE=2BE,∴E(2,4),设直线DE的解析式是y=kx+b把D(0,5)E(2,4)代入得,∴直线DE的解析式是y=﹣x+5;(3)当OD为菱形的边时,则MN=OD=5,且MN∥OD,∵M在直线DE上,∴设M(t,﹣t+5),①当点N在点M上方时,如图2,则有OM=MN,∵OM2=t2+(﹣t+5)2,∴t2+(﹣t+5)2=52,解得t=0或t=4,当t=0时,M与D重合,舍去,∴M(4,3),∴N(4,8);②当点N在点M下方时,如图3,则有MD=OD=5,∴t2+(﹣t+5﹣5)2=52,解得t=2或t=﹣2,当t=2时,N点在x轴下方,不符合题意,舍去,∴M(﹣2,+5),∴N(﹣2,);当OD为对角线时,则MN垂直平分OD,∴点M在直线y=2.5上,在y=﹣x+5中,令y=2.5可得x=5,∴M(5,2.5),∵M、N关于y轴对称,∴N(﹣5,2.5),综上可知存在满足条件的点N,其坐标为(4,8)或(﹣5,2.5)或(﹣2,).【点评】本题为一次函数的综合应用,涉及勾股定理、待定系数法、菱形的性质、分类讨论及方程思想.在(2)中求得E点坐标是解题的关键,在(3)中求得M点的坐标是解题的关键,注意分类讨论.本题考查知识点较多,综合性较强,难度较大.10、如图1,已知正方形ABCD的边长为6,E是CD边上一点(不与点C重合),以CE为边在正方形ABCD的右侧作正方形CEFG,连接BF、BD、FD.计算:(1)当点E与点D重合时,△BDF的面积为;当点E为CD的中点时,△BDF的面积为.证明:(2)当E是CD边上任意一点(不与点C重合)时,猜想S△BDF与S正方形ABCD之间的关系,并证明你的猜想;运用:(3)如图2,设BF与CD相交于点H,若△DFH的面积为,求正方形CEFG的边长.解:计算:(1)∵当点E与点D重合时,∴CE=CD=6,∵四边形ABCD,四边形CEFG是正方形,∴DF=CE=AD=AB=6,∴S△BDF=×DF×AB=18,如图,连接CF,∵四边形ABCD和四边形CEFG均为正方形;∴∠CBD=∠GCF=45°,∴BD∥CF,∴S△BDF=S△BDC=S正方形ABCD=×36=18,故答案为:18,18;证明:(2)S△BDF=S正方形ABCD,理由:连接CF.∵四边形ABCD和四边形CEFG均为正方形,∴∠CBD=∠GCF=45°,∴BD∥CF,∴S△BDF=S△BDC=S正方形ABCD;运用:(3)如图2,∵S△BDF=S正方形ABCD=×36=18,且S△BDF=S△BDH+S△DFH,∴S△BDH=18﹣=,∴×DH×6=,∴DH=,∴S△BDH=××EF=,∴EF=4∴正方形CEFG的边长为4.11、已知如图,点C、D在线段AF上,AD=CD=CF,∠ABC=∠DEF=90°,AB∥EF.(1)若BC=2,AB=2,求BD的长;(2)求证:四边形BCED是平行四边形.(1)解:∵∠ABC=90°,∴AC===2,∵AD=CD,∴BD=AC=;(2)证明:∵AD=CD=CF,∴DF=AC=2,∵∠DEF=90°,∴CE=DF=,∴BD=CE,∵AB∥EF,∴∠A=∠F,在△ABC和△FED中,,∴△ABC≌△FED(AAS),∴BC=ED,∵BD=CE,∴四边形BCED是平行四边形.12、如图,在矩形ABCD中,M是BC上一点,EF垂直平分AM,分别交BC,AM,AD于点E,O,F,连接AE,MF.(1)求证:四边形AEMF是菱形;(2)若AB=6,H为AB的中点,连接OH交AE于点P,OH+OA=9,求△OPE的周长.(1)证明:∵EF垂直平分AM,∴AE=EM,OA=OM.∵四边形ABCD是矩形,∴AD∥BC.∴∠AFO=∠MEO,在△OF和△MOE中,,∴△AOF≌△MOE(AAS).∴OF=OE.∴四边形AEMF是平行四边形.∵AE=EM.∴四边形AEMF是菱形;(2)解:∵O、H分别为AM、AB的中点,∴BM=2OH,AM=2OA,∴AM+BM=2OA+2OH=18.设BM=x,则AM=18﹣x,在Rt△ABM中,由勾股定理得:62+x2=(18﹣x)2,解得:x=8,∴BM=8,AM=10.∴OA=AM=5,设EM=m,则BE=8﹣m,AE=EM=m,在Rt△ABE中,由勾股定理得:62+(8﹣m)2=m2,解得:m=,∴AE=EM=在Rt△AOE中,EO===.∵OP∥EM,∴==1,∴AP=PE,∴OP=EM=,∵PE=AE=,∴△OPE的周长=EO+PE+OP=++=10.。
