2015高考理科数学方程的解与函数的零点考点练习
2015高考数学一轮课件:第2章 第8节 函数与方程

点击此处可返回目录
第九页,编辑于星期五:十三点 四十三分。
第七页,编辑于星期五:十三点 四十三分。
高频考点全通关——函数零点的应用
闯关四:及时演练,强化提升解题技能
2. 若函数 f(x)=xln x-a 有两个零点,则实数 a 的取值范围为( )
A. 0,1e
B. 0,1e
C. 0,1e
D. -1e,0
解析:选 D 令 g(x)=xln x,h(x)=a,则问题可转化成函数 g(x)与 h(x)的
f (b)与0的大小.
第六页,编辑于星期五:十三点 四十三分。
高频考点全通关——函数零点的应用
闯关四:及时演练,强化提升解题技能
1. 函数 f(x)=2x-2-a 的一个零点在区间(1,2)内,则实数 x
a 的取值范围是( ) A.(1,3) B.(1,2)
C.(0,3)
D.(0,2)
解析:选 C 由条件可知 f(1)f(2)<0,即(2-2-a)(4-1-a)<0, 即 a(a-3)<0,解得 0<a<3.
④f(0)·f(3)<0.其中正确结论的序号是( )
A.①③
B.①④
C.②③
D.②④
解析:选 C 由题设知 f(x)=0 有 3 个不同零点. 设 g(x)=x3-6x2+9x,∴g(x)=x(x2-6x+9)=x(x-3)2, 令 g(x)=0,得 x=0 或 x=3,g′(x)=3x2-12x+9, 令 g′(x)>0,得 x<1 或 x>3;令 g′(x)<0,得 1<x<3, 所以 g(x)在(-∞,1),(3,+∞)上是单调递增的;在(1,3) 上是单调递减的.g(1)=4,作出 g(x)的图象,如图所示. ∴f(x)=g(x)-abc,f(x)有 3 个零点,需将 g(x)的图象向下 平移至如图所示位置.由图象观察可知,f(0)f(1)<0 且 f(0)f(3)>0.
高考数学(理科)-基本初等函数中含有参数问题-专题练习(含答案与解析)

高考数学(理科)专题练习 基本初等函数中含有参数问题一、练高考1.【2015高考天津】已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩函数()()2g x b f x =--,其中b R ∈,若函数()()y f x g x =-恰有4个零点,则b 的取值范围是( )A .7,4⎛⎫+∞ ⎪⎝⎭B .7,4⎛⎫-∞ ⎪⎝⎭C .70,4⎛⎫⎪⎝⎭D .7,24⎛⎫ ⎪⎝⎭2.【2015高考山东】设函数()31,1,2,1x x x f x x -<⎧⎪=⎨≥⎪⎩则满足()()()2f af f a =的a 取值范围是( )A .2,13⎡⎤⎢⎥⎣⎦B .[]0,1C .2,3⎡⎫+∞⎪⎢⎣⎭D .[)1,+∞3.【2015高考新课标2】设函数'()f x 是奇函数()()f x x R ∈的导函数,(1)0f -=,当0x >时,'()()0xf x f x -<,则使得()0f x >成立的x 的取值范围是( )A .(,1)(0,1)-∞-B .(1,0)(1,)-+∞C .(,1)(1,0)-∞--D .(0,1)(1,)+∞4.【2015高考湖南】已知32,(),x x af x x x a ⎧≤⎪=⎨>⎪⎩,若存在实数b ,使函数()()g x f x b =-有两个零点,则a 的取值范围是__________.5.【2016高考浙江文数】设函数32 31f x x x =++().已知0a ≠,且2(x )(x ),–f R f A b a x x --∈()()=,则实数a =__________,b =__________.6.【2016高考上海】已知a R ∈,函数21(x)log ()f a x=+. (1)当5a =时,解不等式(x)0f >;(2)若关于x 的方程2()log [(4)25]0f x a x a --+-=的解集中恰好有一个元素,求a 的取值范围; (3)设0a >,若对任意1[,1]2t ∈,函数(x)f 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围. 二、练模拟1.已知函数y A ,集合3{|||,0}B x x a a =-<>,若A B ⋂中的最小元素为2,则实数a 的取值范围是( ) A .(]0,4B .()0,4C .(]1,4D .()1,42.【山西大学附中2017届高三第二次模拟测试】设函数()()21x f x e x ax a =--+,其中1a <,若存在唯一的整数t ,使得()0f t <,则a 的取值范围是( ) A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,24e ⎡⎫-⎪⎢⎣⎭ C .33,24e ⎡⎫⎪⎢⎣⎭D .3,12e ⎡⎫⎪⎢⎣⎭3.【2016届河北省邯郸市一中高三下学期研六】已知函数()y f x =是定义域为R 的偶函数,当0x ≥时()()()5sin ,01421,14xx x f x x π⎧⎛⎫-≤≤ ⎪⎪⎝⎭⎪=⎨⎛⎫⎪> ⎪⎪⎝⎭⎩,若关于x 的方程()()20f x af x b ⎡⎤++=⎣⎦有6个根,则实数a 的取值范围是( )A .59,24⎛⎫-- ⎪⎝⎭B .9,14⎛⎫-- ⎪⎝⎭C .59,24⎛⎫-- ⎪⎝⎭9,14⎛⎫⋃-- ⎪⎝⎭D .5,12⎛⎫-- ⎪⎝⎭4.【2016届河北省衡水中学高三上学期一调】若不等式()()1213lg 1lg33x xa x ++-≥-对任意(),1x ∈-∞恒成立,则a 的取值范围是( ) A .(],0-∞B .[)1,+∞C .(],1-∞D .[)0,+∞5.【宁夏育才中学2017届高三上学期第二次月考】若函数xx k k x f 212)(⋅+-=在定义域上为奇函数,则实数=k __________.6.【山西省孝义市2017届高三上学期二轮模考】函数2()log ()a f x ax x =-在区间[2,4]上是单调增函数,则a 的取值范围是__________.三、练原创1.函数2(),0()1,0x a x f x x a x x ⎧-≤⎪=⎨++>⎪⎩,若(0)f 是()f x 的最小值,则a 的取值范围为( ) A .[1,2]-B .[1,0]-C .[1,2]D .[0,2]2.函数()f x 的导函数为'(x)f ,对x R ∀∈,都有2'()()f x f x >成立,若(ln 4)2f =,则不等式2()exf x =的解是( ) A .ln 4x > B .0ln4x << C .1x >D .01x <<3.已知函数()122,0,log ,0.x a x f x x x ⎧⋅≤⎪=⎨>⎪⎩若关于x 的方程()()0f f x =有且仅有一个实数解,则实数a 的取值范围是( ) A .(),0-∞B .()0,1C .()(),00,1-∞D .()()0,11,+∞4.已知函数2()ln ,af x x a R x=+∈. (1)若函数()f x 在[2,)+∞上是增函数,求实数a 的取值范围;(2)若函数()f x 在[1,e]上的最小值为3,求实数a 的值. 5.已知函数2()(1)1,f x ax a x a R =-++∈. (1)求证:函数()f x 的图象与x 轴恒有公共点; (2)当0a >时,求函数y =(3)若存在0m >使关于x 的方程1()m f x m=+有四个不同的实根,求实数a 的取值范围.高考数学(理科)专题练习 基本初等函数中含有参数问题答 案一、练高考 1~3.DCA4.(,0)(1,)-∞⋃+∞ (0,)⎫+∞⎪⎭;(1,2]{3,4};⎫+∞⎪⎭高考数学(理科)专题练习基本初等函数中含有参数问题解 析1.2.【解析】当1a ≥ 时,()21af a =>,所以,()()()2f aff a = ,即1a >符合题意.当1a < 时,()31f a a =- ,若()()()2f aff a = ,则()1f a ≥ ,即:2311,3a a -≥≥ ,所以213a ≤<适合题意综上,a 的取值范围是2,3⎡⎫+∞⎪⎢⎣⎭,故选C . 3.4.5. 【解析】32323232()()313133f x f a x x a a x x a a -=++---=+--,23222()()(2)(2)x b x a x a b x a ab x a b --=-+++-,所以223223203a b a ab a b a a --=⎧⎪+=⎨⎪-=--⎩,解得21a b =-⎧⎨=⎩.6.1,12t ⎡⎤∈⎢⎥⎣⎦成立.因为0a >,所以函数()211y at a t =++-在区间1,12⎡⎤⎢⎥⎣⎦上单调递增,12t =时,y有最小值3142a -,由31042a -≥,得23a ≥.故a 的取值范围为2,3⎡⎫+∞⎪⎢⎣⎭. 二、练模拟1.2.【解析】 令()()()21,xg x ex h x ax a =-=-.由题意知存在唯一整数t ,使得()g t 在直线()h x 的下方.()()'21x g x e x =+,当12x <-时,函数单调递减,当12x >-,函数单调递增,当12x =-时,函数取得最小值为122e --.当0x =时,(0)1g =-,当1x =时,(1)0g e =>,直线()h x ax a =-过定点()1,0,斜率为a ,故()0a g ->且()113g e a a --=-≥--,解得3,12m e ⎡⎫∈⎪⎢⎣⎭.3.4.5.【解析】122(1)(1)111212k k f f k k k ---=-⇒=-⇒=±++. 6. 【解析】设2()u x ax x =-,则()log ()a f x u x =,要使函数()f x 在区间[2,4]上是单调增函数,由复合函数单调性的判定方法可知()log ()a f x u x =与2()u x ax x =-同为增函数或同为减函数时才能满足,故有1122a a >⎧⎪⎨≤⎪⎩或01142a a<<⎧⎪⎨≥⎪⎩,所以1a >. 三、练原创1. 【解析】因为当0≤x 时,2)()(a x x f -=,因为)0(f 是)(x f 的最小值,所以0≥a ;又因为当0>x 时,221)(a a a xx x f ≥+≥++=,即21≤≤-a .综上所述, a 的取值范围为[]2,0.故应选D . 2.3. 【解析】由函数()122,0,log ,0.x a x f x x x ⎧⋅≤⎪=⎨>⎪⎩可知,在0x ≤部分.当0a >时20x a ⋅>.当0a <时20x a ⋅<.当0a =时20x a ⋅=恒成立.因为关于x 的方程()()0f f x =有且仅有一个实数解,所以只能是()1f x =只有一个解.当0x >时有一个解12x =.所以要使在0x <上没解,有前面可得0a <成立.当0a >时要使01a <<才能成立.故选C .4.③若2a e >,则20x a -<,即()0f x '<在[1,]e 上恒成立,此时()f x 在[1,]e 上是减函数. 所以()()min 213af x f e e ==+=⎡⎤⎣⎦,所以a e =. 5.11 / 11。
2015高考理科数学函数、导数及其应用总复习题(附答案)

2015高考理科数学函数、导数及其应用总复习题(附答案)A组基础演练•能力提升]一、选择题1.(2013年高考江西卷)函数y=xln(1-x)的定义域为()A.(0,1)B.0,1)C.(0,1]D.0,1]解析:根据题意得1-x>0x≥0,解得0≤x答案:B2.已知函数f(x)=2x,x>0,x+1,x≤0.若f(a)+f(1)=0,则实数a的值为()A.-3B.-1C.1D.3解析:当a>0时,由f(a)+f(1)=0得2a+2=0,故此时不存在实数a 满足条件;当a≤0时,由f(a)+f(1)=0得a+1+2=0,解得a=-3,满足条件,故选A.答案:A3.(2014年浙江五校联考)若函数f(x)=+,则f(x)的定义域为()A.-12,0B.-12,0C.-12,+∞D.0,+∞解析:根据题意知log12(2x+1)>0,即0答案:A4.下列函数中,与函数y=13x定义域相同的函数为()A.y=1sinxB.y=lnxxC.y=xexD.y=sin解析:利用正弦函数、指数函数、对数函数及分式型函数定义域的确定方法求解.函数y=13x的定义域为{x|x≠0},选项A中由sinx≠0⇒x≠kπ,k∈Z,故A 不对;选项B中x>0,故B不对;选项C中x∈R,故C不对;选项D 中由正弦函数及分式型函数的定义域确定方法可知定义域为{x|x≠0},故选D.答案:D5.已知函数fx-1x=x2+1x2,则f(3)=()A.8B.9C.11D.10解析:∵fx-1x=x-1x2+2,∴f(3)=9+2=11.答案:C6.具有性质:f1x=-f(x)的函数,我们称为满足“倒负”交换的函数,下列函数:①f(x)=x-1x;②f(x)=x+1x;③f(x)=x,01.满足“倒负”变换的函数是()A.①②B.①③C.②③D.只有①解析:①f1x=1x-x=-f(x)满足.②f1x=1x+x=f(x)不满足.③0x=1时,f1x=0=-f(x),x>1时,f1x=1x=-f(x)满足.答案:B二、填空题7.(2013年高考安徽卷)定义在R上的函数f(x)满足f(x+1)=2f(x).若当0≤x≤1时,f(x)=x(1-x),则当-1≤x≤0时,f(x)=________.解析:设-1≤x≤0,∴0≤x+1≤1,∴f(x)=12f(x+1)=12(x+1)1-(x+1)]=-12x(x+1).答案:-12x(x+1)8.若函数f(x)=2x2+2ax-a-1的定义域为R,则a的取值范围为________.解析:函数f(x)的定义域为R,所以2x2+2ax-a-1≥0对x∈R恒成立,即2x2+2ax-a≥1,x2+2ax-a≥0,恒成立,因此有Δ=(2a)2+4a≤0,解得-1≤a≤0.答案:-1,0]9.已知函数f(x)=x2+1,x≥0,1,xf(2x)的x的取值范围是________.解析:画出f(x)=x2+1,x≥0,1,x如图.由图象可知,若f(1-x2)>f(2x),则1-x2>0,1-x2>2x,即-1得x∈(-1,2-1)答案:(-1,2-1)三、解答题10.(1)已知f2x+1=lgx,求f(x);(2)已知f(x)是一次函数,且满足3f(x+1)-2f(x-1)=2x+17,求f(x);(3)定义在(-1,1)内的函数f(x)满足2f(x)-f(-x)=lg(x+1),求函数f(x)的解析式.解析:(1)令t=2x+1,则x=2t-1,∴f(t)=lg2t-1,即f(x)=lg2x-1.(2)设f(x)=ax+b,则3f(x+1)-2f(x-1)=3ax+3a+3b-2ax+2a-2b=ax+5a+b=2x+17,则有a=2,b+5a=17,∴a=2,b=7,故f(x)=2x+7.(3)x∈(-1,1)时,有2f(x)-f(-x)=lg(x+1).①令x=-x得,2f(-x)-f(x)=lg(-x+1).②由①②消去f(-x),得f(x)=23lg(x+1)+13lg(1-x),x∈(-1,1).11.已知函数f(x)=2x-1,g(x)=x2,,-求fg(x)]和gf(x)]的解析式.解析:当x≥0时,g(x)=x2,fg(x)]=2x2-1,当x∴fg(x)]=2x2-,-∵当2x-1≥0,即x≥12时,gf(x)]=(2x-1)2,当2x-1∴gf(x)]=-,,-1,.(能力提升)甲同学家到乙同学家的途中有一公园,甲从家到公园的距离与乙从家到公园的距离都是2km,甲10时出发前往乙家.如图所示,表示甲从家出发到达乙家为止经过的路程y(km)与时间x(分)的关系.试写出y=f(x)的函数解析式.解析:当x∈0,30]时,设y=k1x+b1,由已知得b1=030k1+b1=2,解得k1=115,b1=0∴y=115x.当x∈(30,40)时,y=2;当x∈40,60]时,设y=k2x+b2,由已知得40k2+b2=260k2+b2=4,解得k2=110b2=-2,∴y=110x -2.综上,f(x)=115x,x∈0,30]2,x∈,-2,x∈40,60] B组因材施教•备选练习]1.已知f(x)=log3x,x>0,ax+b,x≤0,且f(0)=2,f(-1)=3,则f(f(-3))=()A.-2B.2C.3D.-3解析:f(0)=a0+b=1+b=2,解得b=1;f(-1)=a-1+b=a-1+1=3,解得a=12.故f(-3)=12-3+1=9,f(f(-3))=f(9)=log39=2,故选B.答案:B2.现向一个半径为R的球形容器内匀速注入某种液体,下面图形中能表示在注入过程中容器的液面高度h随时间t变化的函数关系的是()解析:从球的形状可知,水的高度开始时增加的速度越来越慢,当超过半球时,增加的速度又越来越快.答案:C3.(1)已知函数f(x)的定义域为(0,1),求f(x2)的定义域;(2)已知函数f(2x+1)的定义域为(0,1),求f(x)的定义域;(3)已知函数f(x+1)的定义域为-2,3],求f(2x2-2)的定义域.解析:(1)∵f(x)的定义域为(0,1),∴要使f(x2)有意义,需使0即-1∴函数f(x2)的定义域为{x|-1(2)∵f(2x +1)的定义域为(0,1),即其中的自变量x的取值范围是0令t=2x+1,∴1∴函数f(x)的定义域为{x|1(3)∵函数f(x+1)的定义域为-2,3],∴-2≤x≤3.令t=x+1,∴-1≤t≤4.∴f(t)的定义域为{t|-1≤t≤4},即f(x)的定义域为{x|-1≤x≤4},要使f(2x2-2)有意义,需使-1≤2x2-2≤4,∴-3≤x≤-22或22≤x≤3,∴函数f(2x2-2)的定义域为x-3≤x≤-22或22≤x≤3.。
考点8 函数与方程(解析版)
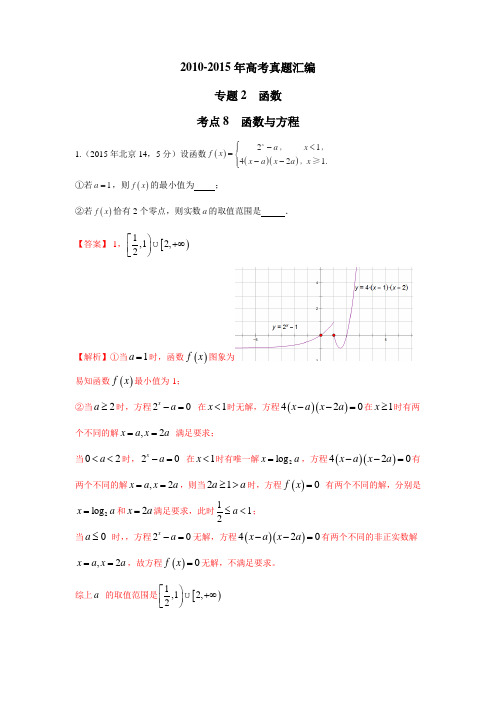
2010-2015年高考真题汇编专题2 函数 考点8 函数与方程1.(2015年北京14,5分)设函数()()()2142 1.x a x f x x a x a x ⎧-<⎪=⎨--⎪⎩‚‚‚≥①若1a =,则()f x 的最小值为;②若()f x 恰有2个零点,则实数a 的取值范围是.【答案】-1,[)1,12,2⎡⎫+∞⎪⎢⎣⎭【解析】①当1a =时,函数()f x 图象为易知函数()f x 最小值为-1;②当2a ≥时,方程20xa -= 在1x <时无解,方程()()420x a x a --=在1x ≥时有两个不同的解,2x a x a == 满足要求;当02a <<时,20xa -= 在1x <时有唯一解2log x a =,方程()()420x a x a --=有两个不同的解,2x a x a ==,则当21a a ≥>时,方程()0f x = 有两个不同的解,分别是2log x a =和2x a =满足要求,此时112a ≤<;当0a ≤ 时,,方程20xa -=无解,方程()()420x a x a --=有两个不同的非正实数解,2x a x a ==,故方程()0f x =无解,不满足要求。
综上a 的取值范围是[)1,12,2⎡⎫+∞⎪⎢⎣⎭2.(2015年湖南15,5分)已知32,(),x x af x x x a⎧≤=⎨>⎩,若存在实数b ,使函数()()g x f x b =-有两个零点,则a 的取值范围是 . 【答案】),1()0,(+∞-∞【解析】分析题意可知,问题等价于方程)(3a xb x ≤=与方程)(2a xb x >=的根的个数和为3.(2015年江苏13,5分)已知函数|ln |)(x x f =,⎩⎨⎧>--≤<=1,2|4|10,0)(2x x x x g ,则方程1|)()(|=+x g x f 实根的个数为 。
【高考数学二轮复习-经典微专题】第12讲 函数的零点问题-原卷及答案

第12讲 函数的零点问题知识与方法1确定函数()f x 零点所在区间的常用方法函数的零点、方程的根、函数图像与x 轴的交点的横坐标,实质是同一个问题的3种不同表达形式.确定零点、方程根、函数图像与x 轴交点所在区间本质上是同一问题的不同表述形式,所以常用解法有3种.(1)解方程法;(2)利用函数零点的存在性定理;(3)数形结合法. 同样,判断函数零点个数也是这3种方法.2已知函数有零点(方程有根),求参数取值常用的方法(1)直接法.直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围. (2)分离参数法.先将参数分离,转化为求函数值域问题加以解决.(3)数形结合法.先对解析式变形,在同一平面直角坐标系中,画出函数的图像,然后数形结合求解.典型例题【例1】已知:,αβ是方程()221420x m x m +-+-=的两个根,且2αβ<<,求m 的取值范围.(2)若220x ax ++=的两个根都小于1-,求a 的取值范围.【例2】(1)已知定义在R 上的奇函数()f x ,满足()()4f x f x -=-,且在区间[]0,2上是增函数,若方程()()0f x m m =>在区间[]8,8-上有4个不同的根1234,,,x x x x ,则1234x x x x +++=(2)设函数()()()20,20,x bx c x f x x ⎧++≤⎪=⎨>⎪⎩若()()()40,22f f f -=-=-,求关于x 的方程()f x x =的解的个数.【例3】设函数()()()2,1,42, 1.x a x f x x a x a x ⎧-<⎪=⎨--≥⎪⎩(1)若1a =,则()f x 的最小值为________.(2)若()f x 恰有2个零点,则实数a 的取值范围是________.【例4】设函数()222f x ax bx =+,若存在实数()00,x t ∈,使得对任意不为零的实数,a b 均有()0f x a b =+成立,则t 的取值范围是________.强化训练1.已知函数()2223f x ax x =+-,如果函数()y f x =在区间[]1,1-上有零点,则实数a 的取值范围为________.2.设()22f x x ax b =++在区间[]1,2上有两个零点(可重合),则a b +的取值范围是________.3.已知函数()254,0,22,0,x x x f x x x ⎧++≤⎪=⎨->⎪⎩若函数()y f x a x =-恰有4个零点,则实数a的取值范围为________.4.若在区间1,2∞⎛⎫+⎪⎝⎭上存在两个不同的实数,a b ,使得2a b k a ++=和2b a k b ++=同时成立,求k 的取值范围.5.(1)若()(0xf x a x a a =-->且1a ≠有2个零点,则实数a 的取值范围是________.(2)函数()2ln f x x x=-的零点所在的区间是(). A.()1,2B.()2,3C.1,1e ⎛⎫ ⎪⎝⎭D.()e,36.若函数()f x 的零点与()422xg x x =+-的零点之差的绝对值不超过0.25,则()f x 可以是().A.()41f x x =-B.()()21f x x =- C.()e 1xf x =-D.()1ln 2f x x ⎛⎫=-⎪⎝⎭7.已知函数()42x xmf x +=是R 上的奇函数. (1)求m 的值. (2)设()12x g x a +=-,若函数()f x 与()g x 的图像至少有一个公共点,求实数a 的取值范围.第12讲 函数的零点问题知识与方法1确定函数()f x 零点所在区间的常用方法函数的零点、方程的根、函数图像与x 轴的交点的横坐标,实质是同一个问题的3种不同表达形式.确定零点、方程根、函数图像与x 轴交点所在区间本质上是同一问题的不同表述形式,所以常用解法有3种.(1)解方程法;(2)利用函数零点的存在性定理;(3)数形结合法. 同样,判断函数零点个数也是这3种方法.2已知函数有零点(方程有根),求参数取值常用的方法(1)直接法.直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围. (2)分离参数法.先将参数分离,转化为求函数值域问题加以解决.(3)数形结合法.先对解析式变形,在同一平面直角坐标系中,画出函数的图像,然后数形结合求解.典型例题【例1】已知:,αβ是方程()221420x m x m +-+-=的两个根,且2αβ<<,求m 的取值范围.(2)若220x ax ++=的两个根都小于1-,求a 的取值范围. 【解析】(1)【解法一】()()()2,220,240αβαβαβαβ<<∴--<∴-++<利用韦达定理1242,mm αβαβ+=-⎧⎨=-⎩代人(1)式得()4221240m m ---+<,解得3m <-.m ∴的取值范围为(),3∞--.【解法2】令()()22142f x x m x m =+-+-,拋物线开口向上.由实根分布2αβ<<,只要()20f <即可,即()()24212420f m m =+-⨯+-<,解得3m <-,即m 的取值范围为(,∞-,()3.-(2)【解法1】设()22f x x ax =++,当两根都小于1-时,函数()f x 的图像与x 轴的交点在一1的左侧,可得)()0,1,3,? .210a a a f ∆≥⎧⎪⎪⎡-<-⇒≤<⎨⎣⎪->⎪⎩即的取值范围为 【解法2】设12,x x 是方程的两个实根,有()()()()111212122212120,0,0,0,1,,10,1101011011020x x x x x x x x x x x x x x ⎧⎧⎧∆≥∆≥∆≥∆≥⎧⎪⎪⎪⎪<-+<⇒++>⇒+++>⎨⎨⎨⎨⎪⎪⎪⎪<-+<+++<++<⎩⎩⎩⎩利用韦达定理,解不等式组得3a ≤<,即a的取值范围为)⎡⎣.【例2】(1)已知定义在R 上的奇函数()f x ,满足()()4f x f x -=-,且在区间[]0,2上是增函数,若方程()()0f x m m =>在区间[]8,8-上有4个不同的根1234,,,x x x x ,则1234x x x x +++=(2)设函数()()()20,20,x bx c x f x x ⎧++≤⎪=⎨>⎪⎩若()()()40,22f f f -=-=-,求关于x 的方程()f x x =的解的个数.【解析】(1)定义在R 上的奇函数,满足()()()()4,4f x f x f x f x -=-∴-=-.∴由()f x 为奇函数得函数图像关于直线2x =对称且()00f =;由()()4f x f x -=-知()()()()8444,f x f x f x f x -=--=--=∴函数是以8为周期的周期函数,又()f x 在区间[0,2上上是增函数,() f x ∴在区间[]2,0-上也是增函数,如图121-所示,则方程()()0f x m m =>在区间[]8,8-上有4个不同的根1234,,,x x x x ,不妨设1234x x x x <<<.由对称性知1234123412,4,1248.x x x x x x x x +=-+=∴+++=-+=- (2)【解法1】由()()()40,22f f f -=-=-,可得164,4,2422,b c c b c b c -+=⎧∴==⎨-+=-⎩.()()()242020x x x f x x ⎧++≤⎪∴=⎨>⎪⎩∴方程()f x x =等价于()0,2,x x f x >⎧⎨==⎩或20,42x x x x≤⎧⎨++=⎩即2x =或20,2320,x x x x ≤⎧∴=⎨++=⎩或1x =-或2x =-,即()f x x =有3个解. 【解法2】同【解法1】可得()()()24204,2,20x x x b c f x x ⎧++≤⎪==∴=⎨>⎪⎩如图122-所示,方程()f x x =解的个数即函数()y f x =与y x =图像交点个数,由图知两图像有3A B C 、、个交点,故方程有3个解.【例3】设函数()()()2,1,42, 1.x a x f x x a x a x ⎧-<⎪=⎨--≥⎪⎩(1)若1a =,则()f x 的最小值为________.(2)若()f x 恰有2个零点,则实数a 的取值范围是________.【解析】()1当1a =时,()()()21,1412,1,xx f x x x x ⎧-<⎪=⎨--≥⎪⎩当1x <时,()11f x -<<,无最小值;当1x ≥时,()()()412f x x x =--=24128.x x -+由二次函数的性质知,32x =时,()f x 的最小值为()1,f x -∴的最小值为 1.- (2)当0a ≤时,20x a -=无解,()()420x a x a --=有两解,分别为a 与2a ,但均小于1,不合题意,故0a ≤时不成立;当0a >时,20xa -=有解()()2log ,420x a x a x a =--=有解x a =或2x a =,要使()f x 恰有2个零点,需3个根中有1个不合题意,只有22log 1,log 11,1,2121a a a a a a ⎧≥<⎧⎪⎪≥<⎨⎨⎪⎪≥≥⎩⎩或综上,实数a 的取值范围是[)1,12,2∞⎡⎫⋃+⎪⎢⎣⎭.【例4】设函数()222f x ax bx =+,若存在实数()00,x t ∈,使得对任意不为零的实数,a b 均有()0f x a b =+成立,则t 的取值范围是________. 【解析】【解法1】(零点存在性定理)由题意222ax bx a b +=+在区间()0,x t ∈上对于任意的0,0a b ≠≠均有解. 故()()222g x ax bx a b =+-+在()0,x t ∈上对于任意的0,0a b ≠≠均有零点.()()()0,1.g a b g a b =-+=+故()()()2010g g a b =-+≤若0a b +=,则t 一定要大于1; 若1t >,则()()()2010g g a b =-+≤. 故()g x 在区间()0,t 上必有零点. 由零点存在性定理可得 1.t > 【解法2】(一“定”一“动”,数形结合)222ax bx a b +=+在区间()0,t 上对于任意的0,0a b ≠≠有解,即212122b x x a ⎛⎫⎛⎫-=--⎪⎪⎝⎭⎝⎭在区间()0,t 上对于任意0,0a b ≠≠均有解. 即2121y x =-与()2102y k x k ⎛⎫=-≠ ⎪⎝⎭在 区间()0,t 上有交点,如图123-所示,故1t >强化训练1.已知函数()2223f x ax x =+-,如果函数()y f x =在区间[]1,1-上有零点,则实数a 的取值范围为________.【解析】若,则得不合题意,故. (i)若时,在上至少有一个零点.有即解得(ii)当时,在上有零点的条件是 解得综上,实数的取值范围为.2.设()22f x x ax b =++在区间[]1,2上有两个零点(可重合),则a b +的取值范围是________. 【解析】0a =()()23,0f x x f x =-=[]31,1.2x =∉-0a ≠()()110f f -⋅()f x []1,1-()()2232230,a a --+-()()25210,a a --15.22a ()()110f f -⋅>()f x []1,1-()()()110,2111,2110,f f a a f f ⎧⎛⎫-⋅ ⎪⎪⎝⎭⎪⎪-<-<⎨⎪⎪-⋅>⎪⎩5.2a >a 1,2∞⎡⎫+⎪⎢⎣⎭【解法1】易知,设, 则故即 【解法2】设的两根为,且.由韦达定理可得将(1)式看作关于的一次函数,又3.已知函数()254,0,22,0,x x x f x x x ⎧++≤⎪=⎨->⎪⎩若函数()y f x a x =-恰有4个零点,则实数a的取值范围为________.【解析】画出函数的图像如答图所示.函数有4个零点,即函数的图像与函数的图像有4个交点根据图像知需.当时,函数的图像与函数的图像有3个交点,故.当与相切时,在整个定义域内,的图像与的图像有5个交点. 此时,由得. 由得,解得或(舍去).则当时,两个函数图像有4个交点,故实数的取值范围是.1124a b f ⎛⎫+=- ⎪⎝⎭()()()12f x x x x x =--121211111.22222f x x x x ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=--=--⎪ ⎪⎪ ⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭121113,,.2222x x ⎛⎫⎛⎫⎡⎤--∈ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦119,,244f ⎛⎫⎡⎤∈⎪⎢⎥⎝⎭⎣⎦[]0,2.a b +∈220x ax b ++=12,x x []12,1,2x x ∈()121212212122,111.,222x x a a b x x x x x x x x x b +=-⎧⎛⎫∴+=-++=--⎨⎪=⎝⎭⎩1x []2211321,2,,.22x x x a b --⎡⎤∈∴+∈⎢⎥⎣⎦][21,2,0,2.x a b ⎡⎤∈∴+∈⎣⎦()f x 121-()y f x a x =-1y a x =()f x (0a >2a =()f x 1y a x =2a <()0y a x x =254y x x =++()f x 1y a x =2,54y ax y x x =-⎧⎨=---⎩()2540x a x +-+=Δ0=2(5)160a --=1a =9a =12a <<a ()1,24.若在区间1,2∞⎛⎫+⎪⎝⎭上存在两个不同的实数,a b ,使得2a b k a ++=和2b a k b ++=同时成立,求k 的取值范围. 【解析】【解法1】将式子和相减并整理,可得,即,故且.方程在区间上有两个不等实根.令结合图像可得解得即 【解法2】将和相减并整理,可得,即. 故且方程在区间上有两个不等实根.令即直线与抛物线有两个不同的交点,结合图像可得,即 5.(1)若()(0xf x a x a a =-->且1a ≠有2个零点,则实数a 的取值范围是________.2a b k a ++=2b a k b ++=2a b +=2b a =-2220a a k -++=2220b b k -++=∴2220x x k -++=1,2∞⎛⎫+ ⎪⎝⎭()222,f x x x k =-++111,22102x f ⎧⎛⎫>= ⎪⎪⎪⎝⎭⎨⎛⎫⎪> ⎪⎪⎝⎭⎩对称轴在右边51,4k -<<-5,1.4k ⎛⎫∈-- ⎪⎝⎭2a b k a ++=2b a k b ++=2a b +=2b a =-222k a a =-+-22 2.k b b =-+-∴222k x x =-+-1,2∞⎛⎫+ ⎪⎝⎭()222,f x x x =-+-y k =()222f x x x =-+-51,4k -<<-5,1.4k ⎛⎫∈-- ⎪⎝⎭【解析】 (1)函数的零点的个数就是函数与函数的交点的个数.如答图所示,由函数的图像可知时两函数图像有两个交点,时两函数图像有唯一交点,故.(2)函数()2ln f x x x =-的零点所在的区间是(). A.()1,2 B.()2,3 C.1,1e ⎛⎫⎪⎝⎭ D.()e,3【解析】 函数在区间内存在零点, 【答案】B.6.若函数()f x 的零点与()422xg x x =+-的零点之差的绝对值不超过0.25,则()f x 可以是().A.()41f x x =-B.()()21f x x =- ()f x xy a =y x a =+122-1a >01a <<1a>()()()210220,2ln 210,3ln 30,3f f f =-=-<=-<=->()()()2110,120,230,f e f e f f e e ⎛⎫=->=--<∴< ⎪⎝⎭∴()2ln f x x x=-()2,3C.()e 1x f x =-D.()1ln 2f x x ⎛⎫=- ⎪⎝⎭【解析】的零点为的零点为, 的零点为的零点为 接下来我们估算的零点, 的零点 又函数的零点与的零点之差的绝对值不超过只有的零点符合此要求,【答案】A.7.已知函数()42x xm f x +=是R 上的奇函数. (1)求m 的值.(2)设()12x g x a +=-,若函数()f x 与()g x 的图像至少有一个公共点,求实数a 的取值范围.【解析】(1)由函数是上的奇函数可知,解得. (2)函数与的图像至少有一个公共点.则方程至少有一个实根, 即方程至少有一个实根.令则方程变为 令,由于, 只需解得实数的取值范围为()41f x x =-()21,(1)4x f x x ==-1x =()e 1x f x =-()10,ln 2x f x x ⎛⎫==- ⎪⎝⎭3.2x =()422x g x x =+-()101,1,2g g ⎛⎫=-= ⎪⎝⎭()g x ∴10,.2x ⎛⎫∈ ⎪⎝⎭()f x ()422xg x x =+-0.25,∴()41f x x =-()f x R ()010f m =+=1m =-()f x ()g x 14122x x x a +-=-4210x x a -⋅+=20,xt =>210.t at -+=()21h t t at =-+()010h =>∴2Δ400,2a a ⎧=-⎪⎨>⎪⎩2,a ∴a [)2,∞+。
2015年陕西高考数学(理科)试题与答案

2015 年普通高等学校招生全国统一考试(陕西卷)理科数学一、选择题(本大题共12 个小题,每小题5 分,共 60 分. 在每小题给出的四个选项中,只有一项是符合题目要求的 .)1. 1.设集合M { x | x2x} ,N{ x | lg x0},则 M N()A .[0,1]B.(0,1]C.[0,1) D .(,1]【答案】 A试题分析:x x 2x0,1,x lg x 0x 0x 1 ,所以0,1,故选.A考点: 1、一元二次方程;2、对数不等式;3、集合的并集运算.【分析及点评】本题主要考察了集合的表示及其相关运算,并结合一元二次方程以及对数运算,属于基础题型,难度不大。
2.某中学初中部共有 110 名教师,高中部共有 150 名教师,其性别比例如图所示,则该校女教师的人数为()A.167B.137C.123D.93【答案】 B考点:扇形图.【分析及点评】本题主要考察了统计以及统计图表的相关知识,难度系数很小,属于基础题型。
3. 如图,某港口一天6时到 18时的水深变化曲线近似满足函数y 3sin( x) k ,据此函数6可知,这段时间水深(单位:m)的最大值为()A .5B.6C.8D.10【答案】 C试题分析:由图象知:y min 2 ,因为y min3k ,所以3 k2 ,解得:k5 ,所以这段时间水深的最大值是y max 3 k358 ,故选C.考点:三角函数的图象与性质.【分析及点评】本题重在转化,将实际问题转化成三角函数问题,对三角函数的图像、性质有较高要求,但作为基础题型,难度不大。
4. 二项式(x 1)n(n N ) 的展开式中x2的系数为15,则n()A .4B .5C.6 D .7【答案】 C考点:二项式定理.【分析及点评】本题主要考察了学生对二项式定理的理解,以及二项式系数的计算,难度不大,属于基础题型。
5. 一个几何体的三视图如图所示,则该几何体的表面积为()A .3B .4C.24D.34【答案】 D试题分析:由三视图知:该几何体是半个圆柱,其中底面圆的半径为1,母线长为 2 ,所以该几何体的表面积是121 1 2 2 2 34,故选 D.2考点: 1、三视图;2、空间几何体的表面积.【分析及点评】三视图以及体积、面积求值几乎每年必考,今年也不例外,题目设置与往年没有改变,难度不大,变化也不大。
高考数学(理科)-基本初等函数中含有参数问题-专题练习有答案
高考数学(理科)专题练习 基本初等函数中含有参数问题一、练高考1.【2015高考天津】已知函数()()22,2,2,2,x x f x x x ⎧-≤⎪=⎨->⎪⎩函数()()2g x b f x =--,其中b R ∈,若函数()()y f x g x =-恰有4个零点,则b 的取值范围是( )A .7,4⎛⎫+∞ ⎪⎝⎭B .7,4⎛⎫-∞ ⎪⎝⎭C .70,4⎛⎫⎪⎝⎭D .7,24⎛⎫ ⎪⎝⎭2.【2015高考山东】设函数()31,1,2,1x x x f x x -<⎧⎪=⎨≥⎪⎩则满足()()()2f af f a =的a 取值范围是( )A .2,13⎡⎤⎢⎥⎣⎦B .[]0,1C .2,3⎡⎫+∞⎪⎢⎣⎭D .[)1,+∞3.【2015高考新课标2】设函数'()f x 是奇函数()()f x x R ∈的导函数,(1)0f -=,当0x >时,'()()0xf x f x -<,则使得()0f x >成立的x 的取值范围是( )A .(,1)(0,1)-∞-B .(1,0)(1,)-+∞C .(,1)(1,0)-∞--D .(0,1)(1,)+∞4.【2015高考湖南】已知32,(),x x af x x x a ⎧≤⎪=⎨>⎪⎩,若存在实数b ,使函数()()g x f x b =-有两个零点,则a 的取值范围是__________.5.【2016高考浙江文数】设函数32 31f x x x =++().已知0a ≠,且2(x )(x ),–f R f A b a x x --∈()()=,则实数a =__________,b =__________.6.【2016高考上海】已知a R ∈,函数21(x)log ()f a x=+. (1)当5a =时,解不等式(x)0f >;(2)若关于x 的方程2()log [(4)25]0f x a x a --+-=的解集中恰好有一个元素,求a 的取值范围; (3)设0a >,若对任意1[,1]2t ∈,函数(x)f 在区间[,1]t t +上的最大值与最小值的差不超过1,求a 的取值范围. 二、练模拟1.已知函数y A ,集合3{|||,0}B x x a a =-<>,若A B ⋂中的最小元素为2,则实数a 的取值范围是( ) A .(]0,4B .()0,4C .(]1,4D .()1,42.【山西大学附中高三第二次模拟测试】设函数()()21x f x e x ax a =--+,其中1a <,若存在唯一的整数t ,使得()0f t <,则a 的取值范围是( ) A .3,12e ⎡⎫-⎪⎢⎣⎭B .33,24e ⎡⎫-⎪⎢⎣⎭ C .33,24e ⎡⎫⎪⎢⎣⎭D .3,12e ⎡⎫⎪⎢⎣⎭3.【河北省邯郸市一中高三下学期研六】已知函数()y f x =是定义域为R 的偶函数,当0x ≥时()()()5sin ,01421,14xx x f x x π⎧⎛⎫-≤≤ ⎪⎪⎝⎭⎪=⎨⎛⎫⎪> ⎪⎪⎝⎭⎩,若关于x 的方程()()20f x af x b ⎡⎤++=⎣⎦有6个根,则实数a 的取值范围是( )A .59,24⎛⎫-- ⎪⎝⎭B .9,14⎛⎫-- ⎪⎝⎭C .59,24⎛⎫-- ⎪⎝⎭9,14⎛⎫⋃-- ⎪⎝⎭D .5,12⎛⎫-- ⎪⎝⎭4.【河北省衡水中学高三上学期一调】若不等式()()1213lg 1lg33x xa x ++-≥-对任意(),1x ∈-∞恒成立,则a 的取值范围是( ) A .(],0-∞B .[)1,+∞C .(],1-∞D .[)0,+∞5.【宁夏育才中学高三上学期第二次月考】若函数xx k k x f 212)(⋅+-=在定义域上为奇函数,则实数=k __________.6.【山西省孝义市高三上学期二轮模考】函数2()log ()a f x ax x =-在区间[2,4]上是单调增函数,则a 的取值范围是__________. 三、练原创1.函数2(),0()1,0x a x f x x a x x ⎧-≤⎪=⎨++>⎪⎩,若(0)f 是()f x 的最小值,则a 的取值范围为( ) A .[1,2]-B .[1,0]-C .[1,2]D .[0,2]2.函数()f x 的导函数为'(x)f ,对x R ∀∈,都有2'()()f x f x >成立,若(ln 4)2f =,则不等式2()exf x =的解是( ) A .ln 4x > B .0ln4x << C .1x >D .01x <<3.已知函数()122,0,log ,0.x a x f x x x ⎧⋅≤⎪=⎨>⎪⎩若关于x 的方程()()0f f x =有且仅有一个实数解,则实数a 的取值范围是( ) A .(),0-∞B .()0,1C .()(),00,1-∞D .()()0,11,+∞4.已知函数2()ln ,af x x a R x=+∈. (1)若函数()f x 在[2,)+∞上是增函数,求实数a 的取值范围;(2)若函数()f x 在[1,e]上的最小值为3,求实数a 的值. 5.已知函数2()(1)1,f x ax a x a R =-++∈. (1)求证:函数()f x 的图象与x 轴恒有公共点; (2)当0a >时,求函数y =(3)若存在0m >使关于x 的方程1()m f x m=+有四个不同的实根,求实数a 的取值范围.高考数学(理科)专题练习 基本初等函数中含有参数问题答 案一、练高考 1~3.DCA4.(,0)(1,)-∞⋃+∞ (0,)⎫+∞⎪⎭;(1,2]{3,4};⎫+∞⎪⎭高考数学(理科)专题练习基本初等函数中含有参数问题解 析1.2.【解析】当1a ≥ 时,()21af a =>,所以,()()()2f aff a = ,即1a >符合题意.当1a < 时,()31f a a =- ,若()()()2f aff a = ,则()1f a ≥ ,即:2311,3a a -≥≥ ,所以213a ≤<适合题意综上,a 的取值范围是2,3⎡⎫+∞⎪⎢⎣⎭,故选C . 3.4.5. 【解析】32323232()()313133f x f a x x a a x x a a -=++---=+--,23222()()(2)(2)x b x a x a b x a ab x a b --=-+++-,所以223223203a b a ab a b a a --=⎧⎪+=⎨⎪-=--⎩,解得21a b =-⎧⎨=⎩.6.1,12t ⎡⎤∈⎢⎥⎣⎦成立.因为0a >,所以函数()211y at a t =++-在区间1,12⎡⎤⎢⎥⎣⎦上单调递增,12t =时,y有最小值3142a -,由31042a -≥,得23a ≥.故a 的取值范围为2,3⎡⎫+∞⎪⎢⎣⎭. 二、练模拟1.2.【解析】 令()()()21,xg x ex h x ax a =-=-.由题意知存在唯一整数t ,使得()g t 在直线()h x 的下方.()()'21x g x e x =+,当12x <-时,函数单调递减,当12x >-,函数单调递增,当12x =-时,函数取得最小值为122e --.当0x =时,(0)1g =-,当1x =时,(1)0g e =>,直线()h x ax a =-过定点()1,0,斜率为a ,故()0a g ->且()113g e a a --=-≥--,解得3,12m e ⎡⎫∈⎪⎢⎣⎭.3.4.5.【解析】122(1)(1)111212k k f f k k k ---=-⇒=-⇒=±++. 6. 【解析】设2()u x ax x =-,则()log ()a f x u x =,要使函数()f x 在区间[2,4]上是单调增函数,由复合函数单调性的判定方法可知()log ()a f x u x =与2()u x ax x =-同为增函数或同为减函数时才能满足,故有1122a a >⎧⎪⎨≤⎪⎩或01142a a<<⎧⎪⎨≥⎪⎩,所以1a >. 三、练原创1. 【解析】因为当0≤x 时,2)()(a x x f -=,因为)0(f 是)(x f 的最小值,所以0≥a ;又因为当0>x 时,221)(a a a xx x f ≥+≥++=,即21≤≤-a .综上所述, a 的取值范围为[]2,0.故应选D . 2.3. 【解析】由函数()122,0,log ,0.x a x f x x x ⎧⋅≤⎪=⎨>⎪⎩可知,在0x ≤部分.当0a >时20x a ⋅>.当0a <时20x a ⋅<.当0a =时20x a ⋅=恒成立.因为关于x 的方程()()0f f x =有且仅有一个实数解,所以只能是()1f x =只有一个解.当0x >时有一个解12x =.所以要使在0x <上没解,有前面可得0a <成立.当0a >时要使01a <<才能成立.故选C .4.③若2a e >,则20x a -<,即()0f x '<在[1,]e 上恒成立,此时()f x 在[1,]e 上是减函数. 所以()()min 213af x f e e ==+=⎡⎤⎣⎦,所以a e =. 5.11 / 11。
【优化指导】2015高考数学总复习 第2章 第8节 函数与方程课时跟踪检测 理(含解析)新人教版
【优化指导】2015高考数学总复习 第2章 第8节 函数与方程课时跟踪检测 理(含解析)新人教版1.(2014·威海模拟)已知函数f (x )的图象是连续不断的,有如下对应值表:x 1 2 3 4 5 6 7 f (x )239-711-5-12-26A .5个B .4个C .3个D .2个解析:选 C 由题意知f (2)·f (3)<0,f (3)·f (4)<0,f (4)·f (5)<0,故函数在区间(2,3),(3,4),(4,5)内各至少有一个零点,故在 [1,6]上至少有3个零点,选C.2.下列函数中,在(-1,1)内有零点且单调递增的是( ) A .y =log 2x B .y =2x-1 C .y =x 2-2D .y =-x 3解析:选B y =log 2x 的零点是1,y =x 2-2的零点是±2,都不在(-1,1)内,尽管y =-x 3的零点在(-1,1)内,但该函数是减函数,只有y =2x -1符合要求.3.(2014·某某检测)函数f (x )=1-x log 2x 的零点所在区间是( )A .⎝ ⎛⎭⎪⎫14,12B .⎝ ⎛⎭⎪⎫12,1 C .(1,2)D .(2,3)解析:选C 因为f (1)=1-log 2 1=1>0,f (2)=1-2log 2 2=-1<0,即f (1)f (2)<0,据零点存在定理可得函数的零点所在的区间为(1,2),故选C.4.(2014·某某模拟)“m <0”是“函数f (x )=m +log 2x (x ≥1)存在零点”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分又不必要条件解析:选A 当m <0时,令f (x )=0得log 2x =-m (x ≥1),x =2-m>1,此时函数f (x )存在零点;反过来,由函数f (x )存在零点不能得知m <0,如取m =0,此时函数f (x )存在零点为x =1.因此,“m <0”是“函数f (x )存在零点”的充分不必要条件,故选A.5.(2011·某某高考)函数f (x )=x -cos x 在[0,+∞)内( ) A .没有零点 B .有且仅有一个零点 C .有且仅有两个零点D .有无穷多个零点解析:选B 令f (x )=0,得x =cos x ,由题意知x ∈[0,+∞),在同一坐标系内画出两个函数y =x 与y =cos x 的图象如图所示,由图象知,两个函数只有一个交点,从而方程x =cos x 只有一个解.故函数f (x )只有一个零点,选B.6.(2013·某某高考)设函数f (x )=e x+x -2,g (x )=ln x +x 2-3.若实数a ,b 满足f (a )=0,g (b )=0,则( )A .g (a )<0<f (b )B .f (b )<0<g (a )C .0<g (a )<f (b )D .f (b )<g (a )<0解析:选A 由f (a )=e a+a -2=0,得0<a <1. 由g (b )=ln b +b 2-3=0得1<b <2. 因为g (a )=ln a +a 2-3<0,f (b )=e b +b -2>0,所以f (b )>0>g (a ),故选A.7.(2014·某某模拟)已知三个函数f (x )=2x+x ,g (x )=x -2,h (x )=log 2x +x 的零点依次为a ,b ,c ,则( )A .a <b <cB .a <c <bC .b <a <cD .c <a <b解析:选B 由于f (-1)=12-1=-12<0,f (0)=1>0,且f (x )为单调递增函数.故f (x )=2x+x 的零点a ∈(-1,0).∵g (2)=0,故g (x )的零点b =2;h ⎝ ⎛⎭⎪⎫12=-1+12=-12<0,h (1)=1>0,且h (x )为单调递增函数,故h (x )的零点c ∈⎝⎛⎭⎪⎫12,1,因此a <c <b .8.(2014·晋中名校联考)函数y =f (x )的最小正周期为2,且f (-x )=f (x ),当x ∈[0,1]时,f (x )=-x +1,那么在区间[-3,4]上,函数y =f (x )的图象与函数y =⎝ ⎛⎭⎪⎫12|x |的图象的交点个数是( )A .8B .7C .6D .5解析:选C 在同一坐标系中画出函数y =f (x )的图象与函数y =⎝ ⎛⎭⎪⎫12|x |的图象,观察图象可知有6个交点,故选C.9.已知函数f (x )=⎝ ⎛⎭⎪⎫13x-log 2x ,正实数a 、b 、c 成公差为正数的等差数列且f (a )f (b )f (c )<0,若实数x 0是方程f (x )=0的一个解,那么下列不等式中不可能成立的是( )A .x 0<aB .x 0>bC .x 0<cD .x 0>c解析:选D 因为a ,b ,c 成等差数列且公差为正数,所以c >b >a >0,又f (x )=⎝ ⎛⎭⎪⎫13x-log 2x 在(0,+∞)上是减函数,所以f (c )<f (b )<f (a ). 又因为f (a )f (b )f (c )<0,则有两种情况:(1)f (a )>f (b )>0>f (c ), 则a <b <x 0<c .(2)f (c )<f (b )<f (a )<0,则x 0<a <b <c .综上所述,不等式中不可能成立的是x 0>c ,故选D.10.(2014·某某四校联考)已知函数f (x )=⎩⎪⎨⎪⎧x 2+12x ,x ≤0,ln x +1,x >0,若函数y =f (x )-kx 有三个零点,则k 的取值X 围为( )A .⎝ ⎛⎭⎪⎫0,12B .()1,+∞C .⎝ ⎛⎭⎪⎫12,1 D .(-∞,0)解析:选C 要使函数y =f (x )-kx 有三个零点,则应该满足f (x )=kx ,只需满足y =f (x )与y =kx 有三个不同交点.当直线y =kx 在原点与y =ln(x +1)相切时的直线为y =x ,这时与y =f (x )有两个交点,不符合题目要求,同样当直线y =kx 在原点与y =x 2+12x 相切时的直线为y =12x ,这时与y =f (x )有1个交点,不符合题目要求,故当12<k <1时,函数y=kx 与y =f (x )有三个交点,故而得出结论12<k <1.故选C.11.若f (x )=⎩⎪⎨⎪⎧x 2-x -1,x ≥2或x ≤-1,1, -1<x <2,则函数g (x )=f (x )-x 的零点为________.解析:1,1+ 2 当x ≥2或x ≤-1时,由x 2-x -1-x =0得x 2-2x -1=0,解得x =1+2或x =1-2(舍去);当-1<x <2时,由1-x =0得x =1.故函数的零点为1,1+ 2.12.(2014·某某段考)已知函数f (x )是定义在(-∞,0)∪(0,+∞)上的奇函数,在(0,+∞)上单调递减,且f ⎝ ⎛⎭⎪⎫12>f (-3)>0,则方程f (x )=0的根的个数为________.解析:2 由于函数f (x )是定义在(-∞,0)∪(0,+∞)上的奇函数,且f (-3)=-f (3)>0,故有f (3)<0,因为函数f (x )在区间(0,+∞)上单调递减,有f ⎝ ⎛⎭⎪⎫12>0,由零点存在定理知,存在c ∈⎝ ⎛⎭⎪⎫12,3,使得f (c )=0,即函数f (x )在(0,+∞)上有唯一零点,由奇函数图象的特点知,函数f (x )在(-∞,0)上也有一个零点,故方程f (x )=0的根的个数为2.13.(2014·日照模拟)已知f (x )=⎩⎪⎨⎪⎧|lg x |,x >0,2|x |,x ≤0,则函数y =2f 2(x )-3f (x )+1的零点个数是________.解析:5 方程2f 2(x )-3f (x )+1=0的解为f (x )=12或1.作出y =f (x )的图象,由图象知零点的个数为5.14.已知函数f (x )=⎩⎪⎨⎪⎧2x -1,x >0,-x 2-2x ,x ≤0,若函数g (x )=f (x )-m 有3个零点,则实数m 的取值X 围是________.解析:[0,1) 在坐标系内作出函数f (x )=⎩⎪⎨⎪⎧2x -1,x >0,-x 2-2x ,x ≤0的图象,如图:发现当0≤m <1时,函数f (x )的图象与直线y =m 有三个交点.即函数g (x )=f (x )-m 有三个零点.1.设方程log 4x -⎝ ⎛⎭⎪⎫14x =0,log 14x -⎝ ⎛⎭⎪⎫14x=0的根分别为x 1,x 2,则( )A .0<x 1x 2<1B .x 1x 2=1C .1<x 1x 2<2D .x 1x 2≥2解析:选A log 14x -⎝ ⎛⎭⎪⎫14x=0的根x 2=12.设f (x )=log 4x -⎝ ⎛⎭⎪⎫14x,因为f (1)·f (2)=⎝ ⎛⎭⎪⎫-14⎝ ⎛⎭⎪⎫12-116<0, 所以1<x 1<2.故0<x 1x 2<1,选A.2.(2014·黄冈中学月考)已知a 是函数f (x )=2x-log 12x 的零点,若0<x 0<a ,则f (x 0)的值满足( )A .f (x 0)=0B .f (x 0)<0C . f (x 0)>0D .f (x 0)的符号不确定解析:选B 函数f (x )=2x+log 2x 在(0,+∞)上是单调递增的,若这个函数有零点,则零点是唯一的,根据函数f (x )在(0,+∞)上是单调递增的及a 为函数f (x )的零点可知,在(0,a )上,这个函数的函数值小于零,即f (x 0)<0.在定义域上单调的函数如果有零点,则只能有唯一的零点,并且以这个零点为分界点把定义域分成两个区间,在其中一个区间内函数值都大于零,在另一个区间内函数值都小于零,故选B.3.(2014·阜宁中学调研)设函数y =x 3与y =⎝ ⎛⎭⎪⎫12x -2的图象的交点为(x 0,y 0),且x 0∈(m ,m +1),m ∈Z ,则m =________.解析:1 令f (x )=x 3-⎝ ⎛⎭⎪⎫12x -2,易知函数y =x 3在R 上单调递增,y =⎝ ⎛⎭⎪⎫12x -2在R 上单调递减,所以y =-⎝ ⎛⎭⎪⎫12x -2在R 上单调递增,所以f (x )在R 上单调递增.又函数y =x 3与y =⎝ ⎛⎭⎪⎫12x -2的图象的交点为(x 0,y 0),所以f (x 0)=0,即x 0为f (x )的零点.又f (1)=1-⎝ ⎛⎭⎪⎫121-2=-1<0,f (2)=8-⎝ ⎛⎭⎪⎫122-2=7>0,f (x )在R 上单调递增,所以x 0∈(1,2),所以m =1.4.已知函数f (x )=4x+m ·2x+1有且仅有一个零点,求m 的取值X 围,并求出该零点. 解:∵f (x )=4x+m ·2x+1有且仅有一个零点,即方程(2x )2+m ·2x+1=0仅有一个实根.设2x =t (t >0),则t 2+mt +1=0. 当Δ=0,即m 2-4=0,∴m =-2时,t =1;m =2时,t =-1(不合题意,舍去), ∴2x=1,x =0符合题意. 当Δ>0,即m >2或m <-2时,t 2+mt +1=0有两正根或两负根,即f (x )有两个零点或没有零点. ∴这种情况不符合题意.综上可知,m =-2时,f (x )有唯一零点, 该零点为x =0.5.已知二次函数f (x )=x 2+(2a -1)x +1-2a .(1)判断命题“对于任意的a ∈R (R 为实数集),方程f (x )=1必有实数根”的真假,并写出判断过程.(2)若y =f (x )在区间(-1,0)及⎝ ⎛⎭⎪⎫0,12内各有一个零点,某某数a 的X 围. 解:(1)“对于任意的a ∈R (R 为实数集),方程f (x )=1必有实数根”是真命题. 依题意:f (x )=1有实根,即x 2+(2a -1)x -2a =0有实根,∵Δ=(2a -1)2+8a =(2a +1)2≥0对于任意的a ∈R (R 为实数集)恒成立即x 2+(2a -1)x -2a =0必有实数根从而f (x )=1必有实数根.(2)依题意知要使y =f (x )在区间(-1,0)及⎝ ⎛⎭⎪⎫0,12内各有一个零点,需满足 ⎩⎪⎨⎪⎧f -1>0,f 0<0,f ⎝ ⎛⎭⎪⎫12>0,即⎩⎪⎨⎪⎧3-4a >0,1-2a <0,34-a >0,解得12<a <34.故所求a 的取值X 围为⎝ ⎛⎭⎪⎫12,34.。
2015高考理科数学《曲线与方程》练习题
2015高考理科数学《曲线与方程》练习题2015高考理科数学《曲线与方程》练习题[A组基础演练·能力提升]一、选择题1.方程x2-y2=0对应的图象是( )解析:由x2-y2=0得,y=x或y=-x,故选C.答案:C2.已知点P是直线2x-y+3=0上的一个动点,定点M(-1,2),Q是线段PM延长线上的一点,且|PM|=|MQ|,则Q点的轨迹方程是( )A.2x+y+1=0 B.2x-y-5=0C.2x-y-1=0 D.2x-y+5=0解析:设Q(x,y),则P为(-2-x,4-y),代入2x-y+3=0得2x-y+5=0.答案:D3.已知A(0,7),B(0,-7),C(12,2),以C为一个焦点的椭圆经过A,B两点,则椭圆的另一个焦点F的轨迹方程是( )A.y2-x248=1(y≤-1) B.y2-x248=1(y≥1)C.x2-y248=1(x≤-1) D.x2-y248=1(x≥1)解析:由题意知|AC|=13,|BC|=15,|AB|=14,又∵|AF|+|AC|=|BF|+|BC|,∴|AF|-|BF|=|BC|-|AC|=2,故点F的轨迹是以A,B为焦点,实轴长为2的双曲线的下支.又c=7,a=1,b2=48,∴点F的轨迹方程为y2-x248=1(y≤-1).答案:A4.有一动圆P恒过定点F(a,0)(a>0)且与y轴相交于点A、B,若△ABP为正三角形,则点P的A .直线B .圆C .椭圆D .双曲线解析:设P (x ,y ),动圆P 的半径为R ,由于△ABP 为正三角形, ∴P 到y 轴的距离d =32R ,即|x |=32R . 而R =|PF |=x -a 2+y 2, ∴|x |=32·x -a2+y 2.整理得(x +3a )2-3y 2=12a 2,即x +3a212a 2-y 24a2=1. ∴点P 的轨迹为双曲线. 答案:D5.已知点A (1,0)和圆C :x 2+y 2=4上一点R ,动点P 满足RA →=2AP →,则点P 的轨迹方程为( ) A.⎝ ⎛⎭⎪⎫x -322+y 2=1 B.⎝ ⎛⎭⎪⎫x +322+y 2=1C .x 2+⎝ ⎛⎭⎪⎫y -322=1D .x 2+⎝⎛⎭⎪⎫y +322=1解析:设P (x ,y ),R (x 0,y 0),则有RA →=(1-x 0,-y 0),AP →=(x -1,y ). 又RA →=2AP →, ∴⎩⎨⎧1-x 0=2x -1,-y 0=2y .∴⎩⎨⎧x 0=-2x +3,y 0=-2y .又R (x 0,y 0)在圆x 2+y 2=4上,∴(-2x +3)2+(-2y )2=4,即⎝⎛⎭⎪⎫x -322+y 2=1.答案:A6.设A 1,A 2是椭圆x 29+y 24=1的长轴两个端点,P 1,P 2是垂直于A 1A 2的弦的端点,则直线A 1P 1与A 2P 2交点的轨迹方程为( )A.x29+y24=1 B.y29+x 24=1 C.x 29-y 24=1 D.y 29-x 24=1 解析:设交点为P (x ,y ),A 1(-3,0),A 2(3,0),P 1(x 0,y 0),P 2(x 0,-y 0), ∵A 1,P 1,P 共线,∴y -y 0x -x 0=yx +3.① ∵A 2,P 2,P 共线,∴y +y 0x -x 0=yx -3.② 由①②解得x 0=9x,y 0=3yx,代入x 209+y 204=1,化简,得x 29-y 24=1.答案:C 二、填空题7.△ABC 的顶点A (-5,0),B (5,0),△ABC 的内切圆圆心在直线x =3上,则顶点C 的轨迹方程是________.解析:如图,|AD |=|AE |=8,|B F |=|BE |=2,|CD |=|CF |, 所以|CA |-|CB |=8-2=6.根据双曲线定义,所求轨迹是以A ,B 为焦点,实轴长为6的双曲线的右支,方程为x 29-y 216=1(x >3).答案:x 29-y 216=1(x >3)8.(2014年成都模拟)P 是椭圆x 2a 2+y 2b 2=1上的任意一点,F 1、F 2是它的两个焦点,O 为坐标原点,有一动点Q 满足OQ →=PF 1→+PF 2→,则动点Q 的轨迹方程是________.解析:由OQ →=PF 1→+PF 2→,又PF 1→+PF 2→=PM →= 2PO →=-2OP →, 设Q (x ,y ), 则OP →=-12OQ →=⎝ ⎛⎭⎪⎫-x2,-y 2,即P 点坐标为⎝ ⎛⎭⎪⎫-x2,-y 2,又P 在椭圆上,则有⎝ ⎛⎭⎪⎫-x 22a 2+⎝ ⎛⎭⎪⎫-y 22b 2=1,即x 24a 2+y 24b2=1. 答案:x 24a 2+y 24b2=19.已知真命题:若A 为⊙O 内一定点,B 为⊙O 上一动点,线段AB 的垂直平分线交直线OB 于点P ,则点P 的轨迹是以O ,A 为焦点,OB 长为长轴长的椭圆.类比此命题,写出另一个真命题:若A 为⊙O 外一定点,B 为⊙O 上一动点,线段AB 的垂直平分线交直线OB 于点P ,则点P 的轨迹是________.解析:如图,连接AP ,由于P 是线段AB 垂直平分线上一点,故有|PA |=|PB |,因此||PA|-|PO||=||PB|-|PO||=|OB|=R=定值,其中R为⊙O的半径.又由于点A在圆外,故||PA|-|PO||=|OB|=R<|OA|,故动点P的轨迹是以O,A为焦点,OB为实轴长的双曲线.答案:以O,A为焦点,OB为实轴长的双曲线三、解答题10.如图所示,直线l1与l2相交于点M,l1⊥l2,点N∈l1,以A、B为端点的曲线段C上的任一点到l2的距离与到点N的距离相等.若△AMN为锐角三角形,|AM|=17,|AN|=3,且|NB|=6,建立适当的坐标系,求曲线段C的方程.解析:以l1为x轴,l2为y轴建立平面直角坐标系,M为坐标原点.作AE⊥l1,AD⊥l2,BF⊥l2,垂足分别为E、D、F.设A(x A,y A),B(x B,y B),N(x N,0).依题意有x A=|ME|=|DA|=|AN|=3,y=|DM|=|AM|2-|DA|2=2 2.A∵△AMN是锐角三角形,∴x N=|ME|+|EN|=|ME|+|AN|2-|AE|2=4,x=|BF|=|BN|=6.B设P(x,y)是曲线段C上任一点,则P∈{(x,y)|(x-x N)2+y2=x2,x A≤x≤x B,y>0}.∴曲线段C的方程为y2=8(x-2)(3≤x≤6,y>0).11.已知圆C的方程为x2+y2=4.(1)求过点P(1,2)且与圆C相切的直线l的方程;(2)直线l过点P(1,2),且与圆C交于A、B两点,若|AB|=23,求直线l的方程;(3)圆C 上有一动点M (x 0,y 0),ON →=(0,y 0),若向量OQ →=OM →+ON →,求动点Q 的轨迹方程,并说明此轨迹是什么曲线.解析:(1)显然直线l 的斜率存在,设切线方程为y -2=k (x -1),则由|2-k |k 2+1=2,得k 1=0,k 2=-43,从而所求的切线方程为y =2和4x +3y -10=0.(2)当直线l 垂直于x 轴时,此时直线方程为x =1,l 与圆的两个交点坐标为(1,3)和(1,-3),这两点的距离为23,满足题意;当直线l 不垂直于x 轴时,设其方程为y -2=k (x -1),即kx -y -k +2=0,设圆心到此直线的距离为d (d >0),则23=24-d 2,得d =1,从而1=|-k +2|k 2+1,得k =34,此时直线方程为3x -4y +5=0,综上所述,所求直线方程为3x -4y +5=0或x =1.(3)设Q 点的坐标为(x ,y ),M 点坐标是(x 0,y 0),ON →=(0,y 0),∵OQ →=OM →+ON →,∴(x ,y )=(x 0,2y 0)⇒x =x 0,y =2y 0.∵x 20+y 20=4,∴x 2+⎝ ⎛⎭⎪⎫y 22=4,即x 24+y 216=1. ∴Q 点的轨迹方程是x 24+y 216=1,轨迹是一个焦点在y 轴上的椭圆.12.(能力提升)(2014年恩施模拟)在直角坐标平面上,O 为原点,M 为动点,|OM →|=5,ON →=255OM →.过点M 作MM 1⊥y 轴于点M 1,过N 作NN 1⊥x 轴于点N 1,OT →=M 1M →+N 1N →.记点T 的轨迹为曲线C ,点A (5,0)、B (1,0),过点A 作直线l 交曲线C 于两个不同的点P 、Q (点Q 在A 与P 之间).(1)求曲线C 的方程;(2)是否存在直线l ,使得|BP |=|BQ |,并说明理由.解析:(1)设点T 的坐标为(x ,y ),点M 的坐标为(x ′,y ′),则M 1的坐标为(0,y ′), ON →=255OM →=255(x ′,y ′),于是点N 的坐标为⎝ ⎛⎭⎪⎫255x ′,255y ′,N 1的坐标为⎝ ⎛⎭⎪⎫255x ′,0,所以M 1M →=(x ′,0),N 1N →=⎝ ⎛⎭⎪⎫0,255y ′.由OT →=M 1M →+N 1N →,有(x ,y )=(x ′,0)+⎝ ⎛⎭⎪⎫0,255y ′,所以⎩⎨⎧x =x ′,y =255y ′.由此得x ′=x ,y ′=52y . 由|OM →|=5,得x ′2+y ′2=5,所以x 2+⎝ ⎛⎭⎪⎫52y 2=5,得x 25+y 24=1,即所求的方程表示的曲线C是椭圆.(2)点A (5,0)在曲线C 即椭圆的外部,当直线l 的斜率不存在时,直线l 与椭圆C 无交点,所以直线l 的斜率存在,并设为k ,直线l 的方程为y =k (x -5).由方程组⎩⎨⎧x 25+y 24=1,y =k x -5得(5k 2+4)x 2-50k 2x +125k 2-20=0.依题意知Δ=20(16-80k 2)>0,得-55<k <55.当-55<k <55时,设交点P (x 1,y 1),Q (x 2,y 2),PQ 的中点为R (x 0,y 0), 则x 1+x 2=50k 25k 2+4,x 0=x 1+x 22=25k 25k 2+4.∴y 0=k (x 0-5)=k ⎝ ⎛⎭⎪⎫25k 25k 2+4-5=-20k25k 2+4.又|BP |=|BQ |⇔BR ⊥l ⇔k ·k BR =-1,k ·k BR =k ·20k 5k 2+41-25k 25k 2+4=20k 24-20k 2=-1⇔20k 2=20k 2-4,而20k 2=20k 2-4不可能成立,所以不存在直线l ,使得|BP |=|BQ |.[B 组 因材施教·备选练习]1.已知点M (-3,0),N (3,0),B (1,0),动圆C 与直线MN 切于点B ,过M 、N 与圆C 相切的两直线相交于点P ,则P 点的轨迹方程为( )A .x 2-y28=1(x >1)B .x 2-y 28=1(x <-1)C .x 2+y 28=1(x >0)D .x 2-y 210=1(x >1) 解析:如图所示,设直线MP 与直线NP 分别与动圆C 切于点E 、F ,则|PE |=|PF |,|ME |=|MB |,|NF |=|NB |.从而|PM |-|PN |=|ME |-|NF |=|MB |-|NB |=4-2=2<|MN |,所以点P 的轨迹是以M 、N为焦点,实轴长为2的双曲线的右支.设对应的双曲线方程为x 2a 2-y 2b 2=1,则a =1,c =3,b 2=8.故P点的轨迹方程为x 2-y 28=1(x >1).答案:A2.到两互相垂直的异面直线的距离相等的点,在过其中一条直线且平行于另一条直线的平面内的轨迹是( )A .直线B .椭圆C .抛物线D .双曲线解析:在棱长为a 的正方体ABCD -A 1B 1C 1D 1中,DC 与A 1D 1是两条相互垂直的异面直线,平面ABCD 过直线DC 且平行于A 1D 1,以D 为原点,分别以DA 、DC 为x 轴、y 轴建立平面直角坐标系,设点P (x ,y )在平面ABCD 内,且到A 1D 1到DC 的距离相等,∴|x |=y 2+a 2,∴x 2-y 2=a 2,故该轨迹为双曲线.答案:D3.由抛物线y 2=2x 上任意一点P 向其准线l 引垂线,垂足为Q ,连接顶点O 与P 的直线和连接焦点F 与Q 的直线交于点R ,则点R 的轨迹方程是________.解析:设P ⎝ ⎛⎭⎪⎫y 202,y 0,则F ⎝ ⎛⎭⎪⎫12,0,Q ⎝ ⎛⎭⎪⎫-12,y 0∴OP 的方程y =2y 0x ①QF 的方程为:y =-y 0⎝ ⎛⎭⎪⎫x -12② 由①、②消去y 0得y 2=-2x 2+x . 答案:y 2=-2x 2+x======*以上是由明师教育编辑整理======。
函数的零点与方程的解(高中数学)
指数函数与对数函数
2
学习目标
核心素养
1.理解函数零点的概念以及函数零 1.借助零点的求法培养数学运算和
点与方程根的关系.(易混点) 逻辑推理的素养.
2.会求函数的零点.(重点) 2.借助函数的零点同方程根的关系,
3.掌握函数零点存在定理并会判断 培养直观想象的数学素养.
25
2.若函数g(x)=f(x知方程 f(x)-a=0有解,即a=f(x)有解. 故a的范围为y=f(x)的值域. 法二:g(x)=f(x)-a有零点,等价于函数y=a与函数y=f(x)的图象有 交点,故可在同一坐标系中分别画出两函数的图象,观察交点情况即 可.
26
【例 3】 已知 0<a<1,则函数 y=a|x|-|logax|的零点的个数为( )
A.1
B.2
C.3
D.4
[思路点拨]
构造函数fx=a|x|0<a<1 与gx=|logax|0<a<1
→
画出fx与 gx的图象
→
观察图象得 零点的个数
27
B [函数y=a|x|-|logax|(0<a<1)的零点的个 数即方程a|x|=|logax|(0<a<1)的根的个数,也就是 函数f(x)=a|x|(0<a<1)与g(x)=|logax|(0<a<1)的图象 的交点的个数.
(4)若 f(x)在(a,b)内有且只有一个零点,则
f(a)·f(b)<0.( )
33
2.函数 f(x)=2x-3 的零点所在
B [∵f(1)=2-3=-1<0,f(2)
的区间是( )
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015高考理科数学方程的解与函数的零点考点练习 1、“0t”是“函数2()fxxtxt在(,)内存在零点”的 ( ) A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件 【答案】A
2、已知函数)0(2)(23abxaxxf有且仅有两个不同的零点1x,2x,则 ( )
A.当0a时,021xx,021xx B.当0a时,021xx,021xx C.当0a时,021xx,021xx D.当0a时,021xx,021xx 【答案】B 3、已知函数2|3|)(3axxxf在)2,0(上恰有两个零点,则实数a的取值范围为 ( )
A.)2,0( B.)4,0( C.)6,0( D.(2,4) 【答案】D 4、若abc,则函数fxxaxbxbxcxcxa的两个零点分别位于区间 ( ) A.,ab和,bc内 B.,a和,ab内 C.,bc和,c
【答案】A. 【解析】因为
()faabac,()()()0fbbcba,()()()0fccacb,
所以()()0fafb,()()0fbfc,所以函数的两个零点分别在(,)ab和(,)bc内,,故选A. 【易错点】不能根据,,abc的大小进行判断函数值的符号,或错误利用零点存在性定理,造成错选B,C, D. 5、函数0.5()2|log|1xfxx的零点个数为 ( ) A.1 B.2 C.3 D.4 【答案】 B.在同一坐标系中作出1()()2xfx与0.5|log|yx,如图,
由图可得零点的个数为2.
6、下列各种说法中正确的个数有 ①函数()yfx满足()()0fafb,则函数()yfx在区间(,)ab内只有一个零点; ②函数()yfx满足()()0fafb,则函数()yfx在区间[,]ab内有零点; ③函数()yfx满足()()0fafb,则函数()yfx在区间(,)ab内没有零点; ④函数()yfx在[,]ab上连续且单调,并满足()()0fafb,则函数()yfx在区间(,)ab内只有一个零点;
⑤函数2()23fxxx的零点是(3,0)与(1,0). ( ) A.0个 B.1个 C.2个 D.3个 【答案】 B.
7、函数2()cosfxxx在区间[0,4]上的零点个数为 ( ) A.4 B.5 C.6 D.7 【答案】 考点分析:本题考察三角函数的周期性以及零点的概念.
解析:0)(xf,则0x或0cos2x,Zkkx,22,又4,0x,4,3,2,1,0k
所以共有6个解.选 C.
8、已知24(0)2(0)axxxfxfxx且方程2fxx恰有3个不同的实数根,则实数a的取值范围是 8,A 4,B 4,0C 0,D
【答案】D 9、已知函数()=lnfxx,则函数()=()'()gxfxfx的零点所在的区间是 ( ) A.(0,1) B.(1,2) C.(2,3) D.(3,4) 【答案】B
解:函数的导数为1'()fxx,所以1()=()'()lngxfxfxxx。因为(1)ln1110g,1(2)ln202g,所以函数()=()'()gxfxfx的零点所
在的区间为(1,2).选 B. 10、函数33,0,(),0xxfxxx的图象与函数()ln(1)gxx的图象的交点个数是 ( ) A.1 B.2 C.3 D.4 【答案】C
11、已知函数21,0,()(1),0.xxfxfxx若方程()fxxa有且只有两个不相等的实数根,则实数a的取值范围是 ( ) A.,1 B.,1 C.0,1 D.0, 【答案】A
12、函数121()()2xfxx的零点个数为 ( ) A.0 B.1 C.2 D.3 【答案】B
【解析】函数121()()2xfxx的零点,即令()0fx,根据此题可得121()2xx,在平面直角坐标系中分别画出这两个函数的图像,可得交点只有一个,所以零点只有一个,故选答案 B.
13、已知函数.0,ln,0,1)(xxxkxxf 则下列关于函数1)(xffy的零点个数的判断正确的是 ( ) A.当0k时,有3个零点;当0k时,有2个零点 B.当0k时,有4个零点;当0k时,有1个零点 C.无论k为何值,均有2个零点 D.无论k为何值,均有4个零点 【答案】B
14、设定义在R上的函数()fx是最小正周期为2的偶函数,()fx是()fx的导函数,当0,x时,0()1fx;当(0,)x且2x时 ,()()02xfx,则函数
()sinyfxx在[2,2]上的零点个数为 ( )
A.2 B.4 C.5 D.8 【答案】B
【解析】由当x∈(0,π) 且x≠2时 ,()()02xfx,知
0,()0,()2xfxfx时,为减函数;()0,()2xfxfx,时,为增函数
又0,x时,0系中作出sinyx和()yfx草图像如下,由图知y=f(x)-sinx在[-2π,2π] 上的零点个数为4个.
【点评】本题考查函数的周期性、奇偶性、图像及两个图像的交点问题.
15、函数()cos2fxxx在区间[0,2]上的零点个数为 ( ) A.2 B.3 C.4 D.5 【答案】 D【解析】由()cos20fxxx,得0x或cos20x;其中,由cos20x,
得22xkkZ,故24kxkZ.又因为0,2xπ,所以π3π5π7π,,,4444x.所以零点的个数为145个.故选 D.
16、设函数141()log()4xfxx、2141()log()4xfxx的零点分别为12xx、,则 ( ) A.1201xx B.1212xx C.121xx D.122xx 【答案】A 17、已知f(x)是定义在R上的奇函数,满足33()()22fxfx,当3(0,)2x
时,f(x)=2ln(1)xx,则函数f(x)在区间[0,6]上的零点个数是 ( ) A.3 B.5 C.7 D.9 【答案】D
18、已知函数2342013()12342013xxxxfxx则下列结论正确的是 ( ) A.()fx在(0,1)上恰有一个零点 B. ()fx在(0,1)上恰有两个零点 C.()fx在(1,0)上恰有一个零点 D.()fx在(1,0)上恰有两个零点
xyo22
1
1sinyx()yfx【答案】C 19、函数3()=2+2xfxx在区间(0,1)内的零点个数是 ( ) A.0 B.1 C.2 D.3 【答案】 【答案】B
【解析】解法1:因为(0)=1+02=1f,3(1)=2+22=8f,即(0)(1)<0ff且函数
()fx在(0,1)内连续不断,故()fx在(0,1)内的零点个数是1.
解法2:设1=2xy,32=2yx,在同一坐标系中作出两函数的图像如图所示:可知B正确. 4
2
2468
510 20、若方程()20fx在(,0)内有解,则()yfx的图象是
【答案】D 21、已知函数||2()(2)xfxfx(11)(11)xxx或与函数()(1)1gxkx有五个不同的交点,则实数k的取值范围为 ( ) A.11(,)46 B.11(,)64 C.1111(,)(,)4664 D.11(,)64
【答案】 C.易知函数()fx以2为周期,函数()gx图象恒过点(1,1),作出两函数图象,当0k时,交点(3,2),(5,2)代入到()gx,分别得1211,46kk,要使有五个不同的交点,则有1164k,由对称性可知:当0k时,1146k.综上,实数k的取值范围为1111(,)(,)4664. 22、函数aaxxf21)(在区间)1,1(上存在一个零点,则实数a的取值范围是________
