20170311相交线与平行线的单元测试题含答案

合集下载

(完整版)相交线与平行线单元测试题.docx

《相交线与平行线》单元测试题姓名 ______________ 学号 ______________一、填空1、把“内角相等”改成“如果⋯⋯，那么⋯⋯”的形式是____________________________________ 。

2、将段 AB 向右平移 3cm 得到段 CD ，如果 AB=5cm ，那么 CD=__________cm.3、如，已知150 ，那么 2 ______ 度。

124、如，已知直AB 与 CD 相交于点 O， OA 平分COE ， 1 65，第 3DOE 的度数是__________。

E D 5、如，已知OE AB ，AOC25，EOD__________度。

1、如，直 a ，b 被直l所截， a∥b，如果165，那么∠度A O B2=_________.6第 47、如，12240 ， b// c ， 3 _________C8、如果两条平行被第三条直所截，一同旁内角的比1:5，那么两个角的度数分_______和_______ 。

9、如， AB ∥ CD，∠ 1=39 °，∠ C 和∠ D 互余，∠ B=________ 。

10、如，已知AB ∥ CD，直 EF 分交 AB 、 CD 于点 E、 F，EG 平分∠ BEF ，若∠ 1=70 °，∠ 2 的度数 _______________ 。

Elb c AD a111A B223OC第5b D第 6第 7二、解答第 911、已知直a、 b 被直c所截，且已知1 2 ，明： a // b 。

12、如， AB // CD ， 3 : 2 5 : 3 ，求 1 的度数。

BA E B12CC F G D第 101ab2c32A B1C D13、如图，∠ ABC = ∠ BCD ，∠ ABC ＋∠ CDG = 180 °，试问： BC 与 GD 平行吗？若平行，请说明理由。

A B GC D14 、如图所示，把一张长方形纸片ABCD 沿 EF 折叠，若EFG 50 ，求AEM 的度数。

七年级数学(下)《相交线与平行线》复习测试题含答案

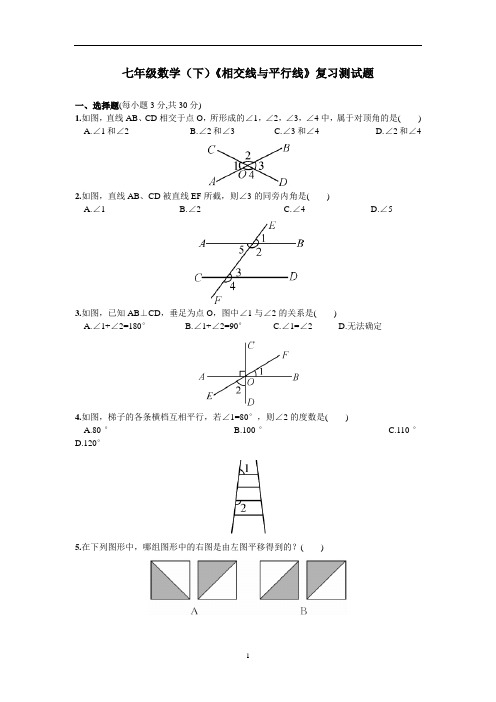
七年级数学（下）《相交线与平行线》复习测试题一、选择题(每小题3分,共30分)1.如图，直线AB、CD相交于点O，所形成的∠1，∠2，∠3，∠4中，属于对顶角的是( )A.∠1和∠2B.∠2和∠3C.∠3和∠4D.∠2和∠42.如图，直线AB、CD被直线EF所截，则∠3的同旁内角是( )A.∠1B.∠2C.∠4D.∠53.如图，已知AB⊥CD，垂足为点O，图中∠1与∠2的关系是( )A.∠1+∠2=180°B.∠1+∠2=90°C.∠1=∠2D.无法确定4.如图，梯子的各条横档互相平行，若∠1=80°，则∠2的度数是( )A.80°B.100°C.110°D.120°5.在下列图形中，哪组图形中的右图是由左图平移得到的？( )6.命题：①对顶角相等；②过一点有且只有一条直线与已知直线平行；③相等的角是对顶角；④同位角相等.其中假命题有( )A.1个B.2个C.3个D.4个7.平面内三条直线的交点个数可能有( )A.1个或3个B.2个或3个C.1个或2个或3个D.0个或1个或2个或3个8.下列图形中，由AB∥CD，能得到∠1=∠2的是( )9.如图，直线a∥b，直线c分别与a、b相交于点A、B.已知∠1=35°,则∠2的度数为( )A.165°B.155°C.145°D.135°10.如图，点E在CD的延长线上，下列条件中不能判定AB∥CD的是( )A.∠1=∠2B.∠3=∠4C.∠5=∠BD.∠B+∠BDC=180°二、填空题(每小题4分，共20分)11.将命题“两直线平行，同位角相等”写成“如果……那么……”的形式是____________________.12.两条平行线被第三条直线所截，同旁内角的度数之比是2∶7，那么这两个角的度数分别是__________.13.如图，AB，CD相交于点O，AC⊥ＣＤ于点Ｃ，若∠BOD=38°，则∠A等于__________.14.如图，BC⊥AE，垂足为点C，过C作CD∥AB.若∠ECD=48°，则∠B=__________.15.如图，直线AB，CD被BC所截，若AB∥CD，∠1=45°，∠2=35°，则∠3=__________度.三、解答题(共50分)16.(7分)如图，已知AB⊥BC，BC⊥CD，∠1=∠2.试判断BE与CF的位置关系，并说明你的理由.解：BE∥CF.理由：∵AB⊥BC,BC⊥CD(已知)，∴∠__________=∠__________=90°(垂直的定义).∵∠1=∠2(已知)，∴∠ABC-∠1=∠BCD-∠2，即∠EBC=∠BCF.∴BE∥CF(____________________).17.(9分)如图，直线AB、CD相交于点O，P是CD上一点.(1)过点P画AB的垂线段PE；(2)过点P画CD的垂线，与AB相交于F点；(3)说明线段PE、PO、FO三者的大小关系，其依据是什么？18.(10分)如图，O是直线AB上一点，OD平分∠AOC.(1)若∠AOC=60°，请求出∠AOD和∠BOC的度数；(2)若∠AOD和∠DOE互余，且∠AOD=13∠AOE，请求出∠AOD和∠COE的度数.19.(12分)如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.(1)AE与FC平行吗?说明理由;(2)AD与BC的位置关系如何?为什么?(3)BC平分∠DBE吗?为什么？20.(12分)如图，已知AB∥CD，分别探究下面四个图形中∠APC和∠PAB、∠PCD的关系，请从你所得四个关系中选出任意一个，说明你探究的结论的正确性.结论：(1)____________________；(2)____________________；(3)____________________；(4)____________________.选择结论：____________________，说明理由.参考答案变式练习1.C2.∵∠AOC=70°，∴∠BOD=∠AOC=70°.∵∠BOE∶∠EOD=2∶3，∴∠BOE=223×70°=28°.∴∠AOE=180°-28°=152°.3.C4.121°5.C6.8 复习测试1.D2.B3.B4.B5.C6.C7.D8.B9.C 10.A11.如果两直线平行，那么同位角相等12.40°，140°13.52°14.42°15.8016.ABC BCD 内错角相等，两直线平行17.（1）（2）图略；（3）PE＜PO＜FO，依据是垂线段最短.18.(1)∵OD平分∠AOC，∠AOC=60°,∴∠AOD=12×∠AOC=30°，∠BOC=180°-∠AOC=120°.(2)∵∠AOD和∠DOE互余，∴∠AOE=∠AOD+∠DOE=90°.∵∠AOD=13∠AOE，∴∠AOD=13×90°=30°.∴∠AOC=2∠AOD=60°.∴∠COE=90°-∠AOC=30°.19.(1)AE∥FC.理由：∵∠1+∠2=180°,∠2+∠CDB=180°, ∴∠1=∠CDB.∴AE∥FC.(2)AD∥BC.理由：∵AE∥CF,∴∠C=∠CBE.又∠A=∠C,∴∠A=∠CBE.∴AD∥BC.(3)BC平分∠DBE.理由：∵DA平分∠BDF,∴∠FDA=∠ADB.∵AE∥CF,AD∥BC,∴∠FDA=∠A=∠CBE,∠ADB=∠CBD.∴∠CBE=∠CBD.∴BC平分∠DBE.20.(1)∠PAB+∠APC+∠PCD=360°(2)∠APC=∠PAB+∠PCD(3)∠APC=∠PCD-∠PAB(4)∠APC=∠PAB-∠PCD(1)过P点作EF∥AB，∴EF∥CD，∠PAB+∠APF=180°.∴∠PCD+∠CPF=180°.∴∠PAB+∠APC+∠PCD=360°.。

相交线与平行线试题含答案

第五章相交线与平行线单元测试题2 .5 cmUCD 的长为_______________ cm一、选择题〔每题5分，共3 0分〕1 .如图，/1 = 6 2°,假设m// n,那么/2的度数为〔〕〔A〕118°〔B〕28°〔C〕62°〔D〕382.在同一平面内, 如果两条直线都和第二条直线垂直, 那么这两条直线〔〕〔A〕互相垂直〔B〕互相平行〔C〕相交〔D〕相等3 .如图，直线m、n相交，那么/1与/2的位置关系为〔〔A〕邻补角〔B〕内错角〔C〕同旁内角〔D〕对顶角11.假设直线a // b , b // c，贝U a ____ c，原因是 _______________________________12.〔1〕连接直线外一点与直线上各点的所有线段中，__________ 最短；〔2〕直线外一点到这条直线的垂线段的长度叫做点到直线的________________ .(A)20°(C)110°(B)70°(D)180°D E5 .以下命题中，真命题的是〔〕〔A〕两个锐角的和为直角〔B〕两个锐角的和为钝角L ____B__ 1C4 .如图，ZC=70 °，当ZAED等于〔〕时，DE//BC〔C〕两个锐角的和为锐角〔D〕互余且非零度的两个角都是锐角三、解答题〔总分值4 0分〕13.〔总分值8分〕如图，vZ1=Z2〔〕，•- ____ //_________ 〔vZ2=Z3〔〕，•- _______ // ________ 〔•- _______ // ________ 〔FD14.〔总分值12分〕著名的比萨斜塔建成于12世纪，从建成之日起就一直在倾斜.目前, 它与地面所成的较小的角为8 5°,它与地面所成的较大的角是多少度？为什么？6.如图，AB丄CD垂足为O, 那么/2等于〔〕〔A〕30°〔B〕45°〔C〕60°〔D〕90°EF经过点O. 如果Z1 = 30、填空题〔每题5分，共3 0分〕7.平行用符号 _________ 表示，直线AB与CD平行，可以记作为8 .如果M N//AB,AC//M N,那么点C在__________________ 上.9.如图，直线a、b相交于点O,假设7 1 = 50°,那么/2 ==_________ ,74= _____________ .10.如图，线段CD是由线段AB经过平移得到的，假设AB的长为D15.(总分值20分)如图，直线AE、CD、EF相交于点O.(1)写出ZCOE的邻补角；(2)分别写出ZCOE和/EOE的对顶角；(3)如果ZBOD=60°, ZBOF=90 求ZAO F和ZFOC的度数.附加题(各10分，共2 0分)1 .如图，根据条件，直线AB与直线CD平行吗？说说你的理由.2 .如图，AD//CE,Z1=Z2，说明AB与CD的位置关系，理由是什么? B2 .解：AE平行于CD. •••AD//CE,「./2=/ADC〔两直线平行，内错角相等〕，V Z1=Z2,A Z1=ZADC〔等量代换〕，•••AE//CD〔内错角相等，两直线平行〕.或：AE//CD. VAD/CE,AZADB = ZE〔两直线平行，同位角相等〕，•••三角形三个角之和为18 0°,即Z1+ZB+ZADB=18O°,Z2+ZCDE+ZE=18O°, .•ZB=18O°-Z1-ZADB,ZCDE=18O°-Z2-ZE, 而/l=/2,.・./B = /CDE,.・.AB//CD〔同位角相等，两直线平行〕第五章相交线与平行线-、选择题二、填空题三、解答题13.〔略〕14.95°.因为它与地面所形成的较大角与较小角互为邻补角15 .解：〔l〕/COE的邻补角为ZCO F和ZDOE;〔2〕ZCOE的对顶角为/ DOF,ZBOE 的对顶角为ZAOF;〔3〕ZAOF=90°,ZFOC=l50°附加题l .解：直线AB与直线CD平行. V ZAGH=110°,A ZBGH=180°-110°=70° 〔邻补角定义〕.而/ DHF=70 °，即/BGH = /DHF,.・.AB//CD〔同位角相等，两直线平行〕.或：•••/CHG = /DHF=7 0 °〔对顶角相等〕，而/AGH + /CHG=11O°+7O°=18O°,.・.AB//CD〔同旁内角互补，两直线平行〕.。

相交线与平行线经典测试题含答案

故选择B.
【点睛】
本题综合考查了平行线的判定及性质.
5．如图，AB∥CD，AE平分∠CAB交CD于点E，若∠C=50°，则∠AED=（）
A．65°B．115°C．125°D．130°
【答案】B
【解析】
试题分析：∵AB∥CD，∴∠C+∠CAB=180°，∵∠C=50°，∴∠CAB=180°﹣50°=130°，∵AE平分∠CAB，∴∠EAB=65°，∵AB∥CD，∴∠EAB+∠AED=180°，∴∠AED=180°﹣65°=115°，故选B．
∴∠1=60°，
故选：B．
【点睛】
此题考查平行线的性质，三角板的知识，熟记性质是解题的关键．
8．如图，，，则（）
A． B． C． D．
【答案】C
【解析】
【分析】
首先证明a∥b，再根据两直线平行同位角相等可得∠3=∠6，再根据对顶角相等可得∠4．
【详解】
解：∵∠1+∠5=180°，∠1+∠2=180°，
B、∵∠3＝∠4，∴AB∥CD（内错角相等，两直线平行），故B能判断；
C、∵∠ABD＝∠BDC，∴AB∥CD（内错角相等，两直线平行），故C能判断；
D、∵∠ABC+∠BCD＝180°，∴AB∥CD（同旁内角互补，两直线平行），故D能判断，
故选A．
【点睛】
本题考查了平行线的判定．掌握同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行是解题的关键．
【详解】
解：∵AB＝AC，∠A＝36°，
∴∠ABC＝∠C＝72°，
∵BD平分∠ABC，
∴∠ABD＝∠DBC＝36°，
∴∠BDC＝180°﹣36°﹣72°＝72°，

第五章《相交线与平行线》单元测试卷(含答案)

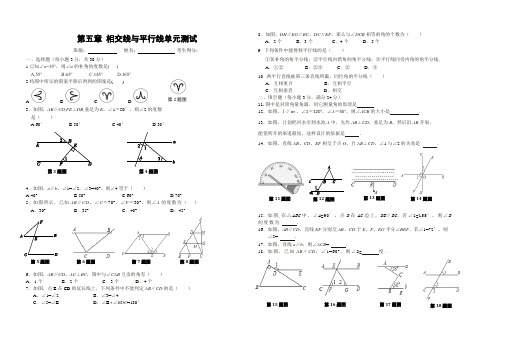
第五章相交线与平行线单元测试班级：姓名：考生得分：一、选择题（每小题3分，共30分） 1.已知∠α=35°，则∠α的补角的度数是( ) A.55° B.65° C.145° D.165° 2.将图中所示的图案平移后得到的图案是( )A. B. C. D.3．如图，AB ∥CD ,FE ⊥DB ,垂足为E ，∠1＝50°，则∠2的度数是（）A.60°B.50°C.40°D.30°4．如图，a ∥b ，∠1=∠2，∠3=40°，则∠4等于（） A.40° B.50° C.60° D.70° 5．如图所示，已知AB ∥CD ，∠C ＝70°，∠F ＝30°，则∠A 的度数为（） A ．30° B ．35° C ．40° D ．45°6．如图，AB ∥CD ，AC ⊥BC ，图中与∠CAB 互余的角有（） A ．1个 B ．2个 C ．3个 D ．4个7．如图，点E 在CD 的延长线上，下列条件中不能判定AB ∥CD 的是（） A ．∠1=∠2 B ．∠3=∠4 C ．∠5=∠B D ．∠B +∠BDC =180°8．如图，DH ∥EG ∥BC ，DC ∥EF ，那么与∠DCB 相等的角的个数为（） A ．2个 B ．3个 C ．4个 D ．5个 9. 下列条件中能得到平行线的是（）①邻补角的角平分线；②平行线内错角的角平分线；③平行线同旁内角的角平分线． A ．①② B ．②③ C ．② D ．③10. 两平行直线被第三条直线所截，同位角的平分线（） A ．互相重合 B ．互相平行 C ．互相垂直 D ．相交二、填空题（每小题3分，满分24分） 11.图中是对顶角量角器，用它测量角的原理是 .12．如图，l ∥m ，∠1＝120°，∠A ＝55°，则∠ACB 的大小是 . 13．如图，计划把河水引到水池A 中，先作AB ⊥CD ，垂足为B ，然后沿AB 开渠，能使所开的渠道最短，这样设计的依据是．14．如图，直线AB ，CD ，EF 相交于点O ，且AB ⊥CD ，∠1与∠2的关系是．15．如图,在△ABC 中，∠A =90°，点D 在AC 边上，DE ∥BC ，若∠1=155°，则∠B 的度数为．16．如图，AB ∥CD ，直线EF 分别交AB 、CD 于E 、F ，EG 平分∠BEF ，若∠1=72°，则∠2= ．1718第2题图第6题图第7题图第8题图第11题图第13题图第14题图第15题图第16题图第17题图第18题图第3题图三、解答题（共46分）19．（7分）读句画图：如图，直线CD与直线AB相交于C，根据下列语句画图：（1）过点P作PQ∥CD，交AB于点Q；（2）过点P作PR⊥CD，垂足为R；（3）若∠DCB=120°，猜想∠PQC是多少度？并说明理由．20．（7分）如图，方格中有一条美丽可爱的小金鱼．（1）若方格的边长为1，则小鱼的面积为；（2）画出小鱼向左平移3格后的图形．（不要求写作图步骤和过程）21．（8分）已知：如图，∠BAP+∠APD =180°，∠1 =∠2.求证：∠E =∠F．22．（8分）已知：如图，∠1 =∠2，∠3 =∠4，∠5 =∠6.求证：ED∥FB．23．（8分）如图，CD平分∠ACB，DE∥BC，∠AED=80°，求∠EDC的度数．24．（9分）如图，已知AB∥CD，∠B=65°，CM平分∠BCE，∠MCN=90°，求∠DCN的度数．25．（10分）如图，直线EF，CD相交于点0，OA⊥OB，且OC平分∠AOF，（1）若∠AOE=40°，求∠BOD的度数；（2）若∠AOE=α，求∠BOD的度数；（用含α的代数式表示）（3）从（1）（2）的结果中能看出∠AOE和∠BOD有何关系？第19题图第五章相交线与平行线检测题参考答案1.C 解析：∵∠α=35°，∴∠α的补角的度数为180°35°=145°,故选C.2. C 解析：根据平移的性质可知C正确.3. C 解析：因为FE⊥DB，所以∠FED=90°，由∠1=50°可得∠FDE=90°-50°=40°.因为AB∥CD，由两直线平行，同位角相等，可得∠2=∠FDE=40°.4. D 解析：因为a∥b，所以∠2=∠4.又∠2=∠1，所以∠1=∠4.因为∠3=40°，所以∠1=∠4==70°.5. C 解析：由AB∥CD可得，∠FEB＝∠C＝70°，∵∠F＝30°，又∵∠FEB＝∠F+∠A，∴∠A＝∠FEB∠F＝70°30°＝40°.故选项C是正确的.6. C 解析：∵AB∥CD，∴∠ABC=∠BCD.设∠ABC的对顶角为∠1，则∠ABC=∠1.又∵AC⊥BC，∴∠ACB=90°，∴∠CAB+∠ABC=∠CAB+∠BCD=∠CAB+∠1=90°，因此与∠CAB互余的角为∠ABC，∠BCD，∠1．故选C．7. A 解析：选项B中，∵∠3=∠4，∴AB∥CD（内错角相等，两直线平行），故正确；选项C中，∵∠5=∠B，∴AB∥CD（内错角相等，两直线平行），故正确；选项D中，∵∠B+∠BDC=180°，∴AB∥CD（同旁内角互补，两直线平行），故正确；而选项A中，∠1与∠2是直线AC、BD被直线AD所截形成的内错角，∵∠1=∠2，∴AC∥BD，故A错误．选A．8. D 解析：如题图所示，∵DC∥EF，∴∠DCB=∠EFB.∵DH∥EG∥BC，∴∠GEF=∠EFB，∠DCB=∠HDC，∠DCB=∠CMG=∠DME，故与∠DCB相等的角共有5个．故选D．9. C 解析：结合已知条件，利用平行线的判定定理依次推理判断．10. B 解析：∵两条平行直线被第三条直线所截，同位角相等，∴它们角的平分线形成的同位角相等，∴同位角相等的平分线平行．故选B．11.对顶角相等解析：根据图形可知量角器测量角的原理是：对顶角相等.12. 65°解析：∵l∥m，∴∠ABC=180°-∠1=180°-120°=60°.在△ABC中，∠ACB=180°-∠ABC-∠A=180°-60°-55°=65°.13. 垂线段定理：直线外一点与直线上所有点的连线中，垂线段最短解析：根据垂线段定理，直线外一点与直线上所有点的连线中，垂线段最短，∴沿AB开渠，能使所开的渠道最短．14. ∠1+∠2=90°解析：∵直线AB、EF相交于O点，∴∠1=∠DOF.又∵AB⊥CD，∴∠2+∠DOF=90°，∴∠1+∠2=90°．15. 65°解析：∵∠1=155°，∴∠EDC=180°-155°=25°.∵DE∥BC，∴∠C=∠EDC=25°.∵在△ABC中，∠A=90°，∠C=25°，∴∠B=180°-90°-25°=65°．故答案为65°．16. 54°解析：∵AB∥CD，∴∠BEF=180°∠1=180°72°=108°，∠2=∠BEG.又∵EG平分∠BEF，∴∠BEG=∠BEF=×108°=54°，故∠2=∠BEG=54°．17. 78°解析：延长BC与直线a相交于点D，∵a∥b，∴∠ADC=∠DBE=50°. ∴∠ACB=∠ADC +28°=50°+28°=78°.故应填78°.18. 120 解析：∵AB∥CD，∴∠1=∠3，而∠1=60°，∴∠3=60°.又∵∠2+∠3=180°，∴∠2=180°-60°=120°．故答案为120．19．解：（1）（2）如图所示.第19题答图（3）∠PQC=60°.理由：∵PQ∥CD,∴∠DCB+∠PQC=180°.∵∠DCB=120°,∴∠PQC=180°120°=60°．20. 解：（1）小鱼的面积为7×621×5×621×2×521×4×221××121×21×11=16.（2）将每个关键点向左平移3个单位，连接即可．第20题答图21.证明：∵ ∠BAP +∠APD = 180°，∴ AB ∥CD .∴ ∠BAP =∠APC . 又∵ ∠1 =∠2,∴ ∠BAP −∠1 =∠APC −∠2.即∠EAP =∠APF .∴ AE ∥FP .∴ ∠E =∠F .22．证明：∵ ∠3 =∠4,∴ AC ∥BD .∴ ∠6+∠2+∠3 = 180°. ∵ ∠6 =∠5，∠2 =∠1,∴ ∠5+∠1+∠3 = 180°. ∴ ED ∥FB .23. 解：∵ DE ∥BC ，∠AED =80°，∴ ∠EDC =∠BCD ，∠ACB=∠AED=80°.∵ CD 平分∠ACB ，∴ ∠BCD = 21∠ACB =40°，∴ ∠EDC =∠BCD =40°．24. 解：∵ AB ∥CD ，∴ ∠B +∠BCE =180°（两直线平行，同旁内角互补）.∵ ∠B =65°，∴ ∠BCE =115°.∵ CM 平分∠BCE ，∴ ∠ECM =21∠BCE =57.5°. ∵ ∠ECM +∠MCN +∠NCD =180°，∠MCN =90°，∴ ∠NCD =180°-∠ECM -∠MCN =180°-57.5°-90°=32.5°．25、解：（1）∵∠AOE +∠AOF =180°（互为补角），∠AOE =40°，∴∠AOF =140°；又∵OC 平分∠AOF ，∴∠FOC =∠AOF =70°，∴∠EOD =∠FOC =70°（对顶角相等）；而∠BOE =∠AOB ﹣∠AOE =50°，∴∠BOD =∠EOD ﹣∠BOE =20°； (2)(3)略。

相交线与平行线单元测试题

相交线与平行线单元测试题一、选择题（每题2分，共10分）1. 两条直线在同一平面内，且不相交，这两条直线叫做平行线。

以下哪项描述不正确？A. 平行线在任何情况下都不会相交B. 平行线之间的距离处处相等C. 平行线可以无限延伸D. 平行线可以相交2. 根据平行线的性质，以下哪个命题是正确的？A. 同位角相等B. 内错角相等C. 同旁内角互补D. 以上都是3. 如果两条直线相交成30度角，那么这两条直线的对顶角是：A. 30度B. 60度C. 90度D. 120度4. 已知直线AB与CD相交于点O，那么OA与OB的关系是：A. OA=OBB. OA垂直于OBC. OA平行于OBD. 无法确定5. 在平面几何中，以下哪个条件不能判定两直线平行？A. 同位角相等B. 内错角相等C. 同旁内角互补D. 两直线没有交点二、填空题（每题2分，共10分）6. 如果两条直线相交所构成的同位角不相等，则这两条直线_________。

7. 平行于同一条直线的两条直线_________。

8. 两条直线相交，如果其中一个角是直角，则这两条直线_________。

9. 如果直线a与直线b相交，且a垂直于直线b，则直线a与直线b所成的角是_________度。

10. 两条平行线被第三条直线所截，同旁内角的度数之和为_________。

三、判断题（每题1分，共5分）11. 两条直线相交所形成的角中，对顶角相等。

（）12. 平行线的性质可以推出同位角相等，内错角相等，同旁内角互补。

（）13. 如果两条直线相交，那么它们一定在某一点相交。

（）14. 两条直线相交所形成的角中，邻角互补。

（）15. 平行线之间的距离处处相等，这是平行线的一个性质。

（）四、简答题（每题5分，共10分）16. 解释什么是“相交线”，并给出相交线的基本性质。

17. 解释什么是“平行线”，并说明平行线的性质有哪些。

五、解答题（每题15分，共15分）18. 在平面直角坐标系中，已知直线L1: y = 2x + 3 和直线L2: y = -x + 5，请判断这两条直线是否平行或相交，并给出证明。

相交线与平行线单元测试(三)(人教版)(含答案).docx

学生做题前请先回答以下问题问题1:看到平行，想什么？为什么这么想？问题2：三角形的内角和等于 _______ •问题3：直角三角形两锐角_______ .问题4：三角形外角定理：三角形的外角等于 _______________________问题5：如果把一个角看作内角，想什么？看作外角，想什么？相交线与平行线单元测试（三）（人教版）一、单选题（共10道，每道10分）1 •如图，AB〃CD, AE 平分ZCAB, CE 平分ZACD,则ZE=（）A.60°B.75°C.90°D.105°答案:c 解题思路:第一步：读题标注；第二步：从已知条件岀发，由平行想同位角、内错角和同旁内角, 因为AB II CD,根据两直线平行，同旁内角互补，可得 ZC^B+ZNCD=180。

，因为」匹平分ZCAB, C£平分厶CD,所以Z1=^ZG15, Z2=^Z.4CZ ),Z 1+Z2= (Z CAB^AACD)= \ X 180°=90°；在中，由三角形的内角和等于180°, 可得 Z£=l 80°-(Z 1+Z2)=180o -90°=90° ・故选C ・试题难度：三颗星知识点：三角形内角和定理2.如图，直线 AB 〃CD, ZEFA=28°, ZEHC=50°,则ZE=( )答案：B 解题思路:A.28°C.32°B.22° D.38° 如图,H D第一步：读题标注；第二步：从已知条件岀发，由平行想同位角、内错角和同旁內角, 因为ABIICD,根据两直线平行，同位角相等，可得ZAGE=Z CHE=50°；厶GE可看作AGEF的一个外角，根据三角形的外角等于与它不相邻的两个内角的和，可得所以ZE=ZAGE-ZEE4=50°-2&Q=22°・故选B.试题难度：三颗星知识点：三角形外角定理3.将一副直角三角板如图放置，已知AE〃BC,则ZAFE的度数为（）A.95°B.100°C.110°D.105°答案：D 解题思路:第一步：读题标注；第二步：从已知条件岀发，由平行想同位角、内错角和同旁内角，因为AEIIBC,根据两直线平行，內错角相等，可得Z1=ZC=3O^；在△型EF中，Zl=30°, ZE=45°f由三角形的内角和等于180°, 可得Z.4FE=180°-Z 1-Z£ =180o-30°-45o=105°.故选D・试题难度：三颗星知识点：三角形内角和定理4.如图，在AABC 中，AE 平分ZBAC, AD1BC,垂足为D,若ZBAC=128°, ZC=36°,则ZDAE的度数为（）A.1O°B.12°C.15°D.18°答案：A解题思路：第一步：读题标注；第二步：从已知条件岀发，因为，匹平分A BAC,且Z SJC=128°,所以ZG4£ = -Z5.4C = 1x128° = 64°,2 2因为00丄PC, ZC=36°,根据直角三角形两锐角互余，可得ZZ)JC=90°-Z C=90°-36°=54°,因此ZZ)J£=ZG4£-Za4C=64°-54o=10°. 故选A.试题难度：三颗星知识点：直角三角形两锐角互余5.如图所示，ZACD是AABC的一个外角，CE平分ZACD, F为CA延长线上的一点，过点F 作FG〃CE,交AB于点G, BC于点H,下列说法正确的是()A.Z2+Z3>Z1B.Z2+Z3<Z1C.Z2+Z3=Z1D.无法判断第一步：读题标注；第二步：结合结i仑，要判断Z2+Z3与Z1的关系，由对顶角相等得Z4=Z2,等量代换得，Z2+Z3=Z4+Z3；Z5可看作的一个外角，得Z5=Z4+Z3；因为C£平分ZACD,所以Z6=Z1, 根据两直线平行，同位角相等，得Z5=Z6,等量代换得Z2+Z3=Z1. 故选C.难度：三颗星知识点：对顶角相等6.如图，EG〃AD, EG交AB于点F,交CA的延长线于点G,若ZB=20°, ZGFA=30°, 则ZADC的度数为（）A.50°B.40°C.45°D.60°答案:A解题思路：如图,第一步：读题标注；第二步：从已知条件岀发，由平行想同位角、内错角和同旁内角，由根据两直线平行，內错角相等，ZQC转到Z1,而Z1可以看作的一个外角，由三角形的外角等于与它不相邻的两个內角的和，得Z1=Z5+Z2,已知ZG屁1=30。

第五单元《相交线与平行线》单元测试卷(较易)(含答案)

人教版初中数学七年级下册第五单元《相交线与平行线》单元测试卷（较易）（含答案解析）考试范围：第五单元；考试时间：120分钟；总分：120分学校:___________姓名：___________班级：___________考号：___________第I卷（选择题）一、选择题（本大题共12小题，共36分。

在每小题列出的选项中，选出符合题目的一项）1. 下列图形中线段PQ的长度表示点P到直线a的距离的是( )A. B. C. D.2. 如图，在线段PA、PB、PC、PD中，长度最小的是( )A. 线段PAB. 线段PBC. 线段PCD. 线段PD3. 如图所示，已知∠1=∠2，要使∠3=∠4，只要( )A.∠1=∠3B.∠2=∠4C.∠1=∠4D. AB//CD4. 在同一平面内，a、b、c是直线，下列说法正确的是( )A. 若a//b，b//c，则a//cB. 若a⊥b，b⊥c，则a⊥cC. 若a//b，b⊥c，则a//cD. 若a//b，b//c，则a⊥c5. 如图，给出下列条件：①∠1=∠2；②∠3=∠4；③∠B=∠DCE；④∠B+∠BAD=180°，其中能推出AB//DC的是( )A. ①②B. ①③C. ②③D. ②④6. 下列说法中，正确的是( )A. “同位角相等”是一个真命题B. 图形的平移是指把图形沿水平方向移动C. “凡直角都相等”是一个假命题D. 在平移的过程中，对应线段互相平行(或在同一条直线上)且相等7. 从操场某处看旗杆是北偏东70°，则从旗杆看此处是( )A. 南偏西70°B. 南偏东70°C. 南偏西20°D. 南偏北20°8. 一副直角三角板如图放置，点C在FD的延长线上，AB//CF，∠F=∠ACB=90∘，∠A= 60∘，∠E=45∘，则∠DBC的度数为( )A. 10°B. 15°C. 18°D. 30°9. 皮影戏是中国民间古老的传统艺术，是一种用兽皮或纸板做成人物剪影来表演故事的民间戏剧．2011年中国皮影戏入选人类非物质文化遗产代表作名录．图1是孙悟空的皮影造型，在下面的四个图中，能由图1经过平移得到的是( )A. B.C. D.10. 如图2是图1将__________平移__________所得到的( )A. △AOB，BC的长度B. △COD，BC的长度C. △AOD，AD的长度D. △BOC，BA的长度11. 如图，多边形的相邻两边互相垂直，则这个多边形的周长为( )A. 21B. 26C. 37D. 4212. 如图，将△ABC沿直线AB向右平移后到达△BDE的位置，连接CD、CE，若△ACD的面积为10，则△BCE的面积为( )A. 5B. 6C. 10D. 4第II卷（非选择题）二、填空题（本大题共4小题，共12分）13. 如图，AB//CD，AB⊥AE，∠CAE=42°，则∠ACD的度数为______．14. 如图，∠1=70∘，直线a平移后得到直线b，则∠2−∠3=___15. 如图，直角三角形ABC的周长为100，在其内部有6个小直角三角形，则6个小直角三角形的周长之和为______．16. 如图，∠3=38°，直线b平移后得到直线a，则∠1+∠2=______°.三、解答题（本大题共9小题，共72分。

相交线与平行线测试题及答案难

相交线与平行线测试题及答案难一、选择题1. 在同一平面内，两条直线的位置关系是（）。

A. 相交或平行B. 相交或重合C. 平行或重合D. 相交、平行或重合答案：D2. 如果两条直线都与第三条直线平行，那么这两条直线的关系是（）。

A. 相交B. 平行C. 重合D. 不确定答案：B3. 两条直线相交成90度角，这两条直线是（）。

A. 相交线B. 垂直线C. 平行线D. 异面直线答案：B二、填空题4. 如果两条直线都与第三条直线相交，且交角相等，则这两条直线（）。

答案：平行5. 在平面几何中，如果两条直线不相交，则它们被称为（）。

答案：平行线三、判断题6. 两条平行线被第三条直线所截，同位角相等。

（）答案：正确7. 垂直于同一直线的两条直线一定平行。

（）答案：错误四、解答题8. 已知直线AB与直线CD相交于点O，且∠AOB=90°，求证：AB⊥CD。

证明：因为∠AOB=90°，所以AB与CD相交成直角，根据垂直的定义，AB⊥C D。

9. 若直线m平行于直线n，直线n平行于直线p，求证：直线m平行于直线p。

证明：根据平行公理，如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

因此，直线m平行于直线p。

五、综合题10. 在平面直角坐标系中，直线l1的方程为y=2x+3，直线l2的方程为y=-x+5，求证：l1与l2相交。

证明：首先，我们可以将两个方程联立求解。

\begin{cases}y = 2x + 3 \\y = -x + 5\end{cases}将第一个方程中的y代入第二个方程，得到：2x + 3 = -x + 5解得：x = 1将x=1代入任意一个方程求得y，例如第一个方程：y = 2(1) + 3 = 5因此，l1与l2的交点为(1,5)，所以l1与l2相交。

11. 已知直线l1平行于直线l2，直线l2平行于直线l3，求证：直线l1平行于直线l3。

证明：根据平行公理，如果两条直线都与第三条直线平行，那么这两条直线也互相平行。

人教版七年级下册数学《平行线与相交线》单元测试卷(含答案)

人教版七年级下册数学《平行线与相交线》单元测试卷姓名：__________班级：__________考号：__________一、选择题（本大题共10小题）1.如图，在ABC △中，D E F 、、分别在AB BC AC 、、上，且EF BC ∥，要使DF AB ∥，只需要在有下列条件中的（）即可．A ．1=2∠∠B ．1=DFE ∠∠C ．1=AFD ∠∠ D ．2AFD ∠=∠2.如图，直线EF 分别与直线AB 、CD 相交于点G 、H ，已知1250∠=∠=︒，GM 平分HGB ∠交直线CD 于点M ．则3∠=（）A ．60︒B ．65︒C ．70︒D ．130︒3.下列说法中正确的有（）①一个角的邻补角只有一个； ②一个角的补角必大于这个角；③若两角互补，则这两个角一定是一个锐角、一个钝角； ④互余的两个角一定都是锐角。

A ．0个B ．1个C ．2个D ．3个 4.下列图中∠1和∠2是同位角的是（）21FE DC BA 321MH FGEDCB AA.⑴、⑵、⑶B.⑵、⑶、⑷C.⑶、⑷、⑸D.⑴、⑵、⑸ 5.下列图形中，由AB CD ∥，能得到12∠=∠的是（）A B C D6.如图，DH EG BC ∥∥，且DC EF ∥，那么图中与BFE ∠相等的角（不包括BFE ∠）的个数是（）A. 2B. 4C. 5D. 67.下列说法中正确的是（）①点到直线的距离是点到直线所作的垂线; ②两个角相等，这两个角是对顶角;③两个对顶角互补，则构成这两个角的两条直线互相垂直; ④连接直线外一点到直线上所有点的线段中垂线段最短. A.①② B. ②③ C.③④ D.②④ 8.如图，若AB CD ∥,70BEF ∠=︒，则B F C ∠+∠+∠的度数为（）A.215︒B.250︒C.320︒D.360︒(1)21(2)12(3)12(4)12(5)21DCB A DCB A A BCDDCBA21122112AB C D F H GED CB A9.如图所示，两直线AB CD 、平行，则l 23456∠+∠+∠+∠+∠+∠= ( )A ．630︒B ．720︒C ．800︒D ．900︒10.如图所示，若AB CD ∥，则角αβλ，，的关系为 ( )A ．360αβλ++=︒ B.180αβλ-+=︒ C ．180αβλ++=︒ D.180αβλ+-=︒二、填空题（本大题共5小题）11.三条直线两两相交有个交点.12.如图，已知．，垂足为，则点到直线的距离为线段的长；线段的长为点到直线的距离．13.有一直的纸带，如图折叠时，α∠=_________．DCFEBA65HG 4321DCF EB AγβαD CE BA90ACB ∠=°CD AB ⊥D A CB DB 图1D CBAα30°EDCBA14.如图，已知AB DE ∥，80ABC ∠=︒，140CDE ∠=︒，则BCD ∠= ．15.如图，直线AB CD ∥，30EFA ∠=，90FGH ∠=，30HMN ∠=，50CNP ∠=，则GHM∠的大小是 .三、解答题（本大题共7小题）16.如图，AB 、CD 、EF 交于点O ，25AOE ∠=°，45DOF ∠=°，求AOD ∠的对顶角和邻补角的度数．17.如图，ABC∆中CD AB ⊥于D ，DE BC ∥，交AC 与E ．过BC 上任意一点F ，作FG AB ⊥于G ，求证：12∠=∠．18.找出下图中用数字表示的各角中，哪些是同位角，内错角？哪些是同旁内角？EDCBA图2OFEBD A CGFE 21D CBA1234图1C EB DA19.如图：已知12∠=∠，A C ∠=∠，求证：①AB DC ∥ ②AD BC ∥证明：∵12∠=∠（） ∵（）∥（）（）． ∴C CBE ∠=∠（）又∵C A ∠=∠（） ∴A ∠= （） ∴（）∥（）（）． 20.如图，已知12C D ∠=∠∠=∠，，求证：A F ∠=∠21.如图，已知12180∠+∠=︒，3B ∠=∠，试判断AED ∠与ACB ∠的大小关系，并对结论进行证明．22.已知如图所示，AB DE ∥,116D ∠=︒，93DCB ∠=︒，求B ∠的度数.12FE DCBA4321FEDCBAD CEBA图EDCB A21人教版七年级下册数学《平行线与相交线》单元测试卷答案解析一、选择题1.B2.B3.B; 一个角有两个邻补角，所以①是错的；一个角的补角可能大于、小于或是等于这个角，所以②是错的；两个直角互补，所以③是错的；④是正确的4.D5.B6.C ；本题考查平行线的性质，由图形找到与BFE ∠相等的角有DCB ∠，GEF ∠，GAC ∠，HDC ∠，DAE ∠7.C 8.B9.D;分别过E F C H ，，，点做AB 的平行线，再求各个角度的和．选D 10.D ．提示：加辅助线：过β角的顶点为E ，作.EF AB ∥二、填空题11.312.AC ，B ，CD 13.75︒ 14.40︒15.40°;过点G ，H 作AB ，CD 的平行线，那么AB OG HQ CD ∥∥∥∵AB OG ∥，HQ CD ∥∴30OGE AFE ∠=∠=︒，50MQR HQP CNP ∠=∠=∠=︒ ∵OG HQ ∥，∴60GHQ OGH HGE EGO ∠=∠=∠-∠=︒ ∵在MHQ ∆中,180MHQ HMQ MQH ∠+∠+∠=︒ 又∵180MQR MQH ∠+∠=︒，∴MHQ HMQ MQR ∠+∠=∠ ∴503020MHQ ∠=︒-︒=︒，∴40GHM GHQ MHQ ∠=∠-∠=︒三、解答题16.由对顶角相等可知，45COE DOF ∠=∠=︒，故254570AOC AOE COE ∠=∠+∠=︒+︒=︒．由AOC ∠、AOD ∠互为邻补角可知，18070110AOD ∠=︒-︒=︒ 由对顶角相等可知，AOD ∠的对顶角110BOC ∠=︒． ∴AOD ∠的对顶角为110︒，AOD ∠的对顶角70︒ 17.略，让学生写出证明过程并写出理由18.1∠与3∠是直线BE 、CD 被直线AC 所截形成的同位角；2∠与4∠是直线BE 、CD被直线19.已知；AB ，CD ；内错角相等，两直线平行；两直线平行，内错角相等；已知；CBE ∠；等量代换；AD ，BC ；同位角相等，两直线平行．20.证明过程略，让学生练习一下过程21.证明过程略,让学生写出证明过程22.29°；过点C 作直线CF AB ∥，因为AB DE ∥,所以AB DE CF ∥∥，因为116D ∠=︒，18011664DCF ∠=︒︒=︒- 因为93C ∠=︒，所以936429BCF ∠=︒-︒=︒，因为B BCF ∠=∠，所以29B ∠=︒．DCFEBA。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

相交线与平行线单元测试一、填空题 1．a、b、c是直线，且a∥b，b⊥c，则a与c的位置关系是________．

2．如图5-1，MN⊥AB，垂足为M点，MN交CD于N，过M点作MG⊥CD，垂足为G，EF 过点N点，且EF∥AB，交MG于H点，其中线段GM的长度是________到________的距离，线段MN的长度是________到________的距离，又是_______的距离，点N到直线MG 的距离是___．

3．如图5-2，AD∥BC，EF∥BC，BD平分∠ABC，图中与∠ADO相等的角有_______ 个，分别是___________． 4．因为AB∥CD，EF∥AB，根据_________，所以_____________． 5．命题“等角的补角相等”的题设__________，结论是__________． 6．如图5-3，给出下列论断：①AD∥BC：②AB∥CD；③∠A=∠C．以上其中两个作为题设，另一个作为结论，用“如果……，那么……”形式，写出一个你认为正确的命题是___________．

7．如图5-4，直线AB、CD、EF相交于同一点O，而且∠BOC=23∠AOC，∠DOF=13∠AOD，那么∠FOC=_____ _ 度． 8．如图5-5，直线a、b被c所截，a⊥l于M，b⊥l于N，∠1=66°，则∠2=________． 9．如图5-6，∠ACB=90°，CD⊥AB，则图中与∠A互余的角有个，它们分别是．∠A=∠ ，根据是． 10．如图5-7，一棵小树生长时与地面所成的角为80°，它的根深入泥土，如果根和小树在同一条直线上，那么∠2等于 °． 11．如图5-8，量得∠1=80°，∠2=80°，由此可以判定 ∥ ，它的根据是．量得∠3=100°，∠4=100°，由此可以判定 ∥ ，它的根据是． 12．猜谜语：（打本章两个几何名称）剩下十分钱：；斗牛．

GHN

EDC

BAFE

DCBA

图5-1 图5-2

DCBA

EOD

CBA

clN

图5-3 图5-4 图5-5 13．a、b、c是直线，且a∥b， b∥c，则a___c; a、b、c是直线，且a⊥b， b⊥c，则a___c;

14．如图5-9，直线AD、BC交于O点，AOBCOD110，则COD的度数为．

15．如图5-10，直线AB与CD交于O点，3180，则2= ． 16．如图5-11，直线AB、EF相交于O点，CDAB于O点，EOD12819，则BOFAOF,的度数分别为．二、选择题 17．若a⊥b，c⊥d则a与c的关系是（） A．平行 B．垂直 C．相交 D．以上都不对 18．如图5-12，∠ADE和∠CED是（） A．同位角 B．内错角 C．同旁内角 D．互为补角

19．如图5-13，ll1211052140//，，，则（）

A． 55 B． 60 C． 65 D． 70

20．如图5-14，能与构成同旁内角的角有（） A． 5个 B．4个 C． 3个 D． 2个

A B O C D

A 4 D 2 1C 3 B

C E

A O B F D

图5-9 图5-10 图5-11

第（11）题EDCB

A l1 1

α2 l2 α

图5-12 图5-13 图5-14

CAD

图1

280°

DEF

123

图3 图5-6 图5-7 图5-8 21．如图5-15，已知ABCD//，等于（） A． 75 B． 80 C． 85 D． 95

A B 120° α

25°C D

B MC A N P D 22．如图5-16，ABCDMPABMN////，，平分AMDAD，，4030，则NMP等于（） A． 10 B． 15 C． 5 D． 75.

23．如果两个角的两边分别平行，而其中一个角比另一个角的4倍少30，那么这两个角是（） A． 42138、 B．都是10 C． 42138、或4210、 D．以上都不对 24．如图5-17，a∥b，∠1与∠2互余，∠3=1150，则∠4等于（） A．115０ B． 155０ C． 135０ D．125０

25．如图5-18，∠1=15０， ∠AOC=90０，点B、O、D在同一直线上，则∠2的度数为（） A．75０ B．15０ C．105０ D． 165０ 26．如图5-19，能表示点到直线（或线段）距离的线段有（） A． 2条 B．3条 C．4条 D．5条 27．下列语句错误的是（） A．连接两点的线段的长度叫做两点间的距离 B．两条直线平行，同旁内角互补 C．若两个角有公共顶点且有一条公共边，和等于平角，则这两个角为邻补角 D．平移变换中，各组对应点连成两线段平行且相等 28．如图5-20，如果AB∥CD，那么图中相等的内错角是（） A．∠1与∠5，∠2与∠6； B．∠3与∠7，∠4与∠8； C．∠5与∠1，∠4与∠8； D．∠2与∠6，∠7与∠3 29．下列语句：①三条直线只有两个交点，则其中两条直线互相平行；②如果两条平行线被第三条截，同旁内角相等，那么这两条平行线都与第三条直线垂直；③过一点有且只有一条直线与已知直线平行，其中（）

d第（18）题43

cba

第（20）题DC

BAO第（19）题

CBA21

图5-17 图5-18 图5-19

图5-15 图5-16

8765432

CBA

图5-20 A．①、②是正确的命题 B．②、③是正确命题 C．①、③是正确命题 D．以上结论皆错 30．下列与垂直相交的洗法：①平面内，垂直于同一条直线的两条直线互相平行；②一条直线如果它与两条平行线中的一条垂直，那么它与另一条也垂直;③平行内，一条直线不可能与两条相交直线都垂直，其中说法错误个数有（） A．3个 B．2个 C．1个 D．0个三、解答题 31．如图5-21，过P点，画出OA、OB的垂线．

1. A PO B

2. A

O P B 32．如图5-22，过P点，画出AB、CD的垂线． 3. B A P C D

CBA

33．如图5-23，是一条河，C河边AB外一点：（1）过点C要修一条与河平行的绿化带，请作出正确的示意图．

34．如图5-24，AB⊥BD，CD⊥MN，垂足分别是B、D点，∠FDC=∠EBA．（1）判断CD与AB的位置关系; （2）BE与DE平行吗?为什么?

NMFE

35．如图5-25，∠1+∠2=180°，∠DAE=∠BCF，DA平分∠BDF．（1）AE与FC会平行吗?说明理由．（2）AD与BC的位置关系如何?为什么? （3）BC平分∠DBE吗?为什么．

图5-21 图5-22

图5-24 图5-23

FE2

A36．如图5-26，已知：CE=DF，AC=BD，1=2．求证：A=B． B A C D

F E 1 2

37．如图5-27，已知：AB//CD，AB=CD，求证：AC与BD互相平分．

O A

B C

38．如图5-27，已知：E、F分别是AB和CD上的点，DE、AF分别交BC于G、H，A=D，1=2，求证：B=C．

2 A B

C F

H G 1

39．如图5-28，已知：在ABC中，C90，AC=BC，BD平分CBA，DEAB于E，求证：AD+DE=BE． E A B C

40．如图5-29，已知：AB//CD，求证：B+D+BED=360（至少用三种方法） E A B

C D

图5-26 图5-26

图5-27 图5-28

图5-29