二0一三学年第一学期单元目标检测题
期中考试卷(试题)-2024-2025学年苏教版二年级数学上册
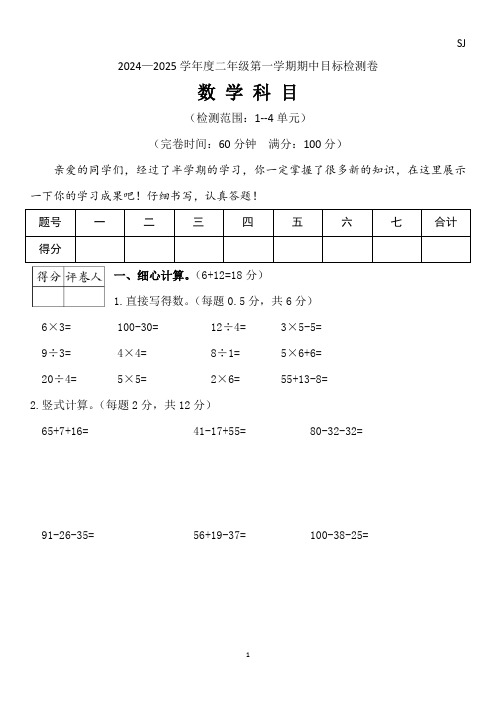
2024—2025学年度二年级第一学期期中目标检测卷数学科目(检测范围:1--4单元)(完卷时间:60分钟满分:100分)亲爱的同学们,经过了半学期的学习,你一定掌握了很多新的知识,在这里展示一下你的学习成果吧!仔细书写,认真答题!题号一二三四五六七合计得分一、细心计算。
(6+12=18分)1.直接写得数。
(每题0.5分,共6分)6×3= 100-30= 12÷4= 3×5-5=9÷3= 4×4= 8÷1= 5×6+6=20÷4= 5×5= 2×6= 55+13-8=2.竖式计算。
(每题2分,共12分)65+7+16= 41-17+55= 80-32-32=91-26-35= 56+19-37= 100-38-25=二、认真填空。
(3、6、 8题各2分,其余每空1分,共27分)3. 30÷6=5读作(),除数是(),被除数是(),商是()。
4.加法算式6+6+6+6可以写成两道乘法算式()和()。
5.每个盒子里有6个皮球,2个盒子里共有()个皮球;如果再增加两个这样的盒子,一共有()个皮球。
6.7.数一数,右图中共有()个平行四边形。
8.我们本学期学习的汉字“杨”有()画,“棉”比“杨”多()画,“棉”有()画,列式()。
9.找规律,填一填。
(1)100、 95、 90、()、()。
(2)5、 10、 16、 23、()、()。
10.有6箱苹果,其中一箱苹果有8个,其余每箱苹果都是5个,列乘加算式是()。
11.在“○”里填上“>”“<”或“=”。
3×3 ○ 3+6 4×6 ○ 5×5 3×5 ○ 7×212.在“○”里填上“+”“-”“×”或“÷”。
5 ○ 5 = 25 1 ○ 2 = 36 ○ 6 = 12 ○ 2 = 4 18 ○3 = 6 7 ○ 2 = 1413. 小军有19枚邮票,芳芳有11枚邮票,小军给芳芳()枚邮票,两个人的邮SJ 票一样多。
安徽省合肥市第一中学2024-2025学年高三上学期期中教学质量检测数学试题+答案

第1⻚/共4⻚合肥⼀中2024—2025学年第⼀学期⾼三年级教学质量检测数学学科试卷时⻓:120分钟分值:150分⼀、单选题:本题共8⼩题,每⼩题5分,共40分.1.已知集合,集合,则()A.B.C.D.2.若,则()A.或 B.或C.D.3.已知函数,则“”是“函数的是奇函数”的()A 充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.函数在上单调,则a 的取值范围是()A.B.C.D.5.在中,内⻆A ,B ,C 的对边分别为a ,b ,c ,已知的外接圆半径为1,且,则的⾯积是()A.B. C.1 D.26.已知⼀个正整数,且N 的15次⽅根仍是⼀个整数,则这个数15次⽅根为().(参考数据:)A.3B.4C.5D.67.已知函数,,若,使得,则实数a 的取值范围是()A.B.第2⻚/共4⻚C.D.8.已知正数x ,y 满⾜,则的最⼩值为()A.1B.2C.3D.4⼆、多项选择题:本题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题⽬要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知关于x 的不等式的解集为,则下列结论正确的是()A. B.的最⼤值为 C.的最⼩值为D.的最⼩值为10.如图是函数的部分图象,A 是图象的⼀个最⾼点,D 是图象与y 轴的交点,B ,C 是图象与x 轴的交点,且的⾯积等于,则下列说法正确的是()A.函数的最⼩正周期为B.函数图象关于直线对称C.函数图象可由的图象向右平移个单位⻓度得到D.函数与在上有2个交点11.已知函数及其导函数的定义域均为R ,若,且是奇函数,令,则下列说法正确的是()第3⻚/共4⻚A.函数是奇函数B.CD.三、填空题:本题共3⼩题,每⼩题5分,共15分.12.已知幂函数在上单调递减,则______.13.已知,且,则________.14.设函数,下列说法正确的有________.①函数的⼀个周期为;②函数的值域是③函数的图象上存在点,使得其到点的距离为;④当时,函数的图象与直线有且仅有⼀个公共点.四、解答题:本题共5⼩题,共77分.解答应写出⽂字说明、证明过程或演算步骤.15.已知命题“”为假命题,命题“在上为增函数”为真命题,设实数a 的所有取值构成的集合为A .(1)求集合;(2)设集合,若是必要不充分条件,求实数m 的取值范围.16.已知函数.(1)若的图象在点处的切线经过点,求;(2)若是的两个不同极值点,且,求实数a 的取值范围.17.已知定义域为的函数满⾜对任意,都有(1)求证:是奇函数;第4⻚/共4⻚(2)当时,.若关于x 的不等在上恒成⽴,求a 的取值范围.18.记的内⻆A ,B ,C 的对边分别为a ,b ,c ,已知.(1)求A 取值的范围;(2)若,求周⻓的最⼤值;(3)若,求的⾯积.19.已知函数,其中.(1)当时,求曲线在点处的切线⽅程;(2)判断函数是否存在极值,若存在,请判断是极⼤值还是极⼩值;若不存在,说明理由;(3)讨论函数在上零点的个数.第1⻚/共22⻚合肥⼀中2024—2025学年第⼀学期⾼三年级教学质量检测数学学科试卷时⻓:120分钟分值:150分⼀、单选题:本题共8⼩题,每⼩题5分,共40分.1.已知集合,集合,则()A.B.C.D.【答案】C 【解析】【分析】根据题意,将集合化简,再结合交集的运算,即可得到结果.【详解】或,,所以,故选:C 2.若,则()A.或 B.或C.D.【答案】B 【解析】【分析】根据,将原式上下同时除以,化简求解即可.【详解】根据题意可知,所以,若,则,与⽭盾故,将其上下同时除以,可得,化简可得,解之得或.故选:B第2⻚/共22⻚3.已知函数,则“”是“函数的是奇函数”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】由是奇函数确定的取值范围,即可判断.【详解】由为奇函数,可得:,即,即恒成⽴,即恒成⽴,即恒成⽴,解得,所以是函数为奇函数的充分不必要条件.故选:A 4.函数在上单调,则a 的取值范围是()A.B.C.D.【答案】D 【解析】【分析】利⽤导数求得其导函数并使其恒⼤于0,再根据分段函数单调性得出不等式即可.【详解】由题意可知时,,时,;第3⻚/共22⻚⼜因为,所以在上单调递增,因此可得时,恒成⽴,可得,⼜,可得;综上可得a 的取值范围是.故选:D 5.在中,内⻆A ,B ,C 的对边分别为a ,b ,c ,已知的外接圆半径为1,且,则的⾯积是()A.B. C.1 D.2【答案】C 【解析】【分析】根据给定条件,利⽤余弦定理求出,利⽤三⻆恒等变换求出,再利⽤正弦定理及三⻆形⾯积公式计算得解.【详解】在中,由及余弦定理,得,解得,⼜,则,由,得,整理得,即,两边平⽅得,⼜,,则,即,由正弦定理得,所以的⾯积是.故选:C6.已知⼀个正整数,且N 的15次⽅根仍是⼀个整数,则这个数15次⽅根为().(参考数据:)第4⻚/共22⻚A.3B.4C.5D.6【答案】C 【解析】【分析】设这个15次⽅根为,则,利⽤对数的运算性质求即可.【详解】设这个15次⽅根为,则,其中且,故,,,,故,,,由于,故.故选:C .7.已知函数,,若,使得,则实数a 的取值范围是()A.B.C.D.【答案】B 【解析】【分析】利⽤导函数证明在区间上单调递增,从⽽得出的值域;同理得出的单调区间和值域,由题意可知,这两个函数值域需要有交集,得出不等式组,从⽽得出范围.【详解】,∴时,,∴在区间上单调递增,∴当时,,令,则,令,则,∵,∴时,,∴单调递增,∴,∴在上单调递增,第5⻚/共22⻚∴,由题意可知,∴.故选:B8.已知正数x ,y 满⾜,则的最⼩值为()A.1 B.2C.3D.4【答案】A 【解析】【分析】应⽤三⻆换元,令,且,结合已知、平⽅关系、和⻆正弦公式得,进⽽有,最后利⽤基本不等式“1”的代换求⽬标式最⼩值.【详解】,由,得,令,且,所以,有,即,故,所以,则,当且仅当,即时取等号,第6⻚/共22⻚所以的最⼩值为1.故选:A【点睛】关键点点睛:根据已知等量关系及三⻆函数的性质,应⽤三⻆换元将已知等式化为是关键.⼆、多项选择题:本题共3⼩题,每⼩题6分,共18分.在每⼩题给出的选项中,有多项符合题⽬要求,全部选对的得6分,部分选对的得部分分,有选错的得0分.9.已知关于x 的不等式的解集为,则下列结论正确的是()A. B.的最⼤值为 C.的最⼩值为D.的最⼩值为【答案】BC 【解析】【分析】由已知结合⼆次不等式与⼆次⽅程的关系可得,然后结合基本不等式的乘“1”法可判断C ,利⽤向量的性质可求解B ,根据⼆次函数的性质可判断D .【详解】因为关于的不等式,的解集为,所以,所以,,所以,A 错误;因为,,所以,当且仅当时取等号,故,由于设,由于,故,当且仅当时等号成⽴,故B 正确;第7⻚/共22⻚,当且仅当,即时取等号,C 正确;,当且仅当时取等号,故最⼩值为,D 错误.故选:BC .10.如图是函数的部分图象,A 是图象的⼀个最⾼点,D 是图象与y 轴的交点,B ,C 是图象与x 轴的交点,且的⾯积等于,则下列说法正确的是()A.函数的最⼩正周期为B.函数的图象关于直线对称C.函数的图象可由的图象向右平移个单位⻓度得到D.函数与在上有2个交点【答案】ABC 【解析】【分析】根据部分图像求出的表达式,再由函数图像平移及正弦函数性质可判断各项.【详解】设的最⼩正周期为,第8⻚/共22⻚由图像可知,,即,可得,故A 正确;且,所以,解得,⼜因为图像过点,可得,即,且,可得,所以.对于选项B :因为,为最⼩值,所以函数的图象关于直线对称,故B 正确;对于选项C :将的图象向右平移个单位⻓度,得到,所以函数的图象可由的图象向右平移个单位⻓度得到,故C 正确;对于选项D :注意到,在同⼀坐标系内,分别作出函数与在上的图象,由图象可知:函数与在上有3个交点,故D 错误;故选:ABC.11.已知函数及其导函数的定义域均为R ,若,且是奇第9⻚/共22⻚函数,令,则下列说法正确的是()A.函数是奇函数B.C.D.【答案】BCD 【解析】【分析】把已知等式中换成,再移项变形可得A 错误;求导令可得,再由是奇函数,再求导可得B 正确;由奇函数的性质得到①,在令,可得,再由已知等式得到④,进⽽得到,然后可得C 正确;由原函数和导函数的奇偶性可得,进⽽可得D 正确;【详解】对于A ,因为,把换成,则,移项化简可得,即,为偶函数,故A 错误;对于B ,由A 中求导可得,令,可得,⼜是奇函数,即,求导可得,即,令,则,所以,故B 正确;对于C ,由B 中可得,①由A 中,②把①中换成可得,③由②③可得,所以:第10⻚/共22⻚故C 正确;对于D ,由B 中,⼜由可得,即,所以所以令可得;令可得;,所以,故D 正确;故选:BCD.【点睛】关键点点睛:本题C 选项的关键在于理解抽象复合函数求导,原函数为奇函数则导函数为偶函数这⼀性质,再利⽤函数的奇偶性解答.三、填空题:本题共3⼩题,每⼩题5分,共15分.12.已知幂函数在上单调递减,则______.【答案】【解析】【分析】先根据函数是幂函数计算求参得出或,最后结合函数的单调性计算得出符合题意的参数.【详解】由题意可得为幂函数,则,解得或.当时,为增函数,不符合题意;当时,在单调递减,符合题意.故答案为:.第11⻚/共22⻚13.已知,且,则________.【答案】【解析】【分析】根据给定条件,利⽤同⻆公式求出,再利⽤和差⻆的余弦公式求出即可.【详解】由,得,,由,得,,由,得,即,则,因此,所以.故答案为:14.设函数,下列说法正确的有________.①函数的⼀个周期为;②函数的值域是③函数的图象上存在点,使得其到点的距离为;④当时,函数的图象与直线有且仅有⼀个公共点.【答案】①④【解析】【分析】利⽤函数的周期性定义结合余弦函数的周期性可判断①;采⽤三⻆代换,利⽤导数判断函数单调性,利⽤函数单调性求解函数值域,判断②;利⽤,结合两点间距离公式可判断③;结合解,根据解的情况判断④,即得答案.第12⻚/共22⻚【详解】对于①,,,故是函数的⼀个周期,①正确;对于②,,需满⾜,即,令,,则即为,当时,在上单调递增,则;当时,,(,故)此时在上单调递减,则,综上,的值域是,②错误;对于③,由②知,,当时,满⾜此条件下的图象上的点到的距离;当时,,满⾜此条件下的图象上的点到的距离第13⻚/共22⻚,当且仅当且时等号成⽴,⽽时,或,满⾜此条件的x 与⽭盾,即等号取不到,故函数的图象上不存在点,使得其到点的距离为,③错误;对于④,由②的分析可知,则,即,⼜,故当且仅当时,,即当时,函数的图象与直线有且仅有⼀个公共点,④正确.故答案为:①④【点睛】关键点点睛:对于函数,先求出定义域,再采⽤换元法令,,得函数,利⽤单调性求其值域.四、解答题:本题共5⼩题,共77分.解答应写出⽂字说明、证明过程或演算步骤.15.已知命题“”为假命题,命题“在上为增函数”为真命题,设实数a 所有取值构成的集合为A .(1)求集合;(2)设集合,若是的必要不充分条件,求实数m 的取值范围.【答案】(1)或(2)或【解析】第14⻚/共22⻚【分析】(1)由:“,”为假命题时,可转化为关于的⼀元⼆次⽅程⽆解,然后利⽤判别式即可,命题q 可利⽤对勾函数的性质求解,取交集即可得a 的取值范围,则集合A 可求,再结合补集运算可得答案;(2)由是的必要不充分条件可得B,然后分为空集和⾮空集两种情况讨论即可.【⼩问1详解】因为命题为假命题,所以关于的⼀元⼆次⽅程⽆解,即,解得,因为命题q 为真命题,当时,在上为增函数,满⾜题意;当时,结合对勾函数的性质可知在上单调递减,不满⾜题意;故集合,所以或;【⼩问2详解】由是的必要不充分条件,则B,当时,,解得,此时满⾜B,当时,则或,解得或,综上所述,的取值范围是或.16.已知函数.(1)若的图象在点处的切线经过点,求;(2)若是的两个不同极值点,且,求实数a 的取值范围.【答案】(1)或(2)【解析】第15⻚/共22⻚【分析】(1)求出函数的导数,利⽤导数的⼏何意义求出切线⽅程即可求解作答.(2)利⽤极值点的意义,结合⻙达定理、根的判别式列出不等式,求解作答.【⼩问1详解】函数,求导得,则,,于是函数的图象在点处的切线⽅程为,即,⽽切线过点,则,整理可得,解得或,所以或【⼩问2详解】由(1)知,⽅程,即有两个不等实根,则,解得,且,于是,由,得,解得,因此,所以实数的取值范围是.17.已知定义域为的函数满⾜对任意,都有(1)求证:是奇函数;(2)当时,.若关于x 的不等在上恒成⽴,求a 的取值范围.【答案】(1)证明⻅解析第16⻚/共22⻚(2)【解析】【分析】(1)利⽤赋值法,先求出及的值,再证明即可;(2)由题意得,构造函数,得出的奇偶性及在上的单调性,继⽽可得,结合题意可得,令,利⽤导数求出在上的最⼤值即可求解.【⼩问1详解】证明:令,得,即,令,得,即,令,,所以是奇函数.【⼩问2详解】,,且,所以,令,因,所以,则,设,则,所以,因为,所以在上是减函数,第17⻚/共22⻚,所以为偶函数,所以在上恒成⽴,即或,即或(负值,舍去),令,即,,令,解得,所以,,单调递增,所以,所以.故的取值范围是.18.记的内⻆A ,B ,C 的对边分别为a ,b ,c ,已知.(1)求A 取值的范围;(2)若,求周⻓的最⼤值;(3)若,求的⾯积.【答案】(1);(2)6;(3).【解析】【分析】(1)根据题意利⽤正弦定理结合三⻆恒等变换分析可得,在利⽤余弦定理结合基本不等式分析运算即可;(2)由(1)可得,结合基本不等式分析运算;(3)根据题意结合正弦定理可求得,利⽤正弦定理以及⾯积公式分析运算.【⼩问1详解】第18⻚/共22⻚由题设,所以,,⼜,则,根据正弦边⻆关系,易得,则,⼜,则,当且仅当时取等号,所以,结合,可得;【⼩问2详解】由(1)有,⼜,⼜,则,所以,当且仅当取等号,所以周⻓的最⼤值6.【⼩问3详解】由,且,所以,⽽,则,由,显然,故,即,结合,可得,由,⽽,由,整理得,可得(负值舍),第19⻚/共22⻚所以,故.19.已知函数,其中.(1)当时,求曲线在点处的切线⽅程;(2)判断函数是否存在极值,若存在,请判断是极⼤值还是极⼩值;若不存在,说明理由;(3)讨论函数在上零点的个数.【答案】(1);(2)答案⻅解析;(3)答案⻅解析.【解析】【分析】(1)求出、,利⽤点斜式可得出所求切线的⽅程;(2)对实数的取值进⾏分类讨论,分析导数在上的符号变化,由此可得出结论;(3)对实数的取值进⾏分类讨论,分析函数在上的单调性,结合零点存在定理可得出结论.【详解】(1)当时,,则,所以,,,所以,曲线在点处的切线⽅程为,即;(2),设,则对任意的恒成⽴,故在上单调递减.所以,,当时,.①若,即时,由零点存在定理可知,存在,使得,第20⻚/共22⻚当时,,此时函数单调递增,当时,,此时函数单调递减.所以,在处取得极⼤值,不存在极⼩值;②若,则,对任意的恒成⽴,此时,函数在上单调递增,此时函数⽆极值.综上所述,当时,函数有极⼤值,⽆极⼩值;当时,函数⽆极值;(3)分以下情况讨论:①若,函数在上单调递增,则,此时,函数在上⽆零点;②若,由(2)可知,由零点存在定理可知,存在,使得,且函数在上单调递增,在上单调递减.从⽽有,设,则对任意的恒成⽴,从⽽当增⼤时,也增⼤.(i )若,此时,此时函数在上单调递减,若,可得或(舍去).此时函数在上⽆零点;第21⻚/共22⻚若,可得,此时函数在上有且只有⼀个零点.当时,,,此时函数在上只有⼀个零点;(ii )当时,此时,此时函数在上单调递增,在上单调递减.,,所以,,设,则对任意恒成⽴,所以,函数在上单调递增,所以,,若,即,即,此时函数在上⽆零点;若,即,即时,此时函数在上有且只有⼀个零点.综上所述,当时,函数在上⽆零点;当时,函数在上有且只有⼀个零点.【点睛】⽅法点睛:利⽤导数解决函数零点问题的⽅法:(1)直接法:先对函数求导,根据导数的⽅法求出函数的单调区间与极值,根据函数的基本性质作出图象,然后将问题转化为函数图象与轴的交点问题,突出导数的⼯具作⽤,体现了转化与化归思想、数形结合思想和分类讨论思想的应⽤;(2)构造新函数法:将问题转化为研究两函数图象的交点问题;第22⻚/共22⻚(3)参变量分离法:由分离变量得出,将问题等价转化为直线与函数的图象的交点问题.。
2012-2013学年第一学期教学目标质量检测题01

图12012-2013学年第一学期教学目标质量检测题七年级数学(一)有理数(1.1—1.3)班别___________姓名__________成绩___________一、选择题(每题4分,共40分) 1.-2的相反数是( )A .4B .2C .-2D .02.在数轴上,原点及原点右边的点表示的数是( )A 正数B 负数C 非正数D 非负数 3. 21-的值是( )A .21- B .21 C .2-D .24.一个正数同它的相反数相加后得( ) A .原数 B .原数的21 C .原数的2倍 D .零5.如图1,在数轴上表示到原点的距离为3个单位的点有( )A .D 点B .A 点C .A 点和D 点D .B 点和C 点6.实数a b ,在数轴上的位置如图所示,下列各式正确的是( )A .0a >B .0b <C .a b >D .a b <7.计算 -4+2的结果是( )A .-2B .-6C .2D .68.-21、-1、2的大小顺序是( )A .-21<-1<2 B .-1<-21<2 C .2<-21<-1 D .-21<2<-19. 黄山的气温由中午的零上2℃下降了7℃后的气温是( ) A. 7℃ B. 5℃ C. -5℃ D. -9℃10. 下列各组数中,互为相反数的是( )A .2和21 B .-2和-21 C . -2和|-2| D .a 和a1二、填空题(每小题4分,共20分)11. 如果河水上涨1米,记作+1米,那么-1.5米表示 .12.数轴上与表示数-3的点的距离是5的点表示的数是________.13. 在2-、0、1、3这四个数中比0大的数是_____________.14. 如果□+2=0,那么“□”内应填的数是________________15. 比-3小2的数是_______________.三、解答下列各题(每小题8分,共40分)16、一条南北走向的公路,规定向南为正.怎样表示向北36千米?向南48千米?20-千米是什么意思?+25千米是什么意思?17.计算:(1)-7–8 + 5.(2)-32 + 92--61.18.在数轴上表示下列各数,并用“<”将它们连接起来. -4,3-,21,0,23.19.检修小组乘汽车沿公路检修线路,约定前进为正,后退为负,某天自A地出发到收工时所走路线(单位:千米)为:+8,-9,+4,-7,+2,+10,-18,-3,问收工时距离A地多少千米?20. 某大楼地上共有12层,地下共有4层,每层高2.8米,请用正负数表示这栋楼每层的楼层号,某人乘电梯从地下3层升至地上7层,电梯一共上了多少米?。
2023年上学期三年级数学第1、3单元测试

2022-2023学年度第二学期第一、三单元质量监测三年级数学科时量:60分钟总分:100分一、认真思考,准确填写(第6小题(5)小题3分,其余每空1分,共20分。
)1.明明在岳麓山顶上看日出,他面向太阳,前面是(),后面是(),右边是(),左边是()。
2.学校操场上的红旗向东南方向飘扬,那么操场上刮的是()方向的风;如果操场上刮东北风,那么红旗会向()方向飘扬。
3.丁丁在贴地图时不小心把地图上下贴反了,现在这张地图的上面是原来地图的()面,右面是原来地图的()面。
(填“东”,“南”,“西”,“北”)4.上体育课时,同学们向南站好队,体育老师喊口令“向右转,向右转”。
这时同学们面向()站立。
5.大自然里有很多的“指南针”。
晴朗的夜空,面对北极星时,你的后面是()面。
在北半球,春天来了,()面的雪融化得快些。
树叶茂盛的一面表示的是()面。
6.下面是三年级上学期获得流动红旗次数的统计表,请你根据统计表的信息完成题目。
(1)从表中看出,上学期()班的卫生情况最好,()班做广播体操的情况最好。
(2)六班的卫生项目获得流动红旗次数比广播体操项目获得流动红旗次数少()次。
(3)七班获得流动红旗的总次数比三班获得流动红旗的总次数多()次。
(4)三年级卫生项目获得的流动红旗和广播体操项目获得的流动红旗数量相差()次。
(5)如果学校要根据流动红旗的评比情况来评选优秀班级,应该选()班,理由是()。
二、仔细推敲,认真辨析(对的打“√”,错的打“×”。
每小题2分,共10分。
)1.冬冬家在学校的北面,放学后明明回家应该向北走。
()2.小红面向西边时,她的左边是北边。
()3.用复式统计表可以计算出总量,单式统计表不可以计算出总量。
()4.单式统计表只能表示一组数据,而复式统计表只能表示两组数据。
()5.当你面向西北时,正面是西北方向,背面就是西南方向。
()三、反复比较,慎重选择(选择正确答案序号填入括号。
每小题2分,共10分。
2023年秋季人教版三年级上册数学第一单元同步检测试卷及答案

单元综合素质评价第一单元时、分、秒一、仔细推敲,选一选。
(将正确答案的序号填在括号里)(每小题2 分,共22 分)1.【新角度】下面钟面显示的时间是4 时5 分30 秒的是( )。
A.B.C.D.2. 下列说法正确的是( )。
A.亮亮跑一百米用了19 秒B.做眼保健操大约需要5 秒C.华华做作业用了1 小时,也就是100 分钟D.龙龙每天睡觉9 分钟3. 下列说法中正确的是( )。
①分针走1 小格,秒针走1 圈。
②妈妈做晚餐大约用了20 秒。
③180 秒=18 分。
④分针从一个数走到下一个数,经过的时间是5 分钟。
A.①②B.①④C.②④D.②③4. 下列选项中,能在1 分钟内完成的是( )。
A.做一遍广播体操B.读一首诗C.唱一首歌D.做一套试卷5.【新考法】三(1)班的学生在进行5分钟的口算测试,开始时间是9:50,口算测试结束时的时间是( )。
A.9:40 B.9:45 C.9:55 D.10:006. 蓝蓝晚上9:00 睡觉,早上6:45 起床,她的睡眠时间接近( )。
A.8 小时B.9 小时C.10 小时D.11 小时7.【新角度】亮亮每天下午2 时上第一节课,该时间在下面直线上的大致位置是( )。
A.①B.②C.③D.④8. 聪聪坚持每天7:00 -7:25 阅读打卡,他每天阅读( )分钟。
A.5 B.25 C.35 D.609. 中央电视台的《新闻联播》是晚上7:00 开始,半小时结束,然后播放2 分钟的广告后是天气预报,天气预报的开始时间是( )。
A.7:30 B.7:32 C.7:31 D.7:3310. 【新情境】福建省教育系统关工委通过“福建省家长网校”某平台直播“名师开讲”家庭教育系列讲座,下午3:10 开始,5:45 结束,这场讲座用时( )。
A.1 小时45 分钟B.2 小时25 分钟C.2 小时35 分钟D.1 小时15 分钟11. 【数学文化】每天(一昼夜)有24 小时。
统编版2024-2025学年第一学期五年级语文上册第四单元达标检测卷(有答案)

2024-2025学年第一学期五年级语文上册第四单元达标检测卷时间:90 分钟满分:100分姓名基础积累·语言运用(共44分)一、下列加点字的读音有误的一项是()。
(2分)A.熏香(xūn)精神抖擞(sǒu)B.鱼鳞(lín)地履其黄(fù)C.剔透(tī)玲珑(líng)D.搅动(jiǎo)舀水(yǎo)二、请在仔细拼读后认真书写。
(6分)圆明园是一座jǔ shì wén míng()的皇家园林。
里面的圆明三园和其他小园如zhòng xīng gǒng yuè()般环绕在圆明园周围。
漫步园内,有如màn yóu ()在tiān nán hǎi běi(),饱览着中外风景名胜,liú lián()其间,仿佛zhì shēn()在幻想的境界里。
三、把下列词语补充完整,并按要求答题。
(填序号)(10分)①惊()动()②()碧()煌③诗()画()④不可()()⑤奇()异()⑥()()剔透上面6个词语中能形容建筑物等异常华丽、光彩夺目的词语是;说明圆明园的建筑损失巨大,无法计算的词语是。
我还能写出形容建筑的词语:、。
四、下列四个句子中没有语病的一句是()(3分)A.走进圆明园,我们就看到满园断壁残垣的景象。
B.通过读这本书,使我受益匪浅。
C.我们阅读课外书籍,可以增长知识和写作水平。
D.六月的运城,是一个炎热的季节。
五、下列哪句诗与其他三句所表达的感情不同?()(3分)A.捐躯赴国难,视死忽如归。
B.但使龙城飞将在,不教胡马度阴山。
C.江山代有才人出,各领风骚数百年。
D.死去元知万事空,但悲不见九州同。
六、根据要求完成句子练习。
(4分)1.读句子,体会加点词的妙处并写在横线上。
(2分)圆明园的毁灭是中国文化史上不可估量的损失,也是世界文化史上不可估量的损失!2.照样子,改写句子。
山西省临汾市2023-2024学年三上数学第三单元《测量》部编版综合诊断试卷
山西省临汾市2023-2024学年三上数学第三单元《测量》部编版综合诊断试卷学校:_______ 班级:__________姓名:_______ 考号:__________(满分:100分时间:45分钟)总分栏题号一二三四五六七总分得分评卷人得分一、认真审题,填一填。
(除标注外,每空1分)1.32千克是吨,写成小数是 吨.2.( )毫米 ( )厘米( )毫米3.填合适的数。
__________分米=3米 3元5角=__________角 2分25秒=__________秒4.把一根4米长的绳子,剪成同样长的5段,每段长( )分米。
5.在横线上填上合适的单位。
小朋友每天大约要睡9_____ 飞机每小时行900____卡车的载重量是3_____ 小明每天大约在6_____起床。
6.700毫米=( )分米 8080千克=( )吨( )千克6吨300千克=( )千克 180秒=( )分7.比较大小905克 9千克 4004千克 4吨3吨 30005克 8吨 8000千克9605克 10千克 3500千克 5吨2吨﹣1吨 600千克 1千克﹣400克 400克.8.如图,这根铅笔的长度是( )厘米( )毫米。
9.5吨= 千克,1000千克= 吨.10.填上合适的单位。
写字时眼离书本约3( ) 一头牛重500( )爸爸每天工作8( ) 你跑100米要12( )11.在括号里填上合适的单位。
冬冬是三年级的学生,身高135( ),体重26( )。
星期日早上8( ),他和妈妈去菜市场,买了一只重2( )的鸡和800( )的青菜,在一辆载重3( )的小货车旁,他们还买了一些水果。
经过90( )他俩回到了家,他赶紧坐在高8( )的书桌旁开始写作业。
12.5吨木材与5吨棉花一样重. .(判断正误)评卷人得分二、仔细推敲,选一选。
(将正确答案的序号填入括号内)(每小题2分,10分)1.英英家离学校3千米,她可以()上学。
2023-2024学年小学数学人教新版三年级上3 测量单元测试(含答案解析)
2023-2024学年人教新版小学数学单元测试学校:__________ 班级:__________ 姓名:__________ 考号:__________注意事项:1.答题前填写好自己的姓名、班级、考号等信息;2.请将答案正确填写在答题卡上;一、选择题(本大题共计2小题,每题3分,共计6分)1.18个1角硬币大约重18( )。
A. 克B. 角C. 千克【答案】A【解析】略2.2袋大米重100()。
A. 千克B. 克C. 吨【答案】A【解析】解答此类题目时,要根据情境选择合适的单位要注意根据实际质量单位和数据的大小灵活地选择.二、填空题(本大题共计7小题,每题3分,共计21分)3.常用的质量单位有________;常用的面积单位有________.【答案】吨、千克、克, 平方厘米、平方分米、平方米、公顷、平方千米【解析】解:常用的质量单位有吨、千克、克;常用的面积单位有平方厘米、平方分米、平方米、公顷、平方千米。
故答案为:吨、千克、克;平方厘米、平方分米、平方米、公顷、平方千米。
4.在()里填上合适的质量单位。
一块橡皮重10(________)。
一根香蕉重110(________)。
一头鲸鱼重8(________)。
一堆水果重5000(________)。
一只小鸡重400(________)。
一艘轮船重200(________)。
【答案】克, 克, 吨, 克, 克, 吨【解析】解答此类题目时,要根据情境选择合适的单位注意根据实际质量单位和数据的大小灵活地选择.5.在横线上填上合适的单位.一个大约重5________ 一袋大约重100________【答案】千克, 克【解析】根据对质量单位的认识可知,一个西瓜的质量用千克作单位,一袋方便面的质量用克作单位,据此解答.6.质量单位有________、________、________,还可以用字母表示为________、________、________.【答案】吨, 千克, 克, t, \kg , \g【解析】略7.说一说,填一填________1把重1 kg ,________把重1吨。
2012年七年级数学上册第一章有理数单元试题
2012年七年级数学上册第一章有理数单元试题2012—2013学年度第一学期单元教学目标检测(第一章有理数)s班级:七年级()班姓名:座号分数:一、用心填一填(1到6每空1分,7到10每空2分,共24分)1、上升5米记作+5米;下降3米记作米;2、的相反数是,倒数是。
3、化简:=,。
4、用“<”号或“>”号填空:⑴3.62.5;⑵-30;⑶-16-1.65、近似数30.15精确到_________位6、用科学记数法表示数:508000=。
7、在-,0,,-6,-3.2,+108,28,-9这些有理数中,(1)正整数有;(2)负整数有;(3)负分数有.8、(1),(2)若,则9、有理数m和n互为相反数,p和q互为倒数,则的值为_________10、用“☆”定义新运算:对于任意实数a、b,都有a☆b=a2+b.例如4☆1=42+1=17,那么3☆2=.精心选一选(每小题2分,共12分)11、已知A地的海拔高度为米,B地比A地高30米,则B地的海拔高度为()米A.-83B.-23C.23D.3012、表示有理数则下列说法正确的是()A.表示正数B.表示负数C.表示正数D.表示的相反数13、下列说法,不正确的是()A.绝对值最小的有理数是0.B.在数轴上,右边的数的绝对值比左边的数的绝对值大.C.数轴上的数,右边的数总比左边的数大D.离原点越远的点,表示的数的绝对值越大。
14、若ab<0,必有()A、a>0,b<0B、a<0,b>0C、a、b同号D、a、b异号15、数轴上与表示2的点的距离为5个单位长度的点表示的数为()A、-3B、7C、-3或7D、-2或516、一种零件的直径尺寸在图纸上是300.03(单位:mm),它表示这种零件的标准尺寸是30mm,加工要求尺寸最大不超过()A、0.03B、0.02C、30.03D、29.97三、细心做一做(共14分)17、如图,填空:(每空1分,共6分)(1)A点表示的数是______,B点表示的数是______,C点表示的数是______,D点表示的数是______;(2)A点与原点的距离等于______,C点与原点的距离等于______:18、(8分)画出数轴,在数轴上表示下列各数,并用“,-1.5,,-4,四、计算题(共36分)19、直接写出计算结果:(12分)(1)(-5)+(-2)=(2)-5-2=(3)(-5)-(-2)=(4)6(-=(5)(-3)2=(6)=20、计算:(24分)五、解答题(共10分)21、(6分)某检修小组乘汽车检修供电线路。
湖北省黄石市大冶市2022-2023学年九年级上学期期中目标检测数学试题
湖北省黄石市大冶市2022-2023学年九年级上学期期中目标检测数学试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.用配方法解一元二次方程x 2+4x+2=0,下列变形中正确的是( ) A .(x+2)2=-2B .(x+2)2=2C .(x+2)2=6D .(x-2)2=22.下列四个图形中,既是轴对称图形又是中心对称图形的是( )A .B .C .D .3.关于x 的一元二次方程2210mx x +-=有两个实数根,则m 的取值范围是( ) A .1m ≤-B .1m ≥-C .1m £且0m ≠D .1m ≥-且0m ≠4.如图,在长为80米,宽为60米的矩形场地上修建两条宽度相等且互相垂直的道路,剩余部分进行绿化,要使绿化面积为24661m ,则道路的宽应为多少米?设道路的宽为x 米,则可列方程为( )A .806080604661x x ⨯--=B .()()280604661x x x --+=C .()()80604661x x --=D .806080604661x x +=⨯-5.根据表格中二次函数y =ax 2+bx +c 的自变量x 与函数值y 的对应值,可以判断方程2三、解答题 19.解下列方程:(1)()()()2323x x x --=-; (2)244116x x ++=.20.如图,在ABC V 和ADE V 中,AB AC =,AD AE =,90BAC DAE ∠=∠=︒,且点D 在线段BC 上,连CE .(1)求证:ABD ACE ≌△△;(2)若60EAC ∠=︒,求CED ∠的度数.21.如图,利用函数243y x x =-+的图象,直接回答:(1)方程2430x x -+=的解是_____________; (2)当2x >时,y 随x 的增大而_______________; (3)当x 满足___________时,函数值大于0; (4)当05x <<时,y 的取值范围是_____________. 22.阅读材料:(1)求抛物线和直线l 的解析式;(2)直线l 与抛物线的对称轴交于点E ,P 为线段BC 上一动点(点P 不与点B C ,重合),过点P 作PF DE ∥交抛物线于点F ,设点P 的横坐标为t . ①当t 为何值时,四边形PEDF 是平行四边形;②设BCF △的面积为S ,当t 为何值时,S 最大?最大值是多少?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二0一三学年第一学期单元目标检测题
小学六年级语文(二)
六()班姓名:_________________ 座号______ 成绩____________一、读拼音,写汉字。
(6分)
shī qī náo zhì ménɡ yì
()工()凉阻()真()()胧()力二、划去括号中加点字不正确的读音。
(4分)
填没.(méi mò) 要.挟(yāo yào) 塞.外(sài sāi) 狂风怒号.(háo hào) 三、组词。
(8分)
艰()讥()频()斑()篇()浆()岔()劣()四、把下列词语补充完整。
(4分)
悬崖()壁可见一()碧空如()水落()出寝不安()思潮起()百折()回牙牙学()五、找出下列词语的近义词。
(8分)
嘲笑()轻易()惊叹()勉励()
六、请删去每组中不是同一类的词语。
(3分)
1、农民工人学生妇女教师
2、桂林上海昆明城市西安
3、阴险英勇可爱漂亮伟大
七、选择恰当的词语填空。
(8分)
周密精密
1、这次活动开展得非常成功,是因为他们事先进行了()的计划。
2、神舟飞船内布满了()的仪器。
不管……总……宁可……也不……
3、李真()自己受苦刑,()愿说出其他同志。
4、()条件怎样恶劣,詹天佑()坚持在野外工作。
八、按要求写句子。
(10分)
1、詹天佑是我国杰出的爱国工程师。
(缩句)
____________________________________________________________________
2、西瓜花没授花粉怎么能结瓜呢?(改为陈述句)
____________________________________________________________________ 3、詹天佑说:“我们的工作首先要精密,不能有一点儿马虎。
”(改为转述句)
____________________________________________________________________ 4、我就不相信,这些小精灵会不爱我们祖国的海岛。
(改成肯定句)
____________________________________________________________________ 5、站长把大西瓜切成薄薄的小片。
(改成“被”字句)
____________________________________________________________________
九、修改病句。
(6分)
1、我们要不断改进学习方法,增加学习效率。
2、全校师生和少先队员都参加了联欢会。
3、在老师的帮助下,我很快克服了错误。
十、阅读短文,回答问题。
(18分)
京张铁路不满四年就全线(jùn)①______工了,比计划提早两年。
这件事给了(miǎo)②______视中国的帝国主义者一个有力的回击。
今天,我们乘火车去八达岭,过青龙桥车站,可以看到一座铜像,那就是詹天佑塑像。
1、在这段文字中①②处拼音后的横线上填上合适的字,然后解释两个字的意思。
(4分)
①_________________________;②__________________________。
2、文中的“京张铁路”指的是从___________到_____________的一段铁路,这是完全由我国工程技术人员设计施工的__________________铁路干线。
(3分)
3、文中“这件事”指的是____________________________________。
(2分)
4、用“║”将这段文字分为两层,然后写出层意。
(4分)
一层:______________________________________________________________ 二层:______________________________________________________________ 5、文中写铜像的作用是什么?(5分)
____________________________________________________________________ 十一、作文。
(25分)
题目:最令你感动的……
提示:选择最令你感动的人或事写,表现自己的真情实感。
