精选中考数学一轮复习第五单元四边形第23讲特殊平行四边形优选习题
中考试题按章节考点分类:第23章特殊的平行四边形

(最新最全)2013年全国各地中考数学解析汇编(按章节考点整理)第二十三章 特殊的平行四边形(2013湖南益阳,7,4分)如图,点A 是直线l 外一点,在l 上取两点B 、C ,分别以A 、C 为圆心,BC 、AB 长为半径画弧,两弧交于点D ,分别连结AB 、AD 、CD ,则四边形ABCD 一定是( ) A .平行四边形 B .矩形 C .菱形 D .梯形【解析】从题目中(BC 、AB 长为半径画弧,两弧交于点D ,)可以得到四边形ABCD 的两组对边分别相等,所以得到四边形ABCD 是平行四边形。
【答案】A【点评】根据尺规作图得到对边相等,只要考生记住两组对边分别相等的四边形是平行四边形这一定义,就可以得到答案,难度不大。
23.1 矩形(2013湖北襄阳,9,3分)如图4,ABCD 是正方形,G 是BC 上(除端点外)的任意一点,DE ⊥AG 于点E ,BF ∥DE ,交AG 于点F .下列结论不一定成立的是A .△AED ≌△BFAB .DE -BF =EFC .△BGF ∽△DAED .DE -BG =FG【解析】由ABCD 是正方形,得AD =BA ,∠BAD =∠ABG =90°,∴∠DAE +∠BAF =90°.又∵DE ⊥AG ,BF ∥DE ,∴BF ⊥AG ,∠BAF +∠ABF =90°.∴∠DAE =∠ABF .而∠AED =∠BFA =90°,∴△AED ≌△BFA .∴DE =AF ,AE =BF .∴DE -BF =AF -AE =EF .由AD ∥BC 得∠DAE =∠BGF 及∠AED =∠GFB =90°,可知△BGF ∽△DAE .可见A ,B ,C 三选项均正确,只有D 选项不能确定.【答案】D 【点评】此题是由人教课标版数学教材八年级下册第104页的第15题改编而成,并将九年级下册第48页练习2融合进来,源于教材而又高于教材,综合考查了正方形的性质、全等三角形、相似三角形知识,是一道不可多得的基础好题.(2013山东泰安,9,3分)如图,在矩形ABCD 中,AB=2,BC=4,对角线AC 的垂直平分线分别交AD 、AC 于点E 、O ,连接CE ,则CE 的长为( ) A. 3 B.3.5 C.2.5 D.2.8图4A C BD E F G ABCDEO【解析】设CE 的长为x,因为EO 垂直平分AC ,所以AE=CE=x,所以ED=4-x, 在Rt △CED 中,由勾股定理得CD 2+ED 2=CE 2,22+(4-x )2=x 2,解得x=2.5. 【答案】C.【点评】本题在矩形中综合考查了线段垂直平分线的性质、勾股定理等知识,用方程的思想解几何问题是一种行之有效的思想方法。
中考数学章节考点分类突破:第23章-特殊的平行四边形(含解析)

(最新最全)2019年全国各地中考数学解析汇编(按章节考点整理)第二十三章 特殊的平行四边形(2018湖南益阳,7,4分)如图,点A 是直线l 外一点,在l 上取两点B 、C ,分别以A 、C 为圆心,BC 、AB 长为半径画弧,两弧交于点D ,分别连结AB 、AD 、CD ,则四边形ABCD 一定是( ) A .平行四边形 B .矩形 C .菱形 D .梯形 【解析】从题目中(BC 、AB 长为半径画弧,两弧交于点D ,)可以得到四边形ABCD 的两组对边分别相等,所以得到四边形ABCD 是平行四边形。
【答案】A【点评】根据尺规作图得到对边相等,只要考生记住两组对边分别相等的四边形是平行四边形这一定义,就可以得到答案,难度不大。
23.1 矩形(2018湖北襄阳,9,3分)如图4,ABCD 是正方形,G 是BC 上(除端点外)的任意一点,DE ⊥AG 于点E ,BF ∥DE ,交AG 于点F .下列结论不一定成立的是A .△AED ≌△BFAB .DE -BF =EFC .△BGF ∽△DAED .DE -BG =FG【解析】由ABCD 是正方形,得AD =BA ,∠BAD =∠ABG =90°,∴∠DAE +∠BAF =90°.又∵DE ⊥AG ,BF ∥DE ,∴BF ⊥AG ,∠BAF +∠ABF =90°.∴∠DAE =∠ABF .而∠AED =∠BFA =90°,∴△AED ≌△BFA .∴DE =AF ,AE =BF .∴DE -BF =AF -AE =EF .由AD ∥BC 得∠DAE =∠BGF 及∠AED =∠GFB =90°,可知△BGF ∽△DAE .可见A ,B ,C 三选项均正确,只有D 选项不能确定.【答案】D 【点评】此题是由人教课标版数学教材八年级下册第104页的第15题改编而成,并将九年级下册第48页练习2融合进来,源于教材而又高于教材,综合考查了正方形的性质、全等三角形、相似三角形知识,是一道不可多得的基础好题.(2018山东泰安,9,3分)如图,在矩形ABCD 中,AB=2,BC=4,对角线AC 的垂直平分线分别交AD 、AC 于点E 、O ,连接CE ,则CE 的长为( )A. 3B.3.5C.2.5D.2.8【解析】设CE 的长为x,因为EO 垂直平分AC ,所以AE=CE=x,所以ED=4-x, 在Rt △CED 中,由勾股定理得CD 2+ED 2=CE 2,22+(4-x )2=x 2,解得x=2.5. 【答案】C.【点评】本题在矩形中综合考查了线段垂直平分线的性质、勾股定理等知识,用方程的思想解几何问题是一种图4D AD行之有效的思想方法。
2019年中考数学第五单元四边形课时训练23多边形及平行四边形练习新版浙教版

课时训练(二十三) 多边形及平行四边形|夯实基础|1.[2018·福建B卷] 一个n边形的内角和是360°,则n等于()A.3B.4C.5D.62.[2018·宜宾] 在▱ABCD中,若∠BAD与∠CDA的角平分线交于点E,则△AED的形状是()A.锐角三角形B.直角三角形C.钝角三角形D.不能确定3.[2017·眉山] 如图K23-1,EF过▱ABCD对角线的交点O,交AD于E,交BC于F.若▱ABCD的周长为18,OE=1.5,则四边形EFCD的周长为 ()图K23-1A.14B.13C.12D.104.[2018·呼和浩特] 顺次连结平面上A,B,C,D四点得到一个四边形,从①AB∥CD,②BC=AD,③∠A=∠C,④∠B=∠D四个条件中任取其中两个,可以得出“四边形ABCD是平行四边形”这一结论的情况共有()A.5种B.4种C.3种D.1种5.[2017·威海] 如图K23-2,在平行四边形ABCD中,∠DAB的平分线交CD于点E,交BC的延长线于点G,∠ABC的平分线交CD于点F,交AD的延长线于点H,AG与BH交于点O,连结BE.下列结论错误的是()图K23-2A.BO=OHB.DF=CEC.DH=CGD.AB=AE6.[2017·镇江] 如图K23-3,点E,F分别在平行四边形ABCD的边BC,AD上,BE=DF,点P在边AB 上,AP∶PB=1∶n(n>1),过点P且平行于AD的直线l将△ABE分成面积为S1,S2的两部分,将△CDF分成面积为S3,S4的两部分,有下列四个等式:①S1∶S2=1∶n,②S1∶S4=1∶(2n+1),③(S1+S4)∶(S2+S3)=1∶n,④(S3-S1)∶(S2-S4)=1∶(n+1).其中成立的有()图K23-3A.①②④B.②③C.②③④D.③④7.[2018·十堰] 如图K23-4,已知▱ABCD的对角线AC,BD交于点O,且AC=8,BD=10,AB=5,则△OCD的周长为.图K23-48.[2018·山西] 图K23-5是我国古代建筑中的一种窗格,其中冰裂纹图案象征着坚冰出现裂纹并开始消溶,形状无一定规则,代表一种自然和谐美,图②是从图①冰裂纹窗格图案中提取的由五条线段组成的图形,则∠1+∠2+∠3+∠4+∠5= 度.图K23-59.如图K23-6,在四边形ABCD中,对角线AC,BD相交于点E,∠CBD=90°,BC=4,BE=ED=3,AC=10,则四边形ABCD的面积为.图K23-610.[2018·长春] 如图K23-7,在▱ABCD中,AD=7,AB=2,∠B=60°.E是边BC上任意一点,沿AE剪开,将△ABE沿BC方向平移到△DCF的位置,得到四边形AEFD,则四边形AEFD周长的最小值为.图K23-711.[2018·朝阳区模拟] 如图K23-8,平行四边形ABCD的对角线AC,BD相交于点O,延长CD到E,使DE=CD,连结AE.(1)求证:四边形ABDE是平行四边形;(2)连结OE,若∠ABC=60°,且AD=DE=4,求OE的长.图K23-812.如图K23-9,分别以Rt△ABC的直角边AC及斜边AB为边向外作等边△ACD及等边△ABE,已知∠BAC=30°,EF⊥AB,垂足为F,连结DF.(1)证明:AC=EF;(2)求证:四边形ADFE是平行四边形.图K23-9|拓展提升|13.[2018·无锡] 如图K23-10,已知∠XOY=60°,点A在边OX上,OA=2.过点A作AC⊥OY于点C,以AC为一边在∠XOY内作等边△ABC.点P是△ABC围成的区域(包括各边)内的一点,过点P作PD∥OY交OX 于点D,作PE∥OX交OY于点E.设OD=a,OE=b,则a+2b的取值范围是.图K23-1014.[2018·重庆B卷] 如图K23-11,在▱ABCD中,∠ACB=45°,点E在对角线AC上,BE=BA,BF⊥AC于点F,BF的延长线交AD于点G.点H在BC的延长线上,且CH=AG,连结EH.(1)若BC=12,AB=13,求AF的长;(2)求证:EB=EH.图K23-11参考答案1.B2.B[解析] 如图,∵四边形ABCD是平行四边形,∴AB∥CD,∴∠BAD+∠ADC=180°.∵AE和DE是角平分线,∴∠EAD=∠BAD,∠ADE=∠ADC,∴∠EAD+∠ADE=(∠BAD+∠ADC)=90°,∴∠E=90°,∴△ADE是直角三角形,故选B.3.C[解析] 因为四边形ABCD是平行四边形,所以AD∥BC,OA=OC,所以∠OAE=∠OCF,又因为∠AOE=∠COF,所以△AOE≌△COF,所以AE=CF,OE=OF,而AB=CD,AD=BC,所以四边形EFCD的周长为AD+CD+EF=×18+2×1.5=12.4.C5.D[解析] ∵AH∥CG,∴∠H=∠HBG.∵∠HBG=∠HBA,∴∠H=∠HBA,∴AH=AB.同理AB=BG,AD=DE,BC=CF.∵AD=BC,∴DF=CE,故B正确.∵AD=BC,∴DH=CG,故C正确.∵AH=AB,AO平分∠HAB,∴BO=HO,故A正确.故选D.6.B[解析] 由题意可得△ABE≌△CDF,设△ABE的面积为S,根据“相似三角形的面积比等于相似比的平方”,则有S1=·S,S2=·S,S3=·S,S4=·S.所以S1∶S2=1∶(n2+2n),S1∶S4=1∶(2n+1),(S1+S4)∶(S2+S3)=(1+2n+1)∶(n2+2n+n2)=1∶n,(S3-S1)∶(S2-S4)=(n2-1)∶(n2+2n-2n-1)=1∶1.故选B.7.148.3609.24[解析] ∵∠CBD=90°,∴△BEC是直角三角形,∴CE==5.又∵AC=10,∴E为AC的中点.∵BE=ED=3,∴四边形ABCD是平行四边形.∵△DBC是直角三角形,∴S△DBC=·DB·BC=×6×4=12.又S△DBC=S△ABD=12,∴S▱ABCD=S△DBC+S△ABD=12+12=24.10.20[解析] 如图,作AE⊥BC.此时四边形AEFD周长最小.在Rt△AEB中,∠AEB=90°,AB=2,∠B=60°,∴AE=AB·sin 60°=2×=3.由平移性质可知,四边形AEFD是矩形,∴四边形AEFD周长为2(AD+AE)=2×(7+3)=20.11.解:(1)证明:∵四边形ABCD是平行四边形,∴AB∥CD,AB=CD.∵DE=CD,∴AB=DE.∴四边形ABDE是平行四边形.(2)∵AD=DE=4,∴AD=AB=4.∴四边形ABCD是菱形.∴AB=BC,AC⊥BD,BO=BD,∠ABO=∠ABC.又∵∠ABC=60°,∴∠ABO=30°.在Rt△ABO中,AO=AB·sin∠ABO=2,BO=AB·cos∠ABO=2, ∴BD=4.∵四边形ABDE是平行四边形,∴AE∥BD,AE=BD=4.又∵AC⊥BD,∴AC⊥AE.在Rt△AOE中,OE==2.12.证明:(1)∵△ABE是等边三角形,EF⊥AB,∴∠AEF=∠AEB=30°,∴∠BAC=∠AEF.又∵∠ACB=90°,∠EFA=90°,∴∠EFA=∠ACB.又AE=AB,∴△AEF≌△BAC,∴AC=EF.(2)∵△ACD是等边三角形,∴AC=AD,∠DAC=60°.由(1)的结论得AC=EF,∴AD=EF.∵∠BAC=30°,∴∠FAD=∠BAC+∠DAC=90°.又∵∠EFA=90°,∴EF∥AD,∴四边形ADFE是平行四边形.13.2≤a+2b≤5[解析] 过P作PH⊥OY交OY于点H,∵PD∥OY,PE∥OX,∴四边形EODP是平行四边形,∠HEP=∠XOY=60°,∴EP=OD=a,Rt△HEP中,∠EPH=30°,∴EH=EP=a,∴a+2b=2(a+b)=2(EH+EO)=2OH,当P在AC边上时,H与C重合,此时OH的最小值=OC=OA=1, 即a+2b的最小值是2;当P在点B时,OH的最大值是1+=,即(a+2b)的最大值是5,∴2≤a+2b≤5.14.解:(1)∵BF⊥AC,∴∠BFC=∠AFB=90°.在Rt△FBC中,sin∠FCB=,而∠ACB=45°,BC=12,∴sin 45°=.∴BF=12×sin 45°=12×=12.在Rt△ABF中,由勾股定理,得AF===5.(2)证明:如图,以点A为圆心,AG为半径作弧,交BG于点M,连结ME,GE,AM.∵∠BFC=90°,∠ACB=45°,∴△FBC是等腰直角三角形.∴FB=FC.∵在▱ABCD中,AD∥BC,∴∠GAC=∠ACB=45°.∴∠AGB=45°.∵AM=AG,AF⊥MG,∴∠AMG=∠AGM=45°,MF=GF.∴∠AMB=∠ECH=135°.∵BA=BE,BF⊥AE,∴AF=EF.∴四边形AMEG是正方形.∴FM=FE.∴BM=CE.又∵CH=AG,∴CH=AM.∴△AMB≌△HCE.∴EH=AB.∴EH=EB.。
(完整版)特殊的平行四边形试题及答案

l l g st he r b ei n ga rgo 9 cm B. 5 cm 和10 cm C. 4 cm 和11 cm D. 7 cm 和8 cm 5.如图,在矩形中,分别为边的中点若,,则图中阴影部分的面积为( B A .3 .6 D .8如图,在菱形中,,∠,则对角线等于(.20 B .15 若正方形的对角线长为2 cm ,则这个正方形的面积为( B ).4 .2 . .矩形、菱形、正方形都具有的性质是( C ).对角线互相平分对角线互相垂直....图14图图,使,则∠. 14.如图,矩形的两条对角线交于点,过点作的垂线,分别交,于点,,连接,已知△的周长为24 cm ,则矩形的周长是48cm.15.已知,在四边形ABCD 中,∠,若添加一个条件即可判定该四边第题图6题an dAl l th i ng si nt he i r b i rf rs 形是正方形,那么这个条件可以是____________.16.已知菱形的周长为,一条对角线长为,则这个菱形的面积为____96_____.17.如图,在矩形ABCD 中,对角线与相交于点O ,且,则BD 的长为____4____cm ,BC 的长为_______cm.三、解答题(共66分)19.(8分)如图,在△ABC 中,AB =AC ,AD 是△ABC 外角的平分线,已知∠BAC =∠ACD .(1)求证:△ABC ≌△CDA ;(2)若∠B =60°,求证:四边形ABCD 是菱形.证明:(1)∵ AB =AC ,∴ ∠B =∠ACB ,∴ ∠FAC =∠B +∠ACB =2∠BCA .∵ AD 平分∠FAC ,∴ ∠FAC =2∠CAD ,∴ ∠CAD =∠ACB .在△ABC 和△CDA 中,∠BAC =∠DCA ,AC =AC ,∠DAC =∠ACB ,∴ △ABC ≌△CDA .(2)∵ ∠FAC =2∠ACB ,∠FAC =2∠DAC ,∴ ∠DAC =∠ACB ,∴ AD ∥BC .∵ ∠BAC =∠ACD ,∴ AB ∥CD ,∴ 四边形ABCD 是平行四边形.∵ ∠B =60°,AB =AC ,∴ △ABC 是等边三角形,∴ AB =BC ,∴ 平行四边形ABCD 是菱形.图19图图图20图图20.(8分)如图,在□ABCD 中,E 为BC 边上的一点,连接AE 、BD 且AE =AB .(1)求证:∠ABE =∠EAD ;(2)若∠AEB =2∠ADB ,求证:四边形ABCD 是菱形.证明:(1)在□ABCD 中,AD ∥BC ,∴ ∠AEB =∠EAD .∵ AE =AB ,∴ ∠ABE =∠AEB ,∴ ∠ABE =∠EAD .(2)∵ AD ∥BC ,∴ ∠ADB =∠DBE .∵ ∠ABE =∠AEB ,∠AEB =2∠ADB ,∴ ∠ABE =2∠ADB ,∴ ∠ABD =∠ABE -∠DBE =2∠ADB -∠ADB =∠ADB ,∴ AB =AD .又∵ 四边形ABCD 是平行四边形,∴ 四边形ABCD 是菱形.图22图图an dAl l h i ng she i r b ei 由勾股定理得+BF x=,即=.23.(8分)如图,在矩形中,相交于点,平分,交于点.,求∠的度数. 平分,所以.又知,所以因为,所以△为等边三角形,所以因为,所以△为等腰直角三角形,所以.所以,,所以=75图23图图图24图图已知:如图,在四边形中,∥,平分∠,,为的b ego od f o rs 试说明:互相垂直平分如图,连接∵图25图图图△中,是的中点,所以是t△的斜边所以,所以.因为平分,所以,所以所以∥.,所以四边形是平行四边形.又,所以平行四边形是菱形,所以互相垂直平分.。
八下册期末复习第五章特殊平行四边形好题精选
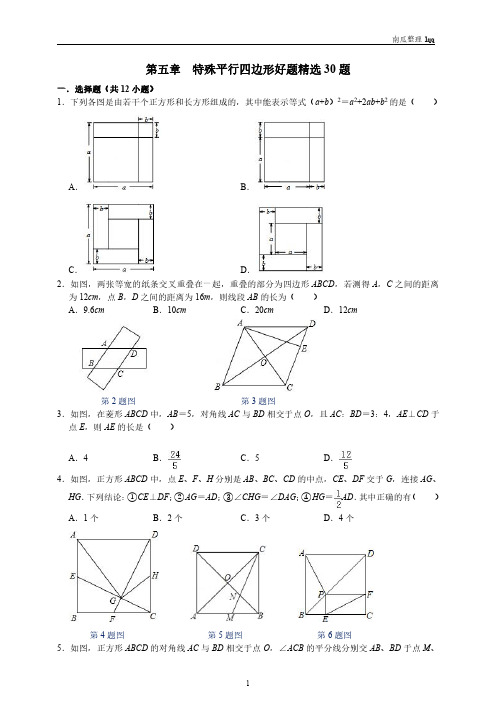
连接 DG.点 E 从点 C 运动到点 D 的过程中,DG 的最小值为
.
19.如图,正方形 ABCD 中,AB=6,点 E 在边 CD 上,且 CD=3DE,将△ADE 沿 AE 对折至△AE,
延长 EF 交边 BC 于点 G,连结 AG,CF,则下列结论:
①△ABG≌△AFG;②BG=CG;③AG∥CF;④S△EGC=S△AFE;⑤S△FGC= ;
30.如图,点 O 为平面直角坐标系的原点,在长方形 OABC 中,OC∥AB,OA∥BC,两边 OC、OA
分别在 x 轴和 y 轴上,且点 B(a,b)满足:
+(2b+6)2=0.
(1)求点 B 的坐标;
(2)如图 1,若过点 B 的直线 BP 与长方形 OABC 的边交于点 P,且将长方形 OABC 的面积分为 1:
为 12cm,点 B,D 之间的距离为 16m,则线段 AB 的长为( )
A.9.6cm
B.10cm
C.20cm
D.12cm
第 2 题图
第 3 题图
3.如图,在菱形 ABCD 中,AB=5,对角线 AC 与 BD 相交于点 O,且 AC:BD=3:4,AE⊥CD 于
点 E,则 AE 的长是( )
A.4
CF 上一点,并且∠ACG=∠AGC,∠GAF=∠GFA,你能证明∠ECB= ∠ACB 吗?
23.如图,在矩形 ABCD 中,AB=6,BC=8,动点 P 在边 AD 上以每秒 2 个单位的速度从 A 出发,
沿 AD 向 D 运动,同时动点 Q 在边 BD 上以每秒 5 个单位的速度从 D 出发,沿 DB 向 B 运动,当
A.25°
B.30°
C.35°
八年级数学下册第五章特殊平行四边形复习试题

特殊四边形平行1.矩形的断定方法有:①_____________________②__________________③_______________ 菱形的断定方法有:①_____________________②__________________③_______________ 正方形断定方法: ①_____________________②__________________③_______________ 2.以下说法中,不正确的有________〔并把它改正〕①对角线互相平分且相等的四边形是正方形②对角线互相垂直的平行四边形是菱形. ③对角线平分一组对的四边形平行是菱形; ④正方形面积等于对角线积的一半3.正方形具有,矩形不一定具有的性质有______________________________________.正方形具有,菱形不一定具有的性质有_____________________________________.4. 〔2021〕四边形ABCD是平行四边形,从四个条件①AB=BC,②∠ABC=90°,③AC=BD,④AC⊥BD中,再选两个作为补充条件后,使得ABCD是正方形,选法有〔写出所有选法〕5.如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.〔1〕求证:四边形AEBD是矩形;〔2〕当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.6.如图,将n个边长都为1cm的正方形按如下图摆放,点A1、A2…A n分别是正方形的中心,①求左边第一个重叠局部的面积,并说明理由②n个这样的正方形重叠局部的面积和为 cm2.7.如图,ABCD是正方形, AD延长线上F, FB与对角线AC 交于G,∠GBC=°,求证: ①AG=AB ②EF=AC8、如图,正方形ABCD的对角线AC、BD相交于点O,E是AC上一点,连EB,过点A作AM⊥BE,垂足为M,AM交BD于点F.〔1〕求证:OE=OF;⑵当AG平分∠BAC时, 求证:GC=2OF作业 1.正方形性质①正方形对边_______,四条边都___ _②正方形四个角___ _;③正方形的对角线__ _____④正方形既是图形,又是图形,对称轴有________条.;2.我们把顺次连接四边形四条边的中点所得的四边形叫中点四边形.....。
呼和浩特专版2022中考数学复习方案第五单元四边形课时训练23多边形与平行四边形试题
课时训练(二十三)多边形与平行四边形(限时:45分钟)|夯实根底|1.[2022·云南]一个十二边形的内角和等于 ()A.2160°B.2080°C.1980°D.1800°2.[2022·泸州]四边形ABCD的对角线AC与BD相交于点O,以下四组条件中,一定能判定四边形ABCD为平行四边形的是()A.AD∥BCB.OA=OC,OB=ODC.AD∥BC,AB=DCD.AC⊥BD3.[2022·遂宁]如图K23-1,▱ABCD中,对角线AC,BD相交于点O,OE⊥BD交AD于点E,连接BE,假设▱ABCD的周长为28,那么△ABE的周长为 ()K23-1A.28B.24C.21D.144.平行四边形两条对角线的长分别为4和6,那么其中一条边长x的取值范围为()A.2<x<3B.1<x<5C.0<x<4D.0<x<65.平面直角坐标系中,▱ABCD的三个顶点坐标分别是A(m,n),B(2,-1),C(-m,-n),那么点D的坐标是()A.(-2,1)B.(-2,-1)C.(-1,-2)D.(-1,2)6.[2022·海南]如图K23-2,在▱ABCD中,将△ADC沿AC折叠后,点D恰好落在DC的延长线上的点E处,假设∠B=60°,AB=3,那么△ADE的周长为()图K23-2A.12B.15C.18D.217.[2022·泰安]如图K23-3,四边形ABCD是平行四边形,点E是边CD上的一点,且BC=EC,CF⊥BE交AB于点F,P是EB延长线上一点,以下结论:①BE平分∠CBF;②CF平分∠DCB;③BC=FB;④PF=PC.其中正确结论的个数为()图K23-3A.1B.2C.3D.48.[2022·龙东地区]如图K23-4,在四边形ABCD中,AD=BC,在不添加任何辅助线的情况下,请你添加一个条件,使四边形ABCD是平行四边形.图K23-49.[2022·益阳]假设一个多边形的内角和与外角和之和是900°,那么该多边形的边数是.10.[2022·枣庄]用一条宽度相等的足够长的纸条打一个结(如图K23-5①所示),然后轻轻拉紧,压平就可以得到如图②所示的正五边形ABCDE.图②中,∠BAC= .图K23-511.[2022·梧州]如图K23-6,▱ABCD中,∠ADC=119°,BE⊥DC于点E,DF⊥BC于点F,BE与DF交于点H,那么∠BHF= 度.图K23-612.[2022·武汉]如图K23-7,在▱ABCD中,E,F是对角线AC上两点,AE=EF=CD,∠ADF=90°,∠BCD=63°,那么∠ADE的大小为.图K23-713.[2022·云南]在平行四边形ABCD中,∠A=30°,AD=4√3,BD=4,那么平行四边形ABCD的面积等于.14.[2022·张家界]如图K23-8,平行四边形ABCD中,连接对角线AC,延长AB至点E,使BE=AB,连接DE,分别交BC,AC于点F,G.(1)求证:BF=CF;(2)假设BC=6,DG=4,求FG的长.图K23-815.[2022·荆门]如图K23-9,平行四边形ABCD中,AB=5,BC=3,AC=2√13.(1)求平行四边形ABCD的面积;(2)求证:BD⊥BC.图K23-916.[2022·福建]在Rt△ABC中,∠ABC=90°,∠ACB=30°.将△ABC绕点C顺时针旋转一个角度α得到△DEC,点A,B的对应点分别为D,E.(1)假设点E恰好落在边AC上,如图K23-10①,求∠ADE的大小;(2)假设α=60°,F为AC的中点,如图②,求证:四边形BEDF是平行四边形.图K23-10|拓展提升|17.[2022·台湾]如图K23-11,将一张面积为14的大三角形纸片沿着虚线剪成三张小三角形纸片与一张平行四边形纸片.根据图中标示的长度,求平行四边形纸片的面积为何? ()图K23-11A.215B.425C.247D.48718.[2022·镇江]在三角形纸片ABC(如图K23-12①)中,∠BAC=78°,AC=10.小霞用5张这样的三角形纸片拼成了一个内外都是正五边形的图形(如图②).(1)∠ABC= °;(2)求正五边形GHMNC的边GC的长.(参考值:sin78°≈0.98,cos78°≈0.21,tan78°≈4.7)①②图K23-12【参考答案】1.D2.B3.D[解析]∵平行四边形的对角线互相平分,OE⊥BD,∴OE垂直平分BD,∴BE=DE,从而△ABE的周长等于AB+AD,即为▱ABCD的周长的一半,∴△ABE的周长为14,应选D.4.B[解析] 如下图,四边形ABCD是平行四边形,∴OA=OC=2,OB=OD=3,∴在△AOB中,OB-OA<AB<OB+OA,∴1<x<5.应选B.5.A6.C[解析]∵折叠后点D恰好落在DC的延长线上的点E处,∴AC⊥DE,EC=CD=AB=3,∴ED=6,∵∠B=60°,∴∠D=60°,∴AD=2CD=6,∴AE=6,∴△ADE的周长=AE+AD+ED=18,应选C.7.D[解析] ∵AB∥CD,∴∠ABE=∠BEC.∵CE=CB,∴∠CBE=∠BEC.∴∠CBE=∠ABE,即BE平分∠ABC,故①正确;∵CE=CB,CF⊥BE,∴CF平分∠DCB,故②正确;∵AB∥CD,∴∠DCF=∠CFB,∵∠DCF=∠FCB,∴∠BCF=∠CFB,∴BC=BF,故③正确;∵BF=CB,CF⊥BE,∴BE垂直平分CF,∴PF=PC,故④正确.8.答案不唯一,AD∥BC或AB=CD或∠A+∠B=180°等9.510.36°[解析]正五边形的内角和为(5-2)×180°=540°,∴∠ABC=540°÷5=108°.∵BA=BC,∴∠BAC=∠BCA=36°.11.61[解析]∵四边形ABCD是平行四边形,∴AD∥BC,DC∥AB,∵∠ADC=119°,DF⊥BC,∴∠ADF=90°,那么∠EDH=29°,∵BE⊥DC,∴∠DEH=90°,∴∠DHE=∠BHF=90°-29°=61°.故答案为61.12.21°[解析]如图,∵四边形ABCD 是平行四边形,∴AD ∥BC ,∴∠1=∠5.∵∠ADF=90°,AE=EF ,∴DE=12AF=AE ,∴∠1=∠2.∴∠5=∠2.∵AE=CD ,DE=AE ,∴DE=CD.∴∠3=∠4.∵∠3=∠1+∠2=2∠2.∴∠4=2∠2.∵∠BCD=63°,∴∠5+∠4=63°,即3∠2=63°,∴∠2=21°,即∠ADE=21°.13.16√3或8√3 [解析]分两种情况,第一种情况:如图①,过D 作DE ⊥AB 于E ,在Rt △ADE 中,∵∠A=30°,AD=4√3,∴DE=12AD=2√3,AE=√32AD=6,在Rt △BDE 中,∵BD=4,∴BE=√BB 2-BB 2=√42-(2√3)2=2,∴AB=8.∴平行四边形ABCD 的面积=AB ·DE=8×2√3=16√3.第二种情况:如图②,同理易求AB=4,∴平行四边形ABCD 的面积=AB ·DE=4×2√3=8√3.故答案为:16√3或8√3.14.解:(1)证明:∵四边形ABCD 是平行四边形,∴AE ∥CD ,AB=CD ,∴∠EBF=∠DCF ,∠BEF=∠CDF ,∵AB=BE ,∴BE=CD ,∴△BEF ≌△CDF ,∴BF=CF.(2)∵BF=CF ,BC=6,∴CF=3.∵AD ∥BC ,∴△ADG ∽△CFG ,∴BB BB =BB BB ,即36=BB 4,解得FG=2.15.解:(1)作CE ⊥AB 交AB 的延长线于点E ,如图.设BE=x ,CE=h ,在Rt △CEB 中:x 2+h 2=9①,在Rt △CEA 中:(5+x )2+h 2=52②,联立①②解得:x=95,h=125,∴平行四边形ABCD 的面积=AB ·h=12.(2)证明:作DF ⊥AB ,垂足为F ,∴∠DFA=∠CEB=90°,∵平行四边形ABCD ,∴AD=BC ,AD ∥BC ,∴∠DAF=∠CBE ,又∵∠DFA=∠CEB=90°,∴△ADF ≌△BCE (AAS),∴AF=BE=95,BF=5-95=165,DF=CE=125, 在Rt △DFB 中,BD 2=DF 2+BF 2=1252+1652=16, ∴BD=4,∵BC=3,DC=5,∴CD 2=DB 2+BC 2,∴BD ⊥BC. 16.解:(1)根据旋转的性质得:∠DCE=∠ACB=30°,∠DEC=∠ABC=90°,CA=CD ,∴∠ADC=∠DAC=180°-∠BBB2=75°.∵∠EDC=90°-∠ACD=60°,∴∠ADE=∠ADC -∠EDC=15°.(2)证明:延长BF 交CE 于点G.在Rt △ABC 中,∠ACB=30°,∴AB=12AC.∵点F 是边AC 的中点,∴BF=FC=12AC=AB ,∴∠FBC=∠ACB=30°.由旋转的性质得AB=DE ,∠DEC=∠ABC=90°,∠BCE=∠ACD=60°,∴DE=BF.∵∠BGE=∠GBC +∠ECB=90°,∴∠DEC=∠BGE=90°,∴BF ∥DE ,∴四边形BFDE 是平行四边形.17.D [解析]如图,设△ADE ,△BDF ,△CEG ,平行四边形DEGF 的面积分别为S 1,S 2,S 3和S ,过点D 作DH ∥EC ,那么由四边形DEGF 为平行四边形,易得四边形DHCE 也为平行四边形,从而△DFH ≌△EGC , ∴S △DFH =S 3,∵DE ∥BC ,∴△ADE ∽△ABC ,DE=3,BC=7,∴B 1B △BBB =949,∵S △ABC =14,∴S 1=949×14,易知S △BDH ∶S=12×4∶3=2∶3,∴S △BDH =23S ,∴23S +S=14-949×14,∴S=487. 应选:D . 18.解:(1)30 [解析] ∵五边形ABDEF 是正五边形,∴∠ABD=(5-2)×180°5=108°,∠DBG=∠BAC=78°,∴∠ABC=∠ABD -∠DBG=30°,故答案为:30.(2)作CQ⊥AB于Q,在Rt△AQC中,,sin∠QAC=BBBB∴QC=AC·sin∠QAC≈10×0.98=9.8.在Rt△BQC中,∠ABC=30°,∴BC=2QC=19.6,∴GC=BC-BG=BC-AC=9.6.。
(全优)浙教版八年级下册数学第五章 特殊平行四边形含答案
浙教版八年级下册数学第五章特殊平行四边形含答案一、单选题(共15题,共计45分)1、如图,矩形ABCD的对角线AC与BD交于点O,过点O作BD的垂线分别交AD,BC于E,F两点.若AC=2 ,∠AEO=120°,则EF的长度为()A.1B.2C.D.2、下列说法中,正确的是()A.两条对角线相等的四边形是平行四边形B.两条对角线相等且互相垂直的四边形是矩形C.两条对角线互相垂直平分的四边形是菱形D.两条对角线互相垂直、平分而且相等的四边形是菱形3、在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,………按这样的规律进行下去,第2012个正方形的面积为()A.5 ( ) 2010B.5 ( ) 2010C.5 ( ) 2012D.5 ( ) 40224、菱形ABCD的对角线AC=24,BD=10,则菱形的周长为()A.20B.48C.52D.605、如图,在矩形ABCD中,AB=6,BC=8,E是BC边上一点,将矩形沿AE折叠,点B落在点B'处,当△B'EC是直角三角形时,BE的长为()A.2B.6C.3或6D.2或3或66、如图,矩形ABCD的周长为18cm,M是CD的中点,且AM⊥BM,则矩形ABCD 的两邻边长分别是()A.3cm和6cmB.6cm和12cmC.4cm和5cmD.以上都不对7、如图,这是用面积为24的四个全等的直角三角形△ABE,△BCF,△CDG和△DAH拼成的“赵爽弦图”,如果AB=10,那么正方形EFGH的边长为()A.1B.2C.3D.48、四边形ABCD的对角线互相平分,要使它变为矩形,需要添加的条件是()A.AB=CDB.AB=BCC.AC⊥BDD.AC=BD9、我们知道:四边形具有不稳定性.如图,在平面直角坐标系中,边长为2的正方形ABCD的边AB在x轴上,AB的中点是坐标原点O,固定点A,B,把正方形沿箭头方向推,使点D落在y轴正半轴上点D′处,则点C的对应点C′的坐标为()A.(,1)B.(2,1)C.(1,)D.(2,)10、在正方形ABCD所在平面内找一点P,使P点与A、B、C、D中两点都连在一个等边三角形,那么这样的P点有()A.5个B.12个C.9个D.15个11、如图,正方形AEFG的边AE放置在正方形ABCD的对角线AC上,EF与CD 交于点M,得四边形AEMD,且两正方形的边长均为2,则两正方形重合部分(阴影部分)的面积为()A.﹣4+4B.4 +4C.8﹣4D. +112、如图,四边形ABCD、CEFG都是正方形,E在CD上且BE平分∠DBC,O是BD中点,直线BE、DG交于H.BD,AH交于M,连接OH,下列四个结论:① BE⊥GD;② OH=BG;③ ∠AHD=45°;④ GD=AM.其中正确的结论个数有()A.1个B.2个C.3个D.4个13、如图,在正方形ABCD中,点E,F分别在CD,BC上,且AF=BE,BE与AF 相交于点G,则下列结论中错误的是()A.BF=CEB.∠DAF=∠BECC.AF⊥BED.∠AFB+∠BEC=90°14、如图,在菱形ABCD中,AB=5,对角线AC=6,若过点A作AE⊥BC,垂足为E,则sinB的值为()A. B. C. D.15、下列结论不一定正确的是( )A.两组对边相等的四边形是平行四边形B.有三个是直角的四边形是矩形C.对角线垂直的四边形是菱形D.对角线互相垂直平分且相等的四边形是正方形二、填空题(共10题,共计30分)16、已知菱形A1B1C1D1的边长为2,且∠A1B1C1=60°,对角线A1C1, B1D1相较于点O,以点O为坐标原点,分别以OA1, OB1所在直线为x轴、y轴,建立如图所示的直角坐标系,以B1D1为对角线作菱形B1C2D1A2,使得∠B1A2D1=60°;再以A2C2为对角线作菱形A2B2C2D2,使得∠A2B2C2=60°;再以B2D2为对角线作菱形B2C3D2A3,使得∠B2A3D2=60°…,按此规律继续作下去,在x轴的正半轴上得到点A1, A2, A3,…,An,则点A2018的坐标为________.17、如图,在矩形ABCD中,,∠ADC的平分线交边BC于点E,AH⊥DE于点H,连接CH并延长交边AB于点F,连接AE交CF于点O,给出下列命题:①∠AEB=∠AEH ②DH= ③ ④其中符合题意命题的序号是________(填上所有符合题意命题的序号).18、如图,四边形ABCD是菱形,∠BAD=60°,AB=6,对角线AC与BD相较于点O,点E在AC上,若OE=2 ,则CE的长为________19、如图,四边形ABCD是菱形,∠A=60°,AB=6,扇形BEF的半径为6,圆心角为60°,则图中阴影部分的面积是________.20、如图,矩形ABCD中,AD=4,AB=2.点E是AB的中点,点F是BC边上的任意一点(不与B、C重合),△EBF沿EF翻折,点B落在B'处,当DB'的长度最小时,BF的长度为________.21、如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为(2,3),则点F的坐标为________.22、如图,在四边形BCDE中,BC⊥CD,DE⊥CD,AB⊥AE,垂足分别为C,D,A,BC≠AC,点M,N,F分别为AB,AE,BE的中点,连接MN,MF,NF。
2020年中考复习之特殊平行四边形练习题及答案(WORD
2020年中考复习之特殊平行四边形练习题一、选择题1.如图,在矩形ABCD中,对角线AC,BD交于点O,以下说法错误的是()A.∠ABC=90°B.AC=BD C.OA=OB D.OA=AD第1题图第2题图第3题图2.如图,在▱ABCD中,对角线AC与BD交于点O,若增加一个条件,使▱ABCD成为菱形,下列给出的条件不正确的是()A.AB=AD B.AC⊥BD C.AC=BD D.∠BAC=∠DAC3.如图,菱形ABCD的对角线AC,BD相交于点O,E,F分别是AD,CD边上的中点,连接EF.若EF=2,BD=2,则菱形ABCD的面积为()A.2 2 B. 2 C.6 2 D.8 2第4题图第5题图第6题图4.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD中,选两个作为补充条件,使▱ABCD成为正方形(如图).现有下列四种选法,你认为其中错误的是()A.①②B.②③C.①③D.②④5.如图,在菱形ABCD中,对角线AC与BD相交于点O,若AB=2,∠ABC=60°,则BD的长为()A.2 B.3 C. 3 D.2 36.如图,在正方形ABCD的外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC 的度数为CA.45°B.55°C.60°D.75°7.如图,菱形ABCD的边长为4,过点A,C作对角线AC的垂线,分别交CB和AD 的延长线于点E,F,AE=3,则四边形AECF的周长为()A.22 B.18 C.14 D.11第7题图第8题图8.如图,四边形ABCD为平行四边形,延长AD到E,使DE=AD,连接EB,EC,DB.添加一个条件,不能使四边形DBCE成为矩形的是()A.AB=BE B.BE⊥DC C.∠ADB=90°D.CE⊥DE9.如图,矩形ABCD中,AB=8,BC=4,点E在AB上,点F在CD上,点G,H在对角线AC上,若四边形EGFH是菱形,则AE的长是()A.2 5 B.3 5 C.5 D.6第9题图第10题图10.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG,BF.给出以下结论:①△DAG≌△DFG;②BG=2AG;③△EBF∽△DEG;④S△BEF=725.其中所有正确结论的个数是()A.1个B.2个C.3个D.4个二、填空题11.如图,菱形ABCD的对角线AC,BD相交于点O,E为AD的中点,若OE=3,则菱形ABCD的周长为________.第11题图第12题图第13题图12.如图,在矩形ABCD中,∠BOC=120°,AB=5,则BD的长为________.13.如图,在菱形ABCD中,AC,BD相交于点O,若∠BCO=55°,则∠ADO=________.14.如图,延长矩形ABCD的边BC至点E,使CE=BD,连接AE,如果∠ADB=30°,则∠E=________°.第14 题图第15题图第16题图15.如图,在正方形ABCD中,对角线AC与BD相交于点O,E为BC上一点,CE=5,F为DE的中点.若△CEF的周长为18,则OF的长为________.16.如图,已知正方形ABCD边长为3,点E在AB边上,BE=1,点P,Q分别是边BC,CD上的动点(均不与顶点重合),当四边形AEPQ的周长最小时,四边形AEPQ的面积是________.三、解答题17.如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.求证:四边形ADCF 是菱形.18如图,在△ABC中,AB=AC,AD是BC边上的中线,AE∥BC,CE⊥AE,垂足为点E.(1)求证:△ABD≌△CAE;(2)连接DE,线段DE与AB之间有怎样的位置和数量关系?请证明你的结论.19.如图,正方形ABCD的边长为8cm,E,F,G,H分别是AB,BC,CD,DA上的动点,AE=BF=CG=DH.(1)求证:四边形EFGH是正方形;(2)判断直线EG是否经过某一定点,说明理由;(3)求四边形EFGH面积的最小值.参考答案与解析1.D 2.C 3.A 4.B 5.D 6.C 7.A 8.B9. C 解析:连接EF 交AC 于O .∵四边形EGFH 是菱形,∴EF ⊥AC ,OE =OF .∵四边形ABCD 是矩形,∴∠B =∠D =90°,AB ∥CD ,∴∠ACD =∠CAB .在△CFO 与△AEO 中,⎩⎪⎨⎪⎧∠FCO =∠EAO ,∠FOC =∠EOA ,OF =OE ,∴△CFO ≌△AEO ,∴AO =CO .∵AC =AB 2+BC 2=45,∴AO =12AC =2 5.∵∠CAB =∠CAB ,∠AOE =∠B =90°,∴△AOE ∽△ABC ,∴AO AB =AE AC ,∴258=AE 45,∴AE =5.故选C. 10.C 解析:由折叠的性质可知DF =DC =DA ,∠DFE =∠C =90°,∴∠DFG =∠A =90°.又∵DG =DG ,∴Rt △DAG ≌Rt △DFG ,∴①正确;∵正方形ABCD 的边长为12,∴BE =EC =EF =6.设AG =GF =x ,则EG =x +6,BG =12-x .由勾股定理得EG 2=BE 2+BG 2,即(x +6)2=62+(12-x )2,解得x =4,∴AG =GF =4,BG =8,∴BG =2AG ,∴②正确;∵BE =EF =6,∴△BEF 为等腰三角形,易知△GDE 不是等腰三角形,∴③错误;∵BE =6,∴BG=8,∴EG =BE 2+BG 2=10,S △BEG =12×6×8=24,∴S △BEF =EF EG ·S △BEG =610×24=725,∴④正确.故选C.11.24 12.10 13.35° 14.1515.72解析:∵CE =5,△CEF 的周长为18,∴CF +EF =18-5=13.∵F 为DE 的中点,∴DF =EF .∵∠BCD =90°,∴CF =12DE ,∴EF =CF =12DE =6.5,∴DE =2EF =13,∴CD =DE 2-CE 2=132-52=12.∵四边形ABCD 是正方形,∴BC =CD =12,O 为BD 的中点,∴OF 是△BDE 的中位线,∴OF =12(BC -CE )=12(12-5)=72. 16.4.5 解析:作点A 关于CD 的对称点A ′,作点E 关于BC 的对称点E ′,连接A ′E ′,交BC ,CD 于点P ,Q ,此时所得四边形AEPQ 的周长最短,易求得其面积为4.5.17.证明:∵AF ∥CD ,∴∠AFE =∠CDE .∵点E 是AC 的中点,∴AE =CE .在△AFE和△CDE 中,⎩⎪⎨⎪⎧∠AFE =∠CDE ,∠AEF =∠CED ,AE =CE ,∴△AEF ≌△CED ,∴AF =CD .∵AF ∥CD ,∴四边形ADCF 是平行四边形.∵∠B =90°,AC =2AB ,∴∠ACB =30°,∴∠CAB =60°.∵AD 平分∠CAB ,∴∠DAC =∠DAB =30°=∠ACD ,∴DA =DC ,∴四边形ADCF 是菱形.18.(1)证明:∵AB =AC ,AD 是BC 边上的中线,∴AD ⊥BC ,BD =CD ,∴∠ADB =∠ADC =90°.∵AE ∥BC ,CE ⊥AE ,∴∠E =∠DCE =90°,∴四边形ADCE 是矩形,∴AD=CE .在Rt △ABD 与Rt △CAE 中,⎩⎪⎨⎪⎧AD =CE ,AB =CA ,∴Rt △ABD ≌Rt △CAE (HL);(2)解:DE∥AB,DE=AB.证明如下:∵四边形ADCE是矩形,∴AE=CD=BD,AE∥BD,∴四边形ABDE是平行四边形,∴DE∥AB,DE=AB.19.(1)证明:∵四边形ABCD是正方形,∴∠A=∠B=90°,AB=DA.∵AE=DH,∴BE =AH.又∵AE=BF,∴△AEH≌△BFE,∴EH=FE,∠AHE=∠BEF.同理:FE=GF=HG,∴EH=FE=GF=HG,∴四边形EFGH是菱形.∵∠A=90°,∴∠AHE+∠AEH=90°,∴∠BEF+∠AEH=90°,∴∠FEH=90°,∴四边形EFGH是正方形;(2)解:直线EG经过正方形ABCD的中心.理由如下:连接BD交EG于点O.∵四边形ABCD是正方形,∴AB∥DC,AB=DC,∴∠EBD=∠GDB.∵AE=CG,∴BE=DG.又∵∠EOB=∠GOD,∴△EOB≌△GOD,∴BO=DO,即点O为BD的中点,∴直线EG经过正方形ABCD的中心;(3)解:设AE=DH=x,则AH=8-x.在Rt△AEH中,EH2=AE2+AH2=x2+(8-x)2=2x2-16x+64=2(x-4)2+32,∴四边形EFGH面积的最小值为32cm2.。
中考数学专题训练:特殊平行四边形(附参考答案)
中考数学专题训练:特殊平行四边形(附参考答案)1.如图,在矩形ABCD和△BDE中,点A在BE上.若矩形ABCD的面积为20,△BDE的面积为24,则△ADE的面积为( )A.10 B.12C.14 D.162.如图,矩形ABCD的对角线AC,BD交于点O,AB=3,BC=4,过点O作OM⊥AC,交BC于点M,过点M作MN⊥BD,垂足为点N,则OM+MN的值为( )A.245B.165C.125D.653.如图,在四边形ABCD中,AB∥CD,AB⊥BD,AB=5,BD=4,CD=3,E是AC 的中点,则BE的长为( )A.2 B.52C.√5D.34.关于菱形的性质,以下说法不正确的是( )A.四条边相等B.对角线相等C.对角线互相垂直D.是轴对称图形5.下列选项中能使□ABCD成为菱形的是( )A.AB=CD B.AB=BCC.∠BAD=90°D.AC=BD6.如图,在菱形ABCD中,∠B=60°,点P从点B出发,沿折线BC-CD方向移动,移动到点D停止.在△ABP形状的变化过程中,依次出现的特殊三角形是( )A.直角三角形→等边三角形→等腰三角形→直角三角形B.直角三角形→等腰三角形→直角三角形→等边三角形C.直角三角形→等边三角形→直角三角形→等腰三角形D.等腰三角形→等边三角形→直角三角形→等腰三角形7.如图,菱形ABCD的对角线AC与BD相交于点O,E为边BC的中点,连接OE.若AC=6,BD=8,则OE=( )A.2 B.52C.3 D.48.如图,在菱形ABCD中,E,F分别是边BC,CD的中点,连接AE,AF,EF.若菱形ABCD的面积为8,则△AEF的面积为( )A.2 B.3C.4 D.59.如图,将矩形ABCD对折,使边AB与DC,BC与AD分别重合,展开后得到四边形EFGH.若AB=2,BC=4,则四边形EFGH的面积为( )A.2 B.4C.5 D.610.一个四边形顺次添加下列条件中的三个条件便得到正方形:a.两组对边分别相等;b.一组对边平行且相等;c.一组邻边相等;d.一个角是直角.顺次添加的条件:①a→c→d ②b→d→c ③a→b→c,则正确的是( )A.仅①B.仅③C.①②D.②③11.如图,在正方形ABCD中,点E,F分别在边CD,AD上,BE与CF交于点G.若BC=4,DE=AF=1,则CG的长是( )A.2 B.√5C.3√22D.12512.如图,已知F,E分别是正方形ABCD的边AB与BC的中点,AE与DF交于点P,则下列结论成立的是( )A.BE=12AE B.PC=PDC.∠EAF+∠AFD=90°D.PE=EC13.如图,在边长为3的正方形ABCD中,∠CDE=30°,DE⊥CF,则BF的长是( )A.1 B.√2C.√3D.214.如图,O为正方形ABCD对角线AC的中点,△ACE为等边三角形.若AB=2,则OE的长度为( )A.√6B.√62C.2√2D.2√315.如图,在△ABC中,D,E,F分别是边AB,BC和AC的中点,请添加一个条件________________________,使四边形BEFD为矩形.(填一个即可)16.如图,点O是菱形ABCD对角线的交点,DE∥AC,CE∥BD,连接OE.若AC=12,BD=16,则OE的长为______.17.如图,在矩形ABCD中,对角线AC,BD相交于点O,E是边AD的中点,点FAC,连接EF.若AC=10,则EF=______.在对角线AC上,且AF=1418.如图,E是矩形ABCD边AD上一点,F,G,H分别是BE,BC,CE的中点,AF=3,则GH的长为_____.19.如图,菱形ABCD的对角线AC,BD相交于点O,OE⊥AD,垂足为点E,AC=8,BD=6,则OE的长为______.20.如图,菱形ABCD的边长为6 cm,∠BAD=60°,将该菱形沿AC方向平移2√3 cm得到四边形A′B′C′D′,A′D′交CD于点E,则点E到AC的距离为_____cm.21.如图,已知菱形ABCD的边长为2,∠DAB=60°,E为AB的中点,F为CE 的中点,AF与DE相交于点G,则GF的长等于______.22.如图,将边长为1的正方形ABCD绕点A顺时针旋转30°得到正方形AB1C1D1,则阴影部分的面积是_________.23.如图,在正方形ABCD中,点E,F分别在BC,CD上,连接AE,AF,EF,∠EAF=45°.若∠BAE=α,则∠FEC一定等于______.24.如图,E,F是正方形ABCD的对角线AC上的两点,AC=8,AE=CF=2,则四边形BEDF的周长是_______.参考答案1.C 2.C 3.C 4.B 5.B 6.C 7.B 8.B 9.B 10.C 11.D 12.C 13.C 14.B15.AB⊥BC(答案不唯一) 16.10 17.52 18.3 19.12520.221.√19422.2-2√3323.2α 24.8√5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最新中小学教育资源
第23讲 特殊平行四边形
基础满分 考场零失误
1.(2018·滨州)下列命题,其中是真命题的为()
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
2.(2018·天津,11,3分)如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上
的一个动点,则下列线段的长等于AP+EP最小值的是()
A.ABB.DE
C.BDD.AF
3.(2018·孝感)如图,菱形ABCD的对角线AC,BD相交于点O,AC=10,BD=24,则菱形ABCD的周
长为()
A.52B.48
C.40D.20
4.(2018·贵州贵阳,5,3分)如图,在菱形ABCD中,E是AC的中点,EF∥CB,交AB于点F,如果
EF=3,那么菱形ABCD的周长为()
A.24B.18C.12D.9
最新中小学教育资源
5.(2018·四川成都,14,4分)如图,在矩形ABCD中,按以下步骤作图:①分别以点A和C为圆
心,以大于AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,
则矩形的对角线AC的长为.
6.(2018·咸宁)如图,将正方形OEFG放在平面直角坐标系中,O是坐标原点,点E的坐标为
(2,3),则点F的坐标为.
7.(2018·盐城)在正方形ABCD中,对角线BD所在的直线上有两点E、F满足BE=DF,连接
AE,AF,CE,CF,如图所示.
(1)求证:△ABE≌△ADF;
(2)试判断四边形AECF的形状,并说明理由.
8.(2018·金华节选)在Rt△ABC中,∠ACB=90°,AC=12,点D在直线CB上,以CA,CD为边作矩
形ACDE,直线AB与直线CE,DE的交点分别为F,G.
如图,点D在线段CB上,四边形ACDE是正方形.
(1)若点G为DE的中点,求FG的长;
(2)若DG=GF,求BC的长.
最新中小学教育资源
能力升级 提分真功夫
9.(2018·山西适应性)如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接
AE,BF,AE与BF交于点G.下列结论错误的是()
A.AE=BFB.∠DAE=∠BFC
C.∠AEB+∠BFC=90°D.AE⊥BF
10.(2018·山西百校联考三)如图,在矩形ABCD中,边AB的长为,∠ABE=30°,将△ABE沿
BE折叠后点A的对应点A'恰好落在矩形的对角线BD上,则边BC的长为()
A.2
11.(2018·太原二模)如图,以正方形ABCD的边CD为边向正方形ABCD外作等边△CDE,AC与
BE交于点F,则∠AFE的度数是()
A.135°B.120°C.60°D.45°
