初三数学第一章证明测试题
北师大版数学九年级上册课本答案

北师大版数学九年级上册课本答案【篇一:北师版九年级数学上册第一章测试卷(含答案)】卷满分120分考试时间120分钟)一、选择题(共10小题,每小题3分,计30分)1、下列各组图形中,是全等三角形的一组是()a.底边长都为15cm的两个等腰三角形b.腰长都为15cm的两个等腰三角形d.边长为12cm的两个等边三角形2、等腰三角形的周长为13,其中一边长为3,则该等腰三角形的底边长为()a.7b.3c.7或3d.53、一个三角形如果有两边的垂直平分线的交点在第三边上,那么这个三角形是()a.等腰三角形b.等边三角形c.直角三角形d.等腰直角三角形4、用反证法证明命题“一个三角形中不能有两个角是直角”,应先假设这个三角形中()a.有两个角是直角b.有两个角是钝角c.有两个角是锐角d.一个角是钝角,一个角是直角6、如图1-2,在一次强台风中一棵大树在离地面5m处折断倒下,倒a.10mb.15mc.25md.30mcba d 图1-1图1-27、下列命题①对顶角相等②如果三角形中有一个角是钝角,那么另外两个角是锐角③若两直线平行,则内错角相等④三边都相等的三角形是等边三角形。
其中逆命题正确的有()a.①③b.②④c.①②d.③④8、如图1-3(1)在△abc中,d、e分别是ab,ac的中点,将△ade沿线段de向下折叠,得到图形1-3(2),下列关于图(2)的四个结论中,一定不成立的是()c.△dba是等腰三角形d.de∥bce c 图1-3 b c (2)(1) aa.1b.2c.3d.4be aa c图1-4图1-5二、填空题(共6小题,每小题3分,计18分)11、已知三条不同的直线a,b,c在同一平面内,下列四个命题:①如果③如果a∥b,a⊥c,那么b⊥c;②如果b∥a,c∥a,那么b∥c;b⊥a,c⊥a,那么b⊥c;④如果b⊥a,c⊥a,那么b∥c 其中属于真命题的是(填写所有真命题的序号)12、一个三角形三边之比为2:5:3,这个三角形的形状是13、把“同角的余交相等”改写成“如果??,那么??”的形式为cd=3,则ab的长度为15、如图1-7,p是正方形abcd内一点,将△abp绕点b顺时针方向旋转能与△cbp?重合,若pb=3,则pp?的长度为a p dbd b cc n c a b ?图1-6 图1-7图1-8三、解答题(共6小题,计72分,解答应写过程)ad图1-918、(10分)已知:如图1-10,de为△abc的边ab的垂直平分线,m d cd为△abc的外角平分线,与de交于点d,dm⊥bc的延长线于点m,dn⊥ac于点n,求证:an=bm。
苏科版九年级上册第一单元《图形与证明》小结+测试题

苏教版数学九年级(上)第一章知识点归纳总结1.1 等腰三角形的性质定理:等腰三角形的顶角平分线、底边上的中线、底边上的高互相重合(简称“三线合一”)。
等腰三角形的两底角相等(简称“等边对等角”)。
等腰三角形的判定定理:如果一个三角形的两个角相等,那么这两个角所对的边也相等(简称“等角对等边”)。
1.2 直角三角形全等的判定定理:斜边和一条直角边对应相等的两个直角三角形全等(简称“HL”)。
角平分线的性质:角平分线上的点到这个角的两边的距离相等。
角平分线的判定:角的内部到角的两边距离相等的点,在这个角的平分线上。
直角三角形中,30°的角所对的直角边是斜边的一半。
1.3 平行四边形的性质与判定:定义:两组对边分别平行的四边形是平行四边形。
定理1:平行四边形的对边相等。
定理2:平行四边形的对角相等。
定理3:平行四边形的对角线互相平分。
判定——从边:1两组对边分别平行的四边形是平行四边形。
2一组对边平行且相等的四边形是平行四边形。
3两组对边分别相等的四边形是平行四边形。
从角:两组对角分别相等的四边形是平行四边形。
对角线:对角线互相平分的四边形是平行四边形。
矩形的性质与判定:定义:有一个角的直角的平行四边形是矩形。
定理1:矩形的4个角都是直角。
定理2:矩形的对角线相等。
定理:直角三角形斜边上的中线等于斜边的一半。
判定:1有三个角是直角的四边形是矩形。
2对角线相等的平行四边形是矩形。
菱形的性质与判定:定义:有一组邻边相等的平行四边形是菱形。
定理1:菱形的4边都相等。
定理2:菱形的对角线相互垂直,并且每一条对角线平分一组对角。
判定:1四条边都相等的四边形是菱形。
2对角线互相垂直的平行四边形是菱形。
正方形的性质与判定:正方形的4个角都是直角,4条边都相等,对角线相等且互相垂直平分,每一条对角线平分一组对角。
正方形即是特殊的矩形,又是特殊的菱形,它具有矩形和菱形的所有性质。
判定:1有一个角是直角的菱形是正方形。
【九年级】初三数学上册第一章证明期末复习试卷

【九年级】初三数学上册第一章证明期末复习试卷第一章证明(二)期末复习试卷一、知识回顾(5分钟,单独学习+演示)1.三角形全等的判定方法有,,,四种,另外直角三角形全等还有。
(用字母表示)2.等腰三角形相互重叠。
(等腰三角形的三条线在一起)。
3.直角三角形的判定方法有:(1)只有一个角的三角形是直角三角形;(2)如果一个三角形,两边的等于第三边的平方,那么这个三角形是直角三有形。
(勾股定理逆定理)4.垂直平分线上各点之间的距离相等。
5.到一条线段两个端点距离相等的点在。
6.角平分线上的点等于该角。
7.在一个角的内部,且到角的两边距离相等的点,在。
8.三角形三条边的垂直平分线相交于一点,从该点到另一点的距离相等。
9.三角形的三个角的平分线相交于一点,并且这一点到的距离相等。
二、必修基本问题(独立学习+展览)16、将下面证明中每一步的理由写在括号内:已知:如图所示,ab=BC,ad=CD求证:∠a=∠c证明:连接BD在△dab和△dcb中∵ab=bc()ad=cd()bd=bd()∴△dab≌△dcb()∴∠a=∠c()17.已知:等腰△abc,cd,be是两腰上的中线验证:CD=be18.求证:等腰三角形的底角必为锐角。
(用反证法)19.在△ ABC,我们知道∠ A.∠ B和∠ C为1:2:3,AB侧中心线CD的长度为5。
计算面积△ ABC。
20.证明:等腰三角形底边上的中点到两腰的距离相等。
(提示:要画图写已知,求证,再证明)21.众所周知,P是平面上的一个点∠ AOB平分线⊥ OA,PD⊥ 产科医生。
验证:(1)oc=cd(2) OP是CD的垂直平分线。
三.能力提高题22.如图所示△ ABC,ab=AC,ab的垂直平分线在点D处与ab相交,在点e处与AC相交。
已知△ EBC为10,AC BC=2。
求AB和BC的长度。
23.如图所示,△abc是等边三角形,d是ac的中点,延长bc到e,使ce=cd(1)用直尺和量规作图的方法,使DBE穿过D点,垂直脚是(不要写字,保持作图痕迹)(2)求证:b=e四、优生学必须回答问题24、请用下图证明勾股定理。
初三数学第一章证明测试题

初三数学第一章证明测试题学号____________姓名___________ 班级_______________得分_____________一、选择题(本题包括 8 小题)1.下列四个命题中,假命题的是( ).A .四条边都相等的四边形是菱形;B .有三个角是直角的四边形是矩形;C .对角线互相垂直平分且相等的四边形是正方形;D .一组对边平行,另一组对边相等的四边形是等腰梯形.2.如图,平行四边形ABCD 中,AB=3,BC=5,AC 的垂直平分线交AD 于E ,则△CDE 的周长是( )A .6B .8C .9D .103.如图所示,正方形ABCD 中,点E 是CD 边上一点,连接AE ,交对角线BD 于点F ,连接CF ,则图中全等三角形共有( )A .1对B .2对C .3对D .4对4.如图,将n 个边长都为1cm 的正方形按如图所示摆放,点A 1、A 2、…、A n 分别是正方形的中心,则n 个这样的正方形重叠部分的面积和为( )A .41cm 2B .4n cm 2C .41 n cm 2D .n )41( cm 2 5.在平面直角坐标系中,□ABCD 的顶点A 、B 、D 的坐标分别是(0,0),(5,0),(2,3),则顶点C 的坐标是( )A.(3,7)B.(5,3)C.(7,3)D.(8,2)6.若等腰梯形两底之差等于一腰的长,那么这个梯形一内角是( )A.︒90B.︒60C.︒45D.︒307.如图,正方形ABCD 的边长为2,点E 在AB 边上.四边形EFGB 也为正方形,设△AFC 的面积为S ,则 ( )A .S=2B .S=2.4C .S=4D .S 与BE 长度有关8.如图2,四边形ABCD 为矩形纸片.把纸片ABCD 折叠,使点B 恰好落在CD 边的中点E处,折痕为AF .若CD =6,则AF 等于 ( )(A )34 (B )33 (C )24 (D )8二、填空题(本题包括 6 小题)9.如图,在菱形ABCD 中,已知AB =10,AC =16,那么菱形ABCD 的面积为 .10.如图,在四边形ABCD 中,E 、F 、G 、H 分别是AB 、BD 、CD 、AC 的中点,要使四边形EFGH 是菱形,四边形ABCD 还应满足的一个条件是 。
九年级数学图形与证明单元试题

第一章图形与证明(二)测试题 (时间 60分钟 满分150分)一、选择题与填空(9×5′+9×6′=99′) 1、若等腰三角形底角为72 0,则顶角为( )A 、1080B 、720C 、540D 、3602、如图,将矩形ABCD 沿AE 折叠,若∠BAD′=30°,则∠AED′ 等于( )A 、30°B 、45°C 、60°D 、75°3、 正方形具有而菱形不一定具有的性质是( )A 、对角线相等B 、对角线互相垂直平分C 、对角线平分一组对角D 、四条边相等4、用两个全等的直角三角形拼下列图形:①平行四边形(不包含菱形、矩形、正方形)②矩形 ③正方形 ④等腰三角形,一定可以拼成的图形的是( )A 、①②③B 、②③④C 、①③④D 、①②④ 5、已知菱形的边长为6cm ,一个内角为600,则菱形较短对角线长是( )ED ′DCA(第2题)A 、6cm B、、3cm D、6、将边长都为1cm 的正方形按如图所示摆放,点A 1、A 2、A 3、A 4分别是正方形的中心,则前5( )A 、14B 、12C 、1D 、27、在梯形ABCD 中,AD ∥BC ,对角线AC ⊥BD ,且AC =12,BD =9.,则梯形两腰中点的连线EF 长是( ) A 、10 B 、212C 、152 D 、128、如图,正方形ABCD 中,E 、F 是对角线AC 上两点,连接BE 、BF 、DE 、DF ,则添加下列哪一个条件可以判定四边形BEDF 是菱形( )A 、∠1=∠2B 、BE =DFC 、∠EDF =600D 、AB =AF9、如图,在梯形ABCD 中,AB ∥CD ,中位线EF 与对角线 AC 、BD交于M 、N 两点,若EF =18cm,MN=8cm,则AB 的长等于( ) A 、10cm B 、13cmFCEDBA 12(第8题图)ADCF BEMN(第9题图)D(第11题图)C、20cmD、26cm10、写出等腰梯形的两个性质,。
初三数学 第一章证明(二)测试题(
培训方案建议书尊敬的XXX公司:感谢您对我们公司的信任和支持。
根据您提供的任务名称,我们为您提供以下培训方案建议书,以满足您的需求。
一、背景和目标1.1 背景随着市场竞争的日益激烈,员工的培训和发展成为提高企业竞争力的重要因素。
为了适应公司发展的需要,提高员工的综合素质和能力,培训方案的制定变得尤为重要。
1.2 目标本培训方案的目标是提供全面的培训计划,以帮助员工掌握相关技能和知识,提高工作效率和质量,促进个人和组织的发展。
二、培训内容和方法2.1 培训内容根据公司的需求和员工的现状,我们建议开展以下培训内容:- 培训课程一:领导力培训通过培训员工的领导力技能,提高他们的团队管理能力和决策能力,从而更好地应对工作中的挑战。
- 培训课程二:沟通与协作培养员工良好的沟通和协作能力,提高团队合作效率,增进员工之间的理解和信任。
- 培训课程三:销售技巧培训培养员工的销售技巧和客户服务意识,提高销售业绩和客户满意度。
- 培训课程四:创新与创业培训培养员工的创新思维和创业精神,激发员工的创造力和创新能力,推动企业的创新发展。
2.2 培训方法为了提高培训效果,我们建议采用多种培训方法的结合:- 理论讲授:通过专业讲师的讲解,向员工传授相关的理论知识和技能。
- 实践演练:通过案例分析、角色扮演等方式,让员工在实际操作中学习和应用所学知识。
- 小组讨论:通过小组讨论的形式,促进员工之间的交流和学习,共同解决问题。
三、培训计划和预算3.1 培训计划我们建议将培训分为多个阶段进行,并制定详细的培训计划,确保培训的顺利进行。
具体的培训计划将根据公司的实际情况和员工的需求进行调整和细化。
3.2 培训预算根据培训内容和方法的复杂程度,我们初步估计培训预算为XXX万元。
具体的费用将根据培训的规模、时长和参与人数进行细化。
四、培训评估和效果监控为了确保培训的有效性和持续改进,我们建议进行培训评估和效果监控:- 培训评估:通过问卷调查、反馈收集等方式,评估培训的满意度和效果,及时发现问题并进行改进。
九年级(上)数学单元测试卷--第一章-证明(二)
九年级(上)数学单元测试卷--第一章-证明(二)本页仅作为文档页封面,使用时可以删除This document is for reference only-rar21year.March2九年级(上)数学单元测试卷 第一章 证明(二)(试卷满分为120分,考试时间为120分钟.)一、选择题(本大题共10小题,每小题3分,共30分)1.已知等腰三角形的两边长分别为5㎝、2㎝,则该等腰三角形的周长是( )A .7㎝B .9㎝C .12㎝或者9㎝D .12㎝2.如图,加条件能满足AAS 来判断⊿ACD ≌⊿ABE 的条件是( )A .∠AEB = ∠ADC ,∠C = ∠D B .∠AEB = ∠ADC , CD = BE C .AC = AB , AD = AE D .AC = AB , ∠C =∠B3.已知△ABC 的三边长分别是6cm 、8cm 、10cm ,则△ABC 的面积是 ( ) A.24cm 2B.30cm 2C.40cm 2D.48cm 24.到△ABC 的三个顶点距离相等的点是△ABC 的( )A.三边中线的交点B.三条角平分线的交点C.三边上高的交点D.三边的垂直平分线的交点5.△ABC 中,∠A ∶∠B ∶∠C=1∶2∶3,若BC=2,则AB 等于( )A.1B. 2C.4D.326、在下列条件中:①∠A+∠B=∠C ,②∠A ∶∠B ∶∠C=1∶2∶3,③∠A=90°-∠B , ④∠A=∠B=12 ∠C 中,能确定△ABC 是直角三角形的条件有( ) A 、1个 B 、2个 C 、3个 D 、4个7.如图,△ABC 中,AB=AC ,点D 在AC 边上,且BD=BC=AD ,则∠A 的度数为( )A.30°B.36°C.45°D.70°8.如图,△ABC ≌△AEF ,AB =AE ,∠B =∠E ,则对于结论①AC =AF .②∠FAB =∠EAB ,③EF =BC ,④∠EAB =∠FAC ,其中正确结论的个数是( )A.1个 B.2个 C.3个 D.4个9.如图,等边△ABC 中,BD=CE ,AD 与BE 相交于点P ,则∠APE 的度数是( )A.45°B.55°C.60°D.75° 10.已知:如图,AB=AC,∠A=36°,AB的垂直平分线交AC于D,则下列结论:①∠C=72°;②BD是∠ABC的平分线;③△ABD是等腰三角形;④△BCD是等腰三角形,其中正确的有( )A.1个 B.2个 C.3个 D.4个7题图 8题图 9题图10题图二、填空题(本大题共8小题,每小题3分,共24分)11.“等边对等角”的逆命题是______________________________.12.已知⊿ABC 中,∠A = 090,角平分线BE 、CF 交于点O ,则∠BOC = 13.在△ABC 中,∠A=40°,AB=AC ,AB 的垂直平分线交AC 与D ,则∠DBC 的度数为 .14.在△ABC 中,AB=5cm ,BC=6cm ,BC 边上的中线AD=4cm ,则∠ADC 的度数是 度.15.⊿ABC 中,∠C= 090,∠A = 030,AC=32,则AB 边上的中线CD= 。
初三数学(上册)《第一章证明(二)》单元测试题(三)
初三数学(上册)《第一章证明(二)》单元测试题(三)一、填空题1.已知:如图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF=.(第1题图) (第5题图) (第6题图)2.在直角三角形中,如果一个锐角为30°,而斜边与较小直角边的和为12,那么斜边长为3.等腰直角三角形中,若斜边为16,则直角边的长为.4.“直角三角形两条直角边的平方和等于斜边的平方”的逆定理是。
5.如图,ED为△ABC的AC边的垂直平分线,且AB=5,△BCE的周长为8,则BC=. 6.如图,在△ABC中,∠C=90°,∠B=15°,AB的垂直平分线交BC于D,交AB于E,若DB=10cm,则AC=.7.在△ABC中,AB=AC,∠A=58°,AB的垂直平分线交AC于N,则∠NBC = . 8.正三角形的边长为a,则它的面积为。
9.命题“线段垂直平分线上的点到这条线段两个端点的距离相等”的条件是,结论是.二、选择题10.至少有两边相等的三角形是( )A.等边三角形B.等腰三角形C.等腰直角三角形D.锐角三角形11.以下命题中,正确的是( )A.一腰相等的两个等腰三角形全等.B.等腰三角形底边上的任意一点到两腰距离之和都大于一腰上的高C.有一角相等和底边相等的两个等腰三角形全等.D.等腰三角形的角平分线、中线和高共7条或3条.12.一架2.5 m长的梯子斜立在一竖直的墙上,这时梯足距离墙底端0.7 m,如果梯子的顶端沿墙下滑0.4 m,那么梯那么梯足将滑( )A.0.9 m B.1.5 m C.0.5 m D.0.8 m13.三角形中,若一个角等于其他两个角的差,则这个三角形是( )A.钝角三角形B.直角三角形C.锐角三角形D.等腰三角形14.已知△ABC中,AB=AC,AB的垂直平分线交AC于D,△ABC和△DBC的周长分别是60 cm和38 cm,则△ABC的腰和底边长分别为( )A.24 cm和12 cm B.16 cm和22 cm C.20 cm和16 cm D.22 cm和16 cm 15.下列定理中,没有逆定理的是( )A.直角三角形的两个锐角互余B.等腰三角形两腰上的高相等C.全等三角形的周长相等D.有一个锐角对应相等的两直角三角形相似16.如图,△ABC中,AC=BC,直线l经过点C,则( )A.l垂直AB B.l平分AB C.l垂直平分AB D.不能确定三、解答题17.已知:如图,等腰三角形ABC中,AC=BC,∠ACB=90°,直线l经过点C(点A、B 都在直线l的同侧),AD⊥l,BE⊥l,垂足分别为D、E.求证:DE=AD+BE。
(数学试卷九年级)第一章证明(二)单元测试题(A)
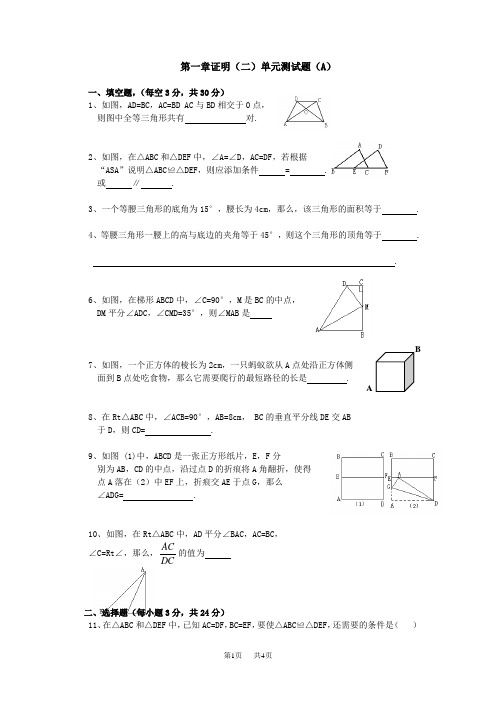
第一章证明(二)单元测试题(A )一、填空题,(每空3分,共30分)1、如图,AD=BC AC=BD A 与BD 相交于则图中全等三角形共有 2、如图,在△ ABC ffiA DEF 中,/ A=Z D, AC=DF 若“ASA 说明△ ABC^A DEF 则应添加条件_「 或 //________ . 3、 一个等腰三角形的底角为 15。
,腰长为4cm 那么,该三角形的面积等 于 .4、 等腰三角形一腰上的高与底边的夹角等于45°,则这个三角形的顶角等于 .5、命题“如果三角形的一个内角是钝角,则其余两个内角一定是锐角”的逆命 题是6、如图,在梯形 ABCD 中, Z C=90,M 是BC 的中点,/ DM 平分/ ADC Z CMD=35,贝UZ MAB 是7、如图,一个正方体的棱长为2cm 一只蚂蚁欲从A 点处沿正方体测 面到B 点处吃食物,那么它需要爬行的最短路径的长是 ___________________ _&在 Rt △ ABC 中, Z ACB=90,AB=8crp BC 的垂直平分线 DE 交 AB 于D,贝卩CD= .点:A9、如图(1)中,ABCD!—张正方形纸片,E, F分别为AB CD的中点,沿过点D的折痕将A角翻折, 点A落在(2)中EF上,折痕交AE于点G那么Z ADG= .10、如图,在Rt △ ABC中,AD平分/ BAC AC=BC/ C=RtZ,那么,-AC的值为DC二、、选择题(每小题3分,共24分)11、在厶ABC^P^ DEF中,已知AC=DF BC=EF要使△ ABC^A DEF还需要的条件是()A、/ A=Z D B 、/ C=Z F C 、/ B=Z E D 、/ C=Z D12、下列命题中是假命题的是()A、两条中线相等的三角形是等腰三角形B、两条高相等的三角形是等腰三角形C、两个内角不相等的三角形不是等腰三角形D三角形的一个外角的平分线平行于这个三角形的一边,则这个三角形是等腰三角形13、如图,已知AB=AC BE=CE D是AE上的一点,则下列结论不一定成立的是()A、/ 仁/ 2 B 、AD=DEC、BD=CD D 、/ BDE/ CDE14、如图,已知AC和BD相交于O点,AD// BC,过O「;—AD=BC 任作一条直线分别交AD BC于点E、F,则下列结论:②OE=OF③AE=CF④OB=OD其中成立的个数是(A、1 B 、2 C 、3 D 、415、若等腰三角形的周长是18, 一条边的长是5,则其他两边的长是()A、5,8 B 、6.5,6.5 C 、5,8或6.5,6.5 D 、8,6.516、下列长度的线段中,能构成直角三角形的一组是()A、■揮3, /$4,■- / 5 B 、6,7,8 ;C 12,25,27 ;D 、2 3, 2 5, 4 217、如图,AC=AD BC=BD则下列结果正确的是()22. (10分)折叠矩形纸片ABCD 先折出折痕(对角线)BD ,再折叠AD 边与对AB=2 BC=1 求 AG 的长.23. (10分) 如图,在 BAC 中,AD 是BC 边上的中线, AB AC 。
初三数学第一章测试题(含答案)
初三数学第一章测试题(含答案)一、选择题(每小题2分,共30分)1. 设 a+b=5,a-b=3,那么a和b的值分别是多少?A. a=4, b=1B. a=3, b=-2C. a=2, b=3D. a=1, b=4 (答案:A)2. 已知正方形面积为36平方厘米,那么正方形的边长是多少?A. 4厘米B. 6厘米C. 9厘米D. 12厘米 (答案:C)3. 一架飞机从A地出发,每小时飞行400千米,飞了2个小时后到达B地,B地与A地相距多少千米?A. 400千米B. 600千米C. 800千米D. 1000千米 (答案:B)4. 有一个长为8厘米的木棍,现需切割成5段,每段长为多少厘米?A. 1厘米B. 2厘米C. 4厘米D. 8厘米 (答案:C)5. 如果80%的学生喜欢数学,且班级共有40名学生,那么班级有多少名学生喜欢数学?A. 8名学生B. 16名学生C. 32名学生D. 64名学生 (答案:B)二、填空题(每空2分,共20分)1. 已知一个数字是3的倍数,则这个数字最小是___。
答案:32. 圆的半径与直径的关系是___。
答案:半径与直径的关系是直径的两倍。
3. 在一部小说中,第一天读了全书的1/4,第二天读了余下的3/4中的一半,剩下的20页需要第三天才能读完,这本小说共有___页。
答案:80页4. 一年有___个月。
答案:12个月5. 设正方形的边长为x,那么它的周长是___。
答案:4x三、解答题(每题10分,共30分)1. 请用代数解方程:已知一个数的五倍减去2等于13,求这个数。
答案:令这个数为x,则方程为5x - 2 = 13,解得 x = 3。
2. 一个数的1/5等于15,这个数是多少?答案:令这个数为x,则方程为x/5 = 15,解得 x = 75。
3. 请用文字说明如何计算一个长方体的体积。
答案:长方体的体积可以通过将长、宽、高相乘来计算,公式为 V = 长 * 宽 * 高。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初三数学第一章证明测试题
学号____________姓名___________ 班级_______________得分_____________
一、选择题(本题包括 8 小题) 1.下列四个命题中,假命题的是(). A.四条边都相等的四边形是菱形; B.有三个角是直角的四边形是矩形;
C.对角线互相垂直平分且相等的四边形是正方形;
D.一组对边平行,另一组对边相等的四边形是等腰梯形. 2.如图,平行四边形ABCD中,AB=3,BC=5,AC的垂直平分线交AD于E,则△CDE的周长是()
A.6 B.8 C.9 D.10
3.如图所示,正方形ABCD中,点E是CD边上一点,连接AE,交对角线BD于点F,连接CF,则图中全等三角形共有() A.1对 B.2对 C.3对 D.4对
4.如图,将n个边长都为1cm的正方形按如图所示摆放,点A1、A2、…、An分别是正方形的中心,则n个这样的正方形重叠部分的面积和为()
A.
41cm2
B.4ncm2 C. D.n)4
1( cm2
5.在平面直角坐标系中,□ABCD的顶点A、B、D的坐标分别是(0,0),(5,0),(2,3),则顶点C的坐标是()
A.(3,7)
B.(5,3)
C.(7,3)
D.(8,2)
6.若等腰梯形两底之差等于一腰的长,那么这个梯形一内角是()
90
60
45
30 7.如图,正方形ABCD的边长为2,点E在AB边上.四边形EFGB也为正方形,设△AFC的面积为S,则()
A.S=2 B.S=2.4 C.S=4 D.S与BE长度有关
8.如图2,四边形ABCD为矩形纸片.把纸片ABCD折叠,使点B恰好落在CD边的中点E处,折痕为AF.若CD=6,则AF等于()
(A)34 (B)33 (C)24
(D)8
二、填空题(本题包括 6 小题)
9.如图,在菱形ABCD中,已知AB=10,AC=16,那么菱形ABCD的面积为 .
10.如图,在四边形ABCD中,E、F、G、H分别是AB、BD、CD、AC的中点,要使四边形EFGH是菱形,四边形ABCD还应满足的一个条件是。
11.如图,将两张长为8,宽为2的矩形纸条交叉,使重叠部分是一个菱形,容易知道当两张纸条垂直时,菱形的周长有最小值8,那么菱形周长的最大值是.
12.如图,将矩形纸ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=3厘米,EF=4厘米,则边AD的长是___________厘米.
13.如图6,在边长为2㎝的正方形ABCD中,点Q为BC边的中点,点P为对角线AC 上一动点,连接PB、PQ,则△PBQ周长的最小值为____________㎝(结果不取近似值).
14.已知平面上四点(00)A,
,(100)B,,(106)C,,(06)D,,直线将四边形ABCD分成面积相等的两部分,则m的值为.三、证明题
15.已知:如图,平行四边形ABCD的对角线AC的垂直平分线与边AD、BC分别相交于
E 、F.求证:四边形AFCE是菱形.
16.如图,在平行四边形ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F.
(1)求证:;
(2)当BC与AF满足什么数量关系时,四边形ABFC是矩形,并说明理由.
四、综合题
17.如图,在边长为5的正方形ABCD中,点E、F分别是BC、DC边上的点,且,(1)求EC∶CF的值;
(2)延长EF交正方形外角平分线CPP于点(如图13-2),试判断AEEP与的大小关系,并说明理由;
(3)在图13-2的AB边上是否存在一点M,使得四边形DMEP是平行四边形?若存在,请给予证明;若不存在,请说明理由.
18.已知:如图①,在RtACB△中,
,,,点P由B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由A出发沿AC方向向点C匀速运动,速度为2cm/s;连接PQ.若设运动的时间为(s)t(),解答下列问题:(1)当t为何值时,PQBC∥?
(2)设AQP△的面积为y(2
cm),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使线段PQ恰好把RtACB△的周长和面积同时平分?若存在,求出此时t的值;若不存在,说明理由;
(4)如图②,连接PC,并把PQC△沿QC翻折,得到四边形,那么是否存在某一时刻t,使四边形为菱形?若存在,求出此时菱形的边长;若不存在,说明理
由.。
