初一数学含中考题412点线面体精品
初一数学《4.1点线面体》检测试试题(人教版)_题型归纳

初一数学《4.1点线面体》检测试试题(人教版)_题型归纳
5分钟训练(预习类训练,可用于课前)
1.圆锥可以看作是由一个_______旋转得到的()
A.矩形(长方形)
B.等腰梯形
C.半圆
D.直角三角形
思路解析:拿一个三角板旋转,不难得出答案?
答案:D
2.包围着几何体的是_______,面与面相交形成______,线与线相交形成_______.答案:面线点
3.数一数长方体、四面体的面数、棱数和顶点数,并填下表:
名称面数(f)顶点数(v)棱数(e)
长方形
四面体
思路解析:利用实物我们不难得到长方体、四面体的面数、棱数和顶点数.
答案:
名称面数(f)顶点数(v)棱数(e)
长方体6812
四面体446
10分钟训练(巩固类训练,可用于课后)
1.五棱柱的面有()
A.5个
B.6个
C.7个
D.8个
思路解析:棱柱有两个底面,关键数清有几个侧面?
答案:C
2.图4-1-11的图形中绕直线l旋转一周,能得到右边立体图形的是()
图4-1-11。
【整合】人教版七年级数学上册412点、线、面、体同步测试题.doc

4・1・2点、线、面、体同步测试题一、填空题1. 长方体有 ______ 个面,有 _________ 条棱,有 _______ 个顶点;圆柱有 ________ 个面,其中有 ________个平面,有 _______ 个曲面.2. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零件的表面积为______________ .3. 薄薄的硬币在桌面上转动时,看上去像球,这说明了 ______________________ •4. 将硬币的直径垂直桌面快速旋转吋,我们看到的几何体是—球 _______ •5. __________________ 如图的几何体有 个面, _______ 条棱, ___________________________ 个顶点,它是由简单的几何体 _________ 和 ___________组成的.6. ____________________________________________________ 将图中的直角三角板ABC 绕AC 边旋转一周得到的儿何体是 _____________________________________________二、选择题7. 下列现象不能体现线动成面的是()A. 用平口铲子铲去墙面上的大片污渍B.用一条拉直的细线切一块豆腐C.流星划过天空留下运动轨迹D.用木板的边缘将沙坑里的沙推平&如果一个直棱柱有12个顶点,那么它的面的个数是A. 10 C.8 D.79. 一个几何体的表面展开图如图所示,A. 四棱锥B.四棱柱C.三棱锥D.三棱柱10. 下列现象不能体现线动成面的是() A. 用平口铲子铲去墙面上的大片污渍B.9B.用一条拉直的细线切一块豆腐C.流星划过天空留下运动轨迹11 .左图屮的图形绕虚线旋转一周,可得到的几何体是()q □ v o ABC12. 下列儿何体的所有面都不是平而图形的是(A. 正方体C.圆柱13. 在球、圆锥、圆柱、棱柱屮,由曲面和平面围成的是(14. 将一个直角梯形绕直线1旋转一周可以得到如图的立体图形,这个直角梯形与直线I 的关系是()15.下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇而,这是因为()A.点动成线B.线动成面C.面动成体D.面面相交形成线16. 若一个棱柱有10个顶点,则下列说法正确的是()A.这个棱柱有4个侧面B.这个棱柱有5个侧面C.这个棱柱的底面是十边形D.这个棱柱是一个十棱柱三、解答题17. 航天飞机拖着“长长的火焰二我们用数学知识可解释为点动成线.用数学知识解释下列现象:(1) 一只小蚂蚁爬行留下的路线可解释为 _________________________ ・(2) _______________________________________________________ 电动车车辐条运动形成的图形可解释为 .18.观察如图所示的图形,写出下列问题的结果:(1) __________________ 这个图形的名称是 ;(2) ______________ 这个儿何体有 _____________ 个面,有 ____________ 个底面,有 _______ 个侧而,底而是 形,侧面是_______ 形.(3)侧血的个数与底血多边形的边数有什么关系?)B.圆锥 D.球 A. 球和圆锥 B. 球和圆柱C. 圆锥和圆柱D. 圆柱和棱柱图V 中的几何体由几个面围成?面与面相交成几条线?它们是直的还是曲的?20.如图所示,长方形绕虚线旋转一周后,形成的图形是什么?旋转半周呢?19 •如图所示:■Z参考答案一、填空题1. 长方体有6 _______ 个面,有_12 ______ 条棱,有—8_个顶点;圆柱有―3_个面,其中有 ___ 2 ___ 个平面,有 ______ 1_个曲面.2. 从棱长为2的正方体毛坯的一角,挖去一个棱长为1的小正方体,得到一个如图所示的零件,则这个零3. 薄薄的硬币在桌面上转动时,看上去像球,这说明了 ____________ .4. 将硬币的直径垂直桌面快速旋转时,我们看到的几何体是 球____ 16_条棱,—9—个顶点,它是由简单的几何体—四棱锥. 和_四棱柱______ 组成的.6. ________________________________________________________ 将图中的直角三角板ABC 绕AC 边旋转一周得到的儿何体是—圆锥 _____________________________________二、选择题7. 下列现象不能体现线动成面的是(C ) A. 用平口铲子铲去墙面上的大片污渍 B. 用一条拉直的细线切一块豆腐 C. 流星划过天空留下运动轨迹 D. 用木板的边缘将沙坑里的沙推平8. 如果一个直棱柱有12个顶点,那么它的面的个数是 (C ) A.10 C.8 D.79. 一个几何体的表面展开图如图所示,A. 四棱锥B. 四棱柱C. 三棱锥D. 三棱柱5.如图的几何体有9 个面,B.910.下列现象不能体现线动成血的是(C )A. 用平口铲子铲去墙面上的大片污渍B. 用一条拉直的细线切一块豆腐C. 流星划过天空留下运动轨迹 11. 左图中的图形绕虚线旋转一周,可得到的几何体是(C )q □ v 9 □AB CD12. 下列几何体的所有而都不是平而图形的是(D )A.正方体B.圆锥C.圆柱D.球13. 在球、圆锥、圆柱、棱柱屮,由曲面和平面围成的是(C )A.球和圆锥B.球和圆柱C.圆锥和圆柱D.圆柱和棱柱14. 将一个直角梯形绕直线1旋转一周可以得到如图的立体图形,这个直角梯形与直线1的关系是(15. 下雨时,司机会打开雨刷器,雨刷器在运动时会形成一个扇面,这是因为( B ) A.点动成线B.线动成面 C •面动成体 D.面面相交形成线 16. 若一个棱柱有10个顶点,则下列说法正确的是(B )A. 这个棱柱有4个侧而B. 这个棱柱有5个侧面C. 这个棱柱的底面是十边形D.这个棱柱是一个十棱柱三、解答题17. 航天飞机拖着“长长的火焰二我们用数学知识可解释为点动成线.用数学知识解释下列现象: (1)_只小蚂蚁爬行留下的路线可解释为 点动成线.(2)电动车车辐条运动形成的图形可解释为 __________________ .18.观察如图所示的图形,写出下列问题的结果:(1) 这个图形的名称是六棱柱 ;(2) 这个几何体有—个面•有2个底面•有—个侧面,底面是六边 形,侧面是 形.(3) 侧面的个数与底而多边形的边数有什么关系? 解:(3)侧面的个数与底面多边形的边数相等.长方19 •如图所示:图V 中的几何体由几个面围成?面与面相交成几条线?它们是直的还是曲的?解:图V 屮的几何体有2个面,其屮一个是平面,一个是曲面,面与面相交有1条线,是一条曲线.20 •如图所示,长方形绕虚线旋转一周后,形成的图形是什么?旋转半周呢?LI解:长方形绕图示虚线旋转一周后形成的图形是圆柱,旋转半周所形成的图形也是圆柱.d ©③,① o 1。
人教版七年级数学上册点线面体同步测试(含答案)

人教版七年级数学上册4.1.2 点线面体同步测试(含答案)一、单选题1.下列几何图形与相应语言描述相符的个数有()A.1 个B.2 个C.3 个D.4 个2.如图,用一个平面去截正方体截面形状不可能...为下图中的()A.B.C.D.3.观察下图,把左边的图形绕着给定的直线旋转一周后,可能形成的立体图形是()A.B.C.D.4.如图,用一个平行于圆锥底面的平面截圆锥,截面的形状是()A.B.C.D.5.用一个平面去截圆柱体,则截面形状不可能是()A.正方形B.三角形C.长方形D.圆6.如图,有一个棱长是4cm的正方体,从它的一个顶点处挖去一个棱长是1cm的正方体后,剩下物体的表面积和原来的表面积相比较()A.变大了B.变小了C.没变D.无法确定变化7.用一个平面去截正方体,截面的形状不可能是()A.四边形B.五边形C.六边形D.七边形8.十个棱长为a的正方体摆放成如图的形状,这个图形的表面积是()A.36a2B.36a C.6a2D.30a29.用一个平面去截圆柱体,则截面形状不可能是()A.梯形B.正方形C.长方形D.圆10.用一个平面去截下列四个几何体,可以得到三角形截面的几何体有()A.1个B.2个C.3个D.4个二、填空题11.如图,正三棱柱的底面周长为9,截去一个底面周长为3的正三棱柱,所得几何体的俯视图的周长是.12.一个长方形绕着它的一条边旋转一周,所形成的几何体是.13.用个平面去截下列几何体:①球体、②圆锥、③圆柱、④正三枝柱、⑤长方体,得到的截面形状可能是三角形的有(写出正确的序号).14.若三棱柱的高为6 cm,底面边长都为5 cm,则三棱柱的侧面展开图的周长为cm,面积为cm2.15.如图,正方体的棱长为a,沿着共一个顶点的三个正方形的对角线裁截掉一个几何体之后,截面△ABC的面积=.三、解答题16.如图所示为一个正方体截去两个角后的立体图形,如果照这样截取正方体的八个角,则新的几何体的棱有多少条?请说明你的理由.17.如图所示,一个长方体的长.宽.高分别是10cm,8cm,6cm,有一只蚂蚁从点A 出发沿棱爬行,每条棱不允许重复,则蚂蚁回到点 A 时,最多爬行多远?并把蚂蚁所爬行的路线用字母按顺序表示出来.18.图中的立体图形是由哪个平面图形旋转后得到?请用线连起来.19.探究:有一弦长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:方案一:以较长的一组对边中点所在直线为轴旋转,如图①;方案二:以较短的一组对边中点所在直线为轴旋转,如图②.(1)请通过计算说明哪种方法构造的圆柱体积大;(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?20.长和宽分别是4cm和2cm的长方体分别沿长、宽所在直线旋转一周得到两个几何体,哪个几何体的体积大?为什么?21.下图是长方体的表面展开图,将它折叠成一个长方体.(1)哪几个点与点N重合?(2)若AE=CM=12cm,LE=2cm,KL=4cm,求这个长方体的表面积和体积. 22.在一块长为7x+5y,宽为5x+3y的长方形铁片的四个角都剪去一个边长为x+y的小正方形,然后折成一个无盖的盒子,求这个盒子的表面积(用含x、y的代数式表示).23.有3个棱长分别是3cm,4cm,5cm的正方体组合成如图所示的图形.其露在外面的表面积是多少?(整个立体图形摆放在地上)24.将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4厘米,宽为3厘米的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?答 案1.C 2.A 3.C 4.B 5.B 6.C 7.D 8.A 9.A 10.B 11.8 12.圆柱体13.②④⑤ 14.42;90 15.√3a 216.解:∵一个正方体有12条棱,一个角上裁出3条棱,即8个角共3×8条棱,∴12+3×8=36条.故新的几何体的棱有36条17.解:由于不能重复且最后回到点 A 处,那么经过的棱数便等于经过的顶点数,当走的路线最长时必过所有顶点,则选择合理的路线时尽可能多地经过长为 10CM 的棱即可. 10×4+8×2+6×2=68(cm) ,所以最多爬行 68CM .路线举例: A →B →C →D →H →G →F →E →A . 18.解:如图.19.解:(1)方案一:π×32×4=36π(cm 3),方案二:π×22×6=24π(cm 3),∵36π>24π,∴方案一构造的圆柱的体积大;(2)方案一:π×(52)2×3=754π(cm 3), 方案二:π×(32)2×5=454π(cm 3), ∵754π>454π, ∴方案一构造的圆柱的体积大;(3)由(1)、(2),得以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大.20.【解答】解:分两种情况:①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).∵16π<32π,∴绕宽所在的直线旋转一周得到圆柱体积大.21.解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;(2)若AE=CM=12cm,LE=2cm,KL=4cm,求这个长方体的表面积和体积.解:由AE=CM=12cm,KL=4cm,可得CH=CM-LK=12-4=8cm,长方体的表面积;2×(8×4+2×4+2×8)=112cm2;体积:4×8×2=64cm3.(1)解:结合图形可知,折叠成一个长方体后,与字母N重合的点有2个:点F和点J;(2)解:由AE=CM=12cm,KL=4cm,可得CH=CM-LK=12-4=8cm,长方体的表面积;2×(8×4+2×4+2×8)=112cm2;体积:4×8×2=64cm3.22.解:由题意,得(7x+5y)(5x+3y)−4(x+y)2=35x2+21xy+25xy+15y2−4(x2+2xy+y2)=35x2+46xy+15y2−4x2−8xy−4y2 =31x2+38xy+11y2.∴这个盒子的表面积为(31x2+38xy+11y2) .23.解:露在外面的表面积:5×5+4×(3×3+4×4+5×5)=25+4×(9+16+25)=225cm2.24.解:绕长所在的直线旋转一周得到圆柱体积为:π×32×4=36πcm3.绕宽所在的直线旋转一周得到圆柱体积:π×42×3=48πcm3。
【人教版数学(2024年)七年级上册同步练习】 6.1.2点线面体(含答案)

【人教版数学(2024年)七年级上册同步练习】6.1.2点线面体一、填空题1.夜晚的流星划过天空时留下一道明亮的光线,由此说明了的数学事实.2.汽车的雨刷把玻璃上的雨水刷干净,是运用了的原理.二、单选题3.在朱自清的《春》中描写春雨“像牛毛、像花针、像细丝,密密麻麻地斜织着”的语句,这里把雨看成了线,这说明了()A.点动成线B.线动成面C.面动成体D.两点确定一条直线4.如图,尉迟恭单鞭救主图罐是南宁博物馆的镇馆之宝,下列平面图形绕轴旋转一周能形成这个瓷罐形状的是()A.B.C.D.5.下图左边的几何体可由()图形绕虚线旋转而成.A.B.C.D.6.如图所示的平面图形绕直线I旋转一周,可以得到的立体图形是()A.B.C .D.7.如图所示的花瓶中,的表面,可以看作由所给的平面图形绕虚线旋转一周形成的.A .B.C.D.三、解答题8.如图所示,有一个长为4cm、宽为3cm的长方形.(1)若分别绕它们的相邻两边所在的直线旋转一周,会得到不同的几何体,请你画出这两个几何体.(2)在你画出的这两个几何体中,哪个体积大?答案解析部分1.【答案】点动成线【知识点】点、线、面、体及之间的联系2.【答案】线动成面【知识点】点、线、面、体及之间的联系3.【答案】A【知识点】点、线、面、体及之间的联系4.【答案】C【知识点】点、线、面、体及之间的联系5.【答案】A【知识点】立体图形的初步认识;点、线、面、体及之间的联系6.【答案】C【知识点】点、线、面、体及之间的联系7.【答案】B【知识点】点、线、面、体及之间的联系8.【答案】【解答】解:(1)如图所示:(2)绕4cm长的边旋转一周所得圆柱的体积=π×33×4=36π;绕3cm长的边旋转一周所得圆柱的体积=π×42×3=48π.答:第二个圆柱体的体积大.【知识点】点、线、面、体及之间的联系。
七年级数学上册41几何图形412点线面体练习新版新人教版128

, 旋转半周所形成的图形也是圆柱 .
创新应用
16. 解 (1) 四面体的棱数为 6; 正八面体的顶点数为 6; 关系式为 V+F-E=2.
(2) 由题意得 , F-8+F- 30=2,
解得 F=20.
(3) 因 为有 24 个顶 点 , 每 个 顶点 处 都有 3 条棱 , 两 点确 定一 条 直线 , 所 以 共有
成, 且有 24 个顶点 , 每个顶点处都有 3 条棱 , 设该多面体外表三角形的个数为 x 个 , 八边形的
个数为 y 个, 求 x+y 的值 .
夯基达标 1. D
答案与解析
4
2. D 要能想象到它转动后的形状 , 面动成体 . 一个梯形以底所在直线为轴旋转 , 上、下两部分
形成圆锥 , 中间形成圆柱 , 是由两个圆锥和一个圆柱组合而成 , 故应选 D.
4.1.2 点、线、面、体
1. 正四面体的顶点数和棱数分别是 (
A.3,4
B.3,6
C.4,4
) D.4,6
2. 如左下图 , 绕虚线旋转得到的实物图是 ( )
3. 下列几何体中 , 有 6 个面的几何图形有 ( )
①长方体 ; ②圆柱 ; ③四棱柱 ; ④正方体 ; ⑤三棱柱 .
A. 1 个
B. 2 个
C. 3 个
D. 4 个
4. 如果一个直棱柱有 12 个顶点 , 那么它的面的个数是 (
)
A.10
B.9
C.8
D.7
5. 下列说法正确的有 ( )
①四面体的各个面都是三角形
方体的面不可能是正方形 .
A. 1 个
B. 2 个
; ②圆柱、圆锥的底面都是圆
七年级数学点、线、面、体典型试题及答案(中考重点考点试题)

七年级数学点、线、面、体典型试题及答案(中考重点考点试题)5分钟训练(预习类训练,可用于课前)1.圆锥可以看作是由一个_______旋转得到的()A.矩形(长方形)B.等腰梯形C.半圆D.直角三角形思路解析:拿一个三角板旋转,不难得出答案答案:D2.包围着几何体的是_______,面与面相交形成______,线与线相交形成_______.答案:面线点3.数一数长方体、四面体的面数、棱数和顶点数,并填下表:名称面数(f) 顶点数(v) 棱数(e)长方形四面体答案:名称面数(f)顶点数(v)棱数(e)长方体 6 8 12四面体 4 4 610分钟训练(巩固类训练,可用于课后)1.五棱柱的面有()A.5个B.6个C.7个D.8个思路解析:棱柱有两个底面,关键数清有几个侧面答案:C2.图4-1-11的图形中绕直线l旋转一周,能得到右边立体图形的是()图4-1-11思路解析:圆锥的锥尖是由角旋转得到的,两个锥尖的几何体是由三角形旋转得到的答案:D3.______棱锥又叫四面体,它的各个面都是______形;它有______条棱,有______个顶点. 思路解析:棱锥当中,只有三棱锥有四个面答案:三三角 6 44.飞机飞行表演在空中留下漂亮的“彩带”,用数学知识解释为_______.思路解析:飞机可以看作一个点,点运动形成线.答案:点动成线5.将图4-1-12中的图形按要求分类:(1)若按柱、锥、球划分;(2)若按组成面的曲或平划分.图4-1-12思路解析:分类时一定要注意把握好特征,做到不重不漏,标准统一.答案:(1)柱体:①,③,④,⑤,⑦;锥体:②;球体:⑥(2)组成的面有曲面:②,⑥,⑦;组成的面是平面:①,③,④,⑤快乐时光繁星点点神探福尔摩斯与华生去露营,两人在繁星之下扎营睡觉.睡至半夜,福尔摩斯突然摇醒华生,问他:“华生,你看这繁星点点,作何感想?”华生:“我看见无数星光,当中可能有些像地球一样,如果真的有跟地球一样,也许会有生命存在.”“华生,你这蠢才,”福尔摩斯说:“有人偷了我们的帐篷……”30分钟训练(巩固类训练,可用于课后)1.图4-1-13所示的几何体中,不完全由平面围成的几何体是()图4-1-13思路解析:关键是分清平面与曲面,仔细观察.答案:D2.在下列立体图形中,有5个面的是()A.四棱锥B.五棱锥C.四棱柱D.五棱柱思路解析:柱体均有两个底面,锥全只有一个底面答案:A3.如图4-1-14,由左面的平面图形绕所给的直线旋转得到的几何体是()图4-1-14思路解析:面动成体,长方形绕着一边旋转形成圆柱答案:B4.如图4-1-15,第二行的图绕直线旋转一周,便能形成第一行的某个几何体,用线连一连,并指出这些几何体的名称.图4-1-15思路解析:线段旋转一周形成一个圆,长方形旋转一周形成一个圆柱,半圆旋转一周会形成球答案:(1)与C;(2)与A;(3)与B连起来.A是圆台;B是球;C是圆柱与圆锥的组合.5.在如图4-1-16所示的3×3的钉板上,能作出多少种不重复的三角形?图4-1-16思路解析:连接不在一条直线上的任意三点,均可以得到三角形,但要注意去掉其中重复的情况.答案:如图,图形是能在3×3钉板上形成的8种三角形:6.如图4-1-17,这个几何体是由几个面组成的?面与面相交成几条线?其中有几条是曲的?图4-1-17思路解析:仔细观察这个几何体,它有两个底面,三个侧面.答案:它是由5个面围成的,面与面相交成9条线,其中有2条是曲的.7.上了年纪的老大爷们常常喜欢用下面的问题来考考青年人的脑筋是不是灵活:一块长方形的桌面,锯掉了一个角,还有几个角?思路解析:长方形切去一个角,关键要考虑如何来切.答案:共分三种情况:(1)还有5个角(2)还有4个角(3)还有3个角8.以前,美国举行了一次“全美初级学术能力测验”,有83万中学生参加,其中有这样一道测验题:有一个三棱锥和一个正四棱锥,它们的棱长都相等,问它们重叠一个侧面后,还露出几个面?标准答案是:7个面,因为两棱锥分开时共有4+5=9(个)面.当它们重叠一个面以后,有两个面被遮住了.可是一位17岁的中学生丹尼尔的回答是5个面,阅卷者当然判他答错.丹尼尔为了证实自己的结论是对的,回家后做了一个模型,当他将这个模型交给老师时,老师不得不承认丹尼尔对了.你知道丹尼尔是怎么做的吗?答案:如图:9.用八根火柴摆成“燕鱼”图形(如图4-1-18),请移动三根火柴,使它头向右.图4-1-18答案:如图:。
七年级数学上册412点线面体习题新版新人教版

(1)如果将图中①~⑤的平面图形绕虚线旋转一周,可 以得到I~Ⅴ的几何体,请你把有对应关系的平面图形 与几 Ⅴ 的 几 何 体 中 , 有 顶 点 的 几 何 体 是 Ⅰ__、__Ⅱ__、__Ⅲ,没有顶点的几何体是__Ⅳ__、__Ⅴ__. (3)图Ⅴ中的几何体由几个面围成?面与面相交成几条 线?它们是直的还是曲的? Ⅴ中的几何体有2个面,其中一个是平面,一个是曲 面,面与面转而成的立体图形 8.(娄底中考)如图,长方形绕它的一条边MN所在的直 线旋转一的平面图形绕轴旋转一周,库文档分 享
13.下列有关圆柱、圆锥相同点和不同点的描述,错 误的是( C ) A.围成圆柱、圆锥的面都有曲面 B.两者都有一个面是圆形的 C.两者都有顶直线l旋转一周可以得到如图的 立体图形,这个直角梯形与直线l的关系是( B )
图1
A.空心圆柱 C.空心球
图2 ____个面,有____1_2___条棱,有 ____8____个顶点;圆柱有____3____个面,其中有 ____2____个平面,有____1____个曲面. 6.旋转门旋转一周,形成了一个圆柱,这说明了 __面_一个多面体的一个面是多边形,其 余各面是有一个公共顶点的三角形,那么这个多面体叫 做棱锥.如图是一个四棱柱和一个六棱锥,它们都有12 条棱.下列棱柱中和九棱锥的棱数相等的是( B ) A.五棱柱 B.六棱柱 C.七棱柱 D.八棱柱
10.将图中的直角三角板ABC绕AC边旋转一周得到的 几何列立体图形中,面数最多的是( C )
A.四棱锥
B.长方体
C.五棱柱
D.六面体
12.下列几何体的所有面都不是平面图形的是( D )
A.正方体
B.圆锥Biblioteka C.圆柱 牛牛文档分 享
人教版初中数学七年级上册《4.1.2 点、线、面、体》同步练习卷(含答案解析
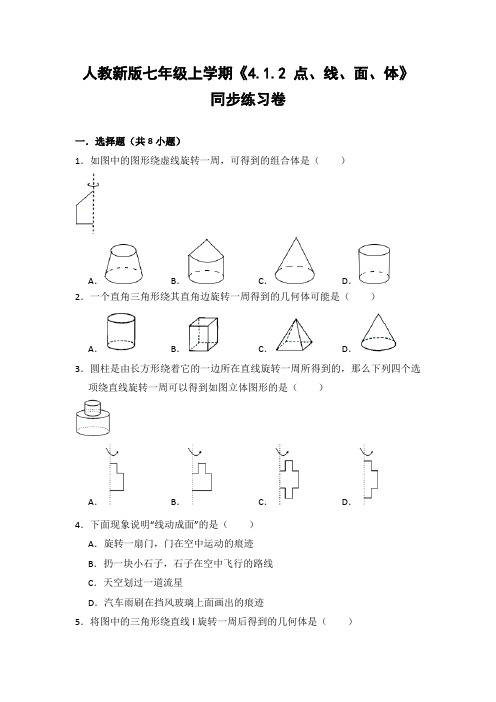
人教新版七年级上学期《4.1.2 点、线、面、体》同步练习卷一.选择题(共8小题)1.如图中的图形绕虚线旋转一周,可得到的组合体是()A.B.C.D.2.一个直角三角形绕其直角边旋转一周得到的几何体可能是()A.B.C.D.3.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是()A.B.C.D.4.下面现象说明“线动成面”的是()A.旋转一扇门,门在空中运动的痕迹B.扔一块小石子,石子在空中飞行的路线C.天空划过一道流星D.汽车雨刷在挡风玻璃上面画出的痕迹5.将图中的三角形绕直线l旋转一周后得到的几何体是()A.B.C.D.6.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是()A.①②③④B.①②③C.②③④D.①③④7.生活中我们见到的自行车的辐条运动形成的几何图形可解释为()A.点动成线B.线动成面C.面动成体D.以上答案都不对8.用钢笔写字是一个生活中的实例,用数学原理分析,它所属于的现象是()A.点动成线B.线动成面C.线线相交D.面面相交二.填空题(共4小题)9.如图,一个边长为2的正方形和等腰直角三角形的一边重合,组成了一个平面图形,如果将它绕AB所在直线按逆时针方向旋转180°,得到一个几何体,=h)则这个几何体的体积为.(圆锥的体积公式为:V圆锥10.如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为.11.将一个长4cm宽2cm的矩形绕它的一边所在的直线旋转一周,所得几何体的体积为cm3.12.写出下面给出的平面图形以虚线为轴旋转一周得到的立体图形名称.由图(1)可得到的立体图形的名称是;由图(2)可得到的立体图形的名称是;由图(3)可得到的立体图形的名称是.三.解答题(共7小题)13.如图是一个长为4cm,宽为3cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1、图2),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大(结果保留π)14.如图,长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题:(1)如图(1),绕着它的宽所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)(2)如图(2),绕着它的长所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)15.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到种大小不同的几何体?(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)16.如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.17.将第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.18.第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.图1旋转形成,图2旋转形成,图3旋转形成,图4旋转形成,图5旋转形成,图6旋转形成.19.如图,把一长方形在直线m上翻滚,请在图中作出A点所经过的路径.人教新版七年级上学期《4.1.2 点、线、面、体》同步练习卷参考答案与试题解析一.选择题(共8小题)1.如图中的图形绕虚线旋转一周,可得到的组合体是()A.B.C.D.【分析】根据面动成体的原理:下面的长方形旋转一周后是一个圆柱,上面的直角三角形旋转一周后是一个圆锥,所以应是圆锥和圆柱的组合体.【解答】解:∵下面的长方形旋转一周后是一个圆柱,上面的直角三角形旋转一周后是一个圆锥,∴根据以上分析应是圆锥和圆柱的组合体.故选:B.【点评】此题主要考查了平面图形与立体图形的联系,可把较复杂的图形进行分解旋转,然后再组合,学生应注意培养空间想象能力.2.一个直角三角形绕其直角边旋转一周得到的几何体可能是()A.B.C.D.【分析】根据面动成体,可得答案.【解答】解:以直角三角形的一条直角边所在直线为对称轴旋转一周,得到一个圆锥,故选:D.【点评】本题考查了点、线、面、体,点动成线,线动成面,面动成体:以直角三角形的一条直角边所在直线为对称轴旋转一周得到圆锥.3.圆柱是由长方形绕着它的一边所在直线旋转一周所得到的,那么下列四个选项绕直线旋转一周可以得到如图立体图形的是()A.B.C.D.【分析】如图本题是一个平面图形围绕一条边为中心对称轴旋转一周根据面动成体的原理即可解.【解答】解:由长方形绕着它的一边所在直线旋转一周可得到圆柱体,如图立体图形是两个圆柱的组合体,则需要两个一边对齐的长方形,绕对齐边所在直线旋转一周即可得到,故选:A.【点评】本题考查面动成体,需注意可把较复杂的体分解来进行分析.4.下面现象说明“线动成面”的是()A.旋转一扇门,门在空中运动的痕迹B.扔一块小石子,石子在空中飞行的路线C.天空划过一道流星D.汽车雨刷在挡风玻璃上面画出的痕迹【分析】根据点动成线,线动成面,面动成体对各选项分析判断后利用排除法求解.【解答】解:A、旋转一扇门,门在空中运动的痕迹是“面动成体”,故本选项错误;B、扔一块小石子,石子在空中飞行的路线是“点动成线”,故本选项错误;C、天空划过一道流星是“点动成线”,故本选项错误;D、汽车雨刷在挡风玻璃上面画出的痕迹是“线动成面”,故本选项正确.故选:D.【点评】本题考查了点、线、面、体的知识,主要是考查学生立体图形的空间想象能力及分析问题,解决问题的能力.5.将图中的三角形绕直线l旋转一周后得到的几何体是()A.B.C.D.【分析】根据面动成体,可得答案.【解答】解:三角形旋转得两个同底的圆锥,故选:B.【点评】本题考查了点线面体,利用面动成体是解题关键.6.下列说法:①一点在平面内运动的过程中,能形成一条线段;②一条线段在平面内运动的过程中,能形成一个平行四边形;③一个三角形在空间内运动的过程中,能形成一个三棱柱;④一个圆形在空间内平移的过程中,能形成一个球体.其中正确的是()A.①②③④B.①②③C.②③④D.①③④【分析】根据点动成线,可以判断①;根据线动成面,可以判断②;根据面动成体,可以判断③;根据平移的性质,可以判断④.【解答】解:①一点在平面内运动的过程中,能形成一条线段是正确的;②一条线段在平面内运动的过程中,能形成一个平行四边形是正确的;③一个三角形在空间内运动的过程中,能形成一个三棱柱是正确的;④一个圆形在空间内平移的过程中,能形成一个圆柱,原来的说法错误.故选:B.【点评】此题考查了点、线、面、体,关键是掌握平面图形与立体图形的联系,培养学生的观察能力和空间想象能力.7.生活中我们见到的自行车的辐条运动形成的几何图形可解释为()A.点动成线B.线动成面C.面动成体D.以上答案都不对【分析】根据从运动的观点来看点动成线,线动成面,面动成体可得答案.【解答】解:生活中我们见到的自行车的辐条运动形成的几何图形可解释为:线动成面,故选:B.【点评】此题主要考查了点、线、面、体,关键是掌握四者之间的关系.8.用钢笔写字是一个生活中的实例,用数学原理分析,它所属于的现象是()A.点动成线B.线动成面C.线线相交D.面面相交【分析】根据点动成线,线动成面,面动成体进行解答.【解答】解:用钢笔写字是点动成线,故选:A.【点评】此题主要考查了点线面体,题目比较简单.二.填空题(共4小题)9.如图,一个边长为2的正方形和等腰直角三角形的一边重合,组成了一个平面图形,如果将它绕AB所在直线按逆时针方向旋转180°,得到一个几何体,=h)则这个几何体的体积为π.(圆锥的体积公式为:V圆锥【分析】将该平面图形绕AB所在直线按逆时针方向旋转180°,得到一个由半个圆锥和半个圆柱组成的几何体,依据圆锥的体积公式和圆柱的体积公式进行计算即可.【解答】解:将该平面图形绕AB所在直线按逆时针方向旋转180°,得到一个由半个圆锥和半个圆柱组成的几何体,这个几何体的体积=(π×22×2+π×22×2)=π,故答案为:π.【点评】本题主要考查了几何体的体积,解决问题的关键是掌握圆锥的体积公式和圆柱的体积公式.10.如图所示,1条直线将平面分成2个部分,2条直线最多可将平面分成4个部分,3条直线最多可将平面分成7个部分,4条直线最多可将平面分成11个部分.现有n条直线最多可将平面分成56个部分,则n的值为10.【分析】n条直线最多可将平面分成S=1+1+2+3…+n=n(n+1)+1,依此可得等量关系:n条直线最多可将平面分成56个部分,列出方程求解即可.【解答】解:依题意有n(n+1)+1=56,解得n1=﹣11(不合题意舍去),n2=10.答:n的值为10.故答案为:10.【点评】考查了点、线、面、体,规律性问题及一元二次方程的应用;得到分成的最多平面数的规律是解决本题的难点.11.将一个长4cm宽2cm的矩形绕它的一边所在的直线旋转一周,所得几何体的体积为16π或32πcm3.【分析】根据圆柱体的体积=底面积×高求解,注意底面半径和高互换得圆柱体的两种情况.【解答】解:分两种情况:①绕长所在的直线旋转一周得到圆柱体积为:π×22×4=16π(cm3);②绕宽所在的直线旋转一周得到圆柱体积为:π×42×2=32π(cm3).故它们的体积分别为16πcm3或32πcm3.故答案为:16π或32π.【点评】本题考查圆柱体的体积的求法,注意分情况讨论,难度适中.12.写出下面给出的平面图形以虚线为轴旋转一周得到的立体图形名称.由图(1)可得到的立体图形的名称是圆柱;由图(2)可得到的立体图形的名称是圆锥;由图(3)可得到的立体图形的名称是球.【分析】根据点动成线,线动成面,面动成体,即可解答.【解答】解:由图(1)可得到的立体图形的名称是圆柱;由图(2)可得到的立体图形的名称是圆锥;由图(3)可得到的立体图形的名称是球;故答案为:圆柱,圆锥,球.【点评】此题主要考查立体图形中的旋转体,也就是把一个图形绕一条直线旋转得到的图形,要掌握基本的图形特征,才能正确判定.三.解答题(共7小题)13.如图是一个长为4cm,宽为3cm的长方形纸片,该长方形纸片分别绕长、宽所在直线旋转一周(如图1、图2),会得到两个几何体,请你通过计算说明哪种方式得到的几何体的体积大(结果保留π)【分析】绕长旋转得到的圆柱的底面半径为4cm,高为6cm,从而计算体积即可;绕宽旋转得到的圆柱底面半径为6cm,高为4cm,从而计算体积进行比较即可.【解答】解:如图1,绕长边旋转得到的圆柱的底面半径为3cm,高为4cm,体积=π×32×4=36πcm3;如图2,绕短边旋转得到的圆柱底面半径为4cm,高为3cm,体积=π×42×3=48πcm3.因此绕短边旋转得到的圆柱体积大.【点评】本题考查了点、线、面、体的知识,熟记常见平面图形旋转可得到什么立体图形是解决本题的关键,另外要掌握圆柱的体积计算公式.14.如图,长方形的长和宽分别是7cm和3cm,分别绕着它的长和宽所在的直线旋转一周,回答下列问题:(1)如图(1),绕着它的宽所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)(2)如图(2),绕着它的长所在的直线旋转一周,所得到的是什么样的几何体?得到的几何体的体积是多少?(π取3.14)【分析】(1)根据矩形绕一条边旋转得到圆柱,根据圆柱的体积公式,可得答案;(2)根据矩形绕一条边旋转得到圆柱,根据圆柱的体积公式,可得答案.【解答】解:(1)得到的是底面半径是7cm,高是3cm的圆柱,V=3.14×72×3=461.58(cm3),答:得到的几何体的体积是461.58cm3;(2)得到的是底面半径是3cm,高是7cm的圆柱,V=3.14×32×7=197.82(cm3),答:得到的几何体的体积是197.82cm3.【点评】本题考查了点、线、面、体,矩形绕一边旋转是圆柱,圆柱的体积公式:πr2h.15.如图所示,已知直角三角形纸板ABC,直角边AB=4cm,BC=8cm.(1)将直角三角形纸板绕三角形的边所在的直线旋转一周,能得到3种大小不同的几何体?(2)分别计算绕三角形直角边所在的直线旋转一周,得到的几何体的体积?(圆锥的体积=πr2h,其中π取3)【分析】(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.(2)如果以AB所在的直线旋转一周得到的圆锥的底面半径是8厘米,高是4厘米;如果以BC所在的直线旋转一周得到的圆锥的底面半径是4厘米,高是8厘米,根据圆锥的体积公式:v=πr2h,把数据代入公式解答.【解答】解:(1)将直角三角形纸板ABC绕三角形的三条边所在的直线旋转一周,能得到3种大小不同的几何体.(2)以AB为轴:×3×82×4=×3×64×4=256(立方厘米);以BC为轴:×3×42×8=×3×16×8=128(立方厘米).答:以AB为轴得到的圆锥的体积是256立方厘米,以BC为轴得到的圆锥的体积是128立方厘米.故答案为:3.【点评】此题考查了点、线、面、体,关键是理解掌握圆锥的特征,以及圆锥体积公式的灵活运用.16.如图,上面的平面图形绕轴旋转一周,可以得出下面的立体图形,请你把有对应关系的平面图形与立体图形连接起来.【分析】根据“面动成体”的原理,结合图形特征进行旋转,判断出旋转后的立体图形即可.【解答】解:连线如下:【点评】本题考查了图形的旋转,注意培养自己的空间想象能力.17.将第一行的图形绕轴旋转一周,便得到第二行的几何体,用线连一连.【分析】根据图形,结合想象,即可选出答案.【解答】解:如图所示,A旋转后得出图形c,B旋转后得出图形d,C旋转后得出图形a,D旋转后得出图形e,E旋转后得出图形b.【点评】本题考查了点、线、面、体等知识点的应用,主要考查学生的理解能力、空间想象能力和观察能力.18.第一行的图形绕虚线转一周,能形成第二行的某个几何体,按要求填空.图1旋转形成d,图2旋转形成a,图3旋转形成c,图4旋转形成f,图5旋转形成b,图6旋转形成e.【分析】根据旋转的特点和各几何图形的特性判断即可.【解答】解:图1旋转形成d,图2旋转形成a,图3旋转形成c,图4旋转形成f,图5旋转形成b,图6旋转形成e.【点评】本题考查了平面图形与立体图形的联系,难度不大,学生应注意培养空间想象能力.19.如图,把一长方形在直线m上翻滚,请在图中作出A点所经过的路径.【分析】由题意可知,A点所经过的路径是先以长方形的长为半径,旋转90°,再以长方形的对角线为半径,旋转90°所对应的弧长.【解答】解:如图所示.【点评】本题考查了点动成线,画图时注意半径的确定.。
