浅析一道坐标几何综合题——2006年镇江市一道中考题评析
2006年数学中考热点试题评析

胱 ∥ 0 / ..△ 0 一△K B /MN ・ A B . P 一△M B . = B,. K B = Q N .’ B O ’ = PA , . B
.
BM :BN.
・
.
.
・ .
.
B B : — M ,即K Q K— M : Q B A M= M. P Q G= C , G 是 ) 中点 ,即点G 与点G 合. 的 重
.
ll
经检 验 , 或 时 , P f 一 个 以A 为腰 的等腰 三 角形. 当: : AA Q  ̄ l _ P
6 ll
( )设A 3 、B O的 中点分 别 为点 、N,则点G随P,Q 动 所形 成 的 运
图形 是 线 段朋
证 明 :如 图2 设MN、即 相 交 于 点G ,过 点P 作 ∥A0交A 于K,
p运 动 所 形 成 的 图 形 是 线 段  ̄ .
・
.
.
练 习题 (0 6 山东省青 岛 市初 级 中学 学业 水平考 试压 轴题 )如 图 20 年
① ,有两个形状完全相 同的直角三角形A C F 叠放在一起 ( 与 B 和E G 点A
点 E重 合 ) 已知 AC 8 m,BC= c , =c 6 m, C= 0 ,EG= c 9。 4 m, EGF 9 。 =0,
评析 :① 这 是 一道 创 新 意识 题 ,其 创 新 意 识 是 :在 P 、Q两 点 的 运 动 变 化 过 程 中 ,探 索何 时 △A 是 一个 以A 为 腰 的等 即 P
腰 三 角 形 :② 考 查 了 考 生 以 下 能 力 :观
察 、 思 维 、作 辅 助 线 、数 形 转 换 、分 析 、
0 △E 斜 边 上 的 中 点 . 是
镇江市中考数学试题分类解析专题9:三角形

江中考数学试题分类解析汇编(12专题)专题9:三角形一、选择题1. (2003江苏镇江3分)如图,Rt△ABC中,∠ACB=900,CD⊥AB,D为垂足,若AC=4,BC=3,则sin∠ACD的值为【】A、4 3B、34C、45D、35【答案】C。
【考点】相似三角形的判定和性质,勾股定理,锐角三角函数定义。
【分析】∵∠A=∠A,∠ADC=∠ACB=90°,∴△ACD∽△ABC。
∴∠ACD=∠B。
∵AC=4,BC=3,∴AB=5。
∴sin∠ACD=sin∠B=AC4AB5。
故选C。
2. (2005江苏镇江3分)如图DE是△ABC的中位线,F是DE的中点,CF的延长线交AB于点G,则AG:GD等于【】A.2:1 B.3:1 C.3:2 D.4:3【答案】A。
【考点】三角形中位线定理,全等、相似三角形的判定和性质。
【分析】过E作EM∥AB与GC交于点M,构造全等三角形把DG转移到和AG相关的中位线处,可得所求线段的比:过E作EM∥AB与GC交于点M,∴△EMF≌△DGF(AAS)。
∴EM =GD 。
∵DE 是中位线,∴CE =12AC 。
又∵EM ∥AG ,∴△CME ∽△CGA 。
∴EM :AG =CE :AC =1:2。
又∵EM =GD ,∴AG :GD =2:1。
故选A 。
3. (2006江苏镇江2分)锐角三角形的三个内角是∠A 、∠B 、∠C ,如果A B α∠=∠∠+, B C β∠=∠∠+,C A γ∠=∠+∠,那么α∠、β∠、γ∠这三个角中【 】A .没有锐角B .有1个锐角C .有2个锐角D .有3个锐角【答案】A 。
【考点】三角形的外角性质。
【分析】根据三角形的外角和锐角三角形的性质作答:∵锐角三角形中三个角∠A 、∠B 、∠C 都是锐角,而由题意知,α∠、β∠、γ∠分别是其外角,∴根据三角形外角的性质,可知α∠、β∠、γ∠这三个角都是钝角。
故选A 。
4. (2009江苏省3分)如图,给出下列四组条件:①AB DE BC EF AC DF ===,,;②AB DE B E BC EF =∠=∠=,,;③B E BC EF C F ∠=∠=∠=∠,,;④AB DE AC DF B E ==∠=∠,,.其中,能使ABC DEF △≌△的条件共有【 】A .1组B .2组C .3组D .4组【答案】C 。
2006年中考动态几何题赏析

2006年中考动态几何题赏析
近年来,涉及动态几何的题目成为中考考试中经常考查的内容。
动态几何是一门研究定义为动态变量的几何问题的学科,具有较强的动手能力与推理能力,是学生自学能力的重要考查对象。
一般而言,动态几何题的特点是:简单、常见、有效。
从简单动态变量的角度来看,可以
从四个方面来分析:(1)通过实验判断解的变化规律,把调整变量理论转化为实践操作;(2)根据运动物体的路径与夹角判断几何图形;(3)联系实际对空间位置进行变换;(4)把动态变量转化为几何关系,有助于理解解题。
此外,中考动态几何题通常出现在解答问题或有关图形变换等形式,要求考生根据运动物
体的变化,来确定直线、点以及圆形等图形上的关系,变换几何图形的位置等。
因此,在应考动态几何题的过程中,应对解题思路进行科学的分析,从多方面解析同一问题,并要灵活地运用几何图形变换的方法来解决实际问题。
此外,还要加强实践能力的训练,把考点用具体的操作来解释。
综上所述,当我们应对动态几何题时,应注重实践能力的发展,以解决实际问题为目标,加强对空间知识的积累,培养解题的分析、研究归纳能力,做到及时发现解题中的问题,
以及把握解题思路的有效解决。
2006年江苏省镇江市中考数学试卷

2006年江苏省镇江市中考数学试卷一、填空题(共8小题,满分18分)1.(3分)3的相反数是,-5的绝对值是,9的平方根是.Y—22.(2分)在函数尸中,自变量x的取值范围是;若分式M的值为零,则x=.3.(2分)若匕q的补角是120°,则匕。
=度,coso=・4.(3分)某校高一新生参加军训,一学生进行五次实弹射击的成绩(单位:环)如下:8,6,10,7,9.则这五次射击的平均成绩是环,中位数是环,方差是环25.(2分)己知扇形的圆心角为120°,半径为2cm,则扇形的弧长是cm,扇形的面积是cm2.6.(2分)己知反比例函数y=^(5)的图象经过点(1,-2),则这个函数的表达式是.当时,y的值随自变量x值的增大而.7.(3分)如图,在△ABC中,D、E分别是AB和AC的中点,F是3C延长线上一点,DF平分CE于点G,CF=1,则BC=,与△ABC的周长之比为,△CFG与的面积之比为.8.(1分)如图,小亮从A点出发,沿直线前进10米后向左转30°,再沿直线前进10米,又向左转30°,…,照这样走下去,他第一次回到出发地A点时,一共走了米.二、选择题(共9小题,每小题2分,满分18分)9.(2分)下列计算正确的是()A. 3x ~ 2«x= 1B. x*x=x^C. 2x+2x=2^D. ( - /) 2= _ 渣10. (2分)如图,已知oo 的半径为5mm,弦则圆心。
到AB 的距离是()B. 2mmC. 3mmD. 4mm11. (2分)小刘同学用10元钱购买两种不同的贺卡共8张,单价分别是1元与2元.设1元的贺卡为x 张,2元的贺卡为y 张,那么x, y 所适合的一个方程组是()8 1 == y 102y + + X -2X o 18 =- y -2 y + +X X 8 - y + %O1 - 2y + %8 - 2y +X A.c.B D 12. (2分)刘翔在出征北京奥运会前刻苦进行110米跨栏训练,教练对他20次的训练成绩进行统计分析,判断他的成绩是否稳定,则教练需要知道刘翔这20次成绩的( )A.众数B.平均数C.频数D.方差13. (2分)图1表示正六棱柱形状的高大建筑物,图2中的阴影部分表示该建筑物的俯视图,P 、Q 、M 、N 表示小明在地面上的活动区域.小明想同时看到该建筑物的三个侧面,他应在( )A. F 区域B.。
2006年中学考试数学精彩试题总汇编及解析汇报汇报 探索型问题
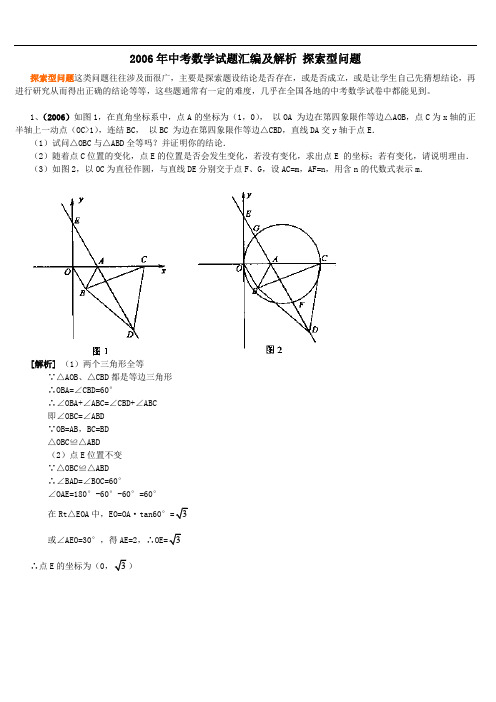
2006年中考数学试题汇编及解析探索型问题探索型问题这类问题往往涉及面很广,主要是探索题设结论是否存在,或是否成立,或是让学生自己先猜想结论,再进行研究从而得出正确的结论等等,这些题通常有一定的难度,几乎在全国各地的中考数学试卷中都能见到。
1、(2006)如图1,在直角坐标系中,点A的坐标为(1,0),•以OA•为边在第四象限作等边△AOB,点C为x轴的正半轴上一动点(OC>1),连结BC,•以BC•为边在第四象限作等边△CBD,直线DA交y轴于点E.(1)试问△OBC与△ABD全等吗?并证明你的结论.(2)随着点C位置的变化,点E的位置是否会发生变化,若没有变化,求出点E•的坐标;若有变化,请说明理由.(3)如图2,以OC为直径作圆,与直线DE分别交于点F、G,设AC=m,AF=n,用含n的代数式表示m.[解析](1)两个三角形全等∵△AOB、△CBD都是等边三角形∴OBA=∠CBD=60°∴∠OBA+∠ABC=∠CBD+∠ABC即∠OBC=∠ABD∵OB=AB,BC=BD△OBC≌△ABD(2)点E位置不变∵△OBC≌△ABD∴∠BAD=∠BOC=60°∠OAE=180°-60°-60°=60°在Rt△EOA中,EO=OA·tan60°3或∠AEO=30°,得AE=2,∴3∴点E的坐标为(03(3)∵AC=m ,AF=n ,由相交弦定理知1·m=n ·AG ,即AG=m n又∵OC 是直径,∴OE 是圆的切线,OE 2=EG ·EF 在Rt △EOA 中,31+ 32=(2-m n)(2+n ) 即2n 2+n-2m-mn=0解得m=222n nn ++.2、(2006)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D . (1)求直线AB 的解析式; (2)若S 梯形OBCD 43,求点C 的坐标; (3)在第一象限是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由. [解析] (1)直线AB 解析式为:y=33-x+3. (2)方法一:设点C坐标为(x ,33-x+3),那么OD =x ,CD =33-x+3. ∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x (舍去)∴ C(2,33) 方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S .由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ×AD =223CD =63.可得CD =33. ∴ AD=1,OD =2.∴C (2,33). (3)当∠OBP =Rt ∠时,如图①若△BOP ∽△OBA ,则∠BOP =∠BAO=30°,BP=3OB=3,∴1P (3,33). ②若△BPO ∽△OBA ,则∠BPO =∠BAO=30°,OP=33OB=1. ∴2P (1,3).当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30° 过点P 作PM ⊥OA 于点M . 方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23.∵ 在Rt △P MO 中,∠OPM =30°, ∴ OM =21OP =43;PM =3OM =433.∴3P (43,433).方法二:设P(x ,33-x+3),得OM =x ,PM =33-x+3 由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM =x x 333+-,tan ∠ABOC=OBOA =3.∴33-x+3=3x ,解得x =43.此时,3P (43,433).④若△POB ∽△OBA(如图),则∠OBP=∠BAO =30°,∠POM =30°. ∴ PM =33OM =43. ∴ 4P (43,43)(由对称性也可得到点4P 的坐标).当∠OPB =Rt ∠时,点P 在x轴上,不符合要求.综合得,符合条件的点有四个,分别是:1P (3,33),2P (1,3),3P (43,433),4P (43,43).3、(2006)如图,在直角坐标系中,以点A为圆心,以x 轴相交于点B C ,,与y 轴相交于点D E ,.(1)若抛物线213y x bx c =++经过C D ,两点,求抛物线的解析式,并判断点B 是否在该抛物线上. (2)在(1)中的抛物线的对称轴上求一点P ,使得PBD △的周长最小.(3)设Q 为(1)中的抛物线的对称轴上的一点,在抛物线上是否存在这样的点M ,使得四边形BCQM 是平行四边形.若存在,求出点M 的坐标;若不存在,说明理由.[解析] (1)OA =∵AB AC ==(B ∴,C 又在Rt AOD △中,AD =OA =3OD ==∴D ∴的坐标为(03)-, 又D C ,两点在抛物线上,231(33)03c c =-⎧⎪⎨++=⎪⎩∴解得3b c⎧=⎪⎨⎪=-⎩ ∴抛物线的解析式为:21333y x x =--当x =0y =∴点(B 在抛物线上 (2)21333y x x =--∵21(43x =- ∴抛物线2133y x x =-的对称轴方程为x = 在抛物线的对称轴上存在点P ,使PBD △的周长最小.BD ∵的长为定值 ∴要使PBD △周长最小只需PB PD +最小. 连结DC ,则DC 与对称轴的交点即为使PBD △周长最小的点. 设直线DC 的解析式为y mx n =+.由30n n =-⎧⎪⎨+=⎪⎩得33m n ⎧=⎪⎨⎪=-⎩∴直线DC的解析式为3y x =-由3y x x ⎧=-⎪⎨⎪=⎩得2x y ⎧=⎪⎨=-⎪⎩ 故点P的坐标为2)-(3)存在,设)Q t为抛物线对称轴x =M 在抛物线上要使四边形BCQM 为平行四边形,则BC QM ∥且BC QM =,点M 在对称轴的左侧.于是,过点Q 作直线L BC ∥与抛物线交于点()m M x t , 由BC QM =得QM =从而m x =-12t =故在抛物线上存在点(M ,使得四边形BCQM 为平行四边形. 4、(2006)把两块全等的直角三角形ABC 和DEF 叠放在一起,使三角板DEF 的锐角顶点D 与三角板ABC 的斜边中点O 重合,其中90ABC DEF ∠=∠=,45C F ∠=∠=,4AB DE ==,把三角板ABC 固定不动,让三角板DEF 绕点O 旋转,设射线DE 与射线AB 相交于点P ,射线DF 与线段BC 相交于点Q .(1)如图9,当射线DF 经过点B ,即点Q 与点B 重合时,易证APD CDQ △∽△.此 时,AP CQ =· .(2)将三角板DEF 由图1所示的位置绕点O 沿逆时针方向旋转,设旋转角为α.其中090α<<,问AP CQ ·的值是否改变?说明你的理由.(3)在(2)的条件下,设CQ x =,两块三角板重叠面积为y ,求y 与x 的函数关系式.[解析] (1)8(2)AP CQ ·的值不会改变.理由如下:在APD △与CDQ △中,45A C ∠=∠= 18045(45)90APD a a ∠=--+=- 90CDQ a ∠=- 即APD CDQ ∠=∠APD CDQ ∴△∽△AP CDAD CQ=∴22182AP CQ AD CD AD AC ⎛⎫==== ⎪⎝⎭∴(3)情形1:当045a <<时,24CQ <<,即24x <<,此时两三角板重叠部分为四边形DPBQ ,过D 作DG AP ⊥于G ,DN BC ⊥于N ,2DG DN ==∴由(2)知:8AP CQ =得8AP x=于是111222y AB AC CQ DN AP DG =--88(24)x x x=--<<情形2:当4590a <≤时,02CQ <≤时,即02x <≤,此时两三角板重叠部分为DMQ △, 由于8AP x =,84PB x=-,易证:PBM DNM △∽△, BEE 图1 图3图3EBGBM PB MN DN =∴即22BM PB BM =-解得28424PB xBM PB x-==+- 84444xMQ BM CQ x x-=--=---∴ 于是1844(02)24xy MQ DN x x x-==--<-≤综上所述,当24x <<时,88y x x=--当02x <≤时,8444xy x x-=---2484y x x x =⎛⎫-+ ⎪-⎝⎭或法二:连结BD ,并过D 作DN BC ⊥于点N ,在DBQ △与MCD △中,45DBQ MCD ∠=∠=45DQB QCB QDC QDC MDQ QDC MDC ∠=∠+∠=+∠=∠+∠=∠DBQ MCD ∴△∽△ MC DBCD BQ=∴4x=- 84MC x =-∴ 284844x x MQ MC CD x x x -+=-=-=--∴ 2148(02)24x x y DN MQ x x-+==<-∴≤法三:过D 作DN BC ⊥于点N ,在Rt DNQ △中, 222DQ DN NQ =+ 24(2)x =+- 248x x =-+于是在BDQ △与DMQ △中45DBQ MDQ ∠=∠= DMQ DBM BDM ∠=∠+∠ 45BDM =+∠ BDQ =∠BDQ DMQ ∴△∽△ BQ DQDQ MQ =∴即4x DQDQ MQ-= 224844DQ x x MQ x x-+==--∴2148(02)24x x y DN MQ x x-+==<-∴≤5、(2006)如图,点O 是坐标原点,点A (n ,0)是x 轴上一动点(n <0)以AO 为一边作矩形AOBC ,点C 在第二象限,且OB =2OA .矩形AOBC 绕点A 逆时针旋转90o 得矩形AGDE .过点A 的直线y =kx +m 交y 轴于点F ,FB =FA .抛物线y=ax 2+bx+c 过点E 、F 、G 且和直线AF 交于点H ,过点H 作HM ⊥x 轴,垂足为点M .(1)求k 的值;(2)点A 位置改变时,△AMH 的面积和矩形AOBC 的面积的比值是否改变?说明你的理由.[解析] (1)根据题意得到:E (3n ,0), G (n ,-n )当x =0时,y =kx +m =m ,∴点F 坐标为(0,m )∵Rt △AOF 中,AF 2=m 2+n 2, ∵FB =AF ,∴m 2+n 2=(-2n -m)2, 化简得:m =-0.75n , 对于y =kx +m ,当x =n 时,y =0, ∴0=kn -0.75n , ∴k =0.75(2)∵抛物线y=ax 2+bx+c 过点E 、F 、G , ∴ ⎪⎩⎪⎨⎧=-++=-++=c c nb a n n cnb a n 75.039022解得:a =n 41,b =-21,c =-0.75n∴抛物线为y=n 41x 2-21x -0.75n解方程组:⎪⎩⎪⎨⎧-=--=nx y n x x n y 75.075.075.021412 得:x 1=5n ,y 1=3n ;x 2=0,y 2=-0.75n∴H 坐标是:(5n ,3n ),HM =-3n ,AM =n -5n =-4n ,∴△AMH 的面积=0.5×HM ×AM =6n 2;而矩形AOBC 的面积=2n 2,∴△AMH 的面积∶矩形AOBC 的面积=3:1,不随着点A 的位置的改变而改变.6、(2006日照)如图(1),在以AB为直径的半圆O有一点P,AP、BP的延长线分别交半圆O于点C、D.求证:AP·AC+BP·BD=AB2.证明:连结AD、BC,过P作PM⊥AB,则∠ADB=∠AMP=90o,∴点D、M在以AP为直径的圆上;同理:M、C在以BP为直径的圆上.由割线定理得:AP·AC=AM·AB,BP·BD=BM·BA,所以,AP·AC+BP·BD=AM·AB+BM·AB=AB·(AM+BM)=AB2.当点P在半圆周上时,也有AP·AC+BP·BD=AP2+BP2=AB2成立,那么:(1)如图(2)当点P在半圆周外时,结论AP·AC+BP·BD=AB2是否成立?为什么?(2)如图(3)当点P在切线BE外侧时,你能得到什么结论?将你得到的结论写出来.[解析](1)成立.证明:如图(2),∵∠PCM=∠PDM=900,∴点C、D在以PM为直径的圆上,∴AC·AP=AM·MD,BD·BP=BM·BC,∴AC·AP+BD·BP=AM·MD+BM·BC,由已知,AM·MD+BM·BC=AB2,∴AP·AC+BP·BD=AB2.(2)如图(3),过P作PM⊥AB,交AB的延长线于M,连结AD、BC,则C、M在以PB为直径的圆上,∴AP·AC=AB·AM,①D、M在以PA为直径的圆上,∴BP·BD=AB·BM,②由图象可知:AB=AM-BM,③由①②③可得:AP·AC-BP·BD=AB·(AM-BM)=AB2.7、(2006)问题背景;课外学习小组在一次学习研讨中,得到了如下两个命题:①如图1,在正三角形ABC中,M,N分别是AC、AB上的点,BM与CN相交于点O,若∠BON=60°.则BM=CN:②如图2,在正方形ABCD中,M、N分别是CD、AD上的点.BM与CN相交于点O,若∠BON=90°.则BM=CN.然后运用类似的思想提出了如下命题:③如图3,在正五边形ABCDE中,M、N分别是CD,DE上的点,BM与CN相交于点O,若∠BON=108°,则BM=CN.任务要求(1)请你从①.②,③三个命题中选择一个进行证明;(2) 请你继续完成下面的探索;①如图4,在正n(n≧3)边形ABCDEF 中,M,N分别是CD、DE上的点,BM与CN相交于点O,试问当∠BON等于多少度时,结论BM =CN 成立(不要求证明)②如图5,在正五边形ABCDE 中,M 、N 分别是DE ,AE 上的点,BM 与CN 相交于点O ,∠BON =108°时,试问结论BM =CN 是否还成立,若成立,请给予证明.若不成立,请说明理由 (I)我选[解析] (1) 如选命题①证明:在图1中,∵∠BON =60°∴∠1+∠2=60° ∵∠3+∠2=60°,∴∠1=∠3又∵BC =CA ,∠BCM =∠CAN =60°∴ΔBCM ≌ΔCAN ∴BM =CN(2)如选命题②证明:在图2中,∵∵∠BON =90°∴∠1+∠2=90° ∵∠3+∠2=90°,∴∠1=∠3又∵BC =CD ,∠BCM =∠CDN =90°∴ΔBCM ≌ΔCDN ∴BM =CN (3)如选命题③证明;在图3中,∵∠BON =108°∴∠1+∠2=108° ∵∠2+∠3=108°∴∠1=∠3 又∵BC =CD ,∠BCM =∠CDN =108° ∴ΔBCM ≌ΔCDN ∴BM =CN(2)①答:当∠BON=0(n-2)180n时结论BM =CN 成立.②答当∠BON =108°时。
江苏省镇江市 中考数学试题【专题12】押轴题(含解析)

专题12:押轴题江苏泰州锦元数学工作室 编辑一、选择题1.(2002江苏镇江3分)如图,正方形ABCD 内接于⊙O,E 为 DC 的中点,直线BE 交⊙O 于点F ,若⊙O 的半径为2,则BF 的长为【 】A 、23B 、22 C 、556 D 、5542. (2003江苏镇江3分)如图,将矩形ABCD 分成15个大小相等的正方形,E 、F 、G 、H 分别在AD 、AB 、BC 、CD 边上,且是某个小正方形的顶点,若四边形EFGH 的面积为1,则矩形ABCD 的面积为【 】A 、2B 、43C 、32D 、533. (2004江苏镇江3分)如图,已知边长为5的等边三角形ABC 纸片,点E 在AC 边上,点F 在AB边上,沿着EF 折叠,使点A 落在BC 边上的点D 的位置,且ED BC ⊥,则CE 的长是【 】(A )10315- (B )1053- (C )535- (D )20103-4. (2005江苏镇江3分)图1是水滴进玻璃容器的示意图(滴水速度不变),图2是容器中水高度随滴水时间变化的图象.给出下列对应:(1):(a )--(e )(2):(b )--(f )(3):(c )--h (4):(d )--(g )其中正确的是【 】A .(1)和(2)B .(2)和(3)C .(1)和(3)D .(3)和(4)5. (2006江苏镇江2分)已知:如图1,点G 是BC 的中点,点H 在AF 上,动点P 以每秒2 cm的速度沿图1的边线运动,运动路径为:G C D E F H →→→→→,相应的△ABP 的面积2()cm y 关于运动时间)(s t 的函数图像如图2,若AB=6 cm ,则下列四个结论中正确的个数有【 】①图1中的BC 长是8cm ②图2中的M 点表示第4秒时y 的值为242cm③图1中的CD 长是4cm ④图2中的N 点表示第12秒时y 的值为182cmA .1个B .2个C .3个D .4个6. (2007江苏镇江3分)在直角坐标系中有两条直线l 1、l 2,直线l 1所对应的函数关系式为y x 2=-,如果将坐标纸折叠,使l 1与l 2重合,此时点(-1,0)与点(0,-1)也重合,则直线l 2所对应的函数关系式为【 】A . y x 2=-B .y x 2=+C .y x 2=--D .y x 2=-+7. (2008江苏镇江3分)福娃们在一起探讨研究下面的题目:函数y=x 2-x +m (m 为常数)的图象如下图,如果x=a 时,y <0;那么x=a -1时,函数值是多少.参考下面福娃们的讨论,请你解该题,你选择的答案是【 】A.y<0 B.0<y<m C.y>m D.y=m8. (2009江苏省3分)下面是按一定规律排列的一列数:第1个数:11122-⎛⎫-+⎪⎝⎭;第2个数:2311(1)(1)1113234⎛⎫⎛⎫---⎛⎫-+++⎪⎪ ⎪⎝⎭⎝⎭⎝⎭;第3个数:234511(1)(1)(1)(1) 11111423456⎛⎫⎛⎫⎛⎫⎛⎫-----⎛⎫-+++++⎪⎪⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭;……第n个数:232111(1)(1)(1)111112342nn n-⎛⎫⎛⎫⎛⎫----⎛⎫-++++⎪⎪ ⎪ ⎪+⎝⎭⎝⎭⎝⎭⎝⎭.那么,在第10个数、第11个数、第12个数、第13个数中,最大的数是【】A.第10个数B.第11个数C.第12个数D.第13个数9. (2010江苏镇江3分)小明新买了一辆“和谐”牌自行车,说明书中关于轮胎的使用说明如下:小明看了说明书后,和爸爸讨论:小明经过计算,得出这对轮胎能行驶的最长路程是【】A .9.5千公里B .113千公里C .9.9千公里D .10千公里10. (2011江苏镇江2分)已知二次函数512-+-=x x y ,当自变量x取m 时对应的值大于0,当自变量x 分别取1-m 、1+m 时对应的函数值为1y 、2y ,则1y 、2y 必须满足【 】A .1y >0、2y >0B .1y <0、2y <0C .1y <0、2y >0D .1y >0、2y <011.(2012江苏镇江3分)边长为a 的等边三角形,记为第1个等边三角形。
【中考12年】江苏省镇江市2001-2012年中考数学试题分类解析 专题5 数量和位置变化
2001-2012年江苏镇江中考数学试题分类解析汇编(12专题)专题5:数量和位置变化一、选择题1. (2001江苏镇江3分)函数y=x 2+5x --的自变量x 的取值范围在数轴上表示应为【 】2. (2001江苏镇江3分)如图,直角三角形AOB 中,AB⊥OB,且AB =OB =3,设直线a :x=t 截此三角形所得的阴影部分的面积为S ,则S 与t 之间的函数关系的图像为【 】【答案】D 。
【考点】二次函数的图象。
【分析】由直角三角形AOB 中,AB⊥OB,且AB =OB =3,知直线a :x=t 截此三角形所得的阴影部分也为等腰直角三角形,所以()21S=a 0a 32≤≤。
则S 与t 之间的函数关系的图像为D 。
故选D 。
3. (2002江苏镇江3分)函数y=2x 1x 1+-的自变量x 的取值范围【 】 A 、 x≥-21. B 、x≠1. C、x≥-21,且x≠1. D、x >-21,且x≠1. 【答案】C 。
【考点】函数自变量的取值范围,二次根式和分式有意义的条件。
【分析】求函数自变量的取值范围,就是求函数解析式有意义的条件,根据二次根式被开方数必须是非负数和分式分母不为0的条件,要使2x 1x 1+-在实数范围内有意义,必须12x 10x 1x 2x 102x 1⎧+≥≥-⎧⎪⇒⇒≥-⎨⎨-≠⎩⎪≠⎩且x≠1。
故选C 。
4. (2005江苏镇江3分)图1是水滴进玻璃容器的示意图(滴水速度不变),图2是容器中水高度随滴水时间变化的图象.给出下列对应:(1):(a )--(e )(2):(b )--(f )(3):(c )--h (4):(d )--(g )其中正确的是【 】A .(1)和(2)B .(2)和(3)C .(1)和(3)D .(3)和(4) 【答案】B 。
【考点】跨学科问题,函数的图象【分析】根据容器的形状,判断对应的函数图象,再对题中的每一种结论进行判断:在只有容器不同的情况下,容器中水高度随滴水时间变化的图象与容器的形状有关。
镇江中考真题数学答案解析
镇江中考真题数学答案解析数学作为一门重要的学科,是中学生中考的一个必考科目。
镇江作为一个历史悠久的城市,也有着相应的中考数学试题。
本文将通过解析镇江中考数学试题的答案,帮助学生更好地理解和应对数学考试。
首先,我们来看一个选择题的例子:1. 在一个凸四边形中,其中一个角是150°,另一个角是80°,第三个角是它的逆时针旋转的角的弧度表示的数值,若这个数值的绝对值小于90°,则这个凸四边形必须是()A. 平行四边形B. 菱形C. 矩形D. 正方形题目中给出了一个凸四边形,要求根据它的角的度数来判断它是何种类型的四边形。
这道题需要考生对几何形状和角度的理解,以及对特定类型几何形状的判定规律的掌握。
解析:我们可以通过推理和计算来求解这个问题。
其中一个角是150°,另一个角是80°,根据凸四边形内角和等于360°,我们可以得出第三个角的度数是360° - 150° - 80° = 130°。
接下来,题目要求我们将角的度数转化为弧度表示。
我们知道一个圆的周长是2π半径长,一个圆的弧度表示角的大小等于该角所对应的弧长与半径的比值。
在单位圆上,一个圆的周长为2π,半径为1,一个角度有360度,所以一个角的弧度表示的数值等于该角度数与2π的乘积再除以360。
根据这个公式我们可以计算出130°对应的弧度值为:130° * 2π / 360 = 13π / 18。
最后,题目要求我们判断这个凸四边形的类型。
根据题目中给出的条件,这个凸四边形的逆时针旋转的角的弧度表示的数值的绝对值小于90°。
根据我们刚刚计算得出的结果,13π / 18这个弧度值转化为度数是234°,显然绝对值小于90°。
所以这个凸四边形必须是A.平行四边形。
通过这道题目的解析,我们可以看出,解题的关键在于对几何形状和角度的理解,以及对转化公式和判定规律的熟悉与掌握。
2006年中考数学试题汇编及解析---动态几何型综合
2006年中考数学试题汇编及解析---动态几何型综合纵观近5年全国各地的中考数学试卷,动态几何型综合题常常出现在一张试卷的压轴题位置,估计这一趋势在今后几年的中考中会越来越明显,这类试题往往综合性较强,往往涉及到函数、直线型、圆等初中数学的重点考察对象中的好几个,应加大训练的力度。
1、(2006山东青岛)如图①,有两个形状完全相同的直角三角形ABC 和EFG 叠放在一起(点A 与点E 重合),已知AC =8cm ,BC =6cm ,∠C =90°,EG =4cm ,∠EGF =90°,O 是△EFG 斜边上的中点.如图②,若整个△EFG 从图①的位置出发,以1cm/s 的速度沿射线AB 方向平移,在△EFG 平移的同时,点P 从△EFG 的顶点G 出发,以1cm/s 的速度在直角边GF 上向点F 运动,当点P 到达点F 时,点P 停止运动,△EFG 也随之停止平移.设运动时间为x (s ),FG 的延长线交 AC 于H ,四边形OAHP 的面积为y (cm 2)(不考虑点P 与G 、F 重合的情况).(1)当x 为何值时,OP ∥AC ?(2)求y 与x 之间的函数关系式,并确定自变量x 的取值范围.(3)是否存在某一时刻,使四边形OAHP 面积与△ABC 面积的比为13∶24?若存在,求出x 的值;若不存在,说明理由.(参考数据:1142 =12996,1152 =13225,1162 =13456或4.42 =19.36,4.52 =20.25,4.62 =21.16)[解析] (1)∵Rt △EFG ∽Rt △ABC ,∴BC FG AC EG =,684FG=. ∴FG =864⨯=3cm .∵当P 为FG 的中点时,OP ∥EG ,EG ∥AC , ∴OP ∥AC .∴ x =121FG=21×3=1.5(s ).∴当x 为1.5s 时,OP ∥AC .(2)在Rt △EFG 中,由勾股定理得:EF =5cm . ∵EG ∥AH ,∴△EFG ∽△AFH .∴FH FGAF EF AH EG ==. ∴FHx AH 3554=+=. ∴ AH =54( x +5),FH =53(x +5).过点O 作OD ⊥FP ,垂足为 D .∵点O 为EF 中点, ∴OD =21EG =2cm . ∵FP =3-x ,∴S 四边形OAHP =S △AFH -S △OFP=21·AH ·FH -21·OD ·FP =21·54(x +5)·53(x +5)-21×2×(3-x ) =256x 2+517x +3 (0<x <3).(3)假设存在某一时刻x ,使得四边形OAHP 面积与△ABC 面积的比为13∶24.则S 四边形OAHP =2413×S △ABC ∴256x 2+517x +3=2413×21×6×8 ∴6x 2+85x -250=0 解得 x 1=25, x 2= -350(舍去). ∵0<x <3, ∴当x =25(s )时,四边形OAHP 面积与△ABC 面积的比为13∶24. 2、(2006河北)如图,在Rt △ABC 中,∠C =90°,AC =12,BC =16,动点P 从点A 出发沿AC 边向点C 以每秒3个单位长的速度运动,动点Q 从点C 出发沿CB 边向点B 以每秒4个单位长的速度运动.P ,Q 分别从点A ,C 同时出发,当其中一点到达端点时,另一点也随之停止运动.在运动过程中,△PCQ 关于直线PQ 对称的图形是△PDQ .设运动时间为t (秒).(1)设四边形PCQD 的面积为y ,求y 与t 的函数关系式; (2)t 为何值时,四边形PQBA 是梯形?(3)是否存在时刻t ,使得PD ∥AB ?若存在,求出t 的值;若不存在,请说明理由;(4)通过观察、画图或折纸等方法,猜想是否存在时刻t ,使得PD ⊥AB ?若存在,请估计t的值在括号中的哪个时间段内(0≤t ≤1;1<t ≤2;2<t ≤3;3<t ≤4);若不存在,请简要说明理由.[解析] (1)由题意知 CQ =4t ,PC =12-3t ,∴S △PCQ =t t CQ PC 246212+-=⋅.∵△PCQ 与△PDQ 关于直线PQ 对称, ∴y=2S △PCQ t t 48122+-=. (2)当CQCP CA CB=时,有PQ ∥AB ,而AP 与BQ 不平行,这时四边形PQBA 是梯形,∵CA =12,CB =16,CQ =4t , CP =12-3t ,∴16412312tt =-,解得t =2. ∴当t =2秒时,四边形PQBA 是梯形.(3)设存在时刻t ,使得PD ∥AB ,延长PD 交BC 于点M ,如下图,若PD ∥AB ,则∠QMD =∠B ,又∵∠QDM =∠C =90°,∴Rt △QMD ∽Rt △ABC ,从而ACQDAB QM =, ∵QD =CQ =4t ,AC =12, AB=20, ∴QM =203t . 若PD ∥AB ,则CP CMCA CB=,得20412331216t t t +-=, 解得t =1211. ∴当t =1211秒时,PD ∥AB .(4)存在时刻t ,使得PD ⊥AB .时间段为:2<t ≤3.3、(2006重庆)如图1所示,一张三角形纸片ABC ,∠ACB=90°,AC=8,BC=6.沿斜边AB 的中线PCD 把这张纸片剪成11AC D ∆和22BC D ∆两个三角形(如图2所示).将纸片11AC D ∆沿直线2D B (AB )方向平移(点12,,,A D D B 始终在同一直线上),当点1D 于点B 重合时,停止平移.在平移过程中,11C D 与2BC 交于点E,1AC 与222C D BC 、分别交于点F 、P.(1) 当11AC D ∆平移到如图3所示的位置时,猜想图中的1D E 与2D F 的数量关系,并证明你的猜想; (2) 设平移距离21D D 为x ,11AC D ∆与22BC D ∆重叠部分面积为y ,请写出y 与x 的函数关系式,以及自变量的取值范围;(3)对于(2)中的结论是否存在这样的x 的值,使重叠部分的面积等于原ABC ∆面积的14. 若存在,求x 的值;若不存在,请说明理由.[解析](1)12D E D F =.因为1122C D C D ∥,所以12C AFD ∠=∠.又因为90ACB ∠=︒,CD 是斜边上的中线,所以,DC DA DB ==,即112221C D C D BD AD === 所以,1C A ∠=∠,所以2AFD A ∠=∠ 所以,22AD D F =.同理:11BD D E =.又因为12AD BD =,所以21AD BD =.所以12D E D F =(2)因为在Rt ABC ∆中,8,6AC BC ==,所以由勾股定理,得10.AB =CB D A 图1122图3C 2D 2C 1BD 1A 图2即1211225AD BD C D C D ====又因为21D D x =,所以11225D E BD D F AD x ====-.所以21C F C E x == 在22BC D ∆中,2C 到2BD 的距离就是ABC ∆的AB 边上的高,为245. 设1BED ∆的1BD 边上的高为h ,由探究,得221BC D BED ∆∆∽,所以52455h x-=. 所以24(5)25x h -=.121112(5)225BED S BD h x ∆=⨯⨯=- 又因为1290C C ∠+∠=︒,所以290FPC ∠=︒.又因为2C B ∠=∠,43sin ,cos 55B B ==. 所以234,55PC x PF x == ,22216225FC P S PC PF x ∆=⨯=而2212221126(5)22525BC D BED FC P ABC y S S S S x x ∆∆∆∆=--=--- 所以21824(05)255y x x x =-+≤≤ (3) 存在. 当14ABC y S ∆=时,即218246255x x -+= 整理,得2320250.x x -+=解得,125,53x x ==.即当53x =或5x =时,重叠部分的面积等于原ABC ∆面积的14.4、(2006山东济南)如图1,以矩形OABC 的两边OA 和OC 所在的直线为x 轴、y 轴建立平面直角坐标系,A 点的坐标为(3)C ,0,点的坐标为(04),.将矩形OABC 绕O 点逆时针旋转,使B 点落在y 轴的正半轴上,旋转后的矩形为11111OA B C BC A B ,,相交于点M . (1)求点1B 的坐标与线段1B C 的长;(2)将图1中的矩形111OA B C 沿y 轴向上平移,如图2,矩形222PA B C 是平移过程中的某一位置,22BC A B ,相交于点1M ,点P 运动到C 点停止.设点P 运动的距离为x ,矩形222PA B C 与原矩形OABC 重叠部分的面积为y ,求y 关于x 的函数关系式,并写出x 的取值范围;(3)如图3,当点P 运动到点C 时,平移后的矩形为333PA B C .请你思考如何通过图形变换使矩形333PA B C 与原矩形OABC 重合,请简述你的做法.[解析](1)如图1,因为15OB OB ===,所以点1B 的坐标为(05),.11541B C OB OC =-=-=.(2)在矩形111OA B C 沿y 轴向上平移到P 点与C 点重合的过程中,点1A 运动到矩形OABC 的边BC 上时,求得P 点移动的距离115x =. 当自变量x 的取值范围为1105x <≤时,如图2,由2122B CM B A P △∽△,得1334x CM +=,此时,2221113334(1)224B A P B CM xy S S x +=-=⨯⨯-⨯+△△. 即23(1)68y x =-++(或23345848y x x =--+).当自变量x 的取值范围为1145x ≤≤时,求得122(4)3PCM y S x '==-△(或221632333y x x =-+).1C 3C(3)部分参考答案:①把矩形333PA B C 沿3BPA ∠的角平分线所在直线对折.②把矩形333PA B C 绕C 点顺时针旋转,使点3A 与点B 重合,再沿y 轴向下平移4个单位长度. ③把矩形333PA B C 绕C 点顺时针旋转,使点3A 与点B 重合,再沿BC 所在的直线对折. ④把矩形333PA B C 沿y 轴向下平移4个单位长度,再绕O 点顺时针旋转,使点3A 与点A 重合.5、(2006山东济南)如图1,已知Rt ABC △中,30CAB ∠= ,5BC =.过点A 作AE AB ⊥,且15AE =,连接BE 交AC 于点P . (1)求PA 的长;(2)以点A 为圆心,AP 为半径作⊙A ,试判断BE 与⊙A 是否相切,并说明理由;(3)如图2,过点C 作CD AE ⊥,垂足为D .以点A 为圆心,r 为半径作⊙A ;以点C 为圆心,R 为半径作⊙C .若r 和R 的大小是可变化的,并且在变化过程中保持⊙A 和⊙C 相切..,且使D 点在⊙A 的内部,B 点在⊙A 的外部,求r 和R 的变化范围.[解析](1) 在Rt ABC △中,305CAB BC ∠==,, 210AC BC ∴==.AE BC ∥,APE CPB ∴△∽△. ::3:1PA PC AE BC ∴==. :3:4PA AC ∴=,3101542PA ⨯==. (2)BE 与⊙A 相切.在Rt ABE △中,AB =15AE =,CCD图1图2tanAE ABE AB ∴∠===60ABE ∴∠= . 又30PAB ∠=,9090ABE PAB APB ∴∠+∠=∴∠=,, BE ∴与⊙A 相切.(3)因为5AD AB ==,r 的变化范围为5r <<当⊙A 与⊙C 外切时,10R r +=,所以R 的变化范围为105R -<;当⊙A 与⊙C 内切时,10R r -=,所以R 的变化范围为1510R <<+ 6、(2006浙江金华)如图,平面直角坐标系中,直线AB 与x 轴,y 轴分别交于A (3,0),B (0,3)两点, ,点C 为线段AB 上的一动点,过点C 作CD ⊥x 轴于点D .(1)求直线AB 的解析式;(2)若S 梯形OBCD 求点C 的坐标; (3)在第一象限内是否存在点P ,使得以P,O,B 为顶点的 三角形与△OBA 相似.若存在,请求出所有符合条件 的点P 的坐标;若不存在,请说明理由.[解析] (1)直线AB 解析式为:y=33-x+3. (2)方法一:设点C坐标为(x ,33-x+3),那么OD =x ,CD =33-x+3. ∴OBCD S 梯形=()2CD CD OB ⨯+=3632+-x . 由题意:3632+-x =334,解得4,221==x x (舍去) ∴ C(2,33)方法二:∵ 23321=⨯=∆OB OA S AOB ,OBCD S 梯形=334,∴63=∆ACD S . 由OA=3OB ,得∠BAO =30°,AD=3CD .∴ ACD S ∆=21CD ×AD =223CD =63.可得CD =33. ∴ AD=1,OD =2.∴C (2,33). (3)当∠OBP =Rt ∠时,如图①若△BOP ∽△OBA ,则∠BOP =∠BAO=30°,BP=3OB=3,∴1P (3,33). ②若△BPO ∽△OBA ,则∠BPO =∠BAO=30°,OP=33OB=1. ∴2P (1,3).当∠OPB =Rt ∠时③ 过点P 作OP ⊥BC 于点P(如图),此时△PBO ∽△OBA ,∠BOP =∠BAO =30°过点P 作PM ⊥OA 于点M .方法一: 在Rt △PBO 中,BP =21OB =23,OP =3BP =23. ∵ 在Rt △P MO 中,∠OPM =30°, ∴ OM =21OP =43;PM =3OM =433.∴3P (43,433). 方法二:设P(x ,33-x+3),得OM =x ,PM =33-x+3 由∠BOP =∠BAO,得∠POM =∠ABO .∵tan ∠POM==OMPM =x x 333+-,tan ∠ABOC=OBOA =3.∴33x+3=3x ,解得x =43.此时,3P (43,433).④若△POB ∽△OBA(如图),则∠OBP=∠BAO =30°,∠POM =30°. ∴ PM =33OM =43. ∴ 4P (43,43)(由对称性也可得到点4P 的坐标). 7、(2006河北课改)图14-1至图14-7的正方形霓虹灯广告牌ABCD 都是20×20的等距网格(每个小方格的边长均为1个单位长),其对称中心为点O .如图14-1,有一个边长为6个单位长的正方形EFGH 的对称中心也是点O ,它以每秒1个单位长的速度由起始位置向外扩大(即点O 不动,正方形EFGH 经过一秒由6×6扩大为8×8;再经过一秒,由8×8扩大为10×10;……),直到充满正方形ABCD ,再以同样的速度逐步缩小到起始时的大小,然后一直不断地以同样速度再扩大、再缩小.另有一个边长为6个单位长的正方形MNPQ 从如图14-1所示的位置开始,以每秒1个单位长的速度,沿正方形ABCD 的内侧边缘按A →B →C →D →A 移动(即正方形MNPQ 从点P 与点A 重合位置开始,先向左平移,当点Q 与点B 重合时,再向上平移,当点M 与点C 重合时,再向右平移,当点N 与点D 重合时,再向下平移,到达起始位置后仍继续按上述方式移动).正方形EFGH 和正方形MNPQ 从如图14-1的位置同时开始运动,设运动时间为x 秒,它们的重叠部分面积为y 个平方单位.(1)请你在图14-2和图14-3中分别画出x 为2秒、18秒时,正方形EFGH 和正方形MNPQ 的位置及重叠部分(重叠部分用阴影表示),并分别写出重叠部分的面积;(2)①如图14-4,当1≤x ≤3.5时,求y 与x 的函数关系式;②如图14-5,当3.5≤x ≤7时,求y 与x 的函数关系式; ③如图14-6,当7≤x ≤10.5时,求y 与x 的函数关系式; ④如图14-7,当10.5≤x ≤13时,求y 与x 的函数关系式.(3)对于正方形MNPQ 在正方形ABCD 各边上移动一周的过程,请你根据重叠部分面积y 的变化情况,指出y 取得最大值和最小值时,相对应的x 的取值情况,并指出最大值和最小值分别是多少. D 图14-2 图 D DD图14-1(P ) D N D[解析] (1)相应的图形如图2-1,2-2.当x =2时,y =3; 当x =18时,y =18.(2)①当1≤x ≤3.5时,如图2-3,延长MN 交AD 于K ,设MN 与HG 交于S ,MQ 与FG 交于T ,则MK =6+x ,SK =TQ =7-x ,从而MS =MK -SK =2x -1,MT =MQ -TQ =6-(7-x )= x -1. ∴y=MT ·MS =(x -1)(2x -1)=2x 2-3x +1.②当3.5≤x ≤7时,如图2-4,设FG 与MQ 交于T ,则 TQ =7-x ,∴MT =MQ -TQ =6-(7-x )=x -1. ∴y=MN ·MT =6(x -1)=6x -6.③当7≤x ≤10.5时,如图2-5,设FG 与MQ 交于T ,则 TQ=x -7,∴MT =MQ -TQ =6-(x -7)=13-x . ∴y = MN ·MT =6(13-x )=78-6x .④当10.5≤x ≤13时,如图2-6,设MN 与EF 交于S ,NP 交FG 于R ,延长NM 交BC 于K ,则MK =14-x ,SK =RP =x -7,图2-4D 图2-5D P图2-6D图2-3DQP 图2-2D 图2-1D QP∴SM=SK-MK=2x-21,从而SN=MN-SM=27-2x,NR=NP-RP=13-x.∴y=NR·SN=(13-x)(27-2x)=2x2-53x+351.(3)对于正方形MNPQ,①在AB边上移动时,当0≤x≤1及13≤x≤14时,y取得最小值0;当x=7时,y取得最大值36.②在BC边上移动时,当14≤x≤15及27≤x≤28时,y取得最小值0;当x=21时,y取得最大值36.③在CD边上移动时,当28≤x≤29及41≤x≤42时,y取得最小值0;当x=35时,y取得最大值36.④在DA边上移动时,当42≤x≤43及55≤x≤56时,y取得最小值0;当x=49时,y取得最大值36.。
江苏省镇江市5年中考数学试卷分析
江苏省镇江市近五年中考数学试卷分析学思堂镇江南大胡凯捷组:王珊珊一、试卷分析1.试卷结构①填空24分②选择15分③解答81分2.试题考试方向主要考察了对基础知识的内在联系以及掌握的熟练程度。
考察了数学的基本能力和综合能力,主要包括计算求解,推理证明,图形处理等,近几年偏向考各种函数的结合问题以及图形的反转(折叠)以及平移。
二、各章节所占分值四边形00105圆8111117统计5660概率6577数据集中和离散9222图形变换610122三、试卷具体内容分析考点内容时间题型分值有理数绝对值、相反数、倒数2015填空1,342014填空122013填空122012填空12有理数的混合运算2015\\2014填空222013填空222012填空22数轴、科学记数法2015填空7、选择135201419(2)22013\\2012\\一元一次方程2015\\2014\\2013选择1632012\\代数式2015\\2014填空1222013填空922012填空32走进图形世界展开与折叠2015\\2014应用28102013应用28102012\\三视图2015选择1432014选择1432013\\2012\\平面图形的认识平行、内错角,同旁内2015填空522014填空5,64角,同位角认识三角形,勾股定理2013填空6,填空104 2012填空6,选择175多边形内角和与外角和2015\\ 2014\\ 2013\\ 2012\\幂的运算2015填空2,18(1)6 2014选择13,18(1)5 2013填空11,选择13,18(1)7 2012选择14,选择176二元一次方程组2015选择3 2014\\ 2013\\ 2012选择153一元一次不等式2015应用19(2)5 2014填空12,选择17,19(2)9 2013选择16,19(2),应用279 201219(2)5整式乘法与因式分解整式乘法2015填空4,选择1552014填空322013填空422012填空52证明三角形全等2015填空8,20(1)5 2014应用206 2013应用216 2012应用216实数平方根、立方根2015应用18(1)2 2014应用18(1)2 2013填空52 2012填空42轴对称图形2015\\ 2014\\ 2013\\ 2012\\平面直角坐标系关于X、Y以及原点对称2015\\2014\\2013\\2012\\一次函数2015应用256 2014填空11,选择17,应用2311 2013填空9,应用276 2012应用24,应用2612数据的收集整理与描述2015\\ 2014应用216 2013应用226 2012应用205中心对称图形平行四边形、矩形、2015填空12,20(2)5菱形、正方形2014应用2810 2013\\ 2012\\旋转2015填空52 2014填空102 2013\\ 2012应用256分式2015填空5,应用题18,1910 2014填空4,18(2),1910 201318(2),198 2012填空11,18(2)6反比例函数2015应用256 2014应用256 2013选择17,应用277 2012应用246二次根式2015应用1842014选择15,18(1)72012选择13,18(1)5一元二次方程2015填空922014填空822013填空822012\\对称图形圆圆2015填空10,23(1),27142014选择1632013填空10,应用2582012应用236扇形面积、圆锥侧面积2015应用23(2)32014填空9,应用2682013选择1532012填空72数据的集中趋势和离散程度平均数、众数、中位数、方差,标准差、极差2015选择16,应用2092014填空722013填空72等可能条件下的概率概率、树状图2015应用2272014应用2272013应用2052012应用226二次函数2015填空11,28122014应用2792013选择14,应用24,26172012选择16,应用2711图形的相似图形(三角形)相似、投影2015填空8,应用2692014应用2662013应用2362012填空10,应用286锐角三角函数2015应用18,24102014选择16,18(2),24132013填空12,应用2382012应用18(1),应用238。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
法解答 问题 的能 力 , 分析 说 明. 现
题 目 如 图 , 平 面 直 角 坐 标 在
系 中 , 坐 标 原 点 。 为 圆 心 , 为 半 径 画 以 2 o o, 是 o o 上 一 动 点 , P 在 第 一 象 限 P 且 内 , 点 P 作 oo 的 切 线 与 X 轴 相 交 于 点 过
维普资讯
浅析一道坐标几何综合题
— —
2 0 年 镇江市一道 中考题评析 06
江苏省丹 阳市实验初 中 朱长安 苏三林
江 苏 省 镇 江 市 2 0 年 中 考 数 学 试 卷 中 的 最 后 一 道 题 是 坐 标 几 06
合题 , 考查 了学 生 “ 读 ・ 解 ・ 用’ 综合 能 力 又 考 查 了 学 生 灵 既 审 理 应 ’ 的 活运 用化 归 、 类 讨论 、 形 结合 等 思 想方 分 数
锐 的观察 力.
本题 考 查 的数 学 思 想 有 转 化 思 想 、 类 讨 论 的 思 想 、 形 结 合 思 想 等 . 分 数 这 些 数 学 思 数 学 思 想 方 法 , 在 可
“ 设’ “ 题 , 结论 ” 间架起 桥 梁 , 和 之 为探 索解 题 途径 起 到“ 航 ” 作 用. 导 的
理 由.
解
( )线段 AB 长度 的最 小值 为 4 理 由如下 : 1 ,
连 接 OP ,・AB 切 o o 于 P , AB上 OP. ’ ’ . 取 AB 的 中 点 C, 接 OC, O 是 Rt AB 斜 边 AB 上 的 中 线 连 则 C A O
’
。
.
.
A B 一 2 C. 0
当 OC — OP 时 , 最 短 , AB 最 短 . OC 即
此 时 ,・ ’ ’OC — OP 一 2 . 。. .AB 一 4 .
( )设 存 在 符 合 条 件 的 点 Q 2
如 图① , 四边形 APOQ 为 平行 四边 形 ,- APo 一 9 。 设 . . 0
.
. . 边 形 APOQ 为 矩 形 . ・四
V
标 为 (g 一 ) 4 , .
V
P
/ \ l 0 一l
一
一
/ \一lO \ \ \ \
.
八
.
图①
图②
如 图 ② , 四 边 形 APQo 为 平 行 四 边 形 , 设
‘
.
‘ OQ ∥ AP, APO 一 9 。 0,
.
‘
.
PoQ 一 9 。 0.
又 oP — OQ ,。 Q 一 4 。 . . 5.
。
.
‘ PQ ∥ Ao ,.P 上 Y轴 , 垂 足 为 点 H. ‘ Q . 设
OQ 一 4 OH , oH — QH 一 √2 于 是 得 g 即 ,
在 Rt OQH 中 ,. △ ‘ 。OQ 一 2 Q 一 4 。 , 5,
又 OP — OQ, ・四边形 APOQ 为正 方形 .。 Q — Q . ̄ QOA ・ 。 . .O A
,
维普资讯
一
45。
.
在 Rt A( Q 中 ,. A ) ‘ ‘OQ
‘ . .
Qo A 一 4 。 5
OA — , 是 得 ( 2 于
A, 与 轴 相 交 于 点 B.
—
口
\一1 1 / A 5 I O \ c
J
. .
辣
( )点 P 在 运 动 时 , 段 AB 的长 度 也 在 发 生 变 化 , 写 出线 段AB 1 线 请
长度 的 最小值 , 说 明理 由; 并 ( )在 o o 上 是 否 存 在 一 点 Q, 得 从 Q、O、A 、P 为 顶 点 的 四 边 2 使 形 是 平 行 四 边 形 ? 若 存 在 , 求 出 Q 点 的 坐 标 ; 不 存 在 , 说 明 请 若 请
。
.
.
Q 点 坐 标 为 (  ̄ , /) 一 /  ̄ . 2 2
。
.
.
符 合 条 件 的 点 Q 的 坐 标 为 (g, √ ) ( √ , 2 . 4 一 2 或 一 2 √ )
评析 该 题 是 试 卷 中 最 后 一 道 压 轴 题 , 是 平 面 直 角 坐 标 它
系 中 的 运 动 型 几 何 问 题 . 题 综 合 运 用 了 圆 的 性 质 、 线 的 性 质 、 角 该 切 直
三 角形斜 边上 的 中线的 性 质 、 线段 最短 、 行 四 边 形 的性 质 、 形 、 垂 平 矩 菱 形 、 方 形 的 判 定 和 性 质 、 象 限 内点 的 坐标 的 特 征 、 腰 直 角 三 角 形 中 正 各 等
三 边 之 比 为 1: 1: 2 平 行 线 的 性 质 等 知 识 , 及 知 识 点 多 , √、 涉 需要 有 敏
