基于Excel的地理数据分析多元线性回归分析
EXCEL在多元线性回归分析中的应用
EXCEL 在多元线性回归分析中的应用高 平/文在一元线性回归分析中,重点放在了用模型中的一个自变量X 来估计因变量Y 。
实际上,由于客观事物的联系错综复杂,一个因变量的变化往往受到两个或多个自变量的影响。
为了全面揭示这种复杂的依存关系,准确地测定它们的数量变动,提高预测和控制的精确度,就要考虑更多的自变量,建立多元回归模型。
多元回归分析的原理和方法同一元线性回归分析基本相同,但有两个不同点:1.不能用散点图来表示变量之间的关系。
2.多元回归的计算难度要远大于简单线性回归,且变量越多,计算越复杂。
但应用EXCEL 来完成计算将变得简单和轻松。
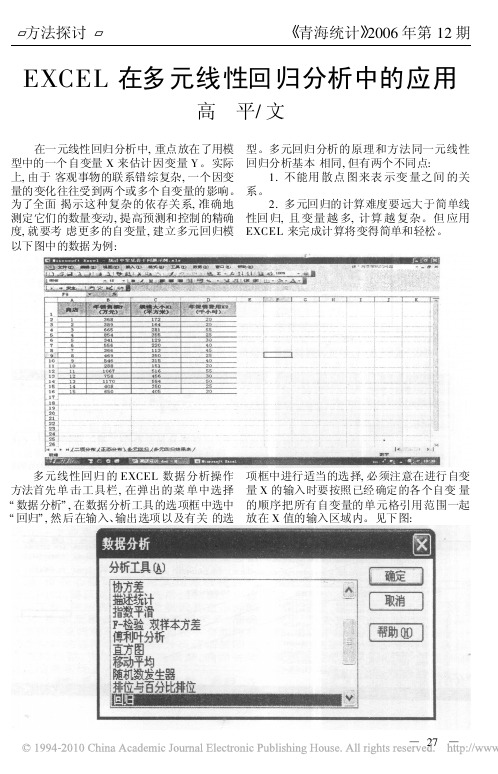
以下图中的数据为例: 多元线性回归的EXCEL 数据分析操作方法首先单击工具栏,在弹出的菜单中选择数据分析 ,在数据分析工具的选项框中选中 回归 ,然后在输入、输出选项以及有关的选项框中进行适当的选择,必须注意在进行自变量X 的输入时要按照已经确定的各个自变量的顺序把所有自变量的单元格引用范围一起放在X 值的输入区域内。
见下图:!27!点击 确定按钮,即可得到线性回归分析的结果。
见下图:!!28根据上图中的显示结果,可直接写出二元线性回归方程:Y i=b0+b1X1i+b2X2i=-51.3127+1. 4053x1i+6.3823x2ib1表示在促销费用固定时,商店的规模大小每增加1平方米,年销售额平均增加1.4053万元;b2表示在商店的规模大小固定时,促销费用每增加1万元,年销售额平均增加6.3823万元。
这里b1即商店的规模大小的回归系数比一元线性回归方程中的回归系数b= 1.6246小,是因为一元线性回归方程只考虑了商店的规模大小对年销售额的影响,忽略了促销费用这一很重要的因素,在商店的规模大小的影响中渗入了促销费用的影响。
这里的截距b0=-51.3127万元,与一元线性回归方程中的截距+99.01万元有很大的不同,因为X1=0和X2 =0都不在X1、X2的样本取值范围之内,因而对截距项的解释要非常谨慎。
excel多元回归模型

excel多元回归模型
Excel可以使用数据分析工具包中的回归分析功能进行多元回归分析。
使用该功能需要满足以下条件:
1. 数据符合多元线性回归的基本假设,即各自变量之间相互独立,且对应因变量的关系为线性关系。
2. 数据已输入Excel表格中,并按照自变量和因变量分列排列。
3. 安装并启用数据分析工具包。
下面是使用Excel进行多元回归的步骤:
步骤1:打开Excel表格,并打开“数据分析工具包”。
步骤2:选择“回归”功能,并点击“确定”。
步骤3:在“回归”对话框中填写以下信息:
i. 输入数据范围:选择自变量和因变量所在的单元格区域。
ii. 选择输出选项:选择需要计算的统计量,例如ANOVA表、系数、标准误差、t值等。
iii. 选择自变量:选择包含自变量的单元格区域。
iv. 选项:选择是否需要新增截距项,以及是否需要输出残差。
步骤4:点击“确定”按钮,Excel会自动对输入数据进行多元回归分析,并在新的工作表中显示回归结果的各项统计量。
需要注意的是,在进行多元回归分析之前,需要进行基本的数据清洗和预处理,例如删除缺失数据、处理异常值等。
此外,在解释回归结果时,还需注意各系数的显著性和实际意义。
用Excel做线性回归分析

用Excel举止一元线性返回分解之阳早格格创做Excel功能强盛,利用它的分解工具战函数,不妨举止百般考查数据的多元线性返回分解.本文便从最简朴的一元线性回纳进脚.正在数据分解中,对付于成对付成组数据的拟合是时常逢到的,波及到的任务有线性形貌,趋势预测战残好分解等等.很多博业读者逢睹此类问题时往往觅供博业硬件,比圆正在化工中经时常使用到的Origin战数教中罕睹的MATLAB等等.它们虽很博业,然而本去使用Excel便真足够用了.咱们已经知讲正在Excel自戴的数据库中已有线性拟合工具,然而是它还稍隐单薄,即日咱们去测验考查使用较为博业的拟合工具去对付此类数据举止处理.文章使用的是2000版的硬件,尔正在其中的一些步调也增加了2007版的注解.1 利用Excel2000举止一元线性返回分解最先录进数据.以连绝10年最大积雪深度战灌溉里积闭系数据为例给予证明.录进截止睹下图(图1).图1第两步,做集面图如图2所示,选中数据(包罗自变量战果变量),面打(H)(excel2007)”..选中数据后,数据形成蓝色(图2).图2面打“图表背导”以去,弹出如下对付话框(图3):图3正在左边一栏中选中“XY集面图”,面打“完毕”按钮,坐时出现集面图的本初形式(图4):图4第三步,返回瞅察集面图,推断面列分集是可具备线性趋势.惟有当数据具备线性分集特性时,才搞采与线性返回分解要领.从图中不妨瞅出,本例数据具备线性分集趋势,不妨举止线性返回.返回的步调如下:⑴最先,挨启“工具”下推菜单,可睹数据分解选项(睹图5)(2007为”数据”左端的”数据分解”):图5用鼠标单打“数据分解”选项,弹出“数据分解”对付话框(图6):图6⑵而后,采用“返回”,决定,弹出如下选项表:图7举止如下采用:X、Y值的输进地区(B1:B11,C1:C11),标记,置疑度(95%),新处事表组,残好,线性拟合图.大概者:X、Y值的输进地区(B2:B11,C2:C11),置疑度(95%),新处事表组,残好,线性拟合图.注意:选中数据“标记”战没有选“标记”,X、Y值的输进地区是纷歧样的:前者包罗数据标记:最大积雪深度x(米)灌溉里积y(千亩)后者没有包罗.那一面务请注意.图8-1 包罗数据“标记”图8-2 没有包罗数据“标记”⑶再后,决定,博得返回截止(图9).图9 线性返回截止⑷末尾,读与返回截止如下:F⑸修坐返回模型,并对付截止举止考验2值不妨曲交从返回截止中读出.本质.有了R值,F值战t值均可预计出去.F值的预计公式战截止为:隐然与表中的截止一般.t值的预计公式战截止为:,而后供残好仄圆战于是图10 y的预测值及其相映的残好等从而,不妨预计DW值(拜睹图11),预计公式及截止为.图11 利用残好预计DW值末尾给出利用Excel赶快预计模型的要领:⑴用鼠标指背图4中的数据面列,单打左键,出现如下采用菜单(图12):图12⑵面打“增加趋势线(R)”,弹出如下采用框(图13):图13⑶正在“分解典型”中采用“线性(L)”,而后挨启选项单(图14):图14⑷正在采用框中选中“隐现公式(E)”战“隐现R仄圆值(R)”(如图14),决定,坐时得到返回截止如下(图15):图15正在图15中,给出了返回模型战相映的测定系数即拟合劣度.。
利用Excel2000进行多元线性回归分析

3 利用Excel2000进行多元线性回归分析【例】某省工业产值、农业产值、固定资产投资对运输业产值的影响分析。
Excel2000的操作方法与一元线性回归分析大同小异:第一步,录入数据(图1)。
图1 录入的原始数据第二步,数据分析⑴沿着主菜单的“工具(T)”→“数据分析(D)…”路径打开“数据分析”对话框,选择“回归”,然后“确定”,弹出“回归”分析对话框,对话框的各选项与一元线性回归基本相同(图2)。
下面只说明x值的设置方法:首先,将光标置于“X值输入区域(X)”中(图2);然后,从图1所示的C1单元格起,至E19止,选中用作自变量全部数据连同标志,这时“X值输入区域(X)”的空白栏中立即出现“$C$1:$E$19”——当然,也可以通过直接在“X值输入区域(X)”的空白栏中输入“$C$1:$E$19”的办法实现这一步骤。
注意:与一元线性回归的设置一样,这里数据范围包括数据标志:工业产值x1 农业产值x2 固定资产投资x3 运输业产值y故对话框中一定选中标志项(图3)。
如果不设“标志”项,则“X值输入区域(X)”的空白栏中应为“$C$2:$E$19”,“Y值输入区域(Y)”的空白栏中则是“$F$2:$F$19”。
否则,计算结果不会准确。
图2 x值以外的各项设置图3 设置完毕后的对话框(包括数据标志)⑵完成上述设置以后,确定,立即给出回归结果。
由于这里的“输出选项”选中了“新工作表组(P)”(图3),输出结果在出现在新建的工作表上(图4)。
从图4的“输出摘要(SUMMARY OUTPUT)”中可以读出:0044.1-=a ,053326.01=b ,00402.02-=b ,090694.03=b ,994296.0=R ,988625.02=R,335426.0=s ,5799.405=F ,940648.21=b t ,28629.02-=b t ,489706.33=b t 。
根据残差数据,不难计算DW 值,方法与一元线性回归完全一样。
excel多元函数线性回归步骤

多元函数线性回归步骤1.加载数据分析第一步:打开2007excel,点击左上角的按钮,如图所示。
第二步:点击右下角的,如图所示。
第三步:点击左侧的加载项,如图所示。
第四步:点击最下面的“转到”,如图所示,然后选中“分析数据库”,点击“确定”。
2.数据的整理已知 和 , 和 , 和 ,将其整理为lnCij B ijP P ,C Bij ij t t -和CB ij ij c c -,见下表。
整理后的数据为:3.数据分析第一步:点击excel2007中工具栏的“数据”,然后点击“数据分析”,弹出数据分析的对话框,如图所示。
第二步:选中“回归”,点击确定,弹出对话框,如图所示。
第三步:“Y值输入区域”选择第一列,“X值输入区域”选择后两列,选择“置信度”,“新工作表组”,“残差”和“标准残差”。
如图所示,点击确定。
4.结果分析结果如图所示。
只需找到如下表所示的内容,Coefficients(系数)Intercept(截距)0.38980452(对应γ)X Variable 1 -0.079587874(对应α)X Variable 2 -0.003868252(对应β)出师表两汉:诸葛亮先帝创业未半而中道崩殂,今天下三分,益州疲弊,此诚危急存亡之秋也。
然侍卫之臣不懈于内,忠志之士忘身于外者,盖追先帝之殊遇,欲报之于陛下也。
诚宜开张圣听,以光先帝遗德,恢弘志士之气,不宜妄自菲薄,引喻失义,以塞忠谏之路也。
宫中府中,俱为一体;陟罚臧否,不宜异同。
若有作奸犯科及为忠善者,宜付有司论其刑赏,以昭陛下平明之理;不宜偏私,使内外异法也。
侍中、侍郎郭攸之、费祎、董允等,此皆良实,志虑忠纯,是以先帝简拔以遗陛下:愚以为宫中之事,事无大小,悉以咨之,然后施行,必能裨补阙漏,有所广益。
将军向宠,性行淑均,晓畅军事,试用于昔日,先帝称之曰“能”,是以众议举宠为督:愚以为营中之事,悉以咨之,必能使行阵和睦,优劣得所。
亲贤臣,远小人,此先汉所以兴隆也;亲小人,远贤臣,此后汉所以倾颓也。
[精品WORD]教你用Excel做回归分析
![[精品WORD]教你用Excel做回归分析](https://img.taocdn.com/s3/m/433c51b9fbb069dc5022aaea998fcc22bcd143c4.png)
[精品WORD]教你用Excel做回归分析用Excel进行回归分析可以很方便地对数据进行分析和预测。
以下是使用Excel进行回归分析的步骤和解释:1.导入数据首先,将需要分析的数据导入Excel中。
可以在Excel的菜单栏中选择“数据”,然后选择“导入外部数据”或“从数据库导入数据”。
导入数据后,将数据放置在一个表格中。
2.选中数据在Excel表格中选中包含数据的区域。
确保包含需要分析的数据,以及任何其他相关的数据列。
3.插入图表在Excel的菜单栏中选择“插入”,然后选择“图表”。
在图表类型中选择适合的数据类型,例如线性图、散点图等。
在弹出的对话框中,选择需要分析的数据区域,并设置图表的其他选项。
4.添加趋势线在图表中单击鼠标右键,选择“添加趋势线”。
在弹出的对话框中,选择要添加趋势线的图表类型,例如线性、指数、对数等。
选择要添加趋势线的数据系列,并设置趋势线的其他选项。
5.显示回归分析结果在趋势线对话框中,选择“显示公式”和“显示R平方值”。
这将显示回归分析的结果,包括回归线的公式和R平方值。
R平方值越接近1,说明回归模型越精确。
6.分析回归结果根据回归分析的结果,可以得出以下结论:•斜率:回归线的斜率表示自变量对因变量的影响程度。
斜率越大,影响程度越大。
•截距:回归线的截距表示因变量在自变量为0时的值。
•R平方值:R平方值表示回归模型对数据的拟合程度。
如果R平方值接近1,说明模型拟合度较高。
•F值:F值是进行回归分析时的统计量,表示整个回归模型的显著性。
如果F值较大,说明模型显著性较高。
•P值:P值表示自变量对因变量的影响是否显著。
如果P值小于0.05,说明自变量对因变量的影响是显著的。
7.使用回归模型进行预测根据回归分析的结果,可以使用回归模型对未来数据进行预测。
将自变量的预测值代入回归模型中,即可得出因变量的预测值。
总之,使用Excel进行回归分析可以方便地得出数据的回归分析结果,以及对未来数据进行预测。
excel线性回归分析
excel线性回归分析Excel性回归分析是一种有用的工具,可以用来探究强相关关系,并用来预测未知的变量与已知变量之间的关系。
它也可以用来确定输入变量和输出变量之间的线性关系。
Excel线性回归分析的发展早在20世纪末就开始了,随着Microsoft Excel的出现,它得到了进一步的发展。
Excel的线性回归分析用于检查两种变量之间的关系。
它使用数学模型来估计数据中各个变量的值,以反映两个量之间的关系。
通过Excel的线性回归分析,可以分析受试者的数据,发现数据之间的相关性。
可以用来确定输出变量和输入变量之间的关系,以及输出变量对输入变量的响应。
Excel线性回归分析可以用来解决很多问题,包括金融预测、统计学研究、政策分析等等。
在统计学研究中,它可以用来评估多个变量的影响,探究它们之间的关系。
它也可以用来预测未知变量的变化,对政策制定做出决策。
使用Excel线性回归分析的过程可以总结为三个步骤:准备数据、分析数据和绘制图表。
准备数据时,首先需要准备要使用的数据集。
要分析的数据可以以数据库、表格或Excel表格的形式准备好。
这些数据应该位于单独的列中,并且要有一个输出变量和一个或多个输入变量。
另外,如果数据集中存在空白,那么这些空白也应该被填充或删除。
然后,就可以开始分析数据了。
首先使用Excel函数来计算多个变量之间的相关系数。
这样可以确定输入变量与输出变量之间的关系。
接下来,要使用Excel的“ Regression”功能,根据以上确定的结果来估计线性模型并获得参数估计值。
最后,用Excel绘制图表来检验估计结果的准确性,帮助用户最大限度地了解结果。
通过以上过程,就可以使用Excel线性回归分析来深入了解两个或多个变量之间的关系,并为制定政策提供有价值的参考。
Excel 线性回归分析不仅可以节省时间,而且可以提高数据分析的准确性和可重复性。
它的使用非常简单,非常适合用于数据科学研究和分析,可以帮助数据分析人员快速准确地分析数据,进行预测和决策。
;2运用EXCEL、SPSS进行相关分析和线性、非线性回归分析
《计量地理学》实验指导§2 运用EXCEL、SPSS进行相关分析和线性、非线性回归分析回归分析是处理两个及两个以上变量间线性依存关系的统计方法。
可以通过软件EXCEL 和SPSS实现。
一、利用EXCEL软件实现回归分析以第4章习题2为例,运用EXCEL进行回归分析。
首先在菜单中选择工具==>加载宏,把“分析工具库”和“规划求解”加载上。
然后在“工具”菜单中将出现“数据分析”选项。
点击“数据分析”中的“回归”,将出现对话框如下图1所示。
图1 回归界面【输入】用以选择进行回归分析的自变量和因变量。
在“Y值输入区域”内输入B7:B11,在“X值输入区域”输入A7:A11,如果是多元线性回归,则X值的输入区就是除Y变量以外的全部解释变量“标志”;置信度水平为95%,输出结果选择在一张新的工作表中;“残差分析”,并绘制回归拟合图,点击“确定”即得到残差表。
【输出选项】用于指定输出结果要显示的内容,包括是否需要残差表及图,参差的正态分布图等。
输出结果解释图 2 回归结果显示回归结果分为三部分:(1)回归统计:包括R^2 及调整后的R^2、标准误差和观测值个数(2)方差分析:包括回归平方和、残差平方和总离差平方和以及它们的自由度、均方差和F通机量(3)回归方程的截距、自变量的系数以及它们的t统计值、95%的上下限值图3 残差与子变量之间的散点图图4 预测值与实际值散点图同样,如果在“数据分析”中点击“相关系数”,可以对多个变量进行相关系数的计算。
二、.利用SPSS软件实现回归分析在SPSS软件中,同样可以简单的实现回归分析,因为回归分析包含了线性回归与曲线拟合两部分内容,首先来看线性回归分析过程(LINEAR)(一)线性回归分析过程(LINEAR)例如,课本中数据,把降水量(P)看作因变量,把纬度(Y)看作自变量,在平面直角坐标系中作出散点图,发现它们之间呈线性相关关系,因此,可以用一元线性回归方程近似地描述它们之间的数量关系。
用EXCEL做线性回归的方法
3.选择XY散点图,然后点击下一步,出现,如下图所示
4.继续点击下一步
5.可以在此输入对应的标题,X轴Y轴值,继续点击下一步,出现
6.点击完成出现生成的曲线,然后用鼠标指着点,右击,选择添加趋势线,出现对话框
选中线性,然后点击确定,出现
7.用鼠标指着直线,然后右击,点击趋势线格式,点击选项
excel做线性回归用excel做线性回归excel线性回归excel非线性回归excel表格线性回归excel多元线性回归excel线性回归方程excel2007线性回归excel线性回归预测excel2010线性回归
用Excel做线性回归的方法
以下列数据为例说明:
1.首先在excel中输入数据,如下
用Excel做线性回归分析报告
用Excel进展一元线性回归分析Excel功能强大,利用它的分析工具和函数,可以进展各种试验数据的多元线性回归分析。
本文就从最简单的一元线性回归入手.在数据分析中,对于成对成组数据的拟合是经常遇到的,涉与到的任务有线性描述,趋势预测和残差分析等等。
很多专业读者遇见此类问题时往往寻求专业软件,比如在化工中经常用到的Origin和数学中常见的MATLAB等等。
它们虽很专业,但其实使用Excel就完全够用了。
我们已经知道在Excel自带的数据库中已有线性拟合工具,但是它还稍显单薄,今天我们来尝试使用较为专业的拟合工具来对此类数据进展处理。
文章使用的是2000版的软件,我在其中的一些步骤也添加了2007版的注解.1 利用Excel2000进展一元线性回归分析首先录入数据.以连续10年最大积雪深度和灌溉面积关系数据为例予以说明。
录入结果见如下图〔图1〕。
图1第二步,作散点图如图2所示,选中数据〔包括自变量和因变量〕,点击“图表向导〞图标;或者在“插入〞菜单中打开“图表〔H〕(excel2007)〞。
图表向导的图标为。
选中数据后,数据变为蓝色〔图2〕。
图2点击“图表向导〞以后,弹出如下对话框〔图3〕:图3在左边一栏中选中“XY散点图〞,点击“完成〞按钮,立即出现散点图的原始形式〔图4〕:灌溉面积y(千亩)01020304050600102030灌溉面积y(千亩)图4第三步,回归观察散点图,判断点列分布是否具有线性趋势。
只有当数据具有线性分布特征时,才能采用线性回归分析方法。
从图中可以看出,本例数据具有线性分布趋势,可以进展线性回归。
回归的步骤如下:⑴ 首先,打开“工具〞下拉菜单,可见数据分析选项〔见图5〕(2007为〞数据〞右端的〞数据分析〞):图5 用鼠标双击“数据分析〞选项,弹出“数据分析〞对话框〔图6〕:图6⑵ 然后,选择“回归〞,确定,弹出如下选项表:图7进展如下选择:X 、Y 值的输入区域〔B1:B11,C1:C11〕,标志,置信度〔95%〕,新工作表组,残差,线性拟合图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于Excel 的地理数据分析多元线性回归分析多元线性回归分析是一元线性回归分析的推广,或者说一元线性回归分析是多元线性回归分析的特例。
掌握了一元线性回归分析,就不能学习多元线性回归分析方法了。
利用Excel 进行多元线性回归与一元线性回归的过程大体相似,操作上有些细节方面的微妙差别。
不过,对于多元线性回归,统计检验的内容相对复杂。
下面以一个简单的实例予以说明。
【例】某省工业产值、农业产值、固定资产投资对运输业产值的影响分析。
通过产值的回归模型,探索影响交通运输业的主要因素。
我们想要搞清楚的是,在工业、农业和固定资产投资等方面,究竟是哪些因素直接影响运输业的发展。
数据来源于李一智主编的《经济预测技术》。
原始数据来源不详。
§2.1 多元回归过程2.1.1 常规分析在Excel 中,多元线性回归大体上可以分为如下几个步骤实现。
第一步,录入数据。
结果如下图所示(图2-1-1)。
第二步,计算过程。
比较简单,分为如下若干个步骤。
(1)打开回归对话框。
沿着主菜单的“工具(T)”→“数据分析(D)…”路径打开(2)“数据分析”对话框,选择“回归”,然后“确定”,弹出“回归”分析选项框,选项框的各(3)选项与一元线性回归基本相同(图2-1-2)。
具体说明如下。
(4)(2)输入选项。
首先,将光标置于“Y值输入区域(Y)”中。
从图2-1-1所示的F1单元(5)格起,至F19止,选中用作因变量全部数据连同标志,这时“Y值输入区域(Y)”的数据区域(6)中立即出现“$F$1:$F$19”。
然后,将光标置于“X值输入区域(X)”中。
从图2-1-1所示的C1单元格起,至E19止,选中用作自变量全部数据连同标志,这时“X值输入区域(X)”中立即出现“$C$1:$E$19”——当然,也可以直接在“X值输入区域(X)”中手动输入地址为“$C$1:$E$19”的单元格范围。
注意,与一元线性回归的设置一样,这里数据范围包括数据标志“工业产值x1”、“农业产值x2”、“固定资产投资x3”和“运输业产值y”。
因此,选项框中一定选中“标志”项(图2-1-3)。
如果不设“标志”项,则“X值输入区域(X)”的对话框中应为“$C$2:$E$19”,“Y值输入区域(Y)”的对话框中则是“$F$2:$F$19”。
否则,计算结果不会准确。
完成上述设置以后,确定,立即给出回归结果。
由于这里的“输出选项”选中了“新工作表组(P)”(图2-1-3),输出结果在出现在新建的工作表上(图2-1-4)。
第三步,结果解读。
这一步与一元线性回归也没有太大差别。
(1)读出回归系数,建立模型。
从图2-1-4所示的“输出摘要(SUMMARY OUTPUT)”中可以读出截距a,以及三个回归系数b1、b2和b3,对应于三个变量工业产值x1、农业产值x1、固定资产投资x2。
数值如下a = −1.0044 , b1 = 0.053326 , b2 = −0.00402 , b3 = 0.090694 .与t统计量等价的时P值。
P小于0.05,表明回归系数的置信度达到95%以上,相应的t检验在显著性水平为α=0.05时可以通过;P小于0.01,表明回归系数的置信度达到99%以上,相应的t 检验在显著性水平为α=0.01时可以通过。
其余依此类推。
为了简明,可以将P值添加到线性回归模型里面,得到展,交通运输业越是受到负面影响。
这在道理上是不通的。
按理说,农业增长应该引起交通运输业的进一步发展才对。
其二,回归系数b2的t检验不能通过。
回归系数的P值高达0.779,置信度只有20%左右,这就有问题了。
其三,回归系数b2的绝对值偏小。
可以判定,自变量之间可能存在多重共线性问题。
2.1.2 偏相关系数的计算和分析在具有多重共线性的线性回归问题中,偏相关系数(partial correlation coefficient)在进行变量取舍判断时具有一定的参考价值。
Excel不能直接给出偏相关系数,但借助有关的函数或命令,可以方便地算出偏相关系数。
计算公式为有了上述公式,可以借助计算矩阵行列式的函数mdeterm计算逆矩阵,然后计算偏相关系数。
最快速的办法是利用矩阵求逆函数minverse。
具体工作可以由以下几个步骤完成。
第一步,计算相关系数相关系数可以借助命令correl或者pearson逐一计算。
为了直观和便捷,不妨给出相关系数矩阵。
首先,沿着“工具(T)→数据分析(D)”的路径,从工具箱的“数据分析”对话框中选择“相关系数”(图2-1-5)。
然后,根据图2-1-1所示的数据分布的单元格范围,在“相关系数”对话框中进行如下设置(图2-1-6)。
注意:“输入区域(I)”中包括自变量和因变量覆盖的数据范围,包括数据标志,并且我们是逐列计算。
确定以后,得到相关系数矩阵。
由于相关矩阵是对称的,Excel只给出了下三角部分(图2-1-7)。
容易根据对称性将上三角部分填补起来(图2-1-8)。
第二步,计算逆矩阵借助函数minverse,非常容易得到相关系数矩阵的逆矩阵。
Minverse的语法如下:Minverse(Array)。
Array为行数和列数相等的数组。
具体到我们的问题,则是先选中一个4×4的数值区域,然后键入“=minverse()”,再然后将光标置于括号中,选中相关的数据——注意不含标志(图2-1-8)。
同时按下Ctrl键和Shift键,回车,立即得到逆矩阵(图2-1-9)。
第四步,偏相关系数分析偏相关系数是假定在一个模型中其他变量不变的情况下,一个自变量与因变量的相关性。
从图2-1-7所示的计算结果可以看出,农业产值与运输业产值的简单相关系数很高,且为正值(0.965)。
但是,在多元线性回归模型中,SPSS给出的偏相关系数很小且为负(-0.076)。
这就是说,单就相关性而言,农业产值与运输业产值肯定是高度正相关的;但是,在模型中,偏相关系数却“说”农业产值对运输业的贡献很小且为负。
这是相互矛盾的。
究其根源,可能是因为农业产值与其他变量具有相关性,因为共线性导致模型回归系数及其检验参量失真。
也可能属于如下情况,农业对运输业的贡献可能是间接的,是通过其他产业部门如工业发生影响。
一言以蔽之,农业产值与运输业产值的偏相关系数暗示两个问题:一是数值太小,表明相关性很低,从而意味着它在线性回归模型中的地位不重要;二是数值为负,表明负相关。
这两种情况都与简单相关系数反映的情况不一致,与我们对现实世界的认识也不尽相符。
这是违背常理的计算结果——农业发展反而导致运输业滞缓。
由此可见,偏相关系数反映的信息与回归系数和t值(或者P值)给出的结果彼此呼应。
§2.2 多重共线性分析2.2.1 共线性判断根据上面的回归参数和相应统计量的初步考察可以判定,模型中存在自变量共线性问题。
有必要对模型中的自变量进行多重共线性判断,然后调整模型的结构。
为了分析多重共线性问题,有必要计算出各个自变量对应的容忍度(Tol)和方差膨胀因子(VIF)。
计算方法如下。
(1) 逐步计算第一步,以工业产值(x1)为因变量,以农业产值(x2)和固定资产投资(x3)为自变量,基于如下模型进行多元线性回归x1 = C + ax2 + bx3 ,从回归结果摘要(Summary Output)的“回归统计”中,可以读到复相关系数(R)的平方值(R Square)为R2=0.97898(图2-2-1),于是得到容忍度1 2 1 0.97898 0.021021 Tol = −R = − = ,相应地,方差膨胀因子为(2) 矩阵计算利用矩阵函数,可以非常方便地计算出VIF值,进而算出Tol值。
首先,借助数据分析的相关系数计算功能,利用前面说明的方法计算自变量的相关系数矩阵(图2-2-2);然后,借助矩阵求逆函数minverse计算相关系数矩阵的逆矩阵(图2-2-3)。
可以看出,这个逆矩阵的对角线上的元素,就是相应的VIF值。
利用矩阵运算,远比逐步计算的效率高。
根据上面的计算结果可以看到,所有的VIF值都大于经验上的检验标准(VIF=10)。
其中工业产值(x1)对应的VIF值最大,这意味着它与其他变量的共线性最强;农业产值(x2)对应的VIF值为次大,固定资产投资(x3)对应的VIF值相对最小。
但是,考虑到回归系数的合理性,首先应该考虑到剔除农业产值,用剩余的变量进行多元线性回归。
2.2.2 剔除异常变量剔除异常变量x2(农业产值),用剩余的自变量x1、x3与y回归(图2-2-4),回归步骤自然是重复上述过程(参见图2-2-5),最后给出的回归结果如下(图2-2-6)。
从图2-2-6中容易读出回归系数估计值和相应的统计量:a = −0.89889 , b1 = 0.051328 , b3 = 0.091229 ;R = 0.994263 , R2 = 0.988558 ;s = 0.324999 ;F = 647.973 ;t b1 = 4.200968 , t b3 = 3.632285 .根据上述结果,建立二元回归模型如下:0.099 0.001 0.00290.8989 0.0513 1 0.0912 3P值y = − + x + x,利用残差或者标准残差容易算出,DW 值约为1.769。
在显著性水平为α=0.05、回归自由度为m=2 时,DW 检验的临界值上下界分别为d l=1.05 的、d u=1.53。
显然,相对于第一次回归结果,回归系数的符号正常,检验参数F值提高了,标准误差s值降低了,t值检验均可通过。
相关系数R有所降低,这也比较正常——一般来说,增加变量数目通常提高复相关系数,减少变量则降低复相关系数。
相对于第一次和第二次回归结果,回归系数的符号正常,但检验参数F值降低了,标准误差s值提高了,t值检验均可通过,相关系数R有所降低。
比较而言,这一次的P值似乎更为合理,回归系数估计值没有任何难以理解之处。
根据上述结果,建立二元回归模型如下§2.3 借助线性回归函数快速拟合2.3.1 直接的公式运算利用线性拟合函数linest可以对模型参数即重要的统计量进行快速估计。
线性拟合函数的语法如下LINEST(known_y's, known_x's, const,stats)这里,known_y’s表示因变量y对应的已知数据集合,known_x’s表示自变量x对应的已知数据集合,const和stats为逻辑值,只能取true或者false,const的默认值为true(这时可以得到正常估计的截距,否则截距为0),stats的默认值为false(这时仅仅给出回归系数,否则会给出斜率和必要的统计参量)。
上述函数可以直接键入,也可以从“编辑栏”中调出函数。
