吉林大学大学物理练习册综合练习二答案
吉林大学大学物理作业答案综合练习题(下)(二)
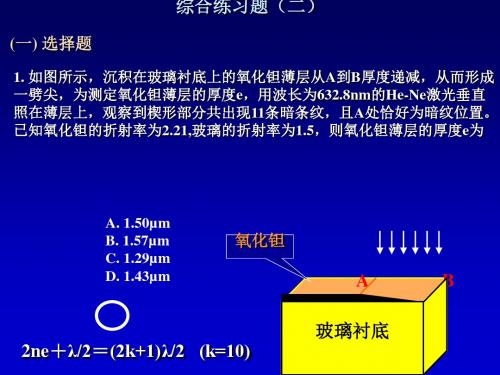
(一) 选择题
1. 如图所示,沉积在玻璃衬底上的氧化钽薄层从A到B厚度递减,从而形成 一劈尖,为测定氧化钽薄层的厚度e,用波长为632.8nm的He-Ne激光垂直 照在薄层上,观察到楔形部分共出现11条暗条纹,且A处恰好为暗纹位置。 已知氧化钽的折射率为2.21,玻璃的折射率为1.5,则氧化钽薄层的厚度e为
2 a b 10 2 4 0 0 n m s i n 3 0
1
4.一平面透射光栅,当用白光垂直照射时,能在30°衍射方向上观察到600nm的第 二级干涉主极大,并能在该处分辨△λ=0.05nm的两条光谱线,但在此30°方向上却 测不到400nm的第三级主极大,计算此光栅的缝宽a和缝距b以及总缝数N 。
6.氢原子中核外电子所处状态的角量子数是l=2,其绕核运动的角动量的 大小 ;该角动量的空间取向可能有 5 种。 一级明
6
a sin 3 ;
a sin k; 2
k1 .5
9.一电磁波在空气中通过某点时,该点某一时刻的电场强度 为E,则同时刻的磁场强度H= ,能流密度S= 。
光栅对第k级主极大的分辨本领为
对于 =600nm的第二级主极大有
0 . 0 5 n m
所以,光栅总缝数
R kN
6 0 0 N 6 0 0 0 k 2 0 . 0 5
5. 在惯性系K中观测到相距 的两地点相隔 8 发生两事 x 9 1 0m 件,而在相对于K系沿x轴正向以匀速度运动的 系中发现此两事件 恰好发生在同一地点,试求在 系中此两事件的时间间隔。 t 5s
m向下拉x时,
kx a J m 2 R k 2 J m 2 R
T2 k ( x x 0 ) mg T 1 ma T R T R J 2 1 a R
吉林大学大学物理练习册综合练习二答案

c′
V
8.1mol刚性双原子分子理想气体,当温度为 时,其 . 刚性双原子分子理想气体, 刚性双原子分子理想气体 当温度为T时 内能为
3 A . RT 2 3 B . kT 2
5 C . RT 2
5 D . kT 2
4
9.对于室温下的双原子分子理想气体,在等压 .对于室温下的双原子分子理想气体, 膨胀的情况下, 膨胀的情况下,系统对外所作的功与从外界吸 收的热量之比 A/Q 等于 A. 1/3 B. 1/4 C. 2/5 D. 2/7 10.一定量的理想气体向真空作绝热自由膨 . 体积由V 增至V 胀,体积由 1增至 2,在此过程中气体的 A. 内能不变,熵增加 内能不变, B. 内能不变,熵减少 内能不变, C. 内能不变,熵不变 内能不变, D. 内能增加,熵增加 内能增加,
m mg µl M f = 2∫ ⋅ dr ⋅ gµr = 0 2l 2
l
M f ⋅ ∆t = 0 − Iω 0 ⇒ 2 lω 0 ∆t = 3 µg
8
5. 如图所示 , 质点 的质量为 . 如图所示, 质点P的质量为 的质量为2kg, 位置矢量 , r r r 的作用。 为 r ,速度为 υ ,它受到力 F 的作用。这三个 −1 量均在xOy平面内,且r = 3m, = 4.0m ⋅ s , 平面内, 量均在 平面内 , υ r F=2N。 则该质点对 点的角动量 12kkgm2s−1, 点的角动量=_________, 。 则该质点对O点的角动量 r 作用在质点上的力对O点的力矩 点的力矩=___________。 作用在质点上的力对 点的力矩 3kNm 。
角动量(动量矩) 角动量(动量矩)
r r r L = r × mυ
r r r M = r ×F
大学物理II练习册答案3课件

大学物理练习三一.选择题1.一力学系统由两个质点组成,它们之间只有引力作用。
若两质点所受外力的矢量和为零,则此系统 [ ] (A) 动量、机械能以及对一轴的角动量都守恒。
(B) 动量、机械能守恒,但角动量是否守恒不能断定。
(C) 动量守恒,但机械能和角动量守恒与否不能断定。
(D) 动量和角动量守恒,但机械能是否守恒不能断定。
解:[ C ] 按守恒条件:∑=0iF 动量守恒,但∑≠0i M 角动量不守恒, 机械能不能断定是否守恒。
2.如图所示,有一个小物体,置于一个光滑的水平桌面上,有一绳其一端连结此物体,另一端穿过桌面中心的小孔,该物体原以角速度ω在距孔为R 的圆周上转动,今将绳从小孔往下拉。
则物体 [ ] (A)动能不变,动量改变。
(B)动量不变,动能改变。
(C)角动量不变,动量不变。
(D)角动量改变,动量改变。
(E)角动量不变,动能、动量都改变。
解:[ E ] 因对o 点,合外力矩为0,角动量守恒3.有两个半径相同,质量相等的细圆环A 和B 。
A 环的质量分布均匀,B 环的质量分布不均匀。
它们对通过环心并与环面垂直的轴的转动惯量分别为J A 和J B ,则 [ ] (A)A J >B J (B) A J < B J (C) A J =B J (D) 不能确定A J 、B J 哪个大。
解:[ C ] 细圆环的转动惯量与质量是否均匀分布无关⎰==220mR dmR J4.光滑的水平桌面上,有一长为2L 、质量为m 的匀质细杆,可绕过其中点且垂直于杆的竖直光滑固定轴O 自由转动,其转动惯量为31m L 2,起初杆静止。
桌面上有两个质量均为m的小球,各自在垂直于杆的方向上,正对着杆的一端,以相同的速率v 相向运动,如图所示。
当两小球同时与杆的两个端点发生完全非弹性碰撞后与杆粘在一起转动,则这一系统碰撞后的转动角速度为 [ ](A)L v 32. (B) L v 54 (C)L v 76 (D) Lv 98解:[ C ]角动量守恒二.填空题1.绕定轴转动的飞轮均匀地减速,t = 0时角速度ω0 =5 rad/s ,t = 20s 时角速度ω=0.8ω0,则飞轮的角加速度β= ,t=0到t=100s 时间内飞轮所转过的角度θ= 。
吉林大学 大学物理下练习册答案

9. 一简谐振动的旋转矢量图如图所示,振幅矢量 长2cm,则该简谐振动的初相位为________ π/4 ,矢 量振动方程为________________ 。 x 0.02cos(πt π/4)
t时刻
πt π / 4 t 0 π/4
x
10. 物体的共振角频率与系统自身性质以及 阻尼大小 有关。系统的__________ 阻尼 越大, ___________ 共振时振幅值越低,共振圆频率越小。
5. 一弹簧振子作简谐振动,振幅为A,周期为T, 运动方程用余弦函数表示,若t=0时, π 。 (1)振子在负的最大位移处,则初相位为_____ (2)振子在平衡位置向正方向运动,则初相位为 _____ 。 -π 2 (3)振子在位移A/2处,向负方向运动,则初相位 π 3 。 为_____ 6. 将复杂的周期振动分解为一系列的 简谐振动之和 ____________,从而确定出该振动包含的频 率成分以及各频率对应的振幅的方法,称为 ___________ 频谱分析 。
7. 上面放有物体的平台,以每秒5周的频率沿竖直方向 作简谐振动,若平台振幅超过_______ 1cm ,物体将会脱离 平台。(g=9.8m/s2) 8. 两个同方向同频率的简谐振动,其合振动的振幅为 20cm,与第一个简谐振动的相位差为 1 π 6 若第一个简谐振动的振幅为 10 3cm 17.3cm 。则第 10cm 。第一、二个简 二个简谐振动的振幅为_________cm 谐振动的相位差1 2 为___________ 。 π/2
π x1 4 cos(2t ), 6 7π x2 3 cos(2t ) 6
则关于合振动有结论:( )
A. 振幅等于1cm,初相等于 π
吉林大学物理B2题册下2013版

大学物理练习册(下册)物理教学与研究中心第十章 机械振动一. 选择题1. 两个相同的弹簧,一端固定,另一端分别悬挂质量为m 1、m 2的两个物体。
若两个物体的振动周期之比T 1∶T 2=2∶1,则m 1∶m 2=( )A.2∶1B.4∶1C.1∶4D.1∶22. 两个质点各自作简谐振动,它们的振幅相同。
第一个质点的振动方程为1cos()x A t ωα=+,当第一个质点从相对平衡位置的正位移回到平衡位置时,第二个质点在正最大位移处,则第二个质点的振动方程为( )A. 2cos()2x A t πωα=++B. 2cos(/2)x A t ωαπ=+-C. 23cos()2x A t ωαπ=+-D. 2cos()x A t ωαπ=++3. 质点作周期为T ,振幅为A 的谐振动,则质点由平衡位置运动到离平衡位置A /2处所需的最短时间是( )A. 4TB. 6TC.8TD.12T4. 一质点在x 轴上作简谐振动,振幅A =4cm ,周期T =2s ,其平衡位置取作坐标原点,若t = 0时刻质点第一次通过2-=x cm 处,且向x 轴正方向运动,则质点第二次通2-=x cm 处的时刻为( )A. 1sB. 23sC. 43sD. 2s5. 一质点同时参与两个在同一直线上的简谐振动,其振动方程分别为14cos(2/6)cm x t π=+,273cos(2)cm 6x t π=+,则关于合振动有结论( )A. 振幅等于1cm ,初相等于π C. 振幅等于1cm ,初相等于76πB. 振幅等于7cm ,初相等于 43π D. 振幅等于1cm ,初相等于/6π6. 一质点作简谐振动,振动方程为cos()x A t ωϕ=+,当时间2Tt =(T 为周期)时,质点的速度为( )A. sin A ωϕ-B. sin A ωϕC. cos A ωϕ-D. cos A ωϕ7. 对一个作简谐振动的物体,下面哪种说法是正确的( )A. 物体处在运动正方向的端点时,速度和加速度都达到最大值B. 物体位于平衡位置且向负方向运动时,速度和加速度都为零C. 物体位于平衡位置且向正方向运动时,速度最大,加速度为零D. 物体处在负方向的端点时,速度最大,加速度为零8. 当质点以f 频率作简谐振动时,它的动能变化频率为( )A. fB. 2fC. 4fD. 0.5f9. 两个振动方向相互垂直、频率相同的简谐振动的合成运动的轨迹为一正椭圆,则这两个分振动的相位差可能为( )A. 0或2πB. 0或32πC. 0或πD. 32π或2π10.竖直弹簧振子系统谐振周期为T ,将小球放入水中,水的浮力恒定,粘滞阻力及弹簧质量不计,若使振子沿铅直方向振动起来,则: ( )A. 振子仍作简谐振动,但周期<TB. 振子仍作简谐振动,但周期>TC. 振子仍作简谐振动,且周期仍为TD. 振子不再作简谐振动二.填空题1. 已知谐振动方程为cos()x A t ωϕ=+,振子质量为m ,振幅为A ,则振子最大速度为 ,最大加速度为 ,振动系统总能量为 ,平均动能为 ,平均势能为 。
吉林大学-大学物理-练习册答案

11. 两根互相平行的长直导线,相距为a,其上均 匀带电,电荷线密度分别为λ1和λ2,则导线单 位长度所受电场力的大小为F0= 。
三、计算题
图中所示为一沿 x 轴放置的长度为l的不均匀 带电细棒,其电荷线密度为 = 0(x-a), 0为一 常量。取无穷远处为电势零点,求坐标原点o处 的电势。
它们定义式是 和 。
路径到B点的场强线积分 = .
7. 在场强为E 均匀电场中,A、B两点间距离为 d,A、B连线方向与E方向一致,从A点经任意
8.半径为R的不均匀带电球体,电荷体密度分布为ρ=Ar,式中 r 为离球心的距离,(r≤R)、A为一常数,则球体上的总电量Q= 。
Π区 大小 ,方向 .
3. 在相对介电常数为εr的各向同性的电介质中,电位移矢量与场强之间的关系是 。
4. 两块“无限大”的带电平行电板,其电荷面密度分别为(>0)及-2 ,如图所示,试写出各区域的电场强度
热
磁
4.涡旋电场由 所激发,其环流数学
左
变化的磁场
表达式为 ,涡旋电场强度E涡与
5. 取自感系数定义式为L=Φ/I, 当线圈几何形状不变,周围无铁磁性物质时,若线圈中电流强度变小,则线圈的自感系数L 。
8. 在没有自由电荷和传导电流的变化电磁场中:
;
;
10/π
9.在自感系数为L=0.05mH线圈中,流过I=0.8A的电流,在切断电路后经t=0.8μs的时间,电流强度近似为零,回路中的平均自感电动势大小
10.长直导线与半径为R的导线圆周相切(两者绝缘),则它们之间互感系数
4. 关于静电场中的电位移线,下列说法中,哪一种是正确的? A.起自正电荷,止于负电荷,不形成闭合线,不中断 B.任何两条电位移线互相平行 C.起自正自由电荷,止于负自由电荷,任何两 条电位移线在无自由电荷的空间不相交 D.电位移线只出现在有电介质的空间
大学物理2习题答案共25页
25、学习是劳动,是充满思想的劳动。——乌申斯基
谢谢!
大学物理2·格林 47、在一千磅法律里,没有一盎司仁 爱。— —英国
48、法律一多,公正就少。——托·富 勒 49、犯罪总是以惩罚相补偿;只有处 罚才能 使犯罪 得到偿 还。— —达雷 尔
50、弱者比强者更能得到法律的保护 。—— 威·厄尔
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
吉林大学大学物理练习册综合练习一答案
R1
R2O
λ1 r P
λ2
D. 0
9. 真空中一半径为 的球面均匀带电 ,在球心 处有一 真空中一半径为R的球面均匀带电 的球面均匀带电Q,在球心O处有一 带电量为q的点电荷 如图所示。 的点电荷, 带电量为 的点电荷,如图所示。设无穷远处为电 势零 则在球内离球心O距离为 距离为r的 点处电势为 点,则在球内离球心 距离为 的P点处电势为
二、填空题 x = 6 t − t 2 ( SI) ,则在 由0至4 s的 1. 一质点的运动方程为 则在t由 至 的 则在 时间间隔内, 时间间隔内,质点的位移大小为 8m ,在t由0到4 s 由 到 的时间间隔内质点走过的路程为 10m 。 2. 半径为 半径为30cm的飞轮 从静止开始以 的飞轮,从静止开始以 的飞轮 从静止开始以0.5rad/s2的匀角加速 度转动, 度转动,则飞轮边缘上一点在飞轮转过 240°时的切向 ° 法向加速度的大小a 加速度的大小 at= 0.15 m/s2 , 法向加速度的大小 n = 0.4π m/s2 。 3.一定量的理想气体处于热动平衡状态时,此热力学 .一定量的理想气体处于热动平衡状态时, 系统不随时间变化的三个宏观量是____________, 系统不随时间变化的三个宏观量是 P,V ,T 2 1 而随时间不断变化的微观量是_________________. 而随时间不断变化的微观量是 υ, 2 mυ , mυ等
m dMf = rµ gdm = rµ g 2 2π rdr πR
mg 2 Mf = ∫ rµ 2 2πrdr = mgµ R 3 πR 0
R
1 2 − Mf θ = 0 − Iω0 2
n =θ
3Rω = 2π 16πµ g
2 0
3. 一卡诺热机 可逆的 ,当高温热源的温度为 一卡诺热机(可逆的 当高温热源的温度为127oC, 低温 可逆的), 热源温度为27 时 其每次循环对外作净功8000J。今维 热源温度为 oC时,其每次循环对外作净功 。 持低温热源的温度不变,提高高温热源温度, 持低温热源的温度不变,提高高温热源温度,使其每次 循环对外作净功10000J 。若两个卡诺循环都工作在相同 循环对外作净功 的两条绝热线之间,试求: 的两条绝热线之间,试求: (1) 第二个循环热机的效率; 第二个循环热机的效率; (2) 第二个循环的高温热源的温度。 第二个循环的高温热源的温度。 T1 − T2 A 解: = η = ⇒Q2 = 24000J T1 Q2 + A 两循环工作在相同的两条绝热线之间, 两循环工作在相同的两条绝热线之间,且低温热源的 温度不变, 不变。 温度不变,故Q2不变。
大学物理(二)习题参考答案
大学物理(二)习题参考答案14-2、 若理想气体的体积为V ,压强为p ,温度为T ,一个分子的质量为m ,k 为玻耳兹曼常量,R 为普适气体常量,则该理想气体的分子数为多少? 解:由理想气体状态方程 N p nkT kT V== 得理想气体的分子数 pV N kT=14-8、温度为0ºC 和100ºC 时理想气体分子的平均平动动能各为多少?欲使分子的平均平动动能等于1e V ,气体的温度需是多少?解:(1)232111331.3810273 5.651022w kT J J --==⨯⨯⨯=⨯ (2)23212233 1.3810(273100)7.721022w kT J J --==⨯⨯⨯+=⨯(3)193323322 1.60107.73107.4610233 1.3810w w kT T K K k --⨯⨯=⇒===⨯≈⨯⨯⨯℃ 14-9、某些恒星的温度可达到约1.0×108K ,这是发生聚变反应(也称热核反应)所需的温度。
通常在此温度下恒星可视为由质子组成。
求: (1)质子的平均动能是多大? (2)质子的方均根速率是多大? 解:(1)质子的平均动能为 23815331.3810 1.0102.071022w kT J J --==⨯⨯⨯⨯=⨯ (2) 质子的方均根速率是2161121.5710rps w mv v s m s --===⋅=⨯⋅或1611.5710rpsv s m s --==⋅=⨯⋅ 14-12、解: (1)KK E E N w w N=⇒=A molMN N M =⋅ 5321234.141032108.27102.66 6.0210k mol A E M w J J MN --⨯⨯⨯∴===⨯⨯⨯(2) 21233228.2710400233 1.3810w w kT T K K k --⨯⨯=⇒==≈⨯⨯ 14-17、解:(1)253122522 6.7510 1.35105 2.010mol mol mol M M PV RT P RT M V M E E P M i iV V E RT M P Pa Pa -⎫=⇒=⎪⎪⇒==⎬⎪=⎪⎭⨯⨯==⨯⨯⨯(2)221223333 6.751027.51055 5.4102w kT E E w J J E i i N N kT N ε-⎫=⎪⨯⨯⎪⇒=⋅===⨯⎬⨯⨯⎪==⎪⎭21223227.510 3.621033 1.3810w T K K k --⨯⨯===⨯⨯⨯ 14-18、解:已知,V ,P ,i22mol mol M i E RT M i E PV M PV RT M ⎫=⎪⎪⇒=⎬⎪=⎪⎭15-2解:已知Q,E ∆由,5552.6610 4.1810 1.5210Q E W W Q E J J J =∆+⇒=-∆=⨯-⨯=-⨯,外界对系统做功。
吉林大学 大学物理 第二章 动力学作业答案
A = '
2
A
+'
2
B
+2' A ' B cos
cos 0
/2
• 4. 一宇宙飞船以恒速在空间中飞行,飞行过程 中遇到一股微尘粒子流,后者以dm/dt的速率沉 积在飞船上,尘粒在落到飞船之前的速度为u方 向与相反,在时刻t飞船的总质量为M(t) ,试 问:要保持飞船匀速飞行,需要多大的力?
2 5. 已知质点质量m=5kg,运动方程 r 2ti t j
s) 则质点在0~2秒内受的冲量I的大小为 20(N· , 在0~2秒内所做的功A= 40J 。 20 j ( N s )
6. 质量为0.25kg 的质点,受力 F ti (SI)的作 用,式中t为时间。t=0 时该质点以 2 j m s 1
以S系为参考系,根据功能原理合外力F做功W 等于系统机械能的增量
1 1 1 2 2 Gm1 m 2 2 Gm1 m 2 W = ( m1 0 + m 2 0 ) - ( m 2 0 ) 2 2 l max 2 l0 = m1 02
6.在光滑的水平桌面上,平放有如图所示的固 定半圆形屏障,质量为m的滑块以速度υ0沿切线 方向进入屏障内,滑块与屏障间的摩擦系数为μ, 试证当滑块从屏障另一端滑出时,摩擦力所做的 1 功为 2 2 A m 0 (e 1) 2 2 d N ma m 解 N m dt r r 1 d d 1 0 e ds ds 0 0 r r
解:首先以B为参考点,F不做功,因此系统机 械能守恒 1 Gm1 m 2 2 Gm1 m 2 m1 0 =2 l0 l max
l max Gm 2 =1 2 Gm 2 0 2 l0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
pa
T2
d
O
b b
T1
c c V
8.1mol刚性双原子分子理想气体,当温度为T时,其 内能为
A. 3 RT 2
B. 3 kT 2
C . 5 RT 2
D. 5 kT 2
3
9.对于室温下的双原子分子理想气体,在等压
膨胀的情况下,系统对外所作的功与从外界吸
收的热量之比 A/Q 等于
A. 1/3
B. 1/4
l 4 0l
r l sin ,dr dl sin
2
2
R1
r
R2
l
U
R2 dr R1 20
2 0
( R2
R1 )
16
5. 一电容为C的空气平行板电容器,接端电压为U的电源 充电后随即断开,试求把两个极板间距离增大至n倍时外 力所作的功。
C S , C' S
6. 关于温度的意义,有下列几种说法:
(1) 气体的温度是分子平均平动动能的量度。
(2) 气体的温度是大量气体分子热运动的集体表现,具
有统计意义。
(3) 温度的高低反映物质内部分子运动剧烈程度的不同。
(4) 从微观上看,气体的温度表示每个气体分子的冷热
程度。上述说法中正确的是:
A. (1)、(2)、(4)
4109 ln 5 3.66108Wb 2
20
角动量(动量矩)
L r m
力矩
气体几种状态变化过程的P-V
图,其中MT为等温线,MQ为绝热线,在AM、
BM、CM三种准静态过程中: p (1) 温度降低的是 AM 过程; M
(2) 气体放热的是 AM、BM 过程。
A
T
Q A E
12
三、计算题
1. 一质量r 为amc的os质点t i在XbOsiYn平面t j上运(动S I,) 其位置矢量为
式中a,b,是正值常数,且a>b。(1) 求质点在A(a,0)点
和B(0,b)点时动能;(2) 求质点所受作用力,以及当质点
从解A点:(1运) 动到B点a过s程in中t的i 分b力cFoxs和Ftjy分别做的功。
哪点是正确的?
A. 电场强度EM < EN;
B. 电势UM < UN;
C. 电势能WM < WN;
M
D. 电场力的功A > 0。
N
5
二、填空题
1.一质点沿x轴运动,其运动方程为x=5+2t-t2(x以m
为单位)。质点的初速度为 2m / s ,第4秒末的速度 为 6m / s 。
2.一质点以(m/s)的匀速率作半径为5m有圆周运动。
12.一质点带有电荷q 8.01019C 以速度 3.0105 m s 在半径为 R 6.0108m 的圆周上做匀速圆周运动,
该带电质点在轨道中心所产生的磁感应强度
B=__0._6_7__1_0_5_T;该带电质点轨道运动的磁矩
pm=__7._2__1_0_2_1_A__m___.
B. (1)、(2)、(3)
C. (2)、(3)、(4)
D. (1)、(3)、(4) 2
7. 如果卡诺热机的循环曲线所包围的面积从图中的abcda
增大为 a bcd a ,那么循环abcda 与a bcd a 所作的功和
热机效率变化情况是:
A. 净功增大,效率提高。 B. 净功增大,效率降低。 C. 净功和效率都不变。 D. 净功增大,效率不变。
C. 2/5
D. 2/7
10.一定量的理想气体向真空作绝热自由膨 胀,体积由V1增至V2,在此过程中气体的
A. 内能不变,熵增加 B. 内能不变,熵减少 C. 内能不变,熵不变 D. 内能增加,熵增加
4
11. 图示为一具有球对称性分布的静电场的E ~ r关系曲
线 , 请指出该静电场E是由下列哪种带电体产生的。
速度大小为 2.5m / s 。(g取10ms-2) 6
4.一质量为m、长为2l匀质棒放在水平桌面上,
如图,棒绕通过棒中心且垂直于桌面轴转动,开
始时转动角速度为0,设棒与桌面间滑动摩擦系 数为μ,棒与轴之间无摩擦力矩,则棒从开始到
停止转动所需时间为 2l0
3g
M f
2
l m dr gr
0 2l
m gl
2
M f t 0 I0 t 2l0 3g
7
5为.r如,图速所度示为,质,点它P受的到质力量为F 的2k作g,用位。置这矢三量个
量均在xOy平面内,且r = 3m, 4.0m s,1
F=2N。则该质点对O点的角动量=_1_2_k_k_g_m_2_s_1, 作用在质点上的力对O点的力矩=__3__k_N__m____。
1 2
ma 2 2
1 2
mb 2 2
Ax A1y3
2.1 mol的理想气体,完成了由两个等容过程和两个等压
过程构成的循环过程(如图),已知状态1的温度为T1,
状态3的温度为T3,且状态2和4在同一等温线上。试求气体
在这一循环过程中作的功。
P
A ( P2 P1 )(V2 V1 )
14
3 一段半径为a的细圆弧,对圆心的张角为0,其上均匀
分布有正电荷 q,如图所示,试以a、q、 0表示出圆心
O处的电场强度。
解: q dq dl ad
q
a0
0 a
dl dE 4 0a2
o
dE
E
l dEx
2dE cos
与导线处于同一平面内的单匝矩形线圈,其边长a=4.0
cm,b=3.0cm,靠近导线的一边与导线
相距d=2.0cm。试求通过线圈的磁通量。
dx
db
Ix
a
m
B dS
S
d
Badx
d
b
o
x
db 0I adx 0Ia ln d b
d 2x
2 d
图 6- 10
(2)F同理mA,a(aB,0m()0点,db:)点x:ma,=b2yajc,0oEsaki,tciEo12ksbmsti12n2mb1t,2jsi2na2 mt
0
2r
dt
A
B
A Fxdx
Fydy
11
10.均匀静电场,电场强度 E (400i 600 j )(V m1)
点a(3,2)和b(1,0)之间电势差_-__2_0_0_0_(__V)。
11.有一内外半径分别为R及2R的金属球壳,在
离其球心O为R/2处放一电量为q的点电荷,则球 心 电场O处强电度势大=小__=_8__3__q0_3R__6__q__0R__2__。__在,离电球势心=_O_1为_2_q3_0R_R_处__的_。
B
Q
对于一个循环过程
C
O
V
E 0 Q A
QCMQ : A 0,Q总 0 QQC 0,QCM 0
QBMQ : A 0,Q总 0 QQB 0,QBM 0 QAMQ : A 0,Q总 0 QQA 0,QAM 0
9
7.一卡诺机(可逆的),低温热源的温度为27oC,热机效
A 匀速直线运动 C 抛物线运动
B 变速直线运动 D 一般曲线运动
1
5.力 F 12 t i (SI)作用在质量m=2 kg的物体上, 使物CA体由原524点7iik从kgg静m m止 s开s1 始1 运动,则BD它在52473ii秒kkgg末 mm的动ss量11 应为:
A. 半径为R的均匀带电球面;
E
B. 半径为R的均匀带电球体; C. 半径为R、电荷体密度为 Ar
E 1 r2
(A为常数)的非均匀带电球体。
D. 半径为R、电荷体密度为 A/ r O R
r
(A为常数)的非均匀带电球体;
12.某电场的电力线分布情况如图所示,一负电荷从M
点移到N点。有人根据这个图得出下列几点结论,其中
该质点在5s内的平均速度的大小
F N
为2m / s 。平均加速度的大小为 0.4m 。/ s302
ts
O
4
7
3.质量m为10kg的木箱放在地面上,在水平拉力F的作用
下由静止开始沿直线运动,其拉力随时间的变化关系如图
所示。若已知木箱与地面间的摩擦系数为0.2,那么在t
=4s时,木箱的速度大小为 4m / s ;在t=7s时,木箱的
l
0 2
0
2ad 4 0a2
cos
x
q
2 0a20
sin 0
2
场强沿x轴的正方向
15
4.
顶角为
的圆台,上、下底面半径分别为R1
和R
,在
2
它的侧面上均匀带电,电荷面密度为,求顶点O的电势.
(以无穷远处为电势零点)
O
U dq 2 rdl
q 4 0l
3. ,质瞬点时在速平率面为上作,某一一般段曲时线间运内动的,平其均瞬速时度速为度为 ,
平均速率为 ,它们之间的关系必定有
A v v, v v
B
v
v,
v
v
C v v, v v
D
v v,
v v
4示. 一式质为点r 在at平2i面 b上t2运j (动其,中已a、知b质为点常位量置)则矢该量质的点表作
d
nd
A W W
Q2
