1振动波
振动与波——精选推荐

振动与波振动与波动⼀、选择题1. 弹簧振⼦作简谐振动,振幅为A ,周期为T ,其运动⽅程⽤余弦函数表⽰.若0t =时,振⼦在负的最⼤位移处,则初相为B(A) 0.(B) π.(C)2π. (D) 2π-. 2. ⼀质量为m 的物体和劲度系数为k 的轻弹簧组成的振动系统,若以物体通过-1/2振幅且向负⽅向运动为计时时刻,该系统的振动⽅程为A(A) 2)3x A π=+. (B) )3x A π=+.(C) cos(2)3x A π=+.(D) 2)3x A π=+.3. 图中所画的是两个简谐振动的振动曲线.若这两个简谐振动可叠加,则合成的余弦振动的初相为 B(A)32π. (B) π. (C) 12π.(D) 0.4. 0t =时,振⼦在位移为/2A 处,且向负⽅向运动,则初相的旋转⽮量为 A5. ⼀个质点作简谐运动,振幅为A ,在起始时刻质点的位移为2A-,且向x 轴正⽅向运动,代表此简谐运动的旋转⽮量为B6. 两个质点各⾃作简谐振动,它们的振幅相同、周期相同.第⼀个质点的振动⽅程为1cos()x A t ωα=+.当第⼀个质点从相对于其平衡位置的正位移处回到平衡位置时,第⼆个质点正在最⼤正位移处.则第⼆个质点的振动⽅程为 B(A) 21cos()2x A t ωαπ=++. (B) 21cos()2x A t ωαπ=+-. (C) 23cos()2x A t ωαπ=+-.(D) 2cos()x A t ωαπ=++.7. ⼀物体作简谐振动,振动⽅程为1cos()4x A t ωπ=+.在/4t T =(T 为周期)时刻,物体的加速度为 B(A) 2A ω.(B)2ω. (C) 2A ω.(D)2A ω. 8. ⼀物体作简谐振动,振动⽅程为1cos()4x A t ωπ=+.在/2t T =(T 为周期)时刻,物体的加速度为 B(A) 2A ω.(B)2ω. (C) 2A ω.(D)2A ω.9. 已知某简谐运动的振动曲线如图所⽰,则此简谐运动的运动⽅程为D(A) 222cos ππ33x t ??=-. (B) 222cos ππ33x t ??=+.(C) 422cos ππ33x t ??=-. (D) 422cos ππ33x t ??=+.10. ⼀质点作简谐振动,周期为T .当它由平衡位置向x 轴正⽅向运动时,从⼆分之⼀最⼤位移处到最⼤位移处这段路程所需要的时间为 C(A) 12T .(B) 8T . (C) 6T . (D) 4T. 11. 把单摆摆球从平衡位置向位移正⽅向拉开,使摆线与竖直⽅向成⼀微⼩⾓度θ,然后由静⽌放⼿任其振动,从放⼿时开始计时.若⽤余弦函数表⽰其运动⽅程,则该单摆振动的初相为 C(A) π. (B) 2π.(C) 0. (D) θ. 12. ⼀个弹簧振⼦和⼀个单摆(只考虑⼩幅度摆动),在地⾯上的固有振动周期分别为1T 和2T .将它们拿到⽉球上去,相应的周期分别为1'T 和2'T .则有 D(A) 11'T T >且22'T T >. (B) 11'T T <且22'T T <.(C) 11'T T =且22'T T =.(D) 11'T T =且22'T T >.13. ⼀质点作简谐振动,已知振动周期为T ,则其振动动能变化的周期是 B(A)4T. (B)2T . (C) T . (D) 2T .14. ⼀弹簧振⼦作简谐振动,当位移为振幅的⼀半时,其动能为总能量的 D(A)14. (B)12. (C). (D)34. 15. ⼀质点作简谐振动,已知振动频率为f ,则振动动能的变化频率是B(A) 4f .(B) 2f .(C) f .(D)2f . 16. 在下⾯⼏种说法中,正确的说法是: C(A)波源不动时,波源的振动周期与波动的周期在数值上是不同的.(B)波源振动的速度与波速相同.(C)在波传播⽅向上的任⼀质点振动相位总是⽐波源的相位滞后(按差值不⼤于π计). (D)在波传播⽅向上的任⼀质点的振动相位总是⽐波源的相位超前(按差值不⼤于π计)17. ⼀质点作简谐振动,振动⽅程为)cos(φω+=t A x ,当时间/2t T =(T 为周期)时,质点的速度为 B(A) φωsin A -. (B) φωsin A .(C) φωcos A -. (D) φωcos A .18. 两个同振动⽅向、同频率、振幅均为A 的简谐运动合成后,振幅为2A ,则这两个简谐运动的相位差为D(A)3π. (B)2π. (C) π.(D) 2π19. 右图中所画的是两个简谐振动的振动曲线。
振动与波复习课件

-1
1
-2
(D)x 2cos(4 t 2 )
33
(C)
5、一弹簧振子作简谐振动,总能量为 E1 ,如果简谐振 动振幅增加为原来的两倍,重物的质量增为原来的四倍, 则它的总能量E2 变为 (D) (A)E1 / 4 (B)E1 / 2 (C) 2E1 (D) 4 E1 6、一弹簧振子作简谐振动,当其偏离平衡位置的位移的 大小为振幅的1/4时,其动能为振动总能量的
对两同频率的谐振动 = 2- 1
当 = 2k , ( k =0,1,2,…),两振动步调相同,称同相
当 = (2k+1) , ( k =0,1,2,…),两振动步调相反 , 称反相。
x
x
A1 A2
x2 x1
同相
T
A1 A2
o
t
o
- A2
- A2
x1
反相
T
t x2
-A1
-A1
若 = 2- 1>0, 则 x2比x1较早达到正最大,
故波动表达式为: y 0.04cos[2( t x ) ] 5 0.4 2
P 0.20 0.40
x (m) 0.60
(2)P处质点的振动方程为:
yP
0.04cos[2( t 5
0.2) 0.4
] 2
0.04cos(0.4t 3) 2
2.如图所示为一平面简谐波在 t 时0 刻的波形图,设此简谐波的频
满足频率相同、振动方向相同、具有恒定的相位差条 件的波为相干波。
考虑两相干波源,振动表达式为:
y1 A1 cos( t 1 )
y2 A2 cos( t 2 )
传播到 P 点引起的振动为:
y1
A1
振动波的阻碍方式

振动波的阻碍方式
振动波在传播过程中可能会遇到各种阻碍,这些阻碍会影响波的传播特性。
常见的阻碍方式包括:
1. 障碍物:实体障碍物如建筑物、山脉、树木等可以阻挡或部分阻挡振动波的传播。
在机械波(如声波、水波)中,障碍物的尺寸、形状和材质会影响波的衍射、折射和反射。
2. 介质变化:振动波在不同介质之间传播时,可能会因为介质性质的突然变化(如密度、压力、温度等)而产生折射现象。
这种介质的不均匀性或非均匀性会影响波的传播路径和速度。
3. 吸收作用:某些介质对振动波具有吸收作用,能够将波的能量转化为热能或其他形式的能量,从而减少波的振幅和能量。
例如,声波在空气中传播时,空气分子会相互碰撞并消耗声能。
4. 散射:当振动波遇到不规则的表面或内部结构时,波会被散射,即波的方向会随机改变。
这种现象在波遇到粗糙表面或小颗粒介质时尤为明显。
5. 反射:振动波遇到界面时,一部分波会被反射回原介质中。
这种现象在波从一种介质传播到另一种介质时发生,如声波在水与空气的交界面上反射。
6. 共振:在特定的频率下,振动波可能会引起系统的共振,导致波的振幅显著增大。
共振现象通常发生在振动系统的自然频率与输入波的频率相匹配时。
7. 波的相互作用:两个或多个振动波在相遇时可能会发生相互
作用,如波的叠加、干涉等。
这种相互作用会影响波的传播和合成。
了解这些阻碍方式有助于我们更好地设计和应用振动波的技术,如声纳、地震勘探、通信系统等,同时也能为波前工程和波控制提供理论基础。
1振动波练习题

一、选择题1、一物体作简谐振动,振动方程为)4/cos(πω+=t A x 。
在t=T/4(T 为周期)时刻,物体的加速度为 (A) 2221ωA -(B) 2221ωA (C) 2321ωA - (D) 2321ωA [ ] 2、对一个作简谐振动的物体,下面哪种说法是正确的?(A) 物体位于平衡位置且向负方向运动时,速度和加速度为零。
(B) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零。
(C) 物体处在运动负方向的端点时,速度和加速度都达到最大值。
(D) 物体处在正方向的端点时,速度最大,加速度为零。
[ ]3、弹簧振子在光滑水平面上作谐振动时,振动频率为v 。
今将弹簧分割为等长的两半,原物体挂在分割后的一支弹簧上,这一系统作谐振动时,振动频率为(A) v (B) v 2(C) 2v (D) 0.5v [ ] 4、一质点沿x 轴作简谐振动,振动方程为))(316cos(1042SI t x ππ+⨯=-。
从t=0时刻起,到质点位置在x =-2cm 处,且向x 轴正方向运动的最短时间间隔为(A) 1/8s (B) 1/4s (C) 1/2s(D) 1/3s (E) 1/6s [ ]5、一质点作简谐振动,周期为T 。
当它由平衡位置向X 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的最短时间为(A) T/4 (B) T/12(C) T/6 (D) T/8 [ ]6、一弹簧振子在光滑水平面上作谐振动,弹簧的倔强系数为k ,物体的质量为m ,振动的角频率为ω=(k/m )1/2,振幅为A ,当振子的动能和势能相等的瞬时,物体的速度为 (A)A ω2 (B) 2/A ω (C) A ω21 (D) A ω [ ] 7、 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是(A) 动能为零,势能最大。
(B) 动能为零,势能为零。
(C) 动能最大,势能最大。
机械振动与机械波:振动图像与波的图像及多解问题
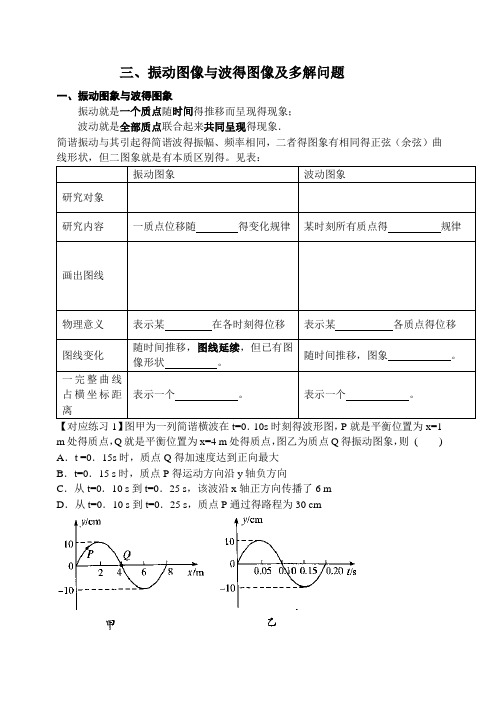
三、振动图像与波得图像及多解问题一、振动图象与波得图象振动就是一个质点随时间得推移而呈现得现象;波动就是全部质点联合起来共同呈现得现象.简谐振动与其引起得简谐波得振幅、频率相同,二者得图象有相同得正弦(余弦)曲振动图象波动图象研究对象研究内容一质点位移随得变化规律某时刻所有质点得规律画出图线物理意义表示某在各时刻得位移表示某各质点得位移图线变化随时间推移,图线延续,但已有图像形状。
随时间推移,图象。
一完整曲线占横坐标距离表示一个。
表示一个。
m处得质点,Q就是平衡位置为x=4 m处得质点,图乙为质点Q得振动图象,则( ) A.t =0.15s时,质点Q得加速度达到正向最大B.t=0.15 s时,质点P得运动方向沿y轴负方向C.从t=0.10 s到t=0.25 s,该波沿x轴正方向传播了6 mD.从t=0.10 s到t=0.25 s,质点P通过得路程为30 cm【对应练习2】如图甲所示,为一列横波在t=0时刻得波动图像,图乙为质点P得振动图像,下列说法正确得就是()A.波沿x轴正方向传播B.波沿x轴负方向传播C.波速为6m/sD.波速为4m/s【对应练习3】一列横波沿x轴正方向传播,a、b、c、d为介质中得沿波传播方向上四个质点得平衡位置。
某时刻得波形如图1所示,此后,若经过3/4周期开始计时,则图2描述得就是()A.a处质点得振动图象B.b处质点得振动图象C.c处质点得振动图象D.d处质点得振动图象【对应练习4】图甲表示一简谐横波在t=20 s时得波形图,图乙就是该列波中得质点P得振动图象,由甲、乙两图中所提供得信息可知这列波得传播速度以及传播方向分别就是( ).A.v=25cm/s,向左传播B.v=50cm/s,向左传播C.v=25 cm/s.向右传播D.v=50 cm/s,向右传播.二、波动图象得多解1、波得空间得周期性:相距为得多个质点振动情况完全相同.2、波得时间得周期性:波在传播过程中,经过时,其波得图象相同.3、波得双向性:波得传播方向及质点得振动方向不确定,要全面考虑。
振动波的微观原理及应用

振动波的微观原理及应用1. 引言振动波是一种在介质中传播的能量传递形式。
它在物理学、工程学和生物学等领域具有广泛的应用。
本文将介绍振动波的微观原理以及一些典型的应用情况。
2. 振动波的微观原理2.1 振动的基本概念振动是物体由于受到外界的扰动而产生的周期性运动。
振动的特点包括频率、振幅和相位等。
2.2 振动波的基本概念振动波是由一系列连续的振动所组成的。
它的传播速度取决于介质性质和波长等因素。
2.3 振动传播的微观机制振动波的传播是通过介质中的粒子之间的相互作用来实现的。
粒子在振动波传输过程中以周期性方式传递能量。
3. 振动波的应用3.1 声波声波是一种机械振动波,其传播介质是气体、液体或固体。
声波在通信、医学、工程等方面有着广泛的应用。
例如,手机中的声音传递即是通过声波传播。
3.2 光波光波是一种电磁波,其频率范围在400-790 THz之间。
光波在光学、通信、显示科技等领域得到广泛应用。
例如,光纤通信利用的即是光波传播的特性。
3.3 地震波地震波是由地壳断裂或地下岩石运动引起的振动。
地震波在地质勘探、地震灾害预警等方面具有重要的应用价值。
3.4 电磁波电磁波是一种在电场和磁场的相互作用下传播的波动现象。
电磁波广泛应用于通信、无线电、雷达等领域。
3.5 机械振动波机械振动波是由固体物体的机械振动引起的波动现象。
例如,地震中的地壳振动即是一种机械振动波。
4. 结论振动波作为一种能量传递形式,在科学、工程和医学等领域广泛应用。
本文介绍了振动波的微观原理,包括振动的基本概念和传播机制。
同时,还列举了几种常见的振动波应用情况,包括声波、光波、地震波、电磁波和机械振动波。
通过了解振动波的微观原理和应用情况,我们可以更好地理解和利用振动波在不同领域中的重要性。
爆破振动波长的计算公式
爆破振动波长的计算公式爆破是一种常见的工程爆炸技术,它可以用于矿山开采、建筑拆除、地质勘探等领域。
在爆破过程中,会产生振动波,这些振动波会对周围的环境和结构物产生影响。
因此,了解爆破振动波的特性和计算方法对于工程设计和环境保护至关重要。
爆破振动波长是指振动波在介质中传播完成一个完整周期所需要的距离。
它是描述振动波传播特性的重要参数,可以用来评估振动波对周围环境和结构物的影响程度。
在工程实践中,我们通常使用以下公式来计算爆破振动波长:λ = V / f。
其中,λ表示振动波长,单位为米(m);V表示振动波在介质中的传播速度,单位为米每秒(m/s);f表示振动波的频率,单位为赫兹(Hz)。
在实际应用中,我们可以通过测量振动波在介质中的传播速度和频率来计算振动波长。
下面,我们将详细介绍如何测量这两个参数以及如何应用上述公式进行计算。
首先,我们来看一下如何测量振动波在介质中的传播速度。
振动波在不同介质中的传播速度是不同的,通常可以通过实地测试或者实验室试验来获得。
在实地测试中,我们可以利用地面振动仪或者加速度计等设备来测量振动波在介质中的传播速度。
在实验室试验中,我们可以通过模拟介质和振动波的实验装置来测量传播速度。
其次,我们来看一下如何测量振动波的频率。
振动波的频率是指单位时间内振动波完成的周期数,通常可以通过振动仪或者频谱分析仪等设备来测量。
在实际应用中,我们可以通过在爆破现场进行实时监测或者在实验室进行模拟试验来获取振动波的频率数据。
一旦我们获取了振动波在介质中的传播速度和频率数据,就可以利用上述公式来计算爆破振动波长。
通过计算振动波长,我们可以评估振动波对周围环境和结构物的影响程度,从而采取相应的控制措施,保护周围环境和结构物的安全。
除了计算爆破振动波长,我们还可以利用振动波长来优化爆破设计。
通过调整爆破参数,如装药量、装药方式、起爆序列等,可以改变振动波的传播特性,从而减小其对周围环境和结构物的影响。
振动与波动振动
y
y
x2
x1
x3
x
1
2 3
x
例3、 图(a)、(b)分别表示t=0s和t=2s时的 某一平面简谐波的波形图。 试写出此平面简谐波波方程。
y/m
y/m
2
2
O
x/m
12
O1
2
x/m
2
2
(a)
(b)
五、波的能量和能流
波不仅是振动状态的传播,而且也是伴随着振动能量的传播。
(1)波长与周期;(2)波源的振动方程;
(3)波方程; (4)离波源0.1m 处质点的振动方程; (5)离波源0.2m和0.3m两点处质点振动的
相位差; (6)在波源振动0.0021s 时的波形方程。
波的干涉
波传播的独立性
?
两不同形状的正(向上)脉冲
两脉冲一正一负, 且位置重合时互为镜象
结论:
(1)波的传播不是介质质元的传播, 是振动状态的传播,是相位的传播
(2) “上游”的质元依次带动“下游”的质元振动。 (3) 某时刻某质元的振动状态将在较晚时刻于“下游”
某处出现---波是振动状态的传播。 (4) 同相点----质元的振动状态相同。
3、波长、周期、波速、频率
三、平面简谐波的波方程
v
这就是右行波的波方程。
y
v
0
P
x
x
左行波的波方程为 y( x ,t ) Acos( t x )
v
y( x ,t ) Acos( t x )
v
y
四、波方程的物理意义
0
1. x x1 (常数)
水下爆破激励堤岸振动主频的衰减规律
doi:10.3969/j.issn.1001 ̄8352.2022.02.010水下爆破激励堤岸振动主频的衰减规律❋李㊀飞①㊀付艳恕②㊀顾㊀云①㊀王海涛①㊀唐㊀毅①①核工业南京建设集团有限公司(江苏南京ꎬ211102)②南昌大学机电工程学院(江西南昌ꎬ330031)[摘㊀要]㊀为了探究水下爆破激励堤岸岩土振动的主频及其传播过程的衰减规律ꎬ采用量纲分析法ꎬ考虑水㊁土介质变化物征ꎬ建立了影响爆破振动主频各物理量之间的泛函ꎮ结合江西省宜春市秀江双桥爆破拆除作业获得的水下爆破振动在堤岸及其近邻域传播测试数据ꎬ通过回归拟合ꎬ求解爆破振动主频公式ꎮ得到爆破振动主频预测值与实测值的平均相对误差为8.87%ꎬ较未考虑水土介质变化特征的预测方法得到的平均相对误差小ꎮ结果表明ꎬ通过引入监测点距爆心之间水㊁土介质传播域距离比值系数ꎬ使得振动主频的预测表达式符合水下爆破振动在堤岸传播的工程物理实际ꎮ[关键词]㊀水下爆破ꎻ量纲分析ꎻ振动主频ꎻ回归分析[分类号]㊀TU746.5ꎻO382AttenuationLawofDominantFrequencyofBankVibrationExcitedbyUnderwaterBlastingLIFei①ꎬFUYanshu②ꎬGUYun①ꎬWANGHaitao①ꎬTANGYi①①NuclearIndustryNanjingConstructionGroupCo.ꎬLtd.(JiangsuNanjingꎬ211102)②SchoolofMechanicalandElectricalEngineeringꎬNanchangUniversity(JiangxiNanchangꎬ330031)[ABSTRACT]㊀Inordertoexplorethemainfrequencyofbankgeotechnicalvibrationexcitedbyunderwaterblastinganditsattenuationlawinpropagationprocessꎬdimensionalanalysismethodwasappliedtoestablishthefunctionalbetweenphysicalparametersthataffectthemainfrequencyofblastingvibrationꎬconsideringtheinfluenceofwaterandgeotechnicalmediumvariation.Combinedwiththeexperimentaldataofunderwaterblastingvibrationpropagationonbankanditssur ̄roundingsintheblastingdemolitionprojectofXiujiangDoubleBridgeinYichunCityꎬJiangxiProvinceꎬtheformulaofdominantfrequencyofblastingvibrationwassolvedthroughregressionfitting.Theaveragerelativeerrorbetweenthepredic ̄tedvalueandthemeasuredvalueofblastingvibrationdominantfrequencyis8.87%ꎬwhichissmallerthanthatobtainedbythepredictionmethodwithoutconsideringthevariationcharacteristicsofwaterandsoilmedia.Resultsshowthatꎬbyintro ̄ducingthedistanceratioofwaterandgeotechnicalmediumbetweenmonitoringpointandblastingcenterꎬformuladeducedbythedimensionalanalysishasbetteraccuracyinpredictingthedominantfrequencyofblastingvibrationinunderwaterblasting.[KEYWORDS]㊀underwaterblastingꎻdimensionalanalysisꎻdominantfrequencyofvibrationꎻregressionanalysis引言众多资料分析表明ꎬ随着传播距离的增加ꎬ爆破振动波振动主频(介质质点最大振幅所对应波的频率)会不断降低ꎬ高频成分振动波衰减速度更快ꎬ而低频成分振动波衰减相对较慢ꎮ因此ꎬ在距离爆源较远处ꎬ爆破振动波的低频成分起主要作用ꎮ而低频率更接近建(构)筑物的固有频率ꎬ从而引起结构共振的可能性更大ꎬ对建(构)筑物造成振动破坏ꎮ㊀㊀振动主频是爆破振动危害三要素之一[1]ꎮ«爆破安全规程»(GB6722 2014)[2]给出建(构)筑物第51卷㊀第2期㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀爆㊀破㊀器㊀材㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Vol.51㊀No.2㊀2022年4月㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀ExplosiveMaterials㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀Apr.2022❋收稿日期:2021 ̄02 ̄22基金项目:核工业南京建设集团有限公司开放基金(BP ̄KFJJ ̄2020 ̄003)第一作者:李飞(1980-)ꎬ男ꎬ本科ꎬ爆破高级工程师ꎬ主要从事工程爆破ꎮE ̄mail:1020403618@qq.com通信作者:付艳恕(1982-)ꎬ男ꎬ副教授ꎬ硕导ꎬ主要从事爆炸与冲击动力学研究及其工程应用ꎮE ̄mail:yshfu@ncu.edu.cn爆破振动安全的判据时ꎬ也考虑了爆破振动主频的影响ꎮ目前ꎬ国内外关于爆破振动主频随传播过程衰减规律的研究包括基于爆破振动强度影响因素提出经验公式[3]ꎬ或基于实验测试给出计算建议[4]ꎬ或基于波的传播理论导出均匀介质中主频衰减规律[5]ꎮ事实上ꎬ爆破振动波传播行为与介质属性紧密关联ꎬ通常采用量纲分析寻找物理现象之间的规律[6 ̄7]ꎮ以上研究都是基于露天爆破ꎬ并没有考虑水域因素ꎮ相比于岩土爆破ꎬ水下爆破对堤岸近邻域结构的振动激励存在两个显著的差异:一是因流体状态的水介质不能承受剪切载荷而无法传递横波ꎬ使得水下爆破对堤岸近邻域结构振动激励天然地过滤掉了横波成分ꎬ而主要呈现为纵波激励ꎻ二是因水介质与岩土介质波阻抗的差异ꎬ使得来自于水下爆破的纵波在水㊁土界面上发生入射㊁反射和透射ꎬ具体的入射波㊁反射波㊁透射波强度与水㊁岩土介质波阻抗相关ꎮ因而ꎬ为了评价水下爆破振动对堤岸及其近邻域建筑结构的影响ꎬ有必要了解爆破振动主频传播过程中随介质变化的衰减规律ꎮ本文中ꎬ结合桥梁爆破拆除项目ꎬ考虑水下爆破振动在堤岸及其近邻域传播所伴随的水㊁土介质变化特征ꎬ运用量纲分析推导出水下爆破振动主频的泛函关系式ꎻ然后ꎬ采用回归拟合方法求解出具体的爆破振动主频预测公式ꎻ最后ꎬ将预测结果与实测结果进行对比ꎬ验证所得水下爆破振动在堤岸近邻域传播主频预测公式的合理性ꎮ1 振动波界面传播行为当振动波从一种介质进入到另一种介质时ꎬ会在两个介质的分界面处发生反射及透射ꎮ假设振动波在介质I和介质II中传播ꎬρ㊁c分别为介质密度和体波声速ꎬ相应的波阻抗分别为ρ1c1和ρ2c2ꎮ在分界面附近ꎬ两种介质由于波动扰动得到的法向速度分别为v1和v2ꎬ得到的压力分别为p1和p2ꎮ如图1所示ꎬ根据介质分界面处的波动边界条件ꎬ两种介质的压力在分界面处连续ꎬ法向速度相等ꎮ即p1=p2ꎻv1=v2ꎮ(1)㊀㊀对于振动波斜入射ꎬ当振动波传播方向在xy平面内ꎬ入射于分界面上时ꎬ与x轴的夹角为θrꎻ反射与透射时ꎬ与x轴的夹角分别为θf和θtꎬ见图2ꎮ㊀㊀通过对振动波斜入射时计算入射㊁反射及透射㊀㊀㊀㊀㊀图1㊀振动波在两种介质传播的分界面Fig.1㊀Interfaceofvibrationwavepropagationintwomedia㊀㊀㊀㊀图2㊀波动斜入射时的反射和透射Fig.2㊀Reflectionandtransmissionofvibrationwaveatobliqueincidence时压力与速度的连续条件ꎬ计算入射波㊁反射波及透射波的压力与速度公式ꎬ见表1ꎮ㊀㊀振动波斜入射时ꎬ根据连续性边界条件ꎬ入射㊁反射及透射时ꎬ在x=0的分界面处ꎬ扰动压力与质点速度有:pr+pf=ptꎻvrx+vfx=vtxꎮ{(2)式中:pr为入射波压力ꎻpf为反射波压力ꎻpt为透射波压力ꎻvrx为入射波质点速度ꎻvfx为反射波质点速度ꎻvtx为透射波质点速度ꎮ㊀㊀再根据斯奈尔声波反射与折射定理[8]ꎬ有θr=θfꎻsinθrsinθt=c1c2ꎮìîíïïï(3)可求得vtx与vrx之比k为:k=vtxvrx=2ρ1c1cosθtρ1c1cosθt+ρ2c2cosθr=21+ρ2tanθtρ1tanθrꎮ(4)㊀㊀本文中ꎬ式(4)中的vtx实际上是爆破振动强度06 ㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀爆㊀破㊀器㊀材㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第51卷第2期表1㊀声波斜入射时入射波㊁反射波及透射波的压力与速度公式Tab.1㊀Pressureformulasandvelocityformulasofincidencewaveꎬreflectionwaveandtransmissionwaveofsoundwaveatobliqueincidence波夹角压力速度入射波α=θrβ=90ʎ-θrγ=90ʎpr=praej(wt-k1xcosθr-k1ysinθr)vrx=cosθrρ1c1pr反射波α=π-θfβ=90ʎ-θfγ=90ʎpf=pfaej(wt+k1xcosθf-k1ysinθf)vfx=cosθfρ1c1pf透射波α=θtβ=90ʎ-θtγ=90ʎpt=ptaej(wt-k2xcosθt-k2ysinθt)vtx=cosθtρ2c2pt的判据ꎮ从式(4)可以看出ꎬ波动在分界面上的vtx由入射波的质点速度㊁波阻抗㊁入射夹角以及透射夹角共同决定ꎮ也即由于界面的存在ꎬ使得入射角与透射角对应的几何参数(图3)影响着爆破振动波的强度ꎬ从而影响着爆破振动主频ꎮ㊀图3㊀振动波从水斜入射到岩土Fig.3㊀Obliqueincidenceofvibrationwavefromwatertorockandsoil2 水土耦合域振动传播主频泛函研究水下爆破振动在堤岸及近邻域传播(图3)时ꎬ由几何关系可知:Ltanθ+Dtanφ=Hꎻ⇔L+Dtanφtanθ=Htanθꎮ(5)将式(5)代入式(4)得:k=v2v1=21+ρ2(H-L)ρ1Dꎮ(6)从式(6)可以看出ꎬ波动在介质界面上的透射由两介质密度与空间几何参数H㊁L㊁D共同决定ꎮ然而ꎬ由于介质物理属性的变化ꎬ水下爆破振动在水㊁土介质中的传播距离和入射角度等因素各异ꎬ使得爆破振动传播规律较为复杂ꎬ建立明确的物理㊁数学方程极为困难ꎬ此时便需要采用量纲分析法[9]建立相应的经验公式ꎬ推导振动主频衰减规律ꎮ影响爆破振动主频的自变量[10 ̄13]分别是炸药量Q㊁爆心距R㊁测点到堤岸的距离RD㊁介质密度ρ和介质中纵波传播速度cpꎮ爆破振动主频f作为因变量ꎬ根据 定理得到以下函数式:f=φ(QꎬRꎬcpꎬρꎬRD)ꎮ(7)由式(7)知ꎬ物理量个数为n=6ꎮ根据 定理ꎬ取基本量为QꎬRꎬcpꎬ故基本量的量纲数为m=3ꎬ导出量与因变量的量纲数为n-m=3ꎬ ㊁ 1㊁ 2代表的是无量纲变量ꎬ则有:㊀㊀㊀㊀㊀㊀㊀㊀ =fQαRβcγpꎻ 1=ρQα1Rβ1cγ1pꎻ2=RDQα2Rβ2cγ2pꎮìîíïïïïïïï(8)式中:α㊁β㊁γ均为待定系数ꎮ以T㊁M㊁L分别表示时间㊁质量及长度的量纲ꎬ则各物理量的量纲如表2所示ꎮ表2㊀水下爆破振动的物理量及量纲Tab.2㊀Physicalparametersanddimensionsinunderwaterblastingvibration物理量fQRcpρRD量纲T-1MLLT-1ML-3L㊀㊀ ㊁ 1㊁ 2都是无量纲变量ꎬ分别有:㊀㊀T-1=MαLβ(LT-1)γ=MαLβ+γT-γꎻML-3=Mα1Lβ1(LT-1)γ1=Mα1Lβ1+γ1T-γ1ꎻL=Mα2Lβ2(LT-1)γ2=Mα2Lβ2+γ2T-γ2ꎮìîíïïï(9)16 2022年4月㊀㊀㊀㊀㊀㊀㊀㊀水下爆破激励堤岸振动主频的衰减规律㊀李㊀飞ꎬ等㊀㊀㊀㊀㊀㊀㊀㊀对式(9)等号两边对应量纲指数进行求解ꎬ可得:α=0ꎬβ=-1ꎬγ=1ꎻα1=1ꎬβ1=-3ꎬγ1=0ꎻα2=0ꎬβ2=1ꎬγ2=0ꎮ于是有:㊀㊀㊀㊀㊀ =fQαRβcγp=fRcpꎻ1=ρQα1Rβ1cγ1p=ρQR-3ꎻ2=RDQα2Rβ2cγ2p=RDRꎮìîíïïïïïïï(10)由上述计算可得无量纲变量之间的函数关系式为:fRcp=φ(ρQR-3ꎬRDR)ꎮ(11)对式(11)进一步转化得:lnfRcp=η1-13η2ln3Qρ3R+η3lnRDRꎮ(12)式中:η1-(1/3)ˑη2ln[3Q/(ρ3R)]是场地因素与炸药量对振动主频的综合影响ꎻη3ln(RD/R)是介质条件对振动主频的影响ꎻη1㊁η2㊁η3分别为爆破点至保护对象间的地形㊁地质与水土耦合条件等有关的系数ꎮ令lnK=η1㊁β1=-η2/3㊁β2=η3ꎬ则爆破振动主频f的计算公式为:f=KcpR(3Qρ3R)β1(RDR)β2ꎮ(13)对于特定的场地ꎬ介质密度ρ及其纵波传播速度cp均可记为常数ꎬ由式(13)可进一步化简得:f=KR(3QR)β1(RDR)β2ꎮ(14)式中:K是场地系数ꎻβ1是衰减系数ꎻβ2是与水陆距离相关的影响系数ꎮ3㊀振动主频函数回归拟合在式(14)中:Q㊁R㊁RD是已知量ꎻK㊁β1㊁β2是待定参数ꎬ即需要根据测试所得振动数据进行拟合求解的参数ꎮ在数学上ꎬ解决这类问题通常采用非线性最小二乘法[14 ̄15]ꎮ用非线性最小二乘法求待定参数K㊁β1㊁β2ꎬ使目标函数最小ꎮ令φi=R-1i(3Qi/Ri)β1(RDi/Ri)β2ꎬ即minf(w)=ð8i=1(Vi-Kφi)2ꎮ(15)式中:w=[Kꎬβ1ꎬβ2]T是待定参数ꎮ㊀㊀目标函数f(w)取最小值的必要条件为:əfəK=0ꎻəfəβ1=0ꎻəfəβ2=0ꎮìîíïïïïïï⇔ð8i=1(Vi-Kφi)φi=0ꎻð8i=1(Vi-Kφi)Kφiln3QR=0ꎻð8i=1(Vi-Kφi)KφilnRDiRi=0ꎮìîíïïïïïï(16)式㊀(16)是一个非线性方程组ꎬ一般采用数值迭代法进行求解ꎮ采用高斯 ̄牛顿迭代法求解[16]ꎬ获得非线性方程组近似解K㊁β1㊁β2ꎬ从而求出式(14)ꎮ㊀㊀对于式(14)中待定参数拟合效果ꎬ可以根据残差平方和Rss来测定:Rss=ð8i=1(Vi-^Vi)2ꎮ(17)㊀㊀张立国等[6]针对岩土爆破振动主频推导出:f=KR(3QR)βꎮ(18)㊀㊀求得的式(14)ꎬ可与式(18)进行对比分析ꎮ4㊀基于实测数据导出主频函数4.1㊀振动测试结果宜春秀江双桥位于在江西省宜春市袁州区城西的秀江河之上ꎬ于1951年建成ꎬ至1984年加建一座桥梁ꎮ桥长193mꎬ为双幅桥ꎬ由主桥和辅桥组成ꎮ由于规划建设需要ꎬ需将双桥爆破拆除ꎮ经现场勘察ꎬ双桥连接宜春南路和宜春北路ꎬ东西方向为秀江下游和上游ꎬ南北两侧为闹市区ꎬ周围环境较复杂ꎮ其中ꎬ在北侧最近处建筑物有东面55m处的培训楼和西面35m的超市ꎻ南侧最近处建筑物有54m处的职业学校ꎻ西面200m处有第二附属医院ꎮ受保护建(构)筑物众多ꎬ爆破振动备受关注ꎮ利用NUBOX ̄6016爆破测振仪对项目水下爆破激励下堤岸振动进行监测ꎬ测点布置方案如图4所示ꎮ新㊁旧两幅桥延时爆破ꎬ4个测点(图4中 号)共得到8组数据ꎬ测点离爆心空间距离见表3ꎮ4.2㊀振动主频函数表达式在采用非线性最小二乘法的基础上ꎬ用Matlab编写的程序对式(14)和式(18)分别进行拟合求解ꎬ得到表4所示结果ꎮ㊀㊀根据表4可以看出ꎬ采用量纲分析推导出的式(14)的残差平方和更小ꎬ故拟合效果更优ꎮ㊀㊀那么根据表4列出的参数ꎬ可知式(18)和式(14)的具体表达式分别为:26 ㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀爆㊀破㊀器㊀材㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第51卷第2期㊀㊀㊀㊀㊀㊀图4㊀测点布置(单位:m)Fig.4㊀Layoutofmeasuringpoints(Unit:m)表3㊀爆破振动监测数据㊀Tab.3㊀Monitoringdataofblastingvibration序号Q/kgR/mRD/mf/Hz1#14.4053.70753.7073.0502#120.1097.98526.8175.4903#71.65126.48754.3583.0504#120.10174.657104.9966.1005#71.65101.89727.8873.0506#120.10148.94679.0336.1007#71.65200.251161.8613.6608#41.50257.857198.1567.320表4㊀拟合参数Tab.4㊀Fittingparameters参数式(18)式(14)K0.1010.418β11.3730.809β20.240Rss15.9701.299f=0.101R(3QR)1.373ꎻ(19)f=0.418R(3QR)0.809(RDR)0.240ꎮ(20)由式(19)㊁式(20)可以分别计算对应的爆破振动主频预测值ꎬ具体结果见表5ꎮ㊀㊀由表5可以看出ꎬ采用式(18)计算出的平均相表5㊀爆破振动主频的实测与预测结果Tab.5㊀Measuredandpredictedresultsofdominantfrequencyofblastingvibration序号实测f/Hz式(19)预测f/Hz相对误差/%式(20)预测f/Hz相对误差/%1#3.051.50650.622.71510.992#5.494.9759.375.1945.393#3.054.32041.653.47814.034#6.106.1721.195.9881.835#3.053.98630.683.60918.336#6.105.8174.655.5509.027#3.665.12840.113.8194.348#7.324.38940.047.8337.00对误差为27.29%ꎬ而采用(14)计算出的平均相对误差为8.87%ꎮ采用量纲分析推导出的式(14)拟合的振动主频能够较准确地反映水土耦合作用下的爆破振动ꎬ预测的水下爆破振动在堤岸近邻域传播主频与实验测试结果相关性更优ꎬ体现了本研究方法的合理性ꎮ5 结论基于江西省宜春市秀江双桥水下墩台爆破拆除项目测试数据ꎬ考虑水㊁土介质变化特征ꎬ采用量纲362022年4月㊀㊀㊀㊀㊀㊀㊀㊀水下爆破激励堤岸振动主频的衰减规律㊀李㊀飞ꎬ等㊀㊀㊀㊀㊀㊀㊀㊀分析法导出了水下爆破激励下堤岸振动主频衰减规律表达式ꎬ并与未考虑水㊁土介质变化特征的预测方法进行对比ꎬ得出以下结论:1)通过综合影响系数呈现水㊁土介质物征变化对振动传播主频的影响ꎬ同时引入监测点距爆心之间水㊁土介质传播域距离比值系数ꎬ使得振动主频预测表达式在物理上尊重水下爆破振动在堤岸传播工程实际ꎬ所得结果更具科学㊁合理性ꎮ2)通过比较回归拟合中的残差平方和可知ꎬ较之于未考虑水㊁土介质变化预测方法而言ꎬ基于量纲分析推导出的公式对于爆破振动主频预测的精度较高ꎬ能够更好地反映水下爆破振动主频衰减规律ꎮ3)通过预测与实测爆破振动主频的相对误差ꎬ可以看出本文研究方法得到的振动主频预测值能够较准确地反映水下爆破在堤岸近邻域振动主频的衰减规律ꎮ参考文献[1]㊀李夕兵ꎬ凌同华ꎬ张义平.爆破震动信号分析理论与技术[M].北京:科学出版社ꎬ2009:22 ̄23.LIXBꎬLINGTHꎬZHANGYP.Analysisofblastvibrationsignals:theoriesandmethods[M].Beijing:SciencePressꎬ2009:22 ̄23.[2]㊀国家安全生产监督管理局.爆破安全规程:GB6722 2014[S].北京:中国标准出版社ꎬ2014.StateAdministrationofWorkSafety.Safetyregulationsforblasting:GB6722 2014[S].Beijing:StandardsPressofChinaꎬ2014.[3]㊀亨利奇.爆炸动力学及其应用[M].北京:科学出版社ꎬ1987:35 ̄37.[4]㊀唐春海ꎬ于亚伦ꎬ王建宙.爆破地震动安全判据的初步探讨[J].有色金属ꎬ2001ꎬ53(1):1 ̄4.TANGCHꎬYUYLꎬWANGJZ.Elementarystudyofsafetycriterionforblastingvibration[J].NonferrousMetalsꎬ2001ꎬ53(1):1 ̄4.[5]㊀孟海利ꎬ郭峰.爆破地震波主频率的试验研究[J].铁道工程学报ꎬ2009(11):81 ̄83ꎬ93.MENGHLꎬGUOF.Experimentalresearchonthemas ̄terfrequencyofblastingseismicwave[J].JournalofRailwayEngineeringSocietyꎬ2009(11):81 ̄83ꎬ93. [6]㊀张立国ꎬ龚敏ꎬ于亚伦.爆破振动频率预测及其回归分析[J].辽宁工程技术大学学报ꎬ2005ꎬ24(2):187 ̄189.ZHANGLGꎬGONGMꎬYUYL.Forecastandregres ̄sionanalysisofblastingvibrationfrequency[J].JournalofLiaoningTechnicalUniversityꎬ2005ꎬ24(2):187 ̄189.[7]㊀卢文波ꎬ周俊汝ꎬ陈明ꎬ等.爆破振动主频衰减公式研究[J].工程爆破ꎬ2015ꎬ21(6):1 ̄6ꎬ24.LUWBꎬZHOUJRꎬCHENMꎬetal.Studyonattenua ̄tionformulaofdominantfrequencyofblastingvibration[J].EngineeringBlastingꎬ2015ꎬ21(6):1 ̄6ꎬ24. [8]㊀杜功焕ꎬ朱哲民ꎬ龚秀芬.声学基础[M].3版.南京:南京大学出版社ꎬ2012:137.[9]㊀谈庆明.量纲分析[M].合肥:中国科学技术大学出版社ꎬ2005.TANQM.Dimensionalanalysis[M].Hefei:UniversityofScienceandTechnologyofChinaPressꎬ2005. [10]㊀李孝林ꎬ王少雄ꎬ高怀树.爆破振动频率影响因素分析[J].辽宁工程技术大学学报ꎬ2006ꎬ25(2):204 ̄206.LIXLꎬWANGSXꎬGAOHS.Analysisoffactorsaffectingblastingvibrationfrequency[J].JournalofLiaoningTechnicalUniversityꎬ2006ꎬ25(2):204 ̄206. [11]㊀王永庆ꎬ魏晓林ꎬ夏柏如ꎬ等.爆破振动频率预测研究[J].爆破ꎬ2007ꎬ24(4):17 ̄20.WANGYQꎬWEIXLꎬXIABRꎬetal.Studyonfore ̄castofblastingseismoticfrequency[J].Blastingꎬ2007ꎬ24(4):17 ̄20.[12]㊀高富强ꎬ侯爱军ꎬ杨小林ꎬ等.基于量纲理论的爆破振动频率分析[J].爆破ꎬ2010ꎬ27(3):1 ̄3ꎬ8.GAOFQꎬHOUAJꎬYANGXLꎬetal.Analysisofblastingvibrationfrequencybasedondimensionalme ̄thod[J].Blastingꎬ2010ꎬ27(3):1 ̄3ꎬ8.[13]㊀费鸿禄ꎬ张超逸ꎬ洪陈超ꎬ等.全断面与台阶法爆破作用下围岩的振动特征[J].爆破器材ꎬ2017ꎬ46(3):52 ̄56.FEIHLꎬZHANGCYꎬHONGCCꎬetal.Dynamicresponseofsurroundingrockunderfullfaceorbenchblastingexcavation[J].ExplosiveMaterialsꎬ2017ꎬ46(3):52 ̄56.[14]㊀谢兰ꎬ高东红.非线性回归方法的应用与比较[J].数学的实践与认识ꎬ2009ꎬ39(10):117 ̄121.XIELꎬGAODH.Theapplicationandcomparisonofdifferentnonlinearfitmethods[J].MathematicsinPrac ̄ticeandTheoryꎬ2009ꎬ39(10):117 ̄121.[15]㊀吕涛ꎬ石永强ꎬ黄诚ꎬ等.非线性回归法求解爆破振动速度衰减公式参数[J].岩土力学ꎬ2007ꎬ28(9):1871 ̄1878.LÜTꎬSHIYQꎬHUANGCꎬetal.Studyonattenua ̄tionparametersofblastingvibrationbynonlinearregres ̄sionanalysis[J].RockandSoilMechanicsꎬ2007ꎬ28(9):1871 ̄1878.[16]㊀马昌凤.最优化方法及其Matlab程序设计[M].北京:科学出版社ꎬ2010:40 ̄48.46 ㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀爆㊀破㊀器㊀材㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀第51卷第2期。
大学物理《波》
1 2 4 2
(3) 振幅 A=1mm,则振动速度的幅值为
vm A 0.1cm 3000s 1 2 1.88 10 cm/s 18.8 m/s
3
其幅值为18.8m/s,远小于波速。
波长和频率
例16-2 设某一时刻绳上横波的波形曲线如下图所示,水平箭 头表示该波的传播方向。试分别用小箭头表明图中 A、B、C、D、 E、F、G、H、I各质点的运动方向,并画出经过1/4周期后的波 形曲线。
解 横波传播过程中各个质点在 其平衡位置附近振动,且振动方向 与传播方向垂直。 右边各点的状态依次向左边传播 经过T/4,波形曲线如下图所示 I A
C
B
D E
I H
G
I
A
C
F
B
B C
D
G H
D
E
F
G
F
A
H
E
u
T
u —波速 T —周期
—波长
—频率
波长和频率
波长、频率和波速之间的关系
u
个
当波长远大于介质分子间的距离时,宏观上介质 可视为是连续的;若波长小到分子间距尺度时,介质 不再具备连续性,此时不能传播弹性波。 弹性波在介质中传播时存在一个频率上限。
波长和频率
(长变情形)
f
(切变情形)
S —横截面积 l l —应变或胁变 f S —应力或胁强
杨氏模量
f —切向力
f /S Y l / l
S —柱体底面积
切变模量
G
f S
波阵面和波射线
流体中的波速
u B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1、一物体作简谐振动,振动方程为)4/cos(πω+=t A x 。
在t=T/4(T 为周期)时刻,物体的加速度为 (A) 2221ωA -(B) 2221ωA (C) 2321ωA - (D) 2321ωA [ ] 2、对一个作简谐振动的物体,下面哪种说法是正确的?(A) 物体位于平衡位置且向负方向运动时,速度和加速度为零。
(B) 物体位于平衡位置且向正方向运动时,速度最大,加速度为零。
(C) 物体处在运动负方向的端点时,速度和加速度都达到最大值。
(D) 物体处在正方向的端点时,速度最大,加速度为零。
[ ]3、弹簧振子在光滑水平面上作谐振动时,振动频率为v 。
今将弹簧分割为等长的两半,原物体挂在分割后的一支弹簧上,这一系统作谐振动时,振动频率为(A) v (B) v 2(C) 2v (D) 0.5v [ ] 4、一质点沿x 轴作简谐振动,振动方程为))(316cos(1042SI t x ππ+⨯=-。
从t=0时刻起,到质点位置在x =-2cm 处,且向x 轴正方向运动的最短时间间隔为(A) 1/8s (B) 1/4s (C) 1/2s(D) 1/3s (E) 1/6s [ ]5、一质点作简谐振动,周期为T 。
当它由平衡位置向X 轴正方向运动时,从二分之一最大位移处到最大位移处这段路程所需要的最短时间为(A) T/4 (B) T/12(C) T/6 (D) T/8 [ ]6、一弹簧振子在光滑水平面上作谐振动,弹簧的倔强系数为k ,物体的质量为m ,振动的角频率为ω=(k/m )1/2,振幅为A ,当振子的动能和势能相等的瞬时,物体的速度为 (A)A ω2 (B) 2/A ω (C) A ω21 (D) A ω [ ] 7、 一平面简谐波在弹性媒质中传播,在某一瞬时,媒质中某质元正处于平衡位置,此时它的能量是(A) 动能为零,势能最大。
(B) 动能为零,势能为零。
(C) 动能最大,势能最大。
(D) 动能最大,势能为零。
[ ]8、 在驻波中,两个相邻波节间各质点的振动(A) 振幅相同,位相相同。
(B) 振幅不同,位相相同。
(C) 振幅相同,位相不同。
(D) 振幅不同,位相不同。
[ ]9、一质点同时参与了三个简谐振动,它们的振动方程分别为)2/cos(1πω+=t A x )6/7c o s (2πω+=t A x )6/c o s (3πω-=t A x其合成运动方程为(A) )2/3cos(πω+=t A x (B) )6/5cos(πω+=t A x(C) )cos(t A x ω= (D) 0=x [ ]10、一横波沿绳子传播时的波动方程为))(104cos(05.0SI t x y ππ-=,则(A) 波长为0.5m (B) 波长为0.05m(C) 波速为25m/s (D) 波速为5m/s [ ]11、沿波的传播方向(X 轴)上,有A ,B 两点相距1/3m (λ>31m ),B 点的振动比A 点滞后1/24秒,相位比A 点落后π/6,此波的频率v 为(A) 2H Z (B) 4H Z(C) 6H Z (D) 8H Z [ ]12、一平面简谐波沿X 轴正向传播,已知L x =(L <λ)处质点的振动方程为t A y ωc o s =,波速为u ,那么x =0处质点的振动方程为(A) ]/[cos u L t A y +=ω (B) ]/[cos u L t A y -=ω(C) ]/cos[u L t A y +=ω (D) ]/cos[u L t A y -=ω[ ]13、一弹簧振子,重物的质量为m ,弹簧的倔强系数为k ,该振子作振幅为A 的简谐振动。
当重物通过平衡位置且向规定的正方向运动时,开始计时。
则其振动方程为: (A) )/cos(π21+=t m k A x (B) )/cos(π21-=t m k A x (C) )/cos(π21+=t k m A x (D) )/cos(π21-=t k m A x (E) t m k A x /cos = [ ]14、一物在光滑水平面上作简谐振动,振幅是12cm ,在距平衡位置63cm 处速度是24cm/s 。
则此振动的角频率ω=(A) 4rad/s (B) 4/3rad/s(C) 1/4rad/s (D) 43rad/s [ ]15、用余弦函数描述一简谐振子的振动。
若其速度~时间(υ~t)关系曲线如图所示,则振动的初相位为(A) π/6 (B) –π/6(C) 5π/6 (D) -5π/6(E) 2π/3 [ ]16、一弹簧振子作简谐振动,当其偏离平衡位置的位移的大小为振幅的1/4时,其动能为振动总能量的(A) 7/16 (B) 9/16 (C) 11/16(D) 13/16 (E) 15/16 [ ]17、一简谐波沿x 轴正方向传播,t=T/4时的波形曲线如图所示,若振动以余弦函数表示,且此题各点振动的初相取-π到π之间的值,则(A) 0点的初位相为φ0=0。
(B) 1点的初位相为φ1=-21π (C) 2点的初位相为φ2=π(D) 3点的初位相为φ3=-21π [ ] 18、一简谐波沿OX 轴正方向传播,t=0时刻波形曲线如图所示,已知周期为2s ,则P 点处质点的振动速度υ与时间t 的关系曲线为: [ ]19、一平面简谐波沿OX 轴正方向传播,t=0时刻的波形图如图所示,则P 处介质质点的振动方程是(A) ))(3/4cos(10.0SI t y P ππ+=(B) ))(3/4cos(10.0SI t y P ππ-=(C) ))(3/2cos(10.0SI t y P ππ+=(D) ))(6/2cos(10.0SI t y P ππ+= [ ]20、一平面简谐波以速度u 沿X 轴正方向传播,O 为坐标原点,已知P 点的振动方程为wt A y cos =,则(A) O 点的振动方程为)/(cos 0u l t A y -=ω(B) 波动方程为)]/()/([cos u x u l t A y --=ω(C) 波动方程为)]/()/([cos u x u l t A y -+=ω(D) C 点的振动方程为)/3(cos u l t A y c -=ω [ ]21、一列机械横波在t 时刻的波形曲线如图所示,则该时刻能量为量大值的媒质质元的位置是:(A) o ',b, d, f(B) a, c, e , g(C) o ', d(D) b, f [ ]22、两相干波源S 1和S 2相距λ/4,(λ为波长),S 1的位相比S 2的位相超前π21,在S 1、S 2的连 线上,S 1外侧各点(例如P 点)两波引起的两谐振动的位相差是:(A) 0 (B) π (C) π21 (D) π23 [ ] 二、填空题1、两个弹簧振子的周期都是0.4s ,设开始时第一振子从平衡位置向负方向运动,经过0.5s 后,第二个振子才从正方向的端点开始运动,则这两振动周相差为 。
2、一简谐振动的旋转矢量图如图所示,振幅矢量长2cm ,则该简谐振动的初位相为 ,振动方程为 。
3、两个同方向、同频率的谐振动,振幅均为A ,若合成振动的振幅仍为A ,则两分振动的初相位差△ф= 。
4、一质点作简谐振动,其振动曲线如图所示。
根据此图,它的周期T= ,用余弦函数描述时初位相ф= 。
5、两个同方向的简谐振动曲线如图所示。
合振动的振幅为 ,合振动的振动方程为 。
6、一简谐波沿x 轴正方向传播,在t=1s 时刻的波形图如图示,波速u =5m/s ,O 处质点振动的初相位ф0= 。
此波的波动方程为y = 。
7、一平面简谐机械波在媒质中传播时,若一媒质质元在t 时刻的波的能量是10J ,则在(t+T)(T 为波的周期)时刻该媒质质元的振动动能是 。
8、如图示,两列平面余弦波分别沿S 1P 和S 2P 传播,波速均为10cm·s -1,t 时刻,在S 1和S 2处质点的振动方程分别为y 1=3cos10t(cm),y 2=4cos10t(cm),振动方向均垂直纸面。
那么,P 处质点振动的振幅为A= cm 。
9、一质点沿x 轴作谐振动,振动方程为x=0.04cos(πt/8)(SI)。
从t=0时刻起,到质点经过平衡位置且向x 轴正方向运动的最短时间间隔为△t= s 。
10、用余弦函数描述一简谐振子的振动。
若其速度~时间(υ~t )关系曲线如图所示,则振动的初相位为ф0= ,周期T= s 。
11、如图(1)所示,一弹簧长为L 倔强系数为k ,系一质量为m 的物体,然后将此弹簧截断为两个等长的弹簧,分别按图(2)和图(3)连接组成简谐振动系数。
则这三个系统的圆频率值平方(ω2)之比为ω12:ω22:ω32= 。
12、已知两简谐振动曲线如图所示,则这两个简谐振动方程(余弦形式)分别为 和 。
13、一质点同时参与了三个简谐振动,它们的振动方程分别为)3/cos(1πω+=t A x )3/5cos(2πω+=t A x其合成运动的运动方程为x = 。
14、一列平面简谐波沿x 轴正向无衰减地传播,波的振幅为2×10-3m ,周期为0.01s ,波速为400m·s -1。
当t=0时x 轴原点处的质元正通过平衡位置向y 轴正方向运动,则该简谐波的表达式为 。
15、图示一简谐波在t=0和t=T/4(T 为周期)时的波形图,试另画出P 处质点的振动曲线。
16、如图所示,一平面简谐波沿O x 轴正方向传播,波长为λ,若P 处质点的振动方程是)cos(ππν212+=t A y P ,则该波的波动方 程是 ;P 处质点在 时刻的振动状态与O 处质点t 1时刻的振动状态相同。
17、如图所示,两相干波源S 1与S 2相距3λ/4,λ为波长。
设两波在S 1S 2连线上传播时,它们的振幅都是A ,并且不随距离变化。
已知在该直线上在S 1左侧各点的合成波强度为其中一个波强度的4倍,则两波源应满足的位相条件是 。
18、设沿弦线传播的一入射波的表达式为])//(2cos[1φλπ+-=x T t A y ,波在L x =处(B 点)发生反射,反射点为固定端(如图)。
设波在传播和反射过程中振幅不变,则反射波的表达式为=2y 。
三、计算题1、一平面简谐波沿X 轴正向传播,其振幅和圆频率分别为A 和ω,波速为u ,设t=0时的波形曲线如图所示。
(1)写出此波的波动方程。
(2)求距O 点为+λ/8处质点的振动方程。
(3)求距O 点为+λ/8处质点在t=0时的振动速度。
2、图示一平面简谐波在t=1s 时刻的波形图,波速s m u /1.0=,求 (1)该波的波动方程;(2)t=0时P 处质点的振动速度υ=?(3)P 处质点在哪些时刻(t=?)其振动状态与O 处质点在t=0时的振动状态相同。
