包络线与方轮
圆的包络线定义

圆的包络线定义
嘿,朋友们!今天咱来唠唠圆的包络线。
你说这圆的包络线啊,就好像是圆的一群“跟班小弟”。
圆在那走,它们就紧紧跟着,形成了一个很特别的形状。
这就好比你出去遛弯,后面跟着一群小狗狗,它们跑的轨迹就有点像包络线呢!
想象一下哈,一个圆在纸上滚动,它身后留下的痕迹可不就是包络线嘛。
这多有意思呀!就像是圆在纸上跳了一支独特的舞蹈,而包络线就是它舞蹈的记录。
咱再打个比方,圆就像是一个明星,那包络线就是这个明星的超级粉丝团,时刻围绕着它,不离不弃。
圆走到哪,包络线就跟到哪,是不是很形象?
其实在生活中啊,我们也能看到圆的包络线的影子呢。
比如说自行车的轮子,当它滚动的时候,在地上留下的印子,那不就是一种包络线嘛。
还有那摩天轮,转呀转的,它的轮廓不也有点像包络线的感觉嘛。
你可别小瞧了这圆的包络线,它在很多地方都有大用处呢!比如在工程设计里,它能帮助工程师们设计出更合理的结构。
在艺术创作中,它能给艺术家们带来灵感,创造出独特的作品。
你说这圆的包络线神奇不神奇?它就这么悄悄地存在着,有时候我们可能都没注意到它,但它却有着自己独特的价值和意义。
说真的,我们的生活中充满了这样看似普通却又不普通的东西。
就像圆的包络线一样,平时可能不显眼,但仔细一琢磨,还真是挺有意思的呢!我们是不是应该多去发现这些小细节呀,说不定能给我们带来很多惊喜呢!
圆的包络线就是这样一个有趣的存在,它不张扬,却有着自己的魅力。
它让我们看到了数学和生活的奇妙结合,让我们感受到了这个世界的丰富多彩。
所以啊,别再忽略它啦,好好去感受它的独特之处吧!。
包络线

c0 I ,
使得
有相同的切线.
l
为曲线族
lc : F ( x, y, c) 0
的一条包络线,
简称为包络.
例如
单参数曲线簇:
( x c) y R
2 2
2
(其中R是常数,c是参数)表示圆心为(c,0)而半 径等于R的一簇圆. 如图
y
x o
从图形可见,此曲线簇的包络显然为:
y R和y R.
注: c 判别曲线有时除包络外还有其它曲线.
2 例1 求曲线族 ( y c) ( x c) 3 0 的包络. 3 2 2 解 记 F ( x, y, c) ( y c) ( x c) 3 0,
2
则
2 2 ( y c) ( x c) 3 0 3 ( y c) ( x c) 2 0
lc
上, 即
Fc 0.
dc 0, dt
因此
因此, 包络线 而且还要满足
l 上任意一点M不仅要满足 F ( x, y, c) 0,
Fc ( x, y, c) 0.
F ( x, y , c ) 0 Fc ( x, y , c) 0
把联立方程组:
中消去参数c得到的方程F(x,y)=0所表示的曲线
lc cI
l*
称为曲线族
的c-判别曲线
F ( x, y, c) 0,
二、包络的求法 曲线族(1)的包络包含在下列两方程
(1)
F ( x, y , c ) 0 ' Fc ( x, y , c) 0
消去参数c而得到的曲线 ( x, y) 0之中, F
曲线F ( x, y) 0称为(1)的 c 判别曲线.
齿轮范成原理实验
齿轮范成原理实验实验指导书一、实验目的1.掌握范成法切制渐开线齿轮的原理,观察齿廓形成的过程。
2.了解渐开线齿轮产生根切的原因、现象和避免根切的方法。
3.分析比较标准齿轮和变位齿轮的异同点。
二、设备及工具1.齿轮范成仪2.工具:剪刀3.自带工具:圆规、三角尺、铅笔(HB)、橡皮、裁好直径230mm圆形图纸一张。
三、原理和方法1.原理范成法是利用一对齿轮相互啮合时,齿轮齿廓互为包络线的原理来加工轮齿的。
加工时,其中一轮为刀具,另一轮为轮坯,他们仍能保持固定的角速比转动,完全和一对真正的齿轮互相啮合传动一样,同时刀具还沿轮坯的轴向作切削运动。
这样切制得到的齿轮齿廓就是刀具刀刃在各位置的包络线。
今若用渐开线作为刀具齿廓,则其包络线也必为渐开线。
由于实际加工时,看不到刀刃在各个位置形成包络线的过程,所以在实验中用齿轮范成仪来实现轮坯与刀具间的传动过程并用铅笔将其记录在纸上,这样我们能清楚地观察到齿轮范成的过程。
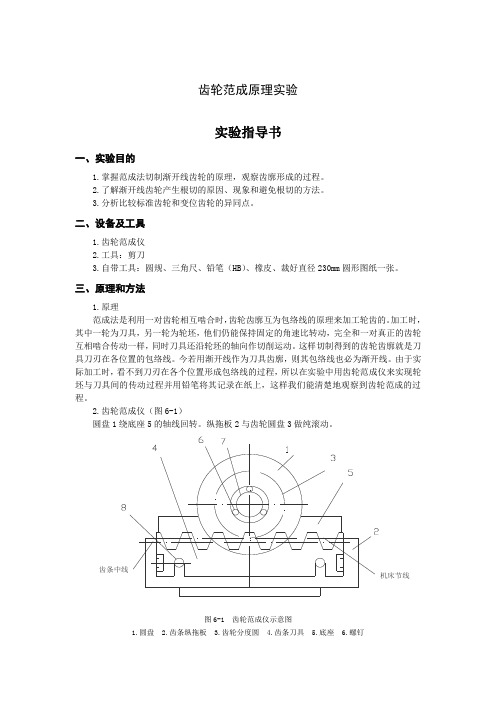
2.齿轮范成仪(图6-1)圆盘1绕底座5的轴线回转。
纵拖板2与齿轮圆盘3做纯滚动。
齿条中线机床节线图6-1 齿轮范成仪示意图1.圆盘2.齿条纵拖板3.齿轮分度圆4.齿条刀具5.底座6.螺钉7.压环 8.调节螺钉圆盘与纵拖板为齿轮齿条传动。
因此两者之间为无滑动的纯滚动。
圆盘上放纸相当于轮坯。
齿条刀具由两个螺钉8与纵拖板相联接,可以使齿条刀具的中心线移近或远离轮坯的中心。
如果当刀具4上的刻度对准“0”时,即齿条刀具的中心线对准机床节线并与分度圆相切时,为切制标准齿轮时刀具的位置;当刀具的中心线远离轮坯中心,即使中线以上的任一分度线与机床节线对准并与轮坯分度圆相切作纯滚动时,为切制正变位齿轮时刀具的位置;反之则为切制负变位齿轮时的位置。
3.齿轮范成仪参数刀具:25.0 1 20 ,20=*=*==c h mm m a α 轮坯:分度圆直径mm d 160=,故齿数8==mdz 四、实验内容绘制:1.标准齿轮(根切齿轮)2.修正齿轮(正变位齿轮)五、实验步骤1.预备工作1)计算:根据下面公式及上面规定的参数算出标准齿轮及正变位齿轮的 d 、 a d 、f d ,变位齿轮参数计算公式:mx d d m x d d a f )22()25.2(++=--=当计算标准齿轮尺寸时,可取上式中0=x ,当切制正变位齿轮时x 的取值为:17)17(min z x -=。
齿轮实验

齿轮范成原理实验一、实验目的1.掌握用范成法切制渐开线齿轮的基本原理,观察轮齿渐开线部分和过渡曲线的形成过程;2.了解渐开线齿轮产生根切现象的原因和避免根切的方法;3.分析比较渐开线标准齿轮和变化齿轮的异同点。
二、设备和工具:1.齿轮范成仪2.圆规、三角板、铅笔等;3.充作毛坯的绘图纸( 260)。
三、原理和方法:1.原理:范成法是利用一对齿轮传动时其共轭齿廓互为包络线的原理来加工齿轮轮齿的方法。
加工时其中一轮为刀具,另一轮为毛坯,它们之间仍保持固定的角速比的传动(强制的),完全和一对真正的齿轮互相啮合传动一样;同时刀具还沿轮坯的轴向作切削运动。
这样所制得齿轮的齿廓就是刀具刀刃在各个位置的包络线。
今若用渐开线作刀具齿廓,则其包络线亦必为渐开线。
刀具可以是轮形插刀,也可以半径为无穷大的齿条刀具。
由于在实际加工时,看不到刀刃在各个位置形成包络线的过程,故通过齿轮范成仪来实现轮坯与刀具间的传动过程,并用铅笔将刀具刀刃的各个位置记录在绘图纸上,这样我们就能清楚地观察到齿轮范成的过程。
2.范成仪的构造范成仪构造如图2-1所示:圆盘1绕其固定轴心O转动。
在圆盘的周缘上刻有凹槽,槽内绕有钢丝2,钢丝绕在凹槽内以后,其中心线所形成的圆应等于被加工齿轮的分度圆(d=Zm)。
钢丝的一端固定在横拖板3上的a处,另一端固定b处。
横拖板3可在机架4上沿水平方向移动,通过钢丝的作用使圆盘相对于横拖板的运动和被加工齿轮相对于齿条的运动一样,即齿轮的节圆和齿条的节线作纯滚,运动学的关系V=r ω。
齿条5装在横拖板上,齿条上有两个槽孔借螺钉6加以固定,齿条刀具中线相对于轮坯中心的位置可借齿条上的槽孔相对于横拖板沿垂直方向移动。
图2-1 齿轮范成仪构造范成仪所用齿条刀具基本参数,被加工齿轮分度直径和齿数,见表2-1。
基本参数齿条刀具模数m(mm)压力角α()(刀具角)齿顶高系数h *a顶隙系数c * 220;1021==m m2010.25被加工齿轮分度圆直径 被加工齿轮的齿数200()d zm mm == d z m==四、实验步骤:1.根据已知的刀具参数(m 、α、h*a 、c*)和被加工齿轮的分度圆直径d ,计算被加工齿轮(标准齿轮、正变位齿轮、负变位齿轮)的齿数和基圆、根圆、顶圆直径,并将上述四个圆画在绘图纸上,然后将纸剪成比顶圆直径图大12(mm )的圆形作为轮坯。
包络线求法

包络线求法
包络线是指一系列曲线的外围线条,它可以用于表示一个复杂的曲线系统中的整体特征。
在实际应用中,包络线求法具有重要的意义。
以下是包络线求法的详细说明:
1. 包络线的绘制方法
包络线的绘制方法有很多种,其中比较常用的是最大值法和追踪法。
最大值法是通过寻找原始曲线在某个区间内的最大值来确定包络线的位置。
而追踪法则是跟随原始曲线中的某个点来确定包络线的位置。
2. 包络线的应用领域
包络线求法在很多领域都有着广泛的应用。
比如,在机器学习中,我们可以使用包络线求法来确定数据的特征,以便更好地进行分类和预测。
在工程领域中,包络线求法可以用于设计机械、电子和航空等设备。
此外,在信号处理和音乐学等领域中,包络线求法也被广泛应用。
3. 包络线求法的研究进展
随着科学技术的发展,包络线求法也在不断地被改进和完善。
目前,研究领域主要集中在如何更准确和高效地绘制包络线上,以及如何将包络线求法应用于更广泛的领域。
一些新的算法和技术也被提出,如基于深度学习的包络线求法、基于多项式拟合的包络线求法等。
总之,包络线求法是一种十分重要的技术,它在许多领域都有着广泛的应用前景。
随着科学技术的不断发展,我们相信包络线求法一
定能够得到更好的应用和更深入的研究。
齿轮齿条介绍

第四章齿轮机构§4-1 齿轮机构的类型一、类型二、特点1、可以用来传递空间任意两轴之间的运动和动力;2、传动准确、平稳、机械效率高;3、使用寿命长,工作安全可靠。
三、功用齿轮机构是现代机械中应用最为广泛的一种传动机构。
如:机械手、汽车变速箱、摄象机、游乐设施等中的传动机构。
§4-2 齿廓啮合基本定律一、齿廓啮合基本定律:过接触点所作两齿廓公法线C:公法线与连心线的交点由三心定理,C点是这对齿廓的相对速度瞬心,则即得齿廓啮合基本定律:两齿廓在任一位置啮合接触时,过接触点所作两齿廓的公法线必通过定点C。
C点:节点节圆:分别以O1、O2为圆心,、为半径所作的圆。
两齿廓的啮合传动相当与一对节圆作纯滚动。
定传动比条件:无论两齿廓在何处啮合,节点C必须为连心线上的一个定点。
变传动比条件:若要求两齿廓作变传动比传动,则节点C不是一个定点,而是按相应的规律在连心线上移动。
二、共轭齿廓共轭齿廓:凡满足齿廓啮合基本定理的一对齿廓称为共轭齿廓共轭曲线:共轭齿廓的齿廓曲线称为共轭曲线共轭:按一定的规律相配的一对三、齿廓曲线的选择1)在给定工作要求的传动比的情况下,只要给出一条齿廓曲线,就可以根据齿廓啮合基本定理求出与其共轭的另一条齿廓曲线。
因此,理论上满足一定传动比规律的共轭曲线有很多。
2)在生产实践中,选择齿廓曲线时还必须综合考虑设计、制造、安装、使用等方面的因素。
3)常用的齿廓曲线有:渐开线、摆线、变态摆线、圆弧曲线、抛物线等,本章主要研究渐开线齿廓的齿轮。
§4-3 渐开线齿廓一、渐开线的形成直线BK沿半径为的圆作纯滚动时,直线上任一点K的轨迹称为该圆的渐开线。
基圆:半径为的圆基圆半径:渐开线的发生线:直线BKK点的展角:二、渐开线的性质1、发生线在基圆上滚过的长度等于基圆上被滚过的圆弧长度。
即=2、渐开线上离基圆越远的部分,其曲率半径越大,渐开线越平直。
发生线BK与基圆的切点B是渐开线在K的曲率中心,是相应的曲率半径,渐开线上离基圆越远的部分,其曲率半径越大,渐开线越平直;渐开线上离基圆越近的部分,其曲率半径越小,渐开线越弯曲;渐开线在基圆上起始点处的曲率半径为零。
包络线原理
包络线原理嘿,朋友们!今天咱来唠唠包络线原理。
你说这包络线原理啊,就好像是一群人在走路。
每个人都有自己的路线,有的走得快,有的走得慢,有的还会绕个弯。
但要是把他们走过的所有痕迹都连起来,哎,那就形成了一条特别的线,这就是包络线啦!想象一下哈,比如咱去爬山。
每个人选择的上山路径都不一样,有的人喜欢沿着陡峭的山坡直冲上去,有的人喜欢绕着平缓的小路慢慢走。
可不管大家怎么走,最后从山下往上看,那些脚印连起来不就是一条包络线嘛。
这包络线就像是一个大框框,把所有人的行动都给框在里面了。
在生活中,包络线原理也到处都是呢!比如说,市场上各种商品的价格波动。
有的商品价格今天高,明天低,后天又不一样了。
但要是把一段时间内的价格都连起来看,是不是就能看出个大概的趋势呀?这就是价格的包络线。
再说说咱的兴趣爱好。
每个人喜欢的东西都不一样,今天喜欢这个,明天可能又迷上那个了。
但要是把这些喜欢的东西串起来,不也能看出一个大致的范围嘛,这也算是一种包络线呀!你看,包络线原理是不是挺有意思的?它就像是生活中的一个小秘密,悄悄地藏在各种现象背后。
有时候你可能没注意到它,但它却一直在那发挥着作用。
咱再深入想想,这包络线原理还能给咱不少启示呢!它告诉咱,虽然每个人都有自己的独特之处,但在大的趋势下,还是有一定规律可循的。
就像那群爬山的人,不管怎么走,最终还是在山的范围内。
那咱在生活中是不是也可以通过观察这些包络线,来更好地把握事情的发展方向呢?而且啊,包络线原理还提醒咱,不要只盯着眼前的一点,要把眼光放长远。
就像看价格波动,不能只看一天两天的,要看长期的趋势。
这样才能做出更明智的决策呀!反正我觉得吧,这包络线原理就像是生活中的一个好朋友,时不时地就给咱提个醒,让咱能更清楚地看到周围的世界。
它不张扬,但却很有用。
你们说是不是呢?所以啊,咱可得好好琢磨琢磨这包络线原理,让它为咱的生活增添更多的色彩和智慧!别小瞧了它哦,说不定哪天就能给你带来意想不到的惊喜呢!。
基于VB生成的RV减速器摆线轮与滚刀包络线
基于VB生成的RV减速器摆线轮与滚刀包络线岳朗; 孙晓超; 张迎辉; 何卫东【期刊名称】《《大连交通大学学报》》【年(卷),期】2019(040)006【总页数】5页(P74-78)【关键词】滚刀; 摆线轮; 包络【作者】岳朗; 孙晓超; 张迎辉; 何卫东【作者单位】大连交通大学机械工程学院辽宁大连 116028; 辽宁加宝石化设备有限公司辽宁营口115000【正文语种】中文摆线针轮传动应用前景十分广阔,但由于其零件精度要求较高,所以加工难度大,尤以摆线齿廓加工是其中主要的难题[1].由于摆线齿廓是比较复杂的曲线,其刀具也一定很复杂.Pennacchi E、Demenego A 和Ta-Shi Lai[2]在齿轮啮合原理和微分几何学的基础上,进行了摆线的包络线计算分析.腾献银[3]等研究了展成加工摆线轮齿廓包络线的数学模型,对确定展成工艺参数、结构优化等有重要的实际价值.陈艾华[4]等利用Solid-Works 的三维造型技术实现了行星摆线齿轮滚刀的基本蜗杆模型的法向齿形到轴向齿形的图形转换.孙俊兰[5]提出利用齿轮啮合原理中的向量矩阵法求解摆线轮滚刀齿形的方法,并分析了滚刀齿形对应于摆线轮的根切和顶切的临界点.徐宏[6]等利用啮合原理设计两齿差摆线轮滚刀,通过包络线法推导得出滚刀的法向齿形.这些学者虽然对滚刀的齿形做了很多工作,但是并没有通过包络线法根据滚刀齿形计算摆线轮齿形,也没有直观的表示出其相互包络的过程.本文在摆线轮及其滚刀的齿形基础上,分别求出其包络线,并通过VB 绘制出摆线轮和滚刀的包络线,为摆线轮及其滚刀的结构设计提供更直观的参考依据.1 摆线轮齿廓方程要求出摆线轮齿形的包络线首先要得出摆线轮的齿形,摆线轮的齿形是按照下面的方法形成的[7].Oa 为摆线轮的圆心,ra 为摆线轮的节圆半径,Ob 为针轮的圆心,rb 为针轮的节圆半径.若假设摆线轮是固定不动的,针轮的节圆相对于摆线轮的节圆作无滑动的滚动(这与实际运转情况是相反的),针轮齿中心Ob 位于针轮节圆之外,它的运动轨迹是摆线轮的理论齿廓,而摆线轮的实际齿形是针轮齿中心形成的理论齿廓的法向等距线,两者的法向距离等于针齿套半径rz .取坐标系XOaY 如图1 所示,中心在摆线轮的中心Oa 处.当转臂(其长度等于偏心距A = rb- ra )相对摆线轮顺时针转动θa .从初始位置转到图示位置时,针轮以其节圆的内圆周在摆线轮节圆的外圆周上相对滚动φ,针轮的中心Ob 从初始位置滚到图示位置.在坐标系XOaY 中,OaM 的矢径为:OaM = OaOb + ObM.图1 摆线轮的齿廓曲线把该矢量等式投影到坐标轴上得M 点运动轨迹的坐标方程:根据θa = Zbφ,方程可写成如下形式:摆线轮的实际齿形是方程的法向等距线[8],即为半径是的rz 针齿套外圆上点的运动轨迹.在图示位置,M 点是针齿套上外圆上K 点的运动轨迹.在图示位置,K 点是针齿套与摆线轮齿形的接触点,因为该点的法线PM 通过节点M (圆的切点).摆线轮实际齿形上任一点K 的矢径为:投影到坐标轴上得摆线轮实际齿形方程:把关系式(1)代入得:式中,rz 为针齿套半径,γ 为摆线轮齿形角.即K点处法线与y 轴的夹角.由于(1)与(3)是法向等距曲线,在对应点它们有共同的法线,因而对应点的切线倾角(齿形角)相等.即存在下列关系:对式(1)进行微分,并带入式(4)整理得:2 滚刀齿形加工摆线齿轮时,是滚刀的齿形曲线包络出摆线齿轮的齿形曲线.同样地,摆线齿轮的齿形曲线也能包络出滚刀的齿形曲线[9].曲线在计算时取摆线轮的外径ReB 作为它的节圆半径,在滚刀的节线上滚动.包络线的等距曲线是滚刀的法向齿形方程,因而滚刀的齿形方程为:参数φHa 的变化范围为0° ~360°Zb/Za.由于整个齿形相对y 轴是对称的,所以计算时只需计算半个齿形即可,此时φHa 的变化范围为是:0°~180°Zb/Za [7].3 摆线轮及其滚刀包络线的形成3.1 滚刀包络线的形成在获得单个滚刀的图形及坐标点集后,需要依据坐标变换来模拟滚刀的包络过程.令齿坯和刀具共同转过1 个-φ 角,相当于齿坯固定不动,齿条刀具在水平移动的同时再转过φ 角.坐标系Oxy 为摆线轮齿坯的定坐标系,O1x1y1 为刀具运动的动坐标系.滚刀经过坐标变换后如图2 所示.图2 滚刀齿廓展成坐标变换由上图的A 点可知平移矩阵为:旋转矩阵为:任一时刻摆线轮上的包络点为:经过坐标变换后的刀具坐标为:摆线轮由于滚刀是绕摆线轮和滚刀接触节线的位置(0,ReB)旋转的,在以针轮圆心为原点的坐标系下,式(7)要写成:将滚刀方程代入,给定不同的φ,然后可求得x、y,即可求得包络线.3.2 摆线轮包络线的形成图3 摆线轮齿廓展成坐标变换刀具可以包络出摆线轮的齿廓,同样,摆线轮也可以包络出刀具的齿形.摆线轮作平移加旋转运动.在求摆线轮包络轨迹线时要进行坐标变换,摆线轮具在水平移动的同时再转过ψ 角.坐标系Oxy为摆线轮齿坯的定坐标系,O1x1y1 为摆线轮运动的动坐标系.摆线轮经过坐标变换如图3 所示.平移矩阵为:由于φ -ψ = φ -Zaφ/Zb = φ/Zb,所以旋转矩阵为:任一时刻包络点为:将上式代入并化简可得摆线轮变换后的坐标为:由于摆线轮是绕摆线轮和滚刀接触节线(0,Rz )的位置旋转的,在以针轮圆心为原点的坐标系下,式(9)要写成:将摆线轮齿廓方程代入即可求其轨迹线.给定不同的φ,求得x、y.4 包络过程仿真实例已知RV-80E 减速器中摆线轮的基本参数:Rz =77 mm,rz =3.5 mm,Zb =44,Za =43,A =1.5 mm.根据以上的坐标变换,用Visual Basic 来实现摆线轮和滚刀各自的包络过程.在程序窗口界面设置了基本参数输入框,程序运行,交汇输入被加工摆线轮的基本参数,在界面模拟区域内,显示动态仿真效果.同时设置退出和清除图形等按钮,在显示出图形后可以选择退出程序或清除图形重新输入参数再观察其他参数下的包络线.绘制滚刀包络出摆线齿廓的图形,首先绘制出滚刀的齿形曲线,也就是加工初始位置处的坐标,然后进行旋转平移变换,旋转平移的过程通过循环语句不断变换出来.利用图片框的PSet 和Line 方法,可在图片框中显示摆线齿廓的范成加工过程.用Picture1.PSet 方法绘制出第一个点,再用Picture1.Line 方法绘制其余的点,并和第一个点连接起来,这样便可以绘制滚刀齿廓当前所处的位置也就是包络线.程序运行效果如图4 所示.用同样的原理绘制摆线轮包络出滚刀的图形,程序运行效果如图5 所示.图4 滚刀包络出摆线轮图5 摆线轮包络出滚刀在对摆线轮的参数进行改变时,摆线轮齿廓变得过大会使图形不能完整显示出来,可以用Picture 的Scale 属性缩放来解决这一问题.5 结论综合上面的研究,应用包络线法计算出了摆线齿轮齿廓的包络曲线方程,以此来作为加工摆线齿轮的滚刀的理论齿廓.同样也可以用滚刀的包络线方程作为摆线轮的齿廓方程.摆线轮加工过程模拟主要算法可归结为点的平移和旋转变换.按照摆线轮的啮合过程,通过VB 将摆线轮加工展成法的过程和原理模拟出来既省工省时省料,而且通过输入摆线轮的基本参数,不局限于固定的尺寸,可以显示各种参数下所加工的齿廓形状.此外,效率很高,可以在短时间内模拟范成加工摆线轮齿廓的全过程.这种加工动态模拟要比实际切削加工具有更好的效果和功能,可通过改变参数值实现任意参数下的包络动态模拟.对于研究摆线轮展成加工、摆线齿廓曲线的形成等具有重要的意义.参考文献:【相关文献】[1]赵君.摆线齿轮蜗杆砂轮磨削方法研究[D].重庆:重庆大学,2016.[2]DEMENEGO A,VECCHIATO D,LITVIN F L,et al.Design and Simulation of Meshing of a Cycloidal Pump[J].Mechanism and Machine Theory,2002,37(3):311-332.[3]滕献银,李克旺,赵新华.摆线齿轮齿廓展成的CAD研究[J].机械科学与技术,2004,21(3):51-52.[4]陈艾华,李必文.行星摆线齿轮滚刀基本蜗杆轴向齿形设计与曲线拟合[J].南华大学学报(自然科学版),2009,23(4):23-26.[5]孙俊兰.摆线齿轮滚刀的齿形设计[J].盐城工业专科学校学报,1995,8(4):6-9.[6]徐宏.两齿差摆线齿轮滚刀的设计[J].工具技术,2009,43(9):74 -75.[7]李儒荀.刀具设计原理与计算[M].南京:江苏科学技术出版社,1985:.607-608.[8]姚继权,张身厚,陈新.摆线齿轮滚刀的三维参数可视化设计[J].辽宁工程技术大学学报(自然科学版),2015,34(6):730-731.[9]张身厚.摆线齿轮滚刀三维参数可视化设计的研究[D].阜新:辽宁工程技术大学,2015.。
包络法求解共轭齿廓曲线(理论)
包络法求解共轭齿廓曲线
共軛曲线及其求法
)。
一对共軛曲线在相对运动过程中互为包络线。
作为共軛曲线的基本条件﹐亦即保证两曲线在嚙合过程连续相切的条件﹐是共軛曲线接触点A 处的相对速度12与通过该点所作这对共軛曲线的公法线-垂直﹐如果这对共軛曲线是一对齿廓曲线﹐这个性质也称作齿廓嚙合基本定律。
公法线与两轮中心连线的交点P 为两轮的瞬心﹐也称为节点。
给出两构件的运动要求和共軛曲线中的一条曲线﹐就可求出另一条曲线﹐常用的有包络法和齿廓法线法。
包络法根据一对共軛曲线在相对运动过程互为包络线的原理﹐如果给定其中一条曲线K 1及两轮相对滚动的一对瞬心线(如图共軛曲线及其求法中的两节圆)使轮1对轮2作相对运动﹐即令轮2固定﹐节圆1在节圆2上滚动﹐可得到K 1在轮2上的一系列相对位置K 1﹑﹑…。
这些曲线形成一个曲线族。
作这个曲线族的包络线K 2﹐即使K 2与曲线族中的每条曲线都相切﹐K 2与K 1即为一对共軛曲线。
机械原理基本概念汇总
机械原理基本概念汇总绪论部分:机械:机械是机器和机构的总称。
机器:机器是执行机械运动的装置,用来完成有用的机械功果转换机械能。
机构:机构能实现预期的机械运动的各构件的基本组合体。
零件:由各种材料做成的制造单元。
构件:由各种材料做成的制造单元经过装配而成的各个运动单元的组合体。
工作机:用来完成有用功的机器。
原动机:将其他形式的能量转换为机械能的机器。
第一章:运动副:两构件直接接触形成的可动连接。
P10低副:面接触的运动副称为低副。
高副:点接触或者线接触的运动副称为高副。
转动副:具有一个独立相对转动的运动副称为转动副。
移动副:具有沿一个方向独立相对运动的运动副称为移动副或者棱柱副。
自由度;构件所具有的独立运动的数目称为自由度。
约束:对独立运动所加的限制称为约束。
运动链:两个以上构件以运动副连接而成的系统称为运动链。
机构运动简图:能准确表达机构运动特性的简单图形称为机构运动简图。
机构示意图:仅仅以构件和运动副的符号表示机构,其图形不按精确比例绘制,而着重表达机构的结构特征的简图称为机构示意图。
复合铰链:当两转动副轴线间的距离缩小到零时,两轴线重合为一。
局部自由度:与输出件运动无关的自由度。
虚约束:不起独立限制作用的约束。
高副低代:在平面机构中用低副代替高副的方法杆组:从动件系统还可以分解为若干个不可再分自由度为零的运动链。
II级杆组:不包含封闭多边形只包含两副构件的杆组第二章:瞬心:瞬心是该两构件上相对速度为零的重合点或者瞬时相同的重合点。
绝对瞬心:如果两构件之一是静止的,则其瞬心为绝对速度瞬心。
相对瞬心:如果两构件都是运动的,则其瞬心为相对速度瞬心。
三心定理:作平面平行运动的三个构件共有的三个瞬心,它们位于同一直线上。
极点:代表构件上速度为零的点。
速度/加速度影像:绘制的加速度三角形abc与原图三角形ABC相似,且顶角字母顺序方向一致,图形abc称为图形ABC的加速度影像。
哥氏加速度:第三章:平面连杆机构:平面连杆机构是由若干刚性构件用低副连接而成的平面机构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
包絡線與方輪
一. 包絡線的概念:
假如有直線族方程:f(x , y , t)=0 , 其中t 是參數, 對於每一
個給定的t 值, 都有一條直線與之對應, 當t 變動時, 便得到一
直線族. 例如:)20(sin cos πθθθ≤≤=+R y x , 其中θ是參
數, 當θ變動時, 得一直線族, 如圖灰色線所示. 細心觀察直
線族, 不難發現這些直線都與一個圓相切, 這個圓就叫做該直
線族的包絡線 .
一般地, 如果一含參數的直線族均與某一條曲線相切, 則這條曲線就稱為這直線族的包絡線 . 二. 方輪的製作:
1. 打開PG_Lab 實驗平台, 作x 軸并在x 軸上取一點G ,以G 為圓心作圓;
2. 以G 為中心作正方形, 使邊心距r 與圓半徑R 之比為9:10(註);
3. 令圓G 向前滾動, 正方形隨之也向前滾動, 則四邊的軌跡形成一波浪形包絡線;
4. 依包絡線的形狀, 制作出波浪形地面, 要注意防止波浪形地面變形,
中間要有受力支柱(牆)﹔
5. 制作一正方柱體(正四棱柱), 使底面邊長等於上述正方形的邊長;
6. 方輪的製作, 成功的關鍵在於波浪曲面的截面上方要依足正方形四邊的包絡線, 使方輪滾動軌道的每一段弧長與正方柱體底面邊長相等 .
註:經過多次的測試, 發現當正方形邊心
距r 與圓半徑R 之比為9:10時, 正方形四邊
的軌跡形成的波浪形包絡線的每一段弧和倒
置懸鏈線上部的一段弧PQ 幾乎重合, 且測量
出每一段弧長與正方形的邊長相等 .
( 倒置懸鏈線方程為
)(2a x a x e e a y -+-= , 這裡取 a = r = 0.9 R )
三. 其它種類的方輪:
正五邊形柱體、正六邊形柱體、星形柱體等滾輪也可用類似的方法製作, 但正三角柱體滾輪就會出問題, 因為正三角形的頂點會撞在軌道上, 不能順利滾動. 如果改成正四面體, 在交錯錐體軌道上就能順利滾動(命名為交錯錐體軌道正四面體滾輪).
注意事項:
1.報告內容要包括:設計圖, 製作過程相片(穿著運動校服), 日程表(如:分工日期, 設計日期, 購買
材料日期, 制作日期等……), 分工安排, 製作心得及感想.
2.報告要打印並要交word檔, 設計圖要交Lab檔.
3.錄影:不少於3分鐘的制作過程(可分段錄影), 並要交以wmv檔或mpg檔儲存的短片.
4.4月10號要檢查每一組完成情況, 4月14號要交齊.
5.要有製作前, 中, 完成的相片及錄影。
