菏泽单县北城三中2017——2018学年第一学期第二次月考数学试卷
大方三中2017-2018学年度第一学期高一第二次月考(数学)-高一年级19班
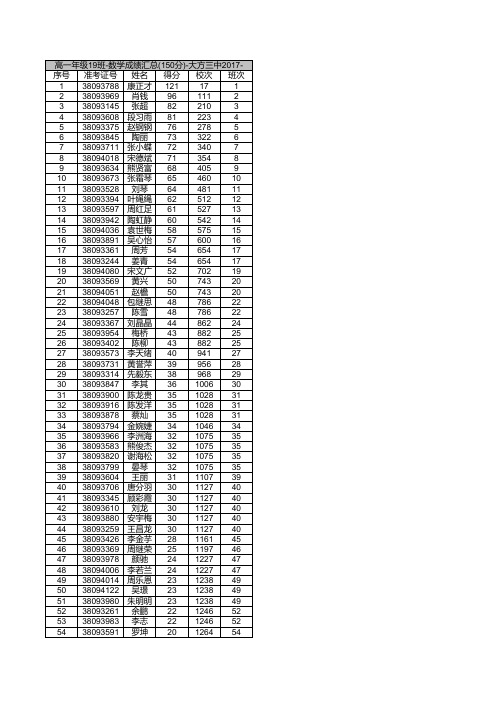
序号准考证号姓名得分校次班次138093788康正才121171238093969肖钱961112338093145张超822103438093608段习雨812234538093375赵钢钢762785638093845陶丽733226738093711张小蝶723407838094018宋德斌713548938093634熊贤富6840591038093673张霜琴65460101138093528刘琴64481111238093394叶绳绳62512121338093597周红足61527131438093942陶虹静60542141538094036袁世梅58575151638093891吴心怡57600161738093361周芳54654171838093244姜青54654171938094080宋文广52702192038093569黄兴50743202138094051赵檐50743202238094048包继思48786222338093257陈雪48786222438093367刘晶晶44862242538093954梅桥43882252638093402陈柳43882252738093573李天绪40941272838093731黄誉萍39956282938093314先毅东38968293038093847李其361006303138093900陈龙贵351028313238093916陈发洋351028313338093878蔡灿351028313438093794金婉婕341046343538093966李洲海321075353638093583熊俊杰321075353738093820谢海松321075353838093799晏琴321075353938093604王丽311107394038093706唐分羽301127404138093345顾彩霞301127404238093610刘龙301127404338093880安宇梅301127404438093259王昌龙301127404538093426李金芋281161454638093369周继荣251197464738093978颜驰241227474838094006李若兰241227474938094014周乐恩231238495038094122吴璟231238495138093980朱明明231238495238093261余鹏221246525338093983李志221246525438093591罗坤20126454
单县二中2017-2018学年高一上学期期末考试数学模拟试题(二)

单县二中2017—2018学年度第一学期期末考试高一数学模拟试题(二) 本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,满分120分.测试时间120分钟.第Ⅰ卷(选择题 共60分)注意事项:1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目涂在答题卡上.2.每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选择其它答案标号.不能答在试题卷上.一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 设集合A ={x |x 2﹣x ﹣6<0},B={x |﹣3≤x ≤1},则A ∪B 等于( )A .[﹣2,1)B .(﹣2,1]C .[﹣3,3)D .(﹣3,3]2. 若函数()1,021,0xx f x x x ⎧⎛⎫<⎪ ⎪=⎨⎝⎭⎪+≥⎩,则()2f f -=⎡⎤⎣⎦( )A .12B .54C .-3D .5 3. 已知直线10ax y a +++=,不论a 取何值,该直线恒过的定点是( )A .()1,1--B .()1,1- C. ()1,1 D .()1,1-4. 函数()()log 101a y x a =-<<的图象大致是( )5. 如图,A B C '''∆是ABC ∆用“斜二测画法”画出的直观图,其中1,O B O C O A ''''''===,那么ABC ∆是一个( ) A .等边三角形 B .直角三角形C. 钝角三角形 D .三边互不相等的三角形6. 圆x 2+y 2﹣2x ﹣8y +13=0的圆心到直线ax +y ﹣1=0的距离为1,则a =( )A .34- B .43- C .3 D .2 7. 设0.30.21231214,,log 82y y y -⎛⎫=== ⎪⎝⎭,则123,,y y y 的大小关系是( )A .312y y y >>B .213y y y >>C. 123y y y >> D .132y y y >>8. 设,m n 是两条不同直线,,αβ是两个不同平面,则下列结论正确的是( )A .若//,//m n m α,则//n αB .若,//m αβα⊥,则m β⊥C. 若,m αββ⊥⊥,则//m α D .若,,m n m n αβ⊥⊥⊥,则αβ⊥9. 函数()f x 是定义在R 上的偶函数,且在[0,)+∞上是增函数,若()()2f a f ≤,则实数a 的取值范围是( )A .(,2]-∞B .(0,2] C.[]2,2- D .(,2][2,)-∞-+∞10. 若实数,x y ,满足250x y --=的最小值是( )A.5 B .1C. D .511. 在正方体1111ABCD A B C D -中,下列结论正确的是( )A .直线1AB 与直线AC 所成的角是45︒B .直线1A B 与平面ABCD 所成的角是30︒C. 二面角1A BC A --的大小是60︒D .直线1A B 与平面11A B CD 所成的角是30︒12. 设方程21210x x -+-=的根为1x ,函数()f x 的零点为2x ,若1214x x -≤,则函数()f x 可以是( )A .()121f x x =-B .()21f x x =-C.()1ln 3f x x ⎛⎫=- ⎪⎝⎭ D .()21x f x =-第Ⅱ卷(非选择题 共90分)二、填空题(每题5分,满分20分,将答案填在答题纸上)13. 若棱长为1的正方体的八个顶点都在同一个球面上,则这个球的表面积为 .14. 若直线220x y +-=与直线460x my ++=平行,则它们之间的距离为 .15. 若496x y ==,则11x y+= . 16. 若函数()21x f x m =--有两个不同的零点,则实数m 的取值范围是 .三、解答题 (本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)17. 已知全集U R =,集合{}(){}12|21,|log 3x A x B x y x -=≤==-.(Ⅰ)求集合()U A B ð; (Ⅱ)设集合{}|C x x a =<,若A C A =,求实数a 的取值范围.18. 已知关于x ,y 的方程C :x 2+y 2﹣2x ﹣4y +m=0.(1)若方程C 表示圆,求m 的取值范围;(2)若圆C 与圆x 2+y 2﹣8x ﹣12y +36=0外切,求m 的值;(3)若圆C 与直线l :x +2y ﹣4=0相交于M ,N 两点,且,求m 的值.19. 在ABC ∆中,点()4,4B ,角A 的内角平分线所在直线的方程为0,y BC =边上的高所在直线的方程为220x y -+=.(Ⅰ) 求点C 的坐标;(Ⅱ) 求ABC ∆的面积20. 根据市场调查,某种新产品投放市场的30天内,每件的销售价格p (千元)与时间x (天)组成有序数对(),x p ,点(),x p 落在下图中的两条线段上,且日销售量q (件)与时间x (天)之间的关系是()*60q x x N =-+∈.(Ⅰ) 写出该产品每件销售价格p 〔千元)与时间x (天)之间的函数关系式;(Ⅱ) 在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品的销售价格⨯日销售量)21. 如图,ABED 是长方形,平面ABED ⊥平面,5,6ABC AB AC BC BE ====,且M 是BC 的中点(Ⅰ) 求证:AM ⊥平面BEC ;(Ⅱ) 求三棱锥B ACE -的体积;(Ⅲ)若点Q 是线段AD 上的一点,且平面QEC ⊥平面BEC ,求线段AQ 的长.22. 已知函数()12121x f x a -=-+(0a >且1a ≠)是定义在R 上的奇函数.(Ⅰ) 求实数a 的值;(Ⅱ) 证明函数()f x 在R 上是增函数;(Ⅲ)当[1,)x ∈+∞时,()22x mf x ≤-恒成立,求实数m 的取值范围.试卷答案一、选择题1-5: DBDAA 6-10: ACDCC 11、12:DB二、填空题13. 3π 14. 15. 2 16.01m <<三、解答题17.解:(Ⅰ){}{}|10|1A x x x x =-≤=≤,{}|1U A x x ∴=>ð 又{}{}|30|3B x x x x =->=<,(){}|13U A B x x ∴=<<ð. (Ⅱ),A C A C A =∴⊆,{}{}|1,|A x x C x x a =≤=<,1a ∴≤.18. 解:(1)方程C :x 2+y 2﹣2x ﹣4y+m=0,配方得:(x ﹣1)2+(y ﹣2)2=5﹣m , 若方程C 表示圆,则5﹣m >0,解得m <5;(2)把圆x 2+y 2﹣8x ﹣12y+36=0化为标准方程得:(x ﹣4)2+(y ﹣6)2=16, 则圆心坐标(4,6),半径为4,则两圆心间的距离d==5,因为两圆的位置关系是外切,所以d=R+r 即4+=5,解得m=4; (3)因为圆C 圆心C 的坐标为(1,2),则圆心C 到直线l 的距离d==, 所以=(|MN|)2+d 2,即5﹣m=1,解得m=4.19. 解:(Ⅰ)由题意知BC 的斜率为-2,又点()4,4B ,∴直线BC 的方程为()424y x -=--,即2120x y +-=.解方程组2200x y y -+=⎧⎨=⎩得20x y =-⎧⎨=⎩∴点A 的坐标为()2,0-.又A ∠的内角平分线所在直线的方程为0y =,∴点()4,4B 关于直线0y =的对称点()4,4B '-在直线AC 上, ∴直线AC 的方程为()223y x =-+,即2340x y ++=. 解方程组21202340x y x y +-=⎧⎨++=⎩得108x y =⎧⎨=-⎩ ∴点C 的坐标为()10,8-. (Ⅱ)BC ==又直线BC的方程是2120x y +-=,∴点A 到直线BC 的距离是d ==, ABC ∴∆的面积是114822S BC d =⨯⨯=⨯=. 20. 解:(Ⅰ)根据图象,每件的销售价格p 与时间x 的函数关系为:()()**40020,602030,x x x N p x x N ⎧+<≤∈⎪=⎨<≤∈⎪⎩ (Ⅱ)设第x 天的日销售金额为y (千元),则()()()()()**4060020,60602030,x x x x N y x x x N ⎧+-+<≤∈⎪=⎨-+<≤∈⎪⎩ 即()()2**202400020,6036002030,x x x x N y x x x N ⎧-++<≤∈⎪=⎨-+<≤∈⎪⎩ 当*020,x x N <≤∈时,()22202400102500y x x x =-++=--+, ∴当10x =时,max 2500y =, 当*2030,x x N <≤∈时,603600y x =-+是减函数,602036002400y ∴<-⨯+=,因此,这种产品在第10天的日销售金额最大.21.(Ⅰ)证明:平面ABED ⊥平面ABC ,平面ABED 平面,ABC AB = ,BE AB BE ⊥⊂平面ABED ,BE ∴⊥平面ABC , 又AM ⊂平面ABC ,BE AM ∴⊥. 又,AB AC M =是BC 的中点,BC AM ∴⊥, 又,BC BE B BC =⊂平面,BEC BE ⊂平面BEC ,AM ∴⊥平面BEC . (Ⅱ)解:由(Ⅰ)知,BE ⊥平面,6ABC h BE ∴==. 在Rt ABM ∆中,4AM =, 又11641222ABC S BC AM ∆=⨯⨯=⨯⨯= 111262433B ACE E ABC ABC V V S h --∆∴==⨯⨯=⨯⨯= (Ⅲ)证明:在平面QEC 内作,QN EC QN ⊥交CE 于点N . 平面QEC ⊥平面BEC ,平面QEC 平面BEC EC -, QN ∴⊥平面BEC ,又AM ⊥平面BEC . //QN AM ∴. QN ∴与AM 共面,设该平面为a ,ABED 是长方形,//AQ BE ∴, 又Q ⊄平面,BEC BE ⊂平面BEC ,//AQ ∴平面BEC , 又,AQ αα⊂平面BEC MN =,//AQ MN ∴, 又//QN AM ,∴四边形AMNQ 是平行四方形.AQ MN ∴=. //,//AQ BE AQ MN ,//MN BE ∴, 又M 是BC 的中点.132MN BE ∴==,3AQ MN ∴==. 22. 解:(Ⅰ)()f x 是定义在R 上的奇函数.()22201102221a a f a a a-∴=-=-==+++,2a ∴=. (Ⅱ)任取12,x x R ∈,且12x x <,则()()()()()1212211212222222211212121212121x x x x x x x x f x f x -⎛⎫⎛⎫-=---=-= ⎪ ⎪++++++⎝⎭⎝⎭ 1212,22x x x x <∴<,即12220x x -< 又12210,210x x +>+> ()()120f x f x ∴-<,即()()12f x f x < ()f x ∴在R 上为增函数(Ⅲ)由题意得,当1x ≥时,212221x x m ⎛⎫-≤- ⎪+⎝⎭即212221x x x m -⋅≤-+恒成立, 1,22x x ≥∴≥,()()()2221121x x x m x -+∴≤≥-恒成立,设()211x t t =-≥,则()()212221t t t t m t t t t-++-≤==-+ 设()21g t t t=-+,则函数()g t 在[1,)t ∈+∞上是增函数. ()()min 10g t g ∴==0m ∴≤∴实数m 的取值范围为0m ≤.。
单县二中2017-2018学年高一上学期期末考试数学模拟试题(三)

单县二中2017—2018学年度第一学期期末考试高一数学模拟试题(三) 21017.12第I 卷(选择题)一、选择题:(本题共12道小题,每小题5分,共60分)1.设集合2{5,log }()3A a =+,集合{,}B a b =,若{2}A B = ,则b a -=( )A .1B .2C .3D .42.已知(1,0,2)A ,(1,3,1)B -,点M 在z 轴上且到A 、B 两点的距离相等,则M 点的坐标为( )A .(3,0,0)-B .(0,3,0)-C .(0,0,3)-D .(0,0,3)3.函数()22x f x =-的定义域为( ) A .[0,1) B .(1,)+∞ C .[0,1)(1,)+∞ D .[0,)+∞4.设m ,n 表示两条不同的直线,α,β表示两个不同的平面,则下列命题不正确的是( )A .m ⊥α,m ⊥β,则α∥βB .m ∥n ,m ⊥α,则n ⊥αC .m ⊥α,n ⊥α,则m ∥nD .m ∥α,α∩β=n ,则m ∥n5. 若直线2y x =-被圆222240x y ax a +-+-=所截得的弦长为,则实数a 的值为( )A. C. 2-或6 D. 0或46 )A B C D 7.设直线0x y a --=与圆224x y +=相交于,A B 两点,O 为坐标原点,若AOB△为等边三角形,则实数a 的值为( )A .B .C .3±D .9±8.已知函数()f x 是R 上的奇函数,且满足(2)(),(3)4,(2017)f x f x f f p +=-<=,则p 的取值范围为( )A .(4,)+∞B .(2,)+∞C .(2,)-+∞D .(4,)-+∞9.在三棱锥S ABC -中,底面ABC △是直角三角形,其斜边4,AB SC =⊥平面ABC ,且3SC =,则此三棱锥的外接球的表面积为( )A .25πB .20πC .16πD .13π10.设函数()|ln |f x x =与2()101g x x x =-++在区间(,2)a a +上均为增函数,则a的取值范围为( )A .(1,3)B .[1,3]C .(1,4)D .[1,4]11.如图,正方体1111ABCD A BC D -中,E 为线段B 1D 1上的一个动点,则下列结论中错误的是( )A .AC ⊥BEB .B 1E ∥平面ABCDC .三棱锥E -ABC 的体积为定值D .B 1E ⊥BC 112.已知函数1,1()|21|,1x x f x x x ⎧>⎪=⎨⎪-≤⎩,若函数()()g x f x k =-有3个零点,则实数k 的取值范围为( )A .(0,)+∞B .(0,1)C .[1,)+∞D .[1,2)第II 卷(非选择题)二、填空题:(本题共5道小题,每小题5分,共25分)13.若2510a b==,则11a b +=__________. 14.已知直线l 过点(-2,-3)且与直线2x-3y+4=0垂直,则直线l 的方程为__________. 15.四面体S-ABC 中,各个侧面都是边长为a 的正三角形,E,F 分别是SC 和AB 的 中点,则异面直线EF 与SA 所成的角等于________.16.已知函数2()2f x x x =+,若对任意1[1,2]x ∈,存在2[1,1]x ∈-,使得12()()f x g x ≥,则实数m 的取值范围是_________.三、解答题:(本题共6道小题,共75分)17.(本小题满分10分)的定义域为B (其中a 为常数). (1)若2a =,求A B 及()A B R ð;(2)若A B A = ,求实数a 的取值范围.18.(本小题满分12分) 如图,已知三棱柱111ABC A B C -中,1AA ⊥平面ABC ,AC BC =,M N 、分别是棱1,CC AB 的中点.(1)求证:CN ⊥平面11ABB A ;(2)求证://CN 平面1AMB .19. (本小题满分12分) 已知定义在(0,)+∞上的函数()log (1)a f x x a =>,且它在1[,3]2上的最大值为1. (1)求a 的值;(2)令11()()()33F x f x f x =++-,判断函数()F x 的奇偶性,并求函数()F x 的值域.20.(本小题满分12分) 已知曲线22:240C x y x y m +--+=.(1)若1m =,过点(2,3)-的直线l 交曲线C 于,M N 两点,且||MN =求直线l 的方程;(2)若曲线C 表示圆,且直线10x y --=与圆C 交于,A B 两点,则是否存在实数m ,使得以AB 为直径的圆过原点,若存在,求出实数m 的值;若不存在,请说明理由.21.(本小题满分12分)“活水围网”养鱼技术具有养殖密度高、经济效益好的特点.研究表明:“活水围网”养鱼时,某种鱼在一定的条件下,每尾鱼的平均生长速度V (单位:千克/年)是养殖密度x (单位:尾/立方米)的函数,当x 不超过4尾/立方米时,V 的值为2千克/年;当420x ≤≤时,V 是x 的一次函数,且当20x =时, 0V =.(1)当020x <≤时,求V 关于x 的函数的表达式.(2)当养殖密度x 为多大时,每立方米的鱼的年生长量(单位:千克/立方米)可以达到最大?并求出最大值.22.(本小题满分12分)如图,在矩形ABCD 中,已知AB =2,AD =M ,N 分别为AD 和BC 的中点,对角线BD 与MN 交于O 点,沿MN 把矩形ABNM 折起,使平面ABNM 与平面MNCD 所成的角为60°,如图.(1)求证:BO ⊥DO ;(2)求AO 与平面BOD 所成角的正弦值.。
山东省菏泽市2017-2018学年高中数学 第一章 解三角形 第二章 数列周测题 新人教A版必修5

解三角形.数列一、选择题(本大题共10小题,共50分)1.△ABC的内角A、B、C的对边分别为a、b、c,若a、b、c成等比数列,且c=2a,则cosB=()A.B.C.D.2.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,若,a=2,,则b的值为()A.B.C.D.3.△ABC的内角A,B,C的对边分别为a,b,c,已知sinB+sinA(sinC﹣cosC)=0,a=2,c=,则C=()A.B.C.D.4.在△ABC中,B=,BC边上的高等于BC,则cosA=()A.B.C.﹣D.﹣5.如图,在△ABC中,D是边AC上的点,且AB=AD,2AB=BD,BC=2BD,则sinC的值为()A.B.C.D.6.已知数列{a n}满足3a n+1+a n=0,a2=﹣,则{a n}的前10项和等于()A.﹣6(1﹣3﹣10)B.C.3(1﹣3﹣10)D.3(1+3﹣10)7.数列{a n}的前n项和为S n,若a1=1,a n+1=3S n(n≥1),则a6=()A.3×44B.3×44+1 C.44D.44+18.等比数列{a n}中,a4=2,a5=5,则数列{lga n}的前8项和等于()A.6 B.5 C.4 D.39.数列{a n}中,对任意n∈N*,a1+a2+…+a n=2n﹣1,则a12+a22+…+a n2等于()A.(2n﹣1)2 B.C.4n﹣1 D.10.《九章算术》是我国古代的数学名著,书中有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各得几何.”其意思为“已知甲、乙、丙、丁、戊五人分5钱,甲、乙两人所得与丙、丁、戊三人所得相同,且甲、乙、丙、丁、戊所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).这个问题中,甲所得为()A.钱 B.钱 C.钱 D.钱二、填空题(本大题共4小题,共20分)11.在△ABC中,B=60°,AC=,则AB+2BC的最大值为.12.已知等差数列{a n}中,满足S3=S10,且a1>0,S n是其前n项和,若S n取得最大值,则n= .13.设△ABC的内角A,B,C的对边分别为a,b,c,且a=2,cosC=﹣,3sinA=2sinB,则c= .14.2011年3月11日,日本9.0级地震造成福岛核电站发生核泄漏危机.如果核辐射使生物体内产生某种变异病毒细胞,若该细胞开始时有2个,记为a0=2,它们按以下规律进行分裂,1 小时后分裂成4个并死去1个,2小时后分裂成6个并死去1个,3小时后分裂成10个并死去1 个,…,记n小时后细胞的个数为a n,则a n= (用n表示).三、解答题(本大题共4题,共50分)15.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.16.设等差数列{a n}的公差为d,前n项和为S n,等比数列{b n}的公比为q,已知b1=a1,b2=2,q=d,S10=100.(1)求数列{a n},{b n}的通项公式(2)当d>1时,记c n=,求数列{c n}的前n项和T n.17.S n为数列{a n}的前n项和,己知a n>0,a n2+2a n=4S n+3(I)求{a n}的通项公式:(Ⅱ)设b n=,求数列{b n}的前n项和.一.填空题:(每题5分,共50分)二、填空题:(每题5分,共20分)11 12、13、 14、三、解答题(12+12+13+13共50分)15、16、17、解三角形.数列答案一.选择题(共10小题)1.B ;2.A ;3.B ;4.C ;5.D ;6.C ;7.A ;8.C ;9.D ;10.B ;二.填空题(共4小题)11.2;12.6或7;13.4;14.2n +1;三.解答题(共4小题)15. 解:(I )由已知及正弦定理得,()2cosC sin cos sin cos sinC A B+B A =, 即()2cosCsin sinC A+B =.故2sinCcosC sinC =.可得1cosC 2=,所以C 3π=.(II )由已知,1sin C 2ab =.又C 3π=,所以6ab =.由已知及余弦定理得,222cosC 7a b ab +-=., 解得,或,当时,当时,a n =(2n+79),b n =9•;(2)当d >1时,由(1)知a n =2n ﹣1,b n =2n ﹣1,∴c n ==,∴T n =1+3•+5•+7•+9•+…+(2n ﹣1)•,∴T n=1•+3•+5•+7•+…+(2n﹣3)•+(2n﹣1)•,∴T n=2+++++…+﹣(2n﹣1)•=3﹣,∴T n=6﹣.17.解:(I)由a n2+2a n=4S n+3,可知a n+12+2a n+1=4S n+1+3两式相减得a n+12﹣a n2+2(a n+1﹣a n)=4a n+1,即2(a n+1+a n)=a n+12﹣a n2=(a n+1+a n)(a n+1﹣a n),∵a n>0,∴a n+1﹣a n=2,∵a12+2a1=4a1+3,∴a1=﹣1(舍)或a1=3,则{a n}是首项为3,公差d=2的等差数列,∴{a n}的通项公式a n=3+2(n﹣1)=2n+1:(Ⅱ)∵a n=2n+1,∴b n===(﹣),∴数列{b n}的前n项和T n=(﹣+…+﹣)=(﹣)=.。
山东单县北城三中2017——2018学年度下学期七年级数学期末模拟八(扫描版无答案)

矿产资源开发利用方案编写内容要求及审查大纲
矿产资源开发利用方案编写内容要求及《矿产资源开发利用方案》审查大纲一、概述
㈠矿区位置、隶属关系和企业性质。
如为改扩建矿山, 应说明矿山现状、
特点及存在的主要问题。
㈡编制依据
(1简述项目前期工作进展情况及与有关方面对项目的意向性协议情况。
(2 列出开发利用方案编制所依据的主要基础性资料的名称。
如经储量管理部门认定的矿区地质勘探报告、选矿试验报告、加工利用试验报告、工程地质初评资料、矿区水文资料和供水资料等。
对改、扩建矿山应有生产实际资料, 如矿山总平面现状图、矿床开拓系统图、采场现状图和主要采选设备清单等。
二、矿产品需求现状和预测
㈠该矿产在国内需求情况和市场供应情况
1、矿产品现状及加工利用趋向。
2、国内近、远期的需求量及主要销向预测。
㈡产品价格分析
1、国内矿产品价格现状。
2、矿产品价格稳定性及变化趋势。
三、矿产资源概况
㈠矿区总体概况
1、矿区总体规划情况。
2、矿区矿产资源概况。
3、该设计与矿区总体开发的关系。
㈡该设计项目的资源概况
1、矿床地质及构造特征。
2、矿床开采技术条件及水文地质条件。
山东省菏泽市2017-2018学年高一下学期期中数学试卷 Word版含解析

山东省菏泽市2017-2018学年高一下学期期中数学试卷 一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.若cosθ>0,且sin2θ<0,则角θ的终边所在象限是() A. 第一象限 B. 第二象限 C. 第三象限 D.第四象限
2.某中学2015届高三年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.则x+y的值为()
A. 7 B. 8 C. 9 D.10 3.设0≤x≤2π,且=sinx﹣cosx,则() A. 0≤x≤π B. C. D.
4.已知集合A={x|2x2﹣x﹣3<0},B={x|y=lg},在区间(﹣3,3)上任取一实数x,则“x∈A∩B”的概率为() A. B. C. D.
5.若函数f(x)=sin(ωx+θ)的图象(部分)如图所示,则ω和θ的取值是()
A. B. C. D. 6.对具有线性相关关系的变量x,y,测得一组数据如下表: x 2 4 5 6 8 y 20 40 60 70 80 根据上表,利用最小二乘法得它们的回归直线方程为=10.5x+,据此模型来预测当x=20时,y的估计值为() A. 210 B. 210.5 C. 211.5 D.212.5
7.总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右一次选取两个数字,则选出来的第5个个体的编号为() 7816 6572 0802 6314 0702 4369 9728 0198 3204 9234 4935 8200 3623 4869 6938 7481
A. 08 B. 07 C. 02 D.01 8.函数向左平移个单位后是奇函数,则函数f(x)在上的最小值为() A. B. C. D.
【月考试卷】2017—2018学年第一学期九年级数学第一次月考试题卷及答案
2017—2018学年第一学期九年级数学第一次月考试题卷一、填空题(本大题共6小题,每小题3分,共18分,每小题只有一个正确选项)1.下列方程中,是一元二次方程的是()A . 2)3(2x x x B . 02cbx ax C . 02132xxD . 122x2.一元二次方程0562x x 配方可变形为()A .14)3(2xB .4)3(2xC .14)3(2x D .4)3(2x3.某商品原价为200元,连续两次降价a %后售价为148元,下列方程正确的是()2.200(1%)148A a .200(12%)148B a 2.200(1%)148C a .200(12%)148D a 4.已知抛物线22yxx 上三点15,Ay ,21,B y ,312,C y ,则1y ,2y ,3y 满足的关系式为()A .1y <2y <3yB .3y <2y <1yC .2y <1y <3y D .3y <1y <2y 5.当0b时,函数yax b 与2yaxbxc 在同一坐标系内的图象可能是()6.对于抛物线21132yx ,下列结论:(1)抛物线的开口向下;(2)对称轴为直线1x ;(3)顶点坐标为1,3;(4)当1x 时,y 随x 的增大而减小。
其中正确结论的个数为()。
A . 1B . 2C . 3D . 4二、填空题(本大题共6小题,每小题3分,共18分)7.方程2437x x的二次项系数是,一次项系数是,常数项是 .8.以3和2为根的一元二次方程是___________ .9.抛物线21y m x 开口向上,则m 的取值范围是 .10.若方程23520xx有一根是a ,则2610aa.11.如图,抛物线212y x 经过平移得到抛物线2122yxx ,其对称轴与两段抛物线所围成的阴影部分的面积为.12.如图,二次函数20yaxbx c a的图象与x 轴交于A B 、两点,与y 轴交于点C ,且OA OC ,则下列结论:2410;20;310;44bac c abcac b OA OBaa其中正确的结论是_____ .(只填写序号)三、(本大题共4小题,13题12分,14、15、16题每题6分,共30分)13.用适当的方法解下列方程:2(1)225x22430xx 33121x x x 245140xx 14.关于x 的一元二次方程012122m xxm 有一个根是0x ,求:(1)m 的值; (2)该一元二次方程的另一根.15.如图,二次函数2yaxbxc 的图象与x 轴交于点A B 、,与y 轴交于点C .(1)写出A B C 、、三点的坐标和对称轴方程;(2)求出二次函数的解析式15题图12题图11题图16.如图,在宽为20m ,长为32m 的矩形耕地上,修筑同样宽的三条道路(互相垂直),把耕地分成大小不等的六块试验田,要使试验田的面积为2570m ,道路应为多宽?四.(本大题共3小题,每小题8分,共24分)17.关于x 的方程222110xk x k有两个实数根12x x 、.(1)求实数k 的取值范围;(2)若12x x 、满足221212+=16+x x x x ,求实数k 的值18.如图,已知抛物线2yxbx c 经过1,0,3,0A B 两点. (1)求b 和c ;(2)当04x 时,求y 的取值范围;(3)点P 为x 轴下方抛物线上一点,试说明P 点运动到哪个位置时PAB S最大,并求出最大面积.19.某个体商户购进某种电子产品的进价是50元/个,根据市场调研发现售价是80元/个时,每周可卖出160个.若销售单价每个降低2元,则每周可多卖出20个.设销售价格每个降低x 元(x 为偶数),每周销售量为y 个.(1)直接写出销售量y 个与降价x 元之间的函数关系式;(2)设商户每周获得的利润为W 元,当销售单价定为多少元时,每周销售利润最大,最大利润是多少元?五.(本大题共2小题,每小题9分,共18分)20.如果关于x 的一元二次方程200axbx c a 有两个实数根,且其中一个根为另一个根的2倍,那么称这样的方程为“倍根方程”.例如,一元二次方程2680xx 的两个根是2和4,则方程2680xx 就是“倍根方程”.(1)若一元二次方程230x x c是“倍根方程”,则c=;(2)若200x mx nm 是“倍根方程”,求代数式2245mmn n 的值;(3)若方程200ax bx ca是倍根方程,且相异两点1,M t s ,4,N t s 都在抛物线2y axbx c 上,求一元二次方程200axbx ca的根.21.已知3,P m 和1,Q m 是抛物线221y xbx 上的两点.(1)求b 的值;(2)判断关于x 的一元二次方程221=0xbx 是否有实数根,若有,求出它的实数根;若没有,请说明理由;(3)将抛物线221yxbx 的图象向上平移k (k 是正整数)个单位,使平移后的图象与x 轴无交点,求k 的最小值.六.(本大题共12分)22.定义:如图1,抛物线20yax bx c a 与x 轴交于A B 、两点,点P 在抛物线上(点P 与A B 、两点不重合),如果ABP 的三边满足222APBPAB ,则称点P 为抛物线20yaxbx c a的勾股点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
菏泽单县北城三中2017-2018学年度
七年级上学期第二次月考数学试卷
(时间:100分钟,满分120分)
一.选择题:(共12小题,每小题3分,满分36分)
1. 10个棱长为a的正方体木块堆成如图所示的形状,则它的表面积是( )
A. 30a2 B. 34a2 C. 36a2 D. 48a2
2.下面四个图形是如图的展开图的是( )
A. B. C. D.
3.如图,点C是线段AB上的点,点D是线段BC的中点,AB=10,AC=6,则线段CD的长是
( )
A.4 B.3 C.2 D.1
4.某大米包装袋上标注着“净含量10kg±150g”,小华从商店买了2袋大米,这两袋大米相
差的克数不可能是( )
A. 100g B. 150g C. 300g D. 400g
5、马小虎做了6道题:
①(﹣1)2013=﹣2013; ②0﹣(﹣1)=1; ③﹣ + =﹣ ;④ ÷(﹣ )=﹣1;
⑤2×(﹣3)2=36;⑥﹣3÷ ×2=﹣3.那么,他做对了( )题.
A. 1道 B. 2道 C. 3道 D. 4道
6..下面是一个被墨水污染过的方程:2x﹣=3x+, 答案显示此方程的解是x=﹣1
,
被墨水遮盖的是一个常数,则这个常数是( )
A. 1 B. -1 C. - D.
7.如果,0)1(22ba那么代数式(a+b)2018的值为( )
A.–2018 B. 2017 C. -1 D. 1
8.受季节影响,某种商品每年按原售价降低10
%后,又降价a元,现在每件售价b元,那
么该商品每件的原售价为( )
A、%101ba B、ba%101
C、%101ab D、ba%101
9..下列图表列出了一项实验的统计数据,表示将皮球从高d处落下时,弹跳高度b
与
下落高度d的关系:
d
50 80 100 150
b
25 40 50 75
则能反映这种关系的式子是( )
.
(A)2bd (B)2bd (C)2db (D)
25bd
10.已知一个单项式的系数是2,次数是3,则这个单项式可以是( )
A. ﹣2xy2 B. 3x2 C. 2xy3 D. 2x3
11 .已知a﹣b=3,c﹣d=2,则(b+c)﹣(a+d)的值是( )
A. -1 B. 1 C. -5 D. 15
12、.若x=1是关于x的方程ax+1=2的解,则a是( )
A. 1 B. 2 C. -1 D. -2
二.填空题:(共12小题,每小题3分,满分36分)
13、方程x+5= (x+3)的解是_______
14.如果a﹣3与a+1互为相反数,那么a=________
15. 如果代数式132xx的值是5,那么代数式2622xx的值等于 .
16、若一个两位数十位上的数是a,个位上的数是b,这个两位数是_________.
17..若关于a,b的多项式(a2+2ab﹣b2)﹣(a2+mab+2b2)中不含ab项,
则m=________.
18.如果0122ba,则aba4035的值为________.
19.若16x2y4和xmyn+3是同类项,那么n﹣m2的值是________
20.单项式﹣ 的系数与次数的积是________
21.甲队有工人272人,乙队有工人196人,如果要求乙队的人数是甲队人数的, 应从
乙队调多少人去甲队.如果设应从乙队调x人到甲队,列出的方程是
22.规定a*b=5a+2b﹣1,则(﹣3)*7的值为________
23.用同样大小的黑色棋子按下图所示的方式摆图形,按照这样的规律摆下去,则第n个
图形需要棋子 枚.
24、若有理数a、b、c在数轴上的位置如图所示,则化简:
c
a b
0
bcbaca
第1个 第2个
第3个
菏泽单县北城三中2017——2018学年度
七年级上学期第二次月考数学试卷
(时间:100分钟,满分:120分)
一、选择(每题3分,共计36分)
题号
1 2 3 4 5 6
选项
题号
7 8 9 10 11 12
选项
二、填空(每题3分,共计36分)
16、 ,17、 ,18、 ,
19、 ,20、 ,21、 ,
22、 ,23、 ,24、 ,
三.
解答题:
25.计算(每小题5分,共10分)
(1)
)48()1214361(
(2)
])3(2[3)21(124
班
级
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
姓
名
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
考
号
26、(1)化简(5分)
22
37432xxxx
(2)(5分)先化简,
再求值: ,其中.
27.(1)(6分)若a是方程的解,
b是方程的解,求a-3b的值.
ababbaabbaba3]4)32(62[3222
3
1
b
3a
32312482xx
51911683xxx
座号
(2)(6分)若式子比式子小1 ,求x的值 .+
28.(1)(8分)一块金与银的合金重250克,放在水中减轻了16克,已知金在水中称重
量减轻119,银在水中称重量减轻110,求这块合金中含金、银各多少克?
312x
0.20.10.3x
(2)、(8分)甲、乙两车同时从A,B两地相向而行,两车的相遇点距A、B两地中点处
8km,已知甲车速度是乙车速度的1.2倍,求A、B两地的路程。
