局部阻力系数ξ公式
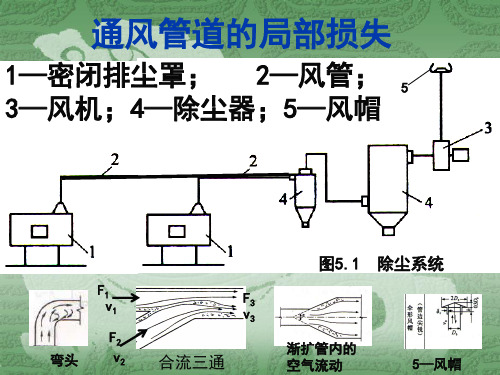
通风管道局部损失(WK).
当合流三通内直管的气流速度大于 支管的气流速度时,会发生直管气流引 射支管气流的作用,有时支管的局部阻 力出现负值,同样直管的局部阻力也会 出现负值,但不可能同时出现负值。为 避免引射时的能量损失,减小局部阻力, 如图5.12,应使
v1≈v2≈v3, 即F1+ F2 =F3,以避 免出现这种现象。
图5.6 矩形弯管
图5.7 内外弧型矩形弯管 导流片的设置
国家标准设计图集各种导流叶片做法
表5.2 内外弧型矩形弯管导流片片数及设置位置
图5.8 内弧、内斜线外直角和内外直角矩形弯管导流片的设置 表5.3 单弧形或双弧形导流片圆弧半径及片距( mm)
2.变径尽量用渐扩、渐缩。(图5.9)
3.管道 与风机接管 处避免局部 涡流。(图 5.10)
图5.12 合流三通
5.风管的进、出口:气流流出时将 流出前的能量全部损失掉,损失值等于 出口动压,因此可采用渐扩管(扩压管) 来降低出口动压损失。图5.13所示,空
气进入风管会产生涡流而 造成局部阻力,可采取措施 减少涡流,降低其局部阻力。
图5.14 风管渐扩进口实物
图5.13 风管进口
局部损失
α=8~10 °(<45°)
图5.9 渐扩管内的空气流动
D叶轮直径
图5.10 风机进出口的管道连接
4.三通的局部阻力大小与断面形 状、两支管夹角、支管与总管的截面比 有关,为减小三通的局部阻力,应尽量 使支管与干管连接的夹角不超过30°, 如图5.12所示。
图5.11 三通支管和干管的连接
图5.12 合流三通
三通、变径、风帽、阀门等。
局部损失计算公式
式中
Pj
v 2
2
Pa
风管阻力计算

通风管道阻力计算对于空调通风专业来说,我们最终的目的是让整个系统达到或接近设计及业主的要求。
对于整套空调系统而言主要应该把握几个关键的参数:风量、温度、湿度、洁净度等。
可见无论空调是否对新风做处理,我们送到房间的风量是一定要达到要求。
否则别的就更不用考虑了。
管道内风量主要是由风管内阻力影响的。
风管内空气流动的阻力有两种,一种是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失,称为摩擦阻力或沿程阻力;另一种是空气流经风管中的管件及设备时,由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失,称为局部阻力。
下边为标准工况且没有扰动的情况下的计算,如实际不是标准工况且有扰动需要进行修正。
一:摩擦阻力(沿程阻力)计算摩擦阻力(沿程阻力)计算一:(公式推导法)根据流体力学原理,无论矩形还是圆形风管空气在横断面形状不变的管道内流动时的摩擦阻力(沿程阻力) 按下式计算:ΔPm=λν2ρL/2D以上各式中:ΔPm———摩擦阻力(沿程阻力),Pa。
λ————摩擦阻力系数【λ根据流体不同情况而改变不具有规律性,不可用纯公式计算,只能靠实验得到许多不同状态的半经验公式:其中最常用的公式为:,《K-管壁的当量绝对粗糙度,mm (见表1-1);D-风管当量直径,mm(见一下介绍) ;Re雷诺数判断流体流动状态的准则数,(见表1-1);其实λ一般由莫台图所得,见图】莫台曲线图表1-1 一般通风管道中K、Re、λ的经验取值ν————风管内空气的平均流速,m/s; 【其中ν=Q/F;Q为管内风量m3/S,F为管道断面积M2 ;其中矩形风管F=a×b;圆形风管F=πD2 /4,一般设计也直接选风速见表1-2】表1-2 一般通风系统中常用空气流速(m/s)ρ————空气的密度,Kg/m3;【在压力B0=101.3kPa、温度t0=20℃、一般情况下取ρ=1.205Kg/m3; 见表1-3】L ———风管长度,m 【横断面形状不变的管道长度】D———风管的当量直径,m; 【矩形风管流速当量直径:;流量当量直径:;圆形风管D为风管直径】摩擦阻力(沿程阻力)计算二:(比摩阻法)由以上计算看出计算V和D较容易而计算λ难度很大,所以我们选择查表更合适快捷。
通风管道沿程摩擦风阻及局部阻力系数计算方法

通风管道沿程摩擦风阻及局部阻力系数计算方法B.1 通风管道沿程摩擦风阻通风管道沿程摩擦风阻可按公式(B.1)~(B.2)计算:55.6d L R f α=.....................................(B.1) =8λρα.......................................(B.2) 式中:α——通风管道摩擦阻力系数(kg/m 3);λ——通风管道达西系数,对柔性通风管进行计算时可取0.019~0.021;ρ——空气密度(kg/m 3);d ——通风管道当量直径(m )。
B.2 通风管道的局部阻力系数通风管道的局部阻力系数取值应根据局部损失的具体形式确定,并可按照以下规定进行取值: a) 突然扩大的异径管接头,其局部阻力系数可按公式(B.3)计算:()212=1/A A ξ-...................................(B.3)式中:A 1——进风处接头的管道截面面积(m 2);A 2——出风处接头的管道截面面积(m 2)。
b) 突然缩小的异径管接头,其局部阻力系数可按公式(B.4)计算: ()221=0.51/A A ξ-..................................(B.4)式中:A 1——进风处接头的管道截面面积(m 2);A 2——出风处接头的管道截面面积(m 2)。
c) 通风管道转弯时,其局部阻力系数可按公式(B.5)~(B.6)计算:0.750.8=0.008/n ξθ...................................(B.5) /n R d =......................................(B.6)式中:θ——转弯角度;R ——转弯处的曲率半径(m );d ——管道直径(m )。
d)管道入口处的局部阻力系数ξ可取为0.6;e)管道出口处的局部阻力系数ξ可取为1.0;f)管道分岔处的局部阻力系数ξ可取为1.0。
风管内空气流动的阻力有两种

1. 风管内空气流动的阻力有两种:(1)是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失,称为摩擦阻力或沿程阻力;(2)另一种是空气流经风管中的管件及设备时,由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失,称为局部阻力。
2. 计算方法:(1)摩擦阻力根据流体力学原理,空气在横断面形状不变的管道内流动时的摩擦阻力按下式计算:ΔPm=λν2ρl/8Rs对于圆形风管,摩擦阻力计算公式可改写为:ΔPm=λν2ρl/2DRs=λν2ρ/2D以上各式中λ————摩擦阻力系数;;ν————风管内空气的平均流速,m/s;ρ————空气的密度,Kg/m3;l ————风管长度,m;Rs————风管的水力半径,m;Rs=f/Pf————管道中充满流体部分的横断面积,m2;P————湿周,在通风、空调系统中既为风管的周长,m;D————圆形风管直径,m。
矩形风管的摩擦阻力计算我们日常用的风阻线图是根据圆形风管得出的,为利用该图进行矩形风管计算,需先把矩形风管断面尺寸折算成相当的圆形风管直径,即折算成当量直径。
再由此求得矩形风管的单位长度摩擦阻力。
当量直径有流速当量直径和流量当量直径两种;流速当量直径:Dv=2ab/(a+b)流量当量直径:DL=1.3(ab)0.625/(a+b)0.25在利用风阻线图计算是,应注意其对应关系:采用流速当量直径时,必须用矩形中的空气流速去查出阻力;采用流量当量直径时,必须用矩形风管中的空气流量去查出阻力。
(2)局部阻力当空气流动断面变化的管件(如各种变径管、风管进出口、阀门)、流向变化的管件(弯头)流量变化的管件(如三通、四通、风管的侧面送、排风口)都会产生局部阻力。
1. 局部阻力按下式计算:Z=ξν2ρ/2ξ————局部阻力系数。
1. 局部阻力在通风、空调系统中占有较大的比例,在设计时应加以注意,为了减小局部阻力,通常采用以下措施:a. 弯头布置管道时,应尽量取直线,减少弯头。
管道阻力的基本计算方法

管道阻力计算空气在风管内的流动阻力有两种形式:一是由于空气本身的黏滞性以及空气与管壁间的摩擦所产生的阻力称为摩擦阻力;另一是空气流经管道中的管件时如三通、弯头等,流速的大小和方向发生变化,由此产生的局部涡流所引起的阻力,称为局部阻力;一、摩擦阻力根据流体力学原理,空气在管道内流动时,单位长度管道的摩擦阻力按下式计算:ρλ242v R R s m ⨯= 5—3 式中 Rm ——单位长度摩擦阻力,Pa /m ;υ——风管内空气的平均流速,m /s ;ρ——空气的密度,kg /m 3;λ——摩擦阻力系数;Rs ——风管的水力半径,m;对圆形风管:4DR s = 5—4式中 D ——风管直径,m;对矩形风管)(2b a abR s += 5—5式中 a,b ——矩形风管的边长,m;因此,圆形风管的单位长度摩擦阻力ρλ22v D R m ⨯= 5—6 摩擦阻力系数λ与空气在风管内的流动状态和风管内壁的粗糙度有关;计算摩擦阻力系数的公式很多,美国、日本、德国的一些暖通手册和我国通用通风管道计算表中所采用的公式如下:)Re 51.27.3lg(21λλ+-=D K 5—7式中 K ——风管内壁粗糙度,mm ;Re ——雷诺数;υvd=Re 5—8式中 υ——风管内空气流速,m /s ;d ——风管内径,m ;ν——运动黏度,m 2/s;在实际应用中,为了避免烦琐的计算,可制成各种形式的计算表或线解图;图5—2是计算圆形钢板风管的线解图;它是在气体压力B =101.3kPa 、温度t=20℃、管壁粗糙度K =0.15mm 等条件下得出的;经核算,按此图查得的Rm 值与全国通用通风管道计算表查得的λ/d 值算出的Rm 值基本一致,其误差已可满足工程设计的需要;只要已知风量、管径、流速、单位摩擦阻力4个参数中的任意两个,即可利用该图求得其余两个参数,计算很方便;图5—2 圆形钢板风管计算线解图例 有一个10m 长薄钢板风管,已知风量L =2400m 3/h,流速υ=16m /s,管壁粗糙度K =0.15mm,求该风管直径d 及风管摩擦阻力R;解 利用线解图5—2,在纵坐标上找到风量L =2400m 3/h,从这点向右做垂线,与流速υ=16m /s 的斜线相交于一点,在通过该点表示风管直径的斜线上读得d =230mm;再过该点做垂直于横坐标的垂线,在与表示单位摩擦阻力的横坐标交点上直接读得Rm =13.5Pa /m;该段风管摩擦阻力为:R =R m l =13.5×10Pa =135Pa无论是按照全国通用通风管道计算表,还是按图5—2计算风管时,如被输送空气的温度不等于20℃,而且相差较大时,则应对R;值进行修正,修正公式如下:t m m K R R ' 5—9式中'mR——在不同温度下,实际的单位长度摩擦阻力,Pa;Rm——按20℃的计算表或线解图查得的单位摩擦阻力,Pa;Kt——摩擦阻力温度修正系数,如图5—3所示;图5—3 摩擦阻力温度修正系数钢板制的风管内壁粗糙度K值一般为0.15mm;当实际使用的钢板制风管,其内壁粗糙度K值与制图表数值有较大出入时,由计算图表查得的单位摩擦阻力Rm值乘以表5—3中相应的粗糙度修正系数;表中υ为风管内空气流速;表5—3 管壁粗糙度修正系数对于一般的通风除尘管道,粉尘对摩擦阻力的影响很小,例如含尘浓度为50g/m3时,所增大的摩擦阻力不超过2%,因此一般情况下可忽略不计;二、局部阻力各种通风管道要安装一些弯头、三通等配件;流体经过这类配件时,由于边壁或流量的改变,引起了流速的大小、方向或分布的变化,由此产生的能量损失,称为局部损失,也称局部阻力;局部阻力主要可分为两类:①流量不改变时产生的局部阻力,如空气通过弯头、渐扩管、渐缩管等;②流量改变时所产生的局部阻力,如空气通过三通等;局部阻力可按下式计算:22ρυξ=Z5—10式中 Z——局部阻力,Pa;ξ——局部阻力系数,见表5—4;υ——空气流速,m/s;ρ—空气密度,kg/m3;上式表明,局部阻力与其中流速的平方成正比;局部阻力系数通常都是通过实验确定的;可以从有关采暖通风手册中查得;表5—4列出了部分管道部件的局部阻力系数值;在计算通风管道时,局部阻力的计算是非常重要的一部分;因为在大多数情况下,克服局部阻力而损失的能量要比克服摩擦阻力而损失的能量大得多;所以,在制作管件时,如何采取措施减少局部阻力是必须重视的问题;表5—4 常见管件局部阻力系数下面通过分析几种常见管件产生局部阻力的原因,提出减少局部阻力的办法;1.三通图5—4为一合流三通中气流的流动情况;流速不同的1、2两股气流在汇合时发生碰撞,以及气流速度改变时形成涡流是产生局部阻力的原因;三通局部阻力的大小与分支管中心夹角、三通断面形状、支管与总管的面积比和流量比即流速比有关;图5—4 合流三通中气流流动状态为了减少三通局部阻力,分支管中心夹角;应该取得小一些,一般不超过30°;只有在安装条件限制或为了平衡阻力的情况下,才用较大的夹角,但在任何情况下,都不宜做成垂直的“T”形三通;为了避免出现引射现象,应尽可能使总管和分支管的气流速度相等,即按υ3=υ1=υ2来确定总管和分支管的断面积;这样,风管断面积的关系为:F3=F1+F2;2.弯头当气流流过弯头时见图5—5,由于气流与管壁的冲击,产生了涡流区Ⅰ;又由于气流的惯性,使边界层脱离内壁,产生了涡流区Ⅱ;两个涡流区的存在,使管道中心处的气流速度要比管壁附近大,因而产生了旋转气流;涡流区的产生和气流的旋转都是造成局部阻力的原因;图5—5 弯头中气流流动状况实验证明,增大曲率半径可以使弯头内的涡流区和旋转运动减弱;但是弯头的曲率半径也不宜太大,以免占用的空间过大,一般取曲率半径R等于弯头直径的1~2倍;在任何情况下,都不宜采用90°的“Г”形直角弯头;3.渐缩或渐扩管渐缩或渐扩管的局部阻力是由于气流流经管件时,断面和流速发生变化,使气流脱离管壁,形成涡流区而造成的;图5—6是渐扩管中气流的流动状况,图5—6 渐扩管中气流流动状况实验证明,渐缩或渐扩管中心角;越大,涡流区越大,能量损失也越大;为了减少渐缩、渐扩管的局部阻力,必须减小中心角α,缓和流速分布的变化,使涡流区范围缩小;通常中心角;不宜超过45°;三、系统阻力整个通风除尘系统的阻力称为系统阻力,它包括吸尘罩阻力、风管阻力、除尘器阻力和出口动压损失4部分;四、通风管道的压力分布图5—7所示为一简单通风系统,其中没有管件、吸尘罩和除尘器,假定空气在进口A和出口C处局部阻力很小,可以忽略不计,系统仅有摩擦阻力;图5—7 仅有摩擦阻力的风管压力分布按下列步骤可以说明该风管压力分布;1定出风管中各点的压力;风机开动后,空气由静止状态变为运动状态;因为风管断面不变,所以各点断面的空气流速相等,即动压相等;各点的动压分布分别为:点A点B全压空气从点A流至点月时要克服风管的摩擦阻力,所以点B的全压即风机吸入口的全压为:式中 Rm——风管单位长度摩擦阻力,Pa/m;——从点A至点B的风管长度,m;l1由式5—11可以看出,当风管内空气流速不变时,风管的阻力是由降低空气的静压来克服的;点C当空气排入大气时,这一能量便全部消失在大气中,称为风管出口动压损失;点B′空气由点B′流至点C需要克服摩擦阻力Rml,所以:22把以上各点的数值在图上标出,并连成直线,即可绘出压力分布图;如图5—7所示;风机产生的风压Hf等于风机进、出口的全压差,即从风管压力分布图和计算结果可以给人们以下启示;①风机产生的风压等于风管的阻力及出口动压损失之和,亦即等于系统阻力;换句话说,系统的阻力是由风机产生的风压来克服的;对于包括有管件、吸尘罩和除尘器的复杂系统,系统阻力中还包括这些部件和设备的阻力;②风机吸入段的全压和静压都是负值,风机压出段的全压和静压一般情况下均是正值;因此,风管连接处不严密时,会有空气漏人和逸出;前者影响吸尘效果,后者影响送风效果或造成粉尘外逸;。
通风管道阻力的计算与公式

风管内空气流动的阻力有两种,一种是由于空气本身的粘滞性及其与管壁间的摩擦而产生的沿程能量损失,称为摩擦阻力或沿程阻力;另一种是空气流经风管中的管件及设备时,由于流速的大小和方向变化以及产生涡流造成比较集中的能量损失,称为局部阻力。
一、摩擦阻力根据流体力学原理,空气在横断面形状不变的管道内流动时的摩擦阻力按下式计算:ΔPm=λν2ρl/8Rs对于圆形风管,摩擦阻力计算公式可改写为:ΔPm=λν2ρl/2D圆形风管单位长度的摩擦阻力(比摩阻)为:Rs=λν2ρ/2D以上各式中λ————摩擦阻力系数ν————风管内空气的平均流速,m/s;ρ————空气的密度,Kg/m3;l————风管长度,mRs————风管的水力半径,m;Rs=f/Pf————管道中充满流体部分的横断面积,m2;P————湿周,在通风、空调系统中既为风管的周长,m;D————圆形风管直径,m。
矩形风管的摩擦阻力计算我们日常用的风阻线图是根据圆形风管得出的,为利用该图进行矩形风管计算,需先把矩形风管断面尺寸折算成相当的圆形风管直径,即折算成当量直径。
再由此求得矩形风管的单位长度摩擦阻力。
当量直径有流速当量直径和流量当量直径两种;流速当量直径:Dv=2ab/(a+b)流量当量直径:DL=1.3(ab)0.625/(a+b)0.25在利用风阻线图计算是,应注意其对应关系:采用流速当量直径时,必须用矩形中的空气流速去查出阻力;采用流量当量直径时,必须用矩形风管中的空气流量去查出阻力。
二、局部阻力当空气流动断面变化的管件(如各种变径管、风管进出口、阀门)、流向变化的管件(弯头)流量变化的管件(如三通、四通、风管的侧面送、排风口)都会产生局部阻力。
局部阻力按下式计算:Z=ξν2ρ/2ξ————局部阻力系数。
局部阻力在通风、空调系统中占有较大的比例,在设计时应加以注意,为了减小局部阻力,通常采用以下措施:1.弯头布置管道时,应尽量取直线,减少弯头。
(完整版)管道阻力的基本计算方法

管道阻力计算空气在风管内的流动阻力有两种形式:一是由于空气自己的黏滞性以及空气与管壁间的摩擦所产生的阻力称为摩擦阻力;另一是空气流经管道中的管件时 (如三通、弯优等 ),流速的大小和方向发生变化,由此产生的局部涡流所引起的阻力,称为局部阻力。
一、摩擦阻力依照流体力学原理,空气在管道内流动时,单位长度管道的摩擦阻力按下式计算:v2R m4R s2(5— 3)式中Rm——单位长度摩擦阻力,Pa/m;υ——风管内空气的平均流速,m/ s;ρ——空气的密度,kg/ m3;λ——摩擦阻力系数;Rs——风管的水力半径,m。
对圆形风管:R s D4(5— 4)式中D——风管直径, m。
对矩形风管R sab2(a b)(5— 5)式中a, b——矩形风管的边长, m。
所以,圆形风管的单位长度摩擦阻力R mv2D 2(5— 6)摩擦阻力系数λ与空气在风管内的流动状态细风管内壁的粗糙度有关。
计算摩擦阻力系数的公式很多,美国、日本、德国的一些暖通手册和我国通用通风管道计算表中所采用的公式以下:1 2 lg(K 2.51)3.7D Re(5— 7)式中K ——风管内壁粗糙度,mm;Re——雷诺数。
Revd(5—8)式中υ——风管内空气流速,m/ s;d——风管内径,m;ν——运动黏度,m2/ s。
在实质应用中,为了防备烦杂的计算,可制成各种形式的计算表或线解图。
图5— 2 是计算圆形钢板风管的线解图。
它是在气体压力B=101. 3kPa、温度 t=20 ℃、管壁粗糙度K = 0.15mm 等条件下得出的。
经核算,按此图查得的Rm 值与《全国通用通风管道计算表》查得的λ/ d 值算出的Rm 值基本一致,其误差已可满足工程设计的需要。
只要已知风量、管径、流速、单位摩擦阻力 4 个参数中的任意两个,即可利用该图求得其余两个参数,计算很方便。
图 5— 2圆形钢板风管计算线解图[例 ]有一个10m长薄钢板风管,已知风量L = 2400m3/ h,流速υ= 16m/ s,管壁粗糙度 K = 0. 15mm,求该风管直径 d 及风管摩擦阻力R。
局部阻力——精选推荐

流体在管路的进口、出口、弯头、阀门、扩大、缩小等局部位置流过时,其流速大小和方向都发生了变化且流体受到干扰或冲击,使涡流现象加剧而消耗能量。
由实验测知,流体即使在直管中为滞流流动,但流过管件或阀门时也容易变为湍流。
在湍流情况下,为克服局部阻力所引起的能量损失有两种计算方法。
一、阻力系数法克服局部阻力所引起的能量损失,也可以表示成动能u2/2的一个函数,即:(1-59)或(1-59a)式中ζ称为局部阻力系数,一般由实验测定。
因局部阻力的形式很多,为明确起见,常对ζ加注相应的下标。
下面列举几种常用的局部阻力系数的求法。
(一)突然扩大与突然缩小图1-27 突然扩大和突然缩小的局部阻力系数管路由于直径改变而突然扩大或缩小,所产生的能量损失按式1-59及1-59a计算。
式中的流速u均以小管的流速为准,局部阻力系数可根据小管与大管的截面积之比从图1-27的曲线上查得。
(二)进口与出口流体自容器进入管内,可看作很大的截面A1突然进入很小的截面A2,即A2/A1≈0,根据图1-27的曲线(b),查出局部阻力系数ζc=0.5,这种损失常称为进口损失,相应的系数ζc,又称为进口阻力系数。
若管口圆滑或喇叭状,则局部阻力系数相应减小,约为0.25~0.05。
流体自管子进入容器或从管子直接排放到管外空间,可看作自很小的截面A1突然扩大到很大的截面A2,即A1/A2≈0,从图1-27中曲线(a),查出局部阻力系数ζe=1,这种损失常称为出口损失,相应的阻力系数ζe又称为出口阻力系数。
流体从管于直接排放到管外空间时,管出口内侧截面上的压强可取为管外空间相同。
应指出,若出口截面处在管出口的内侧,表示流体未离开管路,截面上仍具有动能,出口损失不应计入系统的总能量损失Σhf内,即ζe=0;若截面处在管子出口的外侧,表示流体已离开管路,截面上的动能为零,但出口损失应计入系统的总能量损失内,此时ζe=1。
(三)管件与阀门管路上的配件如弯头、三通、活接头等总称为管件。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
局部阻力系数ξ公式
1 局部阻力系数
局部阻力系数是流体流动阻力的重要参数,它可以用来评估流体在设计时的实际能耗,因此,局部阻力系数ξ的确定对流体力学的应用具有重要的意义。
局部阻力系数ξ的计算常用的一种方法是用局部阻力系数公式,它可以帮助我们估算局部阻力系数:ξ=Δ/V + η/Vf + C,其中Δ、V、η和Vf分别表示静压损失,流体流速,粘度和静态粘度。
确定局部阻力系数ξ的关键要素是流体流速,因为它与局部阻力的大小联系密切。
一般来说,随着流体流速的减小,静压损失和粘度阻力就增大,因此局部阻力系数ξ也会增大。
而当流速增加时,粘度阻力会降低,静压损失也会随之减小,因此局部阻力系数ξ也会随之降低。
此外,粘度也是影响局部阻力系数ξ的重要参数,一般情况下,随着流体粘度增加,局部阻力系数ξ也会增大。
在实际应用中,我们可以根据不同粘度的流体,用局部阻力系数公式来估算局部阻力系数ξ,满足工程要求。
局部阻力系数公式在流体实际应用中被广泛使用,它既提供了一种有效的流体流动参数评估方法,也可以用于估算流体的其他性质,如参数的精度、流动性能以及热传导率等。
要正确使用局部阻力系数
公式,我们需要准确地测定出各项参数,然后使用公式预测出更准确的局部阻力系数ξ。
