清华大学土木工程系土力学第二章(Yu)_726804861
合集下载
土力学-第2章 第2讲

土的分类原则和标准
目 的: • 便于调查研究; • 便于比较、分析、评价; • 便于学术与经验的交流 (基于共同的概念)
原 则: 1)简明原则—采用的指标能综合反映土的主要工程
性质;测定方法简单,使用方便。 2)工程性质差异原则—采用的指标一定程度上反映 不同类工程用土的不同特性。
2.7 土的胀缩性、巨粒湿土 陷性和漂 卵石石冻胀性
1、按沉积年代和地质成因划分
(ii) 运积土
洪积土
2.7 土的分类
建筑地基土的分类
1、按沉积年代和地质成因划分
(ii) 运积土
冲积土
2.7 土的分类
建筑地基土的分类
1、按沉积年代和地质成因划分
(ii) 运积土
风积土,如:黄土
2.7 土的分类
建筑地基土的分类
1、按沉积年代和地质成因划分
B土:粒径大于2mm的没有,粒径大于0.075mm的占全重的52%,属于 砂土。按砂土的分类此土命名为粉砂。
C土:粒径大于2mm的占全重的67%,粒径大于20mm的占全重的13%, 按碎石土分类,该土命名为圆砾或角砾。
2.7 土的分类
分类体系:
1.建筑工程系统分类体系
侧重把土作为建筑地基和环境,研究对象为原状土,例如: 《公路桥涵地基与基础设计规范》(JTJ D63-2007)地基土分类 方法
2.工程材料系统分类体系
侧重把土作为建筑材料,用于路堤、土坝和填土地基工程。研 究对象为扰动土,例如: 《土的分类标准》(GB/T 501452007)工程用土的分类和《公路土工试验规程 》(JTG E402007)土的工程分类
孔密隙实比的e 无黏性土由于压缩性小,抗剪强度高,承载力大, 对可同作一为种建土筑,当物孔的隙良比好小地于基某。一限度时,土体处于密实状态,孔隙
目 的: • 便于调查研究; • 便于比较、分析、评价; • 便于学术与经验的交流 (基于共同的概念)
原 则: 1)简明原则—采用的指标能综合反映土的主要工程
性质;测定方法简单,使用方便。 2)工程性质差异原则—采用的指标一定程度上反映 不同类工程用土的不同特性。
2.7 土的胀缩性、巨粒湿土 陷性和漂 卵石石冻胀性
1、按沉积年代和地质成因划分
(ii) 运积土
洪积土
2.7 土的分类
建筑地基土的分类
1、按沉积年代和地质成因划分
(ii) 运积土
冲积土
2.7 土的分类
建筑地基土的分类
1、按沉积年代和地质成因划分
(ii) 运积土
风积土,如:黄土
2.7 土的分类
建筑地基土的分类
1、按沉积年代和地质成因划分
B土:粒径大于2mm的没有,粒径大于0.075mm的占全重的52%,属于 砂土。按砂土的分类此土命名为粉砂。
C土:粒径大于2mm的占全重的67%,粒径大于20mm的占全重的13%, 按碎石土分类,该土命名为圆砾或角砾。
2.7 土的分类
分类体系:
1.建筑工程系统分类体系
侧重把土作为建筑地基和环境,研究对象为原状土,例如: 《公路桥涵地基与基础设计规范》(JTJ D63-2007)地基土分类 方法
2.工程材料系统分类体系
侧重把土作为建筑材料,用于路堤、土坝和填土地基工程。研 究对象为扰动土,例如: 《土的分类标准》(GB/T 501452007)工程用土的分类和《公路土工试验规程 》(JTG E402007)土的工程分类
孔密隙实比的e 无黏性土由于压缩性小,抗剪强度高,承载力大, 对可同作一为种建土筑,当物孔的隙良比好小地于基某。一限度时,土体处于密实状态,孔隙
清华大学-《土力学》(李广信)学课后习题答案

ms 121.5 g *10 16.9 KN / m3 V 72 则 sat d
d
1-2: 已知:Gs=2.72
设 Vs=1cm3
s 2.72 g / cm3
ms 2.72 g ms 2.72 g *10 16 KN / m3 V 1.7 m V 2.72 0.7 *1 g s V w g *10 20.1KN / m3 V 1.7 则 w 20.1 10 10.1KN / m3
又 hA hB hC 35cm
hA 5cm, hB 10cm, hC 20cm
V kA hA 1*103 cm / s LA
V加水 V * A * t=0.1cm3
2-2 解:
icr
Gs 1 2.70 1 1.076 1 e 1 0.58 h 20 1*9.8* 6.53 N L 30
流塑状态
乙: I L
坚硬(半固态)
I p wL w p 15
属于粉质粘土(中液限粘质土)
乙土较适合作天然地基 1-9:
A甲 I p甲 P0.002甲 53 36 0.31 0.75 55
属非活性粘土
A乙
I p乙 P0.002乙
70 35 1.3 1.25 27
乙:
I p wL wp 8 设Vs 1则ms sVs 2.68 g mw ms w 2.68* 22% 0.4796 g 则VV 0.4796cm3 ms mw 2.68 0.4796 2.14 g / cm3 1 0.4796 Vs VV ms 2.68 1.84 g / cm3 Vs Vw 1.4796
d
1-2: 已知:Gs=2.72
设 Vs=1cm3
s 2.72 g / cm3
ms 2.72 g ms 2.72 g *10 16 KN / m3 V 1.7 m V 2.72 0.7 *1 g s V w g *10 20.1KN / m3 V 1.7 则 w 20.1 10 10.1KN / m3
又 hA hB hC 35cm
hA 5cm, hB 10cm, hC 20cm
V kA hA 1*103 cm / s LA
V加水 V * A * t=0.1cm3
2-2 解:
icr
Gs 1 2.70 1 1.076 1 e 1 0.58 h 20 1*9.8* 6.53 N L 30
流塑状态
乙: I L
坚硬(半固态)
I p wL w p 15
属于粉质粘土(中液限粘质土)
乙土较适合作天然地基 1-9:
A甲 I p甲 P0.002甲 53 36 0.31 0.75 55
属非活性粘土
A乙
I p乙 P0.002乙
70 35 1.3 1.25 27
乙:
I p wL wp 8 设Vs 1则ms sVs 2.68 g mw ms w 2.68* 22% 0.4796 g 则VV 0.4796cm3 ms mw 2.68 0.4796 2.14 g / cm3 1 0.4796 Vs VV ms 2.68 1.84 g / cm3 Vs Vw 1.4796
土力学 第二章

8
2-2 达西定律
1856年法国 学者Darcy 对砂土的渗 透性进行了 研究
h
一、土的层流渗透定律
h h
s
Darcy 渗透试验装置 渗透试验播放
9
2-2 达西定律
一、土的层流渗透定律
※ 达西定律(Darcy's law)
试样全截面积
v
v= ki
Q 土的渗透系数 Δh q= =k A = kiA t Δs q Δh v = = ki = k A Δs
5
2-1 概述
地下自然水位
一级降水水面位置
汲水坑
二级降水水面位置
二级井点降水示意
6
2-1 概述
原地下水位
围 护 桩
降水后的地下水位
渗流量 土的渗透性研究 渗透破坏问题 渗流控制问题
7
第2节 达西定律(*)
一、伯努里方程(Bernoulli equation)(自学) 二、达西定律 ※ 层流(Laminar flow):相邻两个水分子 运动的轨迹相互平行而不交叉的水流。 Darcy(达西)通过大量试验得出了在层 流条件下,土中水的渗透速度与水头损失之 间 关 系 的 渗 流 规 律 , 即 达 西 定 律 ( Darcy's law) 。
kH
∑k H =
i
i
H
= 3.4 × 10−4 cm/s
等效渗透系数由渗透性较强土层控制
与层面垂直的渗流:
1 kV = = 3.0 × 10−7 cm/s ⎛ Hi 1 ⎞ ∑⎜ H k ⎟ 等效渗透系数由渗透性较弱土层控制 Vi ⎠ ⎝
19
2-3 渗透系数的测定
四、影响渗透系数的主要因素
四、影响渗透系数的主要因素 1.土的粒度及矿物成分 2.土的结构 3.土中气体 4.水的性质
2-2 达西定律
1856年法国 学者Darcy 对砂土的渗 透性进行了 研究
h
一、土的层流渗透定律
h h
s
Darcy 渗透试验装置 渗透试验播放
9
2-2 达西定律
一、土的层流渗透定律
※ 达西定律(Darcy's law)
试样全截面积
v
v= ki
Q 土的渗透系数 Δh q= =k A = kiA t Δs q Δh v = = ki = k A Δs
5
2-1 概述
地下自然水位
一级降水水面位置
汲水坑
二级降水水面位置
二级井点降水示意
6
2-1 概述
原地下水位
围 护 桩
降水后的地下水位
渗流量 土的渗透性研究 渗透破坏问题 渗流控制问题
7
第2节 达西定律(*)
一、伯努里方程(Bernoulli equation)(自学) 二、达西定律 ※ 层流(Laminar flow):相邻两个水分子 运动的轨迹相互平行而不交叉的水流。 Darcy(达西)通过大量试验得出了在层 流条件下,土中水的渗透速度与水头损失之 间 关 系 的 渗 流 规 律 , 即 达 西 定 律 ( Darcy's law) 。
kH
∑k H =
i
i
H
= 3.4 × 10−4 cm/s
等效渗透系数由渗透性较强土层控制
与层面垂直的渗流:
1 kV = = 3.0 × 10−7 cm/s ⎛ Hi 1 ⎞ ∑⎜ H k ⎟ 等效渗透系数由渗透性较弱土层控制 Vi ⎠ ⎝
19
2-3 渗透系数的测定
四、影响渗透系数的主要因素
四、影响渗透系数的主要因素 1.土的粒度及矿物成分 2.土的结构 3.土中气体 4.水的性质
土力学第2章-第四讲
14
一、重点讨论——2.5 土的结构
→ 土的结构指的是什么? → 粗粒土结构以什么结构为主?哪种力起主 要作用? → 细粒土结构形成中何种力起主要作用? → 细粒土结构分为哪几种?其沉积环境分别如何? 为什么其环境会导致该结构?
15
习题讨论课
1. 已知某土试样的土粒比重为2.72,孔隙比为0. 95,饱和度为0.37。 若将此土样的饱和度提高到0.90时,1m3的土应加多少水?
能反映土的物理力学性质
无黏性土:颗粒级配 黏性土:液限、塑性指数
《建筑地基基础设计规范》(GB 50007-2002)分类法 《土的分类标准》(GBJ 145-90)分类法
标 准
对同一种土,采用不同的分类标准,得到的土的名称并不相同。在 实践中应该根据具体工程所属的行业,选择适宜的方法。
7
习题讨论课
解: (1)绘制三相草图
(2)加水前:V=1m3,则由
V e = v = 0.95 Vs
Vs = 0.513m3 Vv = 0.487m 3 Va = 0.307m3
(3)加水后:V=1m3,则由
V e = v = 0.95 Vs
Vs = 0.513m3 Vv = 0.487m 3 Va = 0.049m3 Vw= 0.438m 3
上节内容回顾
常用的物理性质指标间的换算关系
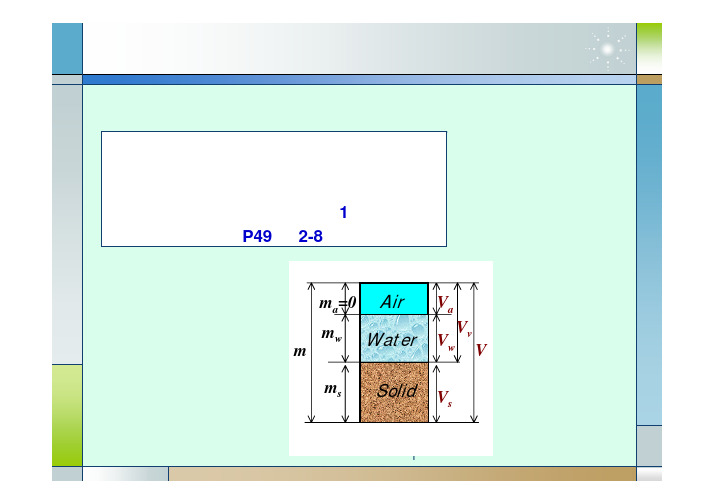
方法:三相草图法 思路:先求解三相草图上的全部质量和体积, 再依据定义求解表达式 技巧:假设任一参数(体积)为1 换算关系:教科书 P49 表2-8
ma=0 m mw ms
Air Water Solid
Va Vw Vs Vv V
质量
1
体积
上节内容回顾
土的物理状态指标
土力学-第二章-平面渗流与流网1 渗透力与渗透变形1 张丙印

智者乐水 仁者乐山
在流场中,流线和等势线(等 水头线)组成的网格称为流网
流线和等势线正交 绘制流网时,如使相邻流线
的和相邻等势线的 保
持不变,则流网中每一个网 格的边长比均为常数
特别的如取 = ,则每
一网格均为曲边正方形
v
+
l
s
q
+
k h l l
vl
l
q v s s
流网及其特性
6
§2.3 平面渗流与流网 –流网画法及应用
§2.3 平面渗流与流网 –求解方法
智者乐水 仁者乐山
数学解析法或近似解析法:求取渗流运动方程
在特定边界条件下的理论解,或者在一些假定 条件下,求其近似解
数值解法:有限元、有限差分、边界元法等,
近年来得到迅速地发展
电比拟试验法:利用电场来模拟渗流场,简便、
直观,可以用于二维问题和三维问题
流网法:简便快捷,具有足够的精度,可分析
vx
φ x
ψ z
vz
φ z
ψ x
智者乐水 仁者乐山
φ x
φ z
ψ x
ψ z
1)势函数和流函数均满足拉普拉斯方程 2)势函数和流函数正交,一点两线的斜率互成负
倒数 3)势函数和流函数是互为共轭的调和函数,两者
均完备 地描述了同一个渗流场
势函数与流函数
5
§2.3 平面渗流与流网 –流网画法及应用
智者乐水 仁者乐山
1)确定边界条件:边界流 线和首尾等势线
2)研究水流的方向:流线 的走向
3)判断网格的疏密大致分 布
4)初步绘制流网的雏形: 正交性、曲边正方形
5)反复修改和检查
《土力学与地基基础》第二章

达西定律只适用于层流 层流: 层流 适用于中砂、细砂、粉砂等 粗砂、砾石、卵石等粗颗粒土不适合。 因为在这些土的孔隙中水的渗流速度较大,已不是层流而是紊流。当水力 梯度较小时,渗流可认为是层流,这时达西定律仍然适用。
Page 18
第二章 土的渗透性
对土渗透性的研究,主要讨论五个问题 对土渗透性的研究,主要讨论五个问题: 渗流模型; 土中水渗透的基本规律(层流渗透定律) ;影响土渗透性的因素 影响土渗透性的因素;渗透系数及其测定; 渗流力及渗流 影响土渗透性的因素 稳定分析。
土力学与地基基础
康晓惠
第二章 土的渗透性
主要内容: 主要内容: 2.1 概述 2.2 达西渗透定律 2.3 渗透系数的测定 2.4 流网及其工程应用
Page 2
第二章 土的渗透性
2.1 概 述
土是具有连续孔隙通道的物质体系,因而水能在其中流动。 渗透: 渗透:在水位差作用下,水穿过土中相互连通的孔隙发生流动的现象,称为 土中水的渗透(渗流)。 渗透性: 渗透性:土能够让水等流体通过的性质叫土的渗透性。
图3-7 常水头渗透试验
Page 25
第二章 土的渗透性
常水头渗透试验装置
Page 26
第二章 土的渗透性
2.变水头渗透试验
– 土样的截面积A,高度为L – 储水管截面积为a – 试验开始储水管水头为h0 – 经过时间t后降为h1 – 时间dt内水头降低dh,水量为:
dQ=-adh
图3-8 变水头渗透试验
第二章 土的渗透性
对土渗透性的研究,主要讨论五个问题 对土渗透性的研究,主要讨论五个问题: 渗流模型; 土中水渗透的基本 规律(层流渗透定律);影响土渗透性的因素;渗透系数及其测定; 渗流 力及渗流稳定分析。
高等土力学第二章课件

A+
f
T
D
g
=
D
D
g
A
+
f
f
T
D
T
D
g
d
= D ep d
Dep=D
Dg
f
T
ห้องสมุดไป่ตู้
D
A+f
T
Dg
不相适应: fg
Dep=D
Df
f
T
D
A+f
T
Df
相适应: f=g
2.6 土的剑桥模型(Cam-clay)
2.6 土的剑桥模型
2.6.1 正常固结粘土的物态边界面(state boundary surface) 2.6.2 超固结土及完全的物态边界面 2.6.3 弹性墙与剑桥模型的屈服函数 2.6.4 修正的剑桥模型
弹性-理想塑性 Elasto-Plastic
刚塑性 Perfectly plastic
增量弹塑性-
Incremental Elastoplastic
不同塑性模型的应用:
刚塑性理论-极限平衡法:刚体滑动法、各 种条分法、滑移线法(不计变形,不计过程)
弹-塑性理论:在一定范围为弹性,超过 某一屈服条件为塑性变形。数值计算中出现
CS:v=常数的Roscoe 面 TS:超固结土的强度线-Hvorslev面 0T:零应力线 包括了正常固结土、重超固结土的 可能的(极限)应力状态
包括超固 结土的完 全的物态 边界面
vi-Ti-Si-Ni
HS
超固结
CS
正常 固结
2.6.3 弹性墙与屈服轨迹
1. 弹性墙 正常固结粘土与轻超固结粘土 (wet clay) 各向等压固结: 加载:NCL
土力学与地基基础——第二章

若干个竖向集中力 Pi (1,2, n) 作用在地基 表面上,按叠加原理则地面下深度处某点的附加应 力应为各集中力单独作用时在点所引起的附加应力 之和
pi 1 z Ki 2 2 z z i 1
n
K P
i 1 i i
n
2.3 地基中的附加应力
讨论:集中力荷载产生的竖向附加应力在地基
2.3 地基中的附加应力
(d)o点在荷载面角点外侧 把荷载面看成由I(ohce)、Ⅳ(ogaf)两个面积中扣除 Ⅱ(ohbf)和Ⅲ(ogde)而成的,所以
z ( Kc1 Kc 2 Kc3 Kc 4 ) p0
2.3 地基中的附加应力
例题 以角点法计算矩形基础甲的基底中心点
垂线下不同深度处的地基附加应力的分布,基 础埋深1.5m,集中力为1940KN,并考虑两相邻 基础乙的影响(两相邻柱距为6m,荷载同基础 甲)。
(b)o点在荷载面内
z ( Kc1 Kc 2 Kc 3 Kc 4 ) p0
(c)o点在荷载面边缘外侧 此时荷载面abcd可看成是由I(ofbg)与Ⅱ(ofah)之差和 Ⅲ(oecg)与Ⅳ(oedh)之差合成的,所以
z ( Kc1 Kc 2 Kc 3 Kc 4 ) p0
如果基础砌置在天然地面上,那末全部基底压 力就是新增加于地基表面的基底附加压力。一 般天然土层在自重作用下的变形早巳结束,因 此只有基底附加压力才能引起地基的附加应力 和变形。
2.2 基底压力
基底压力为均匀分布时:
p0 p 0 p 0 d
基底压力为梯形分布时:
p0 max p0 min
2.1 地基中的自重应力
什么时候考虑土体在自重下的自重应力? 土层一般形成至今有很长的时间,自重应力下
pi 1 z Ki 2 2 z z i 1
n
K P
i 1 i i
n
2.3 地基中的附加应力
讨论:集中力荷载产生的竖向附加应力在地基
2.3 地基中的附加应力
(d)o点在荷载面角点外侧 把荷载面看成由I(ohce)、Ⅳ(ogaf)两个面积中扣除 Ⅱ(ohbf)和Ⅲ(ogde)而成的,所以
z ( Kc1 Kc 2 Kc3 Kc 4 ) p0
2.3 地基中的附加应力
例题 以角点法计算矩形基础甲的基底中心点
垂线下不同深度处的地基附加应力的分布,基 础埋深1.5m,集中力为1940KN,并考虑两相邻 基础乙的影响(两相邻柱距为6m,荷载同基础 甲)。
(b)o点在荷载面内
z ( Kc1 Kc 2 Kc 3 Kc 4 ) p0
(c)o点在荷载面边缘外侧 此时荷载面abcd可看成是由I(ofbg)与Ⅱ(ofah)之差和 Ⅲ(oecg)与Ⅳ(oedh)之差合成的,所以
z ( Kc1 Kc 2 Kc 3 Kc 4 ) p0
如果基础砌置在天然地面上,那末全部基底压 力就是新增加于地基表面的基底附加压力。一 般天然土层在自重作用下的变形早巳结束,因 此只有基底附加压力才能引起地基的附加应力 和变形。
2.2 基底压力
基底压力为均匀分布时:
p0 p 0 p 0 d
基底压力为梯形分布时:
p0 max p0 min
2.1 地基中的自重应力
什么时候考虑土体在自重下的自重应力? 土层一般形成至今有很长的时间,自重应力下
