江西省新余市第四中学2017届高三数学上学期第二次段考试题理
江西省新余市第四中学2024-2025学年 九年级上学期第二次段考数学试卷(无答案)

新余四中2024-2025学年度九上第二次段考数学试卷一、选择题(每小题3分,共18分)1. 下列图形中,既是轴对称图形又是中心对称图形的是 ( )2. 一元二次方程2x²+3x=−1化为一般形式后,二次项系数、一次项系数、常数项分别是 ( )A. 2, 3, 1B. 2, 3, - 1C. 2, - 3, 1D. 2, 3, 03. 下列说法:①三点确定一个圆;②三角形的外心一定在三角形内;③长度相等的弧是等弧;其中错误的有 ( )A. 3个B. 2个C. 1个D. 0个4. 如图,已知一菜园为长10米,宽7米的矩形,为了方便浇水和施肥,修建了同样宽的四条互相垂直的“井”字形道路,余下的部分种青菜,已知种植青菜的面积为54平方米,设小路的宽为x米,则根据题意列出的方程是( )A. (10-2x)(7-2x)=54B. (10-x)(7-x)=54C. (10-x)(7-2x)=54D. (10+2x)(7--2x)=545. 下表是一组二次函数y=x²+3x−5的自变量x与函数值y的对应值,那么方程:x²+3x−5=0的一个近似根是( )A. 1.4B. 1.1C. 1.2D. 1.36. 在平面直角坐标系xOy中,抛物线y=ax²+bx+c(a≠0)的顶点为P(−1,k),,且经过点A(-3,0), 其部分图象如图所示,下面四个结论中,①abc>0;②b=-2a;③若点N(t,n)在此抛物线上且n<c, 则t>0或t<--2; ④对于任意实数t,都有a(t²−1)+b (t+1)≤0成立. 正确的有( ) 个A. 0B. 1C. 2D. 3x1 1.2 1.3 1.4y-0.980.030.6 1.2第4题图第5题表第6题图二、填空题(每小题3分,共18分)7. 点A(-3,4)关于原点的对称点的坐标为 .8. 把抛物线y=x²先向右平移1个单位再向上平移2个单位,所得到抛物线的解析式为 .9. 已知一元二次方程:x²+x−2=0的两个根为x₁、x₂,则(x₁+1)(x₂+1)= .10.用半径为5cm,圆心角为72°的扇形纸片恰好能围成一个圆锥的侧面,则这个圆锥的高为 cm.11. 我国魏晋时期数学家刘徽在《九章算术注》中提到著名的“割圆术”,即利用圆的内接正多边形逼近圆的方法来近似估算. “割圆术”孕育了微积分思想,他用这种思想得到了圆周率π的近似值为3.1416,如图,⊙O的半径为1,运用“割圆术”,以圆内接正八边形面积近似估计⊙O的面积,可得π的估计值为22,若用圆内接正六边形近似估计⊙O的面积,可得π的估计值为 .(结果保留根号)12. 已知等腰AABC内接于半径为5的⊙O,已知圆心O到BC的距离为3,则这个等腰AABC中底边上的高可能是.三、解答题(每小题6分,共30分)13. 解方程: (1)x²=5x;(2)x²−6x+8=0.14. 如图, △ABC绕点A逆时针旋转一定角度后得到△ADE,点D在BC上, ∠EDC=40°,求∠B的度数.15. 已知关于x的一元二次方程:x²+(m+2)x+1=0有两个相等的实数根,求出m的值.16. 如图, 四边形ABCD是⊙O的内接四边形, CD是⊙O的直径, A是BD的中点,请仅用无刻度直尺,按下列要求作图.(保留作图痕迹)(1)在图1中, 作一个以CD为腰的等腰△CDE.(2)在图2中,作一个以OB为对角线的矩形.17. 如图, 点D在⊙O的直径AB的延长线上, CD与⊙O相切于点C. 若∠D=30°,⊙O的半径为1,求阴影部分的面积.四、每小题8分,共24分18. 如图,在边长为12cm的等边三角形ABC中,点P从点A开始沿AB边向点B以每秒钟1cm的速度移动,点Q从点B开始沿BC边向点C以每秒钟2cm的速度移动. 若P、Q分别从A、B同时出发,其中任意一点到达目的地后,两点同时停止运动.(1)经过几秒后,△BPQ是等边三角形?(2)经过几秒△BPQ面积等于:103cm2?19. 秋风起,桂花飘香,到了吃螃蟹的最好季节. 某商店销售一种成本为10元/千克的大闸蟹,若按15元/千克销售,一个月可售出350千克,经调查知销售单价每涨价1元,月销售量就减少10千克,设售价为x元/千克,月销售量为y千克.(1)为了使顾客获得更大的优惠,且月销售利润达到3000元的情况下,售价应为多少元?(2)当售价为多少元时会获得最大利润,并求出最大利润的值.20. 如图, 在四边形ABCD中, AO平分.∠BAD.点 O在AC上, 以点O为圆心, OA为半径, 作⊙O与BC相切于点B, BO延长线交⊙O于点 E, 交AD于点 F, 连接AE, DE.(1)求证: CD是⊙O的切线;(2)若AE =DE=8, 求AF的长.五、每小题9分,共18分21. 设点A(x₁,m),B(x₂,m)是抛物线y=x²+bx+c上的两点(点A 在点B的左侧),且:x₂−x₁=2,抛物线的顶点为C.(1)当b=c=0时,△ABC的是三角形(填“不等边”,“等腰”或“等边”);(2)当b=0且c=1时, 判断△ABC的形状并说明理由;(3)当b,c均不为零时,判断△ABC的形状并说明理由.22. 课本再现: 如图, ⊙O的直径AB为10cm, 弦AC为6cm,∠ACB的平分线交⊙O于点D.(1)求 BC的长; (2)求 BD 的长; (3)直接写出 CD的长..六、每小题12分,共12分23. 如图1, 抛物线y=ax²+bx+c与x轴分别交于点A(−1,0)、B(3,0),与y轴交于点C(0,3).(1)求这条抛物线对应的二次函数的解析式;(2)若其顶点为D,设点P 是抛物线的对称轴l上一点,以点P为圆心的⊙P经过A、B两点,①如图2, 若⊙P与直线CD相切点 E, 求点 P的坐标;②如图3, 若⊙P与直线CD相交于M, N两点(点M在点N的左侧), 且.MN=AB,求点P 的坐标;(3)在(2)的条件下求以点A,B,M,N为顶点的四边形的面积.。
江西省新余市第四中学、宜春中学2017届高三下学期开学联考数学(理)试题含答案

2017届宜春中学新余四中高三开学联考理科数学试卷一。
选择题(60分)1.设集合()22{,|1}416x y A x y =+=,{(,)|3}x B x y y ==,则A B ⋂的子集的个数是:( ) A .4 B .3 C .2 D .12.已知复数313iz i +=-,z 是z 的共轭复数,则z z •=( )A. 14 B 。
12 C.1 D.23. 下列结论正确的...是( )A .命题“如果222p q +=,则2p q +≤”的否命题是“如果2p q +>,则222p q +≠”;B .命题:[0,1],1x p x e ∀∈≥,命题2:,10,q x R x x ∃∈++<则p q ∨为假; C .“若22,am bm <则a b <"的逆命题为真命题;D 。
若31()2nx x-的展开式中第四项为常数项,则n =54. 已知{}2,0,1,3a ∈-,{}1,2b ∈,则曲线221ax by +=为椭圆的概率是( ) A.37 B.47 C.12 D 。
385。
定义22⨯矩阵12142334=a a a a a a a a ⎡⎤-⎢⎥⎦⎣,若cos sin 3()cos(2)cos sin 2x x f x x x x π⎡⎤-⎢⎥=⎢⎥++⎢⎥⎣⎦,则()f x A 。
图象关于(),0π中心对称 B. 图象关于直线2x π=对称C.在区间[,0]6π-上单调递增 D 。
周期为π的奇函数6。
如图所示的流程图,若输出的结果是9,则判断 框中的横线上可以填入的最大整数为( )A .17B .16C .15D .14 7。
如图为某几何体的三视图,求该几何体的内切球的 表面积为( )第6题图A .14πB .3πC . 4πD .43π8.为防止部分学生考试时用搜题软件作弊,命题组指派5名教师对数学卷的选择题、填空题和解答题这3种题型进行改编,则每种题型至少指派一名教师的不同分派方法种数为( )A .150B .180C . 200D .2809。
【全国百强校】江西省新余市第四中学2017届高三上学期第二次段考物理(解析版)

一、选择题(本题共10个小题,共计40分。
其中1-6题为单选题,每题4分,7-10题为多选题,每题4分,少选2分,错选0分)1、滑块a、b沿水平面上同一条直线发生碰撞;碰撞后两者粘在一起运动;经过一段时间后,从光滑路段进入粗糙路段.两者的位置x随时间t变化的图象如图所示.由图象可知()A.相碰前,a在减速,b在加速B.碰撞后,第1秒内a的速度为23m/sC.进入粗糙路段后,a的加速度逐渐减小D.相碰前,a、b的速度方向相同,加速度方向相反【答案】B【解析】考点:x-t图线;牛顿第二定律【名师点睛】本题的关键是掌握位移时间图象的斜率表示速度,斜率的正负表示速度的方向,斜率的大小表示速度的大小。
2、诺贝尔物理学奖授予英国曼彻斯特大学科学家安德烈·海姆和康斯坦丁·诺沃肖洛夫,以表彰他们在石墨烯材料方面的卓越研究.石墨烯是目前世界上已知的强度最高的材料,它的发现使“太空电梯”缆线的制造成为可能,人类将有望通过“太空电梯”进入太空.现假设有一“太空电梯”悬在赤道上空某处,相对地球静止,如图所示,那么关于“太空电梯”,下列说法正确的是( )A.“太空电梯”各点均处于完全失重状态B.“太空电梯”各点运行周期随高度增大而增大C.“太空电梯”上各点线速度与该点离地球球心距离的开方成反比D.“太空电梯”上各点线速度与该点离地球球心距离成正比【答案】AD【解析】考点:万有引力定律的应用;失重和超重【名师点睛】由于太空电梯直接从地面连到了地球同步飞船上,它们的角速度是相同的,这是本题的隐含的条件,抓住这个条件即可解答本题。
3、图示为索道输运货物的情景.已知倾斜的索道与水平方向的夹角为37°,重物与车厢地板之间的动摩擦因数为0.30.当载重车厢沿索道向上加速运动时,重物与车厢仍然保持相对静止状态,重物对车厢内水平地板的正压力为其重力的1.15倍,那么这时重物对车厢地板的摩擦力大小为()A.0.35mg B.0.30mg C.0.23mg D.0.20mg【答案】D【解析】试题分析:由于重物对车厢内水平地板的正压力为其重力的1.15倍,在竖直方向上,由牛顿第二定律得:F N-mg=ma竖直,解得a上=0.15g,设水平方向上的加速度为a水平,则3374atana=︒=竖直水平,解得:a水平=0.2g,对物体受力分析可知,在水平方向上摩擦力作为合力产生加速度,由牛顿第二定律得:f=ma水=0.20mg,故D正确.故选D。
江西省新余市第四中学2024-2025学年高三补习班上学期第一次段考数学试卷及答案

江西省新余市第四中学2024-2025学年高三补习班上学期第一次段考数学试卷命题人:审题人:本试题卷满分150分,考试时间120分钟.一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{(1,2)}M =,则下列关系成立的是()A.1M∈ B.2M∈ C.(1,2)M∈ D.(1,2)M⊆2.2(0,1),sin x x x x ∀∈>-的否定为()A.2(0,1),sin x x x x ∃∉≤- B.2(0,1),sin x x x x∃∈≤-C.2(0,1),sin x x x x ∀∉>- D.2(0,1),sin x x x x∀∈≤-3.函数1()2xf x -=的大致图象为()A.B. C. D.4.已知正数a ,b 满足121a b+=,则2a b +的最小值为()A.9B.6C.4D.35.若函数()2231()69m m f x m m x -+=-+是幂函数且为单调函数,则m 的值为()A.2B.3C.4D.2或46.已知函数21()ln 22f x mx x x =+-在定义域内是增函数,则实数m 的取值范围为()A.[0,)+∞ B.(0,)+∞ C.[3,)-+∞ D.[1,)+∞7.已知函数()2,()log xa f x g x x ==.若对于()f x 图象上的任意一点P ,在()g x 的图象上总存在一点Q ,满足OP OQ ⊥,且||||OP OQ =.则实数a =()A.14B.12C.2D.48.已知函数1()xf x xe-=,若方程1()()1f x a f x +=+有三个不相等的实数解,则实数a 的取值范围为()A.31,2⎛⎫⎪⎝⎭B.(3,1)(1,1)--⋃- C.(1,3)D.3(,1),2⎛⎫-∞-⋃+∞⎪⎝⎭二、选择题:本大题共3小题,每小题6分,共18分.在每小题给出的四个选项中,至少有两项是符合题目要求的.若全部选对得6分,部分选对得部分分,选错或不选得0分.9.若集合{}22,32,8A a a a =++,则实数a 的取值可以是()A.2B.3C.-4D.510.若函数2()ln 2f x a x x bx =-+既有极小值又有极大值,则()A.0ab < B.0a < C.2160b a +> D.||4a b -<11.已知函数22(2)log (1),1()2,1x x x f x x +⎧+>-⎪=⎨≤-⎪⎩,若关于x 的方程()f x m =有四个不等实根()12341234,,,x x x x x x x x <<<,则下列结论正确的是()A.12m <≤B.11sin cos 0x x ->C.3441x x +>-D.2212log mx x ++的最小值为10三、填空题:本题共3小题,每小题5分,共15分.12.曲线()2ln 1f x x =-在点(,1)e 处的切线方程为______.13.若一系列函数的解析式相同,值域相同,但其定义域不同,则称这一系列函数为“同族函数”,试问解析式为y =2x ,值域为{1,2}的“同族函数”共有______个.14.已知函数32()692f x x x x =-+-,给出以下命题:①若函数()3y f x bx =+不存在单调递减区间,则实数b 的取值范围是(1,)+∞;②过点(0,2)M 且与曲线()y f x =相切的直线有三条;③方程2()2f x x=-的所有实数根的和为16.其中真命题的序号是______.四、解答题:本大题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.(本小题13分)已知集合{123}A xm x m =-≤≤+∣,函数()f x =B .(1)当2m =时,求A B ⋂;(2)若A B A ⋂=,求实数m 的取值范围.16.(本小题15分)已知函数21()43ln 2f x x x x =-+.(1)求()f x 的单调区间;(2)求()f x 在区间1,e e⎡⎤⎢⎥⎣⎦上的最大值.17.(本小题15分)已知命题2:,20p x R x ax ∀∈++≥,命题21:3,,102q x x ax ⎡⎤∃∈---+=⎢⎥⎣⎦.(1)若命题p 为真命题,求实数a 的取值范围;(2)若命题q 为真命题,求实数a 的取值范围.18.(本小题17分)定义函数()4(1)2xxa f x a a =-+⋅+,其中x 为自变量,a 为常数.(1)若函数()a f x 在R 上单调递增,求实数a 的取值范围;(2)集合{}{}()32()(0),()(2)(2),a a a R A xf x f B x f x f x f A B =≥=+-=⋂≠∅∣∣ð,求实数a 的取值范围.19.(本小题17分)已知函数2()sin f x x x mx n =-++.(1)当1m =时,求证:函数()f x 有唯一极值点;(2)当30,2m n ==时,求()f x 在区间[0,π]上的零点个数;(3)两函数图像在公共点处的公切线称为“合一切线”.若曲线()y f x =与曲线cos y x =-存在两条互相垂直的“合一切线”,求m ,n 的值.2024-2025学年度上学期补习年级第一次段考数学试卷·参考答案1-8.CBAACDBA 9.BD10.ABC11.ACD12.20x ey e --=13.914.②7.解:设点(),2x P x ,点(),y Q a y当0x =时,点(0,1)P ,根据指数函数与对数函数的性质知,此时(1,0)Q ,显然满足条件;当0,0x y ≠≠,由OP OQ ⊥,知1OP OQ k k ⋅=-,即12x y yx a⋅=-,即2(*)y x y a x =-⋅.又||||OP OQ ==22222x y x y a +=+.将(*)式代入,得()2222222222222222xx x x y y y x y y x x x x ⎛⎫+=+-⋅=+⋅=+ ⎪⎝⎭.由于220,20xx ≥>,有2220x x +>.因此有221y x=,即22y x =,即y x =±.由于0,20yxa >>,所以(*)式可知y x =不满足条件,则有y x =-.代入(*)式得12xy x x x a a a a y y x x x--⎛⎫ ⎪⎝⎭=-=-==-.所以12a =,故12a =.故选:B.8.解:由题意可知:()f x 的定义域为R ,则1()(1)xf x x e '-=-,当1x <时,()0f x '>;当1x >时,()0f x '<;可知()f x 在(,1)-∞内单调递增,在(1,)+∞内单调递减,可得()(1)1f x f ≤=,且当x 趋近于-∞时,()f x 趋近于-∞;当x 趋近于+∞时,()f x 趋近于0;作出()f x 的图象,如图所示,对于关于x 的方程1()()1f x a f x +=+,令()1t f x =≠-,可得11t a t +=+,整理得2(1)10t a t a +-+-=,且-1不为方程2(1)10t a t a +-+-=的根,若方程1()()1f x a f x +=+有三个不相等的实数解,可知2(1)10t a t a +-+-=有两个不同的实数根1212,,t t t t <,且1201t t <<<或1201t t <<=或1201t t =<<,构建2()(1)1g t t a t a =+-+-,若1201t t <<<,则(0)10(1)320g a g a =-<⎧⎨=->⎩,解得312a <<;若1201,1t t <<=,则(1)30g =-=,解得32a =,此时方程为211022t t --=,解得121,12t t =-=,不合题意;若1201t t =<<,则(0)10g a =-=,解得1a =,此时方程为20t =,解得120t t ==,不合题意.综上所述:实数a 的取值范围为31,2⎛⎫⎪⎝⎭.故选:A 11.【答案】ACD解:作出()f x 的图象如下:若1x >-时,2()log (1)f x x =+,令()2f x =,得2log (1)2x +=,即2log (1)2x +=或2log (1)2x +=-,所以212x +=或212x -+=,解得3x =或34x =-,令()1f x =,得2log (1)1x +=,即2log (1)1x +=或2log (1)1x +=-,所以12x +=或112x -+=,解得1x =或12x =-,若1x - 时,2(2)()2x f x +=,令()2f x =,得2(2)22x +=,解得1x =-或-3,令()1f x =,得2(2)21x +=,即2(2)0x +=,解得2x =-,由图可知12343132,21,,1342x x x x -≤<--<≤--≤<-<≤,对于选项,12,()A m f x m <= 有4个根,故A 正确;对于选项B :因为132x -≤<-,所以当13π34x -≤≤-时,11sin cos x x ≥,即11sin cos 0x x -≥,当13π24x -<<-时,11sin cos x x <,即11sin cos 0x x -<,故B 错误;对于选项C :因为()()34f x f x m ==,则3421,21mm x x -=-=-,则3444252m m x x +=+-,因为12m < ,则令2(2,4]mt =∈,则4()5h t t t=+-在(2,4]上单调递增,所以()(2)1h t h >=-,即3441x x +>-,故C 正确;对于选项D :令2212log my x x =++()()2212222,2x x m m +++==,则122,2x x ==,所以())222212log 22log mm y x x =++=++22log 8log m m =++22222log 12log 82log 8log 2log m m m m=++=++,因为12m < ,所以20log 1m < ,所以2212log 828102log y m m =++≥+=,当且仅当2212log 2log m m=,即m =时取等号,所以2212log m x x ++的最小值为10,故D 正确.故选:ACD.14.【答案】②解:因为()()3236932y f x bx x x b x =+=-++-,所以231293y x x b '=-++,若函数326(93)2y x x b x =-++-不存在单调递减区间,则21212(93)0b -+≤,解得1b ≥,所以①错误;设过点(0,2)M 的直线与曲线)y f x =相切于点()00,x y ,则有2000023129(*)y x x x --+=,又点()00,x y 在曲线()y f x =上,所以320000692y x x x =-+-,将()00,x y 代入(*),得()3200000321(1(10x x x x x ⎡⎤⎡⎤-+=--+--=⎣⎦⎣⎦,解得01x =或01x =01x =,所以过点(0,2)M 且与曲线()y f x =相切的直线有三条,②正确;又函数32()692f x x x x =-+-的导数为2()3129f x x x '=-+,令()0f x '>,解得3x >或1x <,所以()f x 递增区间为(,1)-∞和(3,)+∞;令()0f x '<,可得13x <<,所以()f x 递减区间为(1,3).即1x =时取得极大值(1)2,3f x ==时取得极小值(3)2f =-,作出函数()y f x =与函数22y x=-的图像,由图象可得()y f x =的图象与22y x=-的图像有4个交点,它们关于(2,0)对称,则它们的横坐标和为448+=,故③错误.综上所述,真命题的序号为②.故答案为:②.15.【答案】解:由2280x x -++≥得(4)(2)0x x -+≤,所以{24}B xx =-≤≤∣,当时,{14}A B xx ⋂=≤≤∣(2)因为A B A ⋂=,所以A B ⊆,①若A =∅,则123m m ->+,解得4m <-;②若A ≠∅,则21234m m -≤-≤+≤,解得112m -≤≤;∴实数m 的取值范围是4m <-或12m -≤≤.16.【答案】解:(1)易知函数的定义域为3(1)(3)(0,),()4x x f x x x x'--+∞=-+=令()0f x '>,得01x <<或3x >,令()0f x '<得13x <<,故函数()f x 在(0,1)上单调递增,在(1,3)上单调递减,在(3,)+∞上单调递增;(2)由(1)得当11x e<<时,函数()f x 单调递增,当1x e <<时,函数()f x 单调递减,所以max 7()(1)2f x f ==-.17.【答案】解:(1) 命题2:,20p x R x ax ∀∈++≥为真命题,24120a ∴=-⨯⨯≤ ,解得a -≤≤,∴实数a 的取值范围为[-.(2)命题21:3,,102q x x ax ⎡⎤∃∈---+=⎢⎥⎣⎦为真命题,211x a x x x +==+在13,2⎡⎤--⎢⎥⎣⎦上有解,又1y x x =+在[3,1]x ∈--单调递增,在11,2x ⎛⎤∈-- ⎥⎝⎦单调递减,∴当1x =-时,a 取最大值-2,当3x =-时,1103x x +=-,当12x =-时,152x x +=-,∴实数a 的取值范围为10,23⎡⎤--⎢⎥⎣⎦.18.【答案】解:(1)令2,0xt t =>,函数()4(1)2x x a f x a a =-+⋅+在R 上单调递增,2x t =在R 上单调递增,2(1)y t a t a ∴=-+⋅+在(0,)+∞上单调递增,102a +∴,解得1a ≤-,故实数a 的取值范围为(,1]-∞-;(2){}{}2442300log 3x x U A xx x =-⋅+<=<<∣∣ð,{}224(1)24(1)26x x x x B x a a a a --=-+⋅++-+⋅+=∣1644(1)226042x x x x a x a ⎛⎫⎛⎫=+-+++-= ⎪ ⎪⎝⎧⎫⎨⎭⎭⎩⎝⎬⎭,由已知()U A B θ⋂≠ð即1644(1)226042xx x x a a ⎛⎫⎛⎫+-+++-= ⎪ ⎪⎝⎭⎝⎭在()20,log 3内有解,令422xxt =+,则[4,5)t ∈,方程()28(1)260t a t a --++-=在[4,5)上有解,也等价于方程2142t t a t --=-在[4,5)t ∈上有解,21412()122t t h t t t t --==+--- 在[4,5)t ∈上单调递增,()[1,2)h t ∴∈-,故所求a 的取值范围是[1,2)-.19.【答案】解:(1)证明:由2()sin f x x x x n =-++,得()sin cos 2f x x x x x '=--+,且(0)0f '=.当0x >时,()(1cos )sin f x x x x x '=-+-.因为1cos 0,sin 0x x x -≥->,所以()0f x '>.因为()()f x f x ''-=-对任意x R ∈恒成立,所以当0x <时,()0f x '<.所以0x =是()f x 的唯一极值点.(2)()sin cos f x x x x '=--,当π0,2x ⎡⎤∈⎢⎥⎣⎦时,()0f x '≤,所以()f x 在π0,2x ⎡⎤∈⎢⎥⎣⎦上单调递减,因为3π3π(0)0,0222f f -⎛⎫=>=< ⎪⎝⎭,所以由零点存在定理知()f x 在π0,2x ⎡⎤∈⎢⎥⎣⎦上有且仅有一个零点.当π,π2x ⎡⎤∈⎢⎥⎣⎦时,令()()sin cos h x f x x x x '==--,则()2cos sin h x x x x '=-+,当π,π2x ⎛⎫∈ ⎪⎝⎭时,有()0h x '>,所以()h x 在π,π2⎡⎤⎢⎥⎣⎦上单调递增,又因为π10,(π)π02h h ⎛⎫=-<=> ⎪⎝⎭,所以存在π,π2m ⎛⎫∈ ⎪⎝⎭使得()0h m =,当π,2x m ⎛⎫∈⎪⎝⎭时,()()0h x h m <=,所以()f x 在π,2m ⎛⎫⎪⎝⎭上单调递减,所以当π,2x m ⎡⎤∈⎢⎥⎣⎦时,π()02f x f ⎛⎫≤<⎪⎝⎭,故()f x 在π,2m ⎡⎤⎢⎥⎣⎦上无零点,当(,π)x m ∈时,()()0h x h m >=,所以()f x 在(,π)m 上单调递增,又π3()0,(π)022f m f f ⎛⎫<<=>⎪⎝⎭,所以()f x 在(,π)m 上有且仅有一个零点.综上所述:()f x 在[0,π]上有且只有2个零点.(3)设曲线()y f x =与曲线cos y x =-的两条互相垂直的“合一切线”的切点的横坐标分别为12,x x ,其斜率分别为12,k k ,则121k k =-.因为(cos )sin x x '-=,所以1212sin sin 1x x k k ⋅==-.所以{}12sin ,sin {1,1}x x =-.不妨设1sin 1x =,则1π2π,2x k k =+∈Z .因为()1111112sin cos k f x mx x x x '==--,由“合一切线”的定义可知,111112sin cos sin mx x x x x --=.所以112,4ππm k Z x k ==∈+.由“合一切线”的定义可知,2111111sin cos x x x n x x ⋅-+=-,所以0n =.当2,Z,04ππm k n k =∈=+时,取1x =2ππ2π,2π22k x k +=--,则()()()()11221122cos 0,cos 0,sin 1,sin 1f x x f x x f x x f x x ''=-==-=====-,符合题意.所以2,Z,04ππm k n k =∈=+.。
2016-2017年江西省新余四中七年级(下)第二次段考数学试卷(解析版)

(1)A′、B′两点的坐标分别为 A′
B′
;
(2)作出△ABC 平移之后的图形△A′B′C′;
(3)求△ABC 的面积.
19.(8 分)已知关于 x、y 的方程组
的解 x,y 的值是一对正数.
(1)求 m 的取值范围; (2)化简:|m﹣1|+|m+ |.
20.(8 分)如图,周长为 68cm 的长方形 ABCD 被分成 7 个相同的矩形,求长方形 ABCD 的面积.
这样依次得到点 A1,A2,A3,…,An,….若点 A1 的坐标为(3,1),则点 A3 的坐标为
,
点 A2014 的坐标为
;若点 A1 的坐标为(a,b),对于任意的正整数 n,点 An 均在
x 轴上方,则 a,b 应满足的条件为
.
三、解答题(本大题共 5 小题,每小题 6 分,共 30 分)
13.(6 分)解下列方程组或不等式组.
点 Q 到达 A 点整个运动随之结束.AC 的中点 D 的坐标是(1,2),设运动时间为 t(t>
0)秒.问:是否存在这样的 t,使 S△ODP=S△ODQ?若存在,请求出 t 的值;若不存在, 请说明理由
(3)点 F 是线段 AC 上一点,满足∠FOC=∠FCO,点 G 是第二象限中一点,连 OG,使 得∠AOG=∠AOF.点 E 是线段 OA 上一动点,连 CE 交 OF 于点 H,当点 E 在线段 OA
EFB=60°,则∠AED′=( )
A.50°
B.55°
C.60°
D.65°
5.(3 分)已知方程组:
的解是:
,则方程组:
的解是( )
A.
B.
C.
D.
6.(3 分)利用两块相同的长方体木块测量一张桌子的高度.首先按图①方式放置,再交换 两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是( )
江西省新余市第四中学2017届高三上学期第二次段考地理试题 Word版含答案
新余四中2016—2017学年第一学期毕业年级第二次段考地理试卷第Ⅰ卷(选择题共50分)本卷共25个小题,每小题2分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
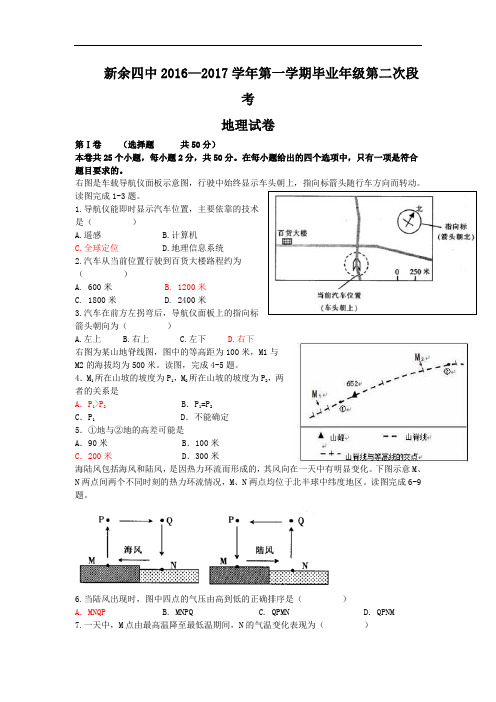
右图是车载导航仪面板示意图,行驶中始终显示车头朝上,指向标箭头随行车方向而转动。
读图完成1-3题。
1.导航仪能即时显示汽车位置,主要依靠的技术是()A.遥感B.计算机C.全球定位D.地理信息系统2.汽车从当前位置行驶到百货大楼路程约为()A. 600米B. 1200米C. 1800米D. 2400米3.汽车在前方左拐弯后,导航仪面板上的指向标箭头朝向为()A.左上B.右上C.左下D.右下右图为某山地脊线图,图中的等高距为100米,M1与M2的海拔均为500米。
读图,完成4-5题。
4.M1所在山坡的坡度为P1,M2所在山坡的坡度为P2,两者的关系是A.P1>P2B.P1=P2C.P1D.不能确定5.①地与②地的高差可能是A.90米 B.100米C.200米 D.300米海陆风包括海风和陆风,是因热力环流而形成的,其风向在一天中有明显变化。
下图示意M、N两点间两个不同时刻的热力环流情况,M、N两点均位于北半球中纬度地区。
读图完成6-9题。
6.当陆风出现时,图中四点的气压由高到低的正确排序是()A. MNQPB. MNPQC. QPMND. QPNM7.一天中,M点由最高温降至最低温期间,N的气温变化表现为()A.一直下降B. 一直上升C.先下降后上升D. 先上升后下降8.若图中M与N之间的海风为正东风,则此时PQ间的水平气流为()A.东北风B.西北风C.东南风D.东北风9.从夏季到冬季的期间,海陆风风力的变化趋势是()A.两者均加强B.两者均减弱C.海风加强,陆风减弱D.陆风加强,海风减弱图乙是北半球1月某地近地面垂直方向的大气示意图。
读图回答10~11题。
甲乙10.图中M地正东方向吹A.东北风B.东南风C.西北风D.西南风11.依据图甲判断该城市该日A.①增强B.②减弱C.③增强D.④减弱某品种桂花在济南和杭州开花的多年平均日期分别是8月27日和9月5日(该种桂花在入秋时开花)。
江西省新余市第四中学、上高第二中学2020届高三数学第二次联考试题 理(含解析)
江西省新余四中、上高二中2020届高三第二次联考数学(理)试题一、选择题:本大题共l2小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合M={},集合N={},(e为自然对数的底数)则=()A. {}B. {}C. {}D.【答案】C【解析】试题分析:,,故=.考点:集合的运算.2.若复数满足(为虚数单位),则复数的共轭复数为()A. B. C. D.【答案】B【解析】由,得,则复数z的共轭复数为.故选:B.3.若为偶函数,且当时,,则不等式的解集为()A. B. C. D.【答案】A【解析】试题分析:因为当时,,成立,所以排除C,当时,不成立,排除B、D,故选A.考点:1、分段函数的解析式;2、分段函数的奇偶性.4. 现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票)的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束,则活动恰好在第4人抽完后结束的概率为()A. B. C. D.【答案】C【解析】试题分析:将张奖票不放回地依次取出共有种不同的取法,若获恰好在第四次抽奖结束,则前三次共抽到张中奖票,第四次抽的最后一张奖票,共有种取法,所以概率为,故选C.考点:古典概型及其概率的计算.5.在等差数列中,,则数列的前11项和( )A. 8B. 16C. 22D. 44【答案】C【解析】【分析】本道题利用,得到,再利用,计算结果,即可得出答案.【详解】利用等差数列满足,代入,得到,解得,故选C.【点睛】本道题考查了等差数列的性质,利用好和,即可得出答案.6.一个几何体的三视图如图所示,该几何体的体积为( )A. B. C. D.【答案】A【解析】【分析】结合三视图,还原直观图,计算体积,即可得出答案.【详解】根据几何体的三视图得该几何体是四棱锥M-PSQN且四棱锥是棱长为2的正方体的一部分,直观图如图所示,由正方体的性质得,所以该四棱锥的体积为:,故A正确.【点睛】本道题考查了三视图还原直观图,题目难度中等,可以借助立方体,进行实物图还原.7.已知函数(,),其图像与直线相邻两个交点的距离为,若对于任意的恒成立, 则的取值范围是()A. B. C. D.【答案】D【解析】【分析】由题意可得函数的周期为=π,求得ω=2.再根据当x∈(﹣,)时,sin(2x+φ)>0恒成立,2kπ<2•(﹣)+φ<2•+φ<2kπ+π,由此求得φ的取值范围.【详解】函数f(x)=2sin(ωx+φ)+1,其图象与直线y=-1相邻两个交点的距离为π,故函数的周期为=π,所以ω=2,于是f(x)=2sin(2x+φ)+1.若f(x)>1对∀x∈恒成立,即当x∈时,sin(2x+φ)>0恒成立,则有2kπ≤2·+φ<2·+φ≤2kπ+π,求得2kπ+≤φ≤2kπ+,k∈Z,又|φ|≤,所以≤φ≤.故答案为:D【点睛】本题主要考查正弦函数的周期性、值域,函数的恒成立问题,属于中档题.对于恒成立问题一般要分离参数,然后利用函数的单调性求函数的最大值或最小值,对于含有不等式的函数问题,一般要构造函数,利用函数的单调性来解决,但涉及技巧比较多,需要多加体会.8.已知抛物线上有三点,的斜率分别为3,6,,则的重心坐标为()A. B. C. D.【答案】C【解析】【分析】设,进而用坐标表示斜率即可解得各点的纵坐标,进一步可求横坐标,利用重心坐标公式即可得解.【详解】设则,得,同理,,三式相加得,故与前三式联立,得,,,则.故所求重心的坐标为,故选C.【点睛】本题主要考查了解析几何中常用的数学方法,集合问题坐标化,进而转化为代数运算,对学生的能力有一定的要求,属于中档题.9.已知函数,满足,则的取值范围是()A. B. C. D.【答案】B【解析】【分析】先分析函数的性质,知函数为奇函数,且在定义域内单调递减,所以可变形为:,进而得,整理得:,利用几何意义可知满足条件的表示的区域是圆的内部(含边界),从而列不等式求解即可.【详解】易知函数的定义域为R,由题意,,可得为奇函数,又是上的减函数,故,所以满足条件的表示的区域是圆的内部(含边界),则点到直线的距离,所以的取值范围是,故选B.【点睛】本题考查函数性质与解析几何中直线与圆位置关系知识点的结合.10.在平面直角坐标系中,已知两圆:和:,又点坐标为,是上的动点,为上的动点,则四边形能构成矩形的个数为()A. 0个B. 2个C. 4个D. 无数个【答案】D【解析】【分析】根据题意画出图形,结合图形得出满足条件的四边形AMQN能构成矩形的个数为无数个.【详解】如图所示,任取圆C2上一点Q,以AQ为直径画圆,交圆C1与M、N两点,则由圆的对称性知,MN=AQ,且∠AMQ=∠ANQ=90°,∴四边形AMQN是矩形,由作图知,四边形AMQN能构成无数个矩形.故答案为:D.【点睛】(1)本题主要考查圆和圆的位置关系,意在考察学生对这些知识的掌握水平和分析推理能力.(2)解答本题的关键是“以AQ为直径画圆,交圆C1与M、N两点”,这样可以得到无数个矩形.11.如图所示,圆形纸片的圆心为,半径为, 该纸片上的正方形ABCD的中心为.,,G,H 为圆上的点, 分别是以,,,为底边的等腰三角形.沿虚线剪开后, 分别以,,,DA为折痕折起使得,,G,H重合,得到四棱锥. 当正方形ABCD的边长变化时,所得四棱锥体积(单位:)的最大值为( )A. B. C. D.【答案】D【解析】【分析】本道题先用a表示四棱锥的体积,构造新函数,求导,结合导函数与原函数的单调性,计算原函数的极值,即可得出答案。
江西省新余市第四中学2021届高三上学期第一次段考数学(文)试题 Word版含答案
新余四中2021届高考年级上学期第一次段考文科数学试卷考试时间:120分钟一.选择题:(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知集合{}20,1,2,3,|0x A B x x -⎧⎫==≥⎨⎬⎩⎭,则A B = A. {}0,1,2 B. {}1,2 C. {}2,3 D.{}0,2,3 2、已知复数z 满足()i z i 2112+=⋅-,则在复平面内复数z 对应的点为A. ⎪⎭⎫⎝⎛--21,1 B. ⎪⎭⎫ ⎝⎛-21,1 C. ⎪⎭⎫ ⎝⎛-1,21 D. ⎪⎭⎫⎝⎛--1,21 3、设θ∈R ,则“ππ||1212θ-<”是“1sin 2θ<”的 A.充分而不必要条件 B.必要而不充分条件 C.充要条件 D.既不充分也不必要条件4、已知命题p :存在R n ∈,使得()nn nxx f 22+=是幂函数,且在()+∞,0上单调递增;命题q :“2,2+∈∃x R x >x 3”的否定是“x x R x 32,2<+∈∀” .则下列命题为真命题的是 A. q p ∧ B.q p ∧⌝ C.q p ⌝∧ D.q p ⌝∧⌝ 5、已知,51log ,41,27log 31313=⎪⎭⎫⎝⎛==c b a 则c b a ,,的大小关系为 A. c b a >> B. c a b >> C.a b c >> D.b a c >> 6. 某地区经过一年的新农村建设,农村的经济收入增加了一倍,实现翻番,为更好地了解该地区农村的经济收入变化情况,统计了该地区新农村建设前后农村的经济收入构成比例,得到如下饼图:建设前经济收入构成比例 建设后经济收入构成比例则下面结论中不正确的是A .新农村建设后,种植收入减少B .新农村建设后,其他收入增加了一倍以上C .新农村建设后,养殖收入增加了一倍D .新农村建设后,养殖收入与第三产业收入的总和超过了经济收入的一半7. 已知平面直角坐标角系下,角顶点与原点重合,始边与X 轴非负半轴重合,终边经过点P(4,3), 则 cos(2)2πα+=A .2425 B. 2425- C .2425或 2425- D.725 8、已知)(x f 是定义在R 上的偶函数,且在区间)0,(-∞上单调递增,若实数a 满足)2()2(|1|->-f f a ,则a 的取值范围是A .)21,(-∞B .),23()21,(+∞-∞C .)23,21(D .),23(+∞9、函数23ln(44)()(2)x x f x x -+=-的图象可能是A B C D10、函数⎪⎭⎫⎝⎛+=62cos πx y 的图像F 向左平移m 个单位后,得到的图像G 关于原点对称,则m 的值可以是A.6π B. 3π C.4π D. 2π11.已知定义在[)+∞,e 上的函数()x f 满足()()0'ln <+x xf x x f 且()02018=f ,其中()x f '是函数()x f 的导函数,e 是自然对数的底数,则不等式()0>x f 的解集为A.[)2018,e B .[)+∞,2018 C .()+∞,e D .[)1,+e e12.设12,F F 分别是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点,M 是C 的右支上的点,射线MN平分21MF F ∠,过原点O 作MN 的平行线交1MF 于点T ,若TM F F 421=,则双曲线C 的离心率为A.52B .2CD 二、填空题:(本大题共4个小题,每小题5分,共20分)13、已知向量(2,1),(m,1)a b ==-,且()a a b ⊥-,则m 的值为 .14、设函数2,3,()(1) 3.x x f x f x x ⎧≥=⎨+<⎩,则2(log 6)f 的值为 .15、若)2ln(21)(2++-=x b x x f 在),1(+∞-上是减函数,则b 的取值范围是 . 16. 已知矩形ABCD 的两边长分别为3=AB ,4=BC ,O 是对角线BD 的中点,E 是AD 边上一点,沿BE 将ABE ∆折起,使得A 点在平面BDC 上的投影恰为O ,则此时三棱锥BCD A -的外接球的表面积是 .三、解答题(本大题共6小题,共70分)17、(12分)设等差数列{}n a 的前n 项和为n S ,若93581,14.S a a =+=, (1)求数列{}n a 的通项公式; (2)设11n n n b a a +=,若{}n b 的前n 项和为n T ,证明:12n T <.18、(12分)如图,在四棱锥ABCD P -中,侧棱⊥PA 底面ABCD ,底面ABCD 为矩形,222===PA AB AD ,E 为PD 上一点,且ED PE 2=.(1)若F 为PE 的中点,求证://BF 平面AEC ; (2)求三棱锥AEC P -的体积.19、(12分)中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分几口井,取得了地质材料。
江西省新余四中、上高二中2019届高三上学期第二次联考数学(文)试题+Word版含答案
绝密★启用前江西省新余四中、上高二中2019届高三上学期第二次联考文科数学试题一、选择题(本大题共12小题,每小题5分,共60分,在每小题列出的四个选项中,选出符合题目要求的一项.)1.已知集合{}0)3)(32(<-+∈=x x Z x A ,{}x y x B ln 1-==,则=B A ( )A .(]e ,0B .{}e ,0C .{}2,1D .)2,1( 2.已知复数z 满足i z i 21211+=+(i 为虚数单位),则z 的虚部为( ) A .4 B .4- C i 4.D .i 4- 3.设5sin π=a ,3log2=b ,3241⎪⎭⎫ ⎝⎛=c ,则( ) A .b c a << B .c a b <<C .b a c <<D .a b c << 4.中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初行健步不为难,次日脚痛减一半,六朝才得到其关,要见次日行里数,请公仔细算相还.”其大意为:“有一个人走了378里路,第一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的地.”问此人第4天和第5天共走了( )A .60里B .48里C .36里D .24里5.设m ,n 是两条不同的直线,α,β是两个不同的平面,则m ∥n 的一个充分不必要条件是( )A . m ⊥α,n ⊥β,α∥βB .m ∥α,n ∥β,α∥βC . m ∥α,n ⊥β,α⊥βD .m ⊥α,n ⊥β,α⊥β6. —只蚂蚁在三边长分别为,,的三角形内自由爬行,某时刻该蚂蚁距离三角形的任意 一个顶点的距离不超过的概率为( )A. B. C. D.7.函数2()(1)cos 1xf x x e =-+图象的大致形状是( )8.已知函数f (x )=Asin (ωx +ϕ)(A >0,ω>0)的图象与直线y=a (0<a <A )的三个相邻交点的横坐标分别是2,4,8,则f (x )的单调递减区间是( )A .[6kπ,6kπ+3](k ∈Z )B .[6kπ﹣3,6kπ](k ∈Z )C .[6k ,6k +3](k ∈Z )D .[6k ﹣3,6k ](k ∈Z )9.一个简单几何体的三视图如图所示,则该几何体的体积为( )A .3696+πB .4872+πC .9648+πD .4824+π10.已知正实数,,满足,则当取得最大值时, 3112a b c+-的最大值为( )A.B.C.D.11. 已知,,是双曲线上的三个点,直线经过原点,经过右 焦,若,且,则该双曲线的离心率为( )A.B.C.D. 12.已知⎪⎩⎪⎨⎧>-+-≤=-0),2(0,)(12x a ax e x x x x f x 是减函数,且bx x f +)(有三个零点,则b 的取值范围为( )A .),1[)22ln ,0(+∞-eB .)22ln ,0(C . ),1[+∞-eD .),1[}22ln {+∞-e 二、填空题(每题4分,满分20分,将答案填在答题纸上)13. 若实数,满足约朿条件,则的最大值为____________.14. 已知锐角三角形ABC 中, 角A 、B 、C 所对的边分别为a 、b 、c ,若2()b a a c =+,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1
江西省新余市第四中学2017届高三数学上学期第二次段考试题 理
一、选择题(本大题共12小题,每小题5分,共60分。在每个小题给出的四个选项中,只有一项
是符合题目要求。)
1.设全集=UR,={x|<0}2xAx,B={x|2<2}x,则图中阴影部分表示的集合为( )
A.{|1}xx B.{|12}xx
C.{|01}xx D.{|1}xx
2.0000cos80cos130sin100sin130等于( )
A.32 B.12 C.12 D. 32
3.已知角的终边经过点(,3)(0)Pxx且10cos10x,则x等于( )
A.1 B.13 C.3 D.223
4.已知1tan()42,则sincossincos的值为( )
A.12 B.2 C.22 D.2
5.已知命题:p函数12xya的图象恒过定点(1,2);命题:q若函数(1)yfx为偶函数,则函
数()yfx的图象关于直线1x对称,则下列命题为真命题的是( )
A.pq B.pq C.pq D.()pq
6.已知ABC中,三内角ABC,,成等差数列,边,,abc成等比数列,则ABC是( )
A.直角三角形 B.等边三角形 C.锐角三角形 D.钝角三角形
7.定义22矩阵12142334=aaaaaaaa,若22cossin3()cos(2)12xxfxx,则()fx( )
A.图象关于,0中心对称 B.图象关于直线2x对称
C.在区间[,0]6上单调递增 D.周期为的奇函数
8.下列结论错误的是 ( )
第1题图
2
A.命题“若p,则q”与命题“若q,则p”互为逆否命题
B.命题q:∃x∈R,sinx-cosx=2。则¬q是假命题
C.为得到函数y=sin(2x-3)图象,只需把函数y=sin(2x+6)的图象向右平移4个长度单位
D.若函数()fx的导数为'()fx,0()fx为()fx的极值的充要条件是0()0fx
9.函数()sin()fxAxB的图象如下图所示,则()fx的解析式与
(0)(1)(2)(3)(2016)Sfffff
的值分别为( )
A、
1
()sin21,20152fxxS
B、1()sin1,201722fxxS
C、
14033
()sin1,222fxxS
D、1()sin1,201622fxxS
10.曲线3yx上一点B处的切线l交x轴于点,AOAB(O是原点)是以A为顶点的等腰三角形,
则切线l的倾斜角为( )
A.030 B.045 C.060 D.0120
11.设函数()(sincos)(02016)xfxexxx,则函数()fx的各极小值之和为( )
A.220152(1)1eee B.22015(1)1eee C.2016211ee D.
22016
2
(1e)1ee
12. 已知函数1()()1()fxaxnxaRx,则下列图像中一定不是()fx图象的是( )
3
二、填空题(本大题共4小题,每小题5分,共20分)
13. 20(1)xdx .
14. 若函数f(x)=2200xxxgxx为奇函数,则f(g(-1))=________.
15. 设x为锐角,若4cos()65x,则sin(2)12x的值为 .
16.设函数sincossincos()()2xxxxfxxR,若在区间0,m上方程3()2fx恰有
4
个解,则实数m的取值范围是 .
三、解答题(本大题共6小题,共70分,解答应写出必要的文字说明,证明过程或演算步骤)
17.(本小题12分)在锐角ABC中,边,ab是方程22320xx的两根,角,AB满足:
2sin()30AB.
(1)求角C的度数;
(2)求边c的长度及ABC的面积.
18.(本小题12分)已知函数22,0,(),0.xxfxxx
(1)判断()fx的奇偶性,并给出证明;
(2)若对任意的221,2,(2)(2)0tfttfkt恒成立,求实数k的取值范围.
19.(本小题12分)已知函数
()cos(2)2sin()sin()344fxxxx
.
(1)求函数()fx的最小正周期和图象的对称轴方程;
(2)求函数()fx在区间,122上的值域.
4
20.(本小题12分)已知函数(),lnxafxaRx
(1)若函数()yfx在(1,e)上是减函数,求实数a的取值范围;
(2)是否存在实数a,使得任意的(0,1)(1,),()xfxx恒成立,若不存在,说明理由。
若存在,求出a的值,并加以证明.
21.(本小题12分)已知函数2()fxaxbxc和函数2()ln,(0)gxaxbxcxabc,
(1)证明:只要0a,无论b取何值,函数()gx在定义域内不可能总为增函数;
(2)在同一函数图象上任意取不同两点1122(,),,AxyBxy,线段AB的中点为0,0()Cxy,记直线
AB
的斜率为k,①对于函数2()fxaxbxc,求证:0()kfx;②对于函数2()lngxaxbxcx,
是否具有与①同样的性质?证明你的结论.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分。
22.(本小题满分10分)选修4-4:坐标系与参数方程
在平面直角坐标系xOy中,已知曲线1C的参数方程为1cos,ysinx(其中为参数),曲线2C参
数方程为221,12xttytt(其中t为参数).
(1)在以原点为极点,x非负半轴为极轴的坐标系下,将曲线1C和曲线2C的方程化为极坐标方程;
(2)若射线:((,),0)43la与曲线1C,2C的交点分别为,AB两点(,AB异于原点),
求OAOB的取值范围.
23.(本小题满分10分) 已知函数()121fxxx.
5
(1)解不等式()5fx;
(2)若不等式()(R)fxaa的解集为空集,求实数a的取值范围.
6
7
8
9
10
11
