第一部分专题三 立体几何-2021届高三数学二轮专题复习精品课件
备战2023年新高考数学二轮专题复习课件立体几何

第三讲立体几何——大题备考【命题规律】立体几何大题一般为两问:第一问通常是线、面关系的证明;第二问通常跟角有关,一般是求线面角或二面角,有时与距离、几何体的体积有关.微专题1线面角保分题[2022·辽宁沈阳二模]如图,在四棱锥P-ABCD中,底面ABCD是正方形,P A⊥平面ABCD,P A=2AB=4,点M是P A的中点.(1)求证:BD⊥CM;(2)求直线PC与平面MCD所成角的正弦值.提分题例1 [2022·全国乙卷]如图,四面体ABCD中,AD⊥CD,AD=CD,∠ADB=∠BDC,E 为AC的中点.(1)证明:平面BED⊥平面ACD;(2)设AB=BD=2,∠ACB=60°,点F在BD上,当△AFC的面积最小时,求CF与平面ABD所成的角的正弦值.听课笔记:【技法领悟】利用空间向量求线面角的答题模板巩固训练1[2022·山东泰安一模]如图,在四棱锥P-ABCD中,底面ABCD是矩形,AB=2AD=2,P A⊥平面ABCD,E为PD中点.(1)若P A=1,求证:AE⊥平面PCD;(2)当直线PC与平面ACE所成角最大时,求三棱锥E-ABC的体积.微专题2二面角保分题[2022·山东临沂二模]如图,AB是圆柱底面圆O的直径,AA1、CC1为圆柱的母线,四边形ABCD是底面圆O的内接等腰梯形,且AB=AA1=2BC=2CD,E、F分别为A1D、C1C的中点.(1)证明:EF∥平面ABCD;(2)求平面OEF与平面BCC1夹角的余弦值.提分题例2 [2022·湖南岳阳三模]如图,在四棱锥P-ABCD中,底面ABCD是菱形,F是PD 的中点.(1)证明:PB∥平面AFC;(2)若直线P A⊥平面ABCD,AC=AP=2,且P A与平面AFC所成的角正弦值为√21,求7锐二面角F-AC-D的余弦值.听课笔记:AD,现例3 [2022·山东日照二模]如图,等腰梯形ABCD中,AD∥BC,AB=BC=CD=12以AC为折痕把△ABC折起,使点B到达点P的位置,且P A⊥CD.(1)证明:平面APC⊥平面ADC;(2)若M为PD上一点,且三棱锥D-ACM的体积是三棱锥P-ACM体积的2倍,求二面角P-AC-M的余弦值.听课笔记:【技法领悟】利用空间向量求二面角的答题模板巩固训练21.[2022·广东韶关二模]如图,在四棱锥P-ABCD中,底面ABCD为矩形,点S是边AB 的中点.AB=2,AD=4,P A=PD=2√2.(1)若O是侧棱PC的中点,求证:SO∥平面P AD;(2)若二面角P-AD-B的大小为2π,求直线PD与平面PBC所成角的正弦值.32.[2022·河北保定一模]如图,在等腰梯形ABCD中,AD∥BC,AD=AB=CD=1,∠BCD =60°,现将DAC沿AC折起至P AC,使得PB=√2.(1)证明:AB⊥PC;(2)求二面角A-PC-B的余弦值.微专题3探索性问题提分题例4 [2022·山东聊城三模]已知四边形ABCD为平行四边形,E为CD的中点,AB=4,△ADE为等边三角形,将三角形ADE沿AE折起,使点D到达点P的位置,且平面APE⊥平面ABCE.(1)求证:AP⊥BE;(2)试判断在线段PB上是否存在点F,使得平面AEF与平面AEP的夹角为45°.若存在,试确定点F的位置;若不存在,请说明理由.听课笔记:【技法领悟】1.通常假设问题中的数学对象存在或结论成立,再在这个前提下进行推理,如果能推出与条件吻合的数据或事实,说明假设成立,并可进一步证明;否则假设不成立.2.探索线段上是否存在满足条件的点时,一定注意三点共线的条件的应用.巩固训练3[2022·湖南岳阳一模]如图,在三棱锥S-ABC中,SA=SB=SC,BC⊥AC.(1)证明:平面SAB⊥平面ABC;(2)若BC=SC,SC⊥SA,试问在线段SC上是否存在点D,使直线BD与平面SAB所成的角为60°,若存在,请求出D点的位置;若不存在,请说明理由.第三讲立体几何微专题1线面角保分题解析:(1)证明:如图,连接AC,∵四边形ABCD是正方形,∴AC⊥BD.又P A ⊥平面ABCD ,BD ⊂平面ABCD ,∴P A ⊥BD , ∵P A ,AC ⊂平面P AC ,P A∩AC =A , ∴BD ⊥平面P AC , 又CM ⊂平面P AC , ∴BD ⊥CM .(2)易知AB ,AD ,AP 两两垂直,以点A 为原点,建立如图所示的空间直角坐标系A - xyz . ∵P A =2AB =4,∴A (0,0,0),P (0,0,4),M (0,0,2),C (2,2,0),D (0,2,0), ∴MC⃗⃗⃗⃗⃗⃗ =(2,2,-2),MD ⃗⃗⃗⃗⃗⃗ =(0,2,-2),PC ⃗⃗⃗⃗ =(2,2,-4). 设平面MCD 的法向量为n =(x ,y ,z ),则{n ·MC⃗⃗⃗⃗⃗⃗ =2x +2y −2z =0n ·MD ⃗⃗⃗⃗⃗⃗ =2y −2z =0,令y =1,得n =(0,1,1).设直线PC 与平面MCD 所成角为θ,由图可知0<θ<π2,则sinθ=|cos 〈n ,PC ⃗⃗⃗⃗ 〉|=|n·PC ⃗⃗⃗⃗⃗||n ||PC ⃗⃗⃗⃗⃗|=√12+12×√22+22+(−4)2=√36.即直线PC 与平面MCD 所成角的正弦值为√36.提分题[例1] 解析:(1)证明:∵AD =CD ,∠ADB = ∠BDC ,BD =BD , ∴△ABD ≌△CBD ,∴AB =CB .∵E 为AC 的中点,∴DE ⊥AC ,BE ⊥AC . ∵DE∩BE =E ,DE ,BE ⊂平面BED , ∴AC ⊥平面BED .∵AC ⊂平面ACD ,∴平面BED ⊥平面ACD .(2)如图,连接EF .由(1)知AC ⊥平面BED . 又∵EF ⊂平面BED , ∴EF ⊥AC . ∴S △AFC =12AC ·EF .当EF ⊥BD 时,EF 的长最小,此时△AFC 的面积最小. 由(1)知AB =CB =2. 又∵∠ACB =60°,∴△ABC 是边长为2的正三角形,∴BE =√3. ∵AD ⊥CD ,∴DE =1,∴DE 2+BE 2=BD 2,∴DE ⊥BE .以点E 为坐标原点,直线EA ,EB ,ED 分别为x 轴、y 轴、z 轴建立空间直角坐标系,则E (0,0,0),A (1,0,0),B (0,√3,0),C (-1,0,0),D (0,0,1),∴AB ⃗⃗⃗⃗⃗ =(-1,√3,0),AD ⃗⃗⃗⃗⃗ =(-1,0,1),DB ⃗⃗⃗⃗⃗ =(0,√3,-1),ED⃗⃗⃗⃗⃗ =(0,0,1),EC ⃗⃗⃗⃗ =(-1,0,0).设DF ⃗⃗⃗⃗⃗ =λDB ⃗⃗⃗⃗⃗ (0≤λ≤1), 则EF ⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +DF ⃗⃗⃗⃗⃗ =ED ⃗⃗⃗⃗⃗ +λDB ⃗⃗⃗⃗⃗ =(0,0,1)+λ(0,√3,-1)=(0,√3λ,1-λ). ∵EF ⊥DB , ∴EF⃗⃗⃗⃗ ·DB ⃗⃗⃗⃗⃗ =(0,√3λ,1-λ)·(0,√3,-1)=4λ-1=0, ∴λ=14,∴EF ⃗⃗⃗⃗ =(0,√34,34),∴CF ⃗⃗⃗⃗ =EF ⃗⃗⃗⃗ −EC ⃗⃗⃗⃗ =(0,√34,34)-(-1,0,0)=(1,√34,34).设平面ABD 的法向量为n =(x ,y ,z ), 则{n ·AB ⃗⃗⃗⃗⃗ =0,n ·AD⃗⃗⃗⃗⃗ =0,即{−x +√3y =0,−x +z =0.取y =1,则x =√3,z =√3,∴n =(√3,1,√3).设当△AFC 的面积最小时,CF 与平面ABD 所成的角为θ,则sin θ=|cos 〈n ,CF ⃗⃗⃗⃗ 〉|=|n·CF ⃗⃗⃗⃗⃗||n ||CF ⃗⃗⃗⃗⃗ |=|√3×1+1×√34+√3×34|√3+1+3× √1+316+916=4√37. 故当△AFC 的面积最小时,CF 与平面ABD 所成的角的正弦值为4√37. [巩固训练1]解析:(1)证明:∵P A ⊥平面ABCD ,CD ⊂平面ABCD ,∴P A ⊥CD , ∵四边形ABCD 为矩形,∴AD ⊥CD ,又AD∩P A =A ,AD 、P A ⊂平面P AD ,∴CD ⊥平面P AD , ∵AE ⊂平面P AD ,∴AE ⊥CD ,在△P AD 中,P A =AD ,E 为PD 的中点,∴AE ⊥PD , 而PD∩CD =D ,PD 、CD ⊂平面PCD , ∴AE ⊥平面PCD .(2)以A 为坐标原点,分别以AB 、AD 、AP 所在直线为x 、y 、z 轴建立空间直角坐标系, 设AP =a (a >0),则C (2,1,0),P (0,0,a ),E (0,12,a2),∴AC ⃗⃗⃗⃗⃗ =(2,1,0),AE ⃗⃗⃗⃗⃗ =(0,12,a 2),PC ⃗⃗⃗⃗ =(2,1,-a ), 设平面ACE 的一个法向量为n =(x ,y ,z ), 则{n ·AC ⃗⃗⃗⃗⃗ =2x +y =0n ·AE⃗⃗⃗⃗⃗ =12y +a 2z =0,取y =-a ,可得n =(a2,-a ,-1).设直线PC 与平面ACE 所成角为θ,则sin θ=|cos 〈n ,PC ⃗⃗⃗⃗ 〉|=|n·FC⃗⃗⃗⃗⃗ ||n ||FC⃗⃗⃗⃗⃗ |=√54a 2+1·√5+a 2=√29+20a2+5a ≤27,当且仅当a =√2时等号成立.即当AP =√2时,直线PC 与平面ACE 所成角最大, 此时三棱锥E - ABC 的体积V =13×12×2×1×√22=√26.微专题2 二面角保分题解析:(1)证明:取AD 的中点M ,连接EM 、MC ,∵E 为A 1D 的中点,F 为CC 1的中点,∴EM ∥AA 1,EM =12AA 1,又CF ∥AA 1,CF =12AA 1, ∴EM ∥CF ,EM =CF ,∴四边形EMCF 为平行四边形,∴EF ∥CM , 又EF ⊄平面ABCD ,CM ⊂平面ABCD , ∴EF ∥平面ABCD .(2)设AB =AA 1=2BC =2CD =4,∵AC ⊥BC ,∴AC =2√3.由题意知CA 、CB 、CC 1两两垂直,故以C 为坐标原点,分别以CA 、CB 、CC 1所在直线为x 、y 、z 轴建立空间直角坐标系.则A 1(2√3,0,4)、O (√3,1,0)、F (0,0,2)、C (0,0,0)、D (√3,-1,0), ∴A 1D 的中点E 的坐标为(3√32,-12,2), ∴OF⃗⃗⃗⃗⃗ =(-√3,-1,2),EF ⃗⃗⃗⃗ =(-3√32,12,0),设平面OEF 的一个法向量为n =(x ,y ,z ),则{n ·OF ⃗⃗⃗⃗⃗ =0n ·EF ⃗⃗⃗⃗ =0,即{−√3x −y +2z =0−3√32x +12y =0,即{√3x +y −2z =03√3x −y =0, 令x =√3,得n =(√3,9,6),∵AC ⊥BC ,AC ⊥CC 1,BC ∩CC 1=C , ∴AC ⊥平面BCC 1,∴平面BCC 1的一个法向量为CA ⃗⃗⃗⃗⃗ =(2√3,0,0),cos 〈n ,CA ⃗⃗⃗⃗⃗ 〉=n·CA ⃗⃗⃗⃗⃗|n |·|CA ⃗⃗⃗⃗⃗|=√3+81+36·2√3=√1020, ∴平面OEF 与平面BCC 1夹角的余弦值为√1020. 提分题[例2] 解析:(1)证明:连接BD 交AC 于O , 易证O 为BD 中点,又F 是PD 的中点, 所以OF ∥PB ,又OF ⊂平面AFC ,且PB 不在平面AFC 内, 故PB ∥平面AFC .(2)取PC 中点为Q ,以O 为坐标原点,OB 为x 轴,OC 为y 轴,OQ 为z 轴建立空间直角坐标系,设OB =m ,则A (0,-1,0),B (m ,0,0),C (0,1,0),P (0,-1,2),D (-m ,0,0)⇒F (-m2,-12,1),AP ⃗⃗⃗⃗⃗ =(0,0,2),OF ⃗⃗⃗⃗⃗ =(-m 2,-12,1),OC⃗⃗⃗⃗⃗ =(0,1,0), 设平面AFC 的法向量为n =(x ,y ,z ),由{n ⊥OF ⃗⃗⃗⃗⃗ n ⊥OC ⃗⃗⃗⃗⃗ ⇒{−m2x −12y +z =0y =0,令x =2,有n =(2,0,m ),由P A 与平面AFC 所成的角正弦值为√217⇒√217=|AP ⃗⃗⃗⃗⃗ ·n||AP⃗⃗⃗⃗⃗ |·|n|=2√4+m 2⇒m =√3, 平面ACD 的法向量为m =(0,0,1),则锐二面角F - AC - D 的余弦值为 |m·n ||m |·|n |=√3√7=√217.[例3] 解析:(1)证明:在梯形ABCD 中取AD 中点N ,连接CN , 则由BC 平行且等于AN 知ABCN 为平行四边形,所以CN =AB , 由CN =12AD 知C 点在以AD 为直径的圆上,所以AC ⊥CD .又AP ⊥CD ,AP∩AC =A, AP ,AC ⊂平面P AC , ∴CD ⊥平面P AC , 又CD ⊂平面ADC , ∴平面APC ⊥平面ADC .(2)取AC 中点O ,连接PO ,由AP =PC ,可知PO ⊥AC ,再由平面P AC ⊥平面ACD ,AC 为两面交线,所以PO ⊥平面ACD ,以O 为原点,OA 为x 轴,过O 且与OA 垂直的直线为y 轴,OP 为z 轴建立空间直角坐标系,令AB =2,则A (√3,0,0),C (-√3,0,0),P (0,0,1),D (-√3,2,0), 由V P - ACM ∶V D - ACM =1∶2,得PM⃗⃗⃗⃗⃗⃗ =13PD ⃗⃗⃗⃗⃗ , 所以OM ⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +PM ⃗⃗⃗⃗⃗⃗ =OP ⃗⃗⃗⃗⃗ +13PD ⃗⃗⃗⃗⃗ =(-√33,23,23), 设平面ACM 的法向量为n =(x ,y ,z ), 则由{n ·OM ⃗⃗⃗⃗⃗⃗ =0n ·OA ⃗⃗⃗⃗⃗ =0得{−√33x +23y +23z =0√3x =0,取z =-1得x =0,y =1,所以n =(0,1,-1),而平面P AC 的法向量m =(0,1,0),所以cos 〈n ,m 〉=m·n |m ||n |=√22. 又因为二面角P - AC - M 为锐二面角,所以其余弦值为√22.[巩固训练2]1.解析:(1)证明:取线段PD 的中点H ,连接SO 、OH 、HA ,如图,在△PCD 中,O 、H 分别是PC 、PD 的中点,所以OH ∥CD 且OH =12CD ,所以OH ∥AS 且OH =AS ,所以四边形ASOH 是平行四边形,所以SO ∥AH ,又AH ⊂平面P AD ,SO ⊄平面P AD ,所以SO ∥平面P AD .(2)取线段AD 、BC 的中点E 、F ,连结PE 、EF .由点E 是线段AD 的中点,P A =PD 可得PE ⊥AD ,又EF ⊥AD ,所以∠PEF 是二面角P - AD - B 的平面角,即∠PEF =23π,以E 为原点,EA⃗⃗⃗⃗⃗ 、EF ⃗⃗⃗⃗ 方向分别为x 轴、y 轴正方向,建立如图所示坐标系,在△P AD 中,AD =4,P A =PD =2√2知:PE =2,所以P (0,-1,√3),D (-2,0,0),B (2,2,0),C (-2,2,0),所以PD⃗⃗⃗⃗⃗ =(-2,1,-√3),PB ⃗⃗⃗⃗⃗ =(2,3,-√3),PC ⃗⃗⃗⃗ =(-2,3,-√3), 设平面PBC 的法向量n =(x ,y ,z ),则{n ·PB ⃗⃗⃗⃗⃗=0n ·PC⃗⃗⃗⃗ =0,即{2x +3y −√3z =0−2x +3y −√3z =0,可取n =(0,1,√3),设直线PD 与平面PBC 所成角为θ, 则sin θ=|cos 〈PD⃗⃗⃗⃗⃗ ,n 〉|=2·2√2=√24,所以直线PD 与平面PBC 所成角的正弦值为√24.2.解析:(1)证明:在等腰梯形ABCD 中,过A 作AE ⊥BC 于E ,过D 作DF ⊥BC 于F ,因为在等腰梯形ABCD 中,AD ∥BC ,AD =AB =CD =1,∠BCD =60°,所以BE =CF =12CD =12,AE =DF =√12−(12)2=√32, 所以AC =BD =√(32)2+(√32)2=√3, BC =2,所以BD 2+CD 2=BC 2,所以BD ⊥CD ,同理AB ⊥AC , 又因为AP =AB =1,PB =√2, ∴AP 2+AB 2=PB 2,∴AB ⊥AP又AC∩AP =A ,AC ,AP ⊂平面ACP , 所以AB ⊥平面ACP , 因为PC ⊂平面ACP , 所以AB ⊥PC .(2)取AC 的中点为M ,BC 的中点为N ,则MN ∥AB , 因为AB ⊥平面ACP ,所以MN ⊥平面ACP ,因为AC ,PM ⊂平面ACP ,所以MN ⊥AC ,MN ⊥PM , 因为P A =PC ,AC 的中点为M ,所以PM ⊥AC , 所以MN ,MC ,MP 两两垂直,所以以M 为原点,以MN 所在直线为x 轴,以MC 所在直线为y 轴,以MP 所在直线为z 轴建立空间直角坐标系,则A (0,-√32,0),B (1,-√32,0),C (0,√32,0),P (0,0,12),PC ⃗⃗⃗⃗ =(0,√32,-12),PB ⃗⃗⃗⃗⃗ =(1,-√32,-12), 平面APC 的一个法向量为m =AB⃗⃗⃗⃗⃗ =(1,0,0), 设平面PBC 的一个法向量为n =(x ,y ,z ),则 {n ·PC⃗⃗⃗⃗ =√32y −12z =0n ·PB ⃗⃗⃗⃗⃗ =x −√32y −12z =0,令y =1,则n =(√3,1,√3),所以cos 〈m ,n 〉=m·n |m ||n |=√31×√7=√217, 因为二面角A - PC - B 为锐角, 所以二面角A - PC - B 的余弦值为√217.微专题3 探索性问题提分题[例4] 解析:(1)证明:因为四边形ABCD 为平行四边形,且△ADE 为等边三角形, 所以∠BCE =120°,又E 为CD 的中点,所以CE =ED =DA =CB ,即△BCE 为等腰三角形, 所以∠CEB =30°.所以∠AEB =180°-∠AED -∠BEC =90°, 即BE ⊥AE .又因为平面AEP ⊥平面ABCE ,平面APE ∩平面ABCE =AE ,BE ⊂平面ABCE , 所以BE ⊥平面APE ,又AP ⊂平面APE ,所以BE ⊥AP .(2)取AE 的中点O ,连接PO ,由于△APE 为正三角形,则PO ⊥AE , 又平面APE ⊥平面ABCE ,平面APE ∩平面ABCE =AE ,PO ⊂平面EAP , 所以PO ⊥平面ABCE ,PO =√3,BE =2√3, 取AB 的中点G ,则OG ∥BE ,由(1)得BE ⊥AE ,所以OG ⊥AE ,以点O 为原点,分别以OA ,OG ,OP 所在的直线为x 轴,y 轴,z 轴,建立如图所示的空间直角坐标系O - xyz ,则O (0,0,0),A (1,0,0),B (-1,2√3,0),P (0,0,√3),E (-1,0,0), 则EA ⃗⃗⃗⃗⃗ =(2,0,0),EB ⃗⃗⃗⃗⃗ =(0,2√3,0),PB ⃗⃗⃗⃗⃗ =(-1,2√3,-√3),EP ⃗⃗⃗⃗ =(1,0,√3), 假设存在点F ,使平面AEF 与平面AEP 的夹角为45°, 设PF⃗⃗⃗⃗ =λPB ⃗⃗⃗⃗⃗ =(-λ,2√3λ,-√3λ),λ∈[0,1], 则EF ⃗⃗⃗⃗ =EP ⃗⃗⃗⃗ +PF ⃗⃗⃗⃗ =(1,0,√3)+(-λ,2√3λ,-√3λ)=(1-λ,2√3λ,√3−√3λ), 设平面AEF 的法向量为m =(x ,y ,z ),由{EF ⃗⃗⃗⃗·m =0EA ⃗⃗⃗⃗⃗ ·m =0得{(1−λ)x +2√3λy +(√3,-√3λ)z =02x =0, 取z =2λ,得m =(0,λ-1,2λ);由(1)知EB⃗⃗⃗⃗⃗ 为平面AEP 的一个法向量, 于是,cos 45°=|cos 〈m ,EB ⃗⃗⃗⃗⃗ 〉|=|m·EB ⃗⃗⃗⃗⃗||m |·|EB ⃗⃗⃗⃗⃗|=2√3|λ−1|2√3·√5λ2−2λ+1=√22,解得λ=13或λ=-1(舍去),所以存在点F ,且当点F 为线段PB 的靠近点P 的三等分点时,平面AEF 与平面AEP 的夹角为45°.[巩固训练3]解析:(1)证明:取AB 的中点E ,连接SE ,CE ,∵SA =SB ,∴SE ⊥AB , ∵BC ⊥AC ,∴三角形ACB 为直角三角形,∴BE =EC , 又BS =SC ,∴△SEC ≌△SEB ,∴∠SEB =∠SEC =90°, ∴SE ⊥EC ,又SE ⊥AB ,AB∩CE =E ,∴SE ⊥平面ABC . 又SE ⊂平面SAB ,∴平面SAB ⊥平面ABC .(2)以E 为坐标原点,平行AC 的直线为x 轴,平行BC 的直线为y 轴,ES 为z 轴建立空间直角坐标系,如图,不妨设SA =SB =SC =2,SC ⊥SA ,则AC =2√2,BC =SC =2知EC =2√3,SE =1,则A (-√2,1,0),B (√2,-1,0),C (√2,1,0),E (0,0,0),S (0,0,1), ∴AB⃗⃗⃗⃗⃗ =(2√2,-2,0),SA ⃗⃗⃗⃗ =(-√2,1,-1), 设D (x ,y ,z ),CD ⃗⃗⃗⃗⃗ =λCS⃗⃗⃗⃗ (0≤λ≤1),则(x -√2,y -1,z )=λ(-√2,-1,1), ∴D (√2−√2λ,1-λ,λ),BD⃗⃗⃗⃗⃗ =(-√2λ,2-λ,λ). 设平面SAB 的一个法向量为n =(x 1,y 1,z 1),则{n ·AB⃗⃗⃗⃗⃗ =2√2x 1−2y 1=0n ·SA ⃗⃗⃗⃗ =−√2x 1+y 1−z 1=0,取x 1=1,得n =(1,√2,0),sin 60°=|n·BD ⃗⃗⃗⃗⃗⃗ ||n ||BD ⃗⃗⃗⃗⃗⃗ |,则√2−2√2λ|√3√2λ2+(2−λ)2+λ2=√32, 得λ2+7λ+1=0,又∵0≤λ≤1,方程无解,∴不存在点D ,使直线BD 与平面SAB 所成的角为60°.。
高三数学二轮复习:立体几何

专题四 立体几何
第1讲 空间几何体
[考情考向分析]
1.以三视图为载体,考查空间几何体面积、体积的计算. 2.考查空间几何体的侧面展开图及简单的组合体问题.
内容索引
热点分类突破 真题押题精练
热规则 俯视图放在正(主)视图的下面,长度与正(主)视图的长度一样,侧(左)视 图放在正(主)视图的右面,高度与正(主)视图的高度一样,宽度与俯视图 的宽度一样.即“长对正、高平齐、宽相等”. 2.由三视图还原几何体的步骤 一般先依据俯视图确定底面再利用正(主)视图与侧(左)视图确定几何体.
跟踪演练3 (1)(2018·咸阳模拟)在三棱锥P-ABC中,PA⊥平面ABC,
AB⊥BC,若AB=2,BC=3,PA=4,则该三棱锥的外接球的表面积为
A.13π C.25π
B.20π
√D.29π
解析 答案
(2)(2018·四川成都名校联考)已知一个圆锥的侧面积是底面积的2倍,
√ 记该圆锥的内切球的表面积为S1,外接球的表面积为S2,则SS12 等于
例3 (1)(2018·百校联盟联考)在三棱锥P-ABC中,△ABC和△PBC均为
边长为3的等边三角形,且PA=326 ,则三棱锥P-ABC外接球的体积为
13 13 A. 6 π
10 10 B. 3 π
√C.5
15 2π
55 D. 6 π
解析 答案
(2)(2018·衡水金卷信息卷)如图是某三棱锥的三视
跟踪演练1 (1)(2018·衡水模拟)已知一几何体的正(主)视图、侧(左)视 图如图所示,则该几何体的俯视图不可能是
√
解析 答案
(2)(2018·合肥质检)在正方体ABCD-A1B1C1D1中,E是棱 A1B1的中点,用过点A,C,E的平面截正方体,则位于 截面以下部分的几何体的侧(左)视图为
北京理工大学附属中学高三数学二轮复习资料立体几何(共22张PPT)

D1 A1 E F B1
C1
D P A
Q
C B
2 6
3 正视图
3
2 3 侧视图
3
俯视图
方法总结: (1)在正视图、左视图、俯视图中投射面 和投射线的关系(在俯视图中,主视图的投 射线向上指) (2)放在正方体或长方体中考虑; (3)检验意识:由三视图得到直观图,一 定再按照画三视图的要求再验证一遍三视图 是否合适。这是解决任何一个数学问题时都 要有的一种意识。
(3)若PF 2FD,判断AF //面PBC?证明你的结论.
谢谢聆听, 恳请指正!
立体几何(理科)二轮 复习建议
北京理工大学附属中学
画面感 (动、静) 操作
空间想象能力 推理论证能力
(作图)
判断
借助头脑中的“画面感”来作出判断, l2 , l3 为空间中三条互相平行且两两间的距离分别为 4, 8.
5,6 的直线.给出下列三个结论: ① Ai li (i 1,2,3) ,使得 A1 A2 A3 是直角三角形; ② Ai li (i 1,2,3) ,使得 A1 A2 A3 是等边三角形; ③三条直线上存在四点 A i (i 1,2,3,4) , 使得四面体 A1 A2 A3 A4 为 在一个顶点处的三条棱两两互相垂直的四面体. 其中,所有正确结论的序号是 A. ① B.①② C. ①③ D. ②③
l
直觉来自哪里?
A
α B C
“几何直观”不同于“直觉”,用数学 来解释生活中的现象。
D1 A1 B1 P D A B
C1
C
教学建议:在此类问题中,要特别注 意将空间线、面的平行、垂直等位置 关系转化到平面,或者利用空间线、 面的垂直等位置关系将距离、角等几 何量转化到平面内,应当熟悉各类圆 锥曲线的定义。
模块二讲重点 立体几何(1)立体几何小题(一) 线面关系及空间角-2021届高考数学二轮复习课件(新

模 块 二 讲 重 点 第 8 讲 立 体 几 何 (1)立 体几何 小题( 一) 线 面 关 系 及空间 角-20 21届高 考数学 二轮复 习课件 (新高 考版)
求二面角的常用方法 (1)传统方法: 定义法:如图,cosθ=APBB. 三垂线法:点P到平面α的距离PA=d,点P到交线l的距离PB= d1,则sinθ=dd1. 关键:求出点P到平面α的距离d.
模 块 二 讲 重 点 第 8 讲 立 体 几 何 (1)立 体几何 小题( 一) 线 面 关 系 及空间 角-20 21届高 考数学 二轮复 习课件 (新高 考版)
⑤精确回答:看准题目要求,是求余弦,还是求正弦还是 正切?是求角还是求三角函数值?
判定面面垂直的方法 (1)利用面面垂直的定义(作出两平面构成的二面角的平面 角,计算平面角为90°); (2)利用面面垂直的判定定理:a⊥β,a⊂α⇒α⊥β. (3)向量法:证明两个平面的法向量m,n垂直,即证m·n=0.
模 块 二 讲 重 点 第 8 讲 立 体 几 何 (1)立 体几何 小题( 一) 线 面 关 系 及空间 角-20 21届高 考数学 二轮复 习课件 (新高 考版)
二、常用方法结论 求异面直线所成的角主要有两种方法
(1)作图法:其解决方法常采用“平移线段法”,平移的方 法一般有三种类型:利用图中已有的平行线平移;利用特殊点 (线段的端点或中点)作平行线平移;补形平移.最终将空间角转 化为平面角,利用解三角形的知识求解.
第8讲 立体几何 第三课时 讲练课件(共86张PPT) 2021届高考(理科)数学二轮复习

【分析】 (1)要证线线垂直,可先证线面垂直.
(2)建立空间直角坐标系,假设BBCP =λ(0≤λ≤1),计算平面
DBB1
的一个法向量
n,以及D→P,然后根据
sinθ=
→ |n·DP|
→
=
33,
|n|·|DP|
计算可得 λ.
【解析】 (1)证明:在直三棱柱 ABC-A1B1C1 中,A1C1⊥ C1C,平面 CC1D⊥平面 ACC1A1,平面 CC1D∩平面 ACC1A1= CC1,A1C1⊂平面 ACC1A1,所以 A1C1⊥平面 CC1D,
(2)把平面图形翻折后,经过恰当连线就能得到三棱锥、四棱 锥,从而把问题转化到我们熟悉的几何体中去解决.
第23页
押题二 二面角 典例 4 (2020·百校联考冲刺金卷)如图,四棱 锥 P-ABCD 中,PA=AD=2,AB=BC=CD=1, BC∥AD,∠PAD=90°,∠PBA 为锐角,平面 PBA⊥平面 PBD. (1)证明:PA⊥平面 ABCD; (2)求平面 PCD 与平面 PAB 所成的锐二面角的余弦值.
第三课时 立体几何大题
01 第三课时
第1页
立体几何大题处于解答题第 2 或第 3 题的位置,属于得分题. 立体几何常见的类型主要有:①考查线线、线面、面面关系 的证明,此类题目常以解答题的第一问出现;②计算空间的角和 距离,此类题目常以解答题的第二问出现. 常见几何体为柱、锥、台等或者它们的组合体.
(1)证明:BD⊥CF; (2)若∠EAC=60°,求异面直线 AE 与 DF 所成角的余弦值.
第4页
【分析】 (1)证明 BD⊥平面 ACFE,再利用线面垂直的定 义,即可得到线线垂直;
(2)证明直线 GM,GA,GB 两两垂直,分别以 GA,GB, GM 为 x,y,z 轴建立空间直角坐标系 G-xyz,求得A→E= - 23,0,32,D→F=-32 3,1,32,再利用向量的夹角公式计算, 即可得到答案.
高三数学第二轮复习:立体几何(2021最新版)
C
例题讲解
例 2、一个多面体的直观图、主视图、侧视图、俯视图如下所示,
(Ⅰ)求该多面体 的体积和全面积
(Ⅱ)若 M 、 N 分别为 A1B 、 B1C1 的中点。
①求证: MN ∥ 平面 ACC1 A1
a
a
②求证: MN 平面 A1BC
a
a
主视图 a
左视图
a 俯视图
例题讲解
A
1
C
1
N B
1
O
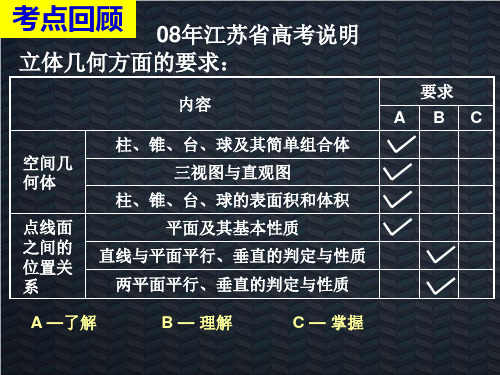
2007年高考山东、海南(宁夏)、广东三省立几考查:
省份
题型
分值
比例
山东 海南 (宁夏) 广东
江苏
选择1题 解答1题 选择1题 解答1题 填空1题 解答1题 选择1题 填空1题 解答1题
17
11.33%
17
11.33%
19
12.67%
22
14.67%
知识点梳理
知识点梳理
课前热身
1. 一个几何体是由若干个相同的正方体组成的,其主视图
a
a
a
a
a
2a
2a
a
a
a
a
a
(1)请画出四棱锥 S-ABCD 的示意图,是否存在一条侧棱垂直于底面? 如果存在,请给出证明;如果不存在,请说明理由;
(2)若 SA 面 ABCD,E 为 AB 中点,证明:平 面SEC 平面 SCD;
(3)求点 D 到面 SEC 的距离。
例题讲解
S
A E
B
M
N
D
M
A
C
B
例题讲解
例 3、正四棱锥 P ABCD 底面的四个顶点 A, B, C, D 在球 O 的
第8讲 立体几何 第一课时 讲练课件(共70张PPT) 2021届高考(理科)数学二轮复习
二、常用方法结论 1.三视图问题的解题策略 (1)由三视图还原直观图的方法: ①还原后的几何体一般为较熟悉的柱、锥、台、球的组合体. ②注意图中实、虚线,实际分别是原几何体中的可视线与被 遮挡线. ③想象原形,并画出草图后进行三视图还原,把握三视图和 几何体之间的关系,与所给三视图比较,通过调整准确画出原几 何体.
第8页
②夹在两个平行平面之间的平行线段相等. ③经过平面外一点有且只有一个平面与已知平面平行. ④两条直线被三个平行平面所截,截得的对应线段对应成比 例. ⑤如果两个平面分别平行于第三个平面,那么这两个平面互 相平行.
第9页
8.判定直线与平面垂直的常用方法 (1)利用线面垂直的定义:若一条直线垂直于平面内任意一条 直线,则这条直线垂直于该平面. (2)利用线面垂直的判定定理:若一条直线与平面内两条相交 直线都垂直,则这条直线与平面垂直. (3)用线面垂直的性质:若两平行线中的一条垂直于平面,则 另一条也垂直于这个平面.
第21页
5.求二面角的常用方法 (1)传统方法: 定义法:如图,cosθ=APBB. 三垂线法:点 P 到平面 α 的距离 PA=d,点 P 到 交线 l 的距离 PB=d1,则 sinθ=dd1. 关键:求出点 P 到平面 α 的距离 d.
第22页
(2)空间向量法: 二面角的范围:θ∈[0,π].
第29页
(3)(2020·九江市第一次统一考试)已知一个几何体的三视图 如图所示,则该几何体的表面积为( C )
A.π2+ 3 C.32π+ 3
B.π+ 3 D.3π+ 3
第30页
【解析】 由三视图知,该几何体是一个底面 半径为 1,高为 3的半圆锥(如图),其正面为圆锥 的轴截面,形状为等边三角形,该截面三角形的面 积为12×2× 3= 3;侧面展开图为扇形,该扇形的弧长为12×2 π×1=π,半径为 ( 3)2+12=2,其面积为12×π×2=π;底 面为半圆,其面积为12×π×12=π2.则该几何体的表面积为32π+ 3. 故选 C.
最新-2021届高考数学文新课标二轮专题复习课件:33 立体几何 精品
证明:MN∥平面 A′ACC′. 思路 本题主要考查线面平行的判定定理,意在考查考生对空 间中的基本定理的掌握情况以及逻辑推理能力与计算能力.
解析 连接 AB′,AC′,
∵四边形 ABB′A′为矩形,M 为 A′B 的中点, 又点 N 为 B′C′的中点, ∴MN∥AC′. 又 MN⊄平面 A′ACC′且 AC′⊂平面 A′ACC′, ∴MN∥平面 A′ACC′.
∵点 E,F 分别是 BC,DC 的中点,∴DF =CE.
又∵AD=DC,∠ADF=∠DCE=90°, ∴△ADF≌△DCE.
∴∠AFD=∠DEC. 又∵∠CDE+∠DEC=90°, ∴∠CDE+∠AFD=90°, ∴∠DOF=180°-(∠CDE+∠AFD)=90°即 AF⊥DE. 又 D1D∩DE=D,∴AF⊥平面 D1DE. 又∵ED1⊂平面 D1DE,∴AF⊥ED1.
(2)∵AA1⊥平面 ABC,AA1⊂平面 AA1C1C,
∴平面 ABC⊥平面 AA1C1C. 作 BE⊥AC,垂足为 E,则 BE⊥平面 AA1C1C.
在 Rt△ABC 中,AC= AB2+AC2= 13.
BE=ABA·CBC=
6 13.
∴四棱锥 B-AA1C1D 的体积 V=13×12(A1C1+AD)·AA1·BE
∵FD⊥B1D,∴易证 Rt△CDF∽Rt△BB1D, ∴BD1FD=BCBD1.
∴DF=13× 10= 310,
∴VB1-ADF=VA-B1DF=13S△B1DF·AD=13×12× 310×
10×2
2=109
2 .
(2016·山东文登统考)如图所示,已知 在四棱锥 P-ABCD 中,CD∥AB,AD⊥AB,BC ⊥PC,且 AD=DC=PA=21AB=a.
人教版高中数学必修立体几何复习课件(共102张PPT)
1 1
1
11.已知某个几何体的三视图如图2,根据图中标出的尺寸 (单位:cm),可得这个几何体的体积是_____8_0__0.0 cm 3
3
2 0 20
主视图
10
10
2 俯0视图
2 侧0视图
第二章 点、直线、平面之间的位置关系
• 四个公理
直线与直线位置关系 • 三类关系 直线与平面位置关系
平面与平面位置关系
(3)
a a
// b
b
(较常用);
(4)
a
//
a
;
(5)
a a
b
a
(面面垂直 线面垂直)
a b
4.面面垂直
向的侧视图(或称左视图)为(
A
A
H
G
Q
B
C
侧视 B
)A
C
I
P
E
图1
F
B
D
E
D
图2
F
B
B
B
E A.
E B.ቤተ መጻሕፍቲ ባይዱ
E C.
E D.
练习10:(1)如图是一个空间几何体的三
视图,如果直角三角形的直角边长均为
正视图 侧视图
1,那么几何体的体积为( ) C
A.1 B.1 C. 1 D.1
俯视图
2
3
6
V1 3S底 h1 31111 3
②判定定理:如果一个平面内的两条相交直线都平行于 另一个平面,那么两个平面互相平行;
符号表述: a,b , a b O, a //,b // //
//
③面面平行的性质定理:
a
a
//
