第9章导体和电介质中的静电场(精)
大学物理下 第九章 静电场中的导体和电介质5
2
ε0S C= d
四,静电场的能量 (1)电容器的能量 )
1 Q2 W = CU 2 = 2 2C
(2)静电场的能量 有电场的地方就有能量 )
1 ωe = D E 2
W = ∫ ωe dV
(3)静电场的能量与功的关系 )
A 静 = W
已知 ε r1 : ε r 2 = 1 : 2 ,问 W1 : W2 = ?
λ o d a
λ λ U = ∫ + dr 2πε0r 2πε0 (d r ) a -λ λ λ d a λ d = Ln ≈ Ln πε0 a πε0 a
λ λ πε 0 ∴ C0 = = = d d λ U Ln Ln a a πε 0
r
d a
P79 99 讨论
1)通电后维持电压不变插入电介质 ) 2)通电后断开再插入电介质 ) 讨论插入前后的 E,D,U,Q. , , , 令插入前为E , , , (令插入前为 0,D0,U0,Q0) 2) Q = Q 0
4a
UBA = UB∞
场具有球对称性
a
3a
解(1)a < r < 3a
∫∫ D dS = ∫∫ DdS = D4πr = QA
2 S S
Q
4a
a
QA D= 2 4πr
D QA E= = 2 ε0εr 4πε0εr r
3a
r > 4a ∫∫ D dS = D 4 πr = Q + Q A
2 S
Q + QA D= 2 4 πr
∫∫ D dS = Q0
S
E = E0 + E'
9-6,8 ,
E0
讨论 p79
大学物理 导体和电介质中的静电场

x
(1 2)S q (3 4)S q
1
2
3
4
q S
q S
0
1 4 0
2 3
ⅠⅡ Ⅲ
2 q / S
3 q / S
----电荷分布在极板内侧面
2020/1/14
由场强叠加原理有:
E1
2 2 0
3 2 0
2 2 0
3 2 0
4 2 0
2 0
q1 q2
2 0 S
E3
1 2 0
2 2 0
3 2 0
4 20/1/14
导体和电介质中的静电场
例: 点电荷 q = 4.0 × 10-10C, 处在不带电导体球壳的 中心,壳的内、外半径 分别为: R1=2.0 × 10-2m , R2=3.0 × 10-2m.
0
+ +
+
+ -
-
-q
+
+ -
+
Q
+
+
q
-+
+q
-
--q-
S
+
++
qi 0
S内
结论
空腔内有电荷q时,空腔内表面感应出等值异号 电量-q,导体外表面的电量为导体原带电量Q与感应 电量q的代数和.
2020/1/14
导体和电介质中的静电场
3. 静电平衡导体表面附近的电场强度与导体表面电荷的关系
3. 导体的静电平衡条件 导体内电荷的宏观定向运动完全停止.
第九章导体和电介质中的静电场

q3 0,
V1
1 4 0
( q1 R1
q2 R2
)
60(V ).
2.提示:未插金属板之前 E0
V d
,则选择题
2
可知两边场强,则所求金属
板的电势V
E
d 2
(E0
2 0
)
d 2
(V d
q )
2 0 S
d 2
V 2
qd 4 o S
。
3 . 提 示 :( 1 ) 据 有 介 质 时 的 高 斯 定 理 , 空 间 任 意 点 的
(1)系统静电能的改变。 (2)电场对电源作的功。 (3)外力对极板作的功。
参考答案 一、 选择题 1.(D) 2.(A) 3.(B) 4.(B) 5.(C) 6.(D) 7.(B) 8.(B) 9.(B) 10.(C)
二、填空题
1. 垂直于导体表面 0
q
2.
4 o R
3. r 一样
3.半径为 R0 的导体球带有电荷 Q,球外有一层均匀介质同心球壳,其内、外
半径分别为 R1, R2 ,相对介电常数为 r ,如图 18。求:
(1)介质内、外的电场 E 和电位移矢量 D。
(2)介质内的电板化强度 P 和表面上的极化电荷面密度 。
4.一平行板电容器极板面积为 S,间距为 d,接在电源上并保持电压为 V,若 将极板的距离拉开一倍,试求:
A
U
(Q2
Q1 )
U
2
(C2
C1 )
0S 2d
U
2
9-1静电场中的导体、空腔导体

q
9-1、2 导体、空腔导体中的静电场 - 、 导体、
导体和电介质中的静电场
作业
书 书 9-7 9-9
下次课内容
§9-4 电介质及其极化 §9-6 介质高斯定理 §9-3 电容器的电容
练习 9-2 练习 9-4
(2)
A
B
(3) 将B板接地 板接地
σ4 = 0
qB = −qA
A、B重新感应
qA
qB
9-1、2 导体、空腔导体中的静电场 - 、 导体、
导体和电介质中的静电场
在一个不带电的金属球旁边放一点电荷q, 例3 在一个不带电的金属球旁边放一点电荷 ,求: (1)感应电荷在球心处的场强; )感应电荷在球心处的场强; R (2)球的电势; )球的电势; r (3)若将球接地,球上的感应电荷 ′。 )若将球接地,球上的感应电荷q o
q'
q
9-1、2 导体、空腔导体中的静电场 - 、 导体、
导体和电介质中的静电场
有一接地的金属球, 用一弹簧吊起, 有一接地的金属球 , 用一弹簧吊起 , 金属球原来不 带电。若在它的下方放置一电量为q的点电荷 的点电荷, 带电。若在它的下方放置一电量为 的点电荷,则 (A) 只有当 只有当q>0时,金属球才下移。 时 金属球才下移。 (B) 只有当 只有当q<0时,金属球才下移。 时 金属球才下移。 (C) 无论 是正是负金属球都下移。 无论q是正是负金属球都下移 是正是负金属球都下移。 (D) 无论 是正是负金属球都不动。 无论q是正是负金属球都不动 是正是负金属球都不动。
1 E1 = (σ1 −σ2 −σ3 −σ4 ) = 0 2ε0
E2 = 1 (σ1 +σ2 +σ3 −σ4 ) = 0 2ε0
《物理学基本教程》课后答案 第九章 静电场中的导体和电介质

第九章 静电场中的导体和电介质9-1 把一厚度为d 的无限大金属板置于电场强度为0E 的匀强电场中,0E 与板面垂直,试求金属板两表面的电荷面密度.分析 对于有导体存在的静电场问题,首先由静电平衡条件分析放入静电场后导体上电荷的重新分布情况,再计算空间电场和电势的分布.本题中,将金属板放入均匀电场后,由于静电感应,平板两面带上等值异号感应电荷.忽略边缘效应,两带电面可视为平行的无限大均匀带电平面.解 设平板两表面的感应电荷面密度分别为σ'和σ'-,如图9-1所示.由例题8-7结果知,带感应电荷的两表面视为带等量异号电荷的无限大平行平面,在导体中产生的场强为0εσ'='E ,方向与0E 相反,由场强叠加原理,平板中任一点的总场强为00εσ'-='-=E E E E 根据静电平衡条件,金属板中场强0=E ,代入上式得000='-εσE 则 00εσE =', 00εσE -='- 结果与板的厚度无关.9-2 一金属球壳的内外半径分别为R 1和R 2,在球壳内距球心为d 处有一电荷量为q 的点电荷,(1)试描述此时电荷分布情况及球心O 处电势;(2)将球壳接地后,以上问题的答案;(3)如原来球壳所带电荷量为Q ,(1)、(2)的答案如何改变.分析 当导体内达到静电平衡后,应用高斯定理可以确定导体上电荷重新分布的情况,然后用电势叠加原理求电势.解 (1)按照静电平衡条件,导体内部0=E ,在球壳内外表面间作同心高斯球面,应用高斯定理,可知球壳内表面上应有q -的感应电荷,为非均匀分布,如图9-2所示.根据电荷守恒定律和高斯定理,球壳外表面上有+q 的感应电荷,且均匀分布.点电荷q 在O 点产生的电势为dq V 0=πε41球壳内外表面上的感应电荷q -和+q 无论分布情况如何,到球心距离分别为R 1和R 2,电势叠加原理表达式为标量求和,所以在O 点产生的电势分别为124R q V 0-=πε 234R q V 0=πεO 点电势为 21321444R qR q d q V V V V 000+-=++=πεπεπε111(421R R d q +-=πε (2)将球壳接地后,外球面上的感应电荷消失,球面上电荷分布不变,得)11(4121R d qV V V -=+=0πε (3)如果原来球壳带电量为Q ,达静电平衡后外球面上电荷Q +q 均匀分布,内球面上电荷分布不变,得2213214)111(4R Q R R d q V V V V 00++-=++=πεπε 球壳接地后,结果与(2)相同.9-3 一无限长圆柱形导体半径为R a ,单位长度带有电荷量λ1,其外有一共轴的无限长导体圆筒,内外半径为分为R b 和R c ,单位长度带有电荷量λ2,求(1)圆筒内外表面上每单位长度的电荷量;(2)a R r <,b c R r R <<,c b R r R <<,c R r >四个区域的电场强度.分析 静电平衡条件下,在圆筒导体内场强为零,用高斯定理和电荷守恒定律可求出感应电荷的分布.解 (1)如图9-3所示,在圆筒形导体内作半径为r ,高为单位长的同轴圆柱形高斯面S ,设导体圆筒内外表面单位长的感应电荷分别为λ'-和λ',由静电平衡条件知导体内0=E , 故有⎰=⋅S E d 0)(1110='-=∑λλεεq即得半径为R b 的圆筒内表面单位长上的感应电荷为-λ1.由电荷守恒定律知,半径为R c 的圆筒外表面上单位长的感应电荷应为λ1,加上原有电荷量λ2,单位长上总带电量为12λλ+.(2)电荷重新分布的结果形成三个同轴的无限长带电圆柱面如图9-3,由于电荷分布具有轴对称性的,产生的电场也是轴对称的,用高斯定理可求出a R r <时,0=Eb a R r R <<时,rE 0=πελ21c b R r R <<时, 0=E c R r >时, rE 0212πελλ+=9-4 证明:两平行放置的无限大带电的平行平面金属板A 和B 相向的两面上电荷面密度大小相等,符号相反,相背的两面上电荷面密度大小相等,符号相同,如果两金属板的面积同为100cm 2,电荷量分别为C 1068A -⨯=Q 和C 1048B -⨯=Q ,略去边缘效应,求两个板的四个表面上的电荷面密度.分析 根据静电平衡条件,一切净电荷都分布在导体表面,本题中的电场空间可视为四个无限大均匀带电平行平面产生的电场的叠加,金属板A 、B 内任意点场强为零.由电荷守恒定律可以建立各表面的电荷面密度与两金属板的总电荷量之间的关系.解 设A 、B 两板的四个表面上的电荷面密度(先假定为正)分别为σ1、σ2、σ3和σ4,如图9-4所示.设向右为正向,由无限大均匀带电平面的场强公式和场强叠加原理,考虑到金属板A 、B 内任意点场强为零,得 金属板A 内0222243201=---000εσεσεσεσ 金属板B 内 0222243201=-++000εσεσεσεσ 解得32σσ-=, 41=σσ又由电荷守恒定律得 A Q S =+21)(σσ,B Q S =+)(43σσ 联立解得 26BA C/m 105-41⨯=+==SQ Q σσ 261A2C/m 101S-⨯=-=σσQ 263C/m 101-2⨯-=-=σσ9-5 三个平行金属板A 、B 和C ,面积都是200cm 2,A 、B 相距4.0mm ,A 、C 相距2.0mm ,B 、C 两板都接地,如图9-5所示,如果A 板带正电C 100.37-⨯,略去边缘效应,(1)求B 板和C 板上感应电荷各为多少?(2)以地为电势零点,求A 板的电势.分析 由静电平衡条件,A 、B 、C 板内各点的场强均为零,A 板上电荷分布在两个表面上,因B 、C 两板均接地,感应电荷应分布在内侧表面上.解 (1)设A 板1、2两面上带电量分别为q 1和q 2,B 、C 两板与A 相对的两内侧表面3、4 上的感应电荷分别为q 1’和q 2’,如图9-5所示.作侧面与平板垂直的高斯面1S ,两端面处E =0,忽略边缘效应,侧面无电场线穿过,由高斯定理0)(11d 110=+'==⋅0⎰∑S S q S S q q ∆∆εεS E 得11q q -=' 同理可得22q q -='.AB 板间和AC 板间为匀强电场,场强分别为S q E 0=ε11 Sq E 0=ε22又已知AC AB V V =,即2211d E d E =因 C 100.3721-⨯==+q q q 由以上各式,得B 、C 两板上的感应电荷分别为C 100.13711-⨯-=-=-='qq q C 100.227122-⨯-=-=-='q q q (2)取地电势为零,A 板电势即为A 、B 间电势差V 103.231111⨯====0Sd q d E V V AB A ε 9-6 半径为cm 0.11=R 的导体球所带电荷量为C 100.110-⨯=q ,球外有一个内外半径分别为cm 0.32=R 和cm 0.43=R 的同心导体球壳,壳上带有电荷量C 111110-⨯=Q ,求:(1)两球的电势;(2)用导线把两球连接起来时两球的电势;(3)外球接地时,两球电势各为多少?(以地为电势零点.)分析 根据静电平衡条件可以确定感应电荷的分布,用导线连接的导体电势相等,外球接地后电势为零.解 (1)根据静电平衡条件,导体球壳内表面感应电荷为-q ,外表面感应电荷为q ,原有电荷量Q .由电势叠加原理,导体球电势为321144R Q q R q R q V 000++-4=πεπεπεV 103.3)(412321⨯=++-=0R Qq R q R q πε导体球壳的电势为V 107.244442333302⨯=+=++-=000R qQ R q Q R q R q V πεπεπεπε(2)球壳和球用导线相连后成为等势体,电势等于半径为R 3带电量为Q +q 的均匀带电球面的电势,以无穷远为电势零点,得V 107.24232⨯=+=0R qQ V πε(3)外球接地后,只乘下内表面的电荷-q ,由电势叠加原理内球电势为V 6044211=-='00R q R q V πεπε外球壳接地与地等势,即02='V另外,求V 1’时还可以用内球产生的电场的线积分计算,即V 60)11(4d 4212221=-=='00⎰R R q r r q V R R πεπε 9-7 半径为R 的金属球离地面很远,并用细导线与地相连,在与球心的距离为R D 3=处有一点电荷q +,试求金属球上的感应电荷.分析 由于导体球接地,其表面上的感应正电荷通过导线与地球内负电荷中和,只剩下负感应电荷在金属球表面不均匀地分布,如图9-7所示.接地后,导体球上各点电势均为零,球心O点的电势应等于点电荷在该点电势与金属球表面感应负电荷在该点电势的代数和.解 设金属球上感应电荷为q ',在金属球表面不均匀地分布,但这些电荷到O 点距离相等,电势叠加后得R q V 0'=πε42点电荷q 在O 点的电势为 R q V 3410=πε043421='+=+=00Rq Rq V V V πεπε得感应电量为 3qq -='由此可以推证,当nR D =时, nqq -='9-8 如图9-8所示,三个“无限长”的同轴导体圆柱面A 、B 和C ,半径分别为A R 、B R 、C R ,圆柱面B 上带电荷,A 和C 都接地,求:B 的内表面单位长度电荷量1λ,外表面单位长度电荷量2λ之比值21/λλ.分析 本题与题9-5的解题思路相似.解 在导体B 内作单位长圆柱面形高斯面,可以说明A 面单位长度上感应电荷为1λ-.同理,可说明C 面单位长度上感应电荷为2λ-.由高斯定理可知场强分布为B A R r R <<时,rE 012=πελ1,方向沿径向由B 指向A . C B R r R <<时,rE 02=πελ22,方向沿径向由B 指向C . BA 间电势差BAV ⎰⋅=A B d 2R R r E ⎰00=-=AB A B 11ln 22R R R R r drπελπελBC 间电势差 BC 02BCln 2R R V πελ=B 为等势体,A 、C 接地,BC BA V V =,从而)/ln()/ln(A B B C 21R R R R =λλ9-9 半径分别为1R 和)(122R R R >的两个同心导体薄球壳,电荷量分别为1Q 和2Q ,今将内球壳用细导线与远处的半径为r 的导体球相联,导体球原来不带电,并假设导线上无电荷分布,试求相连后,导体球所带电荷量q .分析 带电的内球壳与导体球用导线相连后,一部分电荷通过导线转移到导体球表面上.两者相距甚远,可以认为两球壳与球的电场互不影响,已假设导线上无电荷分布,利用内球壳与远处导体球电势相等建立方程求解.解 因两球壳与球的电场互不影响,导体球电势为214r q V 0=πε假设导线上无电荷分布,则内球壳上电荷量变为q Q -1,由电势叠加原理,内球壳的电势为2211244R Q R q Q V 00+-=πεπε内球壳与远处导体球电势相等,即21V V =2211444R Q R q Q r q000+-=πεπεπε 解得)()(121221r R R Q R Q R r q ++=9-10 地球表面的电场强度为150N/C ,方向垂直指向地面,若把地球视为导体,试求地球表面的电荷面密度和地球带的总电荷量.分析 由于地球表面的电场强度方向垂直指向地面,可知地球带负电,将地球视为导体,在静电平衡状态下,电荷分布在表面上.解 设地球表面的电荷面密度为σ,表面附近的场强0εσ=E ,则 292120C/m 1033.1C/m )1085.8150(--⨯-=⨯⨯-==εσE地球半径m 1037.66⨯≈R ,地球带的总电荷量为kC 680C 108.6C 41033.14529-=⨯-=10⨯6.37⨯⨯⨯-==12-2ππσR q9-11 设有一孤立导体球,半径为R .,(1)试求其在真空中的电容表示式;(2)若把地球视为m 1037.66⨯=R 的导体球,它的电容量多大?(3)欲使地球的电势改变1V ,需使其所带电荷量改变多少?解 (1)将孤立导体球视为与无穷远处的同心导体球面组成的球形电容器,利用球形电容器电容表达式,(9-4)式给出孤立导体球的电容R VQC 0==πε4. (2)地球电容F 107F 1037.6446--12⨯=⨯⨯10⨯8.85⨯=πC(3)欲使地球电势改变1伏特,需使地球电量的改变为C 1071107ΔΔ44--⨯=⨯⨯==V C Q这个值很大,所以地球带电量的日常变化不会引起地球电势发生明显的改变,这就是通常可以选取地球作为电势零点的原因.9-12 已知空气的击穿电场强度为V/m 1036⨯,求处于空气中一个半径为1m 的导体球最多能带多少电荷及能达到的最高电势.分析 在带电导体球周围的空气形成一种绝缘介质包围着导体球,当导体球产生的电场足够强时,会使其周围的空气发生电离而成为导体,致使带电导体球放电,通常称为空气被击穿.因均匀带电导体球面的电场强度和电势与带电量成正比,为了不击穿周围的空气,带电导体球所带电量要受到限制.解 由题意击穿电场强度V /m 1036max ⨯=E而 2maxmax 4RQ E 0=πε C 103.3C 11085.841034421262max max --0⨯=⨯⨯⨯⨯⨯==ππεR E Q最高电势为 V 103446max 2max max max ⨯====00RE R R E C Q V πεπε或 V 103V 14103.3464max max ⨯=⨯10⨯8.85⨯⨯==12--0ππεR Q V9-13 收音机里的可变电容器如图9-13(a )所示,其中共有n 块金属片,相邻两片的距离均为d ,奇数片联在一起固定不动(叫定片),偶数片联在一起可一同转动(叫动片),每片的形状如图9-13(b )所示,求当动片转到使两组片重叠部分的角度为θ时,电容器的电容.分析 除了最外侧的两片外,每块金属片的两个表面分别与相邻的金属片表面构成一个电容器,如图9-13(c )所示,所以n 块金属片如此连接等效于(1-n )个平行板电容器并联.当两组片重叠部分的角度为θ时,每个电容器有效极板面积为)(θS ,因此电容器的等效电容是θ的函数.收音机调频的电容器就是根据这个原理设计的.解 当两组片重叠部分的角度为θ时,每个电容器有效极板面积为)(3602212-︒=r r S ππθ(n -1)个极板面积为S ,板间距为d 的平行板电容并联时的等效电容为dr r n d Sn C ⋅︒)-(-=-=0360)1()1(21220θπεε式中θ以度计.9-14 半径都为a 的两根平行长直导线相距为)(a d d >>.(1)设两导线每单位长度上分别带电λ+和λ-,求两导线的电势差;(2)求此导线组每单位长度的电容.分析 因a d >>,可设两导线的电场互不影响,由场强叠加原理可求出两导线间的场强分布,再用场强与电势的积分关系求两导线间电势差,由电容器电容的定义即可求出单位长导线组的等效电容.解 作两导线组合的截面图,以带正电导线轴心为原点建立坐标系如图9-14所示.不难看出,正负电荷在P 点的场强均沿r 轴正向,矢量叠加简化为标量和-11()(2rd r r d r E E E +2=-2+=+=000-+πελπελπελ 两导线间电势差为=-+V r E ad a d ⋅⎰-⎰-0-+=a d a r rd r d 11(2πελa ad -=0ln πελ 由电容器电容的定义,导线单位长电容为aad V C -==-+lnπελ9-15 有两个半径分别为1R 和2R 的导体球放在真空中,两球表面相距为d ,已知1R d >>和2R d >>,试求两导体构成的电容器的电容.分析 按题意 2R d >>,可认为当两导体球分别带电Q +和Q -时,彼此电场互不影响,即各球面上电荷分布仍是均匀的,由场强叠加原理可求出两球球心连线上任一点的场,用与上题相似的方法可以求出两球电势差和两球构成的电容器电容.解 以大球球心为原点,建立如图9-15所示的坐标系,在坐标为r 处的P 点(在连心线上),两球产生的电场均沿r 轴正向,得2212)(44r d R R Qr Q E E E -+++=+=00-+πεπε两带电导体球间电势差为-+V ⎰+⋅=dR R r E 11d ⎰+0-+++=dR R r r d R R r Q 112212d ])(11[4πε)1111(42121R d R d R R Q +-+-+=πε 考虑到1R d >>,2R d >>,可将电势近似表示为)211(421dR R Q V -+=-+πε 此两导体球构成的电容器电容为dR V Q C 21R 421-+1==0-+πε9-16 两只电容器F 81μ=C ,F 22μ=C ,分别把它们充电到1000V ,然后将它们反接,如图9-16所示,求此时两极间电势差.分析 并联电容极板间电压相同,因两电容器电容不等,则反接前两电容器带的电量必定不等.反接后,相连的极板上正负电荷中和,可以计算出中和后电荷量的代数和及并联电容器的等效电容C ,从而求出电势差.解 反接前,设1C 和2C 带电量分别为1Q 和2Q ,充电电压V 10000=U ,则011U C Q = 022U C Q =反接后,正负电荷中和,中和后总电量为21Q Q Q -=,并联等效电容 21C C C +=,则并联电容器两板间电势差为V 600V 1021081000)102108()(666621021=⨯+⨯⨯⨯-⨯=+-==----C C U C C C Q U 9-17 如图9-17所示,F 0.5,F 0.5,F 10321μμμ===C C C ,求:(1)AB 间的电容;(2)在AB 间加上100V 电压时,求每一个电容器上的电荷量和电压;(3)如果C 1被击穿,问C 3上的电荷量和电压各是多少?分析 并联电容器极板电势相等,串联电容器极板上电荷量相等,总电压等于各电容器上电压之和.当1C 上电压超过1C 的额定电压,1C 将被击穿,1C 支路即短路,全部电压就加在3C 上,如超过3C 的额定电压,3C 将被击穿,A 、B 间就发生短路.所以,在设计电容器组合电路时,除应计算等效电容外,还应考虑分配到每个电容器上的电压是否超过所选电容器的额定电压.解 (1)1C 和2C 并联电容为21C C C +=',再与3C 串联后,等效电容为F 75.333μ='+'=C C C C C (2)等效电容所带电量为CU Q =,串联的电容所带电量相等C 1075.343-⨯===CU Q QV 75333==C Q U V 25221121==='==C Q C Q C Q U U又因 Q Q Q =+21可解得 C 105.241-⨯=QC 1025.142-⨯=Q(3)如果C 1被击穿,AB 间电压就加在C 3上,即V 1003==U U则 C 1054333-⨯==U C Q9-18 平板电容器,两极间距离为1.5cm ,外加电压39kV ,若空气的击穿电场强度为30kV/cm ,问此时电容器是否会被击穿?现将一厚度为0.3cm 的玻璃插入电容器并与两板平行,若玻璃的相对电容率为7,击穿电场强度为100kV/cm ,问此时电容器是否会被击穿?结果与玻璃片的位置有无关系?分析 加玻璃片后,电场被分成两部分,应分别计算出空气和玻璃中的电场强度,再判断是否有哪种介质中的场强超过了其击穿场强.可以证明结果与玻璃板的位置无关.解 未加玻璃前平板电容器内场强为kV/cm 30kV/cm 26V/cm 5.139<===d U E 因其量值小于空气的击穿电场强度,电容器不会被击穿.加玻璃后,设电容器极板的电荷面密度为σ,平行板电容器中电位移σ=D .设玻璃和空气中场强分别为1E 和2E ,则有r 01εεσε==DE 002εσε==D E玻璃厚为d 1,则空气层厚为d - d 1,得U d d E d E =-+)(1211由以上各式得kV /cm 48.4)(r111=-+=εd d d UE30kV /cm kV /cm 4.31)(r11r2>=-+=εεd d d U E即空气部分首先被击穿,然后全部电压加在玻璃板上,致使玻璃中场强为kV /cm 100kV /cm 1303.03911>==='d U E 玻璃部分也会被击穿.9-19一平板电容器极板面积为S ,两板间距离为d ,其间充以相对电容率分别为r1ε、r2ε的两种均匀介质,每种介质各占一半体积,若忽略边缘效应,(1)与两种不同介质相对的两部分极板所带电荷面密度是否相等?如果不相等,求:21/σσ=?(2)试证此电容器的电容为⎪⎭⎫⎝⎛+=2210r r d S C εεε 分析 忽略边缘效应,电容器中的电场可视为无限大平行平面间的电场,从而可以确定两种不同介质中场强与极板电势差的关系,以及与两部分极板上的电荷面密度的关系,从而可知极板上的总电荷量.另一种思路是将充入两种介质后的电容器视为由两个电容器并联而成,直接应用并联电容器的计算公式.解1 (1)设电容器端电压为U ,两种介质中场强分别为E 1和E 2,由充满均匀介质的平行板电容器的场强与电压的关系可得dUE E ==21 (1)设1σ、2σ分别为两种不同介质对应部分极板上的电荷面密度,忽略边缘效应,电容器中的电场可视为无限大平行平面间的电场,则有r1011εεσ=E r2022εεσ=E (2) 代入(1)式可得 r2r121εεσσ=即两部分极板所带电荷面密度不相等.由(1)和(2)式可得极板上的总电荷量为)2()(2r2r1021εεεσσ+=+=d SU SQ 由电容器定义得 )2(210r r d S U Q C εεε+==解2 由并联电容器公式求总电容)2(22210201021r r r r d S d S d S C C C εεεεεεε+=+=+= 可见第二种方法计算简单,用第一种方法可对物理过程、电场电荷分布有更明确的概念.另外在第一种方法中亦可用介质中的高斯定理求解.9-20 一球形电容器,在外球壳的半径R 和内外导体间的电势差U 维持恒定的条件下,内球半径R '为多大时才能使内球表面附近的电场强度最小?并求这个最小电场强度的值.分析 导体表面附近的场强与电荷面密度成正比,而当极板间电势差恒定时,极板所带电荷量取决于电容C ,电容器的电容由电介质性质和几何因素决定,根据这些关系可以确定内球半径对内球表面附近电场强度的影响.解 球形电容器电容为R R R R C '-'=πε4 极板上带电量为RR UR R CU q '-'==πε4当外球壳的半径R 和极板间电势差U 恒定时,q 是内球半径R '的函数.内球表面附近的场强大小为)(42R R R RUR q E '-'='==πεεσ 即E 也是R '的函数.欲求场强E 的最小值,令0])(2[d d 22='-'-'='R R R RR RU R E 得 2RR =' 并有2R R ='时,0d d 22>'R E ,即2RR ='时,场强有极小值,且 RUE 4min =9-21 图9-21为水蒸气分子O H 2中氧氢原子核及核外电子云示意图.由于分子的正负电荷中心不重合,故其为有极分子,电矩m C 102.630⋅⨯=-p .(1)水分子有10个正电荷及10个负电荷,试求正负电荷中心之距d=?(2)如将水蒸气置于N/C 105.14⨯=E 的匀强电场中,求其可能受到的最大力矩?(3)欲使电矩与外场平行反向的水分子转到外场方向(转向极化),问电场力作功多少?这功的大小为室温(300K )水分子的平均平动动能kT 23的多少分之一?在室温下实现水分子的转向极化,外加电场强度应该多大?分析 由电矩qd p =及已知的水分子电量可计算正负电荷中心之距d .由电偶极子在外场中受的力矩M E p ⨯=,θsin pE M =,可知,当p 与E 正交时力矩最大.当电矩与外场平行反向)180(︒=θ时,电场力的力矩作功将使θ减小,最后0=θ,注意到在此过程中0d <θ.如果这个功与室温下水分子的平均平动动能kT 23相比较是微不足道的,那么要使水分子在常温下实现极化,外电场作的功至少要等于平均平动动能才能克服热运动的干扰,这就要求外电场足够强.本题的目的在于启发在实际问题中综合各种物理因素的分析方法和数量级分析的方法.解 (1)由题意,水分子正负电荷中心不重合,形成一个电偶极子,电量 e q 10=, ∴ 电矩大小d e qd p )10(==正负电荷中心之距m 109.3106.110102.610121930---⨯=⨯⨯⨯==e p d 题9-21图中,OH 键距为m 10958.010-⨯,d 为这个距离的4%.(2)由电场力作用于电偶极子的力矩M E p ⨯=,力矩大小为θsin PE M =,︒=90θ,M 达极大.m N 103.9105.1102.626430max ⋅⨯=⨯⨯⨯==--PE M(3)力矩作功为⎰=θd M W ,本题中,当转向极化进行时,力矩作正功但0,<θd∴⎰︒-⨯==-=18025109.12d sin J PE PE W θθ 而T =300K 时,水分子的平均平动动能J kT k 2123102.63001038.12323--⨯=⨯⨯⨯==ε32630=Wkε可见在这样大小的外电场中,水分子的转向极化将被分子的热运动干扰,要实现转向极化,使︒=180θ的水分子也转到外电场的方向上 ,电场力作的功至少要等于分子热运动的平均平动动能k ε,从而外场场强值至少要达到N/C 105102.62102.62283021⨯=⨯⨯⨯=='='--p p W E k ε 9-22 平板电容器两级板相距3.0 cm ,其间平行地放置一层0.2=r ε的介质,其位置和厚度如图9-22(a)所示,已知A 板带负电、B 板带正电,极板上电荷面密度为3100C/m 1085.8-⨯=σ,略去边缘效应,求:(1)极板间各区域的D 、E ;(2)极板间距A 极1cm 、2cm 、3cm 处的电势(设A 板电势为零);(3)绘出x D -、x E -、x U -曲线;(4)介质表面的极化电荷面密度.解 (1)作如图9-22(a)所示的高斯面1S 和2S ,由介质中的高斯定理可以证明各区域D 相等,得2100c/m 1085.8-⨯==σD介质外场强 V /m 1000==εDE(3)x D -,x E -,x V -曲线如图9.22(b)所示.(4)介质表面的极化电荷面密度为C/m 10425.4)11(10-⨯=-='σεσr9-23 平板电容器两极间充满某种介质,板间距mm 2=d ,电压600V ,如果断开电源后抽出介质,则电压升高到1800V ,求:(1)介质的相对电容率;(2)介质上的极化电荷面密度;(3)极化电荷产生的电场强度.分析 断开电源后抽出介质意味着极板上的自由电荷电量保持不变,电位移σ=D 也不变,但是电场强度改变,电压也会改变.在计算有均匀各向同性电介质的平行板电容器之间的电场时,电场强度可以表示为0000εσεσ'-='-=E E E ,即自由电荷的电场和极化电荷产生的附加电场的叠加,其中电介质对电场的影响以极化电荷面密度σ'的形式表现出来,反映了空间电场是自由电荷和极化电荷共同产生的;介质中的电场强度也可以直接表示为r00εεσ=E ,其中电介质对电场的影响以相对电容率r ε的形式表现出来,也反映了空间的电场是自由电荷和极化电荷共同产生的.这两种表现形式是等效的.解 (1) 由d U E 00=,dUE =,得相对电容率为 3600180000r ====U U E E ε (2)在平行板电容器两极板间充满均匀电介质时,忽略边缘效应,得C/m 1031.5 )11( )11(600rr-⨯=-=-='εεσεσE(3)极化电荷的分布形成等量异号带电板,忽略边缘效应,得V /m 10650⨯='='εσE9-24 盖革计数器可用来测量电离辐射,它的正极是半径为1R 的金属丝,负极是半径为2R 的同轴圆柱面,当管内充以低压惰性气体,并使两极间建立起强电场,若有辐射粒子进入器壁时将使气体电离,在电子向正极运动的过程中,又会与其他气体原子产生碰撞电离,这样将有更多的电子到达正极并产生一个信号,记录下该辐射,假设m 104.1,m 10252261--⨯=⨯=R R ,管长m 10162-⨯=L ,两级间电势差V 6000=U ,低压惰性气体的相对电容率1r ≈ε,试计算此时阳极上的电荷量和电荷数.分析 由于12,R L R L >>>>,忽略边缘效应,可以把盖革计数器视为带等量异号电荷的无限长同轴圆柱面电容器.解 两级间场强为rE 02πελ=,方向沿径向指向阴极.电势差为 ⎰==211200ln 2d 2R R R R r r U πελπελ 则 120ln R R Uπελ2=阳极上电荷量为)1025/104.1ln(101660002ln 2622120----12⨯⨯⨯⨯⨯10⨯8.85⨯===ππελR R UL L q C 9104.8-⨯= 相应的电荷数为 101991025.5106.1104.8⨯=⨯⨯==--e q N9-25 圆柱形电容器是由半径为1R 的导体圆柱和与它同轴的导体圆筒构成的,圆筒的半径为2R ,电容器的长为L ,其间充满相对电容率为r ε的介质,设沿轴线单位长度上圆柱带电荷量为λ+,圆筒单位长带电荷量为λ-,忽略边缘效应,求:(1)介质中的电位移和电场强度;(2)介质表面的极化电荷面密度;(3)两极之间的电势差U ,从而求电容器电容.分析 已知电荷分布,由介质中的高斯定理可知介质中的D 和E ,由场强叠加原理可求出极化电荷的面密度.解 (1)由于电场具有轴对称性,以半径为r 作高为L 的同轴高斯面,介质中的高斯定理得L D rL λπ=⋅2rD πλ2=rr DE r 2επελπελε0=2==(1) (2)设介质内外表面单位长上的极化电荷分别为λ'和λ'-,在介质内,其内表面极化电荷产生的附加电场的场强为rE 02πελ'-=' 根据场强叠加原理,在介质内电场是导体圆柱表面的自由电荷产生的电场和介质内表面极化电荷产生的附加电场的叠加,即rr E E E 00022πελπελ'-='-= (2) 由(1)和(2)式解得)11(rελλ-='介质内外表面单位长的面积分别为22R π,12R π,则极化电荷面密度分别为)1(22r 11επλπλσ1--='-='-R R )1(22r22επλπλσ1-='='R R (3)电容器两极板电势差为=U ⎰⋅21d R R r E ⎰2==2112r 0r 0ln 2d R R R R r r επελεπελ电容为 12r 012r 0ln 2ln 2R R LR R LUQC επεεπελλ===9-26 在半径为R 的金属球外有一层外半径为R '的均匀介质层,设电介质的相对电容率为r ε,金属球带电量为Q ,求:(1)介质层内外的电场强度;(2)介质层内外的电势;(3)金属球的电势.分析 本题为球对称场,已知电荷分布由介质中的高斯定理可求出D 、E 分布.以无穷远电势为零由场强与电势的积分关系或电势叠加原理可求电势分布.解 (1)如图9-26,作半径为r 的球面为高斯面,由有介质的高斯定理得Q D r =24π24r QD π=在介质内,R r R '<< 2r 0r014r Q DE επεεε==在介质外,R r '> 224rQDE 00==πεε(2)介质内任一点的电势为⎰⎰'∞'+=R rR r E r E V d d 211⎥⎦⎤⎢⎣⎡'+'-=0R R r Q 1)11(14r επε (1) 介质外任一点电势为⎰∞==rrQ dr E V 0224πε(3)金属球的电势可由(1)式中令R r =得到,即⎥⎦⎤⎢⎣⎡'+⎪⎭⎫ ⎝⎛'-=R R R Q V 11114r 00επε 9-27 球形电容器由半径为1R 的导体球和与它同心的导体球壳组成,球壳内半径为3R ,其间有两层均匀电介质,分界面半径为2R ,相对电容率分别为1r ε和r2ε,如图9-27所示,求:(1)当内球所带电荷量为Q +时,电场强度的分布;(2)各介质表面上的束缚电荷面密度;(3)电容器电容.分析 本题电场为球对称的,已知电荷分布,可由介质中的高斯定理先求D ,再求E 的分布.束缚电荷分布在内外两层介质的四个表面上,因为各表面的曲率。
静电场中的导体与电介质-课件

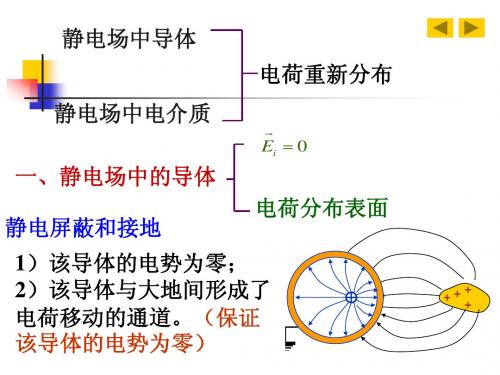
【现象】
☻导体表面出现等量异号的
感应电荷。
☻周围电场分布重新调整使
E
得导体内部 E E E0 0 ,
感应电荷不再增加!静电平衡! E为感应电荷产生的附加电场。
( 金属球 )
( E E E0 )
Chapter 9 静电作者场:中杨茂的田导体与电介质
导体上的感应电荷代数和=0 静电平衡:导体上的感应电
0 Q1
E(r) 40r 2 0
(r R1 ) (R1 r R2 ) (R2 r R3 )
Q1 (Q1 ) Q1 Q2
40r 2
(r R3 )
R3
Q1 Q2
R2
B
A R1 Q1
Q1
验证:导体表面电场强度
E表
0
Chapter 9 静电作者场:中杨茂的田导体与电介质
利用叠加原理同样可求出电势分布:
q
q
q
q
q
q
q
q
q
q
Chapter 9 静电作者场:中杨茂的田导体与电介质
插播录像:
《静电平衡》
Chapter 9 静电作者场:中杨茂的田导体与电介质
三、导体表面的电场强度
E dS
S
E表 dS cos 0o
0dS
上底
下底
E表 dS cos 90o
导体
侧面
E表 S
E
S
表面。
在导体内作任一封闭曲面 S 作
为高斯面 :
E dS
S
1
0
qi
( S内)
SE dS S0 dS 0
qi 0 ( S内)
E 0
E
普通物理学第五版第9章导体和电介质中的静电场章答案
解: (1)由于静电感应,外球内表面电量为 -q,外表面电量为+q q 外球的电势为: U2 = 4pe0 r2 (2)外球内表面电量仍为-q,外表面电量为零 外球的电势为: ´ U2 = 0
(3)设内球电量为q1,内球电势为零 q1 q r1 U1 = q1 = r q 4pe0 r1 + 4pe0 r2 =0 2 q1 q U外 = 4pe0 r2
q1 q2 U1 = 4pe0 R1 + R2 q2 q1 = R1 4pe0 U1 R2
1
2700 -2 = 5.0×10 9.0×109 = 1.0×10-8(C) 8.0×10-9 8.0×10-2
结束 目录
两球接触后,内球电荷q1全部移至外球 壳,两球为等势体。
q1 + q2 U= = 2.03×103(V) 4pe0R2 ΔU内 = 2.7×103 2.03×103 = 6.7×102(V)
d +q
结束 目录
9-6 半径为r1 、 r2 (r1 < r2 )的两个同心导 体球壳互相绝缘,现把+q 的电荷量给予内 球,求: (1)外球的电荷量及电势; (2)把外球接地后再重新绝缘,外球的 电荷量及电势; (3)然后把内球接地,内球的电荷量及 外球的电势的改变(设内球离地球很远)。
结束 目录
结束 目录
9-11 三平行金属板A、B 、C面积均为 200cm2,A、B 间相距4.0mm, A、C 间 相距2.0mm,B 和C 两板都接地。如果使A 板带正电3.0×10-7C ,求: (1)B 、C 板上感应电荷; (2)A 板的电势。 2mm 4mm C A B
目录
解:设A板带电为q =q1+q2,B、C两板的感 应电荷分别为- q1及- q2 。 EAB dAB = EAC dAC UA UB = UA UC q2 q1 EAC = EAB = e0S 2mm 4mm e0 S q1 EAB dAC 1 C A B = E =d = 2 q2 AC AB q1 q2 q1= 1.0×10-7(C) -q1 -q2 q2= 2.0×10-7(C) qB= -q1= -1.0×10-7(C) qC= -q2= -2.0×10-7(C)
第九章静电场中的导体和介质部分习题分析与解答
Q d d 1 2 U BA 0S d d 1 2 Q d d2 1 U AC 0S d 1 d 2
9-6 在真空中,将半径为R的金属球接地,与球心 O相距为r(r>R)处放置一点电荷q,不计接地导线上 电荷的影响。求金属球表面上的感应电荷总量。 解:金属球为等势体,金属 q’ 球上任一点的电势V等于点电 R q 荷q和金属球表面感应电荷q’ O 在球心处激发的电势之和。 r 而金属球接地,总电势为零。 所以球心处的电势为
解: (1)由于静电平衡时电荷只分布于导体的表面上, 故:球A在外表面带电QA=3.0 10-8 C,球壳B内表面 带电-QA= -3.0 10-8 C,球壳B外表面带电QA + QB = 5.0 10-8 C。 由电势的叠加,知球A和球壳B的电势分别为: Q Q Q 3 A A Q A B V 5 . 6 10 V A 4 R R R 0 1 4 0 2 4 0 3
QA qA VB 40R 3
R R Q 8 1 2 A 解得: q 2 . 12 10 C A R R R R R R 1 2 2 3 1 3
Q q 2 A A 得: V 7 . 92 10 V B 4 R 0 3
即,球A的外表面、球壳B的内、外表面所带的电荷 分别为:2.1210-8 C、 -2.1210-8 C、 -0.910-8 C.
( 1 ) Q r P ( 1 ) E ; n r 0 n 2 4 ( R d ) r ( 1 ) Q 8 2 r P 1 . 6 10 C m ; n 2 4 ( R d ) r
在介质内表面:
( 1 ) Q r P ( 1 ) E ; n r 0 n 2 4 rR ( 1 ) Q 8 2 r P 6 . 4 10 C m ; n 2 4 R r
第9章-静电场中的导体和电介质
E 加上外电场后 外 E外
把金属导体置于外电场 中,自由电子将产生宏 观定向运动,导体中电 荷按照外电场特性和导 体形状形成特定的分布
在外电场作用下,引起 导体中电荷重新分布而呈 现出的带电现象,称为
静电感应现象 Electrostatic Induction
问:这种静电感应的过程是否会一直进行下去?
辨析
0 一块无限大均匀带电导体薄板,电荷面密度为 0
问:在它附近一点的场强=?
解:由无限大带电均匀平面两侧的场强公式,得
二、导体处于静电平衡状态时的场强分布
导体外部近表面处场强 E
方向:与该处导体表面垂直
E
0
n
大小:与该处导体表面电荷面密度 成正比。 E(nˆ )
0
S
ES
S 0
ΔS
P
E
0
E内=0
讨论:导体表面附近的场强公式
E
0
指导体表面附近场点近旁的导体电荷面密度
一、静电感应 导体的静电平衡条件
无外电场时
无外电场时,导体中 自由电子在金属内作无 规则热运动,而没有宏 观定向运动,整个导体 呈现电中性
无外电场时
导体的静电感应过程
E 外
加上外电场后
导体的静电感应过程
E 外
+
加上外电场后
导体的静电感应过程
E 外
+
+
加上外电场后
导体的静电感应过程
E 外
+ +
E 外
+ + + + +
9-1电介质导体电容
大小反映了导体本身的电性质。
每升高单位电势所需要的电量。称为孤立导体的电容。 用C来表示。
Q C U
单位: 法拉
F
1F=106μF=1012pF
9.3.2、电容器
1、电容器
+Q -Q 导体B
导体 A
接地 +Q A +Q -Q B 说明:导体A、B组合在一 起, 具有储存电荷的能力; 储存电场的能力; 储存能量的能力; (1)电容器:导体A 、B组合在一起就构成电容器。
E 0, q 0
+Q
结论: 静电平衡下,导体所带电荷只能分布在导体表面上。 导体内无净余电荷。
2 空腔导体,带有+Q的电量
a、腔内无电荷
+ + + + + + + + + s + + + + +Q
1 S E dS q ,E 0 , q 0
导体内,任取高斯面S。
0
总是小于 0 , 合场强 E 的方向与E 的方向相同。
- - - - - -
E0 0 E r 0 r
q q0 (1 1
r
)
根据高斯定理:
取高斯面
S
1 s E dS 0 ( q0 q)
q0 1 1 s E dS 0 ( q0 q0 r ) 0 r
+ P +
+ +
U
r
E dl
R
r
Edr Edr
R
qdr 40 r r
2
R
q 40 r R
可见: U q
§9-3 电容和电容器
9.3.1 孤立导体的电容 孤立导体带电为+Q
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第第九九章章导导体体和和电电介介质质中中的的静静电电场场引言:一、导体、电介质、半导体导体:导电性能很好的材料;例如:各种金属、电解质溶液。
电介质(绝缘体):导电性能很差的材料;例如:云母、胶木等。
半导体:导电性能介于导体和绝缘体之间的材料;二、本章内容简介三、本章重点和难点1. 重点(1)导体的静电平衡性质;(2)空腔导体及静电屏蔽;(3)电容、电容器;2. 难点导体静电平衡下电场强度矢量、电势和电荷分布的计算;第一节静电场中的导体一、静电感应静电平衡1. 静电感应(1)金属导体的电结构从微观角度来看,金属导体是由带正电的晶格点阵和自由电子构成,晶格不动,相当于骨架,而自由电子可自由运动,充满整个导体,是公有化的。
例如:金属铜中的自由电子密度为:nCu=8⨯1028(m-3)。
当没有外电场时,导体中的正负电荷等量均匀分布,宏观上呈电中性。
(2)静电感应当导体处于外电场E0中时,电子受力后作定向运动,引起导体中电荷的重新分布。
结果在导体一侧因电子的堆积而出现负电荷,在另一侧因相对缺少负电荷而出现正电荷。
这就是静电感应现象,出现的电荷叫感应电荷。
2. 静电平衡不管导体原来是否带电和有无外电场的作用,导体内部和表面都没有电荷的宏观定向运动的状态称为导体的静电平衡状态。
(a)自由电子定向运动(b)静电平衡状态3. 静电平衡条件(静电平衡态下导体的电性质)(1)导体内部任何一点处的电场强度为零;导体表面处电场强度的方向,都与导体表面垂直。
(2)在静电平衡时,导体内上的电势处处相等,导体是一个等势体。
E证明:假设导体表面电场强度有切向分量,即τ≠0,则自由电子将沿导体表面有宏观定向运动,导体未达到静电平衡状态,和命题条件矛盾。
dUdU =0,=0E内=0,Eτ=0dldτ因为,所以,即导体为等势体,导体表面为等势面。
二、静电平衡时导体上电荷的分布1. 实心导体(1)处于静电平衡态的实心导体,其内部各处净电荷为零,电荷只能分布于导体外表面。
证明:在导体内包围P点作闭合曲面S,由静电平衡条件 E内=0,所以由高斯定理:内,得。
(2)处于静电平衡的导体,其表面上各点的电荷面密度与表面邻近处场强大小成正比。
证明:在导体表面任取无限小面积元ΔS,认为它是电荷分布均匀的带电平面,电荷面密度为σ,作高斯面(如图:扁平圆柱面),轴线与表面垂直,Δl很小,由高斯定理: S q内 E内⋅dS==0ε0∑q=0 E⋅dS=⎰E⋅dS+⎰S上底下底 E 内⋅dS+⎰E表⋅dS侧=E表∆S+0⋅∆S+E表∆S侧cos=E表∆S=π2σ∆Sε00表,即由此得注意和结论:★ σ∝E表;σ=εE σ E表=nε0 (9-1)★ n为导体表面的外法线方向单位矢量; E ★表由导体上及导体外全部电荷所产生的合场强,而非仅由导体表面该点处的电荷面密度所产生。
例如:孤立的半径为R的均匀带电球面,球面外邻近处P点的场强大小为EP=q4πε0R2=σε0由整个球面上电荷共同产生。
带电球附近有点电荷q1时,同一P点处的场强由球面上原有电荷q和点电荷q1,以及其在球面上的感应电荷所共同产生即,仍σ' '=nEPε0。
然满足(3)静电平衡下的孤立导体,其表面某处面电荷密度σ与该表面曲率有关,曲率越大的地方,电荷密度σ也越大,σ∝R。
(4)尖端放电对于有尖端的带电导体,尖端处电荷面密度大,则导体表面邻近处场强也特别大。
当场强超过空气的击穿场强时,就会产生空气被电离的放电现象,称为尖端放电。
例9-1(书P89)。
'=Eq+Eq1+E感应电荷EP第二节空腔导体内外的静电场一、空腔导体内外的静电场1、空腔导体内部无带电体无论空腔导体是否带电、是否处于外电场中,空腔导体都具有下列性质:(1)空腔内部及导体内部电场强度处处为零,它们形成等电势区。
(2)空腔内表面不带任何电荷。
上述性质可用高斯定律证明。
下面说明性质②。
在导体内做一高斯面,根据静电平衡,导体内部场强处处为零,所以导体内表面电荷的代数和为零。
如内表面某处面电荷密度σ>0 ,则必有另一处σ<0,两者之间就必有电力线相连,就有电势差存在,这与导体内场强为零相矛盾。
所以导体内表面处处 e=0。
这些结论不受腔外电场的影响,腔外电场与腔外表面电荷在腔内场强总贡献为零。
2、腔内有带电体(1)导体中场强为零。
(2)空腔内部的电场决定于腔内带电体,空腔外的电场决定于空腔外表面的电荷分布。
(3)空腔的内表面所带电荷与腔内带电体所带电荷等量异号。
(4)导体接地,则空腔内带电体的电荷变化将不再影响导体外的电场。
证明:(弄清感应电荷的数量。
)二、静电屏蔽electrostatic shielding如图,在空腔导体外,还有一带负电的带电体B,由于静电感应,空腔导体外表面上的电荷及带电体 B 上的电荷将重新分布。
静电平衡时:(1)B使外表面上电荷重新分布;(2)内表面、腔内带电体的电荷分布不变;(3)导体空腔部分的电场等于零;(4)导体接地,腔内电场不影响腔外,腔内各点相对地的电势不再变化。
总之,空腔导体(无论接地与否)将使腔内空间不受外电场的影响,而接地空腔导体将使外部空间不受空腔内的电场的影响,称之为静电屏蔽现象。
例子:屏蔽服、屏蔽线、金属网。
(课 3本P93-P94)。
例题9-2:课本P94。
例题2:一半径为r1,r2(r2〉r1)互相绝缘的两个同心导体球壳,现将 +q 电量给予内球壳,求:(1)外球壳上所带的电荷和外球的电势。
(2)把外球壳接地后再重新绝缘,求外球上所带的电荷及外球的电势。
(3)然后把内球接地,问内球上所带电荷及外球电势改变多少?解:(1)+q 分布在内球壳外表面,静电感应后,外球壳内表面带电-q,外表面带电+q,整个由静电平衡条件得:球壳导体内部场强为零,即: E=0(0<r<r1) qQ 外球壳=0(r1<r<r2) 外球壳总电荷为零,。
由高斯定理得:E=24πε0rqE=(r2<r)24πε0r E内部=0。
所以有:或由电势叠加原理得: U外球=⎰q∞r2 ∞E⋅dl=⎰r2q4πε0r2=dr=q4πε0r2 U外求=4πε0r2-q4πε0r2+q4πε0r2q4πε0r2Q=0Q外球内表=-qQ球U=0,壳=-q。
(2)外球壳接地后再绝缘,则:外球同时外球外表,,即外(3)内球壳接地后,得U内球=0。
此时设内球带正电荷为 e,外球内表面带电荷为-q,则-qr=0e=1q(〉0)4πε0r14πε0r2r2,所以得不为零。
e-qe-q'=U外球+=(≠0)4πεr4πεr4πεr020202因而有: U内球=+e'-U外球=∆U外球=U外球则有:e-qe-q-0=4πε0r24πε0r2。
第三节电容器的电容静电平衡时导体上的电荷只能分布在表面,且与其本身的形状、结构及周围的介质有关。
下面我们讨论的是导体容电本领问题。
一、孤立导体的电容1. 定义设在真空中有一半径为R,带电荷为Q的孤立球形导体,则它的电势(相对于无限远处的零电Q1QV==4πε0R4πεR0势而言)为:而V该比值仅与导体的几何形状和大小有关,与导体所带的电量无关。
由此我们定义孤立导体的电QC=V 容为孤立导体所带的电荷Q与其电势V的比值。
即:电容 C 是反映导体容电能力的物理量。
用单位电势差所能容纳的电量来表征。
2. 单位法拉(F),微法(mF),皮法(pF)1F=106μF=1012pF二、电容器1. 例子和概念两个同心球壳,内球 A 和外球B 分别带 +q 和 -q 电量,中间充以空气或电介质。
当外壳接地后,这样的导体组——非常靠近的中间充满电介质的两个导体组合,称为电容器。
两个导体称为电容器的极板。
2. 电容器的电容C=定义:电容器的电容的电势差。
(1)电容器电容的大小取决于极板的形状、大小、相对位置以及电介质的电容率。
与电容器是否带电无关。
(2)电容器符号:,固定电容器;,可变电容器。
QVA-VB, Q为一个极板所带电量的绝对值,VA-VB为两极板间3. 电容的计算(1)假设电容器的两个极板A、B分别带 +q 和-q 电荷。
B UAB=⎰E⋅dlA (2)求两极板间的电场分布,并由计算两极板间电势差。
C=(3)由定义式qUAB计算电容C。
4. 例子:几种常见的电容器电容的计算(1)平板电容器设有两靠得很近,相距为 d,面积为 S 的平行金属板组成的平行板电容器,板间为真空。
每块极板上的电荷面密度为电场,忽略边缘效应,两极板间的场强为:σ=QS,两极板间的电场为均匀E=两极板间的电势差为σQ=ε0ε0SσQdU=⎰ABE⋅dl=Ed=d=ε0ε0S根据电容的定义得平板电容器的电容为(2)圆柱形电容器设内、外圆柱面各带有+Q和-Q的电荷,则电荷线密度为λ= E面之间距圆柱的轴线为r处的电场强度大小为 Ql。
在两个圆柱E=由电容的定义式可得圆柱形电容器的电容为 E的方向垂直于圆柱轴线。
于是,两圆柱面间的电势差为 RQdrRBQU=⎰lE⋅dr=⎰R=ln2πε0lr2πε0lRA BAλQ1=2πε0r2πε0lrd«RA时,有RR+ddlnB=lnA≈RARARA 于是圆柱形电容器的电容可写成:这正是平板电容器的电容。
可见,当两圆柱面之间的间隙远小于圆柱体半径时,圆柱形电容器可当作平板电容器。
(3)球形电容器:课本P100两半径分别为R1和R2 的同心金属球壳组成球形电容器,两球壳间为真空,求电容。
解:设内外球面分别带 +q 和-q 电量,由高斯定理得两极板间场强方向沿径向,大小为:q(R1〈r〈R2)E=4πε0r2。
两极板间电势差为:2C≈2πε0lRAε0S=dd(圆柱体的侧面积S=2πRAl)U12=⎰由定义得:C0=1R2E⋅dl=⎰R1q4πε0r=2q⎛11⎫-⎪⎪4πε0 ⎝R1R2⎭4πε0R1R2q=U12R2-R14πε0R12ε0SC0≈=dd,和平板电容器一样。
(1)当R2-R1=d<<R1时,(2)当R2→∞时C0=4πε0R1,孤立球形电容器。
三、电容器的并联和串联1. 电容器的并联qq=∑qi,V=Vi=i,C=∑CiCiii 并联电路总电容量增大,电容组耐压值不变。
2. 电容器的串联q=q1=q2=qi,V=∑Vi,i11=∑ CiCi串联电路总电容量减少,电容组耐压值增大。
但如其中一个被击穿,其余电容器会相继被击穿。
例9-3(P105)作业:P148第2题 P149第7题第四节电介质及其极化重点:电介质的极化和极化强度矢量;电位移矢量;有介质时的高斯定理;有介质时电场强度的计算。
难点:电位移矢量电介质:指电阻率很大,导电性能很差的物质。
