强风下高铁连续梁桥最大双悬臂状态抖振时域分析
山区大跨窄悬索桥抖振响应时域有限元分析

摘 要:为了掌握山区窄悬索桥的抗风性能袁以某山区大跨度加 劲 梁窄 悬 索 桥 为研 究 对 象袁 采 用 谐波 合 成 与 F F T 转换 技
术相结合的方法袁构建模拟了山区窄悬索桥三维脉动风场袁并基于 A N SY S 大型有限元分析软件的 A PD L 语言袁建立山区
大跨度窄悬索桥风振响应有限元模型袁分析大跨度窄悬索桥结构抖振响应特性遥 结果表明院窄悬索桥的抖振位移响应时
中图分类号:U 4 4 8 . 2 7
文 献 标 志 码 :B
文章编号:1 009- 7 7 1 6渊 2 01 9冤 1 0- 0061 - 05
0引言
山区大跨度窄悬索桥是一种柔性的高次超静 定结构袁具有跨越能力大尧内力分布均匀尧外形轻 盈美观等优点袁逐渐受到桥梁界的高度关注遥 但该 类桥梁的加劲梁宽度一般设置为 2 ~5 m 袁随着跨 径的增大袁整体结构高跨比和宽跨比急剧降低袁使 得窄悬索桥竖向与横向刚度削弱袁 导致桥梁整体 结构的动力稳定性变差[1 ]遥 在风雨尧车辆和环境激 励下极容易产生较大振幅袁 降低了行人车辆的舒 适度和结构安全性袁 因此开展窄悬索桥结构的风 振响应研究具有重要意义遥
1.1 脉动三维风场理论分析 脉动风能量在频域范围中的分布情况通常采
用脉动风功率谱函数来表达袁 脉动风功率谱函数 反映了脉动风中不同频率成分对湍流脉动总动能 的影响袁根据脉动风风向进行分类袁可以划分为顺 风向脉动风速谱和竖向脉动风速谱遥 我国叶 公路桥 梁抗风设计规范曳渊 JT G _ T F 50要2 01 1 冤 中顺风向脉
收稿日期:2 01 9- 06- 1 0 基金项目:湖北省自然科学基金项目渊 2 01 4 C F B 331 冤 作者简介:周戈渊 1 97 3 要冤 袁男袁大学本科袁工程师袁从事市政公用 基础设施建设和预制混凝土构件生产研究工作遥
某高墩大跨连续刚构桥抖振时域分析

以合 成 . 作者 使 用 P 0D( 特征 正 交分解 ) 型谱 表 示
法L 来对 脉 动风 速过 程 进 行 Mo t— al 拟 , 2 n eC r o模
工 阶 段 的有 限 元 模 型 ( 2 3 . 图 , ) 变截 面箱 梁 和变
截 面 墩 采 用 了 2节 点 空 间 梁 单 元 B AM1 8模 E 8 拟; 主梁 和 墩 采 用 的材 料 均 为 C5 0混 凝 土 , 性 弹
拟 可得 到 响应 时程 结 果 和 统计 值 , 能计 人 多振 型 耦 合效 应且 便 于考 虑 各 种 非线 性 因素 的影 响 , 已 成 为抖 振 计算 的发 展 方 向l. 用 A YS软 件 1使 ] NS 对 某高墩 大跨 连续 刚构桥 的成 桥 阶段 和最不 利施 工 双悬臂 阶段 ( 以下 简称 施工 阶段 ) 进行 了时域抖
3 脉动 风 速场 的 模 拟
铰支 承 , 约束 竖 向平 动 自由度 ; 仅 所有 墩底 均处 理
平 稳 的、 态 的及 各 态 历 经 的零 均值 随机 向量 过 正
为 固结. 型 2为施工 阶段模 型 , 模 即在 主梁 模 型 中
截取的 5 #墩施 工 最 大 双悬 臂 的 部分 , 不 再 含 且
维普资讯
第 2 卷第 1 3 期
20 0 6年 3月
华 中 科
技
大
学
学 报 ( 市科 学版 ) 城
Vo1 3 N o.1 .2 M ar 20 . 06
J f[US .o J T. ( b n S in eEdto Ur a ce c i n) i
斜拉桥风致抖振时域分析

斜拉桥风致抖振时域分析摘要:随着交通事业的快速发展,在我国中西部地区需要建设大量的斜拉桥等大跨度柔性桥梁用于跨越沟谷。
该地区是我国风灾发生较高的区域之一,风环境复杂多变,除了对斜拉桥进行静风稳定的验算,同时也有必要研究脉动风对斜拉桥影响。
本文将通过时域方法分析斜拉桥的抖振。
关键词:斜拉桥脉动风抖振时域分析中图分类号:u4 文献标识码:a 文章编号:1007-0745(2013)05-0178-021.引言我国的中西部山区面积广大,地形复杂,具有山高谷深,风环境复杂等特点,这就需要建设大跨径桥梁以跨越山谷、河流等。
其中斜拉桥是跨越能力比较强的柔性桥型之一。
旧塔科马桥的风毁事故引起人们对桥梁风致振动的关注,其中风对斜拉桥等大跨度桥梁的影响不容忽视。
频域分析、全桥模型风洞试验方法和时域分析方法是现在分析桥梁抖振的主要方法,其中桥梁有限元模型时域分析是比较常用的方法。
2.时域方法的主要步骤桥梁结构抖振时域分析主要包括三个方面:一是空间脉动风场的有效模拟;二是时域风荷载模型的处理;三是非线性时程分析。
2.1.脉动风的模拟1)主梁模型的选择。
在大跨径桥梁全桥的结构分析中,常采用平面和空间杆系结构,塔和墩简化为通过其中心线的两节点两单元,而斜拉索等杆系简化为两节点杆单元。
在三维空间分析中,由于主梁作为横向尺寸较大的实体结构,其纵向还有斜拉索、纵梁等不同构件连接。
都使得不能只用一个空间梁单元进行描述。
大跨径桥梁主梁主要有三种不同的计算模型:三梁式、双梁式以及鱼骨式。
2)风场模拟方法的选择。
抖振响应时域分析,首先依据目标功率谱函数数值模拟空间脉动风场。
对于平稳随机过程,比较常用的方法有谐波合成法与线性滤波法。
谐波合成法计算量较大,但是精度较高,一般常采用这种方法。
2.2.抖振风荷载2.3.非线性时程分析结构几何非线性处理方法。
现代大跨径桥梁的柔性特征十分明显,特别是悬索桥和斜拉桥,对其进行动力分析时必须要考虑几何非线性,才能得到精确的计算结果。
桥梁抗风设计、风洞试验及抗风措施

桥梁抗风设计、风洞试验及抗风措施?46?北方交通201l桥梁抗风设计,风洞试验及抗风措施刘长宏,刘春,宋俊杰(中国华西工程设计建设有限公司大连分公司,大连116000)摘要:桥梁应具有抵抗风作用的能力,特别是大跨度桥梁,其柔性较大,设计时必须考虑颤振,抖振,涡激振动等空气动力问题,通过抗风设计,风洞试验,抗风措施来确定桥梁风荷载和抗风性能是大跨度柔性桥梁抗风研究的主要手段.关键词:桥梁;风荷载;颤振;节段模型;风洞试验中图分类号:U442.59文献标识码:B文章编号:1673—6052(2011)10—0046—021桥梁抗风设计的目的桥梁抗风设计的目的在于保证结构在施工和运营阶段能够:(1)对于可能出现的最大静风荷载,桥梁不会发生强度破坏,变形和静力失稳.(2)为了确保桥梁的抗风安全性,桥梁发生自激发散振动(如颤振)的临界风速必须高于桥梁的设计风速,并具备一定的安全储备,即:临界风速>安全系数X设计风速.对于颤振验算,通常安全系数取为1.2.(3)对于限幅振动,尽管其振幅有限,但因其发生的频率高,可能会引起结构的疲劳损伤或影响结构正常使用,使行人感到不适以及影响施工的Jl~,N进行等,所以也应将桥梁可能发生的限幅振动的振幅减小到可以接受的程度,即:最大响应≤容许值. 2桥梁抗风设计桥梁抗风设计大体可分为结构设计和结构抗风性能检验两个阶段.2.1结构设计阶段这一阶段的工作内容包括对桥位处风速资料的收集,风观测,风的特性参数选取等.根据全国基本风压分布图,并考虑桥址处的地形地貌情况,桥梁高度和桥跨长度,自然风的特征等因素,确定桥梁的设计风速,设计风荷载和自激振动检验风速.设计内容是提出抗风设计对结构设计的多项要求,作为确定桥梁结构体系,各构件的材料,形状,尺寸等的参考.其中最重要的是结构体系的抗风性能设计和结构断面形状的气动选型.2.2结构抗风性能检验阶段该阶段包括静力抗风性能和动力抗风检验两部分.静力抗风检验包括根据规范或通过风洞试验确定结构断面的静力气动力系数,计算出作用在桥梁各个部分的静风荷载,进而计算出在静风荷载作用下的结构内力,变形,检验结构的静力稳定性.动力抗风检验包括桥梁在施工及运营状态时的颤振特性,涡激共振特性,抖振特性检验.采用风洞试验或半试验半理论的方法给出桥梁的颤振临界风速形态,涡激共振的发生风速和振幅估计,抖振振幅及其产生的惯性力.对于颤振临界风速的确定,下面列出VanDerPut的近似公式,以考证临界风速的影响因素.在桥梁初步设计阶段,通常可采用下式估算临界风速U:r厂■——~1U_【l+(8—0~√.721~)Jb式中:一主梁截面几何形状折减系数,对于目前用于悬索桥或斜拉桥的流线型扁平箱梁,该值约为0.7~0.9;对于截面较钝的混凝土箱梁,该值可低达0.3~0.5;8一桥梁的扭转频率与竖弯频率之比;r一主梁截面的惯性半径;一主梁单位长度质量与空气的质量比;(1)一竖弯频率;b一半桥宽.从上式大致可以看出,主梁截面越扁平,流线型越好,临界风速越高;桥梁的刚度越大,固有频率越高;主梁越重,临界风速越高.因此同样截面的混凝土主梁比钢主梁对抗风更为有利.3桥梁动力抗风设计的基本方针对于大跨度柔性桥梁,如悬索桥和斜拉桥的抗第10期刘长宏等:桥梁抗风设计,风洞试验及抗风措施?47? 风设计则应特别注意动力抗风设计.桥梁动力抗风设计的基本方针是:(1)提高结构的临界风速,使之大于设计风速,即不会发生危险性的发散型风致振动;(2)减少各种限幅风致振动(涡激共振,抖振等)的振幅,使之控制在可以接受的范围内.为了使桥梁在使用期间内,在预计的强风作用下不损害桥梁的安全性和使用性,首先应掌握架桥地点的强风特性,决定桥梁的设计风速,并据此推测风对桥梁的作用,校核抗风安全性.如果判断有可能会发生上述有害的振动,就应考虑适当的防止对策或进行设计变更.4风洞试验在确定风引起的桥梁响应时,通常可采用已有的理论分析和风洞模型试验等方法.但由于桥梁断面形状复杂多样,用纯理论分析方法求解作用在桥梁上的空气力及风致振动响应相当困难.因此,采用风洞模型试验仍是目前抗风设计最有效和最可靠的手段.风洞试验是空气动力学研究的一个十分重要且不可替代的手段.它是在风洞实验室模拟大气边界层的实际风环境和实际建筑结构,根据实验室中的模型响应考察实际结构响应.对于复杂环境下,有复杂外形的桥梁结构风效应研究,用其它手段很难进行时,风洞试验只需对实际条件作适当的简化,就可以达到研究目的.风洞试验是目前采用最普遍,最有效的研究手段.通过精心设计的各种风洞试验,可以预测实桥的空气静力稳定性,动力稳定性以及是否有影响正常使用的风致振动现象等.所谓风洞(windtunne1),通常指一个可产生气流的闭合环形管道.风洞的种类很多,一般可依照不同的用途,由其供试验用区域(称作试验段,试验模型置于此段)的截面积和风速大小加以划分.用于进行桥梁空气动力学研究的风洞,在早期都是利用低速航空的风洞,目前已逐步采用专门用于结构风工程研究的大气边界层风洞.大气边界层风洞具有较长的,并可以模拟大气边界层内自然风特性的试验段.试验段的截面积从几平方米至几十平方米不等,试验风速可以从很低的风速(一般为1~2m/s)到每秒数十米.5桥梁风洞模型试验方法根据试验的目的,桥梁风洞模型试验分为主梁节段模型静力试验,动力试验和全桥模型试验等. (1)节段模型静力试验是将主梁(成桥状态时还包括栏杆)按一定的几何比例做成模型,然后支撑在风洞中进行试验,以测定静力三分力系数(C,c和cM)等.(2)动力试验是用弹簧(模拟桥梁其余部分对主梁节段的弹性约束作用)将节段模型悬挂在风洞中进行试验,弹簧常数由相似条件决定.这种试验可以直接给出桥梁颤振临界风速的二维近似试验结果.因试验模型制作容易,费用少,时间省,这种试验得到广泛应用.(3)全桥模型则是将各部分构件的几何外形,质量和刚度按相似关系做成全桥模型,以使模型的固有振动特性与实桥相似,试验的目的是全面测定桥梁的临界风速,涡激振动和紊流引起的抖振的振幅.这种试验具有制作复杂,周期较长,费用昂贵,但真实可靠等特点.6桥梁结构及构件的抗风措施桥梁结构及构件的抗风措施大体上可分为两大类:一是改善结构的振动特性为目的的结构措施;二是以改善结构物的空气动力特性为目的的气动措施.(1)在大跨度斜拉桥或悬索桥的施工阶段中,结构体系处于不断转换区尚未成型,可能会出现比成桥后更为不利的状态,即刚度较小,变形较大,稳定性较差,甚至发生较大的风致振动响应的情况,其中稳定性问题也十分突出.一般说来,大跨斜拉桥在最大双悬臂状态和最大单悬臂状态的颤振稳定性比成桥状态要好.在最大双悬臂状态,主要会发生围绕桥塔的桥平面外的水平摆动以及平面内的竖向"翘翘板"振动,在桥塔中产生较大的内力,设置辅助墩或采用临时墩来减小悬臂长度是常用的方法;在最大单悬臂状态,强风作用下主梁的侧向和竖向抖振产生的惯性力较大,若振动不能接受,可以通过设置阻尼器以及临时风缆等方法来抑制振动.(2)悬索桥在安装初期的结构抗扭刚度主要由主缆提供,其扭转频率随主梁拼装长度的增加而增加.大跨度悬索桥主梁拼装的抗风低谷应避开大风期.若不能避开,可采用不对称施工方法,即不从中央对称拼装,而是偏高中央一定距离开始拼装主梁,待达到一定长度后再进行对称施工.(3)对于刚度相对较小的悬索桥,必须认真地考虑各种改善气动性能的导流措施以便同时解决颤振,涡振,斜振等各类风致振动问题.1500m以上跨度的悬索桥可能还要考虑采用中央开槽的分离箱断面以及增加交叉索形成空间索网等措施以提高结构?48?北方交通2011空心板粱桥拓宽结构新桥截面选取分析罗伟(沈阳公路工程监理有限责任公司,沈阳110000)摘要:应用梁格法建立空间有限元模型,对比分析了当新桥采用普通空心板和宽幅空心板时,旧桥的内力状态.并且分析了新桥截面的刚度以及跨径对旧桥减载效果的影响,对空心板梁桥拓宽结构的设计有一定的参考价值.关键词:空心板;梁格法;刚度;减载中图分类号:U495文献标识码:B文章编号:1673—6052(2011)tO一0048—03 1概述近年来我国的经济不断进步,交通事业繁荣兴盛,国家对基础设施的大力投资推动了公路建设行业的迅猛发展,也对我国公路工程建设提出了越来越高的要求.而我国较早建设的高速公路,如沈大,广佛,沪宁,京津塘,京珠,京沪等高速公路,绝大部分为四车道,随着交通量的不断增加,出现了严重的交通拥堵现象,影响了道路的通行能力与服务水平,为此不得不考虑建设第二通道或者扩建以缓解日趋紧张的交通压力.2国内外研究现状拼宽桥梁的关键是新,旧桥梁拓宽形式的选择,目前我国公路桥梁拓宽基本采用3种方式:(1)新旧桥梁的上,下部结构均不连接.这种方式的优点是新桥与旧桥各自受力明确,互不影响,施工难度小;缺点是在上部活载反复作用下,两桥主梁产生挠度不同,新桥与旧桥之间的沉降差异,可能会造成连接部位沥青铺装层破坏,进而在连接部位形成顺桥向裂缝和横桥墩向错台.(2)新旧桥的上,下部结构均连接.这种方式的优点是新桥与原桥联成整体,减小荷载作用下新老桥连接处产生过大的变形,拼接后桥梁整体性较好;缺点是由于新,旧桥基础沉降的不一致,导致桥梁附加内力增大,使连接处产生裂缝.(3)新旧桥梁的上部结构连接,下部结构分离.优点是由于下部分离,上部结构连接产生的内力对下步构造影响较小;缺点是新旧桥基础沉降的不一致会使上部结构产生较大的附加内力,可以适当增大桩径,减小新旧桥基础沉降的不一致对桥梁上部结构内力的影响.的刚度和气动性能,满足抗风要求.7结语抗风稳定性是控制大跨度桥梁成败的关键因素之一,在大跨度桥梁设计中,不仅要考虑承受风荷载的静力强度问题,还必须考虑空气动力稳定性问题.虽然通过抗风设计,风洞试验,抗风措施为桥梁抗风提供了强有力保障,但还需要进一步充实,完善,改进和提高.Wind—resistantDesign,WindTunnelTestandWind—resistantMeasuresforBridge AbstractThebridgeshouldbewiththecapacityofwind—resistantfunction,especiallythelarge—spanbridgewithhighflexibility,andaerodynamicproblemslikeflutter,buffeting,vortex—inducedvibrationandSOonmustbetakenintoaccountwhendesigning.Bymeansofwind—resistantdesign,windtunneltestandwind—re—sistantmeasurestodeterminewindloadandwind——resistantperformanceofthebridgeisthemainmeansofwind——resistantstudyoflarge—spanflexiblebridge.KeywordsBridge;Windload;Flutter;Segmentalmodel;Windtunneltest。
【国家自然科学基金】_抖振时域分析_基金支持热词逐年推荐_【万方软件创新助手】_20140801
2011年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18
2011年 科研热词 抖振 颤振 结构健康监测 气动弹性 极大似然估计 时域分析 斜拉桥 数据处理 抖振性能 实测风谱 威布尔分布 大迎角 分离涡 分布检验 三角翼 panofsky谱 navier-stokes方程 kaimal谱 推荐指数 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
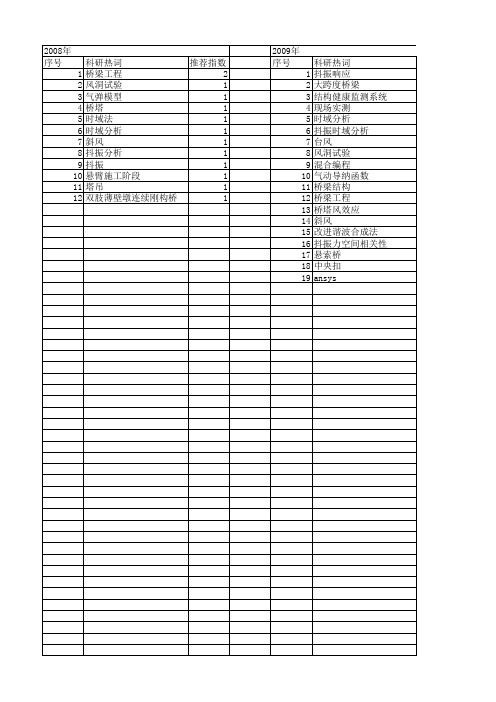
2008年 序号 1 2 3 4 5 6 7 8 9 10 11 12
科研热词 桥梁工程 风洞试验 气弹模型 桥塔 时域法 时域分析 斜风 抖振分析 抖振 悬臂施工阶段 塔吊 双肢薄壁 1 1 1 1 1
2009年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 抖振响应 大跨度桥梁 结构健康监测系统 现场实测 时域分析 抖振时域分析 台风 风洞试验 混合编程 气动导纳函数 桥梁结构 桥梁工程 桥塔风效应 斜风 改进谐波合成法 抖振力空间相关性 悬索桥 中央扣 ansys
推荐指数 4 3 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1
2010年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
科研热词 时域分析 抖振 悬索桥 风效应 风场模拟 随机响应 舒适性 砼桥塔 狄克曼指标 桥塔 极值反应 有限元法 暂态结构 时域抖振分析 抖振响应 大跨悬索桥 塔架 叶片 动力特性
推荐指数 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
某简支梁桥的抖振响应分析

某简支梁桥的抖振响应分析梁桥是桥梁结构中一种常见的结构形式,它由上下两根梁组成,顶部梁用于承受荷载作用,底部梁用于支撑顶部梁。
在梁桥使用过程中,由于荷载作用、风荷载、温度变化等因素的影响,梁桥会发生振动。
而梁桥的抖振响应分析就是研究梁桥在振动作用下的响应情况,以及如何减小梁桥的振动造成的不良影响。
抖振是指梁桥受到荷载作用后出现的大幅度振动现象,如果不及时加以处理,会导致梁桥的结构破坏或者影响梁桥的使用寿命。
抖振响应分析对于确保梁桥的正常运行具有重要意义。
在梁桥的抖振响应分析中,首先需要建立梁桥的动力模型。
动力模型是描述梁桥振动响应的数学模型,它通常包括结构的几何参数、材料力学参数以及外部荷载。
在建立动力模型时,需要考虑梁桥的非线性特性,如接缝间的摩擦、材料的非线性等。
建立好梁桥的动力模型后,就可以进行抖振响应分析了。
抖振响应分析通常是通过求解动力方程得到梁桥的振动响应。
动力方程是描述梁桥振动响应的基本方程,它包含了结构的振动特征以及外部荷载的作用。
在求解动力方程时,可以采用不同的方法,如有限元方法、模态叠加法等。
有限元方法是一种较为常用的数值计算方法,它将结构分成有限的小单元,并利用离散法对结构进行离散化处理。
通过求解离散化后的动力方程,可以得到梁桥的振动响应。
在进行抖振响应分析时,需要考虑梁桥的动力特性。
梁桥的动力特性包括固有频率、振型、阻尼等,它们对梁桥的抖振响应有重要影响。
通过对梁桥的动力特性进行分析,可以得到梁桥的固有频率以及相应的振型,从而判断梁桥是否存在共振等问题。
除了动力特性外,梁桥的阻尼特性也是影响抖振响应的重要参数。
阻尼是指梁桥在振动过程中由于能量的损失而减弱振动幅度的能力。
梁桥的阻尼特性可以通过实验测试或者数值模拟等方法得到,然后可以将其引入到动力方程中进行计算。
根据抖振响应分析的结果,可以对梁桥做出相应的优化设计和改进方案。
可以通过增大梁桥的刚度、改变结构形式、优化材料选型等方式来减小梁桥的抖振响应,以确保梁桥的安全可靠。
普立特悬索桥抖振响应时域分析

普立特悬索桥抖振响应时域分析
黄文锋;邹孔庆;孙建鹏;王美芹
【期刊名称】《西安建筑科技大学学报(自然科学版)》
【年(卷),期】2015(047)003
【摘要】普立特大桥是一座山区大跨悬索桥,为高柔的风敏感结构.在分析抗风性能时,利用ANSYS软件,建立了普立特悬索桥的三维有限元模型,分析了该模型的动力特性,根据Deodatis的谐波合成法模拟了桥梁的随机脉动风场并进行了检验,然后基于准定常理论计算了作用于模型上的抖振力时程,自激力以单元气动剐度及阻尼矩阵的形式在ANSYS中以Matrix27矩阵输入,最后由时程分析求得桥梁在考虑与不考虑自激力作用时的抖振响应.计算结果表明考虑自激力后主要改变了桥梁振动的平衡位置和在部分方向振动中起到正阻尼作用,为同类桥梁的抗风设计计算提供参考.
【总页数】6页(P371-375,381)
【作者】黄文锋;邹孔庆;孙建鹏;王美芹
【作者单位】合肥工业大学,安徽合肥230009;合肥工业大学,安徽合肥230009;中铁四局集团钢结构有限公司,安徽合肥230022;西安建筑科技大学,陕西西安710055;合肥工业大学,安徽合肥230009
【正文语种】中文
【中图分类】TU352.2
【相关文献】
1.普立万进军华南助力精细化工链——本刊联合其他媒体访普立万公司董事长兼首席执行官汤姆·活特迈尔及其亚洲团队 [J],
2.乌江悬索桥抖振响应时域分析 [J], 吴超
3.山区大跨窄悬索桥抖振响应时域有限元分析 [J], 周戈; 盛光祖; 李浩然
4.考虑吊索阻尼比影响的悬索桥抖振响应分析 [J], 刘韡;吴静宇;张卫喜
5.大跨钢桁梁悬索桥风致抖振响应时域分析 [J], 杨镇宇;祝兵
因版权原因,仅展示原文概要,查看原文内容请购买。
陡峭山谷地形大跨连续刚构桥风致响应研究

陡峭山谷地形大跨连续刚构桥风致响应研究
黄东平
【期刊名称】《铁道建筑技术》
【年(卷),期】2024()3
【摘要】为解决陡峭山谷地形连续刚构桥施工时结构的抖动问题,以贵州省剑河至黎平高速公路PPP项目小瑶光特大桥为研究对象,运用现场实测的方法研究了山谷地形的风速场,最大双悬臂施工阶段风致结构加速度和振型响应特征。
结果表明:不同监测点位置的风速存在差异,山谷遮挡和河道宽度突变会影响风速风向,乌下江陡峭山谷地形湍流现象明显;在最大双悬臂施工阶段,桥梁结构的振动以低阶振动为主,结构横弯和纵弯刚度低、抗风能力弱,风荷载对结构的整体稳定性影响较大;大跨连续刚构桥的阻尼比组成复杂,实测阻尼比在0.2~0.8之间,阻尼比在各自振频率中的分布不均,低自振频率低阶振型的阻尼比较大,高自振频率高阶振型的阻尼比较大。
【总页数】5页(P87-90)
【作者】黄东平
【作者单位】中铁十七局集团城市建设有限公司
【正文语种】中文
【中图分类】U448.23;U442.59
【相关文献】
1.高墩大跨连续刚构桥最大悬臂阶段风致响应及其对施工人员的影响
2.大跨连续刚构桥最大双悬臂状态风致内力计算
3.大跨连续刚构桥最大悬臂施工阶段风致抖振
响应4.跨江高墩刚构桥施工期地形风致响应分析5.高墩连续刚构桥施工地形风致响应研究
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
强风下高铁连续梁桥最大双悬臂状态抖振
时域分析
预应力混凝土连续梁桥具有行车平稳、跨越能力大等优点,广泛应用于公路、铁路建设中,成为高铁建设中跨河、跨既有线等障碍的主要桥型.随着交通强国等国家重大战略的推进,大批高铁连续梁桥将建设于华东、华南等强风多发区.为减小桥梁建设对桥下通行、农业生产等的影响,高铁连续梁桥常采用悬臂法施工[2].在此期间,桥梁长期处于墩梁临时固结的长悬臂状态,结构刚度较小,风敏感性加剧,最大双悬臂状态下结构的抗风性能大幅降低[3].因此,需要对双悬臂状态连续梁桥开展抗风安全性能分析,以保证施工期人员、器械和桥梁结构的安全,从而有效控制施工风险.
桥梁结构在风荷载作用下会产生多种风致振动,其中颤振、驰振和涡激共振可以通过在桥梁构件的气动外形优化设计予以避免,但脉动风引起的抖振却无法避免.长期持续的抖振会影响桥梁施工精度,严重时可能引起结构体系破坏.在桥梁抖振分析方面,Davenport首先将概率统计方法推广应用于桥梁抖振响应分析,搭建了经典桥梁风致抖振分析框架.Scanlan引入自激力完善了桥梁风致抖振分析理论,形成了经典桥梁风致抖振频域分析框架.在此基础上,国内外学者针对斜拉桥、悬索桥等大跨度桥梁抖振分析开展了大量工作,逐步实现了大跨度桥梁非平稳、非线性抖振时频域分析.在混凝土桥梁施工期抖振分析方面,韩艳等进行了连续刚构桥平衡悬臂施工阶段的抖振时域分析研究.然而,连续梁桥施工期处于墩梁临时固结状态,其结构刚度与连续刚构桥相比较小,受风荷载的影响尚不明确,且台风等极端风环境下桥梁的抖振问题愈加突出,故需对处于强风多发区的大跨度高铁连续梁悬臂施工阶段的抖振响应进行有效分析及预测.
本文以盐通高铁某大跨连续梁桥为工程背景,该桥位于华东沿海强风、台风多发区,且主跨长达132 m,最大双悬臂阶段施工安全面临重大挑战.本文依照设计参数建立了该桥施工期最大双悬臂状态有限元模型,并采用谐波合成法模拟出施工期该桥的三维脉动风场.利用时域抖振分析理论,开展了最大双悬臂状态结构抖振响应时域分析,研究了不同设计风速和风攻角对抖振响应的影响.
1 桥梁分析模型
1.1 有限元建模
本文工程背景为典型有砟单线轨道预应力混凝土单线连续梁桥.全桥布置见图1.
图1 大跨度连续梁桥全桥布置图(单位:m)
该大跨度高铁连续梁桥计算跨度为269.6 m,沿跨向布置为四墩三跨(68.8+132+68.8) m.该桥采用悬臂灌注法施工,中支点0#梁段在墩顶浇筑,其余各梁段采用挂篮悬臂浇筑,施工期墩顶临时固结,处于最大双悬臂状态时,两侧悬臂长度均为65 m.最大双悬臂状态的三维有限元模型见图2.
图2 桥梁有限元模型
1.2 动力特性分析
基于有限元模型,开展了大跨度连续梁桥施工期最大悬臂状态动力特性分析,并获取了该桥前200阶模态振型和频率.表1列出了前10阶模态频率及其振型特征.由表可知,施工期最大双悬臂状态下的结构基频为0.386 4 Hz,仅为成桥状态基频1.024 5 Hz的37.7%,说明最大双悬臂状态下桥梁刚度较小,抗风安全性较差.最大双悬臂状态下,结构第1、2阶振型出现了全桥整体摆动,第5、6阶振型出现了桥墩的弯曲模态,表明最大双悬臂状态下结构刚度较低,且整体性较差.此外,悬臂施工阶段墩梁处于临时固结状态,结构稳定性将进一步下降.因此,亟需研究大跨度连续梁桥施工期最大双悬臂状态抖振安全性能.
表1 大跨度连续梁桥前10阶振动模态
2 三维脉动风场模拟
参考《公路桥梁抗风设计规范》[12]中附表A.3,可确定桥址区50年一遇、100年一遇、150年一遇和220年一遇距地面10 m高处的10 min平均最大风速分别为29.5、31.7、35.1和40.2 m/s,并以此作为本文采用的设计风速.根据桥址区地形地貌资料确定地表粗糙度为B类.选取适合的风谱模型是保证风场模拟真实性和准确性的首要前提.水平顺风向及竖直方向上脉动风速的功率谱密度函数S u(n)、S w(n)分别为[12]
(1)
(2)
(3)
式中,n为风的脉动频率;u*为气流摩阻速度;U(z)为高度z处的平均风速.由于桥面位于同一水平高度,可假定沿顺桥向分布的各点风场均相同.
基于Deodatis谐波合成法和互谱密度矩阵的显式分解[13],将规范谱作为目标谱,模拟了主梁23个模拟点的顺风向和竖向脉动风速时程.桥墩的脉动风场模拟方法与主梁类似,以式(1)为目标谱,生成了桥墩9个模拟点的顺风向和横风向脉动风速样本.主梁12#模拟点处的顺风向脉动风模拟谱、互相关函数与目标值对比见图3.由图可知,模拟风场功率谱和互相关函数均与理论值基本一致,表明所模拟风场具有较高的保真度.
(a) 功率谱
(b) 互相关函数
图3 模拟风场功率谱与互相关函数校核
3 最大双悬臂状态抖振时域分析
作用于桥梁结构上的风荷载通常可分解为平均风引起的静风力、脉动风引起的抖振力和流固耦合引起的自激力3个部分[4].由于高铁桥主梁断面较小且整体刚度较大,主梁振动时对周围风场的影响较小,故气动自激力对抖振响应的贡献较小.本文基于Davenport抖振分析理论仅考虑静风力和抖振力来开展抖振时域分析.基于准定常理论,Davenport抖振理论框架中将脉动风作用下桥梁结构的升力表示为
(4)
脉动风作用下桥梁结构的阻力为
(5)
脉动风作用下桥梁结构的扭矩为
(6)
式中,ρ为空气密度;B为主梁宽度;α0为平均风攻角;C D、C L、C M分别为阻力系数、升力系数和升力矩系数;分别为阻力系数、升力系数和升力矩系数对攻角α0的导数;u(t)、w(t)分别为水平向和竖向脉动分量.由于缺乏风洞试验,气动导纳偏保守地取为1.气动系数由文献[14]中数值模拟获得,主梁跨中断面三分力系数见表2.
表2 主梁跨中断面三分力系数
3.1 不同设计风速下的抖振响应分析
基于谐波合成法生成了4个设计风速下高铁连续梁桥最大悬臂状态主梁和桥墩的模拟风场,并建立了风荷载模型,进行抖振响应分析.风攻角为0°,设计风速为35.1和40.2 m/s时主梁悬臂端侧向、竖向和扭转抖振位移响应时程见图4.由图可知,主梁抖振主要呈现为围绕静力平衡位置的往复随机振动.
(a) 竖向位移响应
(b) 侧向位移响应
(c) 扭转位移响应
图4 不同设计风速下主梁悬臂端抖振位移响应
将主梁各点处的抖振响应位移中剔除t=0时刻由静风和自重产生的静力响应部分,得到主梁各点的抖振位移响应均方根(RMS)值沿跨度方向的分布情况,结果见图5.由图可知,主梁侧向位移、竖向位移和扭转角RMS值以跨中为对称轴呈对称分布.由于主梁在最大悬臂阶段与桥墩临时固结,故3个方向的抖振位移RMS值均表现出由跨中向两侧非线性递增的规律.
(a) 竖向位移
(b) 侧向位移
(c) 扭转位移
图5 不同设计风速下主梁位移响应RMS值沿跨度方向分布
表3给出了不同风速下主梁悬臂端位移响应峰值和RMS值.由表可知,设计风速为29.5 m/s时,主梁悬臂端最大竖向位移、侧向位移和扭转位移分别为L/1 110、L/756和L/3 196,其中L=132 m为桥梁主跨长度.对于设计时速为350 km/h的单线高速铁路连续梁桥,竖向位移已超过《高速铁路设计规范》(TB 10621—2014)[15]中L/2 500的限定.当设计风速由29.5 m/s增至40.2 m/s时,主梁抖振响应侧向、竖向和扭转位移响应峰值增幅分别为60.5%、55.1%和77.0%,位移响应RMS峰值增幅分别为48.7%、46.9%和54.9%.
表3 不同设计风速下主梁悬臂端位移响应峰值和RMS值
3.2 不同风攻角下的抖振响应分析
由3.1节可知,当设计风速为35.1 m/s时,主梁会产生较明显的抖振响应,此时对应的重现期为150 a,满足高铁桥梁建造和运营使用年限.因此,下文中研究不同风攻角对高铁桥最大悬臂状态抖振响应的影响时,取设计风速为35.1 m/s,得到主梁悬臂端侧向、竖向和扭转抖振响应时程(见图6).剔除静力响应后,3个风攻角下主梁位移响应RMS值沿顺桥向分布见图7.
(a) 竖向位移响应
(b) 侧向位移响应
(c) 扭转位移响应
图6 不同风攻角下主梁悬臂端位移响应
(a) 竖向位移
(b) 侧向位移
(c) 扭转位移
图7 不同风攻角下悬臂端位移响应RMS值沿跨度方向分布
由图6可知,与0°攻角相比,悬臂端竖向位移响应峰值在+3°攻角脉动风作用下明显增大,在-3°攻角作用下有所下降,表明负攻角对竖向抖振位移具有一定的抑制作用.+3°和-3°攻角下侧向位移峰值相差不大.在+3°攻角脉动风作用下,扭转位移响应峰值明显大于-3°和0°攻角的情形.由图7可知,风攻角对悬臂端位移RMS值的影响与对位移峰值的影响规律基本一致.
4 结论
1) 施工期最大双悬臂状态结构基频仅为成桥状态的37.7%,结构刚度较小,抗风安全性较弱,建议在强风多发区高铁连续梁桥悬臂施工期应对结构进行抖振安全评估.
2) 50年一遇设计风速下,主梁悬臂端竖向抖振位移响应峰值达主跨长度的1/1 110,已超规范限值1/2 500,且抖振位移响应峰值随风速增加迅速增大.在强风下高铁连续梁桥施工阶段,应对最大悬臂状态抖振响应采取控制措施.
3) 与零度攻角和负攻角相比,正攻角强风作用下悬臂端抖振响应均明显增大.负攻角对主梁竖向位移有一定的抑制作用,对主梁侧向位移影响不大,悬臂施工期抖振分析应着重考虑正攻角这一不利工况.。
