相似多边形的综合测试题
相似多边形综合

一、知识点分析与例题讲解一、相似多边形的性质知识点1:相似多边形边、角的性质根据相似多边形的定义,可知当两个多边形相似时,它们的对应角相等,对应边对应成比例,其比叫做相似多边形的相似比。
知识点2:相似多边形的周长、面积的性质相似多边形的周长比等于相似比,面积比等于相似比的平方。
由于从多边形的一个顶点出发,可引出(n -3)条对角线,这(n -3)条对角线将多边形分成了(n -2)个三角形,所以相似多边形具有与相似三角形相类似的性质,诸如相似多边形的周长比等于相似比,面积比等于相似比的平方。
例1、已知图中的两个四边形相似,找出图中的成比例线段,并用比例式表示。
例2、如图,在平行四边形ABCD 中,延长AB 到E ,使12BE AB =,延长CD 到F ,使,DF DC EF =交BC 于G ,交AD 于H ,则BEG ∆的周长与CFG ∆的周长的比为_________。
例3、如图,在梯形ABCD 中,E BC AD ,//是AB 上一点,BC EF //,并且EF 将梯形ABCD分成的两个梯形AEFD 、EBCF 相似,若9,4==BC AD ,求EB AE :。
二、位似图形知识点1位似三角形与为似多边形如果两个三角形不仅是相似三角形,而且每组对应点所在的直线都经过同一个点,那么两个三角形叫做位似三角形,它们的相似比又称为位似比,这个点叫做位似中心。
同样,如果两个多边形不仅是相似多边形,而且每组对应点所在的直线都经过同一个点,那么两个多边形叫做位似多边形,它们的相似比又称为位似比,这个点叫做位似中心。
利用多边形的位似可以将一个三角形或多边形缩小或放大。
知识点2位似变换与位似图形若两个几何图形F 与F ’相似,而且对应点连线交于同一点O ,则称F 与F ’关于点O 位似,O 叫做位似中心。
把一个几何图形变换成与之位似的图形,叫做位似变换。
知识点3位似多边形的画法1、连接位似中心与多边形各顶点;2、延长各连线,使得延长线与连线之比为位似比;3、按顺序连接所得各点。
中考数学专题复习:相似多边形与图形位似
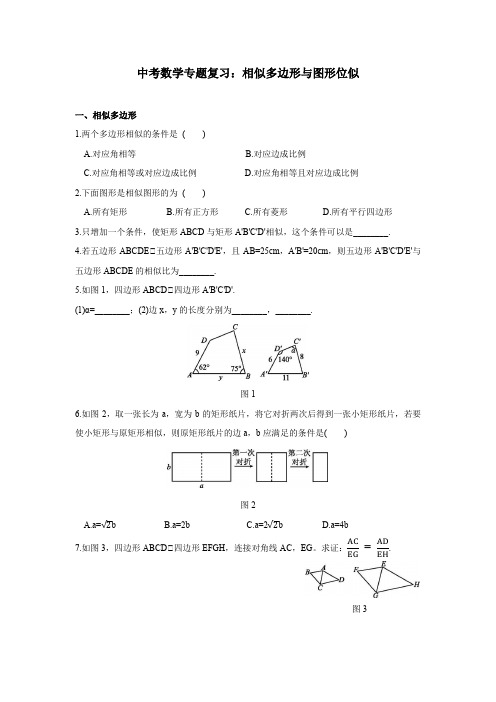
中考数学专题复习:相似多边形与图形位似一、相似多边形1.两个多边形相似的条件是 ( )A.对应角相等B.对应边成比例C.对应角相等或对应边成比例D.对应角相等且对应边成比例 2.下面图形是相似图形的为 ( )A.所有矩形B.所有正方形C.所有菱形D.所有平行四边形 3.只增加一个条件,使矩形ABCD 与矩形A'B'C'D'相似,这个条件可以是________. 4.若五边形ABCDE∽五边形A'B'C'D'E',且AB=25cm ,A'B'=20cm ,则五边形A'B'C'D'E'与五边形ABCDE 的相似比为________. 5.如图1,四边形ABCD∽四边形A'B'C'D'.(1)α=________;(2)边x ,y 的长度分别为________,________.图16.如图2,取一张长为a ,宽为b 的矩形纸片,将它对折两次后得到一张小矩形纸片,若要使小矩形与原矩形相似,则原矩形纸片的边a ,b 应满足的条件是( )图2A.a=√2bB.a=2bC.a=2√2bD.a=4b 7.如图3,四边形ABCD∽四边形EFGH ,连接对角线AC ,EG 。
求证:AC EG=AD EH.图38.在AB=20m,AD=30m的矩形花坛四周修筑小路.(1)如果四周的小路的宽均相等,都是xm,如图4∽,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD相似吗?请说明理由;(2)如果相对着的两条小路的宽均相等,宽度分别为xm,ym,如图∽,那么小路的宽x与y 的比值为多少时,能使得小路四周所围成的矩形A'B'C'D'∽矩形ABCD?图4二、位似图形1.下列各选项的两个图形中,不是位似图形的是( )图52.如图6,以点O为位似中心,把∽ABC放大为原图形的2倍得到∽A'B'C',以下说法中错误的是( )图6A.∽ABC∽∽A'B'C'B.点C,O,C'在同一直线上C.AO∽AA'=1∽2D.AB∽A'B'3.如图7,四边形ABCD与四边形A'B'C'D'位似,位似中心为点O,OC=6,CC'=4,AB=3,则A'B'=________.图74.如图8,∽ABC与∽DEF是位似图形,点B的坐标为(3,0),则其位似中心的坐标为________.图85.如图9,∽ABC三个顶点的坐标分别为A(-1,3),B(-1,1),C(-3,2).(1)请画出∽ABC关于y轴对称的∽A1B1C1;(2)以原点O为位似中心,将∽A1B1C1放大为原来的2倍,得到∽A2B2C2,请在第三象限内画出∽A2B2C2,并求出S△A1B1C1:S△A2B2C2的值.图96.如图10,在5×6的方格中,每个小正方形的边长均为1,∽ABC的顶点均为格点,D为AB的中点,以点D为位似中心,位似比为2,将∽ABC放大,得到∽A'B'C',则BB'等于( )图10A.√52B.√5 C.3√52D.√52或3√527.在平面直角坐标系中,∽ABC和∽A1B1C1的相似比等于12,并且是关于原点O的位似图形,若点A的坐标为(2,4),则其对应点A1的坐标是________.8.如图11,∽ABC与∽A'B'C'是位似图形,点A,B,A',B',O共线,点O为位似中心.(1)AC与A'C'平行吗?为什么?(2)若AB=2A'B',OC'=5,求CC'的长.图119.如图12所示,正方形OEFG和正方形ABCD是位似图形,点F的坐标为(-1,1),点C的坐标为(-4,2),则这两个正方形位似中心的坐标是________.图12参考答案一、相似多边形 1.D2.B [解析] ∽相似多边形的对应边成比例,对应角相等,∽所有正方形都是相似多边形;∽菱形的对应角不一定相等,矩形的边不一定对应成比例,∽所有菱形、所有矩形都不一定是相似图形;∽平行四边形的对应角不一定相等,边不一定对应成比例,∽所有平行四边形不一定是相似图形.3.答案不唯一,如ABA'B' = BCB'C' [解析] ∽矩形的四个角都是直角,∽只要矩形的对应边成比例,则两个矩形相似,∽这个条件可以是ABA'B' = BCB'C'(答案不唯一).4.45 [解析] ∽A'B'AB = 2025 = 45,五边形A'B'C'D'E'∽五边形ABCDE ,∽五边形A'B'C'D'E'与五边形ABCDE 的相似比为45. 5.(1)83° (2)12332[解析] (1)∽四边形ABCD∽四边形A'B'C'D',∽∽A'=∽A=62°,∽B'=∽B=75°,∽α=360°-62°-75°-140°=83°.故答案为83°.(2)∽四边形ABCD∽四边形A'B'C'D',∽x 8 = y 11 = 96,解得x=12,y=332.6.B [解析] 对折两次后的小矩形的长为b ,宽为14a.∽小矩形与原矩形相似,∽a b = b14a,∽a=2b.7.证明:∽四边形ABCD∽四边形EFGH ,∽AD EH = CD GH ,∽D=∽H ,∽∽ADC∽∽EHG ,∽ACEG =AD EH.8.解:(1)如果四周的小路的宽均相等,那么小路四周所围成的矩形A'B'C'D'和矩形ABCD 不相似.理由:∽四周的小路的宽均为x m ,∽A'D'AD=30+2x 30=15+x 15,A'B'AB=20+2x 20=10+x 10.∽x>0,∽15+x 15≠10+x 10,即A'D'AD ≠ A'B'AB,∽小路四周所围成的矩形A'B'C'D'和矩形ABCD 不相似.(2)A'D'AD =30+2y 30=15+y 15,A'B'AB =20+2x 20=10+x 10.当15+y 15=10+x 10时,小路四周所围成的矩形A'B'C'D'∽矩形ABCD ,解得x y =23,∽小路的宽x 与y 的比值为23时,能使得小路四周所围成的矩形A'B'C'D'∽矩形ABCD. 二、位似图形 1.C2.C [解析] ∽以点O 为位似中心,把∽ABC 放大为原图形的2倍得到∽A'B'C',∽∽ABC∽∽A'B'C',点C ,O ,C'在同一直线上,AB∽A'B',AO∽OA'=1∽2,故选项C 错误.故选C.3.5 [解析] ∽四边形ABCD 与四边形A'B'C'D'位似,其位似中心为点O ,OC=6,CC'=4, ∽AB A'B'=OCOC'=610= 35.∽AB=3,∽A'B'=5.4.(1,0) [解析] 如图,连接各对应点A 与D ,C 与F ,直线AD ,CF 的交点Q 即为位似中心,∽位似中心的坐标为(1,0).5.解:(1)如图所示,∽A 1B 1C 1即为所求.(2)如图所示,∽A 2B 2C 2即为所求.∽将∽A 1B 1C 1放大为原来的2倍得到∽A 2B 2C 2,∽∽A 1B 1C 1∽∽A 2B 2C 2,且位似比为12,∽S △A 1B 1C 1∽S △A 2B 2C 2=14.6.D [解析] 如图.∽AC=1,BC=2,∽AB=√5.∽∽A'B'C'∽∽ABC ,位似比为2,∽ABA'B' = 12, ∽A'B'=2√5,∽BB' = 12(A'B'-AB) =√52.同理可得,BB″=A″B″-A″B=3√52.故选D.7.(4,8)或(-4,-8) [解析] ∽∽ABC 和∽A 1B 1C 1的相似比等于12,并且是关于原点O 的位似图形,而点A 的坐标为(2,4),∽点A 的对应点A 1的坐标为(2×2,2×4)或(-2×2,-2×4),即(4,8)或(-4,-8).8.解:(1)AC∽A'C'.理由如下:∽∽ABC 与∽A'B'C'是位似图形,∽∽ABC∽∽A'B'C',∽∽A=∽C'A'B',∽AC∽A'C'.(2)∽∽ABC∽∽A'B'C',∽ABA'B' = ACA'C'.∽AB=2A'B',∽ACA'C' =2.∽AC∽A'C',∽OCOC' = ACA'C' = 2. ∽OC'=5,∽OC=10,∽CC'=OC -OC'=10-5=5. 9.(2,0)或-43,23[解析] 本题分两种情况讨论:∽当两个位似图形在位似中心O'同旁时,位似中心就是直线CF 与x 轴的交点.设直线CF 的函数表达式为y=kx+b(k≠0),将点C(-4,2),F(-1,1)的坐标代入,得,解得,∽y=-,,+23.令y=0,得x=2,∽点O'的坐标是(2,0).∽当位似中心O'在两个正方形之间时,可求直线OC 的函数表达式为y=-12x ,直线DE 的函数表达式为y=14x+1,由, 解得,即O'-,,23.故答案为(2,0)或-43,23.。
27.1.2相似多边形

解:∵AB∥CD,A′B′∥C′D′,∴∠A+∠D=180°,∠B′+∠C′=180°,又 ∵∠A=62°, ∠C′=110°, ∴∠D=118°, ∠B′=70°, 又∵梯形 ABCD 与梯形 A′B′C′D′ x y 9 9.6 相似,∴∠α =∠D=118°,∠β =∠B′=70°,∴ = = = ,解得:x=6,y=12,z 4 8 z 6.4 =6.
27.1 图形的相似 第2课时 相似多边形
1.对于四条线段 a,b,c,d,如果其中两条线段的_ 比 _与另外两条线段的 a c bc) _ 比 _相等,如_b=d(ad=_ ,我们就说这四条线段成比例线段. 2.两个边数相同的多边形,如果它们的角分别 相等_,边_ 成比例 _,那么这 两个多边形叫做相似多边形.相似多边形_对应边 _的比叫做相似比. 3.相似多边形的对应角_ 相等 _,对应边_ 成比例 _.
一、选择题(每小题 6 分,共 18 分) 9.如图,正五边形 FGHMN 与正五边形 ABCDE 相似,若 AB∶FG=2∶3,则下列结论 正确的是( B ) A.2DE=3MN B.3DE=2MN C.3∠A=2∠F D.2∠A=3∠F
2x+y 10.(2014· 牡丹江)若 x∶y=1∶3,2y=3z,则 的值是( A ) z-y A.-5 10 B.- 3 10 C. 3 D.5
证明:∵DE∥BC,∴∠ADE=∠B,∠AED=∠C.又∵AC=9,EC=6,∴AE=3,∵ AD DE AE 1 AD=4,DB=8,∴AB=12,∴ = = = ,∴△ADE 与△ ABC 相似. AB BC AC 3
15.(10 分)如图,在矩形 ABCD 中,AB=2AD,线段 EF=10,在 EF 上取一点 M,分 别以 EM, MF 为一边作矩形 EMNH, 矩形 MFGN, 使矩形 MFGN∽矩形 ABCD, 设 MN=x, 当 x 为何值时,矩形 EMNH 的面积 S 有最大值?最大值是多少?
相似多边形及位似--巩固练习(含答案解析)

相似多边形及位似--巩固练习【巩固练习】一.选择题1.(2016春•高密市期末)两个多边形相似的条件是()A.对应角相等B.对应边成比例C.对应角相等或对应边成比例D.对应角相等且对应边成比例2.下列说法错误的是().A.位似图形一定是相似图形.B.相似图形不一定是位似图形.C.位似图形上任意一对对应点到位似中心的距离之比等于相似比.D.位似图形中每组对应点所在的直线必相互平行.3.(2015•杭州模拟)如图,四边形ABCD∽四边形A1B1C1D1,AB=12,CD=15,A1B1=9,则边C1D1的长是()A.10B.12C.D.4.平面直角坐标系中,有一条“鱼,它有六个顶点”,则()A.将各点横坐标乘以2,纵坐标不变,得到的鱼与原来的鱼位似.B.将各点纵坐标乘以2,横坐标不变,得到的鱼与原来的鱼位似.C.将各点横、纵坐标都乘以2,得到的鱼与原来的鱼位似.D.将各点横坐标乘以2,纵坐标乘以,得到的鱼与原来的鱼位似.5.下列命题:①两个正方形是位似图形;②两个等边三角形是位似图形;③两个同心圆是位似图形;④平行于三角形一边的直线截这个三角形的两边,所得的三角形与原三角形是位似图形.其中正确的有()A.1个B.2个C.3个D.4个6.如图,已知A(4,2),B(2,﹣2),以点O为位似中心,按位似比1:2把△ABO缩小,则点A的对应点A′的坐标为()二.填空题8.如果两个位似图形的对应线段长分别为3cm和5cm,且较小图形周长为30cm,则较大图形周长为______.9.已知ABC,以点A为位似中心,作出ADE,使ADE是ABC放大2倍的图形,则这样的图形可以作出______个,它们之间的关系是__________. 10.(2016•三明)如图,在平面直角坐标系中,已知A(1,0),D(3,0),△ABC与△DEF位似,原点O是位似中心.若AB=1.5,则DE=.11.△ABC中,D、E分别在AB、AC上,DE∥BC,△ADE是△ABC缩小后的图形.若DE把△ABC的面积分成相等的两部分,则AD:AB=________.12.图中的两个四边形相似,则x+y=,α=.13.如图(1),将一个正六边形各边延长,构成一个正六角星形AFBDCE,它的面积为1,取△ABC和△DEF各边中点,连接成正六角星形A1F1B1D1C1E1,如图(2)中阴影部分,取△A1B1C1和△D1E1F1各边中点,连接成正六角星形A2F2B2D2C2E2,如图(3)中阴影部分,如此下去…,则正六角星形A4F4B4D4C4E4的面积为__________________.14.如图,正方形OABC与正方形ODEF是位似图形,位似中心为O,位似比为.若点C的坐标为(0,1),则点E的坐标为.三.综合题15.如图,D、E分别AB、AC上的点.(1)如果DE∥BC,那么△ADE和△ABC是位似图形吗?为什么?(2)如果△ADE和△ABC是位似图形,那么DE∥BC吗?为什么?16.如图,点E是菱形ABCD对角线CA的延长线上任意一点,以线段AE为边作一个菱形AEFG,且菱形AEFG∽菱形ABCD,连接EB,GD.(1)求证:EB=GD;(2)若∠DAB=60°,AB=2,AG=,求GD的长.17.如图1,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF∽矩形ABCO,其相似比为1:4,矩形ABCO的边AB=4,BC=4.(1)求矩形ODEF的面积;(2)将图1中的矩形ODEF绕点O逆时针旋转一周,连接EC、EA,△ACE的面积是否存在最大值或最小值?若存在,求出最大值或最小值;若不存在,请说明理由.【答案与解析】一、选择题1.【答案】D.【解析】∵对应角相等且对应边成比例的多边形相似,∴D符合定义,故选D.2.【答案】D.3.【答案】C.【解析】∵四边形ABCD∽四边形A1B1C1D1,∴=,∵AB=12,CD=15,A1B1=9,∴C1D1==.故选C.4.【答案】C.5.【答案】B【解析】由位似图形的概念可知③和④对,故选B.6.【答案】B.【解析】∵A(4,2),以点O为位似中心,按位似比1:2把△ABO缩小,∴点A的对应点A′的坐标为:(2,1)或(﹣2,﹣1).故选B.7.【答案】B.【解析】∵AB=1,设AD=x,则FD=x-1,FE=1,∵四边形EFDC与矩形ABCD相似,∴EF AD FD AB=,111xx=-,解得11+5=2x ,21-5=2x ,(负值舍去),经检验1=2x 是原方程的解.故选B.二、填空题8.【答案】50cm.9.【答案】2个;全等.10.【答案】4.5.【解析】解:∵△ABC 与DEF 是位似图形,它们的位似中心恰好为原点,已知A 点坐标为(1,0),D 点坐标为(3,0),∴AO=1,DO=3,∴==,∵AB=1.5,∴DE=4.5.故答案为:4.5.11.【答案】;【解析】由BC∥DE 可得△ADE∽△ABC,所以,故.12.【答案】63,85°.【解析】由于两个四边形相似,它们的对应边成比例,对应角相等,∴18:4=x:8=y:6,解得x=36,y=27,则x+y=36+27=63.∴a=360°﹣(77°+83°+115°)=85°.故答案为63,85°.13.【答案】1256.【解析】∵A 1、F 1、B 1、D 1、C 1、E 1分别是△ABC 和△DEF 各边中点,∴正六角星形AFBDCE∽正六角星形A 1F 1B 1D 1C 1E 1,且相似比为2:1,∵正六角星形AFBDCE 的面积为1,∴正六角星形A 1F 1B 1D 1C 1E 1的面积为14,同理可得,第三个六角形的面积为:314=164,第四个六角形的面积为:1111=1644256⨯⨯,故答案为:1256.14.【答案】(﹣,);【解析】∵正方形OABC 与正方形ODEF 是位似图形,位似中心为O ,点C 的坐标为(0,1),∴B 点坐标为:(﹣1,1),∵位似比为,∴点E 的坐标为(﹣,).三.解答题15.【答案与解析】(1)△ADE 和△ABC 是位似图形.理由是:DE∥BC,所以∠ADE=∠B,∠AED=∠C.所以△ADE∽△ABC,所以.又因为点A 是△ADE 和△ABC 的公共点,点D 和点B 是对应点,点E 和点C是对应点,直线BD 与CE 交于点A,所以△ADE 和△ABC 是位似图形.(2)DE∥BC.理由是:因为△ADE 和△ABC 是位似图形,所以△ADE∽△ABC 所以∠ADE=∠B 所以DE∥BC.16.【答案与解析】(1)证明:∵菱形AEFG∽菱形ABCD,∴∠EAG=∠BAD,∴∠EAG+∠GAB=∠BAD+∠GAB,∴∠EAB=∠GAD,∵AE=AG,AB=AD,∴△AEB≌△AGD,∴EB=GD;(2)解:连接BD 交AC 于点P,则BP⊥AC,∵∠DAB=60°,∴∠PAB=30°,∴BP=AB=1,AP==,AE=AG=,∴EP=2,∴EB===,∴GD=.17.【答案与解析】(1)∵矩形ODEF∽矩形ABCO,其相似比为1:4,∴S 矩形ODEF =116S 矩形ABCO =116;(2)存在.2==所以点E 的轨迹为以点O 为圆心,以2为半径的圆,设点O 到AC 的距离为h,8=,解得,∴当点E 到AC 的距离为时,△ACE 的面积有最大值,当点E 到AC 的距离为2-2时,△ACE 的面积有最小值,S 最大=()18282⨯=S 最小=()18282⨯=。
相似图形测试题及答案

相似图形测试题及答案
一、选择题
1. 两个图形相似,那么它们的对应角()
A. 相等
B. 不相等
C. 不一定相等
D. 无法确定
答案:A
2. 如果两个图形相似,那么它们的对应边()
A. 相等
B. 不相等
C. 不一定相等
D. 无法确定
答案:C
3. 相似图形的面积比等于()
A. 边长比的平方
B. 边长比的立方
C. 边长比的四次方
D. 边长比的五次方
答案:A
二、填空题
4. 相似图形的周长比等于它们的________比。
答案:边长
5. 如果两个图形的边长比是2:3,那么它们的面积比是________。
答案:4:9
三、判断题
6. 两个图形的对应角相等,那么这两个图形一定相似。
()
答案:错误
7. 两个图形的对应边成比例,那么这两个图形一定相似。
()
答案:正确
四、解答题
8. 已知两个相似多边形的边长比为3:4,求它们的面积比。
答案:它们的面积比为9:16。
9. 一个三角形的底边长为6cm,高为8cm,另一个相似三角形的底边长为9cm,求另一个三角形的高。
答案:另一个三角形的高为12cm。
10. 一个矩形的长宽比为2:1,如果它的长为8cm,求它的宽。
答案:它的宽为4cm。
第29章《相似形》好题集(31):29.6 相似多边形及其性质

第29章《相似形》好题集(31):29.6 相似多边形及其性质填空题61.两个相似多边形的相似比是,则这两个多边形的对应对角线的比是.62.把一个正多边形放大到原来的2.5倍,则原图与新图的相似比为.63.已知两个相似多边形的周长比为1:2,它们的面积和为25,则这两个多边形的面积分别是和.64.已知一个四边形的各边长分别是3cm、4cm、5cm、8cm,另一个与它相似的四边形的最长边的长是12cm,那么另一个四边形的周长是cm.65.两个相似多边形面积比为9:25,第一个多边形周长为36,则第二个多边形的周长为.66.在菱形ABCD和菱形A′B′C′D′中,∠A=∠A′=60°,若AB:A′B′=1:,则BD:A′C′=.67.已知两个相似五边形的相似比为2:3,且它们的面积之差为15cm2,则较小的五边形的面积为cm2.68.四边形ABCD∽四边形A′B′C′D′,∠A=70°,∠B′=108°,∠C′=92°,则∠D=度.69.如果两个相似多边形的最长边分别为35cm和14cm,那么最短边分别为5cm和cm.70.如图,把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为.71.一个多边形的边长依次为1,2,3,4,5,6,与它相似的另一个多边形的最大边长为8,那么另一个多边形的周长是.72.判断正误:所有的正方形都相似.答:.73.如图,两个相似四边形中,根据已知的数据,图中x=;y=及α=度.74.一个四边形的边长分别是3,4,5,6,与它相似的四边形最小边长为6,则这个四边形的周长是.75.若五边形ABCDE∽五边形MNOPQ,且AB=12,MN=6,AE=7,则MQ=.76.如果多边形ABCDE与多边形A′B′C′D′E′相似,且∠A=48°,则∠A′=度.77.四边形ABCD∽四边形A′B′C′D′,他们的面积之比为36:25,他们的相似比,若四边形A′B′C′D′的周长为15cm,则四边形ABCD的周长为cm.78.在如图所示的相似四边形中,未知边x=.79.如图是两个相似四边形,已知数据如图所示,则x=;y=;α=度.80.已知正方形原来的周长是16cm,现将正方形的各条边扩大到原来的3倍,则此时正方形的周长是cm,面积是m2.82.在比例尺为1:1000的地图上,一块周长为4cm,面积为1cm2的地方所表示的实际周长为米,面积为米2.83.把一个菱形的各边都扩大4倍,则对角平分线之和扩大倍;其面积扩大倍.84.两个相似多边形的一组对应边分别为3cm、6cm,则它们的相似比为.85.在梯形ABCD中,AB∥DC,AB=18cm,DC=8cm,E,F分别是腰AD,BC上的点,且EF∥AB,若梯形DEFC∽梯形EABF,那么EF=cm.86.顺次连接正方形四边中点所得的四边形的面积与原正方形的面积的比为.87.一个六边形的边长依次为1,2,3,4,5,6.与它相似的另一个多边形最大边长为12,则另一个多边形的周长为.88.在一张比例尺为1:30000的地图上,一多边形地区的周长为70cm,面积为340cm2,那么该地区的实际周长为km,面积为km2.89.如图,一张矩形报纸ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比.则a:b=.90.两个相似多边形,其中一个多边形的周长和面积分别是10和8,另﹣多边形的周长为25,则另一个多边形的面积是.第29章《相似形》好题集(31):29.6 相似多边形及其性质参考答案填空题61.;62.2:5;63.5;20;64.30;65.60;66.1:3;67.12;68.90;69.2;70.:1;71.28;72.正确;73.31.5;27;83;74.36;75.;76.48;77.6:5;18;78.27;79.;;80;80.48;144;82.40;100;83.4;16;84.;85.12;86.1:2;87.42;88.21;30.6;89.:1;90.50;。
图形的相似综合测试题(卷)
图形的相似一.选择题〔共15小题〕1.若x:y=1:3,2y=3z,则的值是〔〕A.﹣5 B.﹣C.D.52.如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:DB=3:5,那么CF:CB等于〔〕A.5:8 B.3:8 C.3:5 D.2:53.如果两个相似多边形面积的比为1:5,则它们的相似比为〔〕A.1:25 B.1:5 C.1:2.5 D.1:4.已知矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC 与矩形ABCD相似,则AD=〔〕A.B.C.D.25.如图,在直角梯形ABCD中,AD∥BC,∠ABC=90°,AB=8,AD=3,BC=4,点P为AB边上一动点,若△PAD与△PBC 是相似三角形,则满足条件的点P的个数是〔〕A.1个B.2个C.3个D.4个6.如图,△ABC中,AB=4,AC=3,AD、AE分别是其角平分线和中线,过点C作CG⊥AD于F,交AB于G,连接EF,则线段EF的长为〔〕A.B.1 C.D.77.如图,△ABC的周长为26,点D,E都在边BC上,∠ABC的平分线垂直于AE,垂足为Q,∠ACB的平分线垂直于AD,垂足为P,若BC=10,则PQ的长为〔〕A.B.C.3 D.48.如图,△ABC中,A、B两个顶点在x轴的上方,点C的坐标是〔﹣1,0〕.以点C为位似中心,在x轴的下方作△ABC的位似图形△A′B′C,并把△ABC的边长放大到原来的2倍.设点B的对应点B′的横坐标是a,则点B的横坐标是〔〕A.B. C.D.9.在平面直角坐标系中,点A〔﹣2,1〕与点B关于原点对称,则点B的坐标为〔〕A.〔﹣2,1〕B.〔2,﹣1〕C.〔2,1〕D.〔﹣2,﹣1〕10.〔2015•庆阳〕在如图所示的平面直角坐标系中,△OA1B1是边长为2的等边三角形,作△B2A2B1与△OA1B1关于点B1成中心对称,再作△B2A3B3与△B2A2B1关于点B2成中心对称,如此作下去,则△B2n A2n+1B2n+1〔n是正整数〕的顶点A2n+1的坐标是〔〕A.〔4n﹣1,〕B.〔2n﹣1,〕C.〔4n+1,〕D.〔2n+1,〕11.如图,在△ABC中,AB=BC,∠ABC=90°,BM是AC边中线,点D,E分别在边AC和BC上,DB=DE,EF⊥AC于点F,以下结论:〔1〕∠DBM=∠CDE;〔2〕S△BDE<S四边形BMFE;〔3〕CD•EN=BN•BD;〔4〕AC=2DF.其中正确结论的个数是〔〕A.1 B.2 C.3 D.412.如图,∠ACB=90°,D为AB的中点,连接DC并延长到E,使CE=CD,过点B作BF∥DE,与AE的延长线交于点F.若AB=6,则BF的长为〔〕A.6 B.7 C.8 D.1013.如图,梯形ABCD中,AB∥CD,点E、F、G分别是BD、AC、DC的中点.已知两底差是6,两腰和是12,则△EFG的周长是〔〕A.8 B.9 C.10 D.1214.如图,在梯形ABCD中,AB∥CD,AB=3CD,对角线AC、BD交于点O,中位线EF与AC、BD分别交于M、N 两点,则图中阴影部分的面积是梯形ABCD面积的〔〕A.B.C.D.15.如图,四边形ABCD、CEFG都是正方形,点G在线段CD上,连接BG、DE,DE和FG相交于点O,设AB=a,CG=b〔a>b〕.下列结论:①△BCG≌△DCE;②BG⊥DE;③=;④〔a﹣b〕2•S△EFO=b2•S△DGO.其中结论正确的个数是〔〕A.4个B.3个C.2个D.1个二.填空题〔共10小题〕16.已知,则=.17.已知实数a,b,c满足a+b+c=10,且,则的值是.18.如图,在△ABC中,∠BAC=60°,∠ABC=90°,直线l1∥l2∥l3,l1与l2之间距离是1,l2与l3之间距离是2,且l1,l2,l3分别经过点A,B,C,则边AC的长为.19.如图,正方形ABCD中,E为AB的中点,AF⊥DE于点O,则等于.20.〔2015•高密市一模〕如图,在正三角形ABC中,D,E,F分别是BC,AC,AB上的点,DE⊥AC,EF⊥AB,FD⊥BC,则△DEF的面积与△ABC的面积之比等于.21.〔2015•XX校级模拟〕如图,在△ABC中,点D,E分别在边AB,AC上,且==,则S△ADE:S四边形BCED的值为.22.〔2015•XX〕如图,在△ABC中,CD是高,CE是中线,CE=CB,点A、D关于点F对称,过点F作FG∥CD,交AC 边于点G,连接GE.若AC=18,BC=12,则△CEG的周长为.23.〔2014•XX〕如图,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=6,BC=8,则EF的长为.24.〔2015•XX模拟〕在平面直角坐标系中,点P〔﹣20,a〕与点Q〔b,13〕关于原点对称,则a+b的值为.25.〔2015•XX模拟〕如图,在平面直角坐标系中,点B的坐标是〔1,0〕,若点A的坐标为〔a,b〕,将线段BA绕点B 顺时针旋转90°得到线段BA′,则点A′的坐标是.三.解答题〔共5小题〕26.〔2015•XX〕如图,在△ABC中,AB=AC,点P、D分别是BC、AC边上的点,且∠APD=∠B.〔1〕求证:AC•CD=CP•BP;〔2〕若AB=10,BC=12,当PD∥AB时,求BP的长.27.〔2014•宿迁〕如图,在△ABC中,点D,E,F分别是AB,BC,CA的中点,AH是边BC上的高.〔1〕求证:四边形ADEF是平行四边形;〔2〕求证:∠DHF=∠DEF.28.〔2015•XX〕在Rt△ABC中,∠BAC=90°,过点B的直线MN∥AC,D为BC边上一点,连接AD,作DE⊥AD交MN于点E,连接AE.〔1〕如图①,当∠ABC=45°时,求证:AD=DE;〔2〕如图②,当∠ABC=30°时,线段AD与DE有何数量关系?并请说明理由;〔3〕当∠ABC=α时,请直接写出线段AD与DE的数量关系.〔用含α的三角函数表示〕29.〔2015•XX模拟〕如图,在正方形ABCD中,E、F分别是边AD、CD上的点,,连接EF并延长交BC的延长线于点G.〔1〕求证:△ABE∽△DEF;〔2〕若正方形的边长为4,求BG的长.30.〔2008•贵港〕如图所示,在梯形ABCD中,AD∥BC,点E、F分别为AB、CD的中点.连接AF并延长,交BC 的延长线于点G.〔1〕求证:△ADF≌△GCF;〔2〕若EF=7.5,BC=10,求AD的长.图形的相似综合测试题参考答案一.选择题〔共15小题〕1.A;2.A;3.D;4.B;5.C;6.A;7.C;8.D;9.B;10.C; 11.C;12.C; 13.B; 14.C; 15.B;二.填空题〔共10小题〕16.-;17.;18.;19.;20.1:3;21.1:3;22.27;23.1;24.7; 25.〔b+1,-a+1〕;三.解答题〔共5小题〕26.;27.;28.;29.;30.;。
2019届中考数学复习《相似多边形》专题复习训练(有答案)
2019届初三中考数学复习 相似多边形 专题复习训练1.如图是相似多边形的是( )A .①③B .③④C .①②D .①④2.若△ABC 的每条边长增加各自的10%得△A′B′C′,则∠B′的度数与其对应角∠B 的度数相比( ) A .增加了10% B .减少了10% C .增加了(1+10%)D .没有改变3. 若五边形ABCDE ∽五边形A 1B 1C 1D 1E 1,且五边形ABCDE 与五边形A 1B 1C 1D 1E 1的相似比k 1=5,则五边形A 1B 1C 1D 1E 1与五边形ABCDE 的相似比k 2为( ) A .5 B .15C .6D .14. 如图,小正方形的边长均为1,则下列图中的三角形(阴影部分)与△ABC 相似的是( )5. 在研究相似问题时,甲、乙两同学的观点如下:甲:将边长为3,4,5的三角形按图中的方式向外扩张,得到新三角形,它们的对应边间距均为1,则新三角形与原三角形相似.乙:将邻边为3和5的矩形按图②的方式向外扩张,得到新的矩形,它们的对应边间距均为1,则新矩形与原矩形不相似. 对于两人的观点,下列说法正确的是( )A .两人都对B .两人都不对C .甲对,乙不对D .甲不对,乙对6. 如图,点P 是▱ABCD 边AB 上的一点,射线CP 交DA 的延长线于点E ,则图中相似的三角形有( )A .0对B .1对C .2对D .3对 7. 下列说法正确的是( ) A .所有的等腰三角形都相似B .四个角都是直角的两个四边形一定相似C .所有的正方形都相似D .四条边对应成比例的两个四边形相似8. 如图所示,点E 、F 分别为▱ABCD 的边AD 、BC 的中点,且▱ABFE 相似于▱ADCB ,则AB ∶BC 等于( )A .1∶4B .4∶1C .2∶1D .1∶ 29. 如图,在矩形ABCD 中,AD =2,CD =1,连接AC ,以对角线AC 为边,按逆时针方向作矩形ABCD 的相似矩形AB 1C 1C ,再连接AC 1,以对角线AC 1为边作矩形AB 1C 1C 的相似矩形AB 2C 2C 1,…,按此规律继续下去,则矩形AB n C n C n -1的面积为____.10. 已知:如图是两个形状相同的四边形,则α= ,a = cm.11.已知四边形A′B′C′D′∽四边形ABCD ,其相似比k =23,若A′B′=24,则AB =________.12. 已知两个五边形相似,一个五边形各边长分别为1、2、3、4、5,另一个五边形最大的边长是8,则这个五边形最短的边长是 .13. 下列命题:①所有的正方形都相似;②所有的矩形都相似;③有一个角都是150°的两个菱形相似;④所有的正六边形都相似.其中是真命题的有(填序号).14. 在一矩形花坛ABCD的四周修筑小路,使得相对两条小路的宽均相等.花坛的宽AB=20米,长AD=30米,试问小路的宽x与y的比值为多少时,能使小路四周所围成的矩形A′B′C′D′与矩形ABCD相似?请说明理由.15. 如图所示,一块长为2米,宽为1米的矩形玻璃,为了保护玻璃需要镶上宽10厘米的铝合金边框,那么边框的内外边缘所成的矩形相似吗?为什么?16. 如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩形ABCD相似,AB=4.(1)求AD的长;(2)求矩形DMNC与矩形ABCD的相似比k.17. 某机械厂承接一批焊接矩形钢板业务,已知这种矩形钢板在图纸上(比例尺为1∶400)的长和宽分别为3cm和2cm.此机械厂所用原料是边长为4m的正方形钢板,那么焊接一块这样的矩形钢板,至少要用几块边长为4m的正方形钢板才行?18. 如图,四边形ABCD的对角线相交于点O,A′、B′、C′、D′分别是OA、OB、OC、OD的中点,试判断四边形ABCD与A′B′C′D′是否相似,并说明理由.参考答案:1---8 CDBBA DCD9. 5n22n -110. 87° 2.5 11. 3612. 8513. ①③④ 14. 解:由题意得2020+2y =3030+2x,从而有20(30+2x)=30(20+2y).解得x y =32.∴小路的宽x 与y 的比值为32时,能使矩形A′B′C′D′与矩形ABCD 相似.15. 解:不相似,由条件知,AB EF =2+0.22=1110,BC MF =1+0.21=65,所以AB EF ≠BCMF.所以两个矩形不相似. 16. 解:(1)∵矩形DMNC 与矩形ABCD 相似,∴DM AB =DCAD,设AD =x ,则DM=12x ,∴12x 4=4x ,∴x 2=32,∴x 1=42或x 2=-42(负值舍去),∴AD=4 2.(2)k =DM AB =224=22.17. 解:设要焊接的矩形钢板的长为xcm ,宽为ycm ,则3x =2y =1400,解得x =1200(cm),y =800(cm).故这种钢板的面积为1200×800=960000(cm 2)=96(m 2),96÷(4×4)=6.所以焊接一块这样的矩形钢板,至少要用6块边长为4m 的正方形钢板才行.18. 解:相似.其理由是:由三角形中位线定理可知A′B′AB =A′D′AD =D′C′DC =B′C′BC =12,∠B′A′D′=∠BAD ,∠A′D′C′=∠ADC ,∠D′C′B′=∠DCB,∠A′B′C′=∠ABC,∴四边形A′B′C′D′∽四边形ABCD.。
相似多边形的周长比和面积比训练试题(含答案)
相似多边形的周长比和面积比训练试题(含答案)4.8相似多边形的性质一、目标导航1.相似三角形对应高的比,对应角平分线的比和对应中线的比都等于相似比;2.相似多边形的周长比等于相似比,面积比等于相似比的平方.二、基础过关1.若两个相似多边形面积比为,则它们的周长比是.2.若△ABC∽△ABC,AB=4,BC=5,AC=6,△ABC的最大边长为15,那么它们的相似比是________,△ABC的周长是________.3.两个相似三角形对应角平分线之比为1:4.则它们的周长比为,面积比为.4.若DE为△ABC的中位线,且DE//BC,则△ADE与△ABC的面积比为.5.两个相似三角形的相似比为2∶3,它们周长的差是25,那么较大三角形的周长是________.6.如图,在□ABCD中,延长AB到E,使BE=AB,延长CD到F,使DF=DC,EF交BC于G,交AD于H,则△BEG与△CFG的面积之比是________.7.把一个三角形改做成和它相似的三角形,如果面积缩小到原来的倍,那么边长应缩小到原来的________倍.8.如果两个相似三角形的面积比为9:25,而第一个三角形的周长为36,那么第二个三角形周长是.三、能力提升9.把一个矩形纸片ABCD沿AD和BC的中点连线EF对折,要使矩形AEFB与原矩形相似,则原矩形长与宽的比为()A.2∶1B.∶1C.∶1D.4∶110.在△ABC中,D、E分别是边AB、AC的中点,△ADE和四边形BCED 的面积分别记为S1、S2,那么的值为()A.B.C.D.11.在Rt△ABC中,AD为斜边BC上的高,若S=3S,则AB∶AC等于()A.1∶3B.1∶4C.1∶D.1∶212.顺次连结三角形三边的中点,所成的三角形与原三角形对应高的比是()A.1∶4B.1∶3C.1∶D.1∶213.如图,DF//EG//BC,AD=DE=EB,则面积比S:S:S等于()A.1:1:2B.1:3:5C.1:2:3D.1:4:914.如图,若∠C=90,AD=DB,ED⊥AB,AB=20,AC=12,则四边形ADEC 的面积为()A.75B.58.5C.48D.3715.在梯形ABCD中,AB//CD,若DB,AC交于点O,且△DCO的面积与△DCB的面积比为1:3,则△CDO与△ABO的面积比等于()A.1:9B.1:7C.1:4D.1:516.如图,BE//CD,AB:BC=2:3,则=()A.2:3B.4:15C.4:21D.4:1717.如图,△ABC是一块锐角三角形余料,其中BC=12cm,高AD=8cm,现在要把它裁剪成一个正方形材料备用,使正方形的一边在BC上,其余两个顶点分别在AB、AC上,问这个正方形材料的边长是多少?18.如图,在△ABC中,DE//BC,EF//AB,已知△ADE和△EFC的面积分别是4cm和9cm,求△ABC的面积.19.正方形ABCD中,E是AC上一点,EF⊥AB,EG⊥AD,AB=6,AE:EC=2:1.求四边形AFEG的面积.20.如图,□ABCD中,M为BC中点,AN=3MN,BN的延长线交AC于E,交CD于F.⑴求AE:EC的值;⑵当S=9时,求S.21.如图,△ABC中,AB=4,D在AB边上移动(不与A,B重合),DE//BC 交AC于E,连结CD,设,.⑴当D为AB中点时,求的值;⑵若AD=,,求关于的函数关系式及自变量的取值范围.四、聚沙成塔22.如图,梯形ABCD中,AD//BC,CE平分∠BCD,且CE⊥AB于E,,=14cm.求四边形ADCE的面积.23.△ABC中,AB=AC=10,BC=12,动点D在边AB上,DE⊥AB,点E 在BC上,点F在边AC上,且∠DEF=∠B,当点D在AB上运动时,⑴可能等于的二倍吗?若可能,请求出BD的长;若不可能,请说明理由.⑵可能等于的四倍吗?若可能,请求出BD的长;若不可能,请说明理由.24.在Rt△ABC中,∠C=90,AC=3,BC=4,点E在直角边AC上(点E 与A,C两点均不重合),点F在斜边AB上(点F与A,B均不重合).⑴若EF平分Rt△ABC周长,设AE的长为,试用含的代数式表示△AEF 的面积;⑵是否存在线段EF将Rt△ABC的周长和面积同时平分?若存在,求出此时AE的长;若不存在,说明理由.25.如图,在△ABC中,DE//BC,在AB上取一点F,使.求证:AD=AB•BF.26.某生活小区的居民筹集资金1600元,计划在一块上、下底分别为10米,20米的梯形空地上种植花木如图①,⑴他们在△AMD和△BMC 地带上种植太阳花,单价为8元/㎡,当△AMD地带种满花后(图中阴影部分)共花了160元,请计算种满△BMC地带所需费用.⑵若其余地带要种的有玫瑰和茉莉两种花木可供选择,单价分别为12元/㎡和10元/㎡,应选择哪种花木,刚好用完所筹集的资金.⑶若梯形ABCD 为等腰梯形,面积不变(如图②)请你设计一种花坛图案,即在梯形内找到一点P,使得△APB≌△DPC,且S=S,并说明你的理由.27.将正方形ABCD折叠,使顶点A与CD边上的点M重合,折线交AD于E,交BC于F,边AB折叠后与BC交于点G,⑴如果M为CD的中点,求证:DE∶DM∶EM=3∶4∶5.⑵如果M为CD上任一点,设AB=2a,问△CMG的周长是否与点M的位置有关?若有关,请把△CMG的周长用含DM的长x(即DM=x)的代数式表示;若无关,请说明理由.28.如图,已知△ABC中,AB=5,BC=3,AC=4,PQ∥AB,P点在AC 上(与A、C不重合),Q在BC上.⑴当△PQC的面积与四边形PABQ的面积相等时,求CP的长.⑵当△PQC的周长与四边形PABQ的周长相等时,求CP的长.⑶试问:在AB上是否存在一点M,使得△PQM为等腰直角三角形,若不存在,请简要说明理由;若存在,请求出PQ的长.29.已知,如图,在△ABC中,D是BC的中点,且AD=AC,DE⊥BC 交AB于点E,EC与AD相交于点F.⑴求证:△ABC∽△FCD;⑵若S=5,BC=10,求DE的长.30.如图,已知,在△ABC中,BA=BC=20㎝,AC=30㎝,点P从A点出发,沿AB以4㎝/s的速度向点B运动;同时点Q从C点出发,沿CA以3㎝/s的速度向A点运动,设运动时间为x,⑴当x为何值时,PQ∥BC;⑵当=1:3时,求的值;⑶△APQ能否与△CQB相似,若能,求出AP的长,若不能,请说明理由.31.如图,△ABC中,D为AC上一点,CD=2DA,∠BAC=45°,∠BDC=60°,CE⊥BD于E,连结AE.⑴写出图中所有相等的线段,并加以说明;⑵图中有无相似三角形,若有,请写出一对,若没有,请说明理由;⑶求△BEC与△BEA的面积之比.4.8相似多边形的性质1.2:3;2.2:5,37.5;3.1:4,1:16;4.1:4;5.75;6.1:16;7.;8.60;9.C;10.C;11.C;12.D;13.B;14.B;15.C;16.B;17.4.8cm;18.25;19.16;20.⑴提示:延长AD,BF交于G.AE:EC=3:2.⑵4.21.⑴S:S=1:4.⑵(0<<4).22.提示:延长BA,CD交于点F.面积=.23.⑴可能,此时BD=.⑵不可能,当S的面积最大时,两面积之比=<4.24.⑴S=.⑵存在.AE=.25.略.26.⑴640元.⑵选种茉莉花.⑶略.27.⑴利用勾股定理问题即可解决.⑵答:无关.利用△MCG∽△MDE 的周长比等于相似比可求得△MCG的面积=4.28.⑴CP=2.⑵CP=.⑶分两种情况①PQ=,②PQ=.29.提示:作△ABC的高AG.⑴略.⑵DE=.30.⑴=s.⑵2:9.⑶AP=或20.31.⑴DE=AD,AE=BE=CE.⑵有:△ADE∽△ACE或△BCD∽△ABC.⑶2:1.。
相似多边形题2
相似多边形练习题填空题1、所有矩形都相似.这句话是_________ 的.2、两个相似多边形,其中一个多边形的周长和面积分别是10和8,另﹣多边形的周长为25,则另一个多边形的面积是_________ .3、把一个正方形的周长放大到原来的3倍,则原图形与新图的相似比为_________ .4、两个相似的七边形的相似比为3:4,它们的面积之差为28,则面积之和为_________ .5、两个相似多边形对应边的比为,那么周长的比为_________ ,面积的比为_________ .6、两个相似的五边形,一个各边长分别为1,2,3,4,5,另一个最大边长为10,则后一个五边形的最短边的长为_________ .7、如图,一张矩形报纸ABCD的长AB=acm,宽BC=bcm,E、F分别是AB,CD的中点、将这张报纸沿着直线EF对折后,矩形AEFD的长与宽之比等于矩形ABCD的长与宽之比.则a:b等于_________8、一个六边形的边长依次为1,2,3,4,5,6.与它相似的另一个多边形最大边长为12,则另一个多边形的周长为_________ .9、如图,四边形ABCD∽四边形A′B′C′D′,则∠1=_________ ,AD= _________ .10、在一张比例尺为1:30000的地图上,一多边形地区的周长为70cm,面积为340cm2,那么该地区的实际周长为_________ km,面积为_________ km2.11、两个相似多边形对应边的比为3:2,小多边形的面积为32cm2,那么大多边形的面积为_________ cm2.12、要作一个六边形和已知六边形相似,且使周长是原来的5倍,那么对应边应为原来的_________ 倍.13、已知两个相似多边形的相似比为5:7,若较小的一个多边形的周长为35,则较大的一个多边形的周长为_________ ;若较大的一个多边形的面积是4,则较小的一个多边形的面积是_________ .解答题14、如图,已知在平行四边形ABCD中,点E在边BC上,射线AE交BD于点G,交DC的延长线于点F,AB=6,BE=3EC,则DF= _________ .15、如图,AB∥EF∥CD,已知AC+BD=240,BC=100,EC+ED=192,则CF= _________ .16、如图,在△ABC中,点D、E分别在BC、AC上,BE平分∠ABC,DE∥BA,如果CE=6,AE=4,AB=15,则DE= _________ ,CD= _________ .17、已知:如图,l 1∥l 2∥l 3,AB=3,BC=5,DF=12.则DE= _________ ,EF= _________ .18、如图,F 是平行四边形ABCD 的边AD 上一点,CF 交BA 的延长线于点E ,若,AB=4,则AE= _________ .19、如图,△ABC 的面积是10,点D 、E 、F (与A 、B 、C 不同的点)分别位于AB 、BC 、CA 各边上,而且AD=2,DB=3,如果△ABE 的面积和四边形DBEF 的面积相等,则这个相等的面积值是 _________ .20、如图,射击瞄准时,要求枪的标尺缺口上沿中央A 、准星点B 和瞄准点C 在同一条直线上,这样才能命中目标(不计实际误差).已知某种冲锋枪基线AB 的长为38.5厘米,如果射击距离AC 为100米,当准星尖在缺口内偏差BB′为1毫米时,弹着点偏差CC′= _________ 厘米.(精确到0.001)21、下图中的两个多边形分别是幻灯片上的多边形ABCDEF 和银幕上的多边形A 1B 1C 1D 1E 1F 1,它们的形状相同吗? _________ ;在上图的两个多边形中,是否有相等的内角? _________ .22、设四边形ABCD 与四边形A 1B 1C 1D 1是相似的图形,且A 与A 1、B 与B 1、C 与C 1是对应点,已知AB=12,BC=18,CD=18,AD=9,A 1B 1=8,则四边形A 1B 1C 1D 1的周长为 _________ .答案与评分标准填空题1、所有矩形都相似.这句话是错误的.考点:相似多边形的性质;命题与定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 相似三角形单元测试题 一填空题(每题3分,共36分) 1. 若两个三角形的面积比是1:9,则它们对应边的中线之比为:
2. 若0234xyz,则23xyz . 3. 如图,已知AB⊥BD,ED⊥BD,C是线段BD的中点,且AC⊥CE,ED=1,BD=4,那么AB= .
4.在 ABC中,D为 AB 的中点,AB = 4 ,AC = 7 ,若 AC 上有一点E,且 ΔADE 与
原三角形相似,则 AE = ;
5.在平行四边形ABCD中,E是AB延长线上的一点,连接DE交AC于点G,交BC于点F,则图中有相似三角形 对. 6.某同学利用影子长度测量操场上旗杆的高度,在同一时刻,他测得自己影子长为0.8m,旗杆的影子长为7m,已知他的身高为1.6m,则旗杆的高度为 m. 7.要把一根1m长的铜丝截成两段,用它们围成两个相似三角形,且相似比为 ,那么截成的两段铜丝的长度差应是 m. 8. △ABC的边长分别为AB=14,BC=16,AC=26,P为∠BAC的角平分线上的一点且BP⊥AP,M是BC的中点,则PM的长是 . A1 B1 C1 D1 E1 A
B C D
E 第10题
352
9.已知E是平行四边形ABCD的中点,若平行四边形ABCD的面积为1,则阴影部分的面积为 . 10.如图示的梯形梯子.AB=BC=CD=DE,A1B1=B1C1=C1D1=D1E1,AA1=0.5m,EE1=O.8m,则BB1+CC1+DD1= m. 11.如图示,正方形OEFG和正方形ABCD是位似形,点F的坐标为(1、1),点C的坐标为 (4、2),则两正方形位似的中心坐标是 . 12.在平形四边形ABCD中,F是BC的中点,E是AB上的一点,AE=2BE,BD交EF于点G,则BG:GD= .
二选择题(每题3分,共18分) 13 如图,下列条件中不能判定ACDABC△∽△的是 ( )
(A)ABADBCCD (B)ADCACB (C)ACDB (D)2ACADAB 14.下列四组图形中不一定相似的是.( ) A.有一个角等于40°的两个等腰三角形 B.有一个角为50°的两个直角三角形 C.直角三角形被斜边上的高分成的两个直角三角形 D.有一个角是60°的两个等腰三角形
第11题 A C D
B 第13题 3
15.在同一时刻的阳光下,小明的影子比小强的影子长,那么在同一路灯下:( ) A.小明的影子比小强的影子长 B.小明的影子比小强的影子短 C.小明的影子和比小强的影子一样长 D.谁的影子长不确定 16.在Rt△ACB中,∠ACB=90°,CD⊥AB于D,则图中相似三角形有 ( ) A.1对 B.2对 C.3对 D.4对 17.在四边形ABCD中,E是AB上的一点,EC∥AD,DE∥BC,若S△BEC=1, S△ADE=3,S△CDE= ( ) A.2 B.3:2 C. 3 D.2 18.在四边形ABCD中,一组对边AB=CD.另一组对边AD≠BC,分别取AD、BC中点M、N,连结MN,则AB同MN的关系是 ( ) A.AB=MN B.AB>MN C.AB<MN D.上述三种情况均有可能 19.在矩形FGHN中,点F、G在 BC边上,点N、H分别在 AB、AC边上,且AD⊥BC,垂足为D,AD交NH于E,AD=8cm,BC=24cm,NH=2FN,求此时矩形的面积?(10分)
22. 如图四边形ABCD和四边形ACED都是平行四边形,点R为DE的中点,BR分别交AC、CD于点P、Q。 ⑴请写出图中各对相似三角形(相似比为1 除外);(3分) (2)求BP∶PQ∶QR(7分)
23.如图,M为线段AB的中点,AE与BD交于点C,∠DME=∠A=∠B=,且DM交AC于F,ME交BC于G.
QP
AD
BCE
R4
(1)写出图中三对相似三角形,并证明其中的一对;(5分) (2)连接FG,如果=45°,AB=42,AF=3,求FG的长.(6分)
24.在梯形ABCD中,AD∥BC,AD=6cm,CD=4cm ,BC=BD=10cm,点P由B出发沿BD方向匀速运动,速度为1cm/s;同时线段EF由DC出发沿DA方向匀速运动,速度为1cm/s;交BD于Q,连接PE,若运动时间为t(s)(0﹤t﹤5),解答下列问题: (1)当t为何值知时?PE∥AB?(3分) (2)设△PEQ的面积为y(cm2),求y与t之间的函数关系式;(5分) (3)是否存在某一时刻,使S△PEQ= S△BCD?若存在,求出t的值?若不存在,说明理由?(3分) (4)连接PF,在上述运动过程中,五边形PFCDE的面积是否会发生变化?说明理由?(4
分)
2255
相似图形单元测试题 一.选择题(每小题3分,共30分) 1、如图,在RtABC△内有边长分别为a,b,c的三个正方形.则a,b,c满足的关系
式是( ) A.bac B.bac C.222bac D.22bac
2、如图,小正方形的边长均为1,则图中三角形(阴影部分)与△ABC相似的是( ) 3、如下左图,五边形ABCDE
和五边形A1B1C1D1E1是位似图形,且PA1=32PA,则AB׃A1B1等于( )
A.32 B.23 C. 53 D .35
4、如上中图,在大小为4×4的正方形网格中,是相似三角形的是( ).
A.①和② B.②和③ C.①和③ D.②和④ 5、厨房角柜的台面是三角形,如上右图,如果把各边中点的连线所围成的三角形铺成黑色大理石.(图中阴影部分)其余部分铺成白色大理石,那么黑色大理石的面积与白色大理石面积的比是( )
C E1D1
C1B
1
A1
B
DAC
EP6
A.14 B.41 C.13 D.34 6、在△MBN中,BM=6,点A,C,D分别在MB、NB、MN上,四边形ABCD为平行四边形,∠NDC=∠MDA则□ABCD的周长是 ( ) A.24 B.18 C.16 D.12 7、下列说法“①位似图形都相似;②位似图形都是平移后再放大(或缩小)得到;③直角三
角形斜边上的中线与斜边的比为1∶2;④两个相似多边形的面积比为4∶9,则周长的比为16∶81.”中,正确的有( ) A.1个 B.2个 C.3个 D.4个
8、如图,点M在BC上,点N在AM上,CM=CN,CMBMANAM,下列结论正确的是( ) A.ABM∽ACB B.ANC∽AMB C.ANC∽ACM D.CMN∽BCA
9、已知:如图,小明在打网球时,要使球恰好能打过而且落在离网5米的位置上(网球
运行轨迹为直线),则球拍击球的高度h应为( ). A.0.9m B.1.8m C.2.7m D.6m
10、如图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O)20米的点A处,沿OA所在的直线行走14米到点B时,人影的长度
A.增大1.5米 B.减小1.5米 C.增大3.5米 D.减小3.5米
第8题图 ABCNM7
二、填空题:(30分) 11、如图,在平行四边形ABCD中,M、N为AB的三等分点,DM、DN分别交AC于P、Q
两点,则AP:PQ:QC= .
12、如图,将①∠BAD = ∠C;②∠ADB = ∠CAB; ③BCBDAB2;④DBABADCA;⑤DAACBABC; ⑥ACDABABC中的一个作为条件,另一个作为结论,组成一个真命题,则条件是__________,结论是_______.(注:填序号) 13、如图,RtABC中,AC⊥BC,CD⊥AB于D,AC=8,BC=6,则AD=_________。 14、已知:AM∶MD=4∶1,BD∶DC=2∶3,则AE∶EC=_________。 15、如图, C为线段AB上的一点,△ACM、△CBN都是等边三角形,若AC=3,BC=2,则△MCD与△BND的面积比为 。
16、如图,在矩形ABCD中,沿EF将矩形折叠,使A、C重合,若AB=6,BC=8,则折
痕EF的长为 .
17、如图,已知点D是AB边的中点,AF∥BC,CG∶GA=3∶1,BC=8,则AF= 18、如图,在平面直角坐标系中有两点A(4,0),B(0,2),如果点C在x轴上(C与
A不重合)当点C的坐标为 时,使得△BOC∽△AOB.
19、两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积之和为
130cm2,那么较小的多边形的面积是 cm2.
A B
C
D
M N
第15题
A
B D F
G
C E 第17题
