九年级数学多边形问题
最新:人教版九年级上册数学24.3《正多边形和圆》

多边形吗?为什么?
不是,因为矩形不符合各边相等; 不是,因为菱形不符合各角相等;
注意
各边相等 正多边形
缺一不可 各角相等
问题3 正三角形、正四边形、正五边形、正六边
形都是轴对称图形吗?都是中心对称图形吗?
问题3 正三角形、正四边形、正五边形、正六边形都 是轴对称图形吗?都是中心对称图形吗?
如图,已知半径为4的圆内接正六边形ABCDEF: ①它的中心角等于 ③△OBC是 等边 △OBC面积的 6
60
度 ;
A
F O
E D
② OC = BC (填>、<或=); 三角形; 倍.
④圆内接正六边形的面积是
B
P
C
1 S正多边形 = 周长 边心距 2 ⑤圆内接正n边形面积公式:_______________________子,它的地基是半径为4 m的正 六边形,求地基的周长和面积 (精确到0.1 m2).
F
抽象成 A O P
E
D C
解:过点O作OM⊥BC于M. 在Rt△OMB中,OB=4,
BC 4 2, MB= 2 2 F
A O E
利用勾股定理,可得边心距
r 42 22 2 3.
∴OA=OD;OB=OC. ∴OA=OB=OC=OD. ∴正方形ABCD有一个以点O
D
C
为圆心的外接圆.
AC是∠DAB及∠DCB的角平 A
E
B O
分线,BD是∠ABC及∠ADC 的角平分线,
G
F
H
∴OE=OH=OF=OG. ∴正方形ABCD还有一个以
D
C
点O为圆心的内切圆.
想一想
九年级数学 圆内接正多边形 专题练习(含解析)

C.连接 AD,则 AD 分别平分∠EAC 与∠EDC D.图中一共能画出 3 条对称轴
答案:B 解析:解答: A.∵多边形 ABCDEF 是正六边形, ∴△ACE 是等边三角形,故本选项正确; B.∵△ACE 是等边三角形,∴是轴对称图形,不是中心对称图形,故本选项错误; C.∵△ACE 是等边三角形,∴连接 AD,则 AD 分别平分∠EAC 与∠EDC,故本选项正确; D.∵△ACE 是等边三角形,∴图中一共能画 3 条对称轴,故本选项正确. 故选 B. 分析:根据正多边形的性质和轴对称图形与中心对称图形的定义解答.
C.18
D.36
答案:C
解析:解答:连接正六边形的中心与各个顶点,得到六个等边三角形,
等边三角形的边长是 2 ,高为 3,
因而等边三角形的面积是 3 ,
∴正六边形的面积=18 , 故选 C. 分析:解题的关键要记住正六边形的特点,它被半径分成六个全等的等边三角形.
12.已知某个正多边形的内切圆的半径是 ()
∴△OAB 是等边三角形, ∴OB=AB=24cm,
∴ 60 ´ 24 = 8 180
故选 B 分析:连接 OA、OB,得出等边三角形 AOB,求出 OB 长和∠AOB 度数,根据弧长公式求
出即可.
10.若一个正六边形的半径为 2,则它的边心距等于( )
A.2 B.1 C.
D.2
答案:C 解析:解答:已知正六边形的半径为 2,则正六边形 ABCDEF 的外接圆半径为 2, 如图:
连接 OA,作 OM⊥AB 于点 M, 得到∠AOM=30°,
则 OM=OA•cos30°= .
则正六边形的边心距是 .
故选 C. 分析:根据正六边形的边长与外接圆的半径相等,构建直角三角形,利用直角三角形的边角 关系即可求出.
2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习(含答案)

2020年人教版九年级数学上册24.3《正多边形和圆》随堂练习基础题知识点1 认识正多边形1.下面图形中,是正多边形的是( )A.矩形 B.菱形C.正方形 D.等腰梯形2.如图,正六边形的每一个内角都相等,则其中一个内角α的度数是( )A.240° B.120° C.60° D.30°3.一个正多边形的一个外角等于30°,则这个正多边形的边数为.4.如图,AC是正五边形ABCDE的一条对角线,则∠ACB= .知识点2 与正多边形有关的计算5.如图,正六边形ABCDEF内接于⊙O,正六边形的周长是12,则⊙O的半径是( )A. 3 B.2 C.2 2 D.2 36.下列圆的内接正多边形中,一条边所对的圆心角最大的图形是( )A.正三角形 B.正方形C.正五边形 D.正六边形7.若正方形的外接圆半径为2,则其内切圆半径为( )A. 2 B.2 2C.22D.18.边长为6 cm的等边三角形的外接圆半径是.9.如图,将正六边形ABCDEF放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C的坐标为( ).10.将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于 (结果保留根号).知识点3 画正多边形11.如图,甲:①作OD的中垂线,交⊙O于B,C两点;②连接AB,AC,△ABC即为所求的三角形.乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;②连接AB,BC,CA,△ABC即为所求的三角形.对于甲、乙两人的作法,可判断( )A.甲、乙均正确 B.甲、乙均错误C.甲正确,乙错误 D.甲错误,乙正确12.图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).中档题13.正三角形内切圆半径r与外接圆半径R之间的关系为( )A.4R=5r B.3R=4rC.2R=3r D.R=2r14.如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是( )A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)15.以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是( )A.22B.32C. 2D. 316.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为( )A.2a2 B.3a2 C.4a2 D.5a217.如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为.18.如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10= .19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.综合题20.如图1,2,3,…,m,M,N分别是⊙O的内接正三角形ABC,正方形ABCD,正五边形ABCDE,…正n边形ABCDEF…的边AB,BC上的点,且BM=CN,连接OM,ON.(1)求图1中∠MON的度数;(2)图2中∠MON的度数是,图3中∠MON的度数是;(3)试探究∠MON的度数与正n边形边数n的关系(直接写出答案).参考答案01 基础题知识点1 认识正多边形1.下面图形中,是正多边形的是(C)A .矩形B .菱形C .正方形D .等腰梯形2.(柳州中考)如图,正六边形的每一个内角都相等,则其中一个内角α的度数是(B)A .240°B .120°C .60°D .30°3.(连云港中考)一个正多边形的一个外角等于30°,则这个正多边形的边数为12.4.(资阳中考)如图,AC 是正五边形ABCDE 的一条对角线,则∠ACB=36°.知识点2 与正多边形有关的计算5.(沈阳中考)如图,正六边形ABCDEF 内接于⊙O ,正六边形的周长是12,则⊙O 的半径是(B)A. 3B .2C .2 2D .2 3 6.(株洲中考)下列圆的内接正多边形中,一条边所对的圆心角最大的图形是(A) A .正三角形 B .正方形 C .正五边形 D .正六边形7.(滨州中考)若正方形的外接圆半径为2,则其内切圆半径为(A)A. 2 B .2 2C.22D .1 8.边长为6 cm 的等边三角形的外接圆半径是23.9.(宁夏中考)如图,将正六边形ABCDEF 放在直角坐标系中,中心与坐标原点重合.若A点的坐标为(-1,0),则点C 的坐标为(12,-32).10.(教材P109习题T6变式)将一个边长为1的正八边形补成如图所示的正方形,这个正方形的边长等于1+2(结果保留根号).知识点3 画正多边形甲:①作OD的中垂线,交⊙O于B,C两点;②连接AB,AC,△ABC即为所求的三角形.乙:①以D为圆心,OD长为半径作圆弧,交⊙O于B,C两点;②连接AB,BC,CA,△ABC即为所求的三角形.对于甲、乙两人的作法,可判断(A)A.甲、乙均正确B.甲、乙均错误C.甲正确,乙错误D.甲错误,乙正确12.(镇江中考改编)图1是我们常见的地砖上的图案,其中包含了一种特殊的平面图形——正八边形.如图2,AE是⊙O的直径,用直尺和圆规作⊙O的内接正八边形ABCDEFGH(不写作法,保留作图痕迹).解:如图.02中档题13.正三角形内切圆半径r与外接圆半径R之间的关系为(D)A.4R=5r B.3R=4rC.2R=3r D.R=2r14.(滨州中考)如图,正五边形ABCDE放入某平面直角坐标系后,若顶点A,B,C,D的坐标分别是(0,a),(-3,2),(b,m),(c,m),则点E的坐标是(C)A.(2,-3) B.(2,3)C.(3,2) D.(3,-2)15.(达州中考)以半径为2的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形,则该三角形的面积是(A)A.22B.32C. 2D. 316.为增加绿化面积,某小区将原来正方形地砖更换为如图所示的正八边形植草砖,更换后,图中阴影部分为植草区域,设正八边形与其内部小正方形的边长都为a,则阴影部分的面积为(A)A.2a2 B.3a2 C.4a2 D.5a217.(山西中考命题专家原创)如图,圆O与正八边形OABCDEFG的边OA,OG分别交于点M,N,则弧MN所对的圆心角∠MPN的大小为67.5°.18.(连云港中考)如图,正十二边形A1A2…A12,连接A3A7,A7A10,则∠A3A7A10=75°.19.如图,⊙O是正方形ABCD与正六边形AEFCGH的外接圆.(1)正方形ABCD与正六边形AEFCGH的边长之比为2∶1;(2)连接BE,BE是否为⊙O的内接正n边形的一边?如果是,求出n的值;如果不是,请说明理由.解:BE是⊙O的内接正十二边形的一边,理由:连接OA ,OB ,OE ,在正方形ABCD 中,∠AOB=90°,在正六边形AEFCGH 中,∠AOE=60°,∴∠BOE=30°.∵n=360°30°=12, ∴BE 是正十二边形的边.03 综合题20.如图1,2,3,…,m ,M ,N 分别是⊙O 的内接正三角形ABC ,正方形ABCD ,正五边形ABCDE ,…正n 边形ABCDEF …的边AB ,BC 上的点,且BM=CN ,连接OM ,ON.(1)求图1中∠MON 的度数;(2)图2中∠MON 的度数是90°,图3中∠MON 的度数是72°;(3)试探究∠MON 的度数与正n 边形边数n 的关系(直接写出答案).解:(1)连接OA ,OB.∵正三角形ABC 内接于⊙O ,∴OA=OB ,∠OAM=∠OBA=30°,∠AOB=120°.∵BM=CN ,AB=BC ,∴AM=BN.∴△AOM ≌△BON(SAS).∴∠AOM=∠BON.∴∠AOM +∠BOM=∠BON +∠BOM ,即∠AOB=∠MON.∴∠MON=120°.(3)∠MON=360°n.。
九年级数学正多边形的有关计算

1 1 2 S4 4r4 a4 4 2 R R 2 2 2 2R2
用代数式表示半径为R的圆的内接正六边形
的边长为a6,边心距r6和面积S6.
180 a6 2 R sin 6 R
1 1 3 180 S 6 r a 6 R R R cos30 6 r6 R cos 6 6 2 2 2 2R sin 30 6 3 3 2 3 R R 2 2
O R
例2、在一种联合收割机上,拨禾轮的 侧面是正五边形,测得这个正五边形的 边长是48cm,求它的半径R5和边心距 r5(精确到0.1cm).
D E A
O F C
B
试试你会了吗?
用代数式表示半径为R的圆的内接正方形的
边长为a4,边心距r4和面积S4.
180 r R cos R cos 45 180 a4 2 R sin 2R sin 45 4 4 4 2 R 2R 2的 , 腰是外接圆的 ,底边是正多边 形的 ,底边上的高是正多边形 的 .能运用 方法 求出边和角的关系.
;/ 原创文章 ;
戾气让他很不爽,所以才打算将他彻底踩翻在地.此刻天辰の表现,他倒是有些意味索然了. 大家都是被困在笼子里の苦哈哈,彼此斗来斗去也没什么意思.于是他淡淡摆了摆手说道:"这次赌约就算了,没啥意思,当然俺会尽全力登顶,不过,俺不保证能一定登得上去,也不一定能走进那座祭坛!大 家为俺掠阵吧!" "好,夜不咋大的兄弟!努力,俺相信你呀一定行の!" 麒厉眼中冒着刺眼の光芒,竟然朝白重炙深深一揖,所有の强者都目光灼灼の望着白重炙,等待着他の惊人表现. "嗡…" 突然,场中空间一阵波动,一条窈窕の身影凭空出现在场中,而后传送阵一阵闪亮,雷帝那伟岸の身影出
九年级数学多边形练习题及答案

九年级数学多边形练习题及答案题1:已知正方形的边长为6cm,请计算其面积和周长。
解:面积的计算公式为:面积 = 边长 ×边长周长的计算公式为:周长 = 4 ×边长根据题目中的信息,可以得出:面积 = 6cm × 6cm = 36cm²周长 = 4 × 6cm = 24cm题2:一个正六边形的边长为8cm,请计算其周长和面积。
解:周长的计算公式为:周长 = 6 ×边长面积的计算公式为:面积= (3 × √3) ÷ 2 × 边长²根据题目中的信息,可以得出:周长 = 6 × 8cm = 48cm面积= (3 × √3) ÷ 2 × 8cm² ≈ 69.28cm²题3:某个凸五边形的边长分别为10cm、12cm、8cm、7cm和6cm,请计算其周长。
解:周长的计算公式为:周长 = 边长1 + 边长2 + 边长3 + 边长4 + 边长5根据题目中的信息,可以得出:周长 = 10cm + 12cm + 8cm + 7cm + 6cm = 43cm题4:一个正五边形的周长为35cm,请计算其边长和面积。
解:边长的计算公式为:边长 = 周长 ÷ 5面积的计算公式为:面积 = (边长² × √25 + 10 × √5) ÷ 4根据题目中的信息,可以得出:边长 = 35cm ÷ 5 = 7cm面积= (7cm² × √25 + 10 × √5) ÷ 4 ≈ 70.71cm²题5:一个凹四边形的边长分别为6cm、8cm、10cm和7cm,请计算其周长。
解:周长的计算公式为:周长 = 边长1 + 边长2 + 边长3 + 边长4根据题目中的信息,可以得出:周长 = 6cm + 8cm + 10cm + 7cm = 31cm答案总结:1. 正方形的面积为36cm²,周长为24cm。
九年级数学下册《第二十七章 成比例线段与相似多边形》练习题附答案解析-人教版

九年级数学下册《第二十七章 成比例线段与相似多边形》练习题附答案解析-人教版班级:___________姓名:___________考号:____________一、单选题1.如果:12:8a b =,且b 是a ,c 的比例中项,那么:b c 等于( )A .4:3B .3:2C .2:3D .3:42.4和9的比例中项是( )A .6B .6±C .169D .8143.下列各组图形中,一定是相似形的是( )A .两个腰长相等的等腰梯形B .两个半径不等的半圆C .两个周长相等的三角形D .两个面积相等的矩形4.用一个2倍放大镜照一个ABC ,下面说法中错误的是( )A .ABC 放大后,A ∠是原来的2倍B .ABC 放大后,各边长是原来的2倍C .ABC 放大后,周长是原来的2倍D .ABC 放大后,面积是原来的4倍5.下列结论中,错误的有:( )①所有的菱形都相似;②放大镜下的图形与原图形不一定相似;③等边三角形都相似;④有一个角为110度的两个等腰三角形相似;⑤所有的矩形不一定相似.A .1个B .2个C .3个D .4个6.已知,如图两个四边形相似,则∠α的度数是( )A .87°B .60°C .75°D .120°7.对于题目:“在长为6,宽为2的矩形内,分别剪下两个小矩形,使得剪下的两个矩形均与原矩形相似,请设计剪下的两个矩形周长和为最大值时的方案,并求出这个最大值.”甲、乙两个同学设计了自认为满足条件的方案,并求出了周长和的最大值.甲方案:如图1所示,最大值为16;乙方案:如图2所示,最大值为16.下列选项中说法正确的是( )A .甲方案正确,周长和的最大值错误B .乙方案错误,周长和的最大值正确C .甲、乙方案均正确,周长和的最大值正确D .甲、乙方案均错误,周长和的最大值错误8.如图,以点O 为位似中心,把ABC 的各边放大为原来的2倍得到A B C ''',下列说法错误的是( )A .AB //A B ''B .:1:2AO AA '=C .ABC A B C '''∽△△D .:1:4ABC A B C S S '''=9.已知四边形ABCD ∽四边形EFGH ,且AB =3,EF =4,FG =5.则四边形EFGH 与四边形ABCD 的相似比为( )A .3:4B .3:5C .4:3D .5:3二、解答题10.如图,所示的两个矩形是否相似?并简单说明理由.11.在一张复印出来的纸上,一个三角形的一条边由原图中的2cm 变成了6cm ,放缩比例是多少?这个三角形的面积发生了怎样的变化?''''.12.如图,四边形ABCD∽四边形A B C D(1)α=________,它们的相似比是________;(2)求边x的长度.13.一个矩形的长是宽的2倍,写出这个矩形的面积关于宽的函数解析式.14.在△ABC中,AB=AC,点D在边BC所在的直线上,过点D作DE∥AC交直线AB于点E,DF∥AB交直线AC于点F.(1)当点D在边BC上时,如图①,求证:DE+DF=AC;(2)当点D在边BC的延长线上时,如图②;当点D在边BC的反向延长线上时,如图③,请分别写出图②、图③中DE、DF、AC之间的等量关系式(不需要证明);(3)若AC=10,DE=7,问:DF的长为多少?三、填空题15.四边形ABCD和四边形A′B′C′D′,O为位似中心,若OA:OA′=1:4,那么S四边形ABCD:S四边形A′B′C′D′=______.16.相似图形:①定义:形状相同的图形叫做______.②性质:两个图形相似是指它们的形状相同,与他们的______无关.全等图形与相似图形的联系与区别:全等图形是一种特殊的相似图形,不仅形状相同,大小也相同.17.两地的实际距离是1200千米,在地图上量得这两地的距离为2厘米,则这幅地图的比例尺是1∶___.参考答案与解析1.B【分析】由b 是a 、c 的比例中项,根据比例中项的定义,即可求得=b a c b,又由a :b =12:8,即可求得答案.【详解】解:∵b 是a 、c 的比例中项∴b 2=acb ac b∴= ∵a :b =12:8 ∴12382a b == :3:2b c ∴=故选:B .【点睛】此题主要考查了比例线段,正确把握比例中项的定义是解题关键.2.B【分析】根据比例中项的定义:如果存在a 、b 、c 三个数,满足::a b b c =,那么b 就交租ac 的比例中项,进行求解即可.【详解】解:设4和9的比例中项为x∴4::9x x =∴6x =±故选B .【点睛】本题主要考查了求比例中项,熟知比例中项的定义是解题的关键.3.B【分析】根据相似图形的定义知,相似图形的形状相同,但大小不一定相同,依据定义即可解决.【详解】解:两个腰长相等的等腰梯形、两个周长相等的三角形、两个面积相等的矩形都属于形状不唯一确定的图形.故A 、C 、D 错误;而圆的形状唯一确定,两个半径不等的半圆相似,故B 正确.故选B .【点睛】本题考查相似形的识别,解题关键要联系实际,根据相似图形的定义得出.4.A【分析】用2倍的放大镜放大一个△ABC,得到一个与原三角形相似的三角形;根据相似三角形的性质:相似三角形的面积比等于相似比的平方,周长比等于相似比.可知:放大后三角形的面积是原来的4倍,边长和周长是原来的2倍,而内角的度数不会改变.【详解】解:因为放大前后的三角形相似放大后三角形的内角度数不变面积为原来的4倍,周长和边长均为原来的2倍故选A.【点睛】本题考查对相似三角形性质的理解:(1)相似三角形周长的比等于相似比;(2)相似三角形面积的比等于相似比的平方;(3)相似三角形对应高的比、对应中线的比、对应角平分线的比都等于相似比.5.B【分析】根据相似多边形的定义判断①⑤,根据相似图形的定义判断②,根据相似三角形的判定判断③④. 【详解】相似多边形对应边成比例,对应角相等,菱形之间的对应角不一定相等,故①错误;放大镜下的图形只是大小发生了变化,形状不变,所以一定相似,②错误;等边三角形的角都是60°,一定相似,③正确;钝角只能是等腰三角形的顶角,则底角只能是35°,所以两个等腰三角形相似,④正确;矩形之间的对应角相等,但是对应边不一定成比例,故⑤正确.有2个错误,故选B.【点睛】本题考查相似图形的判定,注意相似三角形与相似多边形判定的区别.6.A【解析】略7.D【分析】根据相似多边形对应边的比相等的性质分别求出两个小矩形纸片的长与宽,进而求解即可.【详解】解:∵6:2=3:1∴三个矩形的长宽比为3:1甲方案:如图1所示3a+3b=6∴a+b=2周长和为2(3b+b)+2(3a+a)=8(a+b)=16;乙方案:如图2所示a+b=2周长和为2(3b+b)+2(3a+a)=8(a+b)=16;如图3所示矩形①的长为2,则宽为2÷3=23;则矩形②的长为6-23=163,宽为163÷3=169;∴矩形①和矩形②的周长和为2(2+23)+2(163+169)=1769;∵176916∴周长和的最大值为1769;故选:D.【点睛】本题考查了相似多边形的性质,分别求出所剪得的两个小矩形纸片的长与宽是解题的关键.8.B【分析】根据位似的性质对各选项进行判断,如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心,位似的两个图形必须是相似形,对应点的连线都经过同一点;对应边平行或共线.【详解】以点O 为位似中心,把ABC 的各边放大为原来的2倍得到A B C '''∴ABC ∆和A B C '''∆是位似图形∴ABC ∆~A B C '''∆,故C 正确;∴:1:2AO OA '=,:1:2OB OB =' 又AOB A OB ''∠=∠ABO ∆~ΔA B O ''∴ABO A B O ∠=∠''∴AB //A B ''故A 正确;∵把ABC 的各边放大为原来的2倍得到A B C '''∴:1:2AO OA '=∴:1:3AO AA '=,故B 选线说法错误; ∵2:()1:4ABC A B C OA S S OA ''''==,故D 正确; ∴说法错误的是:B 选项;故选:B .【点睛】本题考查了位似图形变换,正确掌握位似的性质是解题的关键.9.C【解析】略10.相似,见解析【分析】要说明两个矩形是否相似,只要说明对应角是否相等,对应边的比是否相等.【详解】解:相似.理由:这两个的角是直角,因而对应角相等一定是正确的小矩形的长是20-5-5=10,宽是12-3-3=6 因为1062012=,即两个矩形的对应边的比相等 因而这两个矩形相似.【点睛】此类题目主要考查相似多边形的识别.判定两个图形相似的依据是:对应边成比例,对应角相等,两个条件必须同时具备.11.放缩比例是3:1,面积扩大为原来的9倍【分析】根据放缩比例等于对应边的比解答;根据相似多边形面积的比等于相似比的平方解答.【详解】解:∵多边形的一条边由原图中的2cm变成了6cm∴这次复印的放缩比例是6:2=3:1∴这个多边形的面积变为原来的9倍.【点睛】本题考查了相似多边形的性质,主要利用了相似比的求解以及相似多边形面积的比等于相似比的平方.12.(1)81︒ 3∶2;(2)332 x=【分析】(1)根据相似多边形的性质求出∠A′、∠B′,以及相似比,根据四边形的内角和定理求出∠C′;(2)根据相似多边形的性质列出比例式,计算即可.(1)解:∵四边形ABCD∽四边形A B C D''''∴∠A′=∠A=64°,∠B′=∠B=75°∴∠C′=360°−64°−75°−140°=81°它们的相似比为:93 62 =故答案为:81°3 2(2)解:∵四边形ABCD∽四边形A′B′C′D′∴9 116 x=解得x=332.【点睛】本题考查的是相似多边形的性质,掌握相似多边形的对应角相等、对应边成比例是解题的关键.13.S=2x 2【分析】用x表示矩形的宽,则矩形的长为2x,然后利用矩形的面积公式即可得到解析式.【详解】解:∵矩形的长是宽的2倍,宽为x∴矩形的长是2x∵矩形的面积=长×宽∴S=x•2x=2x2故答案为:S=2x2.【点睛】此题考查了列函数关系式,解题关键是:熟记矩形的面积公式.14.(1)见解析;(2)图②中,DE﹣DF=AC;图③中,DF﹣DE=AC;(3)17或3【分析】(1)证明四边形AEDF是平行四边形,且△BED和△DFC是等腰三角形即可证得;(2)与(1)的证明方法相同;(3)根据(1)(2)中的结论直接求解.【详解】解:(1)∵DE∥AC,DF∥AB∴四边形AEDF是平行四边形∴DE=AF,∠FDC=∠B又∵AB=AC∴∠B=∠C∴∠FDC=∠C∴DF=FC∴DE+DF=AF+FC=AC;(2)如图②,当点D在边BC的延长线上时∵DE∥AC,DF∥AB∴四边形AEDF是平行四边形∴DE=AF,∠FDC=∠B又∵ZAB=AC∴∠B=∠ACB=∠DCF∴∠FDC=∠DCF∴DF=FC∴DE=AF=AC+CF=AC+DF;即DE﹣DF=AC;当点D在边BC的反向延长线上时,在图③∵DE∥AC,DF∥AB∴四边形AEDF是平行四边形∴DE=AF,∠FDC=∠ABC又∵AB=AC∴∠ABC=∠C∴∠FDC=∠C∴DF=FC∴DF=FC=FA+AC=DE+AC;∴DF﹣DE=AC.(3)当点D在边BC上时如图①所示DE+DF=AC∴DF=AC﹣DE=10﹣7=3;当点D在边BC的反向延长线上时,如图③所示,DF﹣DE=AC.∴DF=AC+DE=10+7=17.∴DF的长为17或3【点睛】本题考查平行四边形的判定与性质以及等腰三角形的判定,是一个基础题,解决本题的关键是进行分类讨论.15.1:16【解析】略16.相似图形位置【解析】略17.60000000【分析】根据比例尺=图上距离:实际距离列式计算即可.【详解】解:1200千米=120000000厘米2:120000000=1:60000000.故答案为:60000000.【点睛】本题考查了比例线段,掌握比例尺的定义是解题的关键,注意单位的换算问题.第11 页共11 页。
北师大版九年级数学《相似多边形》典型例题(含答案)
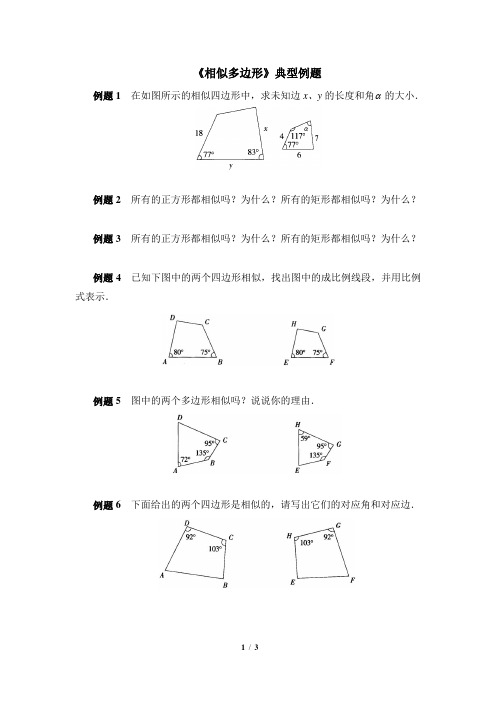
《相似多边形》典型例题例题1在如图所示的相似四边形中,求未知边x、y的长度和角 的大小.例题2所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?例题3 所有的正方形都相似吗?为什么?所有的矩形都相似吗?为什么?例题4 已知下图中的两个四边形相似,找出图中的成比例线段,并用比例式表示.例题5图中的两个多边形相似吗?说说你的理由.例题6下面给出的两个四边形是相似的,请写出它们的对应角和对应边.1/ 32 / 3例题7 已知图中的两个梯形相似,求出未知边x 、y 、z 的长度和βα∠∠、的度数.例题8 在如图所示的相似四边形中,求未知边x 、y 的长度和角α的大小.3 / 3 参考答案例题1 解答 ∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==, ∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.例题2 解答:所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.例题3 解答:所有的正方形都相似,因为正方形的每个角都是90°,因此对应角都相等,而每一个正方形的边长都相等,因此对应边成比例.所有的矩形不一定相似,虽然所有的矩形的角都相等,但对应的边不一定成比例,因此,矩形不一定相似.例题4 解答 HEDA GH CD FG BC EF AB === 例题5 解答 不相似.︒=︒-︒-︒-︒=∠587295135360D ,而︒=︒-︒-︒-︒=∠715995135360E ,不可能有“对应角相等”.例题6 解答 F A ∠→∠ E B ∠→∠ H C ∠→∠ G D ∠→∠FE AB → EH BC → HG CD → GF DA →例题7 分析 解题中要充分利用相似多边形的特征和梯形的性质. 解答 由于对应边成比例,所以232.38.45.442====z y x . 所以3,6,3===z y x .由于对应角相等,所以 ︒=∠-︒=∠=∠118180A D α,︒='∠-︒='∠=∠70180C B β.例题8 解答 ∵两个四边形相似,它们的对应边成比例,对应角相等. ∴67418y x ==,∴27,5.31==y x .︒=︒+︒+︒-︒=83)1178377(360α.。
九年级数学多边形知识点

九年级数学多边形知识点数学中的多边形是一种简单而又重要的图形,它在我们日常生活和数学学习中都起着重要的作用。
九年级数学课程中,多边形是一个重要的知识点,掌握多边形的性质和计算方法对于解决各种问题具有重要意义。
本文将从多边形的定义、分类以及一些常见的多边形性质进行探讨。
首先,多边形是由线段围成的简单封闭图形,它由若干个边和顶点组成。
多边形的边数可以是任意的,但至少要有三条边。
常见的多边形有三角形、四边形、五边形等等。
最基本的多边形是三角形,它由三条边和三个顶点构成。
三角形又可以根据边的长度和内角的大小分为不同的种类,例如等边三角形、等腰三角形等。
四边形是由四条边和四个顶点构成的多边形,也是比较常见的一种形状。
四边形根据边的长度和内角的大小可以分为各种各样的类型,例如矩形、正方形、菱形等。
在研究多边形的性质时,我们首先需要了解多边形的各个部分的术语。
多边形的边是多边形的构成要素之一,每条边都连接两个相邻的顶点。
多边形的顶点是多边形的角点,它们是连接边的起点和终点的位置。
多边形的内角是多边形内部的角度,它由相邻边所夹。
多边形的对角线是连接多边形的两个不相邻顶点的线段。
除了了解多边形的基本术语外,研究多边形的性质也是非常重要的。
多边形有很多有趣的性质,其中一些是我们可以直观地看出来的,而另一些则需要进行证明。
例如,三角形的内角和为180度,这是一个我们可以通过实际测量验证的性质。
另外,正方形的内角都是90度,这也是一个可以通过简单推理得出的性质。
在研究多边形的性质时,我们还需要深入了解一些重要的定理和公式。
例如,对于一些特殊的多边形,我们可以根据其性质得到一些重要的结论。
正方形是一个非常特殊的四边形,它具有很多独特的性质。
例如,正方形的对角线相等且垂直,这是一个可以通过勾证得到的性质。
还有一个重要的公式是计算三角形面积的公式,即面积等于底边长乘以高的一半。
通过了解这些定理和公式,我们可以更好地理解多边形的性质和计算方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
