六年级奥数题_圆和组合图形[含分析答案解析]
六年级奥数题:圆和组合图形(A)(精编文档).doc

【最新整理,下载后即可编辑】圆和组合图形(1)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是 厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的长40厘米, BC 长 厘米.2平方厘米,等腰直角三角形的面7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是度.8.图中扇形的半径OA=OB=6厘米.45∠AOB, AC垂直OB于=C,那么图中阴影部分的面积是平方厘米.)π(=.314459.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知:AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S1的面积是14.13平方厘米,圆S2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O,半径r=9厘米,15=∠,那么阴影部∠1=2分的面积是多少平方厘米?)π.3(≈1414.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方。
小学数学六年级奥数《圆和组合图形(2)》练习题(含答案)
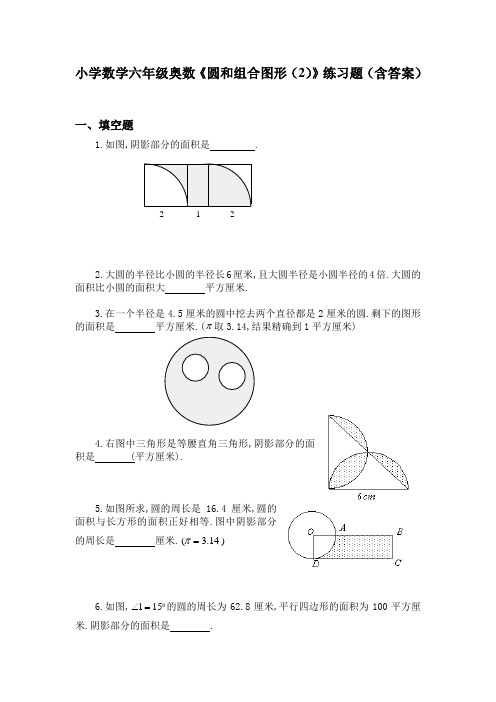
小学数学六年级奥数《圆和组合图形(2)》练习题(含答案)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 . 2 1 27.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题E D C B A GF O D C A B 2 甲 乙11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率22) 取12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?———————————————答 案——————————————————————1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++= 5.204.1645=⨯=(厘米). 6. 6548(平方厘米). 如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为 ⌒61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. 19.1416.花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米). 8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ, 解得x=60.10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米11. 如图,小正方形的边长为2r ,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1) 又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求,它的面积为: )420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).D。
六年级圆的周长奥数题

六年级圆的周长奥数题一、基础题型1. 一个圆的半径是3厘米,它的周长是多少厘米?- 解析:根据圆的周长公式C = 2π r(其中C表示周长,π通常取3.14,r为半径)。
当r = 3厘米时,C=2×3.14×3 = 18.84厘米。
2. 已知圆的直径是8分米,求这个圆的周长。
- 解析:因为圆的周长C=π d(d是直径),当d = 8分米时,C = 3.14×8=25.12分米。
3. 一个圆的半径扩大到原来的2倍,它的周长扩大到原来的几倍?- 解析:设原来圆的半径为r,则原来的周长C_1 = 2π r。
半径扩大2倍后变为2r,此时周长C_2=2π×(2r) = 4π r。
C_2div C_1=(4π r)div(2π r)=2,所以它的周长扩大到原来的2倍。
4. 有一个圆形花坛,半径是5米,在它的周围铺一条宽1米的小路,求小路的外沿周长是多少米?- 解析:小路的外沿半径为5 + 1=6米。
根据圆的周长公式C = 2π r,当r = 6米时,C=2×3.14×6 = 37.68米。
5. 一个半圆的直径是10厘米,求这个半圆的弧长(周长的一半)。
- 解析:圆的周长C=π d,半圆的弧长为(1)/(2)π d。
当d = 10厘米时,弧长=(1)/(2)×3.14×10 = 15.7厘米。
二、组合图形中的圆周长问题6. 正方形的边长为10厘米,在正方形内画一个最大的圆,求这个圆的周长。
- 解析:正方形内最大的圆的直径等于正方形的边长,即d = 10厘米。
根据圆的周长公式C=π d,C = 3.14×10 = 30.4厘米。
7. 长方形的长是12厘米,宽是8厘米,在长方形内画一个最大的半圆,求这个半圆的弧长。
- 解析:因为长方形的长是12厘米,宽是8厘米,所以这个半圆的直径最大为12厘米。
半圆的弧长=(1)/(2)π d=(1)/(2)×3.14×12 = 18.84厘米。
圆和组合图形(B)-六年级奥数题之专题串讲试题(附答案)

十二、圆和组合图形(2)年级 班 姓名 得分一、填空题1.如图,阴影部分的面积是 .平方厘米.平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).厘米.)14.3(=π6.如图,151=∠ . 2 1 21416.3=π,那么花瓣图形的面积是 平方厘米.8.已知:ABC D=2厘米,阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题:阴影部分的面积是多少?四分之一大圆的半径722)为 212.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?120 D1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位. 2. .小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米).3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米).4. .从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. .设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++=5.204.1645=⨯=(厘米).6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为1=∠又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米).7. .花瓣图形的结构是正方形的面积,加上四个43⌒1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x ⨯⨯⨯=⨯⨯ππ,解得x=60.10. .扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).11. 如图,小正方形的边长为2r,则①的面积为:72227224122r r r r =⨯-⎪⎭⎫ ⎝⎛⨯⨯,②的面积为222417272221r r r =-⎪⎭⎫ ⎝⎛⨯⨯,.即阴影部分面积为272r .12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S (1)又9232=-x S ,于是有23184+-=S x ,解得S=6.14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).。
六年级下册数学试题-圆和组合图形(b)全国通用

六年级奥数题:圆和组合图形(B)
、填空题(共10小题,每小题3分,满分30分)
2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大
」方厘米.
3-在一个半径是4” 5厘米的13中挖去两个直径都是2厘米的E1.剩下的图形的面現是
方厘米)
4.圈中三甬形昱笫脛宜第三角務.阴影部分的面积昱平方厘峯*
5-抑險所求.圜的周怅是1阮4厘米T(3的面积与绘方飛附面积正好相等.图中阴盘部分的周弋是
x =3. 143
D C 4如图,Z 1^15'的圆的周^^62. 6厘米,点0为圆心,平行四炖飛■的面积为L00平方厘米.阴影邯井的面积是方厘米).
T.有八个半径为1厘米的小回,用它们的圆周的一邯分達戒一牛花瓣图形(如图).图中黒点是这些圆的凰心.如異風固率n-3. 1416^
那心花融图用的面积臭平方厘采.
10.右图申的正方飛的边怅是2厘米,啖圆弧为分界线的甲、乙两部分的面积羞(大减小〕是平方厘翠.("取3. 13
11.如图:阴影邮廿的面积是多少?四分之一大国的半径为"(计算时回固率取今)
13・有三个面积都是S的圆放在桌上,桌面被回菠盖的面积是2S+2,并且垂仑的两块是等面积的,直线a过两个圆心爪B,如果宜线a下方被E1覆盖的面枳是9・求E]面积S的值.。
六年级奥数题:圆和组合图形 (3)
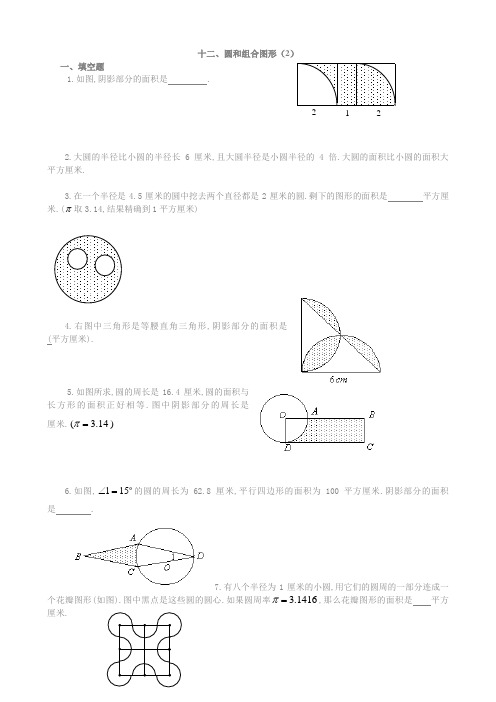
十二、圆和组合图形(2)一、填空题1.如图,阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是 .7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是 平方厘米.2 1 28.已知:ABC D 是正方形, ED =DA =AF =2厘米,阴影部分的面积是 .9.图中,311倍,那么,CAB∠是 度.10.厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题 11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值. 214.如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、C D 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?练习11、 如图18-2所示,AE =ED ,BC=3BD ,S △ABC =30平方厘米。
求阴影部分的面积。
2、 如图18-3所示,AE=ED ,DC =13 BD ,S △ABC =21平方厘米。
六年级奥数题圆和组合图形(A)
六年级奥数题测试(三)圆和组合图形年级 班 姓名 得分一、填空题(共10小题,每小题6分,满分60分) 1.算出圆内正方形的面积为 .2.下图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方厘米. A B 长40厘米,2平方厘米,等腰直角三角形的面积为 .7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.两个阴影部分面积的和是 平方厘米.D 是半圆周的中点, BC 是半圆的直径,已知:AB =?(圆周率14.3=π)4512.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米六年级奥数题测试(三)答案:圆和组合图形1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平方厘米,故半圆面积比三角形ABC 的面积小28平方厘米. 半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43⌒ ⌒圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米.阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米.故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
(完整)六年级奥数题:圆和组合图形(含分析答案)
圆和组合图形(后面有答案分析)一、填空题1.算出圆内正方形的面积为 .2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是平方厘米.3.一个扇形圆心角120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .4.如图所示,以B、C为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是厘米.(保留两位小数)5.三角形ABC是直角三角形,阴影部分①的面积比阴影部分②的面积小28长厘米.6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.45二、解答题11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π14.右图中4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?———————————————答 案——————————————————————1. 18平方厘米.由图示可知,正方形两条对角线的长都是6厘米,正方形由两个面积相等的三角形构成.三角形底为6厘米,高为3厘米,故正方形面积为1822136=⨯⨯⨯(平方厘米).2. 1.14平方厘米.由图示可知,图中阴影部分面积为两个圆心角为45的扇形面积减去直角三角形的面积.即14.12122236045214.32=⨯⨯-⨯⨯⨯(平方厘米).3. 125.6平方厘米.由已知条件可知圆的半径的平方为120平方厘米.故扇形面积为6.12536012012014.3=⨯⨯(平方厘米).4. 3.09厘米.边结BE 、CE ,则BE=CE=BC=1(厘米),故三角形BCE 为等边三角形.于是60=∠=∠BCE EBC .BE=CE=045.136060214.3=⨯⨯(厘米).于是阴影部分周长为09.312045.1=+⨯(厘米).5. 32.8厘米.从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②加上空白部分的面积是三角形ABC 的面积.又已知①的面积比②的面积小28平⌒ ⌒方厘米,故半圆面积比三角形ABC 的面积小28平方厘米.半圆面积为6282124014.32=⨯⎪⎭⎫ ⎝⎛⨯(平方厘米),三角形ABC 的面积为628+28=656(平方厘米).BC 的长为8.32402656=÷⨯(厘米).6. 13937平方厘米. 将等腰直角三角形补成一个正方形,设正方形边长为x 厘米,则圆的半径为2x 厘米.图中阴影部分面积是正方形与圆的面积之差的81,于是有282114.322⨯=⎪⎭⎫ ⎝⎛⨯-x x ,解得1332002=x .故等腰直角三角形的面积为1393721133200=⨯(平方厘米).7. 72.扇形面积是圆面积的511574.31=÷,故扇形圆心角为360的51即72.8. 5.13.三角形ACO 是一个等腰直角三角形,将AO 看作底边,AO 边上的高为3262=÷=÷AO (厘米),故三角形ACO 的面积为93621=⨯⨯(平方厘米).而扇形面积为13.1436045614.32=⨯⨯(平方厘米),从而阴影部分面积为14.13-9=5.13(平方厘米).9. 142.75.由正方形周长是20厘米,可得正方形边长也就是圆的半径为5420=÷(厘米).图形总面积为两个43圆面积加上正方形的面积,即 75.1425243514.322=+⨯⨯⨯(平方厘米).10. 90平方厘米.图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即()902114.3)220(2115122114.3)216(2114.3212222=⨯⨯÷-⨯⨯+⨯⨯÷+⨯⨯÷ (平方厘米).11. 如图作出辅助线,则阴影部分的面积为三角形AED 的面积减去正方形BEDO 的面积再加上圆面积的41. 三角形AED 的面积是21)210()21010(⨯÷⨯÷+;正方形面积是2)210(÷,圆面积的41是2)210(14.341÷⨯⨯,故阴影部分面积为: 22)210(14.341)210(21)210()21010(÷⨯⨯+÷-⨯÷⨯÷+ 125.32625.19255.37=+-=(平方厘米).12. 由已知半圆S 1的面积是14.13平方厘米得半径的平方为914.3213.14=÷⨯(平方厘米),故半径为3厘米,直径为6厘米.又因圆S 2的面积为19.625平方厘米,所以S 2半径的平方为25.614.3625.19=÷(平方厘米),于是它的半径为2.5厘米,直径为5厘米. 阴影部分面积为55)56(=⨯-(平方厘米).13. 因OA=OB ,故三角形OAB 为等腰三角形,即 150215180,151=⨯-=∠=∠=∠AOB OBA ,同理150=∠AOC ,于是602150360=⨯-=∠BOC .扇形面积为:39.42914.3360602=⨯⨯(平方厘米).14. 正方形可以分割成两个底为2,高为1的三角形,其面积为 221221=⨯⨯⨯(平方厘米). 正方形内空白部分面积为4个41圆即一个圆的面积与正方形面积之差,即 2212-=-⨯ππ(平方厘米),所有空白部分面积为)2(2-π平方厘米. 故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为 8)2(22412=-⨯-⨯⨯ππ(平方厘米).。
圆和组合图形练习题B(六年级奥数)
六年级奥数:圆和组合图形(2)一、填空题2.大圆的半径比小圆的半径长 6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面 积大 ________ 平方厘米•3.在一个半径是 4.5厘米的圆中挖去两个直径都是平方厘米.( 取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是(平方厘米).5. 如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好1.如图,阴影部分的面积是 .2厘米的圆.剩下的图形的面积是积是 .7. 有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形 (如图).图中黑点是这些圆的圆心.如果圆周率 3.1416,那么花瓣图形 的面积是—平方厘米.8. 已知:ABCD 是正方形,ED=DA=AF=2厘米,阴影部分的面积是 .S C相等.图中阴影部分的周长是 ________ 厘米.(3.14)6. 如图,1 15的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面C19. 图中,扇形BAC的面积是半圆ADB的面积的1-倍,那么,3CAB是度.10. 右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是平方厘米.(取3.14)二、解答题11. 如图:阴影部分的面积是多少?四分之一大圆的半径为r.22(计算时圆周率取22)12. 已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米.求阴影部分的面积.13. 有三个面积都是S的圆放在桌上,桌面被圆覆盖的面积是2S+2,并且重合的两块是等面积的,直线a过两个圆心A、B,如果直线a下方被圆覆盖的面积是9,求圆面积S的值.14. 如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB、BC、CD滚到2的位置,如果AB、BC、CD的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米?A 120答案一1. 6.两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位. 2.188.4 小圆的半径为6 (4 1) 2(厘米),大圆的半径为2 4 8(厘米).大圆的面积比小圆的面积大(82 22) 3.14 188.4(平方厘米).3. 57.4.52 3.14 (2 2)2 3.14 2 57.305(平方厘米)-57(平方厘米). 4.10.26. 从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即1 3.14 (6 2)2— 62 10.26(平方厘米).25. 20.5.设圆的半径为r,则圆面积即长方形面积为 r 2,故长方形的长为DC r. 阴影部分周长 DC BC BA AD r r ( r r ) 1 2 r - 2 r445 16.420.5(厘米).46.48 5 (平方厘米). 6如图,连结OA 、AC,过A 点作CD 的垂线交CD 于B 形ACD 的面积为100花瓣图形的结构是正方形的面积,加上四个-圆面积后,再割去四个半圆的面积.圆的半4径为1厘米,正方形边长为4厘米.故花瓣图形的面积是223 21 4 1- 4 1- 4 1619.1416(平方厘米).4 28. 2.43平方厘米.如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即1121 245 十… (2 2 3) 2—22—2 -3.14 22.43(平万厘2 22 360米).又圆半径为 6.28 2 50(平方厘米).(3.14 2) 10(厘米),因为 1 15 , 又OA=OD,故AOC15 2 30 ,扇形AOC 的面积为1气(平方厘米).三角形AOC 的面积为5030 23.14 102360261 25 1丄(平方厘米),从而阴影部分的面积为50 11 48— 6 6 6 67. 19.1416.25(平方厘米).方形面积为(平方厘米).DCOE.三角ED A F9. 60.234影部分面积为甘12.将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一x,则有:3S 2x 2S 2,于是 S 2x 2 (1) 色」8 2,解得S=6.半,即阴影部分面积等于622 422 10 (平方厘米).设扇形ABC 圆心角的度数是x,半圆的半径OA=r,有11 3360解得x=60. (2r)210. 0.14.扇形面积为3.14 2213'14(平方厘米)’甲部分面积为222 3^2 0"3(平方厘米),乙部分面积为3.14 1 ;°.57(平方厘米)’甲乙两部分面积差为0.57 0.430.14(平方厘米).11.如图,小正方形的边长为,则①的面积为:21 22 r r71 ②的面积为丄2224「2’①和②的面积和为1手「2r 2 2-r 2.即阴 713.设一个阴影部分的面积为3又2S -x 9 ,于是有x2③23414.圆板的正面滚过的部分如右图阴影部分所求 它的面积为:2 22 (20 2)1 42 6 (20 4) 4 (20 2) 14(4212)22220423D228.07(平方厘米).。
六年级奥数题:圆和组合图形(A)
圆和组合图形(1)
一、填空题
1.算出圆内正方形的面积为 .
2.右图是一个直角等腰三角形,直角边长2厘米,图中阴影部分面积是 平方厘米.
120,以扇形的半径为边长画一个正方形,这个正方形的面积是120平方厘米.这个扇形面积是 .
4.如图所示,以B 、C 为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是
厘米.(保留两位小数)
5.三角形ABC 是直角三角形,阴影部分①的面积比阴影部分②的面积小28平方.
6.如右图,阴影部分的面积为2平方厘米,等腰直角三角形的面积
7.扇形的面积是31.4平方厘米,它所在圆的面积是157平方厘米,这个扇形的圆心角是 度.
8.图中扇形的半径OA =OB =6厘米.45=∠AOB , AC 垂直OB 于C ,那么图中阴影部分的面积是 平方厘米.)14.3(=π
9.右图中正方形周长是20厘米.图形的总面积是 平方厘米.
10.在右图中(单位:厘米),两个阴影部分面积的和是 平方厘米.
45
二、解答题
11. ABC 是等腰直角三角形. D 是半圆周的中点, BC 是半圆的直径,已知: AB =BC =10,那么阴影部分的面积是多少?(圆周率14.3=π)
12.如图,半圆S 1的面积是14.13平方厘米,圆S 2的面积是19.625平方厘米.那么长方形(阴影部分的面积)是多少平方厘米?
13.如图,已知圆心是O ,半径r =9厘米,1521=∠=∠,那么阴影部分的面积是多少平方厘米?)14.3(≈π
14.右图中4个圆的圆心是正方形的4个顶点,它
们的公共点是该正方形的中心.如果每个圆的半径都
是1厘米,那么阴影部分的总面积是多少平方。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆和组合图形(后面有答案分析)
一、填空题
1.算出圆内正方形的面积为.
6厘米
2.右图是一个直角等腰三角形,直角边长 2 厘米 , 图中阴影部分面积是
平方厘米 .
2
3.一个扇形圆心角 120 ,以扇形的半径为边长画一个正方形,这个正方形的面积是 120 平方厘米 .这个扇形面积是.
完美 WORD 格式编辑
4.如图所示 , 以、
C 为圆心的两个半圆的直径都是 2 厘米 ,则阴影部分的周
B
长是厘米 .(保留两位小数 )
E
A B C D
5.三角形 ABC 是直角三角形 ,阴影部分①的面积比阴影部分②的面积小28
C
厘米, BC 长厘米 .
平方厘米 . AB 长 40
②
①
B A
6.如右图 ,阴影部分的面积为 2 平方厘米 ,等腰直角三角形的面积为.
完美 WORD 格式编辑
7.扇形的面积是 31.4 平方厘米 ,它所在圆的面积是157 平方厘米 ,这个扇形的圆心角是度 .
8.图中扇形的半径OA =OB =6 厘米 . AOB 45 , AC 垂直 OB 于 C ,那么图中阴影部分的面积是平方厘米 . ( 3.14 )
A
6
45
O C B
9.右图中正方形周长是20 厘米 .图形的总面积是平方厘米 .
完美 WORD 格式编辑
10.在右图中 (单位 :厘米 ), 两个阴影部分面积的和是平方厘米 .
15
12
20
二、解答题
11.ABC 是等腰直角三角形 . D 是半圆周的中点 , BC 是半圆的直径 ,已知 :
AB=BC =10, 那么阴影部分的面积是多少?( 圆周率 3.14 )
A10 B
D
C
完美 WORD 格式编辑
12.如图 ,半圆 S1的面积是 14.13 平方厘米 ,圆 S2的面积是 19.625 平方厘米 . 那么长方形 (阴影部分的面积 ) 是多少平方厘米 ?
S2
S1
13.如图 ,已知圆心是
O ,半径 =9 厘米, 1 2 15 ,那么阴影部分的面积是r
多少平方厘米 ? ( 3.14 )
A
1 2
完美 WORD 格式编辑
专业资料整理分享
14.右图中 4 个圆的圆心是正方形的 4 个顶点 ,它
们的公共点是该正方形的中心.如果每个圆的半径都是
1 厘米 ,那么阴影部分的总面积是多少平方厘米?
完美 WORD 格式编辑
———————————————答案——————————————————————1.18 平方厘米 .
由图示可知 ,正方形两条对角线的长都是 6 厘米 ,正方形由两个面积相等的三
角形构成 .三角形底为 6 厘米 ,高为 3 厘米 ,故正方形面积为 6 3 1 2 18(平方
2
厘米 ).
2. 1.14 平方厘米 .
由图示可知 ,图中阴影部分面积为两个圆心角为45 的扇形面积减去直角三
角形的面积 .即 3.14 2245 2 2 2 1 1.14 (平方厘米 ).
360 2
3.125.6 平方厘米 .
由已知条件可知圆的半径的平方为120 平方厘米 .故扇形面积为
120
3.14 120 125.6 ( 平方厘米 ).
4. 3.09 厘米 .
边结、,则BE=CE=BC= 1( 厘米 ),故三角形BCE 为等边三角形 .于是BE CE
⌒⌒
EBC BCE 60 .BE=CE= 3.14 2 60
厘米 ). 于是阴影部分周长为
1.045(
360
1.045 2 1 3.09 (厘米 ).
完美 WORD 格式编辑
5.32.8 厘米 .
从图中可以看出阴影部分①加上空白部分的面积是半圆的面积,阴影部分②
加上空白部分的面积是三角形ABC 的面积 .又已知①的面积比②的面积小28 平
方厘米 ,故半圆面积比三角形 ABC 的面积小 28 平方厘米 .
2
1
40
628(平方厘米 ), 三角形 ABC 的面积为半圆面积为 3.14
2
2
628+28=656( 平方厘米 ).BC 的长为 656 2 40 32.8 (厘米 ).
6.37 9平方厘米 .
13
将等腰直角三角形补成一个正方形,设正方形边长为 x 厘米 ,则圆的半径为
x
2 厘米 .图中阴影部分面积是正方形与圆的面积之差的 1 ,于是有
8
2
3200 .故等腰直角三角形的面积为
x2 3.14 1 x8 2 ,解得 x2
2 13
3200 1 37 9 (平方厘米 ).
13 2 13
7. 72.
扇形面积是圆面积的 31.4 157 1 ,故扇形圆心角为 360 的1即72 .
5 5
8. 5.13.
三角形ACO 是一个等腰直角三角形 ,将 AO 看作底边 ,AO 边上的高为
AO 2 6 2 3 (厘米 ), 故三角形 ACO 的面积为1 6 3 9 ( 平方厘米 ). 而扇
形
45 2
面积为 3.14 6 214.13 (平方厘米 ), 从而阴影部分面积为14.13-9=5.13( 平
360
完美 WORD 格式编辑
方厘米 ).
9.142.75.
由正方形周长是 20 厘米 ,可得正方形边长也就是圆的半径为20 4 5( 厘米).图形总面积为两个3圆面积加上正方形的面积 ,即 4
3.14 523 2 52142.75(平方厘米 ).
4
10.90 平方厘米 .
图中阴影部分的面积是从两个以直角三角形直角边为直径的半圆及一个直
角三角的面积和中减去一个以直角三角形斜边为直径的半圆的面积即
12 2 2 3.14 1 (16 2)2 3.14 1 12 15 1 (20 2)2 3.14 1 90
2 2 2 2
(平方厘米 ).
A
10 B E
O D 11.如图作出辅助线 ,则阴影部分的面积为三角形 AED 的面积
1
减去正方形 BEDO 的面积再加上圆面积的. C 三角形 AED 的面积是(10 10 2) (10 2) 1 ;正方形面积是 (10 2)2 ,圆面
积的1是1
2 3.14(10 2)2 ,故阴影部分面积为 :
4 4
1 1
(1010 2) (10 2) (10 2)2 3.14 (10 2) 2
2 4
37.5 25 19.625 32.125(平方厘米) .
12.由已知半圆 S1的面积是 14.13 平方厘米得半径的平方为
14.13 2 3.14 9 (平方厘米 ),故半径为 3 厘米 ,直径为 6 厘米 .
完美 WORD 格式编辑
又因圆 S2的面积为 19.625 平方厘米 ,所以 S2半径的平方为
19.625 3.14 6.25(平方厘米 ), 于是它的半径为 2.5 厘米 ,直径为 5 厘米 .
阴影部分面积为 (6 5) 5 5( 平方厘米 ).
13.因 OA=OB ,故三角形 OAB 为等腰三角形 ,即
OBA 1 15 , AOB 180 15 2 150,
同理 AOC 150 ,于是BOC 360 150 2 60.
602
扇形面积为 : 3.14 9 42.39 (平方厘米 ).
14.正方形可以分割成两个底为 2, 高为 1 的三角形 ,其面积为
1 2 1 2 2(平方厘米 ).
2
正方形内空白部分面积为 4 个1圆即一个圆的面积与正方形面积之差,即
4
12 2 2 (平方厘米 ), 所有空白部分面积为2( 2) 平方厘米 .
故阴影部分面积为四个圆面积之和与两个空白面积之和的差,即为
12 4 2 2( 2) 8 (平方厘米 ).
完美 WORD 格式编辑。
