第3章 超声波发射声场与规则反射体的回波声压
无损检测超声波探伤0第3章 超声波的声场与标准反射体反射声压

矩形波源的半扩散角
φ θ00==ssiinn--11λλ//22ba==5577λλ//22ba
矩形波源的近场区
N=Fs/πλ
3.1.3 纵波声场近场区在两种介质中的分布
近场区公式N=D2/4λ适用均匀介质,不适用近场区存在两种不同介质。 水浸探伤当水层厚度较小时,近场区的计算。
横波声场中第二介质的近场区
N′=N-L=π—λF—SCS2O—CSOβ—Sα— -L1—ttaa—nnαβ—
FS 波源的面积
L1 入射点至波源的距离
β
Λs2 第二介质中的波长 L2 入射点至假想波源的距离
3.2.2.2 横波声场的半扩散角
假想声源的横波声场和纵波声场一样具有良好的指向性,但声束的对称性 与圆形波源不同。
∵ N=D2/4λ ∴ b=1.64N
例:钢纵波声速 CL=5900m/s 频率f=2.5Mhz 晶片直径D=20mm 求近场长度N、半扩散角θ0和未扩散区长度。
解: N=D2/4λ=202/[4×5900/(2.5×106)]=42.4mm θb0==17.06λ4N/≈D=6790.×5m0m.236/20≈8.3°
其变化规律与球孔的直径、距离及有关。
通过计算得知: 球孔的直径一定,距离差一倍差12dB; 距离一定,直径差一倍,差6dB。
3.4.5 大平底的回波声压
PX
如图 X≥3N远场区的大平底返回声压
大小的计算公式
PB=PX/2
P0
PB
PB—大平底返回的声压
PX—波源至X处的声压
从公式可以看出:大平底的返回声压
1.纵波斜入射时在第二介质中产生横波, 其声束不再对称,上下两个半扩散角,上 半扩散角θ上大于下半扩散角θ 下。 2.横波垂直入射时声束对称于轴线。
【超声二级取证】第3章超声发射声场与规则反射体的回波声压
/ P
2P0
sin2
B
F x
1
x F
1 x F
在焦点处,x=F,上式可简化为:
P=πBP0 。焦点处声压随B值增加 而升高。 (B=R2/λf,R为波源半径)
2. 焦柱的几何尺寸 聚焦声束的焦点是一个聚焦区,呈柱形,焦柱直径与长度
的近似表示公式为:
d≈πF/2R ;
L≈πF2/R2 ;
L/ d = 2F/ R
平底孔回波声压:
Pf
P0 FS F f
2 x2
2ax
e 8.68
长横孔回波声压:
Pf
P0 FS
2x
2ax
D ef 8.68 2x
短横孔回波声压:
Pf
P0FSl f
2x2
2ax
D ef 8.68
球孔回波声压:
Pf
P0 FS
x
Df 4x
2 ax
e 8.68
大平底与实心圆柱体回波声压:
PB
P0 FS
2x
3. 聚焦探头的应用
3.4 规则反射体的回波声压
• 当量法:在同样的检测条件下,当自然缺陷回波与某人工规则 反射体回波等高时,则该人工规则反射体的尺寸就是此自然缺 陷的当量尺寸。
3.4.1 平底孔回波声压
超声波波束轴线垂直于平底孔,
超声波在平底孔上全反射,回波声
压为:
Pf
Px F f
x
P0 FS F f
r kbsin
D= p(r, ,90) sin(kbsin ) p(r,0,90) kbsin
b
arcsin
2b
57
2b
矩形晶片(两平面)辐射声压分布(数值结果)
超声波(3)

mm
由上计算表明,横波探头晶片尺寸一定,K值增大,近
2015-4-14 场区长度将减小。 34
例4:试计算2.5MHz、10×12mm方晶片K2.0
横波探头,有机玻璃中入射点至晶片的距离为
12mm,求此探头在钢中的近场区长度N′。(钢
中CS=3230m/s
解: C S 2 3.23 1.29 S2
KFS cos P S 2 x cos
3-21
式中: K — 系数;
2015-4-14
Fs — 波源的面积;
32
λs2 —第二介质中横波波长; x—轴线上某点至假想波源的距离。
⒉近场区长度
横波声场近场区长度N为:
F S cos N S 2 cos
第二介质中的近场区长度N′
2015-4-14
36
在声束轴线与界面法线所决定的入射平面
内,声束不再对称于声束轴线,而是声束上半
扩散角θ上大于声束半扩散角θ下
2015-4-14
37
K tg
上 , 下 1
sin sin cl1 cs2
sin 2 sin 2 C L1 CS 2
sin 1 sin 1 , C CS 2 2015-4-14 L1
1 , 2 38
横波垂直入射时,其声束对称于轴线,半扩
散角θ0 对于圆片形声源: 0 arcsin1.12 s 2 Ds 70 Ds
对于正方形声源:
0 arcsin s 2
λ θ0 70 DS
Ds2 Fs N 4
④ 增加探头的直径、提高探头的频率,半扩散 角将减小,可以改善声束指向性,能量集中, 有利于提高探伤灵敏度。 但增大了近场长度,对探伤反而不利。实
3.4规则反射体回波声压

Df
2x e 8.68
• 球孔回波声压:
•
2x P0 FS D f 8.68 Pf e x 4 x
大平底与实心圆柱体回波声压: PB P0 FS e 8.68 2 x
2x
• 空心圆柱体外圆检测回波声压: • 空心圆柱体外圆检测回波声压:
PF PB 0 S 2 x
d 8.68 e D
3.4.2 长横孔回波声压
• 当X≥3N,超声波垂直入射,全反射,长横孔直径较小, 长度大于波束截面尺寸时,超声波在长横孔表面的反 射类似球面波在柱面镜上的反射。 以a=x, P 1 /a=P0FS /λx,代入球面波在柱面上反射声压 公式,可得长横孔回波声压Pf表达式:
Df P0 Fs P0 Fs D f Px Pf 2x D f 2 x 2x 2 x
3.4.5 大平底回波声压
五、大平底面回波声压 当x≥3N时,超声波在与波束轴线垂直、表面光洁的大 平底面上的反射就是球面波在平面上的反射,其回波声 压PB为:
P0 FS PB 2x
两个不同距离的大平底面回波分贝差为:
12
x2 20 lg x1
大平底距离增加一倍时,其回波声压下降6dB 。
3.4.6圆柱曲底面回波声压
d D
D d
• 考虑到介质衰减的各几何体返回声压公式: • 平底孔回波声压:Pf • 长横孔回波声压:Pf • 短横孔回波声压:Pf
P0 FS F f
2 x 2
2x e 8.68
P0 FS 2 x
Df 2x
2x e 8.68
P F lf 0 S x 2 x
任意两个距离、直径不同的长横孔回波分贝差为:
12 20 lg Pf 1 Pf 2 10 lg
超声波检测(第三章)

式中
FS—波源的面积; λS2—第二介质中横波波长; L1—入射点至波源的距离; L2 —入射点至假想波源的距离。
• 式中 N1 —只有介质Ⅰ时,水中近场长度; • N2 —只有介质Ⅱ时,钢中近场长度 • C1—介质Ⅰ水中波速; • C2—介质Ⅱ钢中波速; • λ1—介质Ⅰ水中波长。 • λ2—介质Ⅱ钢中波长。
例:用2.5MHz,直径14mm纵波直探头水浸探伤钢板,已知 水层厚度为20mm,钢中纵波声速5900m/s,水中纵波声 速1480m/s,求钢中近场区长度N。 解: C 5.9 2.36(mm) 钢中纵波波长 2 f 2.5
0 arcsin1.22 / DS 70 / DS
3、当θ>θ0时,|DC|<0.15,说明半扩散角以外的声压很低, 超声波的能量主要集中在半扩散角以内。2θ0以内的波束称 为主波束(或主声束),只有当缺陷位于主波束范围时, 才容易被发现。以确定的扩散角向固定的方向辐射超声波 的特性称为声束指向性。
析研究常常从液体介质入手,然后在一定
条件下过渡到固体介质。
3.1 纵波声场
一、圆盘波源辐射的纵波声场 波源轴线上声压分布
Z
Q o Y X x
P
P 0 Fs x
x
3Rs2
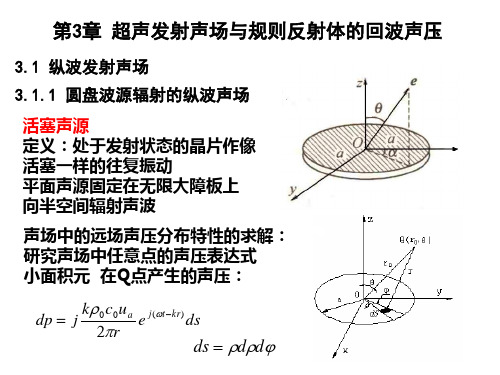
P - 波源轴线上任意一点声压; P0 - 波源的起始声压; FS -波源面积; Rs – 波源半径 λ -波长; x -轴线上Q点至波源的距离。
Z P(r,θ) X x P(r,0)
o Y
)θ
• 波束指向性
Y
3.83 )θ0
Dc
P(r , ) P(r ,0)
• 指向性系数:DC 波前充分远处任意一点的声压P(r,θ)与波 源轴线上同距离处声压P(r,0)之比。
超声波探伤第3讲 (2)

第二章 超声波发射声场与——规则反射体的回波声压§2.1纵波发射声场一、圆盘声源辐射的纵波声场 1.波源轴线上的声压分布如图2.1所示,设液体介质中有一圆盘声源作连续活塞振动,辐射单一频率的连续正弦波。
图2.1圆盘声源轴线上的声压)(2220X X R Sin P P -+=λπR 一波源的半径,波源直径D=2R;当m>D(2R)时,(2.1)式可简化为:λπX DSinP P 8220=当X时,进一步简化:λX F P P 0=式中:F ——波源的面积,。
圆盘声源轴线上的声压分布规律如图2.2所示。
图2.2声学上把由子波的干涉在波源附近的轴线上产生一系列声压极大极小值的区域称为超声场的近场区,又称菲涅耳区。
波源轴线上最后一个声压极大值至波源的距离称为近场区长度,用N 表示。
近场区长度N 可以用下式来计算:λλλ44222D D N =-=2.超声场截面声压分布3.波束指向性与半扩散角超声波的能量主要集中在以内的锥形区域内,此区域称为主波束。
圆晶片辐射的波束半扩散角为:D Dλλθ7022.1arcsin 0==4.未扩散区与扩散区从理想化圆晶片辐射的声场(图 2.5)可以发现,超声波扩散波束并不是从波源开始扩散的,N b 64.1=式中:N 一近场区长度。
二、矩形波源辐射的纵波声场长为α、宽为b 的矩形波源作活塞振动,在液体介质中辐射的纵波声场类似于圆盘源,当x 3N 时,波束轴线上的声压为:λX Fp P 0=(a) (b)图2.6 矩形波源的指向性当a=b 时,波源为正方形。
波束在X 和Y 方向的半扩散角均为za aλλθ57arcsin0==(度)§2.2横波发射声场一、 假想波源图2.9横波声的与假想波源四、指向性和半扩散角图2.10横波声场半扩散声ββθ-2=上1-ββθ=下b a -=1sin β b a +=2sin β21)22.1(1sin Da L λβ-=αλCos DC C b L S L 12122.1=在通过声束轴线入射平面垂直的平面内,声束对称于轴线,这时半扩散角可按下式计算。
超声波发射声场与规则反射体的回波声压PPT课件

P(r,0,0) P0Fs
r
矩形声源辐射的纵波声场 ——声轴线上声压分布
声压计算与声场仿真
矩形声源辐射的纵波声场
——指向性
在 YOZ平 面 内 指 向 性 系 数 :
Dr
P (r,0, ) P (r,0,0)
sin(K b sin ) K b sin
在 YOZ平 面 内 的 半 扩 散 角 为 :
kRs sin
kRs sin
经 查 得 : kRs sin 2.9
所 以 : 12dB
arcsin
2 .9 kRs
arcsin 0.92
Ds
20dB半 扩 散 角 :
2 0 lg 2 J 1 ( k R s s in ) = 2 0 d B, 可 得 :2 J 1 ( k R s s in ) 0 .1
0
arcsin
2b
57
2b
(o )
短边平面
同 样 , 在 XOZ平 面 内 的 半 扩 散 角 为 :
0
arcsin
2a
57
2a
(o )
长边平面
矩形声源辐射的纵波声场 ——近场长度
超声波发射声场与 规则反射体的回波声压
Chapter 3 Sound Field & Echo Sound Pressure
目 录 Contents
纵波发射声场 横波发射声场 聚焦声源发射声场 规则反射体的回波声压 AVG曲线
纵波发射声场 longitudinal Wave Sound Field
Ds
0
arc sin1.22
Ds
自由声场与脉冲反射法指向性的关系:
第2章 超声波发射声场与规则反射体的回波声压汇总

第二章超声波发射声场与规则反射体的回波声压超声波探头(波源)发射的超声场,具有特殊的结构。
只有当缺陷位于超声场内时,才有有可能被发现。
由于液体介质中的声压可以进行线性叠加,并且测试比较方便。
因此对声场的理论分析研究常常从液体介质入手,然后在一定条件下过渡到固体介质。
又由于实际探伤中广泛应用反射法,因此本章在讨论了超声波发射声场以后,还讨论了各种规则反射体的回波声压。
第一节纵波发射声场一、圆盘波源辐射的纵波声场1.波源轴线上声压分布在不考虑介质衰减的条件下,图2.1所示的液体介质中圆盘源上一点波源ds辐射的球面波在波源轴线上Q点引起的声压为式中 P o——波源的起始声压;d s——点波源的面积;λ——波长;r——点波源至Q点的距离;κ———波数,κ=ω/c=2π/λ;ω——圆频率,ω=2πf;‘t——时间。
根据波的迭加原理,作活塞振动的圆盘波源各点波源在轴线上Q点引起的声压可以线性迭加,所以对整个波源面积积分就可以得到波源轴线上的任意一点声压为其声压幅值为(2.1)式中 R s—波源半径;χ——轴线上Q点至波源的距离。
上述声压公式比较复杂,使用不便,特作如下简化。
当χ≥2R,时,根据牛顿二项式将(2.1)式简化为(2.2)根据sinθ≈θ(θ很小时)上式可简化为(2.3)式中 Fs——波源面积,(2.3)式表明,当χ≥3R;/A时,圆盘源轴线上的声压与距离成反比,与波源面积成正比。
波源轴线上的声压随距离变化的情况如图2.2所示。
(1)近场区:波源附近由于波的干涉而出现一系列声压极大极小值的区域,称为超声场的近场区,又叫菲涅耳区。
近场区声压分布不均,是由于波源各点至轴线上某点的距离不同,存在波程差,互相迭加时存在位相差而互相干涉,使某些地方声压互相加强,另一些地方互相减弱,于是就出现声压极大极小值的点。
波源轴线上最后一个声压极大值至波源的距离称为近场区长度,用N表示。
声压P有极大值,化简得极大值对应的距离为式中n=O、1、2、3、……<(D s-一x)/2λ的正整数,共有n+1个极大值,其中n=0为最后一个极大值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
PB1
P0
Fs
2 x1
PB2
P0
Fs
2 x2
dB 20 lg PB2 20 lg x1
PB1
x2
所以,距离相差一倍,其回波声压相差6dB.
平底孔——平底孔回波声压
平底孔处的声压:Px
P0
Fs
x
探头接收到的平底孔回波声压:
Pf
P0
Fs Ff
2x2
式中:Fs ——声源面积;
Ff ——平底孔面积。
计算的前提
所有规则反射体回波声压计算的前提:
1、反射体在声场的足够远处: x>3N 声轴线上声压随声场的变化规律近似球面波:
Px
P0
Fs
x
2、反射体表面光滑、声束垂直入射、声压全反射。
大平底
大平底回波声压:PB
P0
Fs
2 x
规律:
声压与声程成反比、
与频率成正比。
两厚度分别为X1,X
的大平底的回波声压分别为:
应用:底波法调整灵敏度、缺陷当量计算。
长横孔
长横孔回波声压:P1
P0 Fs
2 x
Df 2x
两长横孔回波声压(高度)差:
V12
20 lg
Pf 1 Pf 2
10l g
Df 1x23 Df 2 x13
规律:长横孔回波声压与直径的平方根成正比、
与声程的3/2次方成反比、与频率成正比。
孔径相同,声程差一倍,回波差9dB
两个半扩散角(θ上 >θ下):
上 2 下 1 sin 1 a b,sin 2 a b a sin 1 (1.22L1 )2
Ds
b 1.22L1cs2 cos
DscL1
3.2.2 横波声场的结构
横波垂直入射
对圆形声源:0
arcsin1.22 s2
Ds
70 s2
Ds
对正方形声源:0
lg
D1 D2
x2 x1
平底孔孔径差1倍:回波声压差 12 dB 平底孔声程差1倍:回波声压差 12 dB
平底孔——平底孔与大平底比较
大平底和平底孔的回波声压分别为:
PB
P0
Fs
2 xB
Pf
P0
Fs Ff
2xf 2
两回波的声压(高度)差为:
dB
20 lg
Pf PB
20
lg
d 2
2 xB xf 2
2a
57
2a
(o )
短边平面 长边平面
3.1.2 矩形波源辐射的纵波声场
近场区长度 N Fs
特点:与圆盘波源相同。
3.1.3 纵波声场近场区在两种介质中的分布
钢中剩余近场区长度N’
在水浸法检测中, 如水层距离小于 水中近场长度, 则在钢中的剩余 近场区长度基于 水中近场区计算:
N
'
(
N1
3.1.1 圆盘波源辐射的纵波声场
理论计算
仿真
3.1.1 圆盘波源辐射的纵波声场
近场区(菲涅尔区):在声源附近由于波的干涉 而出现一系列声压极大值和极小值的区域。
在近场区内,声束不扩散。
近场区长度N:波源轴线上最后一个声压极大值到 波源的距离
当 (
Rs2 x2 x)=(2n+1)2 时,声压有极大值:
arcsin
s 2
2a
57 s2
2a
3.3 聚焦声源发射声场
3.3.1 聚焦声场的形成 3.3.2 聚焦声场的特点与应用
3.3.1 聚焦声场的形成
分类:水浸、接触
3.3.2 聚焦声场的特点与应用
声压分布
可见,焦距F越小,B=N/F越大,聚焦效果越好。 若焦距F≥N,B≤1,几乎失去聚焦意义。
P0 Fs
x
Df 4x
两球孔的回波声压(高度)差:
V12 20l g
Pf 1 Pf 2
20lg
Df 1x22 Df 2 x12
规律: 球孔声压直径成正比、与声程的平方成 反比、与频率成正比。
直径一定,声程相差一倍,声压差12dB 声程一定,直径相差一倍,声压差 6dB
大直径圆柱体——实心
声程相同,孔径差一倍,回波差3dB.
短横孔
短横孔回波声压:Pf
P0 Fs
x
lf 2x
Df
两短横孔回波声压(高度)差:
V12
20l
g
Pf Pf
1 2
10
lg
l
f
2 1
l
f
2 2
x24 x14
Df1 Df 2
规律:短横孔回波声压与长度、直径平方根成 正比、与声程的平方成反比、与频率成正比。
球孔
球孔的回波声压:Pf
规则反射体的回波声压
若考虑介质衰减,回波声压应为:
平底孔:Pf 长横孔:Pf
P0 Fs Ff 2 x2
2 ax
e 8.68
P0 Fs
2 x
2 ax
D e f
8.68
2x
短横孔:Pf
P0 Fs
x
lf 2x
2 ax
D e f
8.68
球孔:Pf
P0 Fs
x
2 ax
D e f
8.68
4x
大平底与实心圆柱体:PB
L)
c1 c2
( Ds2 L) c1
4 1
c2
3.1.4 实际声场与理想声场比较
理想声场:连续波均匀激励、理想液体介质; 实际声场:脉冲波非均匀激励、固体介质。
特点: 相同:远场; 不同:近场:实际声场近场的声压分布较均匀, 幅度变化较小,极大值点的数量也少,极小值 远大于0。
3.1.4 实际声场与理想声场比较
3.1.1 圆盘波源辐射的纵波声场
1.波源轴线上声压分布
声轴线上的声压幅值为:
P 2P0 sin (
Rs2 x2 x)
式中:Rs ——声源半径;
x——声程。
当x 2Rs时:
P
2P0
sin(
2
Rs2
x
)
当x 3Rs2 / (足够远)时:
P P0 Rs2 P0Fs x x
3.1.1 圆盘波源辐射的纵波声场
Fs
s 2
cos cos
L1
tan tan
讨论:增大K值,对近场区长度的影响?
3.2.2 横波声场的结构
在钢中的剩余近场长度简便算法:
式中:
N'
N1Hale Waihona Puke L1 tg tg
N1
Fs
l1
——声源在斜楔中的纵波声场近场长度;
L1 ——入射点到声源的距离。
3.2.2 横波声场的结构
纵波折射的横波声场,声束不对称,存在上下
x Ds2 2 (2n 1)2 4(2n 1)
式中:n——正整数,取n 0,即声压的最后极大值出现的声程:
N Ds2 2 Ds2 Rs2 Fs 4 4
3.1.1 圆盘波源辐射的纵波声场
当 (
Rs2 x2 x)=n时,声压有极小值:
x Ds2 (2n)2 8n
n 1、2、3、4...时对应的声程约为N/2、N/4、N/8...
远场区(x》N):轴线上声压最高,偏离中心声
压逐渐降低。同一横截面上声压分布完全对称。
3.1.1 圆盘波源辐射的纵波声场
应用:探头声轴偏移的测量、折射角的测量均 应在远场。
3.1.1 圆盘波源辐射的纵波声场
3.波束指向性和半扩散角 指向性:声束集中向一个方向辐射的性质。
0
3.1.1 圆盘波源辐射的纵波声场
注:波源轴线上最后一个声压为0的距离是0.5N
远场区(x>N):声压随距离增加单调减小;
足够远场(x>3N),P P0Fs / x ——声压与声程
成反比——近似球面波的规律——所有规则反射体 回波声压计算的基础。
3.1.1 圆盘波源辐射的纵波声场
2.超声场横截面声压分布
近场区(x<N):存在中心轴线上声压为0的截面, 中心轴线上声压为0,偏离中心声压较高;
理想声场针对液体,声压线形叠加; 实际声场针对固体,声压方向在连接线上,
叠加干涉少。
3.2 横波发射声场
3.2.1 假想横波波源
3.2.2 横波声场的结构
3.2.1 假想横波波源
假想:把第一介质中的纵波声场转换为轴 线与横波波束一致的横波声场。
假想横波声源为椭圆, 长轴为Ds,短轴为:
Ds'
Ds
cos cos
3.2.1 假想横波波源
在足够远处声轴线上的声压:
P KFs'
s2 x
式中:Fs'
cos cos
Fs ——等效声源面积
规律:与纵波相似。
3.2.2 横波声场的结构
假想横波声源的近场区长度:
N Fs cos s2 cos
横波声场中第二介质中的近场区长度:
N
'
N
L2
圆柱体回波声压:
`
`
P
P0
Fs
2 D
D
可见:与厚度与直径相同的大平底相同。
大直径圆柱体——空心
从外圆周径向入射时回波声压:
PB
P0 Fs
2s
d D
从内圆周径向入射时回波声压:
PB
P0 Fs
2 x
D d
可见,从外圆周面入射时比大平底回波低,因为内壁凸面发散。
从内圆周径入射时比大平底回波高,因为外壁凹面聚焦。
半扩散角θ0 (指向角、第一零值发散角)
当y=kRs sin 3.83, 7.02,10.17...时,Dc=0,即有声压为0点。
