结构力学位移法
结构力学 位移法

6i
12i
3i
l
l2
l
6i
θ=1
3i
1
0 0
3i
l
3i
l2
A
θ=1
i
B i
i
-i
0
10
§7-2 等截面直杆的刚度方程
四、说明:
⑴杆件的线刚度应为杆件的抗弯刚度EI除以杆件长度l。 ⑵转角位移方程中杆端位移若为负应以负值代入以获得杆端弯矩。 ⑶固端弯矩表在应用时,应随实际杆件所受荷载,其固端弯矩作相应变化。
B
ql2/16
EI l
q
A
EI=C
l
l
A
EI l
B EI
C l 3ql2/32
中点
5
§7-2 等截面直杆的刚度方程
一、两端固定杆件的转角位移方程 ⑴杆端位移和杆端弯矩的正负规定 MAB P
①角位移θA、θB顺时针为正。
②Δ=vB-vA A、B两点的相对侧移,使杆件 产生顺时针方向旋转角βAB=Δ/l 的Δ为正。 ③杆端弯矩规定顺时针为正。 ⑵两端固定杆件的转角位移方程 M1AB
1
A
原结构有两个基本未知量 B
1
14
§7-2 等截面直杆的刚度方程
⑷位移法基本结构的构成。 位移法的附加约束法构造基本结构时,在刚结点角位移处加入附加刚臂, 在结点独立线位移处沿线位移方向加入附加链杆。 Δ1 基本结构 Δ3 Δ2 Δ4 Δ5 Δ6
B
Δ2
Δ1 C
基本结构 A
B
Δ3 C
Δ4
A
3
§7-1 位移法基本概念
三、位移法的基本思路(补充说明) 一给定结构在外因作用下,分析其内力和变形(位移)所采用途径有二:
结构力学-位移法的典型方程及计算步骤
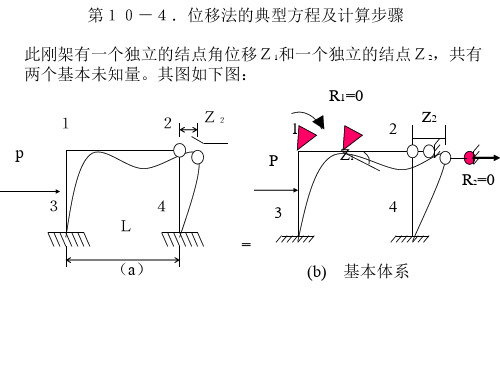
(e)
依题意可知并根据叠加原理上述条件可写为:
R1=R11+R12+R1P=r11 Z1+r12 Z2+R1P=0 R2=R21+R22+R2P=r21 Z1+r22 Z2+R2P=0
上述方程称为位移法基本方程,也称为位移法的典型方程。
为了求出典型方程的系数和自由项,可借助于表10-1,绘出基本
结构图,如下图10-7a,b, 和c所示。然后求出各系数和自由项。
r11 1 3i 4i
r12 6i1 0
R1P PL1 0
l
8
Z1=1
4i 1
2
6i 1l
2
Z2=1 1
2
3i M
3 2i 4
(a)
6i 3 l
3i 4 l
(b)
p
MP
PL 3
4
8
(C)
T10-7
1
2
r21 1
2
r22 1
6i l
0
12i
L2
3i
P
L2
2
2
R2P
0
系数和自由项可分为两类,分别由力矩平衡方程 M1=O求得为:
0
6 2 6 9 12 2 11 l Z1 l 2 Z2 16 P 0
Z1 0.02218 Pl Z2 0.02859 Pl 2
M M1Z1 M 2Z2 M P
转到下一节
者的原理有所不同。
§10-7 有侧移的斜柱刚架
B
B’
C’ C
C”
C
A
D
O A,D
B 结点位移图
O为极点,各结点位移前的位置
结构力学(I)结构静力分析篇(位移法)@@

EI
正对称
q q q
h
反对称
q
哈工大 土木工程学院
29 / 65
q
q
q
对称结构在对称荷载作 用下内力、反力和变形皆对 称,故取半结构计算。由半 结构特点采用位移法较好。
哈工大 土木工程学院
30 / 65
q
q
q
对称结构在反对称荷载 作用下内力、反力和变形皆 反对称,故取半结构计算。 而此半结构仍具有对称结构 特点。继续分解。
A 2EI
l
B
EI c
l
C
原始结构
C
A
Z1
B c
基本结构 基本体系
k R 0 1Z 11 1 C
哈工大 土木工程学院
基本方程
33 / 65
4i
Z1 1
3i
8i
k 11
3i
8i
12 i l 12 i l
M1
1 2 i l
k i 1111
R 1C
3i l
c
3i l
MC
9i R1C c l
哈工大 土木工程学院
15 / 65
3i
Z1 1
k 11
4i
3i
1 Z1 FPl 56i
2i
1 FPl 8 1 FPl 8
M1
4i k i 117
R1P
1 FPl 8
M Z M M 1 1 P
3 FPl 56 8 FPl 56 9 FPl 56
FP
MP
1 R 1P F Pl 8
哈工大 土木工程学院
21 / 65
Z1 1
结构力学位移法

M=1 C
M=1
若求结构两个截面的相对角位移 在两个截面上加两个方向相反单 位力偶
1 d
1 d
A
求结构两个截面的相对角位移 B
d
C 求AB杆的角位移 杆的角位移
若求桁架中AB杆的角位移,应 加一单位力偶,构成这一力偶 的两个集中力取 1/d,垂直作 用于杆端
1 d1
1 d1
A
B 求AB、AC杆的角位移 、 杆的角位移
式中k—考虑剪应力沿截面分布不均匀的修正系数, 考虑剪应力沿截面分布不均匀的修正系数, 式中k 考虑剪应力沿截面分布不均匀的修正系数 与截面形状有关
∆ = ∑∫
FQ FQP FN FNP MMP ds + ∑ ∫ ds + ∑ ∫ k ds EI EA GA
式中 F N FQ M ——虚设单位荷载引起的内力 虚设单位荷载引起的内力
l
q
A B
L
∆Q ∆M
∆Q ∆M
EI = 4.8 GAl 2
= 4.8
E 8 = 2(1 + µ ) = G 3
I h2 = A 12
EI h = 1.067( ) 2 GAl 2 l
∆Q ∆M h = 1.067( ) 2 = 1.067% l
当 h= 1 时 l 10 h 1 当 = 时 l 2
FN FQ FQ
ds ds
M
M
ds dθ=κds
γ0 dη= γ0 ds dλ=εds
ds微段 微段 整根杆 变形体系
dwi12=FN εds+FQ γ0ds +M κds w’i12= ∫ (FN εds+FQ γ0ds +M κds) wi12= ∑∫(FN εds+FQ γ0ds +M κds)
位移法结构力学知识点概念讲解

位移法结构力学知识点概念讲解1.结构位移:结构在受力作用下会发生形变,而位移描述了结构各点之间的距离变化。
位移可以分为水平位移和竖向位移,用于表示结构在水平和竖直方向的变形情况。
2.自由度:结构的自由度是指结构中可以自由变动的独立变量的个数。
自由度越多,结构描述和计算的精度越高。
常见的自由度有平动自由度和转动自由度,平动自由度用于描述结构的水平位移,而转动自由度用于描述结构的转动变形。
3.约束条件:结构中存在的各种约束条件限制了结构的自由度。
约束条件是指结构中一些部分的位移受到限制,不能随意变动。
常见的约束条件有支座和铰链等,它们可以限制结构的平动和转动自由度。
4.单元:位移法将结构划分为若干个单元,每个单元由一组节点和单元内部的位移函数组成。
节点是指结构中的一些特定点,单元内部的位移函数用于描述该单元内部各处的位移情况。
6.节点位移:节点位移是指结构中各个节点的位移,它通过节点的约束条件和单元的位移函数之间的关系得到。
节点位移是位移法计算的核心内容,通过计算节点位移可以得到结构的变形和位移分布。
7.应变:结构在荷载作用下会发生应变,应变描述了结构内部各点的变形情况。
应变是位移的导数,可以通过位移的一阶导数来表示。
应变的计算是位移法中重要的步骤之一8.应力:结构在荷载作用下会发生应力,应力描述了结构各点的受力情况。
应力是力和单位面积的比值,可以通过应变和材料的本构关系得到。
应力的计算是位移法中重要的步骤之一通过以上的概念和知识点,位移法可以对不同类型的结构进行分析和计算。
它是结构力学中常用的方法之一,通过假设结构的位移函数和节点之间的位移关系,得到了结构的变形和位移的近似解。
在实际工程中,位移法广泛应用于桥梁、建筑物和各种结构的设计和分析中,具有重要的理论和实践意义。
结构力学中的位移法

结构力学中的位移法
位移法是基于以下假设的:结构单元之间的约束全部通过边界条件来
体现,结构中的材料是线弹性材料,结构中的每个单元之间是相互独立和
互不干扰的。
位移法的基本思想是首先假设结构的位移场,然后利用位移场的表达
式和边界条件,推导出结构的应力、应变和位移等信息。
具体步骤如下:
1.确定结构的约束条件:根据结构的平衡条件,确定结构各部分之间
的约束关系。
一般包括边界条件和连接条件等。
2.建立位移场:通过将结构的变形分解为一系列位移函数的线性组合,建立位移场。
常用的位移函数包括常数、线性函数、二次函数等。
3.推导位移场的表达式:利用结构的几何关系和材料的力学性质,根
据平衡条件和应力-应变关系,推导出位移场的表达式。
4.边界条件和连接条件:利用结构的边界条件和连接条件,确定位移
场中的待定系数。
5.应力和应变的计算:利用位移场的表达式和应力-应变关系,计算
结构中各点的应力和应变。
6.变形和位移的计算:利用位移场的表达式,计算结构中各点的变形
和位移。
7.校核:通过校核位移场的可行性和合理性,验证所得结果的准确性。
位移法的优点是可以处理各种复杂的边界条件和载荷情况,适用于各
种不规则结构。
但是位移法也存在一些局限性,如要求解一些复杂结构时,可能需要大量的计算和繁琐的推导过程。
总之,位移法是结构力学中一种重要的解决结构问题的方法,通过确定结构的位移场来分析结构的力学性能,具有广泛的应用前景。
在实际工程中,位移法被广泛运用于结构设计和分析中,是一种非常有效的结构分析方法。
力法和位移法的基本方程

力法和位移法的基本方程力法和位移法是结构力学中常用的两种分析方法。
力法是以外力为基础,通过计算结构内力来求解结构的变形和应力状态;位移法则是以结构变形为基础,通过计算结构位移来求解结构的内力和应力状态。
两种方法各有优缺点,应根据具体情况选择合适的方法进行分析。
力法的基本方程为平衡方程和应力-应变关系式。
平衡方程是指结构受到的外力与内力的平衡关系,可以用以下公式表示:∑F = 0其中,∑F表示结构受到的所有外力的合力,等于内力的合力。
这个方程可以用来计算结构的内力分布。
应力-应变关系式是指材料的应力与应变之间的关系,可以用以下公式表示:σ = Eε其中,σ表示应力,E表示弹性模量,ε表示应变。
这个方程可以用来计算结构的应力分布。
位移法的基本方程为位移-力关系式和应力-应变关系式。
位移-力关系式是指结构的位移与内力之间的关系,可以用以下公式表示:u = ∑(k_i)^(-1)F_i其中,u表示结构的位移,k_i表示第i个节点的刚度,F_i表示第i个节点的外力。
这个方程可以用来计算结构的内力分布。
应力-应变关系式同样适用于位移法,可以用来计算结构的应力分布。
需要注意的是,力法和位移法的基本方程只是分析结构的起点,具体的分析方法和计算过程还需要根据具体情况进行选择和确定。
同时,结构的材料性质、几何形状、边界条件等因素也会对分析结果产生影响,需要进行综合考虑。
总之,力法和位移法是结构力学中常用的两种分析方法,它们的基本方程为平衡方程和应力-应变关系式、位移-力关系式和应力-应变关系式。
在实际分析中,应根据具体情况选择合适的方法进行分析,并考虑结构的材料性质、几何形状、边界条件等因素。
结构力学-位移法

DA柱:
MA 0
FQDA
1 4
(M DA
M
AD )
D C
FQDA
MDA
1 4
(3i D
1.5i EH
)
MAD
0.75iD 0.375iEH
A
E
FQEB
MBE
B 28
2kN/m
EB柱 MB 0
FQEB
1 4
M BE
242 4
1 4
(1.5i EH
4)
4
0.375iEH 3
14kN
D C
M BA
3i1 h1
M DC
3i2 h2
M FE
3i3 h3
32
3)建立位移法方程并求解
求各柱剪力。
FQAB
M BA h1
3i1 h12
k1
FQCD
M DC h2
3i2 h22
k2
FQEF
M FE h3
3i3 h32
k3
FP A
h1
E
C
FQAB
FQCD
FQEF
h2 h3
MBA
ql 2 8
M
F AB
ql 2 8
q
BA
B
l
M
F BA
ql 2 8
BB
q
M
F AB
ql 2 8
AA
杆端弯矩顺时针方向为正!
21
§7-3 无侧移刚架的计算
刚架内部结点无线位移,只有角位移。 基本未知量:内部结点的角位移。
8kN/m
Bi
i
A
4m
Di
i
C
4m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/10
讲解:XX
6
力法和位移法的解题思路:
力法:
先求多余未知力
结构内力
解题过程:
超静定结构
拆成基本 结构
结构位移 加上某些条件
原结构的变形协调条件(力法基本方程)
2021/3/10
讲解:XX
7
位移法:
先求某些结点位移
解题过程:
结构内力
结构
拆成单根杆件 的组合体
加上某些条件
1.杆端位移协调条件
单跨超静定梁在梁端、柱顶1处转动 Z1=1时产生的弯矩图 及外荷载作用下产生的弯矩图。
2021/3/10
讲解:XX
19
Z1=1 r11
2021/3/10
讲解:XX
M1
20
R1P
P
1
A
Pl
P
Pl
8
8
MP图
2021/3/10
讲解:XX
21
现取 M 1 图、MP图中的结点1为隔离体,由力矩平衡方
程 M10,求出 :
式(a)变为
r1Z 11R1P0
其物理意义是,基本结构由于转角Z1及外荷载共同作用, 附加刚臂1处所产生的约束反力矩总和等于零。
由此方程可得
Z1
R1P r11
可见,只要有了系数 r11及自由项R1P,Z1值很容易求得。
2021/3/10
讲解:XX
18
为了确定上式中的 R1P 和 r11 ,可先用力法分别求出各
2. 人为地迫使原先被“固定”的结点恢复到结构原 有的位移。
通过上述两个步骤,使基本结构与原结构的受力和变 形完全相同,从而可以通过基本结构来计算原结构的内力 和变形。
2021/3/10
讲解:XX
24
等截面直杆的物理方程
A
位基 移本 法单 中跨 的梁
2021/3/10
A
讲解:XX
B B
25
1.转角位移方程 Slope-Deflection Equation
2.结点的平衡条件
202Hale Waihona Puke /3/10讲解:XX8
适用范围:
力法: 超静定结构 位移法: 超静定结构,也可用于静定结构。
一般用于结点少而杆件较多的刚架。 例:
2021/3/10
讲解:XX
9
用位移法计算图示刚架。
为了使问题简化,作如下 计算假定:
1. 在受弯杆件中,略去杆 件的轴向变形和剪切变 形的影响。
2. 假定受弯杆两端之间的 距离保持不变。
2021/3/10
讲解:XX
10
由此可知,结点1只有转角Z1,而无线位移,汇交 于结点1的两杆杆端也应有同样的转角Z1。
整个刚架的变形只要用未 知转角Z1来描述,如果能设 法求得转角Z1,即可求出刚 架的内力。
2021/3/10
讲解:XX
11
为了求出Z1值,可先对原结构作些修改
P
1
1
B
基本结构
A
基本体系
这样,原结构就被改造成两个单跨梁: lB是两端固定梁,1A是一端固定、另端铰支梁。
2021/3/10
讲解:XX
12
R1P
P
在基本结构上加上原来的
力P,由于附加刚臂不允许结 点1转动,此时只有梁lB发生 变形,梁1A则不变形。
基本结构
此时附加刚臂中产生了反力矩R1P,反力矩规定以顺时 针为正。于是,基本结构与原结构就发生了差别,表现为:
2021/3/10
讲解:XX
14
R1P
P
基本结构
=
+
Z1
R11
Z1
2021/3/10
讲解:XX
15
结点1正好转动一个转角Z1时,所加的附加约束不再 起作用,其数学表达式为:
R1=0 即外荷载和应有的转角Z1共同作用于基本结构时,附 加约束反力矩等于零。
根据叠加原理,共同作用等于单独作用的叠加:
R1=R11+R1P=0
单跨超静定梁在荷载、
符号规定:
温改和支座移动共同作用下
杆端弯矩---绕杆端顺时针为正
杆端剪力---同前
杆端转角---顺时针为正
x 杆端相对线位移---使杆轴顺时针转为正
A
4i A
+
2i A
B
2iB
4iB
y 由线性小变形,由叠加原理可得
+
6iAB/l
P+
AB 6iAB/l
MAB4iA
2iB
6i l
M AB
1.由于加了约束,使结点1不能转动,而原来是能转动 的。
2021/3/10
讲解:XX
13
2.由于加了约束,产生了约束反力矩,而原来是没有 这个约束反力矩的。
为了消除基本结构与原
Z1
结构的差别,在结点1的附
R11
加约束上人为地加上一个外
Z1
力矩R11,迫使结点1正好转
动了一个转角Z1,于是变形
复原到原先给定的结构。
结构 力学Ⅱ
STRUCTURE MECHANICS
南华大学建资学院道桥教研室
2021/3/10
讲解:XX
1
结构力学Ⅱ
讲 授: 课件制作:
刘华良 刘华良
南华大学建资学院道桥教研室 衡阳 2005年
2021/3/10
讲解:XX
2
第八章 位移法
(Displacement Method)
2021/3/10
讲解:XX
3
内容
位移法的基本概念
等截面直杆的物理方程
位移法基本未知量数目的确定
位移法的两种思路:位移法典型方程和直接平衡方程
有侧移的斜柱刚架
剪力静定杆的求算 对称性的利用
联合法和混合法 温度改变时的计算
2021/3/10
支座移动的计算
弹性支座问题
课堂练习
本章小结
讲解:XX
4
位移法的基本概念
求解超静定结构的两种最基本的方法: 力法 位移法
力法适用性广泛,解题灵活性较大。(可选用各 种各样的基本结构)。
位移法在解题上比较规范,具有通用性,因 而计算机易于实现。
位移法可分为:手算——位移法
电算——矩阵位移法
2021/3/10
讲解:XX
5
力法与位移法最基本的区别:基本未知量不同
力法:以多余未知力基本未知量 位移法:以某些结点位移基本未知量
(a)
R11为强制使结点发生转角Z1时所产生的约束反力矩。
R1P为荷载作用下所产生的约束反力矩。
2021/3/10
讲解:XX
16
为了将式(a)写成未知量Z1的显式,将R11写为
Z1=1 R11=r11Z1
R11r11Z1
r11为单位转角(Z1=1) 产生的约束反力矩。
2021/3/10
讲解:XX
17
F AB
MBA 20214/3i/10B
2iA
6i l
M AB
F BA
讲解:XX
t1
转角位t移2 方程
M
F AB
M
F BA
固端弯矩
26
MAB4iA
2iB
r11
7 EI l
1
R1P
8
Pl
2021/3/10
讲解:XX
22
将这些结果代入位移法基本方程中解方程,即得
Z1
Pl 2 56 EI
最后,根据叠加原理 MMPM1Z1 ,即可求出最后弯 矩图 。
2021/3/10
讲解:XX
23
综上所述,位移法的基本思路是:
1. 在原结构产生位移的结点上设置附加约束,使结点 固定,从而得到基本结构,然后加上原有的外荷载;
