第十二章 含运算放大器的电路
集成运算放大器电路-模拟电子电路-PPT精选全文完整版

第4章 集成运算放大器电路
4―3―2差动放大器的工作原理及性能分析 基本差动放大器如图4―12所示。它由两个性能参
数完全相同的共射放大电路组成,通过两管射极连接 并经公共电阻RE将它们耦合在一起,所以也称为射极 耦合差动放大器。
I UE (UEE ) UEE 0.7
RE
RE
第4章 集成运算放大器电路
IC2
R1 R2
Ir
(4―7) (4―8)
第4章 集成运算放大器电路
可见,IC2与Ir成比例关系,其比值由R1和R2确定。 参考电流Ir现在应按下式计算:
UCC
Ir
UCC U BE1 Rr R1
UCC Rr R1
(4―9)
Ir
Rr
IC2
IB1
V1
+
UBE1 -
IE1
R1
IB2 +
UBE2 - R2
(4―11)
Ir
IC1
IB3
IC1
IC3
IC1 IC2,
IC3
3 1 3
IE3
IE3
IC2
IC1
1
IC2
2
若三管特性相同,则β1=β2=β3=β,求解以上各
式可得
IC3
(1 2ຫໍສະໝຸດ 222)Ir
(4―12)
第4章 集成运算放大器电路
利用交流等效电路可求出威尔逊电流源的动态内阻
Ro为
Ro 2 rce
4―2 电流源电路
电流源对提高集成运放的性能起着极为重要的作 用。一方面它为各级电路提供稳定的直流偏置电流, 另一方面可作为有源负载,提高单级放大器的增益。 下面我们从晶体管实现恒流的原理入手,介绍集成运 放中常用的电流源电路。
含电容的运算放大器电路的计算

电容的运算放大器电路是一种常见的电子电路,它可以实现电压放大和滤波功能,广泛应用于许多电子系统中。
本文将从基本概念、电路结构、工作原理和计算方法等方面对含电容的运算放大器电路进行详细介绍,帮助读者更好地理解和应用这一电路。
一、基本概念1. 运算放大器(Operational Amplifier,简称Op-Amp)是一种集成电路,具有高增益、高输入阻抗、低输出阻抗等特点,广泛应用于电子电路中。
2. 电容是一种存储电荷的元件,具有阻抗与频率成反比的特性,可以用于滤波和信号处理。
二、电路结构含电容的运算放大器电路通常由运算放大器、电容和其它元件组成,其中电容可以用来实现滤波、积分、微分等功能。
三、工作原理1. 电容的作用:电容在运算放大器电路中可以用来滤波、积分、微分等。
在滤波电路中,电容可以与电阻配合,实现低通滤波、高通滤波、带通滤波等功能。
2. 电容的阻抗特性:电容的阻抗与频率成反比,即Zc=1/(jωC),其中Zc为电容的阻抗,ω为角频率,C为电容的电容值。
3. 运算放大器的特性:运算放大器具有高输入阻抗、低输出阻抗、无限大的开环增益等特点,在实际应用中可以近似认为是理想运算放大器。
四、计算方法1. 低通滤波电路的计算:对于低通滤波电路,可以通过电容和电阻的组合来实现。
其传递函数为H(jω)=1/(1+jωR1C1),其中R1和C1分别为电阻和电容的取值。
通过调整R1和C1的取值,可以实现不同的频率特性。
2. 高通滤波电路的计算:高通滤波电路同样可以通过电容和电阻的组合来实现。
其传递函数为H(jω)=jωR2C2/(1+jωR2C2),其中R2和C2分别为电阻和电容的取值。
通过调整R2和C2的取值,可以实现不同的频率特性。
3. 带通滤波电路的计算:带通滤波电路通常采用多级滤波电路进行实现,可以组合低通滤波和高通滤波电路来实现。
可以通过串联或并联的方式组合低通和高通滤波电路,来实现不同的频率特性。
运算放大器详细的应用电路(很详细)

§8.1 比例运算电路8.1.1 反相比例电路1. 基本电路电压并联负反馈输入端虚短、虚断特点:反相端为虚地,所以共模输入可视为0,对运放共模抑制比要求低输出电阻小,带负载能力强要求放大倍数较大时,反馈电阻阻值高,稳定性差。
如果要求放大倍数100,R1=100K,Rf=10M2. T型反馈网络(T型反馈网络的优点是什么?)虚短、虚断8.1.2 同相比例电路1. 基本电路:电压串联负反馈输入端虚短、虚断特点:输入电阻高,输出电阻小,带负载能力强V-=V+=Vi,所以共模输入等于输入信号,对运放的共模抑制比要求高2. 电压跟随器输入电阻大输出电阻小,能真实地将输入信号传给负载而从信号源取流很小§8.2 加减运算电路8.2.1 求和电路1.反相求和电路2.虚短、虚断特点:调节某一路信号的输入电阻不影响其他路输入与输出的比例关系3.同相求和电路4.虚短、虚断8.2.2 单运放和差电路8.2.3 双运放和差电路例1:设计一加减运算电路设计一加减运算电路,使 V o=2Vi1+5Vi2-10Vi3 解:用双运放实现如果选Rf1=Rf2=100K,且R4= 100K则:R1=50K R2=20K R5=10K平衡电阻 R3= R1// R2// Rf1=12.5K R6=R4//R5//Rf2= 8.3K例2:如图电路,求Avf,Ri解:§8.3 积分电路和微分电路8.3.1 积分电路电容两端电压与电流的关系:积分实验电路积分电路的用途将方波变为三角波(Vi:方波,频率500Hz,幅度1V)将三角波变为正弦波(Vi:三角波,频率500Hz,幅度1V)(Vi:正弦波,频率500Hz,幅度1V)思考:输入信号与输出信号间的相位关系?(Vi:正弦波,频率200Hz,幅度1V)思考:输入信号频率对输出信号幅度的影响?积分电路的其它用途:去除高频干扰将方波变为三角波移相在模数转换中将电压量变为时间量§8.3 积分电路和微分电路8.3.2 微分电路微分实验电路把三角波变为方波(Vi:三角波,频率1KHz,幅度0.2V)输入正弦波(Vi:正弦波,频率1KHz,幅度0.2V)思考:输入信号与输出信号间的相位关系?(Vi:正弦波,频率500Hz,幅度1V)思考:输入信号频率对输出信号幅度的影响?§8.4 对数和指数运算电路8.4.1 对数电路对数电路改进基本对数电路缺点:运算精度受温度影响大;小信号时exp(VD/VT)与1差不多大,所以误差很大;二极管在电流较大时伏安特性与PN结伏安特性差别较大,所以运算只在较小的电流范围内误差较小。
实验十二集成运算放大器的测试解读
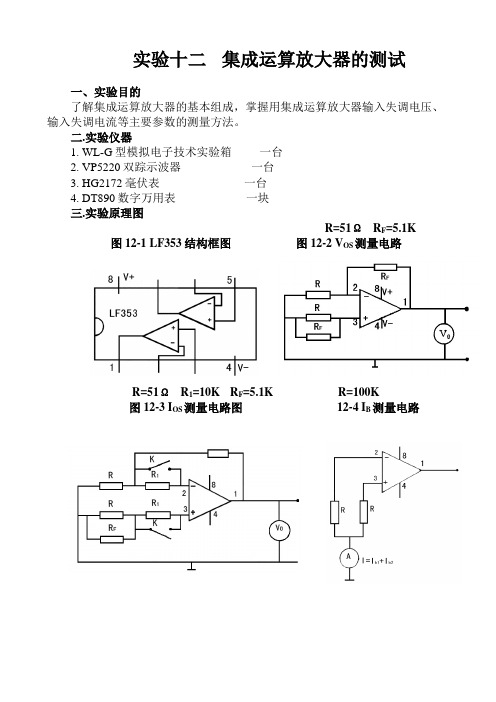
实验十二集成运算放大器的测试一、实验目的了解集成运算放大器的基本组成,掌握用集成运算放大器输入失调电压、输入失调电流等主要参数的测量方法。
二.实验仪器1. WL-G型模拟电子技术实验箱一台2. VP5220双踪示波器一台3. HG2172毫伏表一台4. DT890数字万用表一块三.实验原理图R=51ΩR F=5.1K 图12-1 LF353结构框图图12-2 V OS测量电路R=51ΩR1=10K R F=5.1K R=100K图12-3 I OS测量电路图12-4 I B测量电路C=10uF R1=5.1K R 2=51Ω R F =100K C F =100uF 图12-5 A O 测量电路C=10uF R=1K R F =100K D=1N4148 图12-6 CMRR 测量电路 四、实验步骤与方法1.集成运算放大器 LF353为二运算放大器,该集成电路内含两个独立的运算放大器,内部结构、接线引脚如图12-1 所示。
2.测量输入失调电压V OS输入失调电压V OS 指在室温和标称电源电压下,为使集成运算放大器的输出电压为零,而在其输入端由恒压源提供的补偿电压值。
实验采用在输入信号为零的情况下,测量输出电压V O 的方法,间接的求出输入失调电压V OS ,按照图12-2连接电路,接入±15V 电源,用数字万用表测量输出电压V O 。
则输入失调电压V OS =。
3.测量输入失调电流I OS输入失调电流I OS 指在室温和标称电源电压下,当输入信号为零时,两输入端的基极偏置电流之差,按照图12-3连接电路,接入± 15V 电源,用数字万用表测量输出电压V O 。
当开关断开时为输出电压V O1,开关闭合时为V O2,则输入失调电流 I OS = × 。
R R +RV 2V1R 1R R +R4.测量输入偏置电流I B输入偏置电流I B 指在室温和标称电源电压下,当输入信号为零时,两输入端的基极电流的平均值,按照图12-4连接电路,接入±15V 电源,用数字万用表测量电流I,则基极偏置电流I B =I/2。
运算放大器详细的应用电路(很详细)9页

§8.1 比例运算电路8.1.1 反相比例电路1. 基本电路电压并联负反馈输入端虚短、虚断特点:反相端为虚地,所以共模输入可视为0,对运放共模抑制比要求低输出电阻小,带负载能力强要求放大倍数较大时,反馈电阻阻值高,稳定性差。
如果要求放大倍数100,R1=100K,Rf=10M2. T型反馈网络(T型反馈网络的优点是什么?)虚短、虚断8.1.2 同相比例电路1. 基本电路:电压串联负反馈输入端虚短、虚断特点:输入电阻高,输出电阻小,带负载能力强V-=V+=Vi,所以共模输入等于输入信号,对运放的共模抑制比要求高2. 电压跟随器输入电阻大输出电阻小,能真实地将输入信号传给负载而从信号源取流很小§8.2 加减运算电路8.2.1 求和电路1.反相求和电路虚短、虚断特点:调节某一路信号的输入电阻不影响其他路输入与输出的比例关系2.同相求和电路虚短、虚断8.2.2 单运放和差电路8.2.3 双运放和差电路例1:设计一加减运算电路设计一加减运算电路,使 V o=2Vi1+5Vi2-10Vi3解:用双运放实现如果选Rf1=Rf2=100K,且R4= 100K则:R1=50K R2=20K R5=10K平衡电阻 R3= R1// R2// Rf1=12.5K R6=R4//R5//Rf2= 8.3K例2:如图电路,求Avf,Ri解:§8.3 积分电路和微分电路8.3.1 积分电路电容两端电压与电流的关系:积分实验电路积分电路的用途将方波变为三角波(Vi:方波,频率500Hz,幅度1V)将三角波变为正弦波(Vi:三角波,频率500Hz,幅度1V)(Vi:正弦波,频率500Hz,幅度1V)思考:输入信号与输出信号间的相位关系?(Vi:正弦波,频率200Hz,幅度1V)思考:输入信号频率对输出信号幅度的影响?积分电路的其它用途:去除高频干扰将方波变为三角波移相在模数转换中将电压量变为时间量§8.3 积分电路和微分电路8.3.2 微分电路微分实验电路把三角波变为方波(Vi:三角波,频率1KHz,幅度0.2V)输入正弦波(Vi:正弦波,频率1KHz,幅度0.2V)思考:输入信号与输出信号间的相位关系?(Vi:正弦波,频率500Hz,幅度1V)思考:输入信号频率对输出信号幅度的影响?§8.4 对数和指数运算电路8.4.1 对数电路对数电路改进基本对数电路缺点:运算精度受温度影响大;小信号时exp(VD/VT)与1差不多大,所以误差很大;二极管在电流较大时伏安特性与PN结伏安特性差别较大,所以运算只在较小的电流范围内误差较小。
运算放大器基本电路大全

运算放大器基本电路大全我们经常看到很多非常经典的运算放大器应用图集,但是这些应用都建立在双电源的基础上,很多时候,电路的设计者必须用单电源供电,但是他们不知道该如何将双电源的电路转换成单电源电路。
在设计单电源电路时需要比双电源电路更加小心,设计者必须要完全理解这篇文章中所述的内容。
1.1 电源供电和单电源供电所有的运算放大器都有两个电源引脚,一般在资料中,它们的标识是VCC+和VCC-,但是有些时候它们的标识是VCC+和GND。
这是因为有些数据手册的作者企图将这种标识的差异作为单电源运放和双电源运放的区别。
但是,这并不是说他们就一定要那样使用――他们可能可以工作在其他的电压下。
在运放不是按默认电压供电的时候,需要参考运放的数据手册,特别是绝对最大供电电压和电压摆动说明。
绝大多数的模拟电路设计者都知道怎么在双电源电压的条件下使用运算放大器,比如图一左边的那个电路,一个双电源是由一个正电源和一个相等电压的负电源组成。
一般是正负15V,正负12V和正负5V也是经常使用的。
输入电压和输出电压都是参考地给出的,还包括正负电压的摆动幅度极限Vom以及最大输出摆幅。
单电源供电的电路(图一中右)运放的电源脚连接到正电源和地。
正电源引脚接到VCC+,地或者VCC-引脚连接到GND。
将正电压分成一半后的电压作为虚地接到运放的输入引脚上,这时运放的输出电压也是该虚地电压,运放的输出电压以虚地为中心,摆幅在Vom 之内。
有一些新的运放有两个不同的最高输出电压和最低输出电压。
这种运放的数据手册中会特别分别指明Voh 和Vol 。
需要特别注意的是有不少的设计者会很随意的用虚地来参考输入电压和输出电压,但在大部分应用中,输入和输出是参考电源地的,所以设计者必须在输入和输出的地方加入隔直电容,用来隔离虚地和地之间的直流电压。
(参见1.3节)图一通常单电源供电的电压一般是5V,这时运放的输出电压摆幅会更低。
另外现在运放的供电电压也可以是3V 也或者会更低。
运算放大器详细的应用电路(很详细)
§8.1 比例运算电路8.1.1 反相比例电路1. 基本电路电压并联负反馈输入端虚短、虚断特点:反相端为虚地,所以共模输入可视为0,对运放共模抑制比要求低输出电阻小,带负载能力强要求放大倍数较大时,反馈电阻阻值高,稳定性差。
如果要求放大倍数100,R1=100K,Rf=10M2. T型反馈网络(T型反馈网络的优点是什么?)虚短、虚断8.1.2 同相比例电路1. 基本电路:电压串联负反馈输入端虚短、虚断特点:输入电阻高,输出电阻小,带负载能力强V-=V+=Vi,所以共模输入等于输入信号,对运放的共模抑制比要求高2. 电压跟随器输入电阻大输出电阻小,能真实地将输入信号传给负载而从信号源取流很小§8.2 加减运算电路8.2.1 求和电路1.反相求和电路2.虚短、虚断特点:调节某一路信号的输入电阻不影响其他路输入与输出的比例关系3.同相求和电路4.虚短、虚断8.2.2 单运放和差电路8.2.3 双运放和差电路例1:设计一加减运算电路设计一加减运算电路,使Vo=2Vi1+5Vi2-10Vi3 解:用双运放实现如果选Rf1=Rf2=100K,且R4= 100K则:R1=50K R2=20K R5=10K平衡电阻R3= R1// R2// Rf1=12.5K R6=R4//R5//Rf2= 8.3K例2:如图电路,求Avf,Ri解:§8.3 积分电路和微分电路8.3.1 积分电路电容两端电压与电流的关系:积分实验电路积分电路的用途将方波变为三角波(Vi:方波,频率500Hz,幅度1V)将三角波变为正弦波(Vi:三角波,频率500Hz,幅度1V)(Vi:正弦波,频率500Hz,幅度1V)思考:输入信号与输出信号间的相位关系?(Vi:正弦波,频率200Hz,幅度1V)思考:输入信号频率对输出信号幅度的影响?积分电路的其它用途:去除高频干扰将方波变为三角波移相在模数转换中将电压量变为时间量§8.3 积分电路和微分电路8.3.2 微分电路微分实验电路把三角波变为方波(Vi:三角波,频率1KHz,幅度0.2V)输入正弦波(Vi:正弦波,频率1KHz,幅度0.2V)思考:输入信号与输出信号间的相位关系?(Vi:正弦波,频率500Hz,幅度1V)思考:输入信号频率对输出信号幅度的影响?§8.4 对数和指数运算电路8.4.1 对数电路对数电路改进基本对数电路缺点:运算精度受温度影响大;小信号时exp(VD/VT)与1差不多大,所以误差很大;二极管在电流较大时伏安特性与PN结伏安特性差别较大,所以运算只在较小的电流围误差较小。
集成运算放大器基本运算电路
集成运算放大器的基本运算电路集成运算放大器是一种具有高电压放大倍数的直接耦合多级放大电路。
当外部接入不同的线性或非线性元器件组成负反馈电路时,可以灵活地实现各种特定的函数关系。
在线性应用方面,可组成比例、加法、减法、积分、微分、对数等模拟运算电路。
基本运算电路(1)反相比例运算电路电路如图1所示,对于理想运放,该电路的输出电压与输入电压之间的关系为uO=-ui图1 反相比例运算电路为了减小输入偏置电流引起的运算误差,在同相输入端应接入平衡电阻R2=R1||RF。
(2)同相比例运算电路图2是同相比例运算电路,它的输出电压与输入电压之间的关系为)ui当R1→∞时,uO=ui,即得到如图3所示的电压跟随器。
图中R2=RF,用以减小漂移和起保护作用。
一般RF取10KΩ,RF太小起不到保护作用,太大则影响跟随性。
图2 同相比例运算电路图3 电压跟随器(3)反相加法电路电路如图4所示。
图4 反相加法运算电路输出电压与输入电压之间的关系为uO=()R3=R1||R2||RF (4) 减法运算电路对于图5所示的减法运算电路,当R1=R2,R3=RF时,有如下关系式uO=(ui2-ui1)图5 减法运算电路(5)积分运算电路反相积分电路如图6所示。
在理想化条件下,输出电压uo等于uo(t)= —式中“—”号表示输出信号与输入信号反相。
uc(o)是t=0时刻电容C两端的电压值,即初始值。
图6 积分运算电路如果ui(t)是幅值为E的阶跃电压,并设uc(o)=0,则—即输出电压uo(t)随时间增长而线性下降。
显然时间常数R1C的数值大,达到给定的uo值所需的时间就长。
积分输出电压所能达到的最大值受集成运放最大输出范围的限制。
在进行积分运算之前,首先应对运放调零。
为了便于调节,将图中K1闭合,通过电阻R2的负反馈作用帮助实现调零。
但在完成调零后,应将K1打开,以免因R2的接入造成积分误差。
K2的设置一方面为积分电容放电提供通路,同时可实现积分电容初始电压uc(o)=0。
运放基本电路大全
运算放大器基本电路大全运算放大器电路大全我们经常看到很多非常经典的运算放大器应用图集,但是这些应用都建立在双电源的基础上,很多时候,电路的设计者必须用单电源供电,但是他们不知道该如何将双电源的电路转换成单电源电路。
在设计单电源电路时需要比双电源电路更加小心,设计者必须要完全理解这篇文章中所述的内容。
1.1 电源供电和单电源供电所有的运算放大器都有两个电源引脚,一般在资料中,它们的标识是VCC+和VCC-,但是有些时候它们的标识是VCC+和GND。
这是因为有些数据手册的作者企图将这种标识的差异作为单电源运放和双电源运放的区别。
但是,这并不是说他们就一定要那样使用――他们可能可以工作在其他的电压下。
在运放不是按默认电压供电的时候,需要参考运放的数据手册,特别是绝对最大供电电压和电压摆动说明。
绝大多数的模拟电路设计者都知道怎么在双电源电压的条件下使用运算放大器,比如图一左边的那个电路,一个双电源是由一个正电源和一个相等电压的负电源组成。
一般是正负15V,正负12V和正负5V也是经常使用的。
输入电压和输出电压都是参考地给出的,还包括正负电压的摆动幅度极限Vom 以及最大输出摆幅。
单电源供电的电路(图一中右)运放的电源脚连接到正电源和地。
正电源引脚接到VCC+,地或者VCC -引脚连接到GND。
将正电压分成一半后的电压作为虚地接到运放的输入引脚上,这时运放的输出电压也是该虚地电压,运放的输出电压以虚地为中心,摆幅在Vom 之内。
有一些新的运放有两个不同的最高输出电压和最低输出电压。
这种运放的数据手册中会特别分别指明Voh 和Vol 。
需要特别注意的是有不少的设计者会很随意的用虚地来参考输入电压和输出电压,但在大部分应用中,输入和输出是参考电源地的,所以设计者必须在输入和输出的地方加入隔直电容,用来隔离虚地和地之间的直流电压。
(参见1.3节)图一通常单电源供电的电压一般是5V,这时运放的输出电压摆幅会更低。
含有运算放大器的电阻电路
+
U U Uo 2 1
Uo
R 2
R 1
R f
-
Uo
R
f(
U R
2 2
U1 ) R1
当 R1 R2 Rf Uo ( U1 U2) 11
例 5-3-2 求Uo和Us的关系
解 :( 1 ) 节 点 电 压 分 析
R1
R2
节点1: 设 节 点 如 图
①-
+
② +∞
Us
R3
-
R4
③ ( 1 1 )U- 1 Uo 1 Us
R
R
U O
U in
R
1
in
2
2
1
(
1 R
A )UR
(
1 R
1 R
)U O
0
2
O
2
O
5
整理得:
UO R2(
Uin
R1 ( 1
1
讨论:
RO R2
1 ) ( 1
A RO R2
R2 R1
R2 ) Rin
当运放理想情况下,Rin∝∞ A ∝∞
∴近似有: U O R 2
Uin
R1
注意:分析理想运放电路时,直接利用运放特性列方程求解电
+ R1 R2
R2
R1
Uo 节点2:
- ( 1 1 )U 1 Uo 0
R3 R4
R3
( 2 ) 根 据 运 放 特 性: U- U U o R2R3 R2R 4 U s
R2R4 R1R3
较复杂的电路,列节点方程较合适
12
例5-3 如图所示,R5=R6,试求Uo/Uin
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十二章 含运算放大器的电路
12-1 求图题12-1所示电路的输出电压ou。
图 题12-1
答案
解:43234RuuRR(“虚断”)
43uu (“虚短”)
14121uuiiR
414322222341134[]()oRuRuuiRuRuRRRRRR
4122211341()()RRRRuuRRRR;
12-2 求图题12-2所示电路的开路电压比0iUU。
图 题12-2
答案
解:102iUIIR
11011RUIjCR
)1(1112i0jCRCRUU
12-3 图示题12-3所示电路可用来使一个小电容1CF变成一个大电容,求此大电
容的值,已知510A。
图 题12-3
答案
解: ()IUAUjC
011(1)inUZjACjCI
0(1)0.1CACF
12-4 求图题12-4所示电路的输入阻抗inZ。
图 题12-4
答案
解:(a)21UU 151UIRjC 45II
131UIIR
又340IRIR 即:
1111UUIRRjC
121inUZRjRCI
RjL ,2LRC
(b)同理可得:
12111/inUZRRjLRjCI2LCR。
12-5 图题12-5所示微分电路与输入电压1()ut的波形,画出2()ut的波形。
答案
解:11()()dutitdt
1
21
()()()dut
utitdt
2()ut波形如图(c)
所示。
12-6 图题12-6所示积分电路与输入电压1()ut的波形,画出2()ut的波形。
答案
解:11()()itut
211()()()ttutidud
2()ut波形如图(c)所示。
12-7 图题12-7所示电路,12r,21r,20R。求输入电阻。
图题12-7
答案
解: 1110[]10rAr
2220[]10rAr
12[][][]AAA
12221201002rrrrr
1112212280iARARARA或
21221801iRrrR
12-8 证明图题12-8所示 (a)与(b)两个电路等效。
图 题12-8
答案
证明:(a)12110010[][][]0100aggAAAgg
(b)10[]01bA
[][]abAA (a)(b)两个电路等效。
12-9 求图题12-9所示网络的H参
数矩阵。
图题12-9
答案
解:
''''
1222
()UnUnUU
''
1
2
1
UIg
211IgU
'''
12
1112
11
()UUUnUIIgg
12
2
1n
nUIIgg
21
InI
12UnU
21InI即0[]0nHn
12-10 求图题12-10所示二端口网络
的Z矩阵。
图题12-10
答案
解: 1UnU
21()nIg
12g1g1InIU
00gngnZ
12-11 证明图题12-11中各对电路是等效的。
图 题12-11
答案
(a) 证明011010101rrCrjCjrrA
2
2
01[]110001rjCrr
jrC
Arr
12[][]AA 两电路对应等效。
(b)1101010[]1110ggAggjLjgL
22101101[]1001ggjgLAggjgL
12[][]AA两电路对应等效。
(c)1001[]11010rrRARrrr
2
2
1000[]1110rr
ARRrrrr
12[][]AA两电路对应等效。
12-12 图题12-12所示正弦稳态电路,tVtu2000cos2)(1,求()ut。
图题12-12
答案
解:)(021VUm
根据频域分析法,有:
213113322111(210)150010003000100030001500111(10)1001000100012120nmnnnnUUUUjUjUjUU
得: 111122(22)33nmnUUjUUUj
813542135()2UV
()42cos(2000135)()uttV
