2020年北京市石景山区高三数学理科统一测试卷(石景山一模试卷)人教版
2019-2020年北京市石景山区高三上学期期末考试数学(理)试卷(有答案)【优质版】
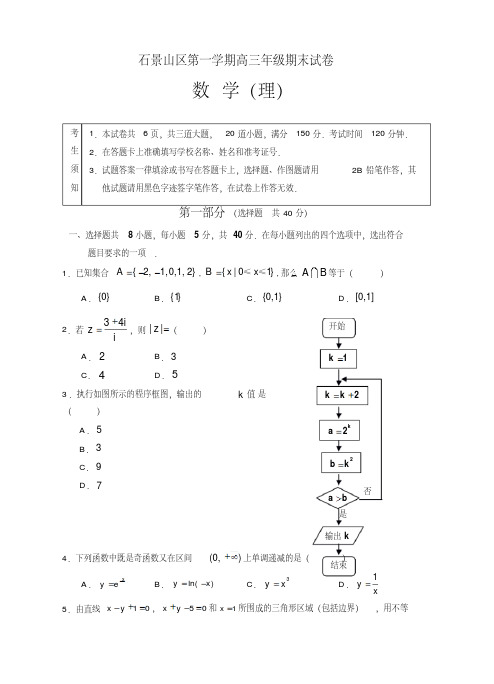
石景山区第一学期高三年级期末试卷数学(理)第一部分(选择题共40分)一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{2,1,0,1,2}A,{|01}Bx x ≤≤,那么AB 等于()A .{0}B .{1}C .{0,1}D .[0,1]2.若34i zi ,则||z ()A .2B .3C .4D .53.执行如图所示的程序框图,输出的k 值是()A .5B .3C .9D .74.下列函数中既是奇函数又在区间(0,)上单调递减的是()A .xy eB .ln()yx C .3yxD .1yx5.由直线10xy ,50x y和1x 所围成的三角形区域(包括边界),用不等考生须知1.本试卷共6页,共三道大题,20道小题,满分150分.考试时间120分钟.2.在答题卡上准确填写学校名称、姓名和准考证号.3.试题答案一律填涂或书写在答题卡上,选择题、作图题请用2B 铅笔作答,其他试题请用黑色字迹签字笔作答,在试卷上作答无效.1k a b 2kk2ka 2b k输出k是否开始结束式组可表示为()A .10,50,1xy xy x B .10,50,1xy xy x C .10,50,1xy xy xD .10,50,1xy xy x6.一个几何体的三视图如右图所示.已知这个几何体的体积为8,则h()A .1B .2C .3D .67.将函数2(3)yx图象上的点2(,(3))P t t向左平移m(m >0)个单位长度得到点Q .若Q 位于函数2y x 的图象上,则以下说法正确的是()A .当2t 时,m 的最小值为3B .当3t 时,m 一定为3C .当4t时,m 的最大值为3D .tR ,m 一定为38.六名同学A 、B 、C 、D 、E 、F 举行象棋比赛,采取单循环赛制,即参加比赛的每两个人之间仅赛一局.第一天,A 、B 各参加了3局比赛,C 、D 各参加了4局比赛,E参加了2局比赛,且A 与C 没有比赛过,B 与D 也没有比赛过,那么F 在第一天参加的比赛局数为()A .1B .2C .3D .4第二部分(非选择题共110分)二、填空题共6小题,每小题5分,共30分.9.在7(3)x的展开式中,5x 的系数是(结果用数值表示).10.已知ABC △中,=3AB ,=1BC ,sin =3cos C C ,则ABC △的面积为.11.若双曲线2214xym的渐近线方程为32yx ,则双曲线的焦点坐标是.12.等差数列{}n a 中,12a ,公差不为零,且1a ,3a ,11a 恰好是某等比数列的前三项,那么该等比数列公比的值等于.侧视图正视图4h俯视图313.有以下4个条件:①a b ;②||||a b ;③a 与b 的方向相反;④a 与b 都是单位向量.其中a //b 的充分不必要条件有.(填正确的序号).14.已知函数11,1,()4ln ,1x x f x x x,①方程()f x x 有________个根;②若方程()f x ax 恰有两个不同实数根,则实数a 的取值范围是____________.三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.(本小题共13分)已知函数π()2sin()sin 3cos22f x x x x .(Ⅰ)求()f x 的最小正周期;(Ⅱ)求()f x 在ππ[,]126上的最大值.16.(本小题共13分)2016年微信用户数量统计显示,微信注册用户数量已经突破9.27亿.微信用户平均年龄只有26岁,97.7%的用户在50岁以下,86.2%的用户在18-36岁之间.为调查大学生这个微信用户群体中每人拥有微信群的数量,现从北京市大学生中随机抽取100位同学进行了抽样调查,结果如下:微信群数量频数频率0至5个006至10个300.311至15个300.316至20个a c20个以上5b合计1001(Ⅰ)求a,b,c的值;(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过15个的概率;(Ⅲ)以这100个人的样本数据估计北京市的总体数据且以频率估计概率,若从全市..大.3人,记X表示抽到的是微信群个数超过15个的人数,求X的分布列学生..中随机抽取和数学期望EX.17.(本小题共14分)如图1,等腰梯形BCDP 中,BC ∥PD ,BAPD 于点A ,3PDBC ,且1ABBC.沿AB 把PAB △折起到P AB △的位置(如图2),使90P AD.(Ⅰ)求证:CD ⊥平面P AC ;(Ⅱ)求二面角AP DC 的余弦值;(Ⅲ)线段P A 上是否存在点M ,使得BM ∥平面P CD .若存在,指出点M 的位置并证明;若不存在,请说明理由.图1图218.(本小题共13分)已知椭圆2222:1(0)xy C a b ab的离心率为32,点(2,0)在椭圆C 上.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)过点(1,0)P 的直线(不与坐标轴垂直)与椭圆交于A B 、两点,设点B 关于轴的对称点为B .直线B A 与轴的交点Q 是否为定点?请说明理由.19.(本小题共14分)已知函数2()11x f x x,2()(0)a xg x x e a.(Ⅰ)求函数()f x 的单调区间;BCAPDB A CP ′ABCD(Ⅱ)若对任意12,[0,2]x x ,12()()f x g x 恒成立,求a 的取值范围.20.(本小题共13分)集合M 的若干个子集的集合称为集合M 的一个子集族.对于集合{1,2,3}n 的一个子集族D 满足如下条件:若,A D BA ,则BD ,则称子集族D 是“向下封闭”的.(Ⅰ)写出一个含有集合{1,2}的“向下封闭”的子集族D 并计算此时(1)AAD的值(其中A 表示集合A 中元素的个数,约定0;AD表示对子集族D 中所有成员A 求和);(Ⅱ)D 是集合{1,2,3}n 的任一“向下封闭的”子集族,对AD ,记max kA ,()max(1)AA Df k (其中ma 表示最大值),(ⅰ)求(2)f ;(ⅱ)若k 是偶数,求()f k .石景山区第一学期期末考试高三数学(理科)参考答案一、选择题共8小题,每小题5分,共40分.题号 12345678答案CDADABBD二、填空题共6小题,每小题5分,共30分.三、解答题共6小题,共80分.15.(本小题共13分)解:(Ⅰ)()2cos sin 3cos2f x x x x……1分sin 23cos2xx……2分π2sin(2)3x,……4分因此)(x f 的最小正周期为π.…………6分(Ⅱ)当ππ[,]126x 时,ππ2π2633x,………8分题号9 10 11 12 13 14答案18932(7,0)4①③1,11[,)4e当ππ232x,πsin(2)3x有最大值1.………10分即π12x时,()f x 的最大值为2.……………13分16.(本小题共13分)解:(Ⅰ)030305100a 解得35a ,5110020b,35710020c.…………………3分(Ⅱ)记“2人中恰有1人微信群个数超过15个”为事件A ,则114060210016()33C C P A C.所以,2人中恰有1人微信群个数超过15个的概率为1633.……………7分(Ⅲ)依题意可知,微信群个数超过15个的概率为25P.X 的所有可能取值0,1,2,3.……………8分则0033270()(1)2255125P XC ,1123541()(1)2255125P XC ,2213362()(1)2255125P XC ,33383()(22551)125P XC .其分布列如下:X123P2712554125361258125所以,2754368601231251251251255EX.……………13分17.(本小题共14分)解:(Ⅰ)因为90P AD ,所以P A ⊥AD .因为在等腰梯形中,AB ⊥AP ,所以在四棱锥中,AB ⊥AP .又ADAB A ,所以P A ⊥面ABCD .因为CD 面ABCD ,所以P A ⊥CD .……3分因为等腰梯形BCDE 中,ABBC ,3PDBC ,且1ABBC.所以2AC ,2CD ,2AD .所以222ACCDAD .所以AC ⊥CD .因为P A AC =A , 所以CD ⊥平面P AC .……5分(Ⅱ)由(Ⅰ)知,PA ⊥面ABCD ,AB ⊥AD ,如图,建立空间直角坐标系,A 0,0,0,B 1,0,0,C 1,1,0,D 0,2,0,P 0,0,1.…………5分所以(1,0,0)AB,(1,1,1)P C.由(Ⅰ)知,平面P AD 的法向量为(1,0,0)AB,设(,,)nx y z 为平面P CD 的一个法向量,则n CD n P C ,即00x y xyz,再令1y ,得(1,1,2)n .cos ,AB n =AB nAB n=66.所以二面角AP DC 的余弦值为66.…………9分(Ⅲ)若线段P A 上存在点M ,使得BM ∥平面P CD .依题意可设AM AP ,其中01.所以(0,0,)M ,(1,0,)BM.由(Ⅱ)知,平面P CD 的一个法向量(1,1,2)n.因为BM ∥平面P CD ,所以BMn ,所以120BM n ,解得12.所以,线段P A 上存在点M ,使得BM ∥平面P CD …………………14分18.(本小题共13分)解:(Ⅰ)因为点(2,0)在椭圆C 上,所以2a .又因为32c ea,所以3c ,221bac.所以椭圆C 的标准方程为:2214xy.……………………5P B A CP ’ABCD xyz分(Ⅱ)设112222(,),(,),(,),(,0)A x y B x y B x y Q n .设直线AB :(1)(0)y k x k.……………………6分联立22(1)440y k x x y和,得:2222(14)8440k x k xk.所以2122814kx x k,21224414kx x k.……………8分直线AB 的方程为121112()y y yy xx x x ,……………9分令0y,解得112122111212()y x x x y x y nx y y y y (11)分又1122(1),(1)y k x y k x ,所以121212()42x x x x nx x .所以直线B A 与轴的交点Q 是定点,坐标为(4,0)Q .………13分19.(本小题共14分)解:(Ⅰ)函数()f x 的定义域为R ,()()()()()()x x x f x x x 2222211111.……2分当x 变化时,()f x ,()f x 的变化情况如下表:x (,)1(,)11(,)1()f x ()f x 所以,函数()f x 的单调递增区间是(,)11,单调递减区间是(,)1,(,)1.…………5分(Ⅱ)依题意,“对于任意12,[0,2]x x ,12()()f x g x 恒成立”等价于“对于任意[0,2]x,minmax ()()f x g x 成立”.由(Ⅰ)知,函数()f x 在[0,1]上单调递增,在[1,2]上单调递减,因为(0)1f ,2(2)115m f ,所以函数()f x 的最小值为(0)1f .所以应满足max ()1g x .………………………………………………7分因为2()e axg x x ,所以2()(+2)e axg x ax x .………8分因为0a,令()0g x 得,10x ,22x a.(ⅰ)当22a,即10a 时,在[0,2]上()0g x ,所以函数()g x 在[0,2]上单调递增,所以函数2max ()(2)4e ag x g .由24e1a得,ln 2a,所以1ln 2a .……………11分(ⅱ)当202a ,即1a时,在2[0,)a上()0g x ,在2(,2]a上()0g x ,所以函数()g x 在2[0,)a 上单调递增,在2(,2]a上单调递减,所以max2224()()eg x g a a .由2241ea 得,2ea,所以1a .……………13分综上所述,a 的取值范围是(,ln 2].……………14分20.(本小题共13分)解:(Ⅰ)含有集合{1,2}的“向下封闭”的子集族{,{1},{2},{1,2}}D……2分此时112(1)(1)(1)(1)(1)0AA D…………4分(Ⅱ)设{1,2,3}n 的所有不超过k 个元素的子集族为kD (ⅰ)易知当2DD 时,(1)AA D达到最大值,所以21122(1)32(2)(1)(1)(1)122n n n n nn f C C n…6分(ⅱ)设D 是使得max kA 的任一个“向下封闭”的子集族,记'''DDD ,其中'D 为不超过2k元的子集族,''D 为1k 元或k 元的子集则(1)AA D='''''(1)(1)(2)(1)AAAA DA DA Df k ………8 分现设''D有l (kn l C )个{1,2,3}n 的k 元子集,由于一个1k 元子集至多出现在1n k个{1,2,3}n 的k 元子集中,而一个k 元子集中有1k kC个1k 元子集,故l 个k 元子集至少产生11k k lC nk个不同的1k 元子集.''11(1)(1)(1)111k Ak k k knnnA DlCkkl l C CCn k n k n k 1(1)(2)()Ak k nnA Df kCC f k 由(ⅰ)得11221()(1)(1)(1)(1)(1)kkk ii nnnni f k CCCC …13分【注:若有其它解法,请酌情给分.】。
北京市石景山区2024届高三下学期3月统一练习数学试卷(解析版)

石景山区2024年高三统一练习数学本试卷共6页,满分为150分,考试时间为120分钟.请务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将答题卡交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}2230A x x x =--<,{}1B x x =>,则A B = ()A.()1,3- B.()3,1- C.()1,1- D.()1,3【答案】D 【解析】【分析】根据一元二次不等式解法可得()13A ,=-,再由交集运算可得结果.【详解】解不等式2230x x --<可得13x -<<,即()13A ,=-;又{}()11,B x x ∞=>=+,因此()1,3A B ⋂=.故选:D2.下列函数中,在区间()1,1-上为减函数的是()A.()sin f x x = B.()cos f x x= C.()()ln 1f x x =+ D.()2xf x -=【答案】D 【解析】【分析】根据三角函数,指数函数和对数函数的性质,即可判断选项.【详解】A ,根据正弦函数的性质可知,()ππ1,1,22⎛⎫-⊆- ⎪⎝⎭,所以sin y x =在()1,1-上为增函数,故A 错误;B ,()cos f x x =是偶函数,关于y 轴对称,()ππ1,1,22⎛⎫-⊆- ⎪⎝⎭,所以cos y x =在()1,0-上是增函数,在()0,1上是减函数,故B 错误;C ,()()ln 1f x x =+的定义域是()1,∞-+,函数()ln 1y x =+是区间()1,1-上是增函数,故C 错误;D ,根据指数函数的性质可知,()2xf x -=在区间()1,1-上是减函数,故D 正确.故选:D3.一袋中有大小相同的4个红球和2个白球.若从中不放回地取球2次,每次任取1个球,记“第一次取到红球”为事件A ,“第二次取到红球”为事件B ,则()P B A =()A.415B.25C.35 D.45【答案】C 【解析】【分析】由条件概率公式求解即可.【详解】()()()43365456P AB P B A P A ⨯===.故选:C .4.设,,αβγ是三个不同平面,且l αγ= ,m βγ= ,则“//l m ”是“//αβ”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】B 【解析】【分析】由充分条件和必要条件的定义结合线面、面面的位置关系对选项一一判断即可得出答案.【详解】由l αγ= ,m βγ= ,//l m ,则,αβ可能相交,故“//l m ”推不出“//αβ”,由l αγ= ,m βγ= ,//αβ,由面面平行的性质定理知//l m ,故“//αβ”能推出“//l m ”,故“//l m ”是“//αβ”的必要不充分条件.故选:B .5.等差数列{}n a 的首项为1,公差不为0.若236,,a a a 成等比数列,则{}n a 的前5项和为()A.15- B.3- C.5D.25【解析】【分析】首先代入等差数列的基本量,由等比数列的概念列式,最后代入求和公式,即可求解.【详解】设等差数列{}n a 的公差为d ,则21a d =+,312a d =+,615a d =+,由题意可知,()()()212115d d d +=++,即22d d =-,解得:2d =-或0d =(舍),则数列{}n a 的前5项和51545520152S a d ⨯=+=-=-.故选:A6.直线1y kx =+与圆()22116x y ++=相交于,A B 两点,则线段AB 的长度可能为()A.5B.7C.9D.14【答案】B 【解析】【分析】根据直线所过定点,求弦长的最小值和最大值,再结合选项,即可求解.【详解】直线1y kx =+恒过点()0,1,且点()0,1在圆()22116x y ++=内,当点()0,1是弦AB 的中点时,此时弦长最短,圆心()0,1-和点()0,1的距离为2,此时弦长AB ==,最长的弦长是直径为8,所以弦长的取值范围是⎡⎤⎣⎦,其中只有B 成立.故选:B7.已知函数()()π2sin 0,2f x x ωϕωϕ⎛⎫=+><⎪⎝⎭的部分图象如图所示,则()πf -的值是()A.B.1C.1- D.【答案】A【分析】由图可得πT =,求得2ω=,再利用图象过点π,212⎛⎫⎪⎝⎭,可得到π3ϕ=,从而得到()π2sin 23f x x ⎛⎫=+ ⎪⎝⎭,再利用诱导公式及特殊角的三角函数值求解即可.【详解】由图象可知π5π112122T ⎛⎫--= ⎪⎝⎭,解得πT =,因为0ω>,所以2πTω=,解得2ω=,将π,212⎛⎫⎪⎝⎭代入解析式化简得πsin 16ϕ⎛⎫+= ⎪⎝⎭,因为π2ϕ<,则ππ62ϕ+=,得π3ϕ=,故()π2sin 23f x x ⎛⎫=+ ⎪⎝⎭,所以()πππ2sin 2π2sin 33f ⎛⎫-=-+== ⎪⎝⎭.故选:A8.设0.32=a ,πsin 12b =,ln2c =,则()A.c b a <<B.b<c<aC.a b c<< D.b a c<<【答案】B 【解析】【分析】根据给定的条件,利用指数、对数函数、正弦函数的性质,借助112,进行比较判断选项.【详解】0.30221a =>=,ππ1sin sin 1262b =<=,2e <<,则1ln 212<<,即112c <<,所以b c a <<.故选:B9.中国民族五声调式音阶的各音依次为:宫、商、角、徵、羽,如果用这五个音,排成一个没有重复音的五音音列,且商、角不相邻,徵位于羽的左侧,则可排成的不同音列有()A.18种 B.24种C.36种D.72种【答案】C 【解析】【分析】先排宫、徽、羽三个音节,然后商、角两个音阶插空即可求解.【详解】解:先将宫、徽、羽三个音节进行排序,且徽位于羽的左侧,有33A 32=,再将商、角插入4个空中的2个,有24A 12=,所以共有31236⨯=种.故选:C .10.对于曲线22:1C x y --+=,给出下列三个命题:①关于坐标原点对称;②曲线C 上任意一点到坐标原点的距离不小于2;③曲线C 与曲线3x y +=有四个交点.其中正确的命题个数是()A.0 B.1C.2D.3【答案】C 【解析】【分析】分析两个曲线的对称性,并结合函数的图象和性质,利用数形结合,即可判断①③,利用基本不等式,即可判断②.【详解】①将曲线22:1C x y --+=中的x 换成x -,将y 换成y -,方程不变,所以曲线关于原点对称,并且关于x 轴和y 轴对称,故①正确;②设曲线C 上任一点为(),P x y()222222222211224y x x y x y xy x y ⎛⎫+=++=++≥+= ⎪⎝⎭,当2222y x x y=,即222x y ==时,等号成立,2≥,曲线C 上任意一点到坐标原点的距离不小于2,故②正确;③曲线3x y +=中的x 换成x -,将y 换成y -,方程不变,所以曲线关于原点对称,并且关于x 轴和y 轴对称,并且将x 换成y ,y 换成x ,方程不变,所以曲线也关于y x =对称,曲线2211:1C x y +=中,21x ≥且21y ≥,将曲线2211:1C x y+=中的x 换成y ,y 换成x ,方程不变,所以曲线C 也关于y x =对称,当0,0x y >>时,联立22111x y y x ⎧+=⎪⎨⎪=⎩,得x y ==,当0,0x y >>时,y ==1x >时,函数单调递减,3<,所以点在直线3x y +=的下方,如图,在第一象限有2个交点,根据两个曲线的对称性可知,其他象限也是2个交点,则共有8个交点,故③错误;故选:C【点睛】关键点点睛:本题的关键是③的判断,判断的关键是对称性的判断,以及将方程转化为函数,判断函数的单调性,即可判断.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.复数z 在复平面内对应的点为(1,2)-,则5z=___________.【答案】12i --##2i 1--【解析】【分析】由复数对应的点写出复数z ,再应用复数除法的法则求解即可.【详解】∵z 对应的点为(1,2)-,∴12i z =-+,∴555(12i)5(12i)12i 12i (12i)(12i)5z ----====---+-+--.故答案为:12i --.12.斜率为1的直线l 经过抛物线24y x =的焦点F ,且与该抛物线相交于A ,B 两点,则AB =______.【答案】8【解析】【分析】求出直线l 的方程,设11()A x y ,、22()B x y ,,直线方程代入抛物线方程应用韦达定理得12x x +,然后由焦点弦长公式可得结论.【详解】抛物线24y x =的焦点坐标为(10)F ,,直线l 方程为1y x =-,设11()A x y ,、22()B x y ,,则由抛物线焦点弦长公式得:12122AB x x p x x =++=++,又A 、B 是抛物线与直线的交点,由241y xy x ⎧=⎨=-⎩得2610x x -+=,则126x x +=,∴||8AB =.故答案为:8.【点睛】结论点睛:焦点弦的一些性质:抛物线22y px =的焦点为F ,AB 是其过焦点的弦,1122(,),(,)A x y B x y ,则(1)12AB x x p =++.(2)112AF BF p +=.(3)2124p x x =,212y y p =-.13.已知向量,a b满足2b = ,a 与b 的夹角为π6,则当实数λ变化时,b a λ- 的最小值为______.【答案】1【解析】【分析】根据题意利用平面向量的几何特征,可知当()b a a λ-⊥ 时,b a λ-取得最小值.【详解】如图所示:设,OA a OB b == ,当()b a a λ-⊥ 时,b a λ-取得最小值,过点B 作BD OA ⊥于点D ,即可得b a λ-的最小值为BD ,又a与b的夹角为π6,即π6AOB ∠=,易知2OB =,所以πsin 16BD OB ==.即b a λ-的最小值为1.故答案为:114.设函数()323,13,1x ax x f x x a x ⎧+≤=⎨+>⎩,①若()f x 有两个零点,则实数a 的一个取值可以是______;②若()f x 是R 上的增函数,则实数a 的取值范围是______.【答案】①.1-(13a <-内的值都可以)②.01a ≤≤或2a ≥【解析】【分析】①分析函数的性质,确定零点所在的区间,通过解方程的方法,即可求解;②根据分段函数的形式,确定两段函数都是单调递增,并根据分界点处函数值的关系不等式,即可求解.【详解】①函数()23f x x a =+在()1,+∞上单调递增,()2130f a =+>,所以函数()f x 在区间()1,+∞上无零点,则函数()33f x x ax =+在(],1-∞上有2个零点,即330x ax +=,()230x x a +=,则0x =,或x =或x =,a<0,1>,解得:13a <-,所以a 的一个值是1-;②函数()23f x x a =+在()1,+∞上单调递增,则在(],1-∞上,()33f x x ax =+也单调递增,且321331a a +≤⨯+,若函数在()33f x x ax =+在区间(],1-∞单调递增,则()2330f x x a '=+≥,即2≥-a x 在区间(],1-∞上恒成立,即()2maxa x≥-,即0a ≥,不等式321331a a +≤⨯+,解得:2a ≥或1a ≤,综上可知,01a ≤≤或2a ≥.故答案为:1-(13a <-内的值都可以);01a ≤≤或2a ≥15.黎曼函数在高等数学中有着广泛应用,其一种定义为:[]0,1x ∈时,()()*1,,N ,0,0,10,1p p x p q q q q R x x ⎧⎛⎫=∈⎪ ⎪=⎨⎝⎭⎪=⎩为既约真分数和内的无理数.若数列*1,n n a R n n -⎛⎫=∈ ⎪⎝⎭N ,给出下列四个结论:①1n a n =;②21n n a a ++<;③1112n i i i a a +=<∑;④11ln 2ni i n a =+≥∑.其中所有正确结论的序号是______.【答案】②③④【解析】【分析】根据黎曼函数的定义和性质逐项分析.【详解】对于①,N ,1n n +∈∴= 时,()11001a R ==≠,故①错误;对于②,111n a n +=+,212n a n +=+,+12n n a a +∴>,故②正确;对于③,11223341111111123341ni i n n i a a a a a a a a a a n n ++==++++=⨯+⨯++⋅+∑ 11111111123341212n n n =-+-++-=-<++ ,故③正确;对于④,123111123ni n i a a a a a n==++++=+++∑ ,()2n ≥,构造函数()e 1xg x x =--,()0x >,则()e 10xg x ='->,()g x 单调递增,()(0)0g x g ∴>=,即当0x >时e 1xx >+,11132111e 1,e 1,,e 123n n>+>+>+ ,11123345111111eln 2342232nn n n n n ++++++⎛⎫>⨯⨯⨯⨯=∴+++> ⎪⎝⎭,当1n =时,110ni i a a ===∑,11ln 02+=,11ln 2ni i n a =+⎛⎫∴≥ ⎪⎝⎭∑,故④正确.故选:②③④.【点睛】方法点睛:新定义题型的特点是:通过给出一个新概念,或约定一种新运算,或给出几个新模型来创设全新的问题情景,要求考生在阅读理解的基础上,依据题目提供的信息,联系所学的知识和方法,实现信息的迁移,达到灵活解题的目的:遇到新定义问题,应耐心读题,分析新定义的特点,弄清新定义的性质,按新定义的要求,“照章办事”,逐条分析、验证、运算,使问题得以解决.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.在锐角ABC 中,角,,A B C 的对边分别为,,a b c,且2sin 0b A -=.(1)求角B 的大小;(2)求cos cos A C +的取值范围.【答案】(1)π3B =(2),12⎛⎤ ⎥⎝⎦【解析】【分析】(1)由正弦定理边化角求解即可;(2)由(1)可知π3B =,所以2π3A C +=,所以将cos cos A C +转化为同一个角的三角函数,最后求其值域即可.【小问1详解】因为2sin 0b A =,由正弦定理边化角得:2sin sin 0B A A =,所以(2sin sin 0B A =,由于在ABC 中,sin 0A ≠,所以2sin 0B =,即3sin 2B =,又π02B <<,所以π3B =.【小问2详解】由(1)可知π3B =,所以2π3A C +=,所以2π2π2πcos cos cos cos cos cos cos sin sin 333A C A A A A A⎛⎫+=+-=++⎪⎝⎭1313πcos cos cos sin 22226A A A A A A ⎛⎫=-+=+=+ ⎪⎝⎭由于在锐角ABC 中,2ππ032π02A A ⎧<-<⎪⎪⎨⎪<<⎪⎩,所以ππ62A <<,所以ππ2π363A <+<,所以πππsin sin sin 362A ⎛⎫<+≤ ⎪⎝⎭,所以πsin 126A ⎛⎫<+≤ ⎪⎝⎭,所以cos cos A C +的取值范围为3,12⎛⎤ ⎥ ⎝⎦.17.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,2PA AD CD ===,3BC =,PC =.(1)求证:CD ⊥平面PAD ;(2)再从条件①、条件②这两个条件中选择一个作为已知,求平面PBC 与平面PAD 所成锐二面角的大小.条件①:AB =条件②://BC 平面PAD .注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.【答案】(1)证明见解析(2)所选条件见解析,π4【解析】【分析】(1)连接AC ,由题目条件可推得ADC △为等腰直角三角形,且π4ACD ∠=,π2ADC ∠=,即CD AD ⊥,再PA CD ⊥,由线面垂直的判定定理即可证明;(2)选条件①或选条件②均可证明BC CD ⊥,建立以A 为原点的空间直角坐标系,求出平面PBC 与平面PAD 的法向量,由二面角求解即可.【小问1详解】如图,连接AC ,因PA ⊥平面ABCD ,,AC CD ⊂平面ABCD ,则PA AC ⊥,PA CD ⊥.又2PC PA ==,则AC =注意到2AD DC ==,则ADC △为等腰直角三角形,其中π4ACD ∠=,π2ADC ∠=.所以CD AD ⊥,又因为PA CD ⊥,,AD PA ⊂平面PAD ,AD PA A ⋂=,所以CD ⊥平面PAD ;【小问2详解】若选条件①,由余弦定理可得,222222cos AC BC AB ACB AC BC +-∠===⋅,结合ACB ∠为三角形内角,得π4ACB ∠=,又π4ACD ∠=,则π2BCD ∠=,即BC CD ⊥.若选条件②,因BC //平面PAD ,BC ⊂平面ABCD ,平面ABCD ⋂平面PAD AD =,则BC AD ∥,又π2ADC ∠=,则π2BCD ∠=,即BC CD ⊥.故建立以A 为坐标原点,如下图所示空间直角坐标系(x 轴所在直线与DC 平行)又23,PA AD CD BC ====,AB =则()()()()0,0,02,1,02,2,00,2,0A B C D -,,,,()0,0,2P ,则()0,3,0BC = ,()2,2,2CP =-- ,()2,0,0DC =.平面PAD 法向量为()2,0,0DC =,设平面PBC 法向量为(),,n x y z = ,则03022200n BC y x y z n CP ⎧⋅==⎧⎪⇒⎨⎨--+=⋅=⎩⎪⎩.令1x =,则0,1y z ==,所以()1,0,1n =,设面PBC 与平面PAD 所成角为θ,2cos cos ,2n DC n DC n DCθ⋅====⋅,根据平面角的范围可知π4θ=.18.为研究北京西部地区油松次生林和油松人工林的森林群落植物多样性问题,某高中研究性学习小组暑假以妙峰山油松次生林和老山油松人工林为研究对象进行调查,得到两地区林下灌木层,乔木层,草本层的抽样调查数据.其中两地区林下灌木层获得数据如表1,表2所示:表1:老山油松人工林林下灌木层植物名称植物类型株数酸枣灌木28荆条灌木41孩儿拳头灌木22河朔荛花灌木4臭椿乔木幼苗1黑枣乔木幼苗1构树乔木幼苗2元宝槭乔木幼苗1表2:妙峰山油松次生林林下灌木层植物名称植物类型株数黄栌乔木幼苗6朴树乔木幼苗7栾树乔木幼苗4鹅耳枥乔木幼苗7葎叶蛇葡萄木质藤本8毛樱桃灌木9三裂绣线菊灌木11胡枝子灌木10大花溲疏灌木10丁香灌木8(1)从抽取的老山油松人工林林下灌木层的植物样本中任选2株,求2株植物的类型都是乔木幼苗的概率;(2)以表格中植物类型的频率估计概率,从妙峰山油松次生林林下灌木层的所有植物中随机抽取3株(假设每次抽取的结果互不影响),记这3株植物的植物类型是灌木的株数为X,求X的分布列和数学期望;(3)从老山油松人工林的林下灌木层所有符合表1中植物名称的植物中任选2株,记此2株植物属于不同植物名称的概率估计值为1P;从妙峰山油松次生林的林下灌木层所有符合表2中植物名称的植物中任选2株,记此2株植物属于不同植物名称的概率估计值为2P.请直接写出1P与2P大小关系.(结论不要求证明)【答案】(1)1 495;(2)分布列见解析,期望95(3)12P P <【解析】【分析】(1)根据古典概型概率公式,以及组合数公式,即可求解;(2)根据二项分布概率公式,即可求解;(3)根据两个表格中的植物类型分布的数据,即可求解.【小问1详解】表1中的灌木有284122495+++=株,乔木幼苗有1+1+2+1=5株,共有100株,所以252100C 1C 495P ==,所以求2株植物的类型都是乔木幼苗的概率为1495;【小问2详解】表2中的灌木有9111010848++++=株,乔木幼苗有674724+++=株,木质藤本有8株,抽取1株是灌木的概率为483482485=++,由题意可知,0,1,2,3X =,33,5X B ⎛⎫⎪⎝⎭()32805125P X ⎛⎫=== ⎪⎝⎭,()21332361C 55125P X ⎛⎫⎛⎫==⨯= ⎪⎪⎝⎭⎝⎭,()22332542C 55125P X ⎛⎫⎛⎫==⨯=⎪ ⎪⎝⎭⎝⎭,()332735125P X ⎛⎫=== ⎪⎝⎭,分布列如下,X0123P8125361255412527125()39355E X np ==⨯=;【小问3详解】表1中植物间的数量差距较大,表2中每种植物的数量差不多,所以选出来不同种类,表2的概率更大,所以12P P <.19.已知函数()()e0axf x x a =>.(1)求曲线()y f x =在点()()0,0f 处的切线方程;(2)求()f x 在区间[]1,1-上的最大值与最小值;(3)当1a =时,求证:()ln 1f x x x ≥++.【答案】(1)y x =(2)见解析(3)证明见解析【解析】【分析】(1)根据导数的几何意义,求切线方程;(2)首先求函数的导数,再讨论01a <≤和1a >两种情况求函数的单调性,求函数的最值;(3)首先根据不等式构造函数()e ln 1xg x x x x =---,再利用导数求函数的最小值,即可证明.【小问1详解】()()1e ax f x ax '=+,()01f '=,()00f =,所以曲线()y f x =在点()()0,0f 处的切线方程为y x =;【小问2详解】()()1e ax f x ax '=+,0a >当01a <≤时,()0f x '≥在区间[]1,1-上恒成立,()f x 在区间[]1,1-上单调递增,所以函数()f x 的最小值为()1e axf --=-,最大值为()1e af =,当1a >时,()0f x '=,得()11,0x a=-∈-,()f x '在区间11,a ⎡⎫--⎪⎢⎣⎭小于0,函数()f x 单调递减,()f x '在区间1,1a ⎡⎤-⎢⎥⎣⎦大于0,函数()f x 单调递增,所以函数()f x 的最小值为11e f a a ⎛⎫-=- ⎪⎝⎭,()1e ax f --=-,()1e a f =,显然()()11f f >-,所以函数()f x 的最大值为()1e a f =,综上可知,当01a <≤时,函数()f x 的最小值为()1e axf --=-,最大值为()1e af =,当1a >时,函数()f x 的最小值为11e f a a ⎛⎫-=- ⎪⎝⎭,最大值为()1e a f =;【小问3详解】当1a =时,()e xf x x =,即证明不等式e ln 1x x x x ≥++,设()e ln 1xg x x x x =---,0x >,()()11e ⎛⎫'=+-⎪⎝⎭xg x x x ,设()1e xh x x =-,0x >,()21e 0xh x x'=+>,所以()h x 在()0,∞+单调递增,并且1202h ⎛⎫=<⎪⎝⎭,()1e 10h =->,所以函数()h x 在1,12⎛⎫⎪⎝⎭上存在唯一零点0x ,使()0001e 0x h x x =-=,即()00g x '=,则在区间()00,x ,()0g x '<,()g x 单调递减,在区间()0,x +∞,()0g x '>,()g x 单调递增,所以()g x 的最小值为()00000e ln 1xg x x x x =---,由()0001e 0x h x x =-=,得001x x e =,且00ln x x =-,所以()00g x =,所以()e ln 10xg x x x x =---≥,即()ln 1f x x x ≥++.20.已知椭圆()2222:10x y C a b a b +=>>的离心率为32,短轴长为(1)求椭圆C 的方程;(2)设O 为坐标原点,过点31,2P ⎛⎫--⎪⎝⎭分别作直线12,l l ,直线1l 与椭圆相切于第三象限内的点G ,直线2l 交椭圆C 于,M N 两点.若2PG PM PN =⋅,判断直线2l 与直线OG 的位置关系,并说明理由.【答案】(1)22182x y +=(2)2//l OG ,理由见解析【解析】【分析】(1)根据条件,列出关于,,a b c 得到方程,即可求解;(2)首先设出直线1l 的方程,并与椭圆方程联立,求出点G 的坐标,设出直线2l 的方程,与椭圆方程联立,利用韦达定理表示PM PN ,再根据2PG PM PN =⋅,求出直线2l ,即可判断直线2l 与直线OG 的位置关系.【小问1详解】由条件可知,222322c a b a b c ⎧=⎪⎪⎪=⎨⎪=+⎪⎪⎩,解得:28a =,22b =,26c =,所以椭圆C 的方程为22182x y +=;【小问2详解】设直线13:12l x m y ⎛⎫=+- ⎪⎝⎭,联立2248312x y x m y ⎧+=⎪⎨⎛⎫=+- ⎪⎪⎝⎭⎩,得()()222294323704m y m m y m m ++-+--=,(*)()()22229Δ32443704m m m m m ⎛⎫=--+--= ⎪⎝⎭,整理为212280m m --=,解得:2m =-或14m =,由题意结合图形可知,0m <,所以2m =-,当2m =-时,代回(*)得2210y y ++=,即1y =-,321122x ⎛⎫=--+-=- ⎪⎝⎭,所以点G 的坐标为()2,1--,31,2P ⎛⎫--⎪⎝⎭,所以254PG =设直线23:12l x n y ⎛⎫=+- ⎪⎝⎭,联立,()11,M x y ,()22,N x y ,2248312x y x n y ⎧+=⎪⎨⎛⎫=+- ⎪⎪⎝⎭⎩,得()()222294323704n y n n y n n ++-+--=,(*)()()22229Δ32443704n n n n n ⎛⎫=--+--= ⎪⎝⎭,整理为212280n n --<,解得:214n -<<,2122234n n y y n -+=+,212293744n n y y n --=+,132PM y ⎛⎫=+⎪⎝⎭,232PN y ⎛⎫=+ ⎪⎝⎭,()()()221212123339112224PM PN n y y n y y y y ⎛⎫⎛⎫⎡⎤=+++=++++ ⎪⎪⎢⎥⎝⎭⎝⎭⎣⎦,()222229373239414244n n n n n n n ⎛⎫-- ⎪-=++⨯+ ⎪++ ⎪⎝⎭()22214n n +=+,即()2221544n n +=+,解得:2n =±(2-舍去),即2n =,则直线2l 的斜率为12,而1122OG k -==-,所以2//l OG.12y y -表示两点间的距离,21.已知集合(){}{}()12,,,,0,1,1,2,,2n n i S X X x x x x i nn ==⋅⋅⋅∈=⋅⋅⋅≥,对于()12,,,nA a a a =⋅⋅⋅,()12,,,n n B b b b S =⋅⋅⋅∈,定义A 与B 之间的距离为()1,ni i i d A B a b ==-∑.(1)已知()41,1,1,0A S =∈,写出所有的4B S ∈,使得(),1d A B =;(2)已知()1,1,,1n I S =⋅⋅⋅∈,若,n A B S ∈,并且()(),,d I A d I B p n ==≤,求(),d A B 的最大值;(3)设集合n P S ⊆,P 中有()2m m ≥个元素,若P 中任意两个元素间的距离的最小值为t ,求证:12n t m -+≤.【答案】(1)()0,1,1,0、()1,0,1,0、()1,1,0,0、()1,1,1,1;(2)()()max 2,2,2,2p p nd A B n p p n ≤⎧=⎨->⎩;(3)见解析【解析】【分析】(1)根据题中定义可得B 的所有情形;(2)分2p n ≤、2p n >两种情况,利用绝对值三角不等式可求得(),d A B 的最大值;(3)表示出()()121121'{,,,|,,,,,}n t n t n P c c c c c c c P -+-+=∈ ,结合定义,可得()()121121,,,,,,n t n t a a a b b b -+-+≠ ,即P '中任意两元素不相等,可得P '中至多有12n t -+个元素,即可得证.【小问1详解】已知()41,1,1,0A S =∈,4B S ∈,且(),1d A B =,所以,B 的所有情形有:()0,1,1,0、()1,0,1,0、()1,1,0,0、()1,1,1,1;【小问2详解】设()12,,,n A a a a = ,()12,,,n B b b b = ,因为()()11,=11n niii i d I A a a p ==-=-=∑∑,则12n aa a n p +++=- ,同理可得12n b b b n p +++=- ,当2n p ≥时,()1111,11112n n n niiiiiii i i i d A B a b a b a bp =====-=-+-≤-+-=∑∑∑∑;当2n p <时,()111,22nnniiiii i i d A B a b a bn p ====-≤+=-∑∑∑.当11,1,,1,0,0,,0p A ⎛⎫ ⎪= ⎪⎝⎭ 个,10,0,0,1,1,,1p B ⎛⎫⎪= ⎪⎝⎭个时,上式等号成立.综上所述,()()max 2,2,2,2p p nd A B n p p n ≤⎧=⎨->⎩;【小问3详解】记()()121121{,,,|,,,,,}n t n t n P c c c c c c c P -+-+='∈ ,我们证明P P '=.一方面显然有P P '≤.另一方面,,n A B S ∀∈且A B ≠,假设他们满足112211,,,n t n t a b a b a b -+-+=== .则由定义有(),1d A B t ≤-,与P 中不同元素间距离至少为t 相矛盾.从而()()121121,,,,,,n t n t a a a b b b -+-+≠ .这表明P '中任意两元素不相等.从而P P m '==.又P '中元素有1n t -+个分量,至多有12n t -+个元素.从而12n t m -+≤.【点睛】方法点睛:解决以集合为背景的新定义问题,要抓住两点:(1)紧扣新定义,首先分析新定义的特点,把定义所叙述的问题的本质弄清楚,并能够应用到具体的解题过程之中,这是新定义型集合问题难点的关键所在;(2)用好集合的性质,解题时要善于从试题中发现可以使用集合性质的一些因素,在关键之外用好集合的运算与性质.。
北京市石景山区2023届高三一模数学试题 (解析版)

北京市石景山区2023届高三一模数学试题一、单选题1.已知集合{}22A x x =-≤≤,{}220B x x x =+-≤,则A B ⋃=( )A .[]22-,B .[]2,1-C .[]0,1D .[]0,22.在复平面内,复数z 对应的点的坐标为()2,1--,则iz=( ) A .12i -- B .2i -- C .12i -+ D .2i -3.已知双曲线()222104x y b b-=>的离心率是2,则b =( )A.12 B .C D4.下列函数中,是奇函数且在定义域内单调递减的是( ) A .()sin f x x =B .()2xf x =C .()3f x x x =+ D .()()1e e 2x xf x -=-5.设0x >,0y >,则“2x y +=”是“1xy ≤”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件 D .既不充分也不必要条件6.已知数列{}n a 满足:对任意的,m n *∈N ,都有m n m n a a a +=,且23a =,则10a =( ) A .43B .53C .63D .103【答案】B【分析】根据对任意的,m n *∈N ,有m n m n a a a +=,且23a =,求得48,a a 的值,即可得10a 的值.【详解】对任意的,m n *∈N ,都有m n m n a a a +=,且23a =,所以222249a a a a ===,则2444881a a a a ===,所以510283813a a a ==⨯=.故选:B.7.若函数()()πsin 0,0,02f x A x A ωϕωϕ⎛⎫=+>><< ⎪⎝⎭的部分图象如图所示,则ϕ的值是( )A .π3B .π6C .π4D .π12【答案】A【分析】根据正弦型函数的对称性可得对称中心π,03⎛⎫⎪⎝⎭,即可求得最小正周期T ,从而可求ω的值,结合图象代入已知点坐标即可得ϕ的值.【详解】由图可知()2π0,3f m f m ⎛⎫==- ⎪⎝⎭,所以π,03⎛⎫⎪⎝⎭是()f x 的一个对称中心,由图象可得最小正周期T 满足:1πππ2362T ⎛⎫=--= ⎪⎝⎭,则2ππT ω==,又0ω>,所以2ω=, 则由图象可得π2π6k ϕ⎛⎫⨯-+= ⎪⎝⎭,Z k ∈,所以ππ3k ϕ=+,Z k ∈,又π02ϕ<<,所以π3ϕ=.故选:A.8.在不考虑空气阻力的条件下,火箭的最大速度v (单位:/km s )与燃料的质量M (单位:kg ),火箭(除燃料外)的质量m (单位:kg )的函数关系是2000ln 1M v m ⎛⎫=+ ⎪⎝⎭.当燃料质量与火箭质量的比值为0t 时,火箭的最大速度可达到0/v km s .若要使火箭的最大速度达到02/v km s ,则燃料质量与火箭质量的比值应为( ) A .202t B .200t t +C .02tD .2002t t +【答案】D【分析】根据对数运算法则可求得()200022000ln 12v t t =++,由此可得结果.【详解】由题意得:()002000ln 1v t =+,9.已知直线l :220kx y k --+=被圆C :()22125x y ++=所截得的弦长为整数,则满足条件的直线l 有( ) A .6条 B .7条 C .8条 D .9条10.已知正方体1111ABCD A B C D -的棱长为2,点P 为正方形ABCD 所在平面内一动点,给出下列三个命题:①若点P 总满足11PD DC ⊥,则动点P 的轨迹是一条直线;②若点P 到直线1BB 与到平面11CDD C 的距离相等,则动点P 的轨迹是抛物线; ③若点P 到直线1DD 的距离与到点C 的距离之和为2,则动点P 的轨迹是椭圆. 其中正确的命题个数是( ) A .0 B .1C .2D .3【答案】C【分析】根据正方体中的线面垂直以及线线垂直关系,即可确定满足满足11PD DC ⊥的动点P 的轨迹,从而可判断①;利用线线关系将点线距离转化为点点距离,结合圆锥曲线的定义即可判断动点P 的轨迹,即可得判断②③,从而可得答案. 【详解】对于①,如图在正方体1111ABCD A B C D -中,连接11,BD CD ,在正方体中,因为四边形11CDD C 为正方形,所以11DC CD ⊥, 又BC ⊥平面11CDD C ,1DC ⊂平面11CDD C ,所以1BC DC ⊥, 又11,,CD BC C CD BC ⋂=⊂平面1BCD ,所以1DC ⊥平面1BCD ,平面1BCD ⋂平面ABCD BC =,P ∈平面ABCD ,点P 总满足11PD DC ⊥, 所以P ∈平面1BCD ,所以P BC ∈,则动点P 的轨迹是一条直线,故①正确;对于②,1BB ⋂平面ABCD B =,P ∈平面ABCD ,则点P 到直线1BB 等于P 到B 的距离, 又P 到平面11CDD C 的距离等于P 到DC 的距离,则P 到B 的距离等于P 到DC 的距离,由抛物线的定义可知,动点P 的轨迹是抛物线,故②正确;对于③,点P 到直线1DD 的距离等于P 到D 的距离,所以P 到D 的距离与到点C 的距离之和为2,即2PD PC DC +==,则点P 的轨迹为线段DC ,故③不正确. 所以正确的命题个数是2. 故选:C.二、填空题11.向量()2sin ,cos a θθ=,()1,1b =,若//a b ,则tan θ=_________. 【答案】12##0.5【分析】根据平面向量的坐标平行运算得cos 2sin θθ=,利用同角三角函数的商数关系θ【详解】向量(2sin a θ=,()1,1b =,若//a b ,则2sin sin 2sin θθ=.12.若nx⎛⎝的展开式中含有常数项,则正整数n 的一个取值为_________.13.项数为(),2k k k *∈≥N 的有限数列{}n a 的各项均不小于1-的整数,满足123123122220k k k k k a a a a a ----⋅+⋅+⋅+⋅⋅⋅+⋅+=,其中10a ≠.给出下列四个结论:①若2k =,则22a =;②若3k =,则满足条件的数列{}n a 有4个; ③存在11a =的数列{}n a ;④所有满足条件的数列{}n a 中,首项相同. 其中所有正确结论的序号是_________.一列举得数列{}n a ,即可判断②.【详解】由于有限数列{}n a 的各项均不小于1-的整数,所以1n a ≥-,*N ,Z n n a ∈∈,又因为123123122220k k k k k a a a a a ----⋅+⋅+⋅+⋅⋅⋅+⋅+=,所以()()123231112312222222121k k k k k k k k a a a a a -------⋅=-⋅+⋅+⋅⋅⋅+⋅+≤++++=-所以1111112k a -⎛⎫-≤≤-< ⎪⎝⎭,且10a ≠,1a 为整数,所以11a =-,故③不正确,④正确;当2k =时,得1220a a +=,所以11a =-,则22a =,故①正确;当3k =时,得123420a a a ++=,因为11a =-,所以2324a a +=,则23245a a =-≤, 所以2512a -≤≤,2a 为整数,则2a 的可能取值为1,012-,,,对应的3a 的取值为6,4,2,0, 故数列{}n a 可能为1,1,6--;1,0,4-;1,1,2-;1,2,0-,共4个,故②正确. 故答案为:①②④.【点睛】思路点睛:项数为(),2k k k *∈≥N 的有限数列{}n a 的性质入手1n a ≥-,*N ,Z n n a ∈∈从各项1n a ≥-,结合不等式放缩,确定1a 的范围,从而得1a 的值,逐项验证即可.三、解答题14.如图,在ABC 中,42AC =,π6C =,点D 在边BC 上,1cos 3ADB ∠=.(1)求AD 的长;(2)若ABD △的面积为2AB 的长. 【答案】(1)3AD = (2)3AB =15.某高校“植物营养学专业”学生将鸡冠花的株高增量作为研究对象,观察长效肥和缓释肥对农作物影响情况.其中长效肥、缓释肥、未施肥三种处理下的鸡冠花分别对应1,2,3三组.观察一段时间后,分别从1,2,3三组随机抽取40株鸡冠花作为样本,得到相应的株高增量数据整理如下表.假设用频率估计概率,且所有鸡冠花生长情况相互独立.(1)从第1组所有鸡冠花中随机选取1株,估计株高增量为(]7,10厘米的概率; (2)分别从第1组,第2组,第3组的所有鸡冠花中各随机选取1株,记这3株鸡冠花中恰有X 株的株高增量为(]7,10厘米,求X 的分布列和数学期望EX ;(3)用“1k ξ=”表示第k 组鸡冠花的株高增量为(]4,10,“0k ξ=”表示第k 组鸡冠花的株高增量为(]10,16厘米,1,2,3k =,直接写出方差1D ξ,2D ξ,3D ξ的大小关系.(结论不要求证明))1125=)29100=所以21112936012310025100505EX =⨯+⨯+⨯+⨯=. (3)132D D D ξξξ<< 理由如下: ()()1129111,04040P P ξξ====,所以22112911292929291131910,10404040404040401600E D ξξ⎛⎫⎛⎫=⨯+⨯==-⨯+-⨯=⎪ ⎪⎝⎭⎝⎭; ()()2220111,04022P P ξξ=====,所以22221111111140010,10222222241600E D ξξ⎛⎫⎛⎫=⨯+⨯==-⨯+-⨯==⎪ ⎪⎝⎭⎝⎭; ()()3325531,04088P P ξξ=====,所以223353555531537510,108588888641600E D ξξ⎛⎫⎛⎫=⨯+⨯==-⨯+-⨯==⎪ ⎪⎝⎭⎝⎭; 所以132D D D ξξξ<<.16.如图,在四棱锥P ABCD -中,底面ABCD 是边长为2的正方形,侧面PAD 为等腰直角三角形,且π2PAD ∠=,点F 为棱PC 上的点,平面ADF 与棱PB 交于点E .(1)求证://EF AD ;(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面PCD 与平面ADFE 所成锐二面角的大小.条件①:2AE条件②:平面PAD ⊥平面ABCD ; 条件③:PB FD ⊥.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分. 【答案】(1)证明见解析 (2)π3【分析】(1)根据条件可以证明//AD 平面PBC ,再利用线面平行的性质定理即可证明出结论;(2)选条件①②可以证明出,,AB AD AP 两两垂直,建立空间直角坐标系A xyz -,求出相应坐标,再求出两平面的法向量,进而求出结果;选条件①③或②③同样可以证明求解.【详解】(1)证明:因为底面ABCD 是正方形,所以//AD BC ,BC ⊂平面PBC ,AD ⊄平面PBC ,所以//AD 平面PBC ,又因为平面ADF 与PB 交于点E .AD ⊂平面ADFE ,平面PBC ⋂平面,ADFE EF =所以//EF AD . (2)选条件①②侧面PAD 为等腰直角三角形,且π,2PAD ∠= 即2PA AD ==,PA AD ⊥平面PAD ⊥平面ABCD ,平面PAD ⋂平面ABCD AD =,PA ⊂平面PAD , 则PA ⊥平面ABCD ,又ABCD 为正方形, 所以,,PA AB PA AD AB AD ⊥⊥⊥.以点A 为坐标原点,,,AB AD AP 分别为x 轴,y 轴,z 轴正方向,建立如图所示空间直角坐标系A xyz -,则(0,0,0),(0,0,2),(2,2,0),(2,0,0),(0,2,0)A P C B D 因为2AE =,所以点E 为PB 的中点,则(1,0,1)E 从而:(2,2,2),(0,2,0),(1,0,1)PC AD AE =-==, 设平面ADFE 的法向量为:(,,)n x y z =, 则020n AE x z n AD y ⎧⋅=+=⎪⎨⋅==⎪⎩,令1x =,可得(1,0,1)n =-设平面PCD 的法向量为:(,,)n a b c =,则 2202220n PD b c n PC a b c ⎧⋅=-=⎪⎨⋅=+-=⎪⎩, 令1b =,可得(0,1,1)n = 所以1cos ,2PB n PB n PB n⋅== 则两平面所成的锐二面角为π3选条件①③侧面PAD 为等腰直角三角形,且,2PAD π∠=即2,PA AD PA AD ==⊥,AD AB PA AB A ⊥⋂=,且两直线在平面内,可得AD ⊥平面PAB ,PB ⊂平面PAB ,则AD PB ⊥.,所以PAB 为等腰三角形,所以点,所以PAB 为等腰直角三角形,为等腰直角三角形,且AD ABCD ,,所以PAB 为等腰三角形,所以点17.已知椭圆C :()222210x y a b a b+=>>过点(,且离心率为12.(1)求椭圆C 的方程;(2)过点()1,1P -且互相垂直的直线1l ,2l 分别交椭圆C 于M ,N 两点及,S T 两点.求PM PN PS PT的取值范围.18.已知函数()()e 1sin xf x m x m =--∈R .(1)当1m =时,(ⅰ)求曲线()y f x =在点()()0,0f 处的切线方程;(ⅱ)求证:0,2πx ⎛⎫∀∈ ⎪⎝⎭,()0f x >.(2)若()f x 在π0,2⎛⎫⎪⎝⎭上恰有一个极值点,求m 的取值范围.1m 时,所以)e x x m =-1m 时,f 时,(f x 'x 与y =-0f x,因此π2⎫⎪⎭上恰有一个极小值点,19.若无穷数列{}n a 满足以下两个条件,则称该数列为τ数列. ①11a =,当2n ≥时,122n n a a --=+;②若存在某一项5m a ≤-,则存在{}1,2,,1k m ∈⋅⋅⋅-,使得4k m a a =+(2m ≥且m *∈N ). (1)若20a <,写出所有τ数列的前四项;(2)若20a >,判断τ数列是否为等差数列,请说明理由; (3)在所有的τ数列中,求满足2021m a =-的m 的最小值.【答案】(1)τ数列的前四项为:1,1,1,1--;1,1,1,5-;1,1,3,3--;1,1,3,7- (2)τ数列为首项为1公差为4的等差数列,理由见解析 (3)m 的最小值为1517【分析】(1)先根据条件①去绝对值可得1n n a a -=-或14n n a a -=+,由20a <得21a =-,再根据条件逐个列举即可;(2)由条件①知,当2n ≥时,1n n a a -=-或14n n a a -=+,由20a >得25a =,利用反证法假设τ数列中存在最小的正整数i (3i ≥),使得1i i a a -=-,根据单调性结合条件②可知假设不成立,即可得结论;(3)先根据条件②可得()431506n b n n =-+≤≤必为数列{}n a 中的项,再结合条件①可得31n n a b -=分析即可.【详解】(1)由条件①知,当2n ≥时,1n n a a -=-或14n n a a -=+, 因为20a <,由条件①知21a =-,所以τ数列的前四项为:1,1,1,1--;1,1,1,5-;1,1,3,3--;1,1,3,7-. (2)若20a >,τ数列是等差数列由条件①知,当2n ≥时,1n n a a -=-或14n n a a -=+, 因为20a >,所以25a =假设τ数列中存在最小的正整数i (3i ≥),使得1i i a a -=-, 则1231,,,,i a a a a -单调递增,由11a =则1231,,,,i a a a a -均为正数,且125i a a -≥=.所以15i i a a -=-≤-.由条件②知,则存在 {}1,2,3,,1k i ∈-,使得41k i a a =+≤-此时与1231,,,,i a a a a -均为正数矛盾,所以不存在整数i (3i ≥),使得1i i a a -=-,即14n n a a -=+. 所以τ数列为首项为1公差为4的等差数列. (3)由2021m a =-及条件②, 可得1,5,9,,2017,2021-----必为数列{}n a 中的项,记该数列为{}n b ,有()431506n b n n =-+≤≤,不妨令n j b a =,由条件①,143j j a a n +=-=-或1447j j a a n +=+=-+均不为141n b n +=--; 此时243j a n +=-+或41n +或47n -或411n -+,均不为141n b n +=-- 上述情况中,当143j a n +=-,241j a n +=+时,32141j j n a a n b +++=-=--= 结合11a =,则有31n n a b -=.由5062021b =-,得350611517m =⨯-=即为所求.四、双空题20.抛物线C :24x y =的焦点坐标为_________,若抛物线C 上一点M 的纵坐标为2,则点M 到抛物线焦点的距离为_________.21.设函数()33,,x x x af x x x a ⎧-≤=⎨->⎩,①若0a =,则()f x 的最大值为_________;②若()f x 无最大值,则实数a 的取值范围是_________.。
【精校】2020年北京市石景山区高考一模试卷数学文

2020年北京市石景山区高考一模试卷数学文一、选择题共8小题,每小题5分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.设集合A={x|(x+1)(x-2)<0},集合B={x|1<x <3},则A ∩B=( ) A.{x|-1<x <3} B.{x|-1<x <1} C.{x|1<x <2} D.{x|2<x <3}解析:A={x|-1<x <2},∴A ∩B={x|1<x <2}. 答案:C2.下列函数中既是奇函数,又在区间(0,+∞)上是单调递减的函数为( )A.y =B.y=-x 3C.12log y x =D.1y x x=+解析:对于A ,(x ≥0)是非奇非偶的函数,不满足条件;对于B ,y=-x 3,是定义域R 上的奇函数,且在区间(0,+∞)上是单调减函数,满足条件; 对于C ,12log y x =,定义域是(0,+∞),是非奇非偶的函数,不满足条件;对于D ,1y x x=+,是定义域(-∞,0)∪(0,+∞)上的奇函数,但在区间(0,+∞)上不是单调减函数,也不满足题意. 答案:B3.执行如图所示的程序框图,输出的结果是( )A.3B.11C.38D.123解析:模拟程序的运行,可得a=1,满足条件a<10,执行循环体,a=3,满足条件a<10,执行循环体,a=11,不满足条件a<10,退出循环,输出a的值为11. 答案:B4.设x,y满足约束条件2239x yx yx+≤⎧⎪-≤⎨⎪≥⎩,,,则下列不等式恒成立的是( )A.x≥1B.y≤1C.x-y+2≥0D.x-3y-6≤0解析:作出x,y满足约束条件2239x yx yx+≤⎧⎪-≤⎨⎪≥⎩,,,对应的平面区域如图:则A(0,2),易知x ≥1,y ≤1不成立,直线z=x-y+2经过A 时取得最小值为0,直线z=x-3y-6经过A 时取得最小值为:-12, 由图象可知x-3y-6≤0不成立,恒成立的是x-y+2≥0. 答案:C5.已知平面向量a b r r ,满足32a b ==r r ,,a r 与b r 的夹角为120°,若()a mb a +⊥r r r ,则实数m 的值为( )A.1B.32C.2D.3解析:∵32a b ==r r,,a r 与b r 的夹角为120°, ∴1cos1203232a b a b ⋅=︒=⎛⎫⨯⨯-=⎪⎝-⎭r r r r .∵()()22330a mb a a mb a a ma b m +⊥∴+⋅=+⋅=-=r r r r r r r r r,,解得m=3.答案:D6.“a >b >1”是“log a 3<log b 3”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件 解析:由log a 3<log b 3得3311log log a b<,若a >b >1,则log 3a >log 3b >0,则3311log log a b<成立,即充分性成立, 若log 3a <0,log 3b >0时,满足条件,但此时0<a <1,b >1,则a >b >1不成立, 即“a >b >1”是“log a 3<log b 3”的充分不必要条件. 答案:A7.若某多面体的三视图(单位:cm)如图所示,则此多面体的体积是( )A.78cm 3B.23cm 3C.56cm 3D.12cm 3 解析:由三视图知几何体是一个正方体减去一个三棱柱, 正方体的棱长是1,∴正方体的体积是1×1×1=1,三棱柱的底面是腰长是12的直角三角形,高是1, ∴三棱柱的体积是111112228⨯⨯⨯=,∴几何体的体积是171.88-=答案:A8.如图,已知线段AB 上有一动点D(D 异于A 、B),线段CD ⊥AB ,且满足CD 2=λAD ·BD(λ是大于0且不等于1的常数),则点C 的运动轨迹为( )A.圆的一部分B.椭圆的一部分C.双曲线的一部分D.抛物线的一部分解析:以AB所在直线为x轴,以AB的垂直平分线为y轴,建立平面直角坐标系,设AB中点为O,设C(x,y),AB=2a,则D(x,0),A(-a,0),B(a,0),∵线段CD⊥AB,且满足CD2=λAD·BD(λ是大于0且不等于1的常数),∴y2=λ(x+a)(x-a)=λx2-λa2,∴λx2+y2=λa2.∴点C的运动轨迹为椭圆的一部分. 答案:B二、填空题共6小题,每小题5分,共30分.9.复数31ii=+.解析:()()()31111. 1111222i ii i iii i i i-----====--+++-答案:11 22i --10.双曲线2212xy-=的焦距是,渐近线方程是 .解析:双曲线2212xy-=中,1a b c===,∴焦距是2c=,渐近线方程是y x=.答案:y x=.11.若圆C的半径为1,其圆心与点(1,0)关于直线y=x对称,则圆C的标准方程为 . 解析:圆心与点(1,0)关于直线y=x对称,可得圆心为(0,1),再根据半径等于1,可得所求的圆的方程为x2+(y-1)2=1,答案:x2+(y-1)2=1.12.在△ABC中,A=60°,AC=4,,则△ABC的面积等于 .解析:∵△ABC中,A=60°,AC=4,由正弦定理得:4sin sin sinBC ACA B B==,,解得sinB=1,∴B=90°,C=30°,∴△ABC的面积=14sin302⨯⨯︒=答案:.13.在等差数列{a n}中a3=0,如果a k是a6与a k+6的等比中项,那么 . 解析:在等差数列{a n}中,由a3=0,得a k=a3+(k-3)d=(k-3)d,a6=a3+3d=3d,a k+6=a3+(k+3)d=(k+3)d,∵a k是a6与a k+6的等比中项,∴a k2=a6·a k+6,即(k-3)2d2=3d·(k+3)d,∵d≠0,∴k2=9k,得k=9.答案:914.已知函数f(x)=224x x x m x x m⎧--≤⎨-⎩,,,>.①当m=0时,函数f(x)的零点个数为;②如果函数f(x)恰有两个零点,那么实数m的取值范围为 .解析:①令-x2-2x=0可得x=-2或x=0,令x-4=0得x=4.∴当m=0时,f(x)有3个零点.②若m<-2,则f(x)在(-∞,m]上无零点,在(m,+∞)上有1个零点x=4,不符合题意;若-2≤m<0,则f(x)在(-∞,m]上有1个零点x=-2,在(m,+∞)上有1个零点x=4,符合题意;若0≤m<4,则f(x)在(-∞,m]上有2个零点x=-2,x=0,在(m,+∞)上有1个零点x=4,不符合题意;若m≥4,则f(x)在(-∞,m]上有2个零点x=-2,x=0,在(m,+∞)上无零点,符合题意;∴-2≤m<0或m≥4.答案:①3,②[-2,0)∪[4,+∞).三、解答题共6小题,共80分.解答应写出文字说明,演算步骤或证明过程.15.已知函数()22cos cos1f x x x x=+-.(Ⅰ)求函数f(x)的最小正周期; (Ⅱ)求函数f(x)在区间[2π,π]上的最小值和最大值. 解析:(Ⅰ)利用二倍角公式以及两角和与差的三角函数化简函数的解析式,然后求函数f(x)的最小正周期;(Ⅱ)通过角的范围求解相位的范围,利用正弦函数的单调性求解函数的最值即可. 答案:(Ⅰ)()22cos cos 1f x x x x =+-1cos 222cos 222sin 2226x x x x x π⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝=+⎝⎭+=+⎭=, 所以周期为T=22π=π. (Ⅱ)因为2π≤x ≤π,所以7132666x πππ≤+≤.所以当13266x ππ+=时,即x=π时,f(x)max =1.当3262x ππ+=时,即x=23π时,f(x)min =-2.16.等差数列{a n }中,a 2=4,其前n 项和S n 满足S n =n 2+λn(λ∈R). (Ⅰ)求实数λ的值,并求数列{a n }的通项公式; (Ⅱ)若数列{1nS +b n }是首项为λ、公比为2λ的等比数列,求数列{b n }的前n 项的和T n . 解析:(I)利用a 2=S 2-S 1=4+2λ-1-λ=4,求出λ=1,再利用数列中a n 与S n 关系a n =S n ,n=1, S n -S n-1,n ≥2,求通项公式.(II)求出数列{1S n +b n }的通项公式,再得出数列{b n }的通项公式,最后根据通项公式形式选择相应方法求和.答案:(I)因为a 2=S 2-S 1=4+2λ-1-λ=4,解得λ=1,∴S n =n 2+n ,当n ≥2时,则a n =S n -S n-1=n 2+n-(n-1)2-(n-1)=2n , 当n=1时,也满足,所以a n =2n. (II)由已知数列{1nS +b n }是首项为1、公比为2的等比数列, 其通项公式为111112n n n b b S S -⎛⎫ ⎪⎝⎭+=+,且首项1111b S +=,故()11111111111112222211n n n n n n n b b b b S S n n n n ----=+=+⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭==-=--++,,, 11()1111112212122311n nn n T n n n -⎡⎤⎛⎫⎛⎫⎛⎫ ⎪ =++⋯+⋯--⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦+-+⋯+-=--++.17.抢“微信红包”已经成为中国百姓欢度春节时非常喜爱的一项活动.小明收集班内20名同学今年春节期间抢到红包金额x(元)如下(四舍五入取整数):102 52 41 121 72162 50 22 158 4643 136 95 192 5999 22 68 98 79对这20个数据进行分组,各组的频数如下:(Ⅰ)写出m,n的值,并回答这20名同学抢到的红包金额的中位数落在哪个组别;(Ⅱ)记C组红包金额的平均数与方差分别为v1、s12,E组红包金额的平均数与方差分别为v2、s22,试分别比较v1与v2、s12与s22的大小;(只需写出结论)(Ⅲ)从A,E两组所有数据中任取2个,求这2个数据差的绝对值大于100的概率.解析:(Ⅰ)由题意求出m=4,n=2,从而能求出这20名同学抢到的红包金额的中位数落在B 组.(Ⅱ)记C组红包金额的平均数与方差分别为v1、s12,E组红包金额的平均数与方差分别为v2、s22,由此能比较v1与v2、s12与s22的大小.(Ⅲ)A组两个数据为22,22,E组两个数据为162,192,任取两个数据,利用列举法能求出这2个数据差的绝对值大于100的概率.答案:(Ⅰ)由题意求出m=4,n=2,这20名同学抢到的红包金额的中位数落在B组. (Ⅱ)记C组红包金额的平均数与方差分别为v1、s12,E组红包金额的平均数与方差分别为v2、s22,则v1<v2,s12<s22.(Ⅲ)A组两个数据为22,22,E组两个数据为162,192任取两个数据,可能的组合有6种结果,分别为:(22,22),(22,162),(22,192),(22,162),(22,192),(162,192),记数据差的绝对值大于100为事件A,事件A包括4种结果,∴这2个数据差的绝对值大于100的概率P(A)=42 63 .18.如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.(1)求三棱锥D-ABC 的体积; (2)求证:AC ⊥平面DEF ;(3)若M 为DB 中点,N 在棱AC 上,且CN=38CA ,求证:MN ∥平面DEF. 解析:(1)直接利用体积公式,求三棱锥D-ABC 的体积; (2)要证AC ⊥平面DEF ,先证AC ⊥DE ,再证AC ⊥EF ,即可.(3)M 为BD 的中点,连CM ,设CM ∩DE=O ,连OF ,只要MN ∥OF 即可. 答案:(1)∵△BCD 是正三角形,AB ⊥平面BCD ,AB=BC=a ,∴三棱锥D-ABC 的体积2313V a =⨯=. (2)取AC 的中点H ,∵AB=BC ,∴BH ⊥AC.∵AF=3FC ,∴F 为CH 的中点.∵E 为BC 的中点,∴EF ∥BH.则EF ⊥AC. ∵△BCD 是正三角形,∴DE ⊥BC. ∵AB ⊥平面BCD ,∴AB ⊥DE.∵AB ∩BC=B ,∴DE ⊥平面ABC.∴DE ⊥AC. ∵DE ∩EF=E ,∴AC ⊥平面DEF. (3)连CM ,设CM ∩DE=O ,连OF. 由条件知,O 为△BCD 的重心,CO=23CM. 当CN=38CA 时,CF=23CN ,∴MN ∥OF. ∵MN ⊄平面DEF ,OF ⊂平面DEF ,∴MN ∥平面DEF.19. 已知椭圆E :22221x y a b+=(a >b >0)的离心率e=2,焦距为(Ⅰ)求椭圆E 的方程;(Ⅱ)若C ,D 分别是椭圆E 的左、右顶点,动点M 满足MD ⊥CD ,连接CM ,交椭圆E 于点P.证明:OM OP ⋅u u u u r u u u r为定值(O 为坐标原点).解析:(Ⅰ)根据题意,分析可得椭圆中c 的值,结合椭圆的离心率公式可得a 的值,计算可得b 的值,将a 、b 的值代入椭圆的方程,即可得答案;(Ⅱ)根据题意,设l CM :x=my-2,联立直线与椭圆的方程,用根与系数的关系分析,用m 表示P 的坐标结合直线的方程分析可得M 的坐标,进而可以用m 表示OM OP ⋅u u u u r u u u r,分析可得答案.答案:(Ⅰ)根据题意,椭圆E的焦距为2c=,所以,因为c e a ==所以c=2, 因为a 2=b 2+c 2,所以b 2=2,所以椭圆方程为22142x y +=. (Ⅱ)因为直线CM 不在x 轴上,故可设l CM :x=my-2.由221422x y x my ⎧+=⎪⎨⎪=-⎩,,得(m 2+2)y 2-4my=0, ∴22224422P P m m y x m m -==++,,即P(22224422m mm m -++,).在直线x=my-2中令x=2,则4M y m =,即M(2,4m). ∴2224816422m OM OP m m -⋅=+=++u u u u r u u u r .∴OM OP ⋅u u u u r u u u r 为定值4.20.设函数f(x)=lnx+mx,m ∈R. (Ⅰ)当m=e(e 为自然对数的底数)时,求f(x)的极小值; (Ⅱ)讨论函数g(x)=f ′(x)-3x零点的个数; (Ⅲ)若对任意b >a >0,()()f b f a b a--<1恒成立,求m 的取值范围.解析:(Ⅰ)m=e 时,f(x)=lnx+e x ,利用f ′(x)判定f(x)的增减性并求出f(x)的极小值; (Ⅱ)由函数g(x)=f ′(x)-3x ,令g(x)=0,求出m ;设φ(x)=m ,求出φ(x)的值域,讨论m 的取值,对应g(x)的零点情况;(Ⅲ)由b >a >0,()()f b f a b a--<1恒成立,等价于f(b)-b <f(a)-a 恒成立; 即h(x)=f(x)-x 在(0,+∞)上单调递减;h ′(x)≤0,求出m 的取值范围. 答案:(Ⅰ)当m=e 时,f(x)=lnx+e x ,∴f ′(x)=2x e x -; ∴当x ∈(0,e)时,f ′(x)<0,f(x)在(0,e)上是减函数;当x ∈(e ,+∞)时,f ′(x)>0,f(x)在(e ,+∞)上是增函数;∴x=e 时,f(x)取得极小值为f(e)=lne+e e=2; (Ⅱ)∵函数g(x)=f ′(x)-2133x m x x x =--(x >0), 令g(x)=0,得m=-13x 3+x(x >0); 设φ(x)=-13x 3+x(x >0), ∴φ′(x)=-x 2+1=-(x-1)(x+1);当x ∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上是增函数,当x ∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上是减函数;∴x=1是φ(x)的极值点,且是极大值点,∴x=1是φ(x)的最大值点,∴φ(x)的最大值为φ(1)=23; 又φ(0)=0,结合y=φ(x)的图象,如图;可知:①当m >23时,函数g(x)无零点; ②当m=23时,函数g(x)有且只有一个零点;③当0<m <23时,函数g(x)有两个零点; ④当m ≤0时,函数g(x)有且只有一个零点; 综上,当m >23时,函数g(x)无零点; 当m=23或m ≤0时,函数g(x)有且只有一个零点; 当0<m <23时,函数g(x)有两个零点; (Ⅲ)对任意b >a >0,()()f b f a b a--<1恒成立, 等价于f(b)-b <f(a)-a 恒成立;设h(x)=f(x)-x=lnx+m x-x(x >0),则h(b)<h(a). ∴h(x)在(0,+∞)上单调递减;∵h ′(x)=211m x x--≤0在(0,+∞)上恒成立, ∴m ≥-x 2+x=-(x-12)2+14(x >0),∴m ≥14; 对于m=14,h ′(x)=0仅在x=12时成立;∴m 的取值范围是[14,+∞). 考试高分秘诀是什么?试试这四个方法,特别是中考和高考生谁都想在考试中取得优异的成绩,但要想取得优异的成绩,除了要掌握好相关的知识定理和方法技巧之外,更要学会一些考试技巧。
2023年北京石景山区高三一模数学试卷(解析版)

2023年北京石景山区高三一模数学试卷(详解)一、单选题1.A.B.C.D.【答案】【解析】已知集合,,则( )A 【分析】解一元二次不等式得集合,再根据并集运算得结果.【详解】由解得,所以,又,所以.故选:A.2.A.B.C.D.【答案】【解析】在复平面内,复数对应的点的坐标为,则( )C 【分析】根据复数对应点坐标得的值,再利用复数的除法可得结果.【详解】复数对应的点的坐标为,则,所以.故选:C.3.A.12B.C.D.已知双曲线的离心率是2,则( )【答案】【解析】B 【分析】根据双曲线离心率公式即可求出结果.【详解】由题意可得,解得,故选:B.4.A. B.C.D.【答案】【解析】下列函数中,是奇函数且在定义域内单调递减的是( )D 【分析】根据函数的奇偶性,基本初等函数的单调性,逐项判断即可.【详解】对于A ,函数为奇函数,但在定义域上函数不单调,故A 不符合;对于B ,的定义域为,,则为偶函数,故B 不符合;对于C ,的定义域为,,则为奇函数,又函数在上均为增函数,故在上为增函数,故C 不符合;对于D ,的定义域为,,则为奇函数,又函数在上为减函数,在上为增函数,故在上为减函数,故D 符合.故选:D.5.设,,则“”是“”的( )A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】【解析】A 【分析】根据基本不等式判断充分性,根据举反例说明必要性不成立,即可得结论.【详解】因为,,则,当且仅当时等号成立,故充分性成立;若,满足,但,故必要性不成立,所以“”是“”的充分而不必要条件.故选:A.6.A.B.C.D.【答案】【解析】已知数列满足:对任意的,都有,且,则( )B 【分析】根据对任意的,有,且,求得的值,即可得的值.【详解】对任意的,都有,且,所以,则,所以.故选:B.7.A.B. C. D.【答案】【解析】若函数的部分图象如图所示,则的值是( )A 【分析】根据正弦型函数的对称性可得对称中心,即可求得最小正周期,从而可求的值,结合图象代入已知点坐标即可得的值.【详解】由图可知,所以是的一个对称中心,由图象可得最小正周期满足:,则,又,所以,则由图象可得,,所以,,又,所以.故选:A.ππ8.A.B.C.D.【答案】【解析】在不考虑空气阻力的条件下,火箭的最大速度(单位:)与燃料的质量(单位:),火箭(除燃料外)的质量(单位:)的函数关系是.当燃料质量与火箭质量的比值为时,火箭的最大速度可达到.若要使火箭的最大速度达到,则燃料质量与火箭质量的比值应为( )D 【分析】根据对数运算法则可求得,由此可得结果.【详解】由题意得:,,,即当火箭的最大速度达到,则燃料质量与火箭质量的比值为.故选:D.9.A.6条B.7条C.8条D.9条【答案】【解析】已知直线:被圆:所截得的弦长为整数,则满足条件的直线有( )B 【分析】圆C 的圆心为,半径,直线l 过定点,故直线l 被圆C 截得的弦长范围为,结合圆的对称性,再检验斜率不存在的直线l 的情况即可得出答案.【详解】圆的圆心为,半径,直线l 化为,则直线l 过定点,则,在圆内,当时,直线l 被圆C 截得的弦长最短为,当过圆心C 时,直线l 被圆C 截得的弦长最长为10,故直线l 被圆C 截得的弦长范围为,因为弦长为整数,则弦长的取值为7,8,9,10,由圆的对称性,故满足弦长为整数的直线有7条.故选:B.10.已知正方体的棱长为2,点为正方形所在平面内一动点,给出下列三个命题:①若点总满足,则动点的轨迹是一条直线;A.0B.1C.2D.3【答案】【解析】②若点到直线与到平面的距离相等,则动点的轨迹是抛物线;③若点到直线的距离与到点的距离之和为2,则动点的轨迹是椭圆.其中正确的命题个数是( )C 【分析】根据正方体中的线面垂直以及线线垂直关系,即可确定满足满足的动点的轨迹,从而可判断①;利用线线关系将点线距离转化为点点距离,结合圆锥曲线的定义即可判断动点的轨迹,即可得判断②③,从而可得答案.【详解】对于①,如图在正方体中,连接,在正方体中,因为四边形为正方形,所以,又平面,平面,所以,又平面,所以平面,平面平面,平面,点总满足,所以平面,所以,则动点的轨迹是一条直线,故①正确;对于②,平面,平面,则点到直线等于到的距离,又到平面的距离等于到的距离,则到的距离等于到的距离,由抛物线的定义可知,动点的轨迹是抛物线,故②正确;对于③,点到直线的距离等于到的距离,所以到的距离与到点的距离之和为2,即,则点的轨迹为线段,故③不正确.所以正确的命题个数是2.故选:C.二、填空题11.【答案】【解析】【踩分点】向量,,若,则 ./ 0.5【分析】根据平面向量的坐标平行运算得,利用同角三角函数的商数关系式即可得的值.【详解】向量,,若,则,所以则.故答案为:.12.【答案】【解析】【踩分点】若的展开式中含有常数项,则正整数的一个取值为 .3(只要是3正整数倍即可)【分析】根据二项式通项公式即可求出结果.【详解】的展开式的通项为,的展开式中含有常数项需要满足,即,所以只要是3正整数倍即可.故答案为:3(只要是3正整数倍即可).13.【答案】【解析】项数为的有限数列的各项均不小于的整数,满足,其中.给出下列四个结论:①若,则;②若,则满足条件的数列有4个;③存在的数列;④所有满足条件的数列中,首项相同.其中所有正确结论的序号是 .①②④【分析】根据有限数列的性质,,及满足,其中,利用不等式放缩,结合等比数列求和可得,即可确定的值,从而可判断①③④的正误,若,得,结合,求得的关系,根据不等式求得的范围,一一列举得数列,即可判断②.【详解】由于有限数列的各项均不小于的整数,所以,,又因为,所以所以,且,为整数,所以,故③不正确,④正确;当时,得,所以,则,故①正确;当时,得,因为,所以,则,所以,为整数,则的可能取值为,对应的的取值为,故数列可能为;;;,共4个,故②正确.故答案为:①②④.【踩分点】【点睛】思路点睛:项数为的有限数列的性质入手,从各项,结合不等式放缩,确定的范围,从而得的值,逐项验证即可.三、双空题14.【答案】【解析】【踩分点】抛物线:的焦点坐标为 ,若抛物线上一点的纵坐标为2,则点到抛物线焦点的距离为 .3$【分析】根据抛物线标准方程可得焦点坐标,利用抛物线定义可得点到抛物线焦点的距离.【详解】抛物线:中,所以的焦点坐标为;由抛物线的定义可得.故答案为:;.\displaystyle{\left(0 ; }15.【答案】【解析】设函数,①若,则的最大值为 ;②若无最大值,则实数的取值范围是 . ; ①若,,当时,,单调递减,,当时,,,所以在单调递增,在单调递减,则此时,所以的最大值为;【踩分点】②当时,当时,,单调递减,所以,当时,在单调递增,所以,因为无最大值,所以,解得;当时,当时,,单调递减,,当时,在单调递增,在单调递减,所以,因为无最大值,所以,此种情况无解,舍去;当时,当时,,单调递减,,当时,在单调递增,在单调递减,在单调递增,所以,因为无最大值,所以,此种情况无解,舍去;所以实数的取值范围是故答案为:① ;②四、解答题16.【答案】【解析】如图,在中,,,点在边上,.(1)求的长;(2)若的面积为,求的长.(1)(2)【分析】(1)根据三角形中邻补角互补,,由平方关系得,再结合正弦定理即可求得的长;(2)由得面积可得,再结合余弦定理即可求得的长.【详解】(1)因为,所以在中,因为所以在中,由正弦定理得,所以;(2)的面积为,得因为,所以又因为,所以在中,由余弦定理得所以.【踩分点】17.某高校“植物营养学专业”学生将鸡冠花的株高增量作为研究对象,观察长效肥和缓释肥对农作物影响情况.其中长效肥、缓释肥、未施肥三种处理下的鸡冠花分别对应1,2,3三组.观察一段时间后,分别从1,2,3三组随机抽取40株鸡冠花作为样本,得到相应的株高增量数据整理如下表.株高增量(单位:厘米)第1组鸡冠花株数92092第2组鸡冠花株数416164第3组鸡冠花株数1312132假设用频率估计概率,且所有鸡冠花生长情况相互独立.(1)从第1组所有鸡冠花中随机选取1株,估计株高增量为厘米的概率;(2)分别从第1组,第2组,第3组的所有鸡冠花中各随机选取1株,记这3株鸡冠花中恰有株的株高增量为厘米,求的分布列和数学期望;(3)用“”表示第组鸡冠花的株高增量为,“”表示第组鸡冠花的株高增量为厘米,,直接写出方差,,的大小关系.(结论不要求证明)【答案】【解析】(1)(2)分布列见解析,(3)【分析】(1)根据表格数据,第1组所有鸡冠花中随机选取1株,得厘米的总数,由古典概型概率公式可得结果;(2)首先估计各组鸡冠花增量为厘米的概率,然后可确定所有可能的取值,根据独立事件概率公式可求得每个取值对应的概率,由此可得分布列;根据数学期望计算公式可求得期望;(3)由两点分布方差计算公式可求得,,的值,由此可得大小关系.【详解】(1)设事件为“从第1组所有鸡冠花中随机选取1株,株高增量为厘米”,根据题中数据,第1组所有鸡冠花中,有20株鸡冠花增量为厘米,所以估计为;(2)设事件为“从第2组所有鸡冠花中随机选取1株,株高增量为厘米”,设事件为“从第3组所有鸡冠花中随机选取1株,株高增量为厘米”,根据题中数据,估计为,估计为,根据题意,随机变量的所有可能取值为0,1,2.3,且;;;,则的分布列为:0123【踩分点】所以.(3)理由如下:,所以;,所以;,所以;所以.18.如图,在四棱锥中,底面是边长为2的正方形,侧面为等腰直角三角形,且,点为棱上的点,平面与棱交于点.(1)求证:;(2)从条件①、条件②、条件③这三个条件中选择两个作为已知,求平面与平面所成锐二面角的大小.条件①:;条件②:平面平面;条件③:.【答案】【解析】注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.(1)证明见解析(2)【分析】(1)根据条件可以证明平面,再利用线面平行的性质定理即可证明出结论;(2)选条件①②可以证明出两两垂直,建立空间直角坐标系,求出相应坐标,再求出两平面的法向量,进而求出结果;选条件①③或②③同样可以证明求解.【详解】(1)证明:因为底面是正方形,所以,平面,平面,所以平面,又因为平面与交于点.平面,平面平面所以.(2)选条件①②侧面为等腰直角三角形,且即,平面平面,平面平面,平面,则平面,又为正方形,所以.以点为坐标原点,分别为轴,轴,轴正方向,建立如图所示空间直角坐标系,则因为,所以点为的中点,则从而:,设平面的法向量为:,则,令,可得设平面的法向量为:,则,令,可得所以则两平面所成的锐二面角为选条件①③侧面为等腰直角三角形,且即,且两直线在平面内,可得平面,平面,则.又因为且两直线在平面内,则平面平面则因为,所以为等腰三角形,所以点为的中点又因为,所以为等腰直角三角形,下面同①②选条件②③侧面为等腰直角三角形,且,即【踩分点】平面平面,平面平面,平面,则平面为正方形,所以.又因为且两直线在平面内,则平面,平面则因为,所以为等腰三角形,所以点为的中点.下面同①②19.【答案】【解析】已知椭圆:过点,且离心率为.(1)求椭圆的方程;(2)过点且互相垂直的直线,分别交椭圆于,两点及两点.求的取值范围.(1)(2)【分析】(1)根据椭圆过点,且离心率为列方程组求得的值,即可得椭圆的方程;(2)讨论直线的斜率不存在时,直线的斜率不存在时,求各交点坐标即可得的取值,再讨论直线,的斜率均存在,不妨设直线的方程为,则直线的方程为,,联立直线与椭圆得交点坐标关系,利用弦长公式即可求得的范围,综合可得答案.【详解】(1)椭圆:过点,且离心率为所以,解得,所以椭圆的方程为;(2)当直线的斜率不存在时,则直线:,代入椭圆方程得,,【踩分点】所以;直线:,代入椭圆方程得,所以,所以;当直线的斜率不存在时,同理可得;当直线,的斜率均存在,不妨设直线的方程为,则直线的方程为,,则,消去得,恒成立,所以,所以;同理可得,将换成可得所以,综上所述,的取值范围是.20.【答案】已知函数.(1)当时,(ⅰ)求曲线在点处的切线方程;(ⅱ)求证:,.(2)若在上恰有一个极值点,求的取值范围.(1)(ⅰ)切线方程为;(ⅱ)证明见解析(2)【解析】【分析】(1)当时,求导,根据导数几何意义求解切点坐标与斜率,即可得切线方程;根据导函数的正负确定函数的单调性,即可得函数的最值,即可证明结论;(2)根据极值点与函数的关系,对进行讨论,确定导函数是否存在零点进行判断,即可求得的取值范围.【详解】(1)当时,(ⅰ),又,所以切线方程为.(ⅱ),,因为,所以,所以,所以所以在单调递增,所以;(2),当时,所以,,由(1)知,,所以在上单调递增.所以当时,没有极值点,当时,,因为与在单调递增.所以在单调递增.所以,.所以使得.所以当时,,因此在区间上单调递减,当时,,因此在区间上单调递增.故函数在上恰有一个极小值点,的取值范围是.【踩分点】21.【答案】【解析】若无穷数列满足以下两个条件,则称该数列为数列.①,当时,;②若存在某一项,则存在,使得(且).(1)若,写出所有数列的前四项;(2)若,判断数列是否为等差数列,请说明理由;(3)在所有的数列中,求满足的的最小值.(1)数列的前四项为:;;;(2)数列为首项为1公差为4的等差数列,理由见解析(3)的最小值为【分析】(1)先根据条件①去绝对值可得或,由得,再根据条件逐个列举即可;(2)由条件①知,当时,或,由得,利用反证法假设数列中存在最小的正整数(),使得,根据单调性结合条件②可知假设不成立,即可得结论;(3)先根据条件②可得必为数列中的项,再结合条件①可得分析即可.【详解】(1)由条件①知,当时,或,因为,由条件①知,所以数列的前四项为:;;;.(2)若,数列是等差数列由条件①知,当时,或,因为,所以假设数列中存在最小的正整数(),使得,则单调递增,由则均为正数,且.所以.由条件②知,则存在,使得此时与均为正数矛盾,所以不存在整数(),使得,即.所以数列为首项为1公差为4的等差数列.(3)由及条件②,可得必为数列中的项,记该数列为,有,不妨令,由条件①,或均不为;此时或或或,均不为上述情况中,当,时,结合,则有.由,得即为所求.【踩分点】。
2020届北京市石景山区高三4月统一测试数学试题(带答案解析)

2020届北京市石景山区高三4月统一测试数学试题1.设集合{}1,2,3,4P =,{}3,Q x x x R =≤∈,则P Q I 等于( )A .{}1B .{}1,2,3C .{}3,4D .{}3,2,1,0,1,2,3---2.在复平面内,复数56i +,32i -对应的点分别为A ,B .若C 为线段AB 的中点,则点C 对应的复数是( )A .84i +B .28i +C .42i +D .14i + 3.下列函数中,既是奇函数又在区间()0,∞+上单调递减的是( )A .22y x =-+B .2x y -=C .ln y x =D .1y x = 4.圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a =( )A .43-B .34-CD .25.将4位志愿者分配到进博会的3个不同场馆服务,每个场馆至少1人,不同的分配方案有( )种.A .72B .36C .64D .816.如图,网格纸的小正方形的边长是1,粗线表示一正方体被某平面截得的几何体的三视图,则该几何体的体积为( )A .2B .4C .5D .87.函数()cos 6f x x πω⎛⎫=+ ⎪⎝⎭(0>ω)的最小正周期为π,则()f x 满足( ) A .在0,3π⎛⎫ ⎪⎝⎭上单调递增 B .图象关于直线6x π=对称C .3f π⎛⎫= ⎪⎝⎭D .当512x π=时有最小值1-8.设{}n a 是等差数列,其前n 项和为n S .则“1322S S S +>”是“{}n a 为递增数列”的( )A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件9.设()f x 是定义在R 上的函数,若存在两个不等实数12,x x R ∈,使得()()121222f x f x x x f ++⎛⎫= ⎪⎝⎭,则称函数()f x 具有性质P ,那么下列函数: ①()1,00,0x f x x x ⎧≠⎪=⎨⎪=⎩;②()2f x x =; ③()21f x x =-; 具有性质P 的函数的个数为( )A .0B .1C .2D .310.点M ,N 分别是棱长为2的正方体1111ABCD A B C D -中棱BC ,1CC 的中点,动点P 在正方形11BCC B (包括边界)内运动.若1//PA 面AMN ,则1PA 的长度范围是( )A.⎡⎣ B.2⎡⎢⎣ C.,32⎡⎤⎢⎥⎣⎦ D .[]2,311.已知向量1,22BA ⎛= ⎝⎭u u u r,1,22BC ⎛⎫= ⎪ ⎪⎝⎭u u u r ,则ABC ∠=______.12.已知正项等比数列{}n a 中, 11a =,其前n 项和为()*n S n N ∈,且123112a a a -=,则4S =__________.13.能够说明“设a ,b 是任意非零实数”,若“a b >,则11a b<”是假命题的一组整数a ,b 的值依次为______.14.已知F 是抛物线C :24y x =的焦点,M 是C 上一点,FM 的延长线交y 轴于点N .若M 为FN 的中点,则FN =______.15.长沙市为了支援边远山区的教育事业,组织了一支由13名教师组成的队伍下乡支教,记者采访队长时询问这个团队的构成情况,队长回答:“(1)有中学高级教师;(2)中学教师不多于小学教师;(3)小学高级教师少于中学中级教师;(4)小学中级教师少于小学高级教师;(5)支教队伍的职称只有小学中级、小学高级、中学中级、中学高级;(6)无论是否把我计算在内,以上条件都成立.”由队长的叙述可以推测出他的学段及职称分别是____.16.如图,在正四棱锥P ABCD -中,AB PB ==AC BD O =I .(1)求证:BO ⊥平面PAC ;(2)求二面角A PC B --的余弦值.17.2020年,北京将实行新的高考方案.新方案规定:语文、数学和英语是考生的必考科目,考生还需从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目.若一个学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定,例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.某校为了解高一年级840名学生选考科目的意向,随机选取60名学生进行了一次调查,统计选考科目人数如下表:(1)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?(2)从选考方案确定的16名男生中随机选出2名,求恰好有一人选“物理、化学、生物”的概率;(3)从选考方案确定的16名男生中随机选出2名,设随机变量01ξ⎧=⎨⎩两名男生选考方案不同两名男生选考方案相同,求ξ的分布列和期望. 18.已知锐角ABC V ,同时满足下列四个条件中的三个:①3A π=②13a =③15c =④1sin 3C = (1)请指出这三个条件,并说明理由;(2)求ABC V 的面积.19.已知椭圆C :22221x y a b +=(0a b >>)的右焦点为()1,0F ,.直线l 过点F 且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 的中点为M .(1)求椭圆C 的方程;(2)证明:直线OM 的斜率与l 的斜率的乘积为定值;(3)延长线段OM 与椭圆C 交于点P ,若四边形OAPB 为平行四边形,求此时直线l 的斜率.20.已知函数()2f x x =(0x >),()ln g x a x =(0a >). (1)若()()f x g x >恒成立,求实数a 的取值范围;(2)当1a =时,过()f x 上一点()1,1作()g x 的切线,判断:可以作出多少条切线,并说明理由.21.有限个元素组成的集合{}12,,,n A a a a =⋅⋅⋅,n *∈N ,记集合A 中的元素个数为()card A ,即()card A n =.定义{},A A x y x A y A +=+∈∈,集合A A +中的元素个数记为()card A A +,当()()12n n card A A ++=时,称集合A 具有性质P . (1){}1,4,7A =,{}2,48B =,,判断集合A ,B 是否具有性质P ,并说明理由;(2)设集合{}123,,,2020A a a a =,1232020a a a <<<且i a N *∈(1,2,3i =),若集合A 具有性质P ,求123a a a ++的最大值;(3)设集合{}12,,,n A a a a =⋅⋅⋅,其中数列{}n a 为等比数列,0i a >(1,2,,i n =⋅⋅⋅)且公比为有理数,判断集合A 是否具有性质P 并说明理由.参考答案1.B【解析】【分析】 由333x x ≤⇒-≤≤,又因为{}1,2,3,4P =.所以P Q =I {}1,2,3.【详解】 由{}3,Q x x x R =≤∈得:333x x ≤⇒-≤≤,又因为{}1,2,3,4P =所以P Q =I {}1,2,3.故选:B【点睛】本题主要考查两个集合的交集,属于基础题目.2.C【解析】【分析】根据复数z a bi =+ 在复平面内所对应点的坐标为(,)a b ,得出A ,B 的坐标,进而得出点C 的坐标,进而得出答案.【详解】因为复数56i +,32i -对应的点分别为A ,B ,所以在复平面内点A 的坐标为()5,6A , 点B 的坐标为()3,2B -,又因为C 为线段AB 的中点,所以点C 的坐标为5362,(4,2)22+-⎛⎫= ⎪⎝⎭,所以点C 对应的复数是42i +. 故选:C【点睛】主要考查复数在复平面内所对应点的坐标知识,属于基础题目.3.D【解析】【分析】根据函数的奇偶性及单调性对4个选项一一判断,即可得出答案.【详解】由基本函数的性质得:22y x =-+为偶函数,2x y -=为非奇非偶函数,ln y x =为非奇非偶函数,1y x=为奇函数,且在区间()0,∞+上单调递减. 故选:D【点睛】本题主要考查函数的奇偶性与单调性,属于基础题目.4.A【解析】试题分析:由2228130x y x y +--+=配方得22(1)(4)4x y -+-=,所以圆心为(1,4),因为圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,所以1=,解得43a =-,故选A. 【考点】 圆的方程,点到直线的距离公式【名师点睛】直线与圆的位置关系有三种情况:相交、相切和相离. 已知直线与圆的位置关系时,常用几何法将位置关系转化为圆心到直线的距离d 与半径r 的大小关系,以此来确定参数的值或取值范围.5.B【解析】【分析】先从4个人中选出2个作为一个元素看成整体,再把它同另外两个元素在三个位置全排列,根据分步乘法原理得到结果.【详解】解:Q 将4位志愿者分配到3个不同场馆服务,每个场馆至少1人,∴先从4个人中选出2个作为一个元素看成整体,再把它同另外两个元素在三个位置全排列,共有234336C A =.【点睛】本题考查排列组合及简单的计数问题,是一个基础题,本题又是一个易错题,排列容易重复,注意做到不重不漏.6.B【解析】如图所示,题中的几何体是棱长为2的正方体被平面ABCD 截得的正方体的下部分,很明显截得的两部分是完全一致的几何体,则该几何体的体积为31242V =⨯=. 本题选择B 选项.7.D【解析】由函数()cos 6f x x πω⎛⎫=+ ⎪⎝⎭(0ω>)的最小正周期为π得2ω=,则()cos 26f x x π⎛⎫=+ ⎪⎝⎭, 当(0,)3x π∈时,52(,)666x πππ+∈,显然此时()f x 不单调递增,A 错误; 当6x π=时,()cos 062f ππ==,B 错误;5()cos 36f ππ==,C 错误;故选择D. 8.C【解析】【分析】先由1322S S S +>进行化简,能推出0d >,即{}n a 为递增数列. 再由{}n a 为递增数列,得321a a a >>,能推出1322S S S +> 故“1322S S S +>”是“{}n a 为递增数列”的充分必要条件.【详解】设{}n a 的公差为d .充分性证明:由1322S S S +>得:112312322()a a a a a a a a +++>+⇒> ,即:0d >. 所以{}n a 为递增数列.必要性证明:由{}n a 为递增数列得:321a a a >> ,所以11231122122132()2a a a a a a a a a S S a S =+++>+++=+=+ 所以“1322S S S +>”是“{}n a 为递增数列的充分必要条件故选:C.【点睛】本题主要结合等差数列考查充分条件及必要条件的判断.属于基础题目. 9.C【解析】【分析】对于①,取121,1x x ==-便可得出答案.对于②,运用反证法,即可证明()2f x x =不具有性质P .对于③,取12x x =,代入便可得出答案.【详解】对于①:取121,1x x ==-,则 12()1,()1f x f x ==- 此时,12(0)02x x f f +⎛⎫==⎪⎝⎭,()()121(1)022f x f x ++-==. 所以()()121222f x f x x x f ++⎛⎫=⎪⎝⎭故函数①具有性质P .对于②:假设存在两个不等实数12,x x R ∈,使得()()121222f x f x x x f ++⎛⎫=⎪⎝⎭, 则222121211222224x x x x x x x x f +++⋅+⎛⎫⎛⎫==⎪ ⎪⎝⎭⎝⎭. ()()22121222f x f x x x ++=. 所以22112224x x x x +⋅+22122x x +=,化简得:2221212122()0044x x x x x x +--=⇒=即:12x x =.与“存在两个不等实数12,x x R ∈,使得()()121222f x f x x x f ++⎛⎫=⎪⎝⎭” 矛盾. 故函数②不具有性质P .对于③:取12x x =,则 12()1,()1f x f x == 此时,12(0)12x x f f +⎛⎫==⎪⎝⎭,()()1211122f x f x ++== 所以()()121222f x f x x x f ++⎛⎫= ⎪⎝⎭故函数③具有性质P . 故选:C. 【点睛】本题主要考查对函数性质的理解,属于中档题目. 10.B 【解析】【分析】取11B C ,1B B 中点E ,F ,得平面1A EF ∥平面AMN .进而得到点P 的轨迹为线段EF , 又因为1A EF V 为等腰三角形,进而便可得出答案. 【详解】取11B C ,1B B 中点E ,F , 连接1A E 、1A F . 则1A E ∥AM .EF ∥MN .又因为1A E EF E ⋂= . 所以平面1A EF ∥平面AMN .又因为动点P 在正方形11BCC B (包括边界)内运动, 所以点P 的轨迹为线段EF .又因为正方体1111ABCD A B C D -的棱长为2,所以11A E A F =EF =.所以1A EF V 为等腰三角形.故当点P 在点E 或者P 在点F 处时,此时1PA当点P 为EF 中点时,1PA 2= .故选:B.【点睛】本题主要考查点、线、面间的距离问题,考查学生的运算能力及推理转化能力,属于中档题目,解决本题的关键是通过构造平行平面寻找点P 的位置. 11.6π; 【解析】 【分析】由向量的数量积公式得:cos BA BCABC BA BC⋅∠=⋅u u u r u u u r u u u r u u u r ,代入化简,便可求得答案. 【详解】由1,22BA ⎛= ⎝⎭u u u r,1,22BC ⎛⎫= ⎪ ⎪⎝⎭u u u r得:2cos 1BA BC ABC BA BC⋅∠===⋅u u u r u u u ru u u r u u u r 又因为[]0,ABC π∠∈,所以6ABC π∠=.故答案为: 6π. 【点睛】本题主要考查向量的数量积知识,属于基础题目. 12.15 【解析】解:由题意可知:2111111a a q a q -= ,结合11,0a q => 解得:2q = , 则4124815S =+++= . 13.2,1-;(答案不唯一) 【解析】 【分析】取2,1a b ==-,再使用反证法即可得出答案. 【详解】取2,1a b ==- ,则a b >,但是1121>-,即11.a b> 故答案为:2,1-. 【点睛】本题考查了真假命题的定义及反例的应用,属于基础题目.14.3; 【解析】 【分析】由题意得:(1,0)F ,又因为M 为FN 的中点,且点N 在y 轴上,设点(0,)N N y ,所以点M 为1(,)22Ny ,又因为点M 在抛物线上,代入抛物线便可得出N y ,进而求得 3FN =. 【详解】根据题意画出图象,如下图所示:因为F 是抛物线C :24y x =的焦点,所以点F 坐标为(1,0)F . 设点N 为(0,)N N y ,因为M 为FN 的中点,所以点M 为1(,)22Ny , 因为点M 在抛物线上,则214()22N y =⨯.则28Ny = .故:3FN == . 故答案为:3. 【点睛】本题主要考查抛物线的几何性质,属于基础题目. 15.小学中级 【解析】 【分析】设小学中级、小学高级、中学中级、中学高级人数分别为a b c d ,,,,根据条件列不等式组,推出a b c d ,,,取法,根据取法推测队长的学段及职称. 【详解】设小学中级、小学高级、中学中级、中学高级人数分别为a b c d ,,,, 则13,1,,,a b c d d c d a b b c a b +++=≥+≤+<< 所以13(),7,6a b a b a b c d -+≤+∴+≥+≤,若7,a b +=则6,3,4,5,1c d a b a b c d Q +=<∴====, 若8,a b +≥则5,14,3,5c d d c b c b a b +≤≥∴≤∴≤≥Q Q 矛盾 队长为小学中级时,去掉队长则2,4,5,1a b c d ====, 满足11,64,45,24d c d a b b c a b =≥+=≤+==<==<=; 队长为小学高级时,去掉队长则3,3,5,1a b c d ====,不满足a b <; 队长为中学中级时,去掉队长则3,4,4,1a b c d ====,不满足b c <; 队长为中学高级时,去掉队长则3,3,5,0a b c d ====,不满足1d ≥; 综上可得队长为小学中级. 【点睛】本题考查不等式性质,考查论证推理能力,属难题.16.(1)证明见解析.(2【解析】 【分析】(1)P ABCD -为正四棱锥.所以ABCD 为正方形,PO ⊥面ABCD ,PO BO ⊥. 因为ABCD 为正方形,所以AC BD ⊥ . PO AC O =I ,所以BO ⊥面PAC .(2)要求二面角A PC B --的余弦值,通过建立空间直角坐标系,运用向量法即可得出答案. 【详解】(1)证明:联结PO .在正四棱锥P ABCD -中,PO ⊥底面ABCD . 因为BO ⊂平面ABCD ,所以PO BO ⊥. 在正方形ABCD 中,BO AC ⊥,又因为PO AC O =I ,所以BO ⊥面PAC . (2)解:由(1)知,PO ,AO ,BO 两两垂直, 以O 为坐标原点建立如图所示空间直角坐标系. 在正方形ABCD中,因为AB = 所以2AO =.又因为PB = 所以2PO =.所以点P 的坐标为()002P ,,,点C 的坐标为()2,0,0C -, 点B 的坐标为()0,2,0B .则()2,0,2PC =--u u u r ,()2,2,0CB =u u u r.由(1)知,BO ⊥平面PAC .所以平面PAC 的一个法向量为()10,2,0n OB ==u r u u u r. 设平面PBC 的一个法向量()2,,n x y z =u u r.则2200n PC n CB ⎧⋅=⎪⎨⋅=⎪⎩u u v u u u v u u v u u u v ,即220,220.x z x y --=⎧⎨+=⎩ 令1y =,则1x =-,1z =.故平面PBC 的一个法向量()21,1,1n =-u u r. 121212cos ,n n n n n n ⋅==u r u u ru r u u r u r u u r 所以二面角A PC B --的余弦值为3. 【点睛】本题主要考查线面垂直及空间向量求面面角的应用,属于中档题目. 17.(1)392人.(2)815.(3)分布列答案见解析,期望为310【解析】 【分析】(1)计算男生和女生确定选考生物的人数,进行估算即可.(2)根据表格数据可得选考方案确定的男生中选择“物理、化学、生物”的人数,进而得到答案.(3)求出随机变量的数值和对应的概率,即可得到分布列和期望. 【详解】(1)由数据知,60人中选考方案确定的学生中选考生物的学生有82028+=人 所以该学校高一年级选考方案确定的学生中选考生物的学生有2884039260⨯=人 (2)选考方案确定且为“物理,化学,生物”的男生共有8人. 设“恰好有一人选物理、化学、生物”为事件A()1188216815C C C P A ==(3)由数据可知,选考方案确定的男生中有8人选择物理、化学和生物;有4人选择物理、化学和历史;有2人选择物理、化学和地理;有2人选择物理、化学和政治.ξ的可能取值为0,1.()1111118844222167010C C C C C C P C ξ++=== ()222284222163110C C C C P C ξ+++===所以ξ的分布列为:73301101010E ξ=⨯+⨯= 【点睛】本题主要考查统计与概率的综合知识,涉及到离散型随机变量、数学期望的求法,考查了频数分布表、古典概型的知识,题目难度稍大.18.(1)ABC V 同时满足①,②,③,理由见解析.(2)【解析】 【分析】(1)判断三角形的满足条件,推出结果即可.(2)利用余弦定理求出b ,利用面积公式求解ABC V 的面积. 【详解】(1)ABC V 同时满足①,②,③. 理由如下:若ABC V 同时满足①,④,则在锐角ABC V 中,11sin 32C =<,所以06C π<< 又因为3A π=,所以32A C ππ<+<所以2B π>,这与ABC V 是锐角三角形矛盾,所以ABC V 不能同时满足①,④, 所以ABC V 同时满足②,③. 因为c a >所以C A >若满足④. 则6A C π<<,则2B π>,这与ABC V 是锐角三角形矛盾.故ABC V 不满足④. 故ABC V 满足①,②,③.(2)因为2222cos a b c bc A =+-, 所以222113152152b b =+-⨯⨯⨯. 解得8b =或7b =.当7b =时,22271315cos 02713C +-=<⨯⨯所以C 为钝角,与题意不符合,所以8b =. 所以ABC V的面积1sin 2S bc A ==【点睛】本题主要考查解三角形中余弦定理的应用及面积公式的应用,属于中档题目.19.(1)2212x y +=.(2)证明见解析.(3)直线l的斜率:2±【解析】 【分析】(1)由题意知1c =,2c a =,可得a =1c =,1b =.故得到椭圆方程. (2)设直线l 的方程为()1y k x =-(0k ≠),将直线与椭圆进行联立,利用中点坐标公式,结合韦达定理得到12M OM M y k x k-==,进而得解. (3)四边形OAPB 为平行四边形,则OA OB OP +=u u u r u u u r u u u r .所以2122421P k x x x k =+=+, 2221P ky k -=+,又因为点P 在圆上,把点P 坐标代入椭圆方程,即可得出答案. 【详解】(1)由已知1c =,c e a ==, 又222a b c =+,解得a =1b =所以椭圆方程为2212x y +=.(2)设直线l 的方程为()1y k x =-(0k ≠)联立()()221210x y y k x k ⎧+=⎪⎨⎪=-≠⎩消去y 得()2222214220kx k x k +-+-=,不妨设()11,A x y ,()22,B x y则2122421k x x k +=+,因为M 为线段AB 的中点 所以21222221M x x k x k +==+,()2121M M k y k x k -=-=+ 所以12M OM M y k x k-== 所以1122OM l k k k k -⨯=⨯=-为定值. (3)若四边形OAPB 为平行四边形,则OA OB OP +=u u u r u u u r u u u r所以2122421P k x x x k =+=+ ()()()1212122211221P ky y y k x k x k x x k -=+=-+-=+-=+因为点P 在椭圆上,所以2222242222121k k k k ⎛⎫-⎛⎫+⨯= ⎪ ⎪++⎝⎭⎝⎭解得212k =,即2k =±所以当四边形OAPB 为平行四边形时,直线l的斜率为2k =± 【点睛】本题主要考查直线与椭圆的位置关系,属于中档题目. 20.(1)02e a <<.(2)2条切线,理由见解析 【解析】 【分析】(1)把()()f x g x >转化为:()()()h x f x g x =-,要使得()()f x g x >恒成立,即满足()h x 的最小值大于0.(2)设切点()00,P x y ,则()00011y g x x -'=-,对方程化简,判断0x 的个数即可,得出切线的条数.【详解】(1)令()()()2ln h x f x g x x a x =-=-(0x >) 所以()2222a x a x x h x x='-=- 令()2220x x xh a -'==,解得x . 当x 变化时,()h x ',()h x 的变化情况如下表:所以在()0,∞+的最小值为ln 2222a a a a h a =-=- 令0h >,解得02e a <<.所以当02e a <<时,()0h x >恒成立,即()()f x g x >恒成立.(2)可作出2条切线.理由如下:当1a =时,()ln g x x =.设过点()1,1的直线l 与()ln g x x =相切于点()00,P x y ,则()00011y g x x -'=-即000ln 111x x x -=- 整理得000ln 210x x x -+=令()ln 21x x m x x -=+,则()m x 在()0,∞+上的零点个数与切点P 的个数一一对应. ()ln 1m x x '=-,令()ln 10x m x '=-=解得x e =.当x 变化时,()m x ',()m x 的变化情况如下表:所以()m x 在()0,e 上单调递减,在(),e +∞上单调递增. 且2222211124ln 110m e e e e e ⎛⎫=⨯-+=-+> ⎪⎝⎭()ln 2110m e e e e e =⨯-+=-+<()2222ln 2110m e e e e =⨯-+=>所以()m x 在21,e e ⎛⎫ ⎪⎝⎭和()2,e e 上各有一个零点,即ln 210x x x -+=有两个不同的解. 所以过点()1,1可作出ln y x =的2条切线.【点睛】本题主要考查利用导数解决恒成立问题及切线的问题,考查了逻辑思维能力,属于中档题目. 21.(1)集合A 不具有性质P ,集合B 具有性质P ,理由见解析.(2)6050.(3)集合A 具有性质P ,理由见解析.【解析】【分析】(1)根据定义即可判断,进而得出答案.(2)运用反证法即可得出答案.(3)设11n n a a q -=,假设当i k l j <≤<时有i j l k a a a a +=+成立,进而结合反证法证明假设不成立,进而得出答案.【详解】(1)集合A 不具有性质P ,集合B 具有性质P .{}2,5,8,11,14A A +=,()()33152card A A ++=≠不具有性质P ; {}4,6,8,10,12,16B B +=,()()33162card B B ++==具有性质P . (2)若三个数a ,b ,c 成等差数列,则{},,A a b c =不具有性质P ,理由是2a c b +=.因为1232020a a a <<<且i a N *∈(1,2,3i =)所以32019a ≤,要使123a a a ++取最大,则32019a =;22018a ≤,易知{}2018,2019,2020不具有性质P ,要使123a a a ++取最大, 则22017a =;12016a ≤,要使123a a a ++取最大,检验可得12014a =;()123max 6050a a a ++=(3)集合A 具有性质P .设等比数列的公比为为q ,所以11n n a a q -=(10a >)且q 为有理数,假设当i k l j <≤<时有i j l k a a a a +=+成立,则有1j i k i l i q q q ---=+-因为q 为有理数,设m q n=(m ,n *∈N )且(m ,n 互质),因此有 1j i k i l i m m m n n n ---⎛⎫⎛⎫⎛⎫=+- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭即j i k i j k l i j l j i m m n m n n ------=+-(1), (1)式左边是m 的倍数,右边是n 的倍数,又m ,n 互质,显然i j l k a a a a +=+不成立.所以()() 1212n nn ncard A A C C ++=+=,所以集合A具有性质P.【点睛】本题考查了集合新定义问题,考查了等比数列的应用,以及学生的阅读能力,属于难题.。
2022年北京市石景山区高考数学一模试卷+答案解析(附后)
2022年北京市石景山区高考数学一模试卷1.设全集,集合,则( )A. B. C. D.2.复数z满足,则( )A. B. i C. D. 13.从1,2,3,4,5中不放回地抽取2个数,则在第1次抽到偶数的条件下,第2次抽到奇数的概率是( )A. B. C. D.4.设l是直线,,是两个不同的平面,则下列命题中正确的是( )A. 若,,则B. 若,,则C. 若,,则D. 若,,则5.已知圆C:,过点的直线l与圆C交于A,B两点,则弦AB长度的最小值为( )A. 1B. 2C. 3D. 46.函数的图象大致为( )A. B.C. D.7.在等差数列中,,设数列的前n项和为,则( )A. 12B. 99C. 132D. 1988.在中,,若,则的大小是( )A. B. C. D.9.“”是“在上恒成立”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件10.设A,B为抛物线C:上两个不同的点,且直线AB过抛物线C的焦点F,分别以A,B为切点作抛物线C的切线,两条切线交于点则下列结论:①点P一定在抛物线C的准线上;②;③的面积有最大值无最小值.其中,正确结论的个数是( )A. 0B. 1C. 2D. 311.函数的定义域是______.12.在的展开式中,的系数是______用数字填写答案13.正项数列满足,若,,则的值为______.14.设点,分别为椭圆C:的左,右焦点,点P是椭圆C上任意一点,若使得成立的点恰好是4个,则实数m的一个取值可以为__________.15.已知非空集合A,B满足:,,函数对于下列结论:①不存在非空集合对,使得为偶函数;②存在唯一非空集合对,使得为奇函数;③存在无穷多非空集合对,使得方程无解.其中正确结论的序号为__________.16.已知函数只能同时满足下列三个条件中的两个:①函数的最大值为2;②函数的图象可由的图象平移得到;③函数图象的相邻两条对称轴之间的距离为请写出这两个条件的序号,说明理由,并求出的解析式;在中,内角A ,B ,C 所对的边分别为a ,b ,c ,,,求面积的最大值.17.某学校高中三个年级共有300名学生,为调査他们的课后学习时间情况,通过分层抽样获得了20名学生一周的课后学习时间,数据如表单位:小时:高一年级789高二年级78910111213高三年级671117试估计该校高三年级的学生人数;从高一年级和高二年级抽出的学生中,各随机选取一人,高一年级选出的人记为甲,高二年级选出的人记为乙,求该周甲的课后学习时间不大于乙的课后学习时间的概率:再从高中三个年级中各随机抽取一名学生,他们该周的课后学习时间分别是8,9,单位:小时,这三个数据与表格中的数据构成的新样本的平均数记为,表格中的数据平均数记为,试判断与的大小.结论不要求证明18.如图1,在平面四边形PDCB 中,,,,将沿BA 翻折到的位置,使得平面平面ABCD ,如图2所示.设平面SDC 与平面SAB 的交线为l ,求证:;在线段SC 上是否存在一点点Q 不与端点重合,使得二面角的余弦值为,请说明理由.19.设函数若,①求曲线在点处的切线方程;②当时,求证:若函数在区间上存在唯一零点,求实数m 的取值范围.20.已知椭圆C:的短轴长等于,离心率求椭圆C的标准方程;过右焦点F作斜率为k的直线l,与椭圆C交于A,B两点,线段AB的垂直平分线交x轴于点P,判断是否为定值,请说明理由.21.若数列中存在三项,按一定次序排列构成等比数列,则称为“等比源数列”.已知数列为4,3,1,2,数列为1,2,6,24,分别判断,是否为“等比源数列”,并说明理由;已知数列的通项公式为,判断是否为“等比源数列”,并说明理由;已知数列为单调递增的等差数列,且,,求证为“等比源数列”.答案和解析1.【答案】A【解析】解:全集,集合,则故选:求出集合A,利用补集定义能求出本题考集合的运算,考查补集定义等基础知识,考查运算求解能力,是基础题.2.【答案】A【解析】解:,故选:根据已知条件,结合复数的运算法则,即可求解.本题主要考查复数的运算法则,属于基础题.3.【答案】D【解析】解:设事件为第i次抽到偶数,,2,则,,在第1次抽到偶数的条件下,第2次抽到奇数的概率为:故选:设事件为第i次抽到偶数,,2,利用条件概率计算公式能求出在第1次抽到偶数的条件下,第2次抽到奇数的概率.本题考查在第1次抽到偶数的条件下,第2次抽到奇数的概率的求法,考查条件概率等基础知识,考查运算求解能力,是基础题.4.【答案】B【解析】解:设l是直线,,是两个不同的平面,对于A,若,,则与相交或平行,故A错误;对于B,若,,则由面面垂直的判定定理得,故B正确;对于C,若,,则l与平行或,故C错误;对于D,若,,则l与相交、平行或,故D正确.故选:对于A,与相交或平行;对于B,由面面垂直的判定定理得;对于C,l与平行或;对于D,l与相交、平行或本题考查命题真假的判断,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力,是中档题.5.【答案】B【解析】解:设点为D点,圆C:,圆心,半径,当直线DC垂直于直线l时,弦AB最短,故选:根据已知条件,结合垂径定理,以及两点之间的距离公式,即可求解.本题主要考查垂径定理,以及两点之间的距离公式,属于基础题.6.【答案】D【解析】解:函数的定义域为,当时,;当时,则在单调递减;在单调递增,故选:求得的定义域,讨论,时,的单调性,结合图象可得结论.本题考查函数的图象的判断,注意运用单调性判断,考查分类讨论思想和数形结合思想,属于基础题.7.【答案】C【解析】解:,,解得,故选:根据已知条件,结合等差中项的定义,以及等差数列的前n项和公式,即可求解.本题主要考查等差中项的定义,以及等差数列的前n项和公式,属于基础题.8.【答案】C【解析】解:在中,,,,,,即,,故选:利用三角形的内角和定理及诱导公式得到,再利用两角和与差的余弦函数公式化简,把A的度数代入已知等式求出的值,代入计算求出的值,再利用两角和与差的余弦函数公式求出的值,进而得到,即可求出的度数.此题考查了正弦定理,两角和与差的余弦函数公式,以及特殊角的三角函数值,熟练掌握正弦定理是解本题的关键.9.【答案】B【解析】解:“在上恒成立”,则在上恒成立,又在上为增函数,则,即,又“”是“”的必要不充分条件,即”是“在上恒成立”的必要不充分条件,故选:先由不等式恒成立问题求出m的范围,再结合充分必要条件判断即可.本题考查了不等式恒成立问题,重点考查了充分必要条件,属基础题.10.【答案】C【解析】解:由抛物线知焦点,可设直线AB的方程为,,,联立直线与抛物线方程得,有,,,,切线AP的方程为,化简得,同理切线BP的方程为,联立解得,故①正确;,,故②正确;,当时,有最小值,无最大值,故③错误.故选:由直线与抛物线的有关知识,结结论依次判断.本题考查抛物线的几何性质,判断直线与直线的位置关系,以及三角形的面积的最值问题,属中档题.11.【答案】【解析】解:根据题意,由,得,所以函数的定义域为,故答案为:,由题意可得,从而求出不等式组的解集即可.本题考查求函数定义域的应用问题,解题关键是列出使解析式有意义的不等式组,属于基础题.12.【答案】35【解析】解:的展开式中的通项公式为,令,解得,即的系数是,故答案为:先求展开式的通项公式,再求展开式的项系数即可.本题考查了二项式定理,重点考查了展开式的项系数的求法,属基础题.13.【答案】【解析】解:,,是等比数列,设公比为q,且,由,得,,故答案为:根据可知该数列为等比数列,根据,求出其公比和首项即可求本题考查了数列的递推式,属于基础题.14.【答案】答案不唯一【解析】【分析】本题考查了点与椭圆的位置关系,属于中档题.当时,说明椭圆上存在4点满足条件.【解答】解:当时,,则,由椭圆方程可知,,,,因为,所以以为直径的圆与椭圆有4个交点,使得成立的点恰好有4个,所以实数m的一个取值可以为故答案为:答案不唯一15.【答案】①③【解析】【分析】本题主要考查集合间的基本关系与函数的奇偶性,属于难题.通过求解可以得到在集合A,B含有何种元素的时候会取到相同的函数值,因为存在能取到相同函数值的不同元素,所以即使当x与都属于一个集合内时,另一个集合也不会产生空集的情况,之后再根据偶函数的定义判断①是否正确,根据奇函数的定义判断②是否正确,解方程判断③是否正确.【解答】解:①若,,则,,,若,,则,,,若,,则,,,若,,则,,,综上不存在非空集合对,使得为偶函数,故①正确;②若,则或,当,时,,满足当时,所以可统一为,此时为奇函数,当,时,,满足当时,所以可统一为,此时为奇函数,所以存在非空集合对,使得为奇函数,且不唯一,故②错误;③解的,解的,当非空集合对满足且,则方程无解,又因为,,所以存在无穷多非空集合对,使得方程无解,故③正确。
北京市石景山区2020届高三数学3月统一测试(一模)试题文
北京市石景山区2020 届高三数学 3 月一致测试(一模)试题文本试卷共 6 页,满分为150 分,考试时间为120 分钟.请务势必答案答在答题卡上,在试卷上作答无效,考试结束后上交答题卡.第一部分(选择题共 40分)一、选择题共8 小题,每题 5 分,共40 分.在每题列出的四个选项中,选出切合题目要求的一项.1.已知会合 P { x R | x ≥ 1} , Q{1, 2} ,则以下关系中正确的是=Q B. PüQ C. QüP D.PUQ RA. P2.设 i 是虚数单位,若复数z 1 i ,则复数z的模为A. 1B.2C.3D. 23.某几何体的三视图如右图所示,该几何体的体积为A. 2B.4C.6D.124.若 x 0 y ,则以下各式中必定正确的选项是A. sin x sin yB. ln x ln( y)C. e x e yD. 11 x y5.中国南宋期间的数学家秦九韶提出了一种多项式简化算法,右图是实现该算法的程序框图,如输入的 n2, x 1 ,依次输入的 a 为 1, 2, 3,运转程序,输出的 s 的值为A.1B.2C.3D.6r r(1,1), k R ,则 k r r6. 已知平面向量a( k , 2) , b 2 是 a 与 b 同向的A.充足不用要条件B.必需不充足条件C. 充要条件D. 既不充足也不用要条件7.已知 f ( x)sin( 2πx) ,则 f (0) f (1) f (2) f (3) L f (2019) 5A.0B. 505C.1010D. 20208.当 x0,1 时,以下对于函数y mx2的图象与 y x m 的图象交点个1数说法正确的选项是A.当 m0,1时,有两个交点B.当 m1,2时,没有交点C. 当m2,3 时,有且只有一个交点D. 当m3,时,有两个交点第二部分(非选择题共110 分)二、填空题共 6 小题,每题 5 分,共 30分.9.在平面直角坐标系xOy 中,角和角均以 Ox 为始边,它们的终边对于x轴对称.若 sin1,则 sin =__________.3x y ≥ 1,10.若变量 x, y 知足拘束条件y x ≤ 1, 则 z2x y 的最小值为_________.x ≤ 1,11.已知抛物线 y2 2 px( p0) 的准线为 l , l 与双曲线x2y 21的渐近线分别交于4A, B 两点.若 | AB | 4 ,则p______ .12.九连环是我国从古到现在宽泛流传的一种益智游戏.在某种弄法中,用a n表示解下 n(n ≤ 9, n N * ) 个圆环所需的最少挪动次数,已知a1 1 ,a n 2a n11,n为偶,则解下 4个圆环所需的最少挪动次数a4为______.2a n12,数13.已知会合 A { 5, 1, 2, 4, 5} ,请写出一个一元二次不等式,使得该不等式的解集与会合A有且只有一个公共元素,这个不等式能够是______________.14.在直角坐标系xOy 中,点 A x1 , y1和点 B x2 , y2是单位圆x2y2 1 上两点,AB =1,则AOB =______; | y1 2 | | y2 2 | 的最大值为_.三、解答题共 6 小题,共80 分.解答应写出文字说明,演算步骤或证明过程.15.(本小题 13 分)设数列 { a n } 的前n项和为 S n,若 a1 2 且 S n S n 12n (n≥2, n N*).(Ⅰ)求 S n;(Ⅱ)若数列{ b n } 知足 b n2a n,求数列 { b n } 的前n项和 T n.16.(本小题 13 分)1在△ABC 中,角A,B,C的对边分别为 a ,b,c , b = 23 , c= 3 , cos B =.(Ⅰ)求 sinC 的值;(Ⅱ)求△ ABC的面积.17.(本小题14 分)如图,在四棱锥E ABCD 中,平面ABCD平面AEB,且四边形ABCD为矩形.BAE = 90, AE= 4,AD= 2 ,F,G, H分别为BE, AE, AD 的中点.(Ⅰ)求证:CD ∥平面FGH;(Ⅱ)求证:平面FGH平面ADE ;(Ⅲ)在线段DE 求一点 P ,使得 AP FH ,并求出 AP 的值.已知某单位全体员工年纪频次散布表为:年纪(岁)[25,30) [30, 35) [35,[40,[45, 50) [50, 55)共计40)45)人数(人)61850311916140经统计,该单位35 岁以下的青年员工中,男员工和女员工人数相等,且男员工...的年纪频率散布直方图和以下:(Ⅰ)求 a ;(Ⅱ)求该单位男女员工的比率;(Ⅲ)若从年纪在[25 , 30)岁的员工中随机抽取两人参加某项活动,求恰巧抽取一名男员工和一名女员工的概率.设函数 f ( x)e x ax a, a 0 .2(Ⅰ)若曲线 y f ( x) 在点 (1, f (1)) 处的切线与x轴平行,求a;(Ⅱ)当 x 1 时,函数 f ( x) 的图象恒在x 轴上方,求 a 的最大值.20.(本小题满分14 分)已知椭圆 C : x2y21(a b 0) 的离心率为1,右焦点为 F ( c,0) ,左极点为A,右顶a 2b22点 B 在直线l:x2上.(Ⅰ)求椭圆 C 的方程;(Ⅱ)设点 P 是椭圆C上异于 A , B 的点,直线 AP交直线l于点 D ,当点 P 运动时,判断以BD 为直径的圆与直线PF的地点关系,并加以证明.2020 年石景山区高三一致测试数学(文)试卷答案及评分参照一、选择题:本大题共8个小题,每题 5 分,共 40 分.题号12345678答案C B C D D C A B 二、填空题:本大题共6个小题,每题 5 分,共 30 分.9.1;10.1;11.8;312.7;13. ( x4)(x6)0 ;(答案不独一)14.π, 3 4.3三、解答题:本大题共6个小题,共80分.解答题应写出文字说明,证明过程或演算步骤.15.(本小题13 分)解:(Ⅰ)因为 S n Sn 12n (n≥2, n N*),所以 a n S n Sn 12n (n≥2, n N*).又因为 a1 2 ,所以 a n2n ( n N*).所以 S n n(22n)n2n .2(Ⅱ) b n 2a n4n,所以 T n44n4n 4 .14316.(本小题 13 分)解: ( Ⅰ) 在△ABC中,cosB = 1 ,3∴ sin B = 1 cos2 B = 1(1)2 2 2,33∵ b = 2 3 , c= 3 ,由正弦定理b c233,sin B得22sinC sinC36∴ sinC =.3(Ⅱ)由余弦定理b2 = a2 + c22ac cosB 得 12= a2 + 9 2 3a ( 1) ,3∴ a 22a3= 0,解得 a= 1 或 a= 3 (舍)∴S V ABC =1acsinB 211322 2 .2317.(本小题 14 分)(Ⅰ)证明:在矩形ABCD 中, CD ∥AB,∵ F ,G 分别为 BE ,AE 的中点,∴FG∥AB,且 FG = 1AB, 2∴CD∥FG,∵CD平面FGH,FG平面FGH,∴CD ∥平面 FGH .(Ⅱ)证明:在矩形 ABCD 中,AD AB,又∵ BAE 90 ,∴ AB AE,又ADI AE= A∴AB 平面 ADE ,又GF //AB∴ GF平面ADE ,∵ GF平面FGH,∴平面 FGH平面 ADE .(Ⅲ)解:作AP DE于P,∵ GF平面 ADE ,且 AP平面 ADE ,∴ GF AP ,∵G, H 分别为 AE, AD 的中点,∴GH AP∵GFI GH=G,∴AP 平面FGH,∵FH 平面FGH,∴AP FH,∵矩形 ABCD平面AEB,且平面ABCD I 平面AEB= AB,∴AE 平面ABCD,∴AE 平面AD,在直角三角形 AED 中, AE= 4 , AD= 2,可求得AP 4 5 .518.(本小题13 分)解:(Ⅰ)由男员工的年纪频次散布直方图可得:0.025 0.025) 51 .所以.(Ⅱ)该单位 [25,35) 岁员工共24 人,因为 [25,35) 岁男女员工人数相等,所以 [25, 35)岁的男员工共 12 人.由(Ⅰ)知,男员工年纪在[25, 35) 岁的频次为0.15,所以男员工共有1280人,所以女员工有140 - 80=60人,所以男女比率为4∶ 3.(Ⅲ)由男员工的年纪频次散布直方图可得:男员工年纪在[25, 30)岁的频次为.由(Ⅱ)知,男员工共有80 人,所以男员工年纪在[25, 30)岁的有 4 人,分别记为A1, A2 , A3, A4.又全体员工年纪在[25, 30)岁的有 6人,所以女员工年纪在 [25, 30) 岁的有 2 人,分别记为B1, B2.从年纪在 25~30 岁的员工中随机抽取两人的结果共有(A1,A2) ,(A1,A3 ) ,(A1,A4 ) ,(A1,B1) ,(A1,B2 ),(A2,A3) ,(A2,A4 ) ,(A2,B1 ),(A2,B2 ) ,(A3,A4 ),(A3,B1) ,(A3,B2) ,(A4,B1 ) ,(A4,B2 ) ,(B1,B2 ) 15 种状况,此中一男一女的有(A1,B1) ,(A1,B2 ),(A2,B1) ,(A2,B2 ) ,(A3,B1) ,(A3,B2 ) ,(A4,B1 ) ,(A4,B2 ) 8 种状况,所以恰巧抽取一名男员工和一名女员工的概率为8 .1519.(本小题 13 分)解:(Ⅰ) f ( x)e x ax a ,2f ( x)e x a ,f (1)e a ,由题设知f(1)0,即 e a0 ,解得 a e.经考证 a e 知足题意。
