054奥数天天练丨分数与繁分数化简
小学繁分数化简专题

小学奥数知识点汇编第一章计算1.1四则混合运算1.1.1繁分数的化简技巧繁分数的定义如果分数形式中,分子或分母含有四则运算或分数, 或分子与分母都含有四则运算或分数的数,叫“繁分数”;其对应于“简分数”。
1.1.1.2繁分数化简的基本方法1.1.1.2.1可利用分数与除法的关系把繁分数写成分子除以分母的形式。
141.1.1.2.2利用分数的基本性质, 去掉分子、分母上分数的分母后化为最简分数。
一般情况下,分子、分母所乘上的适当非零整数为分子、分母部分的两个分数分母的最小公倍数。
1.1.1.3繁分数化简的常用技巧 1.1.1.3.1化带分数为假分数:繁分数中的分子或分母若含有带分数,则把带分数化为假分数 再化简。
,1 6 6 , -1155 - 5 - 5 -18 9 28 8 “ 40 -202— 153331.1.1.3.2化小数为分数:繁分数中的分子或分母若含有小数,则一般可把小数化成分数再化 简。
3 3200.15 20 — 20 31 3 _ 3 3155—20 4 4 46例: 76 5 • - 6 14 X 57 14 7 5125 例:67 5 14 614 7 5 14 1412 51.1.133化分数为小数:繁分数中的分子或分母部分所含有的分数可化为有限小数,则可把 分子或分母中的分数化为小数再化简。
0.15 0.15 15 1■ - --- — _3 一 0.75 一 75 一 541.1.1.3.4化小数为整数:若分子、分母都是小数还可以利用分数的基本性质,分子与分母同 时扩大相同的倍数,把小数化成整数再化简。
-2.4 _ 24 _ 2 3.6 _ _ 31.1.1.3.5化复杂为简单:繁分数的分子或分母部分若含有加减运算,则先加减运算再按繁分 数化简方法进行化简。
繁分数的分子、分母都是连乘运算可以分子、分母直接约分化简。
1 3 1 30.26(2)厘 4 1 0.52 1.5 72走进奥数繁分数1_ 1 _ 1_ 1 _ 1_ 1 _ 12 丄1-亠11-丄1-丄5-292922222 —J \J222 22 2122 1555221.1.1.3.6化多层为单层:化简复杂的繁分数要学会分层化简O12767 17 “ 70——20 =1 _ 6 20 63201.5 3.75 0.26 0.52 1.5 7.51 1 1 12 12 4346 6 2 上20 一 20根据实际问题列出的分数,有时它的分子或分母里又含有分 数,或者分子和分母里都含有分数,我们把这样的分数叫做繁繁分数中,把分子部分和分母部分分开的那条分数线,叫 做繁分数的主分数线(也叫主分线)。
分数化简的方法

分数化简的方法分数是数学中常见的一种数形式,它由分子和分母组成,通常以分数线将两者分开。
在实际运用中,我们经常需要对分数进行化简,以便更好地进行计算和比较。
那么,接下来我将介绍一些常见的分数化简方法,希望能够帮助大家更好地理解和运用分数化简。
首先,我们来看一下最基本的分数化简方法——约分。
约分就是将分子和分母同时除以它们的最大公约数,使得分数的分子和分母没有公因数。
例如,对于分数6/9,我们可以将分子和分母同时除以它们的最大公约数3,得到化简后的分数2/3。
这种方法简单易行,是分数化简的基本手段。
其次,我们可以通过因式分解来进行分数化简。
当分子和分母均为多项式时,我们可以尝试对它们进行因式分解,然后进行约分。
例如,对于分数(x^2-4)/(x^2-2x),我们可以将分子和分母分别因式分解为(x+2)(x-2)和x(x-2),然后进行约分,得到化简后的分数x+2。
这种方法适用于复杂的分数化简,可以将分数化简为最简形式。
另外,我们还可以利用分数的性质来进行化简。
例如,分数的乘法性质和除法性质可以帮助我们简化分数。
当两个分数相乘时,我们可以将它们的分子相乘、分母相乘,然后进行约分;当两个分数相除时,我们可以将它们的分子相除、分母相除,然后进行约分。
这样可以将复杂的分数化简为最简形式,提高计算效率。
此外,我们还可以利用分数的小数形式来进行化简。
有些分数在小数形式下会呈现循环小数或者有限小数的形式,我们可以将它们化简为最简形式。
例如,分数1/3在小数形式下为0.3333…,我们可以直接将其化简为0.3;分数4/9在小数形式下为0.4444…,我们可以直接将其化简为0.4。
这种方法适用于将分数化简为小数形式的情况。
最后,我们需要注意的是,在进行分数化简时,要特别注意分母不能为0的情况。
因为分母为0会导致分数无意义,所以在化简分数时,要确保分母不为0,避免出现错误的结果。
总的来说,分数化简是数学中常见的运算,通过约分、因式分解、分数性质和小数形式等方法,我们可以将复杂的分数化简为最简形式,以便更好地进行计算和比较。
繁分数化简技巧[1]
![繁分数化简技巧[1]](https://img.taocdn.com/s3/m/2fc3b254376baf1ffc4fad79.png)
什么叫做繁分数?_计算奥数专题_繁分数问题在一个分数的分子和分母里,至少有一个又含有分数,这样形式的分数,叫做繁分数。
繁分数中,把分子部分和分母部分分开的那条分数线,叫做繁分数的主分数线(也叫主分线)。
主分线比其他分数线要长一些,书写位置要取中。
在运算过程中,主分线要对准等号。
如果一个繁分数的分子部分和分母部分又是繁分数,我们就把最长的那条主分线,叫做中主分线,依次向上为上一主分线,上二主分线……;依次向下叫下一主分线,下二主分线……;两端的叫末主分线。
如:根据分数与除法的关系,分数除法的运算也可以写成繁分数的形式。
什么叫做繁分数化简?_计算奥数专题_繁分数问题把繁分数化为最简分数或整数的过程,叫做繁分数的化简。
繁分数化简一般采用以下两种方法:(1)先找出中主分线,确定出分母部分和分子部分,然后这两部分分别进行计算,每部分的计算结果,能约分的要约分,最后写成“分子部分÷分母部分”的形式,再求出最后结果。
此题也可改写成分数除法的运算式,再进行计算。
(2)繁分数化简的另一种方法是:根据分数的基本性质,经繁分数的分子部分、分母部分同时扩大相同的倍数(这个倍数必须是分子部分与分母部分所有分母的最小公倍数),从而去掉分子部分和分母部分的分母,然后通过计算化为最简分数或整数。
繁分数的分子部分和分母部分,有时也出现是小数的情况,如果分子部分与分母部分都是小数,可依据分数的基本性质,把它们都化成整数,然后再进行计算。
如果是分数和小数混合出现的形式,可按照分数、小数四则混合运算的方法进行处理。
即:把小数化成分数,或把分数化成小数,再进行化简。
繁分数的运算基本法则_计算奥数专题_繁分数问题繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.繁分数运算典型问题解析1_计算奥数专题_繁分数问题繁分数运算典型问题解析1繁分数运算典型问题解析2繁分数运算典型问题解析3繁分数运算典型问题解析4繁分数运算典型问题解析5繁分数运算典型问题解析6繁分数运算典型问题解析7繁分数运算典型问题解析8繁分数运算典型问题解析9繁分数运算典型问题解析10繁分数运算典型问题解析11繁分数运算典型问题解析12繁分数运算典型问题解析13繁分数运算典型问题解析14繁分数运算典型问题解析15数学计算公式(常用公式)繁分数的计算练习题及答案讲解1_计算奥数专题_繁分数问题繁分数的计算练习题及答案讲解1繁分数的计算练习题及答案讲解2_计算奥数专题_繁分数问题繁分数的计算练习题及答案讲解2繁分数的计算练习题及答案讲解3_计算奥数专题_繁分数问题繁分数的计算练习题及答案讲解3繁分数的计算练习题及答案讲解4_计算奥数专题_繁分数问题繁分数化简技巧(化多层为单层)_计算奥数专题化多层为单层:化简复杂的繁分数要学会分层化简。
六年级奥数第四讲_繁分数的计算精编版
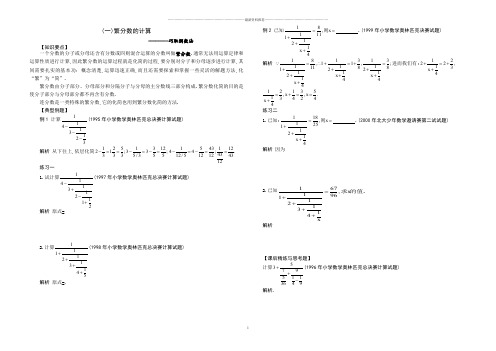
(一)繁分数的计算--------巧取倒数法【知识要点】一个分数的分子或分母还含有分数或四则混合运算的分数叫做繁分数.通常无法用运算定律和运算性质进行计算,因此繁分数的运算过程就是化简的过程,要分别对分子和分母逐步进行计算,其间需要扎实的基本功:概念清楚,运算迅速正确,而且还需要探索和掌握一些灵活的解题方法,化“繁”为“简”.繁分数由分子部分、分母部分和分隔分子与分母的主分数线三部分构成.繁分数化简的目的是使分子部分与分母部分都不再含有分数.连分数是一类特殊的繁分数,它的化简也用到繁分数化简的方法.【典型例题】例1计算11413123---(1995年小学数学奥林匹克总决赛计算试题)解析从下往上,依层化简125131221;33;3335/355-==-=-=154311244;.4312/512124312-=-==练习一1.试计算1141312112-+-+(1997年小学数学奥林匹克总决赛计算试题)解析原式=2.计算1111213145++++(1998年小学数学奥林匹克总决赛计算试题)解析原式=. 例2已知==+++xx则,1184112111.(1999年小学数学奥林匹克决赛试题)解析181313,11,;111118812211121444x xx=∴+=+=+++++++进而我们有:1222,134x+=++12135,,.134244x xx=+==+练习二1.已知:==+++xx则,25184112111.(2000年北大少年数学邀请赛第二试试题) 解析因为2.已知167,1961121314xx=++++求的值.解析【课后精练与思考题】计算53795113649++-(1996年小学数学奥林匹克总决赛计算试题)解析.(二)分数的简便计算1 3x4 +14x5+15x6+16x7+17x8+18x9=1 1x2 +12x3+13x4+……+12005X2006+12006=1 6 +112+120130+142+156172+190=1+2120+3130+4142+5156+6172+7190+81110+91132=3 2 +76+1312+2120+3130+4342+5756=1+11+2+11+2+3+11+2+3+4+11+2+3+4+5+ …+11+2+3+4+5 (50)=1 1x3 +13x5+15x7+……+197x99=2 3 +215+235+263+299+2143= 32x5 +35x8+38x11+311x14+314x17=4 1X5 +45X9+49X13+413X17+417X21=1 2 +14+18+116+132+164=56-712+920-1130+1342=1+12-56+712-920+1130-1342+1556-1772=12+(23+13)+(34+24+14)+…+(3940+3840+…+240+140)=7116×67+6115×56+5114×45+4113×34+3112×23=112×113×114×115×……×1199×11100=(1+12)×(1+14)×(1+16)×…×(1+120)×(1-13)×(1-15)×…×(1—119)×(1—121)=(1+12+13+14)×(12+13+14+15)-(1+12+13+14+15)×(12+13+14)=(9-1639×4)+(8-1639×5)+……+(4-1639×9)=155+255+355+…+955+1055+11155+121551355+……+19155+20155=251+451+651+……+5051-151-351-551-……-4951=。
小学数学中常见的分数化简方法

小学数学中常见的分数化简方法分数是数学中一个重要的概念,它由分子和分母组成。
在小学数学中,我们需要学习如何将分数化简为最简形式。
下面将介绍一些常见的分数化简方法。
一、约分法约分是将分数化简为最简形式的常见方法。
当分子和分母有相同的因子时,我们可以将它们同时除以这个因子,从而得到一个相等但分子与分母都较小的分数。
例如,对于分数6/12,我们可以发现分子和分母都可以被2整除。
因此,我们可以将分子和分母同时除以2得到1/2,这就是6/12的最简形式。
二、质数分解法在质数分解法中,我们将分子和分母都用质数的乘积表示,然后将相同的质数因子约掉。
举例来说,对于分数8/16,我们可以分别质数分解分子和分母,得到的结果分别是2*2*2和2*2*2*2。
然后,我们发现分子和分母都有三个2这个质数因子,因此,我们将它们约掉,得到1/2,这就是8/16的最简形式。
三、最大公约数法最大公约数法是一种使用最大公约数来进行化简的方法。
我们可以通过求出分子和分母的最大公约数,然后将其同时除以最大公约数,得到最简形式的分数。
例如,对于分数15/25,我们可以求出它们的最大公约数为5,然后将分子和分母同时除以5,得到3/5,这就是15/25的最简形式。
四、小数转分数法有些时候,我们需要将小数转化为分数并化简。
这时,我们可以将小数的小数部分化为分数形式,然后将分数与小数的整数部分相加,即可得到最简分数。
举例来说,对于小数1.25,我们可以将小数部分0.25转化为分数1/4。
然后,我们将1/4与整数部分1相加,得到5/4,这就是1.25的最简分数形式。
总结:小学数学中常见的分数化简方法有约分法、质数分解法、最大公约数法和小数转分数法。
掌握了这些方法,我们就可以将分数化简为最简形式,更好地理解和应用分数。
通过约分法,我们可以将分数的分子和分母同时除以相同的因子,得到最简形式的分数。
质数分解法将分子和分母分别用质数的乘积表示,并约掉相同的质数因子。
分数复数的化简

分数复数的化简
分数是分子和分母中都有分数的分数。
因此,繁分数有时也被称为是“叠分数”。
根据分子和分母中分数的个数、变量的个数以及变量的复杂度的不同,化简繁分数的难易程度也不同。
阅读本文,学习如何化简繁分数。
方法1反转相乘法化简繁分数
1必要的话,将分子和分母化简成一个分数。
并不是所有的繁分数都很难算,事实上,分子和分母中分别只含有一个分数的繁分数就很容易化简。
所以,如果繁分数的分子或分母。
2求分母位置上分数的倒数。
根据定义,除以一个数,就相当于乘以这个数的倒数。
现在,繁分数的分子和分母上都只有一个分数,我们可以利用除法的这一性质,化简繁分数。
首先,求出繁分数分母位置上分数的倒数。
方法很简单,只需要交换分子和分母即可。
本例中,繁分数。
3用繁分数的分子部分乘以最小公分母。
求出最小公分母之后,再用它乘以繁分数的分子部分。
换句话说,我们需要用整个繁分数乘以注意事项
计算过程中,最好把每一步都写出来。
在化简分数的过程中,计算过快或者心算,很容易出现计算错误。
在网上或者课本上找一个繁分数,然后按照上文的方法尝试化简。
奥数繁分数计算定义及解题技巧
奥数繁分数计算定义及解题技巧
奥数繁分数计算定义及解题技巧
1、繁分数的定义
如分数形式,分子或分母含有分数,或分子与分母都含有分数的.数,叫繁分数。
2、繁分数计算的技巧
(1)先找出繁分数中主分数线,确定分子部分和分母部分,然后这两部分分别进行计算,每部分的计算结果能约分的要约分,最后改成“分子部分/分母部分”的形式,再求出结果。
(2)繁分数化简的另一种方法是:根据分数的基本性质,将繁分数的分子部分和分母部分同时扩大相同的倍数(这个倍数必须是分子部分与分母部分所有分母的最小公倍数),从而却掉分子部分和分母部分的分母,然后通过计算划分为最简分数或整数。
下载全文。
分数化简的方法
分数化简一般采用以下四种方法:
(1)先找出中主分线,确定分子部分和分母部分,然后这两部分分别进行计算,每部分的计算结果能约分的要约分,最后改成“分子部分÷分母部分”的形式,再求出结果.
(2)繁分数化简的另一种方法是:根据分数的基本性质,经繁分数的分子部分和分母部分同时扩大相同的倍数(这个倍数必须是分子部分与分母部分所有分母的最小公倍数),从而去掉分子部分和分母部分的分母,然后通过计算化为最简分数或整数.
(3)繁分数的化简一般由下至上,由左到右,逐次进行化简.
繁分数的分子部分和分母部分有时也出现是小数的情祝,如果是分数和小数混合出现的形式,可按照分数、小数四则混合运算的方法进行处理.即:把小数化成分数,或把分数化成小数后再进行化简.
当分子部分和分母部分都统一成小
数后,化简的方法是:中间约分时,把小数看成整数,但要注意小数点不要点错位置.
也可以根据分数的基本性质,把繁分数的分子部分和分母部分都变成整数连乘,然后交叉约分算出结果来.
通过观察可以看到:分子部分的各个因数一共有三位小数;分母部分的各个因数一共有两位小数.针对这个情况,分子和分母同时扩大1000倍,就都变成了整数.
在此基础上进行约分,即可得出最后的结果.
1、征服畏惧、建立自信的最快最确实的方法,就是去做你害怕的事,直到你获得成功的经验。
2、忍别人所不能忍的痛,吃别人所别人所不能吃的苦,是为了收获得不到的收获。
就像驴子面前吊着个萝卜就会往前走。
正因为有那个目标,你才有劲儿往前走。
分数化简练习题及答案
分数化简练习题及答案第一章计算1.1四则混合运算1.1.1繁分数的化简技巧1.1.1.1繁分数的定义如果分数形式中,分子或分母含有四则运算或分数,或分子与分母都含有四则运算或分数的数,叫“繁分数”;其对应于“简分数”。
1.1.1.2繁分数化简的基本方法1.1.1.2.1可利用分数与除法的关系把繁分数写成分子除以分母的形式。
6561412例:?÷?×?571475141.1.1.2.2利用分数的基本性质,去掉分子、分母上分数的分母后化为最简分数。
一般情况下,分子、分母所乘上的适当非零整数为分子、分母部分的两个分数分母的最小公倍数。
6?141277例:??55?1414141.1.1.3繁分数化简的常用技巧1.1.1.3.1化带分数为假分数:繁分数中的分子或分母若含有带分数,则把带分数化为假分数再化简。
1166151898840202153331.1.1.3.2化小数为分数:繁分数中的分子或分母若含有小数,则一般可把小数化成分数再化简。
33?200.153133155??204441.1.1.3.3化分数为小数:繁分数中的分子或分母部分所含有的分数可化为有限小数,则可把分子或分母中的分数化为小数再化简。
0.150.151510.75755?41.1.1.3.4化小数为整数:若分子、分母都是小数还可以利用分数的基本性质,分子与分母同时扩大相同的倍数,把小数化成整数再化简。
2.4242.63631.1.1.3.5化复杂为简单:繁分数的分子或分母部分若含有加减运算,则先加减运算再按繁分数化简方法进行化简。
繁分数的分子、分母都是连乘运算可以分子、分母直接约分化简。
12347??71770??20?23?66?6?? 1154162063??45202020131?3?0.261.5?3.75?0.261?1?11 10.52?1.5?7.52?1?240.52?1.5?721.1.1.3.6化多层为单层:化简复杂的繁分数要学会分层化简。
奥林匹克数学题型分式的简化与运算
奥林匹克数学题型分式的简化与运算分式是数学中常见且重要的概念,它在奥林匹克数学竞赛中也经常出现。
分式可以表示为两个整数之间的比值,通常由一个分子和一个分母组成。
本文将探讨奥林匹克数学题型中关于分式的简化和运算的方法与技巧。
一、分式的简化在奥林匹克数学竞赛中,简化分式是一个基础而又重要的步骤。
为了简化分式,我们需要找到分子和分母的最大公因数,并将其约分。
例如,考虑分式$\frac{12}{18}$。
我们可以观察到12和18都可以被2整除,因此它们的最大公因数是2。
通过将分子和分母都除以最大公因数2,我们可以得到简化后的分式$\frac{6}{9}$。
这个分式仍然存在可以约分的因子,进一步简化为$\frac{2}{3}$。
我们得到了最简形式的分式。
二、分式的乘法奥林匹克数学题型中常常涉及到多个分式的乘法运算。
在进行分式乘法时,我们需要将分式的分子与分子相乘,分母与分母相乘,并约分得到结果。
考虑以下示例:$\frac{1}{2} \times \frac{3}{4}$。
我们将分子1与分子3相乘,得到3;将分母2与分母4相乘,得到8。
最后,我们对结果$\frac{3}{8}$进行简化。
三、分式的除法除法是分式运算中的另一个常见问题。
当我们需要将两个分式相除时,可以通过将除式取倒数,再进行分式乘法来实现。
例如,考虑分式$\frac{\frac{2}{3}}{\frac{4}{5}}$。
我们可以将除式$\frac{4}{5}$取倒数,得到$\frac{5}{4}$。
然后,我们可以将原始分式转化为$\frac{2}{3} \times \frac{5}{4}$的形式。
最后,按照分式乘法的规则进行计算,得到结果$\frac{10}{12}$。
我们可以对结果进行简化,得到最终的答案$\frac{5}{6}$。
四、分式的加法与减法在奥林匹克数学竞赛中,有时候需要进行分式的加法和减法运算。
为了实现这些操作,我们需要找到两个分式的公共分母,并按照相应的运算法则进行计算。
