自动控制原理习题分析第三章3
自动控制原理习题及其解答第三章

第三章例3-1 系统的结构图如图3-1所示。
已知传递函数 )12.0/(10)(+=s s G 。
今欲采用加负反馈的办法,将过渡过程时间t s减小为原来的0.1倍,并保证总放大系数不变。
试确定参数K h 和K 0的数值。
解 首先求出系统的传递函数φ(s ),并整理为标准式,然后与指标、参数的条件对照。
一阶系统的过渡过程时间t s 与其时间常数成正比。
根据要求,总传递函数应为)110/2.0(10)(+=s s φ即HH K s K s G K s G K s R s C 1012.010)(1)()()(00++=+= )()11012.0(101100s s K K K HHφ=+++=比较系数得⎪⎩⎪⎨⎧=+=+1010110101100H HK K K 解之得9.0=H K 、100=K解毕。
例3-10 某系统在输入信号r (t )=(1+t )1(t )作用下,测得输出响应为:t e t t c 109.0)9.0()(--+= (t ≥0)已知初始条件为零,试求系统的传递函数)(s φ。
解 因为22111)(ss s s s R +=+=)10()1(10109.09.01)]([)(22++=+-+==s s s s s s t c L s C 故系统传递函数为11.01)()()(+==s s R s C s φ 解毕。
例3-3 设控制系统如图3-2所示。
试分析参数b 的取值对系统阶跃响应动态性能的影响。
解 由图得闭环传递函数为1)()(++=s bK T Ks φ系统是一阶的。
动态性能指标为)(3)(2.2)(69.0bK T t bK T t bK T t s r d +=+=+= 因此,b 的取值大将会使阶跃响应的延迟时间、上升时间和调节时间都加长。
解毕。
例 3-12 设二阶控制系统的单位阶跃响应曲线如图3-34所示。
试确定系统的传递函数。
解 首先明显看出,在单位阶跃作用下响应的稳态值为3,故此系统的增益不是1,而是3。
自动控制原理第3章习题解答

(2) k (t ) = 5t + 10 sin( 4t + 45 )
0
(3) k (t ) = 0.1(1 − e 解: (1) Φ ( s ) =
−t / 3
)
0.0125 s + 1.25
1
胡寿松自动控制原理习题解答第三章
(2) k (t ) = 5t + 10 sin 4t cos 45 + 10 cos 4t sin 45
3s 4 + 10s 3 + 5s 2 + s + 2 = 0
试用劳思稳定判据和赫尔维茨判据确定系统的稳定性。 解: 列劳思表如下:
s4 s3 s2 s1 s0
3 5 2 10 1 47 2 10 1530 0 − 47 2
由劳思表可以得到该系统不稳定。 3-12 已知系统特征方程如下,试求系统在 s 右半平面的根数及虚根值。 (1)
2ξω n = 70
ξ=
7 2 6
根据(3-17)
h(t ) = 1 +
e − t / T1 e − t / T12 + T2 / T1 − 1 T1 / T2 − 1
解:根据公式(3-17)
3
胡寿松自动控制原理习题解答第三章
《自动控制原理》第三章 3-4 稳定性分析
第三章 线性系统的时域分析法
赫尔维茨稳定判据: 线性系统稳定的充要条件: i 0, i 1,2, n
能源与动力学院
第三章 线性系统的时域分析法
15
3. 劳思-赫尔维茨稳定判据…
例3 2 s 4 s 3 3s 2 5s 10 0
1 5 4 0 1 0 2
系统不稳定
0 5 3
0 0 0 10
能源与动力学院
第三章 线性系统的时域分析法
11
1. 稳定性的基本概念
稳定性:扰动作用 偏离平衡状态 产生初始偏差 扰动消失 恢复到原平衡状态
例1. 单摆 例2. 曲面坡
大范围稳定 小范围稳定
稳定平衡点 不稳定平衡点
能源与动力学院
第三章 线性系统的时域分析法
12
2. 线性系统稳定的充要条件
第三章 线性系统的时域分析法
3
重点回顾
R(s) E(s)
1
n s(s 2n )
2
C(s)
Td s
n s(s 2n )
2
R(s)
E (s )
C(s)
Kt s
能源与动力学院
第三章 线性系统的时域分析法
4
重点回顾
主导极点: 如果在所有的闭环极点中,距虚轴 最近的极点周围没有闭环零点,而其他闭 环极点又远离虚轴,那么距虚轴最近的极 点在系统响应过程中起主导作用,这样的 闭环极点称为主导极点 非主导极点:除主导极点外的其他闭环极点
《自动控制原理》习题及解答03

t1
T[ln(
T
T
)
ln
0.9]
则
tr
t2
t1
T
ln
0.9 0.1
2.2T
3) 求 ts
h(ts )
0.95
1
T T
e ts
/T
ts
T[ln
T T
ln 0.05]
T[ln
T T
ln 20]
T[3
ln
T T
]
3-3 一阶系统结构图如题 3-3 图所示。要求系统闭环增益 K 2 ,调节时间 ts 0.4 (s),试确定参数 K1, K 2 的值。
3-15 虚根。
h() lim s (s) 1 2.5
s0
s
已知系统的特征方程,试判别系统的稳定性,并确定在右半 s 平面根的个数及纯
4 1 )(s
1)
T1
T2
T1
T2
1 0.25
C(s) (s)R(s)
4
= C0 C1 C2
s(s 1)(s 4) s s 1 s 4
C0
lim s (s) R(s)
s0
lim
4
s0 (s 1)(s
4)
1
C1
lim (s
s1
1) (s)
R(s)
lim
s0
4 s(s
4)
4 3
考虑初始条件,对微分方程进行拉氏变换
s 2C(s) s c(0) c(0) 5 s C(s) c(0) 62.5C(s) 0 整理得 s 2 5s 62.5 C(s) s 5c(0) c(0)
对单位反馈系统有 e(t) r(t) c(t) , 所以
自动控制原理第3章 习题及解析

自动控制原理(上)习 题3-1 设系统的结构如图3-51所示,试分析参数b 对单位阶跃响应过渡过程的影响。
考察一阶系统未知参数对系统动态响应的影响。
解 由系统的方框图可得系统闭环响应传递函数为/(1)()()111K Ts Ks Kbs T Kb s Ts +Φ==++++ 根据输入信号写出输出函数表达式:111()()()()()11/()K Y s s R s K s T Kb s s s T bK =Φ⋅=⋅=-++++对上式进行拉式反变换有1()(1)t T bKy t K e-+=-当0b >时,系统响应速度变慢;当/0T K b -<<时,系统响应速度变快。
3-2 设用11Ts +描述温度计特性。
现用温度计测量盛在容器内的水温,发现1min 可指示96%的实际水温值。
如果容器水温以0.1/min C ︒的速度呈线性变化,试计算温度计的稳态指示误差。
考察一阶系统的稳态性能分析(I 型系统的,斜坡响应稳态误差)解 由开环传递函数推导出闭环传递函数,进一步得到时间响应函数为:()1t T r y t T e -⎛⎫=- ⎪⎝⎭其中r T 为假设的实际水温,由题意得到:600.961Te-=-推出18.64T =,此时求输入为()0.1r t t =⋅时的稳态误差。
由一阶系统时间响应分析可知,单位斜坡响应的稳态误差为T ,所以稳态指示误差为:lim ()0.1 1.864t e t T →∞==3-3 已知一阶系统的传递函数()10/(0.21)G s s =+今欲采用图3-52所示负反馈的办法将过渡过程时间s t 减小为原来的1/10,并保证总的放大倍数不变,试选择H K 和0K 的值。
解 一阶系统的调节时间s t 与时间常数成正比,则根据要求可知总的传递函数为10()(0.2/101)s s Φ=+由图可知系统的闭环传递函数为000(10()()1()0.211010110()0.21110H HHHK G s K Y s R s K G s s K K K s s K ==++++==Φ++)比较系数有101011011010HHK K K ⎧=⎪+⎨⎪+=⎩ 解得00.9,10H K K ==3-4 已知二阶系统的单位阶跃响应为1.5()1012sin(1.6+53.1t y t e t -=-)试求系统的超调量%σ,峰值时间p t ,上升时间r t 和调节时间s t 。
自动控制原理-第3章

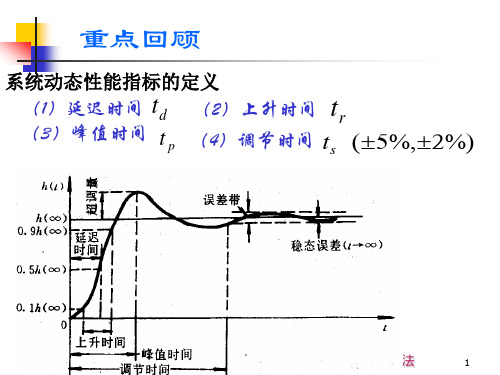
响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4<ζ<0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
自动控制原理第三章3
ω n =1/ LC
RC ζ= 2L
ω n2 = 1/LC
第三节 二阶系统性能分析
二、二阶系统的单位阶跃响应 2 ωn C(s)=Ф(s)R(s)= 2 ζ (S +2 ω n S+ω n2 )S
闭环特征方程: 闭环特征方程: S2+2 ωn S+ω n2= 0 ζ 闭环极点: 闭环极点: S1.2 = -ζ ωn ± ω n ζ
欠阻尼二阶系统动态性能指标(总结): 欠阻尼二阶系统动态性能指标(总结):
1)上升时间tr )上升时间
π −β π -β tr = = ωd ωn 1 − ξ 2
2)峰值时间tp )峰值时间 3)超调量σ% )超调量σ% 4)调节时间ts )调节时间
π π tp = = ωd ω n 1 − ξ 2
[
c(t)=1sin(ωd n sin(ω 1-ζ2 cos(ωdt2p+β) -ζ ωt+β) dtp+β)]
e
− ζω n t
sin(ωdc(tp) -ζ ωntp -1 1-ζ2ωne tg(ωdsin(ωdtp+β) dtp+β) tp+β)=tgβ = 1-ζ2 [-ζ = 即 dt ζ cos(ωdtp+β) π -ζ ωntp π cos(ωdtp+β)]=0 ωdtp = 0,π,2π…+ωde tp= ωd =ωn 1-ζ2
第三节 二阶系统性能分析
三、二阶系统的性能指标
)、欠阻尼二阶系统的性能指标 (一)、欠阻尼二阶系统的性能指标 主要性能 指标有
1
c(t)
σ%
ess
性能指标 求取如下
0
tr t
《自动控制原理》第三章-3-5-稳态误差计算
伺服电动机
R(s)
E(s)
1
C(s)
-
s(s 1)
K 1, 1
r(t) 1(t),k p , ess 0
r(t) t, kv 1, ess 1
r(t)
1 2
t2, ka
0, ess
位置随动系统
能源与动力学院 第三章 线性系统的时域分析法
14
4.扰动作用下稳态误差
R(s)
-
E(s)
R(s) E(s) 20
s4
N (s)
+
2
C(s)
s(s 2)
能源与动力学院 第三章 线性系统的时域分析法
28
3-20
R
-
K1
U
K2 S(T1S 1)
C
G(s)
K1K 2
B
s(T1s 1)(T2s 1)
1 T2S 1
(s)
C(s) R(s)
T1T2 s 3
K1K2 (T2s 1) (T1 T2 )s2 s
1
能源与动力学院 第三章 线性系统的时域分析法
7
3.输入作用下稳态误差计算
(1)阶跃作用下的稳态误差
r(t) R 1(t), R(s) R s
ess
Lim sR(s) s0 1 G(s)H (s)
Lim s1R(s)
s0
K Lim s
s0
1
R LimG(s)H (s)
Lim s R
s0
K Lim s
27
参考答案: Kp= ,kv=5,ka=0,essr=0.4,essn=-0.2
四、控制系统如图, r(t) 1 2t, n(t) 1(t), 试计算
自动控制原理第三章课后习题 答案(最新)
3-1 设系统的微分方程式如下:(1) )(2)(2.0t r t c =&(2) )()()(24.0)(04.0t r t c t c t c =++&&&试求系统闭环传递函数Φ(s),以及系统的单位脉冲响应g(t)和单位阶跃响应c(t)。
已知全部初始条件为零。
解:(1) 因为)(2)(2.0s R s sC = 闭环传递函数ss R s C s 10)()()(==Φ 单位脉冲响应:s s C /10)(= 010)(≥=t t g单位阶跃响应c(t) 2/10)(s s C = 010)(≥=t t t c(2))()()124.004.0(2s R s C s s =++ 124.004.0)()(2++=s s s R s C 闭环传递函数124.004.01)()()(2++==s s s R s C s φ 单位脉冲响应:124.004.01)(2++=s s s C t e t g t 4sin 325)(3-= 单位阶跃响应h(t) 16)3(61]16)3[(25)(22+++-=++=s s s s s s Ct e t e t c t t 4sin 434cos 1)(33----=3-2 温度计的传递函数为11+Ts ,用其测量容器内的水温,1min 才能显示出该温度的98%的数值。
若加热容器使水温按10ºC/min 的速度匀速上升,问温度计的稳态指示误差有多大?解法一 依题意,温度计闭环传递函数11)(+=ΦTs s 由一阶系统阶跃响应特性可知:o o T c 98)4(=,因此有 min 14=T ,得出 min 25.0=T 。
视温度计为单位反馈系统,则开环传递函数为Tss s s G 1)(1)()(=Φ-Φ=⎩⎨⎧==11v TK 用静态误差系数法,当t t r ⋅=10)( 时,C T Ke ss ︒===5.21010。
自动控制原理 第3章习题解答
1−ζ 2 = π
ζ
3
2π
tr
=
π −β ωd
=
3 3
=
23 9
π
;t p
=π ωd
=
π 3
=
3π 3
−ζ π
M p = e 1−ζ 2 ×100% = 16.3% ;
t
5% s
=3 ζω n
=
3s,
t
2% s
=4 ζω n
= 4s
3-6 系统结构图如题 3-6 图所示,试求当τ = 0 时,
系统的ζ 和ωn 之值,如要求ζ =0.7,试确定参数τ 。
s2
0.8
1+ K
s1 0.8(2 + K ) − (1 + K ) 0
0.8
s0 1+ K
Q 系统临界稳定
∴ 0.8(2 + K ) − (1 + K ) = 0
即K = 3 即系统的临界增益K = 3
由s 2行构成辅助多项式:0.8s 2 + (1 + K ) = 0
即0.8s 2 + 4 = 0 ∴ s1,2 = ± j 5 = ± j2.24 ∴系统的振荡频率为ωn = 2.24rad / s
= 150.5°
h(t) = 1 − 0.06e−5.76t + 1.07e−0.37t cos(1.27t + 150.5°)
3-4
已知根据主导极点 s1,2 确定的调整时间为 10.82s,考察这一时刻系统单位阶跃响应中
的指数项值 − 0.06e−5.76t |t=10.82 = −5.15 ×10−29 ,可见指数项值在 ts = 10.82 时已经衰减到 微不足道的程度。事实上,在峰值时间 t p = 2.48s ,指数项的值为 − 3.7 ×10−8 ,可见对
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
自动控制原理习题分析第三章3-1(1)
以知单位反馈系统的开环传递函数,试用捞斯判据判断系统的稳定性。
50
()(1)(5)
G s s s s =
++
自动控制原理习题分析第三章3-1(4
=
++ 3已知位反系的函,用思判据判系的定性.4
G(s)s (s 2)(s 3)
自动控制原理习题分析第三章3-2(3)
+++++= 5432已知系特征方程,用思判据判定系定性.若系不定,指出右半s平面特征根的目.
s s 3s 9s 16s 100
自动控制原理习题分析第三章3-2(4)
++++= 543已知系特征方程,用思判据判定系定性.若系不定,指出右半s平面特征根的目.s 3s s 2s 100
自动控制原理习题分析第三章3-3(2)
++++= 432已知系特征方程,用思判据判定使系定取值范.s Ks s s 10
自动控制原理习题分析第三章3-6
;==+++ 32
已知位反系的函,用思判据判系是否定和是否具有σ1的定裕度..4
G(s)2s 10s 13s 5
=--+-+-+=+-=∴= 323
2
(2).用s z 1代入特征方程:2(z 1)10(z 1)13(z 1)50
展得新特征方程:2z 4z z 0;缺常,且一次方系,系不具σ1定裕度.
自动控制原理习题分析第三章3-8
ς= n s 已知系如.K 8,求:(1)系的特征量和ω;(2)系的性能指σ%和t .
自动控制原理习题分析第三章3-9
ς-= s 38系,若加入速度反,求使0.5,
(1)τ的取值;(2)σ%和t .
ςς-+=
=+++++==
++++=
==+++++++=+==⨯⨯=⇒==⨯= '
2
n n 1
1s(0.5s 1)局部:Φ(s)1
s(0.5s 1)τs 1τs s(0.5s 1)
系88/(1τ)
:G(s)函s(0.5s 1)τs s(0.5s/(1τ)1)
G(s)816
Φ(s)1G(s)s(0.5s 1)τs 8s 2(1τ)s 16
ω4不;2(1τ)2ω20.544τ1
此:σ%e 100%
1ςς≈
=≈=s s n n 6.3%
311t 1.5秒,或t ln 1.57秒
ωω 自动控制原理习题分析第三章3-11(1)
+=
+++-++-=--=--=--=-±-=-⨯∴≈
++- 7.6(s 2.1)
Φ(s)(s 8)(s 2)(s 0.5j0.866)(s 0.5j0.866)
零s 2.1和极s 2很靠近(构成偶极子)可忽略其影.又另一极s 8的模(8)比共复极s 0.5j0.866的模(1)大8倍,故s 8非主极,
可忽略其性能影.7.6 2.1
Φ(s)2(s 8)(s 0.5
j0.866)(s ςςς++⨯≈====⨯++++≈=≈== n 22
s s n n 0.5j0.866)7.6 2.10.9975;主极ω1,0.5,σ%16.3%,82(s s 1)s s 1
311t 6秒,或t ln 6.28秒(Δ0.05)
ωω
自动控制原理习题分析第三章3-11(1
----=-+︒+--0.5t 0.5t 8t 2t
c(t)0.9975(1 1.1547e sin(0.866t 60))0.1139392e sin0.866t 0.0163888e 0.0211111e
自动控制原理习题分析第三章3-11(2)
ςς--=
=≈=
++++++==⇒===∴=-====∴=====-+
++++=-+ 2n 2s s s s t 6t 1661
Φ(s)17
(s 1)(s 6)6(s 1)s 1s s 166
117,2T T 1.429,σ%0T 66
t 求法1:由319:t /T 7.8,t 7.8T 3.184s 法2:由主极T 1s,t 3T 3s
1611 1.20.2
c(s)Φ(s)s (s 1)(s 6)s s s 1s 6
c(t)1 1.2e 0.2e =,c(3.17)0.9496
自动控制原理习题分析第三章3-14
--=
+=++++=+⋅=++⋅ 10n n 1
n n 110
2某位反系的函:Φ(s)a s a C(s)
.系定,分求R(s)a s a s a s a (1)r(t)(12t)1(t);(2)r(t)(12t t )1(t),系差.
自动控制原理习题分析第三章3-14
---------+++++==
--
++++++==++++++ 10
n n 1n n 11010n n 1n n 110
01
1020
n n 122n 2n 3n n 1n n 1222a s a a s a s a s a Φ(s)
G(s)1Φ(s)1a s a s a s a a a (s 1)
a s a a a ;a a a s
a s a s s (s s 1)
a a
自动控制原理习题分析第三章3-17
==⋅= ss d 12312某复合控制系的构如所示.在定入作用和扰入作用同加入,且r(t)n(t)Bt 1(t),使差e 0,求K 的值.(K ,K ,K ,T ,T ,τ均正.)
自动控制原理习题分析第三章3-17
→→→→-∴==+-++=++++--==
++++2c ssR R s 0
s 0
12
1d 12
s 0
13
111d
1d s 0
131
311G G e lim sE (s)lim s
1G G K K s 1s(Ts 1)(τs 1)B
lim s
K s 1K s(Ts 1)
(Ts 1)(τs 1)K K B K K B lim B
s(Ts 1)(τs 1)K K (τs 1)K K
自动控制原理习题分析第三章3-17
→→→→-==+-∴==+-
+-+-===++++++----=+=
+=N 3
12ssN N 3
s 0
s 0
12
2
22122s 0s 0112312313
11d 21d ss ssR ssN 3131E (s)1令R(s)0,G N(s)1G G 1
e limsE (s)limsG N(s)
1G G K T s 1K (Ts 1)BK B lims lim B K s s(Ts 1)(T s 1)K K (T s 1)K K 1K s(Ts 1)
B K K B BK B(1K K K e e e K K K K -== 22
d ss 311
)1K ,K ,e 0K K K。
