中考数学命题研究 第一编 教材知识梳理篇 第三章 函数及其图象 第二节 一次函数的图象及性质(精练)试题
中考数学总复习 基础知识梳理 第3单元 函数及其图象 3.3 一次函数的应用课件

12/10/2021
第二页,共十页。
知识(zhī shi)体系图
要点 梳理 (yàodiǎn)
一次函数的应用
利润问题 方案选择问题 其他问题
12/10/2021
第三页,共十页。
利用(lìyòng)一次函数知识解应用题的一般步骤
1.设定实际(shíjì)问题中的变量. 2.建立变量与变量之间的函数关系. 3.确定自变量的取值范围,保证自变量具有实际意义. 4.利用函数的性质解决问题. 5.写出答案.
第三单元 函数及其图象。1.设定实际问题中的变量.。2.建立变量与变量之间的函数关系(guān xì).。3.确定自变量的取值范围,保证自变量 具有实际意义.。4.利用函数的性质解决问题.。3.求运动过程中的函数解析式——关键:以静制动.。【答案】A
12/பைடு நூலகம்0/2021
第十页,共十页。
因为
2 (小时)乙两小时内运动路程与时间的关系也分段,分为两2 2段0,1第2一 段5 图象为倾斜线段,过原点与
点
,且斜率小于甲的第一段,大于甲的第三段.第二段图象也为平行于x轴的线3段,故可以排除C, 53 所,20以 选
择A选项.
12/10【/20答21 案】A
第九页,共十页。
内容(nèiróng)总结
12/10/2021
第六页,共十页。
三种 题型 (sān zhǒnɡ)
学法指导
1.选择题——关键(guānjiàn):读懂函数图象,学会联系实际. 2.综合题——关键:运用数形结合思想. 3.求运动过程中的函数解析式——关键:以静制动.
12/10/2021
第七页,共十页。
经典 考题 (jīngdiǎn)
12/10/2021
中考数学总复习 第一部分 基础篇 第三章 函数及其图象 考点11 一次函数课件

第三章 函数(hánshù)及其图象 11 一次函数
2021/12/9
第一页,共十四页。
目标(mùbiāo)方向
进一步理解正比例函数和一次函数的概念,能结合图象讨 论这些函数的基本性质,以及分析和解决(jiějué)简单的实际问题.
加深对一次函数与方程(组)及不等式的关系的理解,从 运动变化的角度更深层次地了解方程(组)及不等式等内 容,构建和发展相互联系的知识体系. 中考中多以选择题、填
空题、解答题以及与方程、不等式相结合的综合应用题形式考查 .
2021/12/9
第二页,共十四页。
考点聚焦
考点(kǎo diǎn)一 一次函数和正比例函数的定义
2021/12/9
第三页,共十四页。
考点(kǎo diǎn)二 一次函数的图象与性质
2021/12/9
第四页,共十四页。
2021/12/9
第五页,共十四页。
考点(kǎo 三 diǎn) 一元函数解析式的确定
2021/12/9
第六页,共十四页。
考点四 一次函数与方程(fāngchéng)(组)及不等式的关系
2021/12/9
第七页,共十四页。
2021/12/9
第八页,共十四页。
真题探源
2021/12/9
第九页,共十四页。
2021/12/9
第十页,共十四页。
2021/12/9
第十一页,共十四页。
2021/12/9
第十二页,共十四页。
2021/12/9
第十三页,共十四页。
内容 总结 (nèiróng)
第一部分 基 础 篇。第三章 函数及其图象。目标方向。进一步理解正比例函数和一次函数的概念, 能结合图象讨论这些函数的基本性质,以及分析和解决简单的实际问题.加深对一次函数与方程(组)
中考数学 第1编 教材知识梳理篇 第3章 函数及其图象 第9讲 一次函数及其应用(精讲)试题
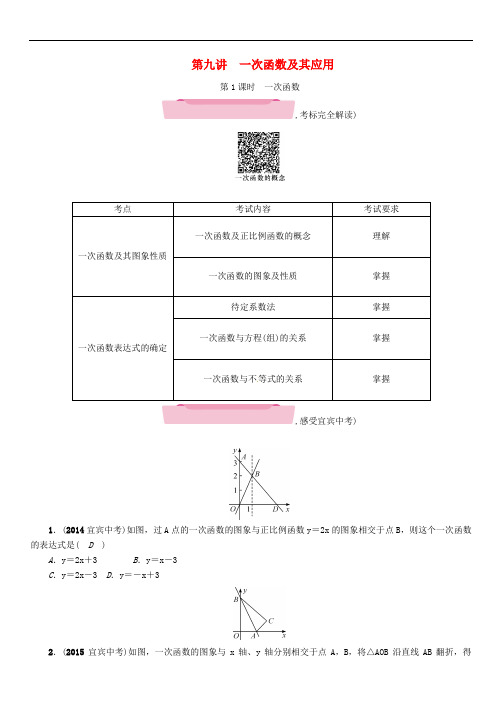
第九讲 一次函数及其应用第1课时 一次函数,考标完全解读)一次函数与不等式的关系,感受宜宾中考)1.(2014宜宾中考)如图,过A 点的一次函数的图象与正比例函数y =2x 的图象相交于点B ,则这个一次函数的表达式是( D )A .y =2x +3B .y =x -3C .y =2x -3D .y =-x +32.(2015宜宾中考)如图,一次函数的图象与x 轴、y 轴分别相交于点A ,B ,将△AOB 沿直线AB 翻折,得△ACB.若C ⎝ ⎛⎭⎪⎫32,32,则该一次函数的表达式为.,核心知识梳理)一次函数及其图象性质1.一次函数及正比例函数的概念一般地,形如__y =kx +b(k ,b 为常数,且k≠0)__的函数,叫做一次函数.形如__y =kx(k 为常数,且k≠0)__的函数叫做正比例函数.【温馨提示】正比例函数是一次函数的特殊形式,正比例函数是一次函数,反之不一定成立,定义中k≠0是非常重要的条件,若k =0,则函数就成为y =b(b 为常数),此函数是常数函数,不是一次函数.2.一次函数的图象及性质 一次函数y =kx +b(k≠0)大致图象续表【针对练习】函数y =-3x +2经过__第一、二、四__象限,其中y 随x 的增大而__减小__.一次函数表达式的确定3.利用坐标确定一次函数表达式的常用方法:__待定系数法__. 4.具体步骤(1)设出一次函数表达式__y =kx +b(k≠0)__;(2)将两对对应的x ,y 值代入表达式y =kx +b 中,得到含有待定系数k ,b 的方程组; (3)求出待定系数k ,b 的值;(4)将所求待定系数的值代入所设的函数表达式中.【针对练习】若一次函数y =kx +b 经过(0,1),(1,2)两点,则一次函数的表达式为__y =x +1__.一次函数与方程、不等式的关系5.一次函数与方程(组)的关系(1)一次函数y =kx +b(k ,b 为常数,且k≠0)可转化为二元一次方程kx -y +b =0; (2)一次函数y =kx +b 的图象与x 轴交点的__横坐标__是方程kx +b =0的解;(3)一次函数y =kx +b 与y =k 1x +b 1图象交点的横、纵坐标值是方程组⎩⎪⎨⎪⎧y =kx +b ,y =k 1x +b 1的解.6.一次函数与不等式的关系(1)①函数y =kx +b 中函数值y >0时,自变量x 的取值范围就是不等式kx +b >0的解集,对应的函数图象为位于x 轴上方的部分,即x <a ,如图①;②函数y =kx +b 中函数值y <0时,自变量x 的取值范围就是不等式kx +b <0的解集,对应的函数图象为位于x 轴下方的部分,即x >a ,如图①;(2)当两个一次函数有交点时,联立两个函数表达式组成方程组,求出交点坐标,两个一次函数可将平面分成四部分,比较两函数交点左右两边函数的增减性来判断不等式的解集.即k 1x +b 1>k 2x +b 2的解集为x >a ;k 1x +b 1<k 2x +b 2的解集为x <a ,如图②.,重点难点解析)一次函数的图象及性质【例1】已知一次函数y =kx +b -x 的图象与x 轴的正半轴相交,且函数值y 随自变量x 的增大而增大,则k ,b 的取值情况为( )A .k >1,b <0B .k >1,b >0C .k >0,b >0D .k >0,b <0【解析】一次函数y =kx +b -x =(k -1)x +b , ∵函数值y 随x 的增大而增大,∴k -1>0,即k >1;∵图象与x 轴的正半轴相交,∴图象与y 轴的负半轴相交,∴b <0.∴选项A 是正确的. 【答案】A 【针对训练】1.(2017白银中考)在平面直角坐标系中,一次函数y =kx +b 的图象如图所示,观察图象可得( A )A .k>0,b>0B .k>0,b<0C .k<0,b>0D .k<0,b<0待定系数法求一次函数表达式【例2】已知函数y =kx +b(k≠0)的图象与y 轴交点的纵坐标为-2,且当x =2时y =1,那么此函数表达式为________.【解析】由题意知,图象过(0,-2),(2,1)两点,将(0,-2)与(2,1)代入y =kx +b 中,得⎩⎪⎨⎪⎧2k +b =1,b =-2,解得⎩⎪⎨⎪⎧k =32,b =-2.则函数表达式为y =32x -2.【答案】y =32x -2.【针对训练】2.已知一次函数y =kx +3的图象经过点(1,4).(1)求这个一次函数的表达式;(2)求关于x的不等式kx+3≤6的解集.解:(1)将(1,4)代入一次函数y=kx+3中,得4=k+3,解得k=1,∴一次函数的表达式为y=x+3;(2)将k=1代入kx+3≤6中得,x+3≤6,解得x≤3.一次函数综合应用【例3】如图,把Rt△ABC放在直角坐标系内,其中∠CAB=90°,BC=5,点A,B的坐标分别为(1,0),(4,0),将△ABC沿x轴向右平移,当点C落在直线y=2x-6上时,线段BC扫过的面积为____cm2.【解析】如图所示.∵点A,B的坐标分别为(1,0),(4,0),∴AB=3.∵∠CAB=90°,BC=5,∴AC=4.∴A′C′=4.∵点C′在直线y=2x-6上,∴2x-6=4,解得 x=5.即OA′=5.∴CC′=5-1=4.∴S▱BB′C′C=4×4=16 (cm2).即线段BC扫过的面积为16 cm2.【答案】16【针对训练】3.如图,若一次函数y=-2x+b的图象交y轴于点A(0,3),则不等式-2x+b>0的解集为( C)A .x >32B .x >3C .x <32D .x <34.已知函数y 1=2x +4与函数y 2=-2x +8. (1)求两函数图象与x 轴围成的三角形的面积;(2)当x 为何值时,y 1=y 2,y 1>y 2.解:(1)⎩⎪⎨⎪⎧y =2x +4,y =-2x +8,解得⎩⎪⎨⎪⎧x =1,y =6,即交点坐标(1,6).∴两函数图象与x 轴围成的三角形的面积为:12×6×6=18;(2)x =1时,y 1=y 2, x >1时,y 1>y 2.,当堂过关检测)1.(2017宁德中考)如图,直线l 是一次函数y =kx +b 的图象,若点A(3,m)在直线l 上,则m 的值是( C )A .-5B .32C .52D .7,(第1题图)) ,(第2题图))2.(2017葫芦岛中考)一次函数y =(m -2)x +3的图象如图所示,则m 的取值范围是( A )A .m <2B .0<m <2C .m <0D .m >23.(2017陕西中考)若一个正比例函数的图象经过A(3,-6),B(m ,-4)两点,则m 的值为( A )A .2B .8C .-2D .-84.(2017成都中考)如图,正比例函数y 1=k 1x 和一次函数y 2=k 2x +b 的图象相交于点A(2,1).当x<2时,y 1__<__y 2.(选填“>”或“<”)5.已知:如图,在平面直角坐标系xOy 中,一次函数y =34x +3的图象与x 轴和y 轴分别交于A ,B 两点,将△AOB 绕点O 顺时针方向旋转90°后得到△A′OB′.(1)求直线A′B′的表达式;(2)若直线A′B′与直线AB 相交于点C ,求S △A ′BC ∶S △ABO . 解:(1)由y =34x +3,得A(-4,0)和B(0,3),∴A ′(0,4),B ′(3,0).设A′B′的表达式为y =kx +b ,将A′, B ′坐标代入,得⎩⎪⎨⎪⎧b =4,3k +b =0,∴⎩⎪⎨⎪⎧k =-43,b =4,∴直线A′B′的表达式为y =-43x +4;(2)由旋转得:∠A=∠A′, ∠ABO =∠A′BC, ∴∠A ′CB =∠AOB=90°, ∴△A ′CB ∽△AOB. 又∵AB=42+32=5,∴S △A ′ BC ∶S △ABO =⎝ ⎛⎭⎪⎫A ′B AB 2=⎝ ⎛⎭⎪⎫4-352=125.请完成精练本第20页作业教后反思:________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________ ________________________________________________________________________第2课时 一次函数的实际应用,考标完全解读),感受宜宾中考)(2013宜宾中考)某棵果树前x 年的总产量y 与x 之间的关系如图所示,从目前记录的结果看,前x 年的年平均产量最高,则x 的值为( C )A .3B .5C . 7D .9,核心知识梳理)一次函数的实际应用1.用一次函数解决实际问题的一般步骤为: (1)设定实际问题中的自变量与因变量;(2)__通过列方程(组)与待定系数法求一次函数关系式__; (3)__确定自变量的取值范围__; (4)利用函数性质解决问题;(5)__检验所求解是否符合实际意义__; (6)答. 2.方案最值问题对于求方案问题,通常涉及两个相关量,解题方法为根据题中所要满足的关系式,通过__列不等式__,求解出某一个事物的__取值范围__,再根据另一个事物所要满足的条件,即可确定出有多少种方案.【方法点拨】求最值的本质为求最优方案,解法有两种: (1)可将所有求得的方案的值计算出来,再进行比较;(2)直接利用所求值与其变量之间满足的一次函数关系式求解,由一次函数的增减性可直接确定最优方案及最值;若为分段函数,则应分类讨论,先计算出每个分段函数的取值,再进行比较.显然,第②种方法更简单快捷.,重点难点解析)一次函数的实际应用【例1】甲、乙两人利用不同的交通工具,沿同一路线从A 地出发前往B 地.甲出发1 h 后,乙出发.设甲与A 地相距y 甲(km ),乙与A 地相距y 乙(km ),甲离开A 地的时间为x(h ),y 甲,y 乙与x 之间的函数图象如图所示.(1)甲的速度是________km /h ;(2)当1≤x≤5时,求y 乙关于x 的函数表达式; (3)当乙与A 地相距240 km 时,甲与A 地相距______km .【解析】(1)根据图象确定甲的路程与时间即可求出速度;(2)利用待定系数法确定出y 乙关于x 的函数表达式即可;(3)求出乙距A 地240 km 时的时间,乘以甲的速度即可得结果.【答案】解:(1)60; (2)当1≤x≤5时,设y 乙关于x 的函数表达式为y 乙=kx +b. ∵点(1,0),(5,360)在其图象上,∴⎩⎪⎨⎪⎧0=k +b ,360=5k +b ,解得⎩⎪⎨⎪⎧k =90,b =-90. ∴y 乙关于x 的函数表达式为y 乙=90x -90(1≤x≤5);(3)220 【针对训练】1.某片果园有果树80棵,现准备多种一些果树提高果园产量,但是如果多种树,那么树之间的距离和每棵树所受光照就会减少,单棵树的产量随之降低.若该果园每棵果树产果量y(kg ),增种果树x(棵),它们之间的函数关系如图所示.(1)求y 与x 之间的函数关系式;(2)在投入成本最低的情况下,增种果树多少棵时,果园可以收获果实6 750 kg? (3)当增种果树多少棵,果园的总产量w(kg )最大?最大产量是多少? 解:(1)设函数的表达式为y =kx +b.该一次函数过点(12,74),(28,66),根据题意,得⎩⎪⎨⎪⎧74=12k +b ,66=28k +b ,解得⎩⎪⎨⎪⎧k =-0.5,b =80. ∴该函数的表达式为y =-0.5x +80; (2)根据题意,得(-0.5x +80)(80+x)=6 750, 解得x 1=10,x 2=70. ∵投入成本最低,∴x =10.∴增种果树10棵时,果园可以收获果实6 750 kg ; (3)根据题意,得 w =(-0.5x +80)(80+x) =-0.5x 2+40x +6 400 =-0.5(x -40)2+7 200,∵a =-0.5<0,则抛物线开口向下,函数有最大值. ∴当x =40时,w 最大值为7 200 kg .∴当增种果树40棵时,果园的最大产量是7 200 kg.利用一次函数进行方案选择【例2】为了贯彻落实市委市政府提出的“精准扶贫”精神.某校特制定了一系列关于帮扶A ,B 两贫困村的计划.现决定从某地运送152箱鱼苗到A ,B 两村养殖,若用大小货车共15辆,则恰好能一次性运完这批鱼苗,已知这两种大小货车的载货能力分别为12箱/辆和8箱/辆,其运往A ,B 两村的运费如下表:(1)求这15辆车中大小货车各多少辆;(2)现安排其中10辆货车前往A 村,其余货车前往B 村,设前往A 村的大货车为x 辆,前往A ,B 两村总费用为y 元,试求出y 与x 的函数表达式;(3)在(2)的条件下,若运往A 村的鱼苗不少于100箱,请你写出使总费用最少的货车调配方案,并求出最少费用.【解析】(1)设大货车用x 辆,小货车用y 辆,根据大、小两种货车共15辆,运输152箱鱼苗,列方程组求解;(2)设前往A 村的大货车为x 辆,则前往B 村的大货车为(8-x)辆,前往A 村的小货车为(10-x)辆,前往B 村的小货车为[7-(10-x)]辆,根据表格所给运费,求出y 与x 的函数关系式;(3)结合已知条件,求x 的取值范围,由(2)的函数关系式求使总运费最少的货车调配方案.【答案】解:(1)设大货车用x 辆,小货车用y 辆.根据题意,得⎩⎪⎨⎪⎧x +y =15,12x +8y =152,解得⎩⎪⎨⎪⎧x =8,y =7.∴大货车用8辆,小货车用7辆;(2)y =800x +900(8-x)+400(10-x)+600[7-(10-x)]=100x +9 400.(3≤x≤8,且x 为整数); (3)由题意,得12x +8(10-x)≥100, 解得x≥5.又∵3≤x≤8,∴5≤x ≤8且为整数.∵y =100x +9 400,k =100>0,y 随x 的增大而增大, ∴当x =5时,y 最小,最小值为y =100×5+9 400=9 900(元).答:使总运费最少的调配方案是:5辆大货车、5辆小货车前往A 村;3辆大货车、2辆小货车前往B 村,最少运费为9 900元.【针对训练】2.新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为 4 000元/m 2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120 m 2.若购买者一次性付清所有房款,开发商有两种优惠方案: 方案一:降价8%,另外每套楼房赠送a 元装修基金; 方案二:降价10%,没有其他赠送.(1)请写出售价y(元/m 2)与楼层x(1≤x≤23,x 取整数)之间的函数关系式;(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算. 解:(1)当1≤x≤8时,y =4 000-(8-x)×30=30x +3 760, 当9≤x≤23时,y =4 000+(x -8)×50=50x +3 600,∴y =⎩⎪⎨⎪⎧30x +3 760(1≤x≤8),50x +3 600(9≤x≤23);(2)第十六层楼房每平方米的价格为:50×16+3 600=4 400(元/m 2), 按照方案一所交房款为:W 1=4 400×120×(1-8%)-a =485 760-a(元), 按照方案二所交房款为:W 2=4 400×120×(1-10%)=475 200(元), 当W 1>W 2时,即485 760-a >475 200, 解得0<a <10 560,当W 1<W 2时,即485 760-a <475 200, 解得a >10 560,∴当0<a <10 560时,方案二合算; 当a =10 560时,两种方案一样; 当a >10 560时,方案一合算.利用一次函数解决分段函数型问题【例3】某企业接到一批粽子生产任务,按要求在15天内完成,约定这批粽子的出厂价为每只6元,为按时完成任务,该企业招收了新工人,设新工人李明第x 天生产的粽子数量为y 只,y 与x 满足下列关系式:y =⎩⎪⎨⎪⎧54x (0≤x≤5),30x +120(5<x≤15). (1)李明第几天生产的粽子数量为420只?(2)如图,设第x 天每只粽子的成本是p 元,p 与x 之间的关系可用图中的函数图象来刻画.若李明第x 天创造的利润为w 元,求w 与x 之间的函数表达式,并求出第几天的利润最大,最大利润是多少元?(利润=出厂价-成本)(3)设(2)小题中第m 天利润达到最大值,若要使第(m +1)天的利润比第m 天的利润至少多48元,则第(m +1)天每只粽子至少应提价几元?【解析】(1)把y =420代入y =30x +120,解方程即可求得;(2)根据图象求得成本p 与x 之间的关系,然后根据利润等于订购价减去成本价,然后整理即可得到W 与x 的关系式,再根据一次函数的增减性和二次函数的增减性解答;(3)根据(2)得出m +1=13,根据利润等于订购价减去成本价得出提价a 与利润w 的关系式,再根据题意列出不等式求解即可.【答案】解:(1)设李明第n 天生产的粽子数量为420只,由题意可知30n +120=420,解得n =10.答:第10天生产的粽子数量为420只;(2)由图象得,当0≤x≤9时,p =4.1;当9≤x≤15时,设p =kx +b ,把点(9,4.1),(15,4.7)代入,得⎩⎪⎨⎪⎧9k +b =4.1,15k +b =4.7, 解得⎩⎪⎨⎪⎧k =0.1,b =3.2, ∴p =0.1x +3.2,①0≤x ≤5时,w =(6-4.1)×54x=102.6x ,当x =5时,w 最大=513元;②5<x≤9时,w =(6-4.1)×(30x+120)=57x +228,当x =9时,w 最大=741元;③9<x≤15时,w =(6-0.1x -3.2)×(30x+120)=-3x 2+72x +336,∵a =-3<0,∴当x =-b 2a=12时,w 最大=768(元). ∵513<741<768,∴第12天的利润最大,最大利润是768元;(3)由(2)可知m =12,m +1=13,设第13天提价a 元.由题意,得w 13=(6+a -p)(30x +120)=510(a +1.5),∴510(a +1.5)-768≥48,解得a =0.1.答:第13天每只粽子至少应提价0.1元.【针对训练】3.甲、乙两人匀速从同一地点到1 500 m 处的图书馆看书,甲出发5 min 后,乙以50 m /min 的速度沿同一路线行走.设甲、乙两人相距s(m ),甲行走的时间为t(min ),s 关于t 的函数图象的一部分如图所示.(1)求甲行走的速度;(2)在坐标系中,补画s 关于t 的函数图象的其余部分; (3)问甲、乙两人何时相距360 m?解:(1)甲行走的速度:150÷5=30(m /min );(2)当t =35时,甲行走的路程为:30×35=1 050(m ),乙行走的路程为:(35-5)×50=1 500(m ),∴当t =35时,乙已经到达图书馆,甲距图书馆的路程还有1 500-1 050=450 m ,∴甲到达图书馆还需时间:450÷30=15(min ),∴35+15=50(min ),∴当s =0时,横轴上对应的时间为50.补画的图象如图所示(横轴上对应的时间为50);(3)设乙出发经过x min 和甲第一次相遇.根据题意,得150+30x =50x ,解得x =7.5,7.5+5=12.5(min ),由函数图象可知,当t =12.5时,s =0,∴点B 的坐标为(12.5,0),当12.5≤t≤35时,设BC 的表达式为s =kt +b ,把C(35,450),B(12.5,0)代入可得⎩⎪⎨⎪⎧12.5k +b =0,35k +b =450, 解得⎩⎪⎨⎪⎧k =20,b =-250, ∴s =20t -250,当s =360时,20t -250=360,解得t =30.5.当35<t≤50时,设CD 的表达式为s =k 1t +b 1,把D(50,0),C(35,450)代入,得⎩⎪⎨⎪⎧50k 1+b 1=0,35k 1+b 1=450, 解得⎩⎪⎨⎪⎧k 1=-30,b 1=1 500,∴s =-30t +1 500,∵当s =360时,-30t +1 500=360,解得t =38.∴当甲行走30.5 min 或38 min 时,甲、乙两人相距360 m .,当堂过关检测)1.(2017鄂州中考)小东家与学校之间是一条笔直的公路,早饭后,小东步行前往学校,途中发现忘带画板,停下给妈妈打电话,妈妈接到电话后,带上画板马上赶往学校,同时小东沿原路返回,两人相遇后,小东立即赶往学校,妈妈沿原路返回16 min 到家,再过5 min 小东到达学校.小东始终以100 m /min 的速度步行,小东和妈妈的距离y(单位:m )与小东打完电话后的步行时间t(单位:min )之间的函数关系如图所示,下列四种说法:①打电话时,小东和妈妈距离是 1 400 m ;②小东与妈妈相遇后,妈妈回家速度是50 m /min ;③小东打完电话后,经过27 min 到达学校;④小东家离学校的距离为2 900 m .其中正确的个数是( D )A .1个B .2个C .3个D .4个2.小丁每天从某都市报社以每份0.3元买出报纸200份,然后以每份0.5元卖给读者,若报纸卖不完,当天可退回报社,但报社只按每份0.2元退给小丁.如果小丁平均每天卖出报纸x 份,纯收入为y 元.(1)求y 与x 之间的函数关系式(要求写出自变量x 的取值范围);(2)如每月以30天计,小丁每天至少要卖多少份报纸才能保证每月收入不低于1 000元?解:(1)y =(0.5-0.3)x -(0.3-0.2)(200-x),即y =0.3x -20(0≤x≤200,且x 为整数),(2)依题意,得(0.3x -20)×30≥1 000,解得x≥17779, ∵x 为整数,∴x 取178.答:小丁每天至少应卖出报纸178份,才能保证月收入不低于1 000元.3.某学校组织了一次野外长跑活动,参加长跑的同学出发后,另一些同学从同地骑自行车前去加油助威.如图,线段L 1,L 2分别表示长跑的同学和骑自行车的同学行进的路程y(km )随时间x(min )变化的函数图象.根据图象,解答下列问题:(1)分别求出长跑的同学和骑自行车的同学的行进路程y 与时间x 的函数表达式;(2)求长跑的同学出发多少时间后,骑自行车的同学就追上了长跑的同学?解:(1)长跑:y =16x , 骑车:y =12x -10, (2)联立以上两个方程组,得⎩⎪⎨⎪⎧y =16x ,y =12x -10,解得⎩⎪⎨⎪⎧x =30,y =5. 答:长跑的同学出发了30 min 后,骑自行车的同学就追上了长跑的同学.。
中考数学总复习 基础知识梳理 第3单元 函数及其图象 3.2 一次函数课件

12/9/2021
第十页,共十四页。
有关正比例函数的两个(liǎnɡ ɡè)区别
学法 指导 (xué fǎ)
1.正比例函数和一次函数的区别
正比例函数是一次函数的特殊情况,一次函数包括正比例函数.也就是 说:如果一个函数是正比例函数,那么(nàme)一定是一次函数,但是,一个 函数是一次函数,不一定是正比例函数.
就行了.
0,
b
,
b k,Leabharlann 012/9/2021
第六页,共十四页。
要点 梳理 (yàodiǎn)
2.一次函数y=kx+b(k≠0)的图象所经过(jīngguò)的象限及增减性.
12/9/2021
第七页,共十四页。
3.2.4 待定系数(xìshù)法求一次函数的解析式
要点 梳理 (yàodiǎn)
No 求待定系数的值代入所设的函数解析式中.。经典考题
Image
12/9/2021
第十四页,共十四页。
y y
k1x k2x
b1 b2
12/9/2021
第九页,共十四页。
要点 梳理 (yàodiǎn)
2.一次函数与不等式的关系
(1)函数y=kx+b的函数值y大于0时,自变量x的取值范围就是(jiùshì)不等式kx+b >0的解集,即函数图象位于x轴的上方; (2)函数y=kx+b的函数值y小于0时,自变量x的取值范围就是不等式kx+b <0的解集,即函数图象位于x轴的下方.
3.2.5 用函数(hánshù)观点看方程(组)与不等式
要点 梳理 (yàodiǎn)
1.一次函数与方程(fāngchéng)(组)的关系
(1)一次函数的解析式y=kx+b就是一个二元一次方程;
广东地区中考复习课件第三章函数第2节一次函数

增大而增大.
(2)当m,n满足
即
时,
函数图象经过原点. (3)若图象经过第一、二、三象限,则
即
考点2 用待定系数法求一次函数的解析式
考点精讲
【例2】(2014深圳)已知函数y=ax+b经过(1,3),(0,-2),
则a-b等于
()
A. -1
B. -3
C. 3
D. 7
思路点拨:分别把(1,3),(0,-2)代入函数y=ax+b求
y=kx(k≠0)中的常数k.确定一个一次函数,需要确定一次函数 定义式y=kx+b(k≠0)中的常数k和b.解这类问题的一般方法是
待定系数法. 2. 一次函数与一元一次方程的关系
任何一元一次方程都可以转化为ax+b=0 (a, b为常数, a≠0)的形式,所以解一元一次方程可以转化为:当某个一次
函数的值为0时,求相应的自变量的值. 从图象上看,相当于
减小,图象从左至右下降. 5. 一次函数的性质
一般地,一次函数y=kx+b有下列性质: (1)当k>0时,y随x的增大而增大; (2)当k<0时,y随x的增大而减小; (3)当b>0时,直线与y轴交点在y轴正半轴上; (4)当b<0时,直线与y轴交点在y轴负半轴上.
方法规律
1. 正比例函数和一次函数解析式的确定 确定一个正比例函数,就是要确定正比例函数定义式
思路点拨:(1)根据函数图象,当x≤1时,直线y=kx+b 没有在直线y=mx-n的下方,即满足kx+b≥mx-n;
(2)观察函数图象,写出直线y=kx+b在x轴下方所对应
的自变量的范围即为所求; (3)利用函数图象的交点坐标为两函数解析式组成的方
中考数学总复习 第一部分 基础篇 第三章 函数及其图象 考点11 一次函数数学课件

第三章 函数及其图象
11 一次函数
12/10/2021
目标方向
进一步理解正比例函数和一次函数的概念,能结 合图象讨论这些函数的基本性质,以及分析和解决简 单的实际问题.加深对一次函数与方程(组)及不等式 的关系的理解,从运动变化的角度更深层次地了解、填空题、解答题以及与方 程、不等式相结合的综合应用题形式考查.
12/10/2021
12/10/2021
12/10/2021
12/10/2021
12/10/2021
12/10/2021
考点聚焦
考点一 一次函数和正比例函数的定义
12/10/2021
考点二 一次函数的图象与性质
12/10/2021
12/10/2021
考点三 一元函数解析式的确定
12/10/2021
考点四 一次函数与方程(组)及不等式的关系
12/10/2021
12/10/2021
真题探源
中考数学 第一部分 教材知识梳理 第三单元 第11课时 一次函数及其应用
【解析】不等式x+b>kx+4的解集在图象上就表示:一 次函数y1=x+b的图象在一次函数y2=kx+4的图象上方 部分所对应的横坐标的取值范围,结合图象可知即x >1.
一题多解:把P(1,3)分别代入y1=x+b和y2=kx+4中, ∴3=1+b,即b=2,∴y1=x+2;3=k+4,即k=-1,∴y2= x+4,∴x+2>-x+4,解得x>1.
考点2 一次函数表达式的确定 1. 利用坐标确定一次函数表达式常用待定 系数法.(2011版新课标新增内容)
2. 确定一次函数表达式的一般步骤:
(1)设出一次函数表达式y=kx+b; (2)将x,y的对应值代入表达式y=kx+b, 得到含有待定系数的方程或方程组; (3)求待定系数k,b的值; (4)将所求待定系数的值代入所设的函数 表达式中即可得函数表达式.
(1)不等式kx+b>0的解集为一次函数y=kx+b图 象位于x轴上方部分对应x的取值范围;
(2)不等式kx+b<0的解集为一次函数y=kx+b图 象位于x轴下方部分对应x的取值范围;
(3)设点C的坐标为(m,n),那么不等式
kx+b≤k1x+b1的解集是 15__x__m __.
考点4 一次函数的实际应用 1. 利用一次函数的性质解决实际问题的步骤:
拓展 已知正比例函数y=kx(k≠0)的函数值y随x的增 大而减小,则一次函数y=x+k的图象大致是 ( B)
【解析】∵正比例函数y=kx(k≠0)的函数值y随x增 大而减小,∴k<0,∴一次函数y=x+k的图象经过 第一、三、四象限.故选B.
中考数学 第一部分 教材知识梳理 第三单元 第11课时 一次函数及其应用课件
最新中小学教案、试题、试卷、课 件
6
考点3
一次函数与方程、不等式的关系
1. 一次函数与方程的关系 (1)一次函数的表达式就是一个二元一次方程; (2)点14 B __________ 的横坐标 是方程kx+b=0的解; (3)点C的坐标(x,y)中的x,y的
ì y = kx + b ï 值是方程组 í 的解. ï î y = k1 x + b1
最新中小学教案、试题、试卷、课 件 15
【解析】∵函数的图象 y=kx+b与y轴交点的纵坐标为
-5,且当x=1时,y=2,∴函数的图象过点 (0,
ì ì ïb =-5 k =7 ï \ , -5),(1,2), í k + b = 2 解得 í ,故此函 ï î ï î b =-5
数的表达式为:y=7x-5.
最新中小学教案、试题、试卷、课 件
8
考点4
一次函数的实际应用
1. 利用一次函数的性质解决实际问题的步骤:
(1)设定实际问题中的变量; (2)建立一次函数关系式; (3)确定自变量的取值范围; (4)利用函数的性质解决问题.
最新中小学教案、试题、试卷、课 件
9
2. 一次函数的应用有如下常用题型: (1)根据实际问题中给出的数据列出相应的 函数表达式,解决实际问题;
第一部分
教材知识梳理
第三单元 函数
第11课时 一次函数及其应用
最新中小学教案、试题、试卷、课 件
1
中考考点清单
考点1 一次函数及其图象性质(高频考点) 考点2 考点3 一次函数表达式的确定 一次函数与方程、不等式的关系
考点4
一次函数的实际应用
最新中小学教案、试题、试卷、课 件
【中考数学考点复习】第二节一次函数的图象与性质课件
拓展训练
8.已知正比例函数 y=kx(k≠0)的图象过点(2,3),把正比例函数 y= k x (k ≠0) 的 图 象 平 移 , 使 它 过 点(1 , - 1) , 则 平 移 后 的 函 数 图 象 大 致 是 ( D)
一 平移前表
次
达式
函
平移方向(m>0)
平移后表达式
数
向左平移m个单位长度 y=k(x m )+b
图
直线
向右平移m个单位长度 y=k(x m )+b
象
的 y=kx+b 向上平移m个单位长度 y=kx+b m
平
(k≠0)
移
向下平移m个单位长度 y=kx+b m
口诀
横坐标左加 右减
等号右边整 体上加下减
4.一次函数 y=(2m-1)x+2 的值随 x 值的增大而增大,则常数 m 的取 1
值范围为 m>2 . 5.已知一次函数 y=(k-3)x+1 的图象经过第一、二、四象限,则 k 的 取值范围是 k<3 .
6.在平面直角坐标系中,已知一次函数 y=2x+1 的图象经过 P1(x1,y1), P2(x2,y2)两点,若 x1<x2,则 y1 < y2.
.
第 12 题图
一次函数表达式的确定
13.(2021 甘肃省卷)将直线 y=5x 向下平移 2 个单位长度,所得直线的表
达式为( A )
A.y=5x-2
B.y=5x+2
C.y=5(x+2)
D.y=5(x-2)
14.已知一次函数y=kx+b的图象经过M(0,2),N(1,3)两点,则k,b
第10课时 一次函数的图象及其性质 课件 2025年中考数学一轮总复习
么过原点O且将△AOB的面积平分的直
线l2的解析式为( D )
D
A. y= x
B. y=x
C. y= x
D. y=2x
(2)如图2,已知一条直线经过点A
(0,2),点B(1,0),将这条直线
向左平移与x轴、y轴分别交于点C,D.
若DB=DC,则直线CD的函数解析式
y= x-
考点三 一次函数与方程(组)、不
等式
例3 (1)(2024·广东)已知不等式
kx+b<0的解集是x<2,则一次函数y
=kx+b的图象大致是( B )
B
A B C D
一、
二、三
一、
三
一、
三、四Βιβλιοθήκη 一、 二、四
二、
四
二、
三、
四
增大
减小
(1)k的符号决定直线的增减性;
的大小决定直线的倾斜程度,即 越
大,直线与x轴相交的锐角的度数越大
(直线越 ); 越小,直线与x
轴相交的锐角的度数越小(直线越 ).(2)b(称为截距)表示直线y=kx+
图象
关系
一次函数y=kx+b的图象可由正
比例函数y=kx的图象平移得到.
当b>0时,向上平移b个单位长
度;当b<0时,向下平移 个单
位长度
(0,b)
(- ,0)
知识点2 一次函数y=kx+b(k≠0)的
图象与性质
函
数
y=kx+b(k,b为常数,且k≠0)
k>0
k<0
b>0
b=0
b<
0
b>0
b=0
为 ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
精选教案
可编辑
第二节 一次函数的图象及性质
1.(2016南宁中考)已知正比例函数y=3x的图象经过点(1,m),则m的值为( B )
A.31 B.3 C.-31 D
.-3
2.(2016郴州中考)当b<0时,一次函数y=x+b的图象大致是( B )
,A) ,B)
精选教案
可编辑
,C) ,D)
3.(2016呼和浩特中考)已知一次函数y=kx+b-x的图象与x轴的正半轴相交,且函数值y随自变量x的
增大而增大,则k,b的取值情况为( A )
A.k>1,b<0 B
.k>1,b>0
C.k>0,b>0 D
.k>0,b<0
4.(2016广州中考)若一次函数y=ax+b的图象经过第一、二、四象限,则下列不等式中总是成立的是( C )
A.ab>0 B
.a-b>0
C.a2+b>0 D
.a+b>0
5.(2016陕西中考)已知一次函数y=kx+5和y=k′x+7,假设k>0且k′<0,则这两个一次函数图象的交
点在( A )
A.第一象限 B
.第二象限
C.第三象限 D
.第四象限
6.(2016雅安中考)若式子+(k-1)0有意义,则一次函数y=(1-k)x+k-1的图象可能是( C )
精选教案
可编辑
,A) ,B)
,C) ,D)
7.(2016枣庄中考)若关于x的一元二次方程x2-2x+kb+1=0有两个不相等的实数根,则一次函数y=
kx+b的图象可能是( B )
精选教案
可编辑
,A) ,B)
,C) ,D)
8.(2016天津中考)若一次函数y=-2x+b(b为常数)的图象经过第二、三、四象限,则b的值可以是__-
1__.(写出一个即可)
9.(2016永州中考)已知一次函数y=kx+2k+3的图象与y轴的交点在y轴的正半轴上,且函数值y随x
的增大而减小,则k所能取到的整数值为__-1__.
10.(2016娄底中考)将直线y=2x+1向下平移3个单位长度所得直线的表达式是__y=2x-2__.
11.(2016巴中中考)已知二元一次方程组x+2y=-2x-y=-5,的解为y=1,x=-4,则在同一平面直角坐标系中,直线
l1:y=x+5与直线l2:y=-21x-1的交点坐标为__(-4,1)__.
精选教案
可编辑
12.(2016绍兴中考)根据卫生防疫部门要求,游泳池必须定期换水、清洗.某游泳池周五早上8∶00打开
排水孔开始排水,排水孔的排水速度保持不变,期间因清洗游泳池需要暂停排水,游泳池的水在11∶30全部排
完.游泳池内的水量Q(m3)和开始排水后的时间t(h)之间的函数图象如图所示,根据图象解答下列问题:
(1)暂停排水需要多少时间?排水孔的排水速度是多少?
(2)当2≤t≤3.5时,求Q关于t的函数表达式.
解:(1)暂停排水时间为30 min(半小时),排水孔的排水速度为300 m3/h;(2)设当2≤t≤3.5时,Q关于t
的函数表达式为Q=kt+b,把(2,450),(3.5,0)代入得0=3.5k+b.450=2k+b,解得k=-300,b=1 050,∴函数表达式为Q=-
300t+1 050.
精选教案
可编辑
13.(2016吉林中考)甲、乙两人利用不同的交通工具,沿同一路线从A地出发前往B地,甲出发1 h后,
乙出发.设甲与A地相距y甲(km),乙与A地相距y乙(km),甲离开A地的时间为x(h).y甲,y乙与x之间的函
数图象如图所示.
(1)甲的速度是__60__km/h;
(2)当1≤x≤5时,求y乙关于x的函数表达式;
(3)当乙与A地相距240 km时,甲与A地相距__220__km.
解:(2)解法一:当1≤x≤5时,设y乙关于x的函数表达式为y乙=kx+b.∵点(1,0),(5,360)在其图象
上,∴360=5k+b,0=k+b,解得b=-90.k=90,∴y乙关于x的函数表达式为y乙=90x-90(1≤x≤5);解法二:由图象得y乙=
精选教案
可编辑
90,∴y乙=90(x-1)=90x-90(1≤x≤5).
14.(2016北京中考)如图,在平面直角坐标系xOy中,过点A(-6,0)的直线l1与直线l2:y=2x相交于
点B(m,4).
(1)求直线l1的表达式;
(2)过动点P(n,0)且垂于x轴的直线与l1,l2的交点分别为C,D,当点C位于点D上方时,写出n的取值
范围.
解:(1)由题可知,点B(m,4)在直线l2:y=2x上,∴4=2m,m=2,∴B(2,4).∵l1过点A(-6,0),
B(2,4),2k+b=4,-6k+b=0,解得b=3,,∴y=21x+3;(2)由题可知:C(n,21n+3),D(n,2n),∵点C在点D上方,∴
2
1
n+3>2n,解得n<2,∴当n<2时,点C在点D上方.
15.(2016宜昌中考)如图,直线y=x+与两坐标分别交于A,B两点.
(1)求∠ABO的度数;
(2)过点A的直线l交x轴正半轴于点C,AB=AC,求直线l的函数表达式.
精选教案
可编辑
解:(1)对于y=x+,令x=0,则y=,∴A的坐标为(0,),∴OA=,令y=0,则x=-1,∴OB=1.在
Rt△AOB中,tan
∠ABO=OBOA=,∴∠ABO=60°;(2)在△ABC中,AB=AC,又AO⊥BC,∴BO=CO,∴C点的
坐标为(1,0),设直线l的函数表达式为y=kx+b(k,b为常数),依题意有0=k+b.3=b,解得,3,∴直线l的函数表达
式为y=-x+.
16.(2016丽水中考)2016年3月27日“丽水半程马拉松竞赛”在莲都举行,某运动员从起点万地广场西
门出发,途经紫金大桥,沿比赛路线跑回终点万地广场西门.设该运动员离开起点的路程s(km)与跑步时间
t(min)之间的函数关系如图所示,其中从起点到紫金大桥的平均速度是0.3 km/min,用时35 min,根据图象提
供的信息,解答下列问题:
(1)求图中a的值;
(2)组委会在距离起点2.1 km处设立一个拍摄点C,该运动员从第一次经过点C到第二次经过点C所用的时
间为68 min.
①求AB所在直线的函数表达式;
②该运动员跑完赛程用时多少分钟?
精选教案
可编辑
解:(1)∵从起点到紫金大桥的平均速度是0.3 km/min,用时35 min,∴a=0.3×35=10.5;(2)①∵直线OA
经过点O(0,0),A(35,10.5),∴直线OA的函数表达式是s=0.3t(0≤t≤35),∴当s=2.1时,0.3t=2.1,解得
t=7.∵该运动员从起点到第二次过点C所用的时间为68 min,∴该运动员从第一次过点C到第二次过点C用的
时间是7+68=75(min),∴AB所在直线经过(35,10.5),(75,2.1)两点.设AB所在直线的函数表达式为s=kt
+b,则75k+b=2.1,35k+b=10.5,解得b=17.85.k=-0.21,∴AB所在直线的函数表达式是s=-0.21t+17.85;②∵该运动员跑完
赛程所用的时间即为直线AB与横轴交点的横坐标的值,∴当s=0时,-0.21t+17.85=0,解得t=85,∴该运
动员跑完赛程用时85 min.
