广东省肇庆第四中学高二数学上学期第二次月考试题 文(无答案)
广东省肇庆第四中学2014-2015学年高一上学期第一次月考数学试卷(无答案)

一、选择题(共10题,每小题5分,共50分) 1.下列四个关系式中,正确的是 ( )A.{}a ∈φB.{}a a ∉C.{}{}b a a ,∈D.{}b a a ,∈2.若集合}3,2,1,0{=A ,}4,2,1{=B ,则集合=B A ( )A .{0,1,2,3,4}B .{1,2,3,4}C .{1,2}D .{0}3.若集合}12|{<≤-=x x A ,}20|{≤<=x x B ,则=B A ( )A .}22|{≤≤-x xB .}02|{<≤-x xC .}10|{<<x xD . }21|{≤<x x4.若集合}{5,3,2,0=A ,则集合A 的真子集共有 ( )A.7个B.8个C.15个D.16个5.下列函数中哪一个与函数x y =是同一个函数( ) A.2)(x y = B.xx y 2= C.33x y = D.2x y = 6.方程组⎩⎨⎧-=-=+11y x y x 的解集是 ( )A {}1,0==y xB {}1,0C {})1,0(D {}(,)|01x y x y ==或7.设函数x a y )12(-=在R 上是增函数,则有( )A .21≥aB .21≤aC .21>aD .21<a 8.已知奇函数)(x f y =在区间[-b ,-a ]上为减函数,且在此区间上,)(x f y =最小值为2, 则函数)(x f y =在区间[a ,b ]上是( )A .增函数且最大值为2B .增函数且最小值为-2C .减函数且最大值为-2D .减函数且最小值为29.函数x x x f 2)(2-=的单调增区间是 ( )A .),(+∞-∞B .(]1,∞-C .[)+∞,1D .(]0,∞-10.如果函数)(x f =2)1(22+-+x a x 在区间(-∞,4)上是减函数,则实数a 的取值范围是( )A .a ≥-3 B. a ≤-3 C. a ≤5 D.a ≥3 二、填空题(共4题,每小题5分,共20分)11.函数xx y 1+=的定义域为________. 12.函数12)(2++=x x x f 在区间]2,2[-上的值域是 .13.已知函数⎩⎨⎧< ≥ =00)(2x x x x x f ,))2((-f f = . 14.已知()5412-+=-x x x f ,则()x f =______________________.三、解答题,请写出详细过程(共6题,共80分)15.(14分)已知2)(,11)(2+=+=x x g x x f (1)求)]2([),2(),2(g f g f ;(2)求)]([x g f 的解析式.}{}{}{).()(),()(),()(,,11,15,35)12.(16B A C B A C B C A C B C A C B C A C x x B x x A x x U U U U U U U U U ⋃⋂⋃⋂<≤-=-<≤-=≤≤-=,求,已知,全集分17.(12分)已知集合{}12,3,1-=m A ,集合}{2,3m B =,若A B ⊆,求实数m 的值.18.(14分) 已知函数xkx x f 1)(-= ,且1)1(=f . (1)求实数k 的值及函数的定义域;(2)判断函数在()+∞,0上的单调性,并用定义加以证明.19.(14分)已知函数()x f 是定义在R 上的偶函数,当x ≥0时,x x x f 4)(2-= (1)求)1(-f 的值;(2)当x <0时,求)(x f 的解析式.20.(14分)函数12)(2--=ax x x f ,[]2,0∈x(1)若1=a ,写出函数)(x f 在[]2,0上的单调区间(不必证明)(2)求函数)(x f 在[]2,0上的最值.。
2024-2025学年广东省广州四中高二(上)月考数学试卷(10月份)(含答案)

2024-2025学年广东省广州四中高二(上)月考数学试卷(10月份)一、单选题:本题共8小题,每小题5分,共40分。
在每小题给出的选项中,只有一项是符合题目要求的。
1.从分别写有1,2,3,4,5,6的六张卡片中,无放回地随机抽取两张,则抽到的两张卡片上的数字之积是5的倍数的概率为( )A. 13B. 25C. 35D. 152.如图,空间四边形OABC 中,OA =a ,OB =b ,OC =c ,点M 在OA 上,且OM =23OA ,点N 为BC 中点,则MN 等于( )A. 12a +12b−12c B. −23a +12b +12c C. 23a +23b−12c D. 23a +23b−12c3.在正方体ABCD−A 1B 1C 1D 1中,E 为线段A 1B 1的中点,则异面直线D 1E 与BC 1所成角的余弦值为( )A.55B.105C.155 D.2 554.若直线l 1:y =kx−k +2与直线l 2关于点(2,1)对称,则直线l 2恒过定点( )A. (3,1)B. (3,0)C. (0,1)D. (2,1)5.已知事件A 、B ,且P(A)=0.6,P(B)=0.7,如果A 与B 互斥,那么P(AB)=p 1;如果A 与B 相互独立,那么P(A +−B )=p 2,则p 1,p 2分别为( )A. p 1=0,p 2=0.9 B. p 1=0.42,p 2=0.9C. p 1=0,p 2=0.72D. p 1=0.42,p 2=0.456.在三棱锥P−ABC 中,PA ,PB ,PC 两两垂直,且PA =1,PB =2,PC =3,三角形ABC 重心为G ,则点P 到直线AG 的距离为( )A. 23B.53 C. 21717 D.221177.已知实数x ,y 满足y =15x−35,且−2≤x ≤3,则y−2x +1的取值范围( )A. (−∞,−12]∪[3,+∞) B. [−12,3]C. (−∞,−1]∪[3,+∞)D. [−1,3]8.直线l 1:x +(m +1)y−2m−2=0与直线l 2:(m +1)x−y−2m−2=0相交于点P ,对任意实数m ,直线l 1,l 2分别恒过定点A ,B ,则|PA|+|PB|的最大值为( )A. 4B. 8C. 22D. 42二、多选题:本题共3小题,共18分。
广东省肇庆市第四中学高二下学期第一次月考数学(文)试题

一、选择题(本大题共12小题,每小题5分,共60分)1、复数31ii--等于( ). A .i 21+ B.12i - C.2i + D.2i -2、在复平面内,复数12z i =-+对应的点位于 ( )A .第一象限B .第二象限C .第三象限D .第四象限3、已知函数63)(23-+=x ax x f ,若4)1('=-f ,则实数a 的值为( ) A .319B .316C .313D .310 4、一物体作直线运动,其运动方程为t t t s 2)(2+-=,则t =1时其速度为( )A. 4B. -1C. 1D. 05、000(3)()lim 1x f x x f x x∆→+∆-=∆,则0()f x '等于( )A.1B.0C.3D.136、已知回归直线的斜率的估计值是1.23,样本点的中心为(4,5),则回归直线的方程是( )A. 1.234y x =+B. 1.235y x =+C. 1.230.08y x =+D. 0.08 1.23y x =+ 7 、若i x x x )23()1(22+++-是纯虚数,则实数x =( )A. -1B. 1C. -1或1D. 08、用反证法证明命题“三角形的内角至少有一个不大于60︒”时,应该先( )A. 假设三内角都不大于60︒B. 假设三内角都大于60︒C. 假设三内角至多有一个大于60︒D. 假设三内角至多有两个大于60︒9、函数)(x f 的定义域为开区间),(b a ,导函数)(x f '在),(b a 内 的图象如图所示,则函数)(x f 在开区间),(b a 内有极小值点( )A.1个B.2个C.3个D. 4个10.若函数4)(23+-=ax x x f 在(0,2)内单调递减,则实数a 的取值范围为A .[)+∞,3B .{3}C .(]3,∞-D .(0,3)11、已知函数f (x )=32261x x m ++-(m 为常数)在[22]-,上有最大值2,则此函数在[22]-,上的最小值为( ) A.38- B.30- C.6- D.12-12、已知数列{n a }的通项公式2)1(1+=n a n ,记123()(1)(1)(1)(1)n f n aaa a =---⋅⋅⋅-,通过计算)1(f ,)2(f ,)3(f ,)4(f 的值,猜想)(n f 的值为 A.2)1(12+-n n B. )1(2++n n n C. 12++n n D.)1(22++n n 二、填空题(本大题共4小题,每小题5分,共20分) 13、复数()2i 1+i 的实部是 .14、曲线x x y 43-=在点(1,3)- 处的切线倾斜角为____________15、若复数 z 满足(1+i )=1z (i 是虚数单位),则其共轭复数z =__________________ .16、经过圆222r y x =+上一点M (0x ,0y )的切线方程为200r y y x x =+. 类比上述性质,可以得到椭圆12222=+b y a x 类似的性质为:经过椭圆12222=+by a x 上一点P(0x ,0y )的切线方程为 ▲ .17、(10分)求函数f (x )=2x 3-6x 2+7的极值和单调区间.18.(本小题满分12分)求当a 为何实数时,复数i a a a a z )12()32(22-++--=满足:(Ⅰ)z 为实数; (Ⅱ)z 为纯虚数;(Ⅲ)z 位于第四象限。
广东省肇庆四中高二数学上学期第二次月考试卷(含解析)

2015-2016学年广东省肇庆四中高二(上)第二次月考数学试卷一、选择题(共12小题,每小题5分,满分60分)1.若直线l经过原点和点A(﹣2,﹣2),则它的斜率为()A.﹣1 B.1 C.1或﹣1 D.02.已知直线l1经过两点(﹣1,﹣2)、(﹣1,4),直线l2经过两点(2,1)、(x,6),且l1∥l2,则x=()A.2 B.﹣2 C.4 D.13.过点(﹣1,3)且平行于直线x﹣2y+3=0的直线方程为()A.x﹣2y+7=0 B.2x+y﹣1=0 C.x﹣2y﹣5=0 D.2x+y﹣5=04.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.108cm3B.100cm3C.92cm3D.84cm35.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊥α,n∥α,则m⊥n②若α∥β,β∥γ,m⊥α,则m⊥γ③若m∥α,n∥α,则m∥n④若α⊥γ,β⊥γ,则α∥β其中正确命题的序号是()A.①和②B.②和③C.③和④D.①和④6.圆(x+2)2+y2=5关于y轴对称的圆的方程为()A.x2+(y+2)2=5 B.x2+(y﹣2)2=5 C.(x﹣2)2+y2=5 D.(x﹣2)2+(y﹣2)2=57.经过两圆x2+y2=9和(x+4)2+(y+3)2=8的交点的直线方程为()A.8x+6y+13=0 B.6x﹣8y+13=0 C.4x+3y+13=0 D.3x+4y+26=08.不论k为何实数,直线(2k﹣1)x﹣(k+3)y﹣(k﹣11)=0恒通过一个定点,这个定点的坐标是()A.(5,2)B.(2,3)C.(5,9)D.(﹣,3)9.已知直线l1:x+my+6=0,l2:(m﹣2)x+3y+2m=0,若l1∥l2,则实数m的值是()A.3 B.﹣1,3 C.﹣1 D.﹣310.若直线ax+by=1与圆x2+y2=1有两个公共点,则点P(a,b)与圆的位置关系是()A.在圆上B.在圆外C.在圆内D.以上皆有可能11.若直线x﹣y=2被圆(x﹣a)2+y2=4所截得的弦长为,则实数a的值为()A.﹣1或B.1或3 C.﹣2或6 D.0或412.已知直线l:y=x+m与曲线y=有两个公共点,则实数m的取值范围是()A.(﹣2,2)B.(﹣1,1)C.[1,)D.(﹣,)二、填空题(共4小题,每小题5分,满分20分)13.如果点P在z轴上,且满足|PO|=1(O是坐标原点),则点P到点A(1,1,1)的距离是.14.已知斜率为且与两坐标轴围成的三角形的面积为4的直线方程是.15.当动点P在圆x2+y2=2上运动时,它与定点A(3,1)连线的中点Q的轨迹方程是.16.在平面直角坐标系xOy中,已知圆x2+y2=4上有且仅有四个点到直线12x﹣5y+c=0的距离为1,则实数c的取值范围是.三、解答题(共6小题,满分70分)17.一个长、宽、高分别是80cm、60cm、55cm的水槽中有水200000cm3,现放入一个直径为50cm的木球,且木球的三分之二在水中,三分之一在水上,那么水是否会从水槽中流出?18.在平面直角坐标系中,有三个点的坐标分别是A(﹣4,0),B(0,6),C(1,2).(1)证明:A,B,C三点不共线;(2)求过A,B的中点且与直线x+y﹣2=0平行的直线方程;(3)求过C且与AB所在的直线垂直的直线方程.19.已知圆心为C的圆经过点 A(1,1)和B(2,﹣2),且圆心C在直线L:x﹣y+1=0上,求圆C的标准方程.20.如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.(1)证明:PE⊥DE;(2)如果PA=2,求异面直线AE与PD所成的角的大小.21.如图,正方体ABCD﹣A1B1C1D1的棱长为a,E为DD1的中点.(1)求证:BD1∥平面EAC;(2)求点D1到平面EAC的距离.22.已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的上方(1)求圆C的方程;(2)设过点P(1,1)的直线l1被圆C截得的弦长等于2,求直线l1的方程;(3)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.2015-2016学年广东省肇庆四中高二(上)第二次月考数学试卷参考答案与试题解析一、选择题(共12小题,每小题5分,满分60分)1.若直线l经过原点和点A(﹣2,﹣2),则它的斜率为()A.﹣1 B.1 C.1或﹣1 D.0【考点】斜率的计算公式.【专题】计算题.【分析】把原点坐标(0,0)和点A的坐标(﹣2,﹣2)一起代入两点表示的斜率公式k=,即可得到结果.【解答】解:根据两点表示的斜率公式得:k===1,故选 B.【点评】本题考查用两点表示的斜率公式得应用,注意公式中各量所代表的意义,体现了代入的思想.2.已知直线l1经过两点(﹣1,﹣2)、(﹣1,4),直线l2经过两点(2,1)、(x,6),且l1∥l2,则x=()A.2 B.﹣2 C.4 D.1【考点】两条直线平行与倾斜角、斜率的关系.【分析】根据条件可知直线l1的斜率不存在,然后根据两直线平行的得出x的值.【解答】解:∵直线l1经过两点(﹣1,﹣2)、(﹣1,4),∴直线l1的斜率不存在∵l1∥l2 直线l2经过两点(2,1)、(x,6),∴x=2故选:A.【点评】本题考查了两直线平行的条件,同时考查斜率公式,属于基础题.3.过点(﹣1,3)且平行于直线x﹣2y+3=0的直线方程为()A.x﹣2y+7=0 B.2x+y﹣1=0 C.x﹣2y﹣5=0 D.2x+y﹣5=0【考点】直线的一般式方程;两条直线平行的判定.【专题】计算题.【分析】由题意可先设所求的直线方程为x﹣2y+c=0再由直线过点(﹣1,3),代入可求c 的值,进而可求直线的方程【解答】解:由题意可设所求的直线方程为x﹣2y+c=0∵过点(﹣1,3)代入可得﹣1﹣6+c=0 则c=7∴x﹣2y+7=0故选A.【点评】本题主要考查了直线方程的求解,解决本题的关键根据直线平行的条件设出所求的直线方程x﹣2y+c=0.4.已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.108cm3B.100cm3C.92cm3D.84cm3【考点】由三视图求面积、体积.【专题】立体几何.【分析】由三视图可知:该几何体是一个棱长分别为6,6,3,砍去一个三条侧棱长分别为4,4,3的一个三棱锥(长方体的一个角).据此即可得出体积.【解答】解:由三视图可知:该几何体是一个棱长分别为6,6,3,砍去一个三条侧棱长分别为4,4,3的一个三棱锥(长方体的一个角).∴该几何体的体积V=6×6×3﹣=100.故选B.【点评】由三视图正确恢复原几何体是解题的关键.5.设m,n是两条不同的直线,α,β,γ是三个不同的平面,给出下列四个命题:①若m⊥α,n∥α,则m⊥n②若α∥β,β∥γ,m⊥α,则m⊥γ③若m∥α,n∥α,则m∥n④若α⊥γ,β⊥γ,则α∥β其中正确命题的序号是()A.①和②B.②和③C.③和④D.①和④【考点】空间中直线与平面之间的位置关系;命题的真假判断与应用;空间中直线与直线之间的位置关系;平面与平面之间的位置关系.【专题】证明题;压轴题;空间位置关系与距离.【分析】根据线面平行性质定理,结合线面垂直的定义,可得①是真命题;根据面面平行的性质结合线面垂直的性质,可得②是真命题;在正方体中举出反例,可得平行于同一个平面的两条直线不一定平行,垂直于同一个平面和两个平面也不一定平行,可得③④不正确.由此可得本题的答案.【解答】解:对于①,因为n∥α,所以经过n作平面β,使β∩α=l,可得n∥l,又因为m⊥α,l⊂α,所以m⊥l,结合n∥l得m⊥n.由此可得①是真命题;对于②,因为α∥β且β∥γ,所以α∥γ,结合m⊥α,可得m⊥γ,故②是真命题;对于③,设直线m、n是位于正方体上底面所在平面内的相交直线,而平面α是正方体下底面所在的平面,则有m∥α且n∥α成立,但不能推出m∥n,故③不正确;对于④,设平面α、β、γ是位于正方体经过同一个顶点的三个面,则有α⊥γ且β⊥γ,但是α⊥β,推不出α∥β,故④不正确.综上所述,其中正确命题的序号是①和②故选:A【点评】本题给出关于空间线面位置关系的命题,要我们找出其中的真命题,着重考查了线面平行、面面平行的性质和线面垂直、面面垂直的判定与性质等知识,属于中档题.6.圆(x+2)2+y2=5关于y轴对称的圆的方程为()A.x2+(y+2)2=5 B.x2+(y﹣2)2=5 C.(x﹣2)2+y2=5 D.(x﹣2)2+(y﹣2)2=5【考点】关于点、直线对称的圆的方程.【专题】计算题;方程思想;综合法;直线与圆.【分析】求出关于y轴对称的圆的圆心坐标为(2,0),半径还是2,从而求得所求的圆的方程.【解答】解:已知圆关于y轴对称的圆的圆心坐标为(2,0),半径不变,还是2,故对称圆的方程为(x﹣2)2+y2=5,故选:C.【点评】本题主要考查求圆的标准方程,求出关于y轴对称的圆的圆心坐标为(2,0),是解题的关键,属于基础题.7.经过两圆x2+y2=9和(x+4)2+(y+3)2=8的交点的直线方程为()A.8x+6y+13=0 B.6x﹣8y+13=0 C.4x+3y+13=0 D.3x+4y+26=0【考点】圆系方程.【专题】计算题;函数思想;直线与圆.【分析】利用圆系方程,求解即可.【解答】解:联立x2+y2=9和(x+4)2+(y+3)2=8,作差可得:8x+6y+26=0,即6x﹣8y+13=0.故选:B.【点评】本题考查圆系方程的应用,考查计算能力.8.不论k为何实数,直线(2k﹣1)x﹣(k+3)y﹣(k﹣11)=0恒通过一个定点,这个定点的坐标是()A.(5,2)B.(2,3)C.(5,9)D.(﹣,3)【考点】恒过定点的直线.【专题】计算题.【分析】直线方程即 k(2x+y﹣1)+(﹣x+3y+11)=0,一定经过2x﹣y﹣1=0和﹣x﹣3y+11=0 的交点,联立方程组可求定点的坐标.【解答】解:直线(2k﹣1)x﹣(k+3)y﹣(k﹣11)=0即 k(2x﹣y﹣1)+(﹣x﹣3y+11)=0,根据k的任意性可得,解得,∴不论k取什么实数时,直线(2k﹣1)x+(k+3)y﹣(k﹣11)=0都经过一个定点(2,3).故选B【点评】本题考查经过两直线交点的直线系方程形式,直线 k(ax+by+c)+(mx+ny+p)=0 表示过ax+by+c=0和mx+ny+p=0的交点的一组相交直线,但不包括ax+by+c=0这一条.9.已知直线l1:x+my+6=0,l2:(m﹣2)x+3y+2m=0,若l1∥l2,则实数m的值是()A.3 B.﹣1,3 C.﹣1 D.﹣3【考点】直线的一般式方程与直线的平行关系.【专题】直线与圆.【分析】直接利用两直线平行对应的系数关系列式求得m的值.【解答】解:∵l1:x+my+6=0,l2:(m﹣2)x+3y+2m=0,若l1∥l2,则,解得:m=﹣1.故选:C.【点评】本题考查了直线的一般式方程与直线平行的关系,关键是对两直线系数所满足关系的记忆,是基础题.10.若直线ax+by=1与圆x2+y2=1有两个公共点,则点P(a,b)与圆的位置关系是()A.在圆上B.在圆外C.在圆内D.以上皆有可能【考点】点与圆的位置关系.【专题】直线与圆.【分析】由于直线ax+by=1与圆x2+y2=1有两个公共点,可得圆心(0,0)到直线ax+by=1的距离d<r.利用点到直线的距离公式和点与圆的位置关系判定即可得出.【解答】解:∵直线ax+by=1与圆x2+y2=1有两个公共点,∴圆心(0,0)到直线ax+by=1的距离d<r.∴,化为.∴点P(a,b)在圆的外部.故选:B.【点评】本题考查了直线与圆的位置关系、点到直线的距离公式和点与圆的位置关系,属于中档题.11.若直线x﹣y=2被圆(x﹣a)2+y2=4所截得的弦长为,则实数a的值为()A.﹣1或B.1或3 C.﹣2或6 D.0或4【考点】直线与圆相交的性质.【专题】计算题.【分析】由圆的方程,得到圆心与半径,再求得圆心到直线的距离,由求解.【解答】解:∵圆(x﹣a)2+y2=4∴圆心为:(a,0),半径为:2圆心到直线的距离为:∵解得a=4,或a=0故选D.【点评】本题主要考查直与圆的位置关系及其方程的应用,是常考题型,属中档题.12.已知直线l:y=x+m与曲线y=有两个公共点,则实数m的取值范围是()A.(﹣2,2)B.(﹣1,1)C.[1,)D.(﹣,)【考点】函数的零点与方程根的关系.【专题】函数的性质及应用.【分析】画出图象,当直线l经过点A,C时,求出m的值;当直线l与曲线相切时,求出m.即可.【解答】解:画出图象,当直线l经过点A,C时,m=1,此时直线l与曲线y=有两个公共点;当直线l与曲线相切时,m=.因此当时,直线l:y=x+m与曲线y=有两个公共点.故选C.【点评】正确求出直线与切线相切时的m的值及其数形结合等是解题的关键.二、填空题(共4小题,每小题5分,满分20分)13.如果点P在z轴上,且满足|PO|=1(O是坐标原点),则点P到点A(1,1,1)的距离是或.【考点】空间两点间的距离公式.【专题】空间位置关系与距离.【分析】设P(0,0,z),由于|OP|=1,可得,即|z|=1,解得z.再利用两点间的距离公式即可得出|PA|.【解答】解:设P(0,0,z),∵|OP|=1,∴,即|z|=1,解得z=±1.∴|PA|=或.故答案为:或.【点评】本题考查了空间中的两点间的距离公式,属于基础题.14.已知斜率为且与两坐标轴围成的三角形的面积为4的直线方程是y=±2.【考点】直线的截距式方程.【专题】直线与圆.【分析】设直线的方程为y=+m,分别令x=0,y=0,可得A(0,m),B(﹣2m,0).可得=4,解出即可.【解答】解:设直线的方程为y=+m,分别令x=0,y=0,可得A(0,m),B(﹣2m,0).∵=4,解得m=±2.∴直线方程为:y=±2,故答案为:y=±2.【点评】本题考查了直线的方程及其应用、三角形面积计算公式,考查了推理能力与计算能力,属于基础题.15.当动点P在圆x2+y2=2上运动时,它与定点A(3,1)连线的中点Q的轨迹方程是(2x ﹣3)2+(2y﹣1)2=2 .【考点】轨迹方程.【专题】计算题;转化思想;综合法;直线与圆.【分析】根据已知,设出中点Q的坐标(x,y),根据中点坐标公式求出点P的坐标,根据点P在圆x2+y2=2上,代入圆的方程即可求得中点Q的轨迹方程.【解答】解:设中点Q(x,y),则动点P(2x﹣3,2y﹣1),∵P在圆x2+y2=2上,∴(2x﹣3)2+(2y﹣1)2=2,故答案为:(2x﹣3)2+(2y﹣1)2=2.【点评】此题是个基础题.考查代入法求轨迹方程和中点坐标公式,体现了数形结合的思想以及分析解决问题的能力.16.在平面直角坐标系xOy中,已知圆x2+y2=4上有且仅有四个点到直线12x﹣5y+c=0的距离为1,则实数c的取值范围是(﹣13,13).【考点】直线与圆的位置关系.【专题】直线与圆.【分析】求出圆心,求出半径,圆心到直线的距离小于1即可.【解答】解:圆半径为2,圆心(0,0)到直线12x﹣5y+c=0的距离小于1,即,c的取值范围是(﹣13,13).【点评】考查圆与直线的位置关系.(圆心到直线的距离小于1,此时4个,等于3个,等于1,大于1是2个.)是有难度的基础题.三、解答题(共6小题,满分70分)17.一个长、宽、高分别是80cm、60cm、55cm的水槽中有水200000cm3,现放入一个直径为50cm的木球,且木球的三分之二在水中,三分之一在水上,那么水是否会从水槽中流出?【考点】函数模型的选择与应用.【专题】应用题.【分析】根据长方体的体积公式求出水槽的体积,再根据球的体积公式求出木球的体积,结合题意,根据水槽中水的体积与木球在水中部分的体积之和与水槽的体积比较,即可确定答案.【解答】解:∵水槽是一个长、宽、高分别是80cm、60cm、55cm的长方体,根据长方体的体积公式可得,水槽的容积为V水槽=80×60×55=264000(cm3),∵木球的三分之二在水中,∴木球在水中部分的体积为(cm3),又∵水槽中有水200000cm3,∴水槽中水的体积与木球在水中部分的体积之和为(cm3),∴V<V水槽,故水不会从水槽中流出.【点评】本题考查了长方体的体积公式,考查了球体的体积公式,解题的关键是抓住水槽中水的体积与木球在水中部分的体积之和与水槽的体积之间的关系.属于中档题.18.在平面直角坐标系中,有三个点的坐标分别是A(﹣4,0),B(0,6),C(1,2).(1)证明:A,B,C三点不共线;(2)求过A,B的中点且与直线x+y﹣2=0平行的直线方程;(3)求过C且与AB所在的直线垂直的直线方程.【考点】直线的一般式方程与直线的垂直关系.【专题】直线与圆.【分析】(1)利用斜率计算公式分别计算出K AB,K AC,即可判断出;(2)利用中点坐标公式、点斜式即可得出;(3)利用相互垂直的直线斜率之间的关系、点斜式即可得出.【解答】解:(1)∵,,∴K AB≠K AC,∴A,B,C三点不共线.(2)∵A,B的中点坐标为M(﹣2,3),直线x+y﹣2=0的斜率k1=﹣1,所以满足条件的直线方程为y﹣3=﹣(x+2),即x+y﹣1=0为所求.(3)∵,∴与AB所在直线垂直的直线的斜率为,所以满足条件的直线方程为,即2x+3y﹣8=0.【点评】本题考查了中点坐标公式、相互垂直的直线斜率之间的关系、点斜式、三点共线与斜率之间的关系,考查了计算能力,属于基础题.19.已知圆心为C的圆经过点 A(1,1)和B(2,﹣2),且圆心C在直线L:x﹣y+1=0上,求圆C的标准方程.【考点】圆的标准方程.【专题】计算题;直线与圆.【分析】设圆心坐标为C(a,a+1),根据A、B两点在圆上利用两点的距离公式建立关于a 的方程,解出a值.从而算出圆C的圆心和半径,可得圆C的方程.【解答】解:∵圆心在直线x﹣y+1=0上,∴设圆心坐标为C(a,a+1),根据点A(1,1)和B(2,﹣2)在圆上,可得=,解之得a=﹣3∴圆心坐标为C(﹣3,﹣2),半径r=5因此,此圆的标准方程是(x+3)2+(y+2)2=25.【点评】本题给出圆C满足的条件,求圆的方程.着重考查了两点间的距离公式和圆的标准方程等知识,属于基础题.20.如图,PA⊥平面ABCD,矩形ABCD的边长AB=1,BC=2,E为BC的中点.(1)证明:PE⊥DE;(2)如果PA=2,求异面直线AE与PD所成的角的大小.【考点】直线与平面垂直的判定;异面直线及其所成的角.【专题】空间位置关系与距离;空间角.【分析】(1)首先利用勾股定理的逆定理证明DE⊥AE,及PA⊥平面ABCD,根据三垂线定理即可证明PE⊥DE;(2)取PA的中点M,AD的中点N,连MC、NC、MN、AC.利用三角形的中位线定理可知∠MNC 的大小等于异面直线PD与AE所成的角或其补角的大小.再利用余弦定理即可得出.【解答】(1)证明:连接AE,由AB=BE=1,得,同理,∴AE2+DE2=4=AD2,由勾股定理逆定理得∠AED=90°,∴DE⊥AE.∵PA⊥平面ABCD,DE⊂平面ABCD,根据三垂线定理可得PE⊥DE.(2)取PA的中点M,AD的中点N,连MC、NC、MN、AC.∵NC∥AE,MN∥PD,∴∠MNC的大小等于异面直线PD与AE所成的角或其补角的大小.由PA=2,AB=1,BC=2,得,,∴,.∴异面直线PD与AE所成的角的大小为.【点评】熟练掌握勾股定理的逆定理、线面垂直的判定与性质定理、三垂线定理、三角形的中位线定理、异面直线所成的角、余弦定理是解题的关键.21.如图,正方体ABCD﹣A1B1C1D1的棱长为a,E为DD1的中点.(1)求证:BD1∥平面EAC;(2)求点D1到平面EAC的距离.【考点】点、线、面间的距离计算;直线与平面平行的判定.【专题】计算题;证明题.【分析】(1)欲证BD1∥平面EAC,只需在平面EAC内找一条直线BD1与平行,根据中位线定理可知EF∥D1B,满足线面平行的判定定理所需条件,即可得到结论;(2)设D 1到平面EAC的距离为d,根据建立等式关系可求出d,即可求出点D1到平面EAC的距离.【解答】解:(1)证明:连接BD交AC于F,连EF.(1分)因为F为正方形ABCD对角线的交点,所长F为AC、BD的中点.(3分)在DDD1B中,E、F分别为DD1、DB的中点,所以EF∥D1B.(5分)又EFÌ平面EAC,所以BD1∥平面EAC.(7分)(2)设D1到平面EAC的距离为d.在DEAC中,EF^AC,且,,所以,于是.(9分)因为,(11分)又,即,(13分)解得,故D1到平面EAC的距离为.(14分)【点评】本题主要考查了线面平行的判定以及点到平面距离的度量,同时考查了空间想象能力,转化能力和计算求解的能力,属于中档题.22.已知直线l:4x+3y+10=0,半径为2的圆C与l相切,圆心C在x轴上且在直线l的上方(1)求圆C的方程;(2)设过点P(1,1)的直线l1被圆C截得的弦长等于2,求直线l1的方程;(3)过点M(1,0)的直线与圆C交于A,B两点(A在x轴上方),问在x轴正半轴上是否存在点N,使得x轴平分∠ANB?若存在,请求出点N的坐标;若不存在,请说明理由.【考点】直线和圆的方程的应用.【专题】计算题;直线与圆.【分析】(1)设出圆心C坐标,根据直线l与圆C相切,得到圆心到直线l的距离d=r,确定出圆心C坐标,即可得出圆C方程;(2)根据垂径定理及勾股定理,由过点P(1,1)的直线l1被圆C截得的弦长等于2,分直线l1斜率存在与不存在两种情况求出直线l1的方程即可;(3)当直线AB⊥x轴,则x轴平分∠ANB,当直线AB斜率存在时,设直线AB方程为y=k(x ﹣1),联立圆与直线方程,消去y得到关于x的一元二次方程,利用韦达定理表示出两根之和与两根之积,由若x轴平分∠ANB,则k AN=﹣k BN,求出t的值,确定出此时N坐标即可.【解答】解:(1)设圆心C(a,0)(a>﹣),∵直线l:4x+3y+10=0,半径为2的圆C与l相切,∴d=r,即=2,解得:a=0或a=﹣5(舍去),则圆C方程为x2+y2=4;(2)由题意可知圆心C到直线l1的距离为=1,若直线l1斜率不存在,则直线l1:x=1,圆心C到直线l1的距离为1;若直线l1斜率存在,设直线l1:y﹣1=k(x﹣1),即kx﹣y+1﹣k=0,则有=1,即k=0,此时直线l1:y=1,综上直线l1的方程为x=1或y=1;(3)当直线AB⊥x轴,则x轴平分∠ANB,当直线AB斜率存在时,设直线AB方程为y=k(x﹣1),N(t,0),A(x1,y1),B(x2,y2),联立得:,消去y得:(k2+1)x2﹣2k2x+k2﹣4=0,∴x1+x2=,x1x2=,若x轴平分∠ANB,则k AN=﹣k BN,即+=0, +=0,整理得:2x1x2﹣(t+1)(x1+x2)+2t=0,即﹣+2t=0,解得:t=4,当点N(4,0),能使得∠ANM=∠BNM总成立.【点评】此题考查了直线与圆的方程的应用,涉及的知识有:垂径定理,勾股定理,圆的标准方程,点到直线的距离公式,以及斜率的计算,熟练掌握定理及公式是解本题的关键.。
广东省肇庆市第四中学高二数学下学期第一次月考试题
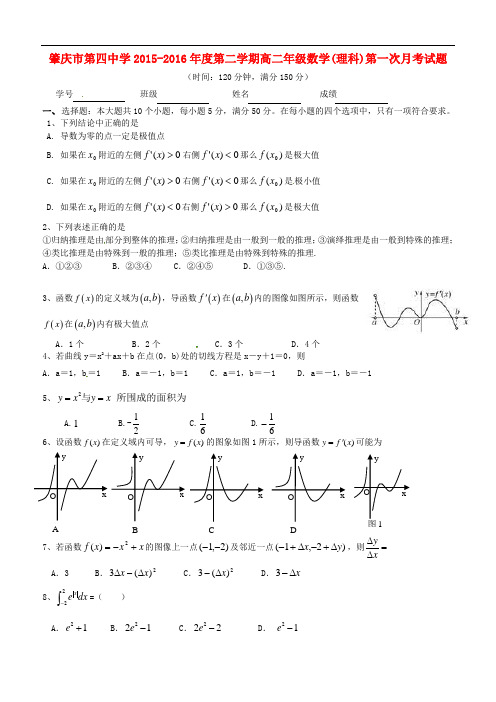
肇庆市第四中学2015-2016年度第二学期高二年级数学(理科)第一次月考试题 (时间:120分钟,满分150分) 学号 班级 姓名 成绩一、 选择题:本大题共10个小题,每小题5分,满分50分。
在每小题的四个选项中,只有一项符合要求。
1、下列结论中正确的是A. 导数为零的点一定是极值点B. 如果在0x 附近的左侧0)('>x f 右侧0)('<x f 那么)(0x f 是极大值C. 如果在0x 附近的左侧0)('>x f 右侧0)('<x f 那么)(0x f 是极小值D. 如果在0x 附近的左侧0)('<x f 右侧0)('>x f 那么)(0x f 是极大值2、下列表述正确的是①归纳推理是由部分到整体的推理;②归纳推理是由一般到一般的推理;③演绎推理是由一般到特殊的推理;④类比推理是由特殊到一般的推理;⑤类比推理是由特殊到特殊的推理.A .①②③B .②③④C .②④⑤D .①③⑤.3、函数()f x 的定义域为(),a b ,导函数()f x '在(),a b 内的图像如图所示,则函数()f x 在(),a b 内有极大值点A .1个B .2个C .3个D .4个4、若曲线y =x 2+ax +b 在点(0,b)处的切线方程是x -y +1=0,则A .a =1,b =1B .a =-1,b =1C .a =1,b =-1D .a =-1,b =-15、2y x y x ==与 所围成的面积为A.1B.-12C.16D.16- 6、设函数()f x 在定义域内可导,()y f x =的图象如图1所示,则导函数()y f x '=可能为7、若函数x x x f +-=2)(的图像上一点)2,1(--及邻近一点)2,1(y x ∆+-∆+-,则=∆∆x y A .3 B .2)(3x x ∆-∆ C .2)(3x ∆- D .x ∆-38、22x e dx -⎰=( )A .21e +B .221e -C .222e -D . 21e -x y OAx y O B x y O C y O D x x y O9、已知点P 在曲线41x y e =+上,α为曲线在点P 处的切线的倾斜角,则α的取值范围是( ) A.3[,)4ππ B.[,)42ππ C.3(,]24ππ D.[0,4π) 10、函数()1ln 212+++=ax x x x f 在()+∞,0上是增函数,则实数a 的取值范围是( ) A.[2,)-+∞ B.[2,)+∞ C.(,2]-∞- D.(-2,+∞)11、设f (x ),g (x )分别是定义在R 上的奇函数和偶函数,当x < 0时,f ′(x )g (x )+f (x )g ′(x )>0,且(3)0g -=,则不等式f (x )g (x )<0的解集是A . (-3,0)∪(3,+∞) B. (-3,0)∪(0,3)C . (-∞,-3)∪(3,+∞) D. (-∞,-3)∪(0,3)12、已知()1sin cos f x x x =+,()1n f x +是()n f x 的导函数,即()()21f x f x '=,()()32f x f x '=,…,()()1n n f x f x +'=,n ∈*N ,则()2016f x =( )A .sin cos x x -B . sin cos x x --C .sin cos x x -+D .sin cos x x +二、填空题:本大题共4个小题,每小题5分,满分20分。
肇庆市第四中学高三数学上学期第一次月考试题 文(无答案)新人教A版

肇庆市第四中学2014届高三第一次月考数学文试题班级:学号:姓名:成绩:一、选择题:本大题共10小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设i为虚数单位,则复数43ii+=()A. -4-3iB. -4+3iC. 4+3iD.4-3i2.设集合U={1,2,3,4,5,6}, M={1,3,5} 则C u M=()A. {2,4,6}B.{1,3,5}C.{1,2,4}D.U3.若向量AB=(1,2),BC=(3,4),则AC=()A.(4,6)B.(-4,-6)C.(-2,-2)D.(2,2)4.下列函数为偶函数的是()A .y=sinx B.y=3x C. y=x e5.已知变量x,y满足约束条件 x +y≤1,则z =x +2y的最小值为()x–y≤1x +1≥0A.3B.1C.-5D.-66.在△ABC中,若∠A=60°,∠B=45°,BC=AC=()A. B.7.某几何体的三视图如图1所示,它的体积为()A.72πB.48πC.30πD.24π8.在平面直角坐标系xOy中,直线3x+4y-5=0与圆x²+y²=4相交于A、B两点,则弦AB的长等于()A. D.19.执行如图2所示的程序框图,若输入n的值为6,则输出s的值为()A.105B.16C.15D.110. 对任意两个非零的平面向量α和β,定义α·β=αβββ⋅⋅。
若平面向量a,b 满足|a|≥|b|>0,A 与b 的夹角(0,)4πθ∈,且a ·b 和b ·a 都在合集{|}2n n Z ∈中,a ·b= ( )A .12 B.1 C. 32 D. 52二、填空题:本大题共5小题,考生作答4小题,每小题5分,满分20分。
(一)必做题(11~13题)11.函数y =_____ _____。
12.若等比数列{a n }满足a 2a 4=,则 。
广东省肇庆市高二上学期数学第二次月考试卷
广东省肇庆市高二上学期数学第二次月考试卷姓名:________ 班级:________ 成绩:________一、单选题 (共12题;共24分)1. (2分)已知命题,则()A .B .C .D .2. (2分) (2018高二上·玉溪期中) 已知高一(1)班有48名学生,班主任将学生随机编号为01,02,……,48,用系统抽样方法,从中抽8人,若05号被抽到了,则下列编号的学生被抽到的是()A . 16B . 22C . 29D . 333. (2分)设随机变量,且则P等于()A . 0.1B . 0.2C . 0.3D . 0.44. (2分)回归直线方程,其中a=3,样本中心点为(1,2 )则回归直线方程为()A . y=x+3B . y=-x+3C . y=-2x+3D . y=x-35. (2分)记集合A={(x,y)|x2+y2≤16},集合B={(x,y)|x+y﹣4≤0,(x,y)∈A}表示的平面区域分别为Ω1 ,Ω2 .若在区域Ω1内任取一点P(x,y),则点P落在区域Ω2中的概率为()A .B .C .D .6. (2分)若ab,c为实数,则下列命题正确的是()A . 若a>b,则B . 若a<b<0,则C . 若a<b<0,则D . 若a<b<0,则7. (2分)“x<-1”是“x2-1>0”的()A . 充分而不必要条件B . 必要而不充分条件C . 充要条件D . 既不充分也不必要条件8. (2分)(2019·延安模拟) 宋元时期数学名著《算学启蒙》中有关“松竹并生”的问题:松长五尺,竹长两尺,松日自半,竹日自倍,竹松何日而长等.如图是源于思想的一个程序框图,若输入的,分别为和,则输出的()A .B .C .D .9. (2分) (2016高一上·西安期末) 已知0<k<4直线L:kx﹣2y﹣2k+8=0和直线M:2x+k2y﹣4k2﹣4=0与两坐标轴围成一个四边形,则这个四边形面积最小值时k值为()A . 2B .C .D .10. (2分)(2018·中山模拟) 如右图,在正方体中,异面直线与所成的夹角为()A .B .C .D .11. (2分)为准线的抛物线的标准方程为()A .B .C .D .12. (2分)已知双曲线的左、右焦点分别是、,其一条渐近线方程为,点在双曲线上,则()A .B .C .D .二、填空题 (共4题;共4分)13. (1分) (2016高二上·宝应期中) 五个数1,2,3,4,a的平均数是3,这五个数的方差是________.14. (1分)(2020·杨浦期末) 椭圆的焦点为为椭圆上一点,若 ,则________.15. (1分)(2018·鞍山模拟) 已知向量满足,,则的夹角为________.16. (1分)(2013·江苏理) 在平面直角坐标系xOy中,椭圆C的标准方程为(a>b>0),右焦点为F,右准线为l,短轴的一个端点为B,设原点到直线BF的距离为d1 , F到l的距离为d2 ,若d2= ,则椭圆C的离心率为________.三、解答题 (共6题;共55分)17. (5分)(2018高二上·潮州期末) 已知 ,命题,命题.(1)若为真命题,求实数的取值范围;(2)若命题是假命题, 命题是真命题,求实数的取值范围.18. (5分)(2020·随县模拟) 已知函数 .(1)解不等式;(2)设函数的最小值为,已知,且,求的最小值.19. (15分)(2017·新课标Ⅱ卷理) 海水养殖场进行某水产品的新、旧网箱养殖方法的产量对比,收获时各随机抽取了100 个网箱,测量各箱水产品的产量(单位:kg),其频率分布直方图如图:(Ⅰ)设两种养殖方法的箱产量相互独立,记A表示事件“旧养殖法的箱产量低于50kg,新养殖法的箱产量不低于50kg”,估计A的概率;(Ⅱ)填写下面列联表,并根据列联表判断是否有99%的把握认为箱产量与养殖方法有关:箱产量<50kg 箱产量≥50kg 旧养殖法新养殖法(Ⅲ)根据箱产量的频率分布直方图,求新养殖法箱产量的中位数的估计值(精确到0.01).附:P(K2≥k)0.0500.010 0.001K 3.841 6.635 10.828 K2= .20. (10分) (2019高二下·金山月考) 如图,几何体中,是边长为2的正方形,为直角梯形,,,, .(1)求异面直线和所成角的大小;(2)求几何体的体积;(3)若平面ABCD内有一经过点B的曲线,该曲线上的任一动点都满足与所成角的大小恰等于与所成角.试判断曲线的形状并说明理由.21. (10分) (2019高三上·双鸭山月考) 如图,在四棱柱中,侧棱底面,,,,,且点和分别为和的中点.(1)求证:平面;(2)求二面角的正弦值.22. (10分)(2018·孝义模拟) 在平面直角坐标系中,以原点为极点,轴的非负半轴为极轴建立极坐标系.已知曲线的极坐标方程为,为曲线上的动点,与轴、轴的正半轴分别交于,两点.(1)求线段OP中点Q的轨迹参数方程;(2)若M是(1)中点Q的轨迹上的动点,求△MAB面积的最大值.参考答案一、单选题 (共12题;共24分)1-1、2-1、3-1、4-1、5-1、6-1、7-1、8-1、9-1、10-1、11-1、12-1、二、填空题 (共4题;共4分)13-1、14-1、15-1、16-1、三、解答题 (共6题;共55分) 17-1、17-2、18-1、18-2、19-1、20-1、20-2、20-3、21-1、21-2、22-1、22-2、。
广东省肇庆第四中学高一数学上学期第二次月考试题(无答案)
广东省肇庆第四中学2014-2015学年高一数学上学期第二次月考试题(无答案)1.指数函数x y a =的图像经过点(2,16)则a 的值是( )A .14 B .12 C .2 D .42.设0.3log 4a =,3log 4b =,20.3c = , 则,,a b c 的大小关系是 ( )A .a b c <<B .a c b <<C .c b a <<D .b a c <<3. 已知集合{}{}|1,|21x M x x N x =<=>,则M N I =( )A .∅B .{}|0x x <C .{}|1x x <D .{}|01x x <<4.若函数()y f x =是函数(0,1)x y a a a =>≠且的反函数,且(2)1f =,则()f x =() A .2log x B .12x C . 12log x D .22x -5.若函数x x x f -+=33)(与x x x g --=33)(的定义域均为R ,则 ( )A .)(x f 为奇函数,)(x g 为偶函数B .)(x f 为偶函数,)(x g 为奇函数C .)(x f 与)(x g 均为奇函数D .)(x f 与)(x g 均为偶函数6.函数()2x f x e x =+-的零点所在的区间是( )A.(-2,-1)B.(-1,0)C.(0,1)D.(1,2)7.函数()()22log 6f x x x =-++的单调减区间是( ) A.1,2⎛⎤-∞ ⎥⎝⎦ B. 1+2⎡⎫∞⎪⎢⎣⎭, C.12,2⎛⎫- ⎪⎝⎭ D. 132⎛⎫⎪⎝⎭,8.函数122x y =-()的图象必过 ( )A .第一、三、四象限B .第二、三、四象限C .第一、二、三象限D .第一、二、四象限9.函数()1xxa y a x =>的图象的大致形状是( )10.已知函数⎩⎨⎧≥<-+-=1,1,16)23()(x a x a x a x f x 在),(+∞-∞上单调递减,则实数a 的取值范围是( ) A.)1,0( B.)32,0( C.)32,83[ D.)1,83[二、填空题(共4题,每小题5分,共20分)11.已知幂函数y =f (x )的图象经过点(2,2),那么这个幂函数的解析式为________.12. 计算:22(lg 5)(lg 2)2lg 2-+=___________. 13.若函数(1)f x +的定义域为[]-23,,则函数(21)f x -的定义域是 . 14. 设函数f (x )是定义在R 上的偶函数,且)2()(-=x f x f ,当x∈[0,1]时,1)(+=x x f , )23(f =_____________. 三、解答题:本大题共6小题,满分80分.15.(本小题满分12分)设全集R U =,集合{}|13A x x =-≤<,{}|242B x x x =-≥-(1)求B A ⋂ (2)A B C U ⋃)(;16.(本小题满分12分)已知函数()2xf x =.(1)若0()2f x =,求0(3)f x 的值;(2)若)42()13(22-+≤+-x x f x x f ,求x 的取值范围.17、(本题满分14分)已知函数2()(3)3,f x kx k x k =+++其中为常数,且满足(2)3f =(1)求函数()f x 的表达式;(2)求函数()f x 在[1,4]-上的最大值和最小值;(3)设函数()()g x f x mx =-,若()[2,2]g x -在区间上是单调函数,求实数m 的取值范围;18.(本小题满分14分)某租赁公司拥有汽车100辆. 当每辆车的月租金为3000元时,可全部租出.当每辆车 的月租金每增加50元时,未租出的车将会增加一辆. 租出的车每辆每月需要维护费150元,未租出的车每辆每月需要维护费50元.(1)当每辆车的月租金定为3600元时,能租出多少辆车?(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?19.(本小题满分14分)设函数()21x f x x -=-, (1)判断并证明()f x 在()1+∞,的单调性; (2)求函数在[]2,6x ∈的最大值和最小值.20.(本小题满分14分) 已知函数2)1()(++-=x mx k x f ,其中R m k ∈,,且0≠m .(1)求函数)(x f 的定义域;(2)k 如何取值时,函数)(x f 存在零点,并求出零点.。
广东省肇庆第四中学高二上学期第二次月考数学(文)试题
1、圆锥的底面半径是3,高是4,则它的侧面积是( )2、已知空间两点A(6,0,1),B(3,5,7),则它们之间的距离为 ( ) A 、 B 、5 C 、70 D 、6 3.设k 是直线4x +3y -5=0的斜率,则k 等于( ) A - B C D -4.如果直线ax +2y +2=0与直线3x -y -2=0平行,那么系数a 的值为( ) A -3 B -6 C - D5.方程x 2+y 2+2ax -by +c =0表示圆心为C (2, 3),半径为3的圆,则a 、b 、c 的值依次为( )(A )2、6、4; (B )-2、6、4; (C )2、-6、4; (D )2、-6、-4 6.直线3x -4y +1=0被圆(x -3)2+y 2=9截得的弦长为( )(A) (B)4 (C) (D)2 7.若直线(1+a )x +y -1=0与圆x 2+y 2+4x =0相切,则a的值为( )A 、1或-1B 、或C 、1D 、8.已知直线l 方程为2x -5y +10=0,且在x 轴上的截距为a ,在y 轴上的截距为b ,则︱a +b ︱等于( )A 3B 7C 10D 59、直线3x +4y -13=0与圆1)3()2(22=-+-y x 的位置关系是:( ) A 、相离 B 、相交 C 、相切 D 、无法判定 10、圆C 1: 1)2()2(22=-++y x 与圆C 2:的位置关系是( ) A 、外离 B 、相交 C 、内切 D 、外切二、填空题(本大题共4小题,每小题5分,共20分)11.以点A( -1,4)、B(3, 2)为直径的两个端点的圆的方程为 . 12.过点P(-1,2)且与圆4)2()3(22=-++y x 相切的直线方程是________________. 13.圆上的点到直线的距离的最小值是 .14.若为圆的弦的中点,则直线的方程是三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤) 15、(12分)已知三角形ABC 的顶点坐标为A (-1,5)、B (-2,-1)、C (4,3),M 是BC 边上的中点。
广东省肇庆市四会中学2021-2022学年高二数学文月考试题含解析
广东省肇庆市四会中学2021-2022学年高二数学文月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 如图,△ABC中,||=3,||=1, D是BC边中垂线上任意一点,则·(-)的值是( )A.1 B. C.2D.4参考答案:D2. 某奶茶店的日销售收入y(单位:百元)与当天平均气温x(单位:℃)之间的关系如下:通过上面的五组数据得到了x与y之间的线性回归方程: =﹣x+2.8;但现在丢失了一个数据,该数据应为()A.3 B.4 C.5 D.2参考答案:B【考点】线性回归方程.【分析】求出的值,代入方程,求出的值,从而求出丢失了的数据.【解答】解:设该数据是a,=0,故=﹣x+2.8=2.8,∴(5+a+2+2+1)=2.8,解得:a=4,故选:B.3. 某个命题与正整数有关,若当时该命题成立,那么可推得当时该命题也成立,现已知当时该命题不成立,那么可推得A. 当时,该命题不成立B. 当时,该命题成立C. 当时,该命题成立D. 当时,该命题不成立参考答案:D略4. 某单位为了了解用电量y(千瓦时)与气温x(℃)之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:( ).A.58千瓦时B .66千瓦时 C .68千瓦时D .70千瓦时参考答案:C5. 已知双曲线的离心率为,则m=()A.7 B.6 C.9 D.8参考答案:C【考点】双曲线的简单性质.【分析】根据题意,由双曲线的标准方程分析可得其焦点在x轴上,以及a、b的值,由双曲线的几何性质可得c的值,又由该双曲线的离心率为,结合双曲线的离心率公式可得=,解可得m的值,即可得答案.【解答】解:双曲线的方程为:﹣=1,则其焦点在x轴上,且a==4,b=,则c==,若其离心率为,则有e===,解可得m=9;故选:C.6. 命题p: x0∈R,+10<0,则p:()A. x0∈R,+10>0B. x0∈R,+10≥0C. x∈R,+10>0D. x∈R,+10≥0参考答案:D7. 圆x2+y2﹣6x+4y+12=0与圆(x﹣7)2+(y﹣1)2=36的位置关系是()A.外切B.相交C.内切D.外离参考答案:A【考点】圆与圆的位置关系及其判定.【专题】计算题;方程思想;综合法;直线与圆.【分析】将圆的方程分别化为标准方程,找出圆心坐标和半径,利用两点间的距离公式求出两圆心的距离d,可得出d=R﹣r,可得出两圆内切.【解答】解:将圆x2+y2﹣6x+4y+12=0化为标准方程得:(x﹣3)2+(y+2)2=1,又,(x﹣7)2+(y﹣1)2=36,∴圆心坐标分别为(3,﹣2)和(7,1),半径分别为r=1和R=6,∵两圆心距d==5,∴d=R﹣r,则两圆的位置关系是内切.故选:A.【点评】此题考查了圆与圆的位置关系及其判定,圆与圆的位置关系可以由圆心距d与R及r的关系来判定,当d<R﹣r时,两圆内含;当d=R﹣r时,两圆内切;当R﹣r<d<R+r时,两圆相交;当d=R+r时,两圆外切;当d>R+r时,两圆外离.8. 已知A,B两地的距离为10 km,B,C两地的距离为20 km,现测得∠ABC=120°,则A,C两地的距离为 ( ) A.10 km B.10km C.10km D.10km 参考答案:D9. 函数的图象可能是()A. B.C. D.参考答案:D10. 若k可以取任何实数,则方程x2+ky2=1所表示的曲线不可能是()A.抛物线B.圆C.直线D.椭圆或双曲线参考答案:A二、填空题:本大题共7小题,每小题4分,共28分11. 由曲线y=sinx,y=cosx与直线x=0,x=所围成的平面图形(下图中的阴影部分)的面积是.参考答案:2﹣2考点:余弦函数的图象.专题:三角函数的图像与性质.分析:三角函数的对称性可得S=2,求定积分可得.解答:解:由三角函数的对称性和题意可得S=2=2(sinx+cosx)=2(+)﹣2(0+1)=2﹣2故答案为:2﹣2点评:本题考查三角函数的对称性和定积分求面积,属基础题.12. 江苏省高中生进入高二年级时需从“物理、化学、生物、历史、地理、政治、艺术”科目中选修若干进行分科,分科规定如下:从物理和历史中选择一门学科后再从化学、生物、地理、政治中选择两门学科作为一种组合,或者只选择艺术这门学科,则共有_________种不同的选课组合.(用数字作答)参考答案:13【分析】先从物理和历史中选择一门学科,再从化学、生物、地理、政治中选择两门学科作为一种组合,再根据题意求解.【详解】先从从物理和历史中选择一门学科有种,再从化学、生物、地理、政治中选择两门学科作为一种组合有种,所以共有种.故答案为:13【点睛】本题主要考查排列组合的综合应用,意在考查学生对这些知识的理解掌握水平和分析推理能力.13. 如图是函数的导函数的图象,给出下列命题:①-2是函数的极值点;②1是函数的极值点;③在处切线的斜率小于零;④在区间(-2,2)上单调递增.则正确命题的序号是_______.(写出所有正确命题的序号)参考答案:①④【分析】根据导函数的图象和极值点和单调性之间的关系,对四个命题逐一判断.【详解】命题①:通过导函数的图象可以知道,当时,,所以函数单调递减,当时,,所以函数单调递增,故-2是函数的极值点,故本命题是真命题;命题②:通过导函数的图象可以知道,当时,,所以函数单调递增,当时,,所以函数单调递增,故1不是函数的极值点,故本命题是假命题;命题③:由图象可知,所以在处切线的斜率大于零,故本命题是假命题;命题④:由图象可知当时,,所以函数单调递增,故本命题是真命题,故正确命题的序号是①④.14. 已知|2x﹣1|+(y+2)2=0,则(xy)2016= .参考答案:1【考点】有理数指数幂的化简求值.【分析】根据指数幂的运算法则计算即可.【解答】解:∵|2x﹣1|+(y+2)2=0,∴x=,y=﹣2,∴xy=﹣1,∴(xy)2016=1,故答案为:115. 求函数在区间上的值域为▲.参考答案:略16. 第二十九届北京奥运会吉祥物“福娃迎迎”,按如下的方式构造图形,图(1)、(2)、(3)、(4)分别包含1个、5个、13个、25个,第n个图形包含个“福娃迎迎”,则=_____.(答案用含n的解析式表示)参考答案:【分析】本题可根据题意及图写出前4个算式的表达式,然后观察规律可得及,即可算出结果.【详解】由题意及图,可发现规律:通过已知的这四个算式的规律,可得:,,通过上面两个算式,可得:,故答案为:.【点睛】本题主要考查了归纳推理的应用,其中解答中结合图形与题干的理解,先写出前面的简单项,发现规律并归纳是解答的关键,着重考查了推理与运算能力,属于中档试题.17. 已知1<a<5,5<b<12,则2a-b的取值范围是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
广东省肇庆第四中学2014-2015学年高二数学上学期第二次月考试题
文(无答案)
1、圆锥的底面半径是3,高是4,则它的侧面积是( )
2
15π
A 、 π12
B 、 π15
C 、 π30
D 、 2、已知空间两点A(6,0,1),B(3,5,7),则它们之间的距离为 ( ) A 、70 B 、5 C 、70 D 、6 3.设k 是直线4x +3y -5=0的斜率,则k 等于( ) A -
34 B 34 C 43 D -4
3 4.如果直线ax +2y +2=0与直线3x -y -2=0平行,那么系数a 的值为( ) A -3 B -6 C -23 D 3
2
5.方程x 2
+y 2
+2ax -by +c =0表示圆心为C (2, 3),半径为3的圆,则a 、b 、c 的值依次为( ) (A )2、6、4; (B )-2、6、4; (C )2、-6、4; (D )2、-6、-4 6.
直
线
3x -4y +1=0
被
圆
(x -3)2
+y 2
=9
截得的弦长为
( )
7.若直线(1+a )x +y -1=0与圆
x 2+y 2+4x =0
相切,则a 的值为
( )
A 、1或-1
B 、
14或14- C 、1 D 、14
- 8.已知直线l 方程为2x -5y +10=0,且在x 轴上的截距为a ,在y 轴上的截距为b ,则︱a +b ︱等于( )
A 3
B 7
C 10
D 5
9、直线3x +4y -13=0与圆1)3()2(2
2
=-+-y x 的位置关系是:( ) A 、相离 B 、相交 C 、相切 D 、无法判定
10、圆C 1: 1)2()2(2
2
=-++y x 与圆C 2:16)5()2(22=-+-y x 的位置关系是( ) A 、外离 B 、相交 C 、内切 D 、外切
二、填空题(本大题共4小题,每小题5分,共20分)
11.以点A( -1,4)、B(3, 2)为直径的两个端点的圆的方程为 . 12.过点P(-1,2)且与圆4)2()3(22=-++y x 相切的直线方程是________________. 13.圆12
2=+y x 上的点到直线02543=-+y x 的距离的最小值是 .
14.若)1,2(-P 为圆25)1(22=+-y x 的弦AB 的中点,则直线AB 的方程是
三、解答题(本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤) 15、(12分)已知三角形ABC 的顶点坐标为A (-1,5)、B (-2,-1)、C (4,3),M 是BC 边上的中点。
(1)求AB 边所在的直线方程;(2)求BC 边上的垂直平分线所在直线方程;(3)求以线段AM 为直径的圆的方程。
16.(14分)已知两圆04026,010102
222=--++=--+y x y x y x y x ,
求(1)它们的公共弦所在直线的方程;(2)公共弦长。
17.(14分)求满足下列条件的圆的方程
(1)、求过点(5,2),(3,2)M N 且圆心在直线32-=x y 上的圆的方程。
(2)、过圆x 2
+y 2
-x +y -2=0和x 2
+y 2
=5的交点,且圆心在直线3x +4y -1=0上的圆的方程为
18、(12分)已知:在空间四边形ABCS中,AC=AS,BC=BS
CS
求证:AB⊥
19.(14分)如下图所示,在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AB=5,AA1=4,点D是AB的中点.
(1)求证: AC⊥平面CBB1C1
(2)求证:AC1∥平面CDB1;
20. (14分)在ABC ∆中,已知B 在原点,C 点坐标为(0,2),AB
AC
=且,求点A 的轨
迹方程,并说明轨迹是什么图形。
肇庆市第四中学2014-2015年度第一学期
高二年级数学(文科)新课程模块二考试试题(答题卡)
(时间:120分钟,满分150分)
班级 学号 姓名 成绩
一、选择题:本大题共8个小题,每小题5分,满分40分。
在每小题的四个选项中,只有一项符合要求。
二、填空题:本大题共4个小题,每小题5分,满分20分。
11. 12. 13. 14. 三、解答题:本大题共6个小题,满分80分。
15.(12分)
16.(14分)
17.(14分)
18.(12分)
S
C
B A
19.(14分)解:
20.(14分)。
