图的实例解析与编程实现
图算法及应用案例分析

图算法及应用案例分析图算法是图论中研究图的结构和性质的数学工具,它在许多领域都有重要的应用,如社交网络分析、交通网络优化、电力网络分析等。
本文将介绍几种常见的图算法,并通过相应的应用案例进行分析。
一、最短路径算法最短路径算法用于寻找两个节点之间的最短路径,常见的算法有Dijkstra算法和Floyd算法。
其中,Dijkstra算法适用于单源最短路径问题,而Floyd算法适用于多源最短路径问题。
在交通网络优化中,最短路径算法可以用于选择最优的路径来减少行驶时间和交通拥堵。
例如,一位司机想要从A地到达B地,可以使用最短路径算法找到从A到B的最短路径,避开拥堵路段,减少行驶时间。
二、最小生成树算法最小生成树算法用于找出一棵包含所有节点的树,并且树上边的权重之和最小。
常见的算法有Prim算法和Kruskal算法。
在电力网络分析中,最小生成树算法可以用于选择最优的输电线路布局,减少电力传输的损耗和成本。
例如,一个电力公司想要在某个区域内建设输电线路,可以使用最小生成树算法找到连接所有电力站点的最小成本的输电线路布局。
三、社交网络分析算法社交网络分析算法用于研究和分析社交网络中的节点间关系,常见的算法有PageRank算法和社区发现算法。
在社交网络中,PageRank算法可以用于确定网页的重要性,根据节点之间的连接关系,将节点进行排序。
例如,在搜索引擎中,搜索结果页面的排序可以基于PageRank算法。
四、流网络算法流网络算法用于研究图中节点之间的流量分配和优化问题,常见的算法有最大流算法和最小割算法。
在管道网络优化中,最大流算法可以用于确定管道中液体或气体的最大流量。
例如,在石油管道系统中,最大流算法可以用于确定从油井到储罐的最大输送能力。
综上所述,图算法在许多应用中起着重要的作用,能够帮助解决各类问题。
从最短路径算法到流网络算法,不同的图算法有不同的应用场景,在各个领域都发挥着巨大的作用。
PLC流程图法编程及实例

PLC流程图法编程及实例可编程逻辑控制器(PLC)是一种广泛应用于工业自动化领域的设备,它通过接收输入信号,执行内部程序,从而控制输出信号,实现对设备的控制。
PLC编程的方法有很多种,其中,流程图法是一种常用的编程方法。
本文将介绍PLC流程图法编程的基本概念、优点、实例及应用实践经验。
PLC流程图法编程是一种图形化的编程语言,它将PLC程序转换成直观的流程图形式,通过在流程图中定义输入、输出变量,以及各个步骤之间的逻辑关系,来实现对PLC程序的编写和控制。
流程图法编程具有直观易懂、易于学习、易于维护等优点,因此,它成为了很多工程师和技术人员首选的PLC编程方法。
直观易懂:流程图使用图形化的方式来表示PLC程序,可以直观地展示程序的结构和逻辑关系,方便工程师和技术人员理解和分析。
易于学习:相比于传统的文本编程语言,流程图法编程更加简单易懂,即使是没有PLC编程经验的人也可以快速上手。
易于维护:在PLC程序调试过程中,流程图法可以更快速地找到程序中的错误和漏洞,方便工程师和技术人员进行程序的修改和维护。
提高效率:使用流程图法编程,可以减少程序调试的时间和成本,提高PLC程序的开发效率。
下面以一个简单的PLC程序为例,介绍如何使用流程图法进行编程。
实例:设计一个控制设备,当按下启动按钮后,设备开始工作,当按下停止按钮后,设备停止工作。
输入变量:启动按钮(X0)、停止按钮(X1)在绘制流程图时,我们需要将输入变量和输出变量在图中表示出来,并使用图形符号来表示输入输出之间的逻辑关系。
根据上面的实例,我们可以绘制如下流程图:开始 -->启动按钮(X0) -->设备状态(Y0) -->工作| ||---------->停止按钮(X1) <--|设备状态(Y0) -->工作状态 <--停止状态 <--结束根据流程图,我们可以编写如下的PLC程序:LD X0 //检查启动按钮是否按下OUT Y0 //将设备状态输出为工作状态LD X1 //检查停止按钮是否按下OUT Y0 //将设备状态输出为停止状态在编写PLC程序时,有些问题需要特别注意:变量的命名:为了避免程序出错和便于维护,变量命名要规范、有含义、易记忆。
西门子s7200PLC编程实例解析
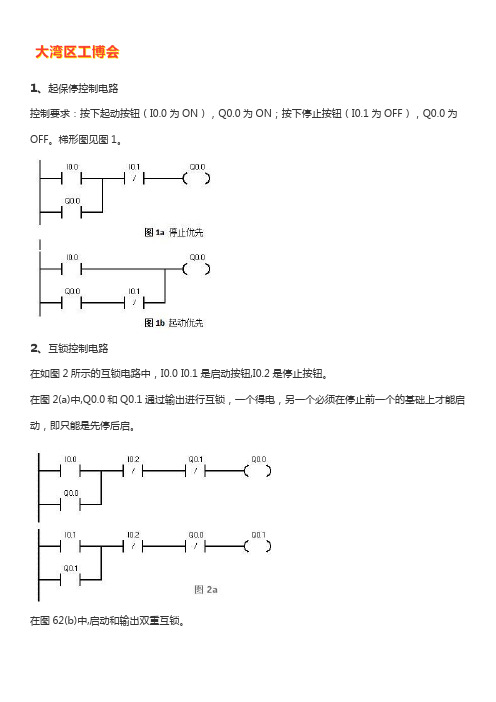
1、起保停控制电路控制要求:按下起动按钮(I0.0为ON),Q0.0为ON;按下停止按钮(I0.1为OFF),Q0.0为OFF。
梯形图见图1。
2、互锁控制电路在如图2所示的互锁电路中,I0.0 I0.1是启动按钮,I0.2是停止按钮。
在图2(a)中,Q0.0和Q0.1通过输出进行互锁,一个得电,另一个必须在停止前一个的基础上才能启动,即只能是先停后启。
在图62(b)中,启动和输出双重互锁。
3、多地控制电路图3所示是一个多地控制电路梯形图。
I0.0、I0.1、I0.2是多地启动按钮,I0.3、I0.4、I0.5是多地停止按钮。
4、顺序控制电路比如有3台电动机,按启动按钮I0.0,3台电动机Q0.0、Q0.1、Q0.2依次启动;按停止按钮I0.1,3台电动机Q0. 0\Q0.1、Q0.2依次反向停止。
这个程序在诸如皮带机控制等顺序控制机械中应用广泛。
顺序控制梯形图如图4所示。
在图中,启动时,I0. 0为ON,用通电延时时间继电器T37通过比较指令来依次启动电动机,当T37的当前值等于100时,即定时10 s时,启动Q0.1,20 s时,启动Q0.2。
停止时,I0.1为ON,用断电延时时间继电器T38通过比较指令来依次反向停止电动机。
5、二分频电路二分频电路也叫单按钮电路。
在许多控制场合,需要对控制信号进行分频,有时为了节省一个输人点,也需要采用此种电路。
图5是实现二分频运行时序控制的两种梯形图。
在图5(a)中,10.0第一一个脉冲到来时,PC第一次扫描,MO.0为ON ,Q0.0为ON ,第二次扫描,00.0自锁;10.0第二个脉冲到来时,PC第一次扫描,MO.0 为ON ,MO.1为ON,Q0.0断开,第二次扫描,M0.0断开,Q0.0保持断开;依次类推。
图5b前面梯形图的原理差不多,不再作说明。
此电路多用于一个按钮控制一盏灯的两种状态。
I0.0下面可并联多个输入按钮,就可实现多个开关控制一盏灯。
C#实现图(Graph)

C#实现图(Graph)简介图表示点之间的关系,在C#中通过节点对象的集合来表示点(Vertex),用邻接矩阵(adjacency matrix)来表示点之间的关系。
下面来看C#实现。
PS:本片文章是我复习的笔记,代码注释很全。
勿吐槽。
表示点的对象下面实现代码:每个节点包含两个字段,分别为节点数据以及表示是否被访问过的一个布尔类型。
表示图的对象图中除了需要点的集合和邻接矩阵之外,还需要一些基本的向图中添加或删除元素的方法,以及一个构造方法来对图进行初始化。
//图中所能包含的点上限private const int Number = 10;//顶点数组private Vertex[] vertiexes;//邻接矩阵public int[,] adjmatrix;//统计当前图中有几个点int numVerts = 0;//初始化图public Graph(){//初始化邻接矩阵和顶点数组adjmatrix = new Int32[Number, Number]; vertiexes = new Vertex[Number];//将代表邻接矩阵的表全初始化为0for (int i = 0; i < Number; i++){for (int j = 0; j < Number; j++){adjmatrix[i, j] = 0;}}}//向图中添加节点public void AddVertex(String v){vertiexes[numVerts] = new Vertex(v); numVerts++;}拓扑排序(TopSort)拓扑排序是对一个有向的,并且不是环路的图中所有的顶点线性化。
需要如下几个步骤1.首先找到没有后继的节点。
2.将这个节点加入线性栈中3.在图中删除这个节点4.重复步骤1,2,3因此,首先需要找到后继节点的方法:此外还需要删除图中点的方法,这个方法不仅需要删除图中对应位置的点,还需要删除邻接矩阵对应的行和列,因此设置了两个辅助方法,见代码。
plc可编程序控制器应用实例(梯形图+解析)
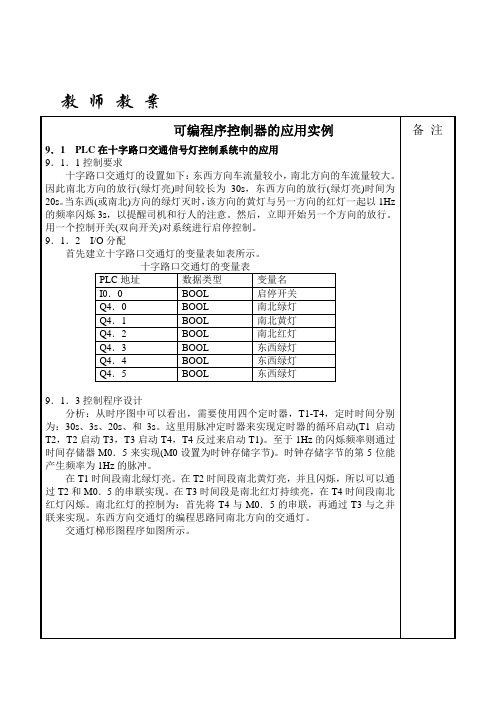
教师教案交通灯梯形图程序9.2 PLC在节日彩灯控制系统中的应用9.2.1控制要求用PLC实现对节日彩灯的控制,结构简单,变幻形式多样、价格低。
彩灯形式及变幻尽管花样繁多,但其负载不外乎三种:长通类负载、变幻类负载及流水类负载。
长通类负载是指彩灯中用以照明或起衬托底色作用之类的负载,其特点是只要彩灯投入工作,则这类负载长期接通。
变幻类负载则指某些在整个工作过程中定时进行花样变换的负载,如字形的变换,色彩的变幻或位置的变幻之类,其特点是定时通断,但频率不高。
流水、闪烁类负载则指变幻速度快,犹如行云流水、星光闪烁、万马奔腾,其特点虽也是定时通断,但频率较高(通常间隔几十毫秒至几百毫秒)。
对于长通类负载,其控制十分简单,只需一次接通或断开。
而对变幻类及流水、闪烁类负载的控制,则是按预定节拍产生一个“环形分配器”(一般可用SHRB、ROL-W产生),有了环形分配器,彩灯就能得到预设频率和预设花样的闪亮信号。
彩灯就可实现花样的变幻。
通常先根据花样变幻的规律例出动作时序表,再按预设彩灯变幻花样在表中“打点”,然后再依据动作时序表输出即可。
9.2.1控制程序设计本例所选彩灯变幻花样为跳闪方式:1隔1跳2,回跳1,隔1跳2,回跳1┈。
其动作时序表如表所示。
节日彩灯动作时序表即本例的节拍是16位,输出是8位,环形分配器由ROL-W产生彩灯闪烁频率固定为1Hz,如果需要现场改变频率,则T33的PT端需采用VWZ写入。
节日彩灯控制的梯形图如图所示。
节日彩灯控制的梯形图9.3 PLC在自动送料车控制系统中的应用9.3.1控制要求如图所示,当小车处于后端时,按下起动按钮,小车向前运行,行至前端压下前限位开关,翻斗门打开装货,7s后,关闭翻斗门,小车向后运行,行至后端,压下后限位开关,打开小车底门卸货,5s后底门关闭,完成一次动作。
要求控制送料小车的运行,并具有以下几种运行方式:1)手动操作:用各自的控制按钮,一一对应地接通或断开各负载的工作方式。
turtle例题

turtle例题摘要:1. turtle库简介2.turtle库的基本功能与应用3.turtle例题解析4.总结与拓展正文:一、turtle库简介turtle库是Python中一个有趣的绘图库,它的名称来源于乌龟。
这个库可以方便地进行绘图、计算、动画制作等操作。
它的特点是用简单的代码就可以实现复杂的图形和算法,非常适合初学者学习和实践。
二、turtle库的基本功能与应用1.绘制基本图形:turtle库可以轻松地绘制线段、多边形、圆形等基本图形,只需几句简单的代码。
2.控制画笔:我们可以通过设置画笔的速度、颜色、填充颜色等属性,使绘图更加丰富多样。
3.数学计算:turtle库还提供了许多数学函数,如三角函数、对数、指数等,可以方便地进行数学计算。
4.动画制作:利用turtle库可以制作简单的动画,如旋转、平移等。
三、turtle例题解析1.绘制正方形:```pythonimport turtlefor i in range(4):turtle.forward(100)turtle.left(90)turtle.done()```2.绘制圆形:```pythonimport turtleturtle.circle(50)turtle.done()```3.计算勾股定理:```pythonimport turtlea = 3b = 4c = turtle.sqrt(a**2 + b**2)turtle.write(f"{a} + {b} = {c}", align="center", font=("Arial", 16, "normal"))turtle.done()```4.绘制螺旋线:```pythonimport turtleturtle.speed(0)turtle.penup()turtle.goto(0, 0)turtle.pendown()for i in range(36):turtle.forward(2)turtle.right(10)turtle.done()```四、总结与拓展turtle库作为一个有趣且实用的Python库,可以帮助初学者轻松地完成各种绘图和计算任务。
DPU编程示例与实例解析
DPU在大数据处理中的性能优化
DPU在大数据处理中的未来发展趋势
DPU在大数据处理中的应用场景
DPU在大数据处理中的优势
DPU在大数据处理中的具体实现
实例3:解析DPU在人工智能领域的应用
DPU在人工智能领域的应用背景
DPU在人工智能领域的优势
DPU在人工智能领域的具体应用案例
DPU在人工智能领域的发展趋势和挑战
DPU编程示例与实例解析
汇报人:XXX
目录
01
DPU编程概述
02
DPU编程示例
03
DPU实例解析
04
DPU编程技巧和优化
05
DPU编程的挑战和未来发展
DPU编程概述
DPU的定义和作用
DPU可以处理各种类型的数据,包括图像、音频、视频等
DPU(Data Processing Unit)是一种专门用于数据处理的硬件设备
实例1:解析DPU在密码学中的应用
密码学简介:介绍密码学的基本概念和原理
结论:总结DPU在密码学中的应用优势和局限性,以及对未来发展的展望
实例解析:通过具体的密码学实例,解析DPU在其中的应用和实现过程
DPU在密码学中的应用:详细解析DPU在密码学中的应用场景和实现方法
实例2:解析DPU在大数据处理中的应用
编程接口:DPU编程需要调用特定的编程接口,如CUDA、OpenCL等
性能优化:DPU编程需要进行性能优化,以提高数据处理效率和降低能耗
DPU编程的流程和工具
流程:编写代码、编译、链接、加载、运行
工具:DPU编程器、DPU编译器、DPU链接器、DPU加载器、DPU运行器
示例:编写一个简单的DPU程序,包括输入、处理、输出
PLC编程各类经典案例解析
任务一十字路口交通信号灯控制实验一、控制要求:该实验在十字路口交通信号灯控制实验区内完成,交通灯分1、2两组,控制规律相同,工作时序图如下:起动┌┐─┘└──────────────────────────────┌──────┐┌┐┌┐┌┐1绿─┘└┘└┘└┘└─────────────────←20秒→←3秒→┌──1黄──────────────┘2秒└───────────────┐┌──────────────1红└───────────────┘┌──────┐┌┐┌┐┌┐2绿─────────────────┘└┘└┘└┘└─1─┐┌─2黄└────────────────────────────┘┌───────────────┐2红─┘└──────────────二、I/O分配:三、梯形图设计四.实验梯形图五.实验问题.今天的实验中,我们先在绿灯的闪烁上遇到了问题,后经同学讲解,运用了P -1s 解决了闪烁问题;在运行的时候,计时器出现了不工作的问题,老师说可以从灯100.00中看出计时器没有运行,在调整后就可以运行基本程序了;按钮的开关控制问题通过利用一个新线圈的引用,实现了0.00按下后整体的指示灯工作,0.01按下后整体停止。
实现了交通灯的指示控制。
以上为我们组今天实验中遇到的所有问题。
通过对这些问题的解决,让我们对PLC 实验更进一步的了解,对日后的实际操作会有很大的帮助。
任务二混料罐控制实验一、控制要求:该实验在混料罐实验区内完成。
液面在最下方时,按下起动按钮后, 可进行连续混料。
首先,液体A阀门打开,液体A流入容器;当液面升到M传感器检测位置时, 液体A阀门关闭,液体B阀门打开; 当液面升到H传感器检测位置时, 液体B阀门关闭,搅拌电机开始工作。
搅拌电机工作6秒钟后,停止搅拌,混合液体C阀门打开,开始放出混合液体。
当液面降到L传感器检测位置时,延时2秒后,关闭液体C阀门, 然后再开始下一周期操作。
C语言典型例题——关于图形输出
在C语言学习中我们会遇到各种输出图形的题目,下面我们就来看一些这种题目。
一、编写程序输出下图所示的图形。
(1)(2)(3)(11)下面我们分别以i、j、k分别表示行数,空格数,星号数。
(1)i j k (2) i j k (3) i j k1 0 1 1 6 1 1 0 92 0 2 2 5 2 2 1 73 0 3 34 3 3 2 54 0 4 4 3 4 4 3 35 0 5 5 2 5 5 4 16 0 6 6 1 6 j<=i-17 0 7 7 0 7 k<=11-2*iK<=i j<=7-iK<=i发现行数、空格、星号有如上关系,用for循环便可实现。
(1)#include"stdio.h"void main(){int i,j;for(i=1;i<=7;i++){for(j=1;j<=i;j++) printf("*");printf("\n");}}(2)#include"stdio.h"void main(){int i,j,k;for(i=1;i<=7;i++){for(j=1;j<=7-i;j++) printf(" ");for(k=1;k<=i;k++) printf("*");printf("\n");}}(3)#include"stdio.h"void main(){int i,j,k;for(i=1;i<=6;i++){for(j=1;j<=i-1;j++) printf(" ");for(k=1;k<=11-2*i;k++) printf("*");printf("\n");}}然后我们在进行扩展。
Turtle画图的方法及案例
Turtle画图的方法及案例Turtle是一个图形绘制库,它可以在屏幕上绘制各种形状和图案。
通过控制Turtle的移动和旋转,可以绘制直线、曲线、多边形等各种图形。
它的特点就是简单易用,只需要几行代码,就可以实现复杂的图形绘制,并且绘制过程是实时可视化的,即绘制的过程会立即显示在屏幕上。
这样可以方便地观察Turtle 的移动和绘制结果,帮助用户理解和调试代码,是学习Python最好的开端,而且可以培养出浓厚的兴趣。
本文给出了Turtle编程最基础的语法,从易到难给出了几个案例的源代码。
一、Turtle基础1.导入模块:在Python程序中导入turtle模块,使用命令import turtle。
2.创建画布:使用命令turtle.Screen()创建一个画布,即绘图窗口。
3.创建画笔:使用命令turtle.Turtle()创建一个画笔,即绘图工具。
4.绘制基本图形:通过调用画笔对象的方法,只需利用几个基础命令即可实现绘图。
这些基础的方法包括:turtle.forward(distance):以指定的距离distance前进。
turtle.backward(distance):以指定的距离distance后退。
turtle.right(angle):向右转动指定的角度angle。
turtle.left(angle):向左转动指定的角度angle。
turtle.goto(x,y):将画笔移动到指定的坐标(x,y)。
turtle.penup():抬起画笔,即移动时不绘制图像。
turtle.pendown():放下画笔,即移动时绘制图像。
turtle.pensize(width):设置画笔的宽度。
turtle.pencolor(color):设置画笔的颜色。
turtle.fillcolor(color):设置填充颜色。
turtle.begin_fill():开始填充形状。
turtle.end_fill():结束填充形状。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
图的 实例 解析 与编 程实 现
解:(1) 每个顶点的出度和入度如下: (2) 邻接矩阵如下所示:
目录
图的 实例 解析 与编 程实 现
(3) 邻接表如下图所示。
目录
图的 实例 解析 与编 程实 现
(4) 逆邻接表如下图所示。
目录
图的 实例 解析 与编 程实 现
【例6-9】 用深度优先遍历和广度优先遍历对如下 图所示的无向图G进行遍历(从顶点1出发),给出遍历 序列,并画出对应的深度优先生成树和广度优先生成 树。
目录
图的 实例 解析 与编 程实 现
解:图中的深度优先序列为1, 2, 4, 7, 5, 3, 8, 6;广度优先序列为1, 2, 3, 4, 5, 6, 8, 7。深度优 先生成树如下图(a)所示,广度优先生成树如下图(b)所 示。
接矩阵对图的存储。 参考程序见算法例6-10 。 该算法的执行时间是O(n+n2+e),由于e<n2,算法的 时间复杂度是O(n2)。 无向图的邻接矩阵是对称矩阵,对于规模大的邻接 矩阵可采取压缩存储方式存储。
目录
图的 实例 解析 与编 程实 现
【例6-11】编程实现邻接表对图的存储。 参考程序见算法例6-11 。
【例6-12】 编程求有向赋权图的最短路径(使用迪 杰斯特拉算法)。 参考程序见算法例6-12 。
项目
数据结 构(C 语言描 述)
谢谢观看!
目录
图的 实例 解析 与编 程实 现
第6章 图
项目
数据结 构(C 语言描 述)
图的实例解析与 编程实现
目录
图的 实例 解析 与编 程实 现
图的实例解析与编程实现
【例6-8】已知如下图所示的有向图,请给出该图的: (1) 每个顶点的出度和入度。 (2) 邻接矩阵。 (3) 邻接表。 (4) 逆邻接表。
