多结点样条插值曲面的图像放大方法探微

基于双线性插值改进算法的图像放大技术实现(精)

2006・ 10月号・软件导刊 91基于双线性插值改进算法的图像放大技术实现王杉, 范学峰(同济大学电子信息与工程学院, 上海 200433摘要:针对双线性插值算法在图像放大过程中处理图像边缘部分的不足, 提出了一种新的改进算法。

该算法通过分析图像的局部结构对图像分别进行插值。

同质区域采用双线性插值算法, 边缘区域采用基于圆形孔径的方法进行放大。

此外, 通过与传统算法进行比较, 利用实例说明了该算法在图像处理细节部分的优越性。

关键字 :双线性插值; 图像放大技术; 图像处理技术中图分类号:TP317.4文献标识码:A文章编号:1672-7800(2006 10-0091-020前言数字图像处理技术起源于 20世纪 20年代, 经过半个多世纪的发展, 已经广泛应用于工业、医疗保健、航空航天等各个领域, 在国民经济中发挥着越来越重要的作用。

图象处理技术的一个基本内容是图像的放大和缩小 (简称放缩 , 它在图像显示、传输 (通信、分析及动画制作等方面有着广泛的应用。

图像放大的基本要求是能够以较快速度得到较好的放大效果, 即放大后所需要的图像处理细节部分仍然清晰。

在图像放大时要进行插值运算, 理想的插值是辛格函数插值 [1]。

但由于它的运算量太大, 所以在实际应用中, 重复平移象素法 [2](Du-plicatePixels和双线性插值法 [3](BilinearIn-terpolation 是最常用的图像放大算法。

虽然这两种算法都有较快的速度, 但是在放大效果方面有所不足。

重复平移象素法只是简单地复制源象素点最邻近的象素点 (最邻近取样 , 其结果是产生象素块 (即马赛克 ,使得图像整体不清楚。

而双线性插值法则利用了源象素点周围邻近的 4个象素点的线性平均权值计算目标象素点值, 这样虽然可以得到较好的整体效果, 但图像的边缘模糊, 细节部分不够清晰。

笔者提供了一种基于双线性插值的改进算法, 该算法针对双线性插值算法在边缘处理上的不足, 加以了改进, 从而使得放大后的图像处理细节部分仍然清晰。

一种基于Newton-Thiele型有理插值曲面的图像缩放方法

一种基于Newton-Thiele型有理插值曲面的图像缩放方法胡敏;檀结庆
【期刊名称】《计算机科学》
【年(卷),期】2002(029)0z2
【摘要】@@ 1.引言rn为获得较好的视觉效果或适应某些特殊场合的需要,常要对图像进行缩放处理.图像的缩放可归结为对图像进行几何运算,它分两步进行:首先对图像进行空间变换;其次对图像进行灰度级插值.一般的方法是使用简单的比例变换,但这种方法时常会引起比较严重的图像走样,尤其是当图像中包含像素之间灰度级有变化的细微结构时,会在图像中产生人工的痕迹,图像带有大量锯齿形.
【总页数】3页(P49-51)
【作者】胡敏;檀结庆
【作者单位】合肥工业大学计算机信息学院,合肥,230009;合肥工业大学计算机信息学院,合肥,230009
【正文语种】中文
【中图分类】TP3
【相关文献】
1.基于Ferguson曲面插值的图像缩放方法 [J], 韩忠杰;饶道娟;穆国旺
2.对图像缩放中有理插值方法的一种新讨论 [J], 盛敏
3.一种三元Newton-Thiele型有理插值方法 [J], 崔蓉蓉;顾传青
4.一种含参数的双线性有理插值的图像缩放方法 [J], 丁剑
5.一种基于Sobel算子和混合有理插值的图像缩放方法 [J], 陈宝国;李宁
因版权原因，仅展示原文概要，查看原文内容请购买。

利用双线性插值法实现图像放大

利用双线性插值算法实现图像放大
一、双线性插值算法的原理
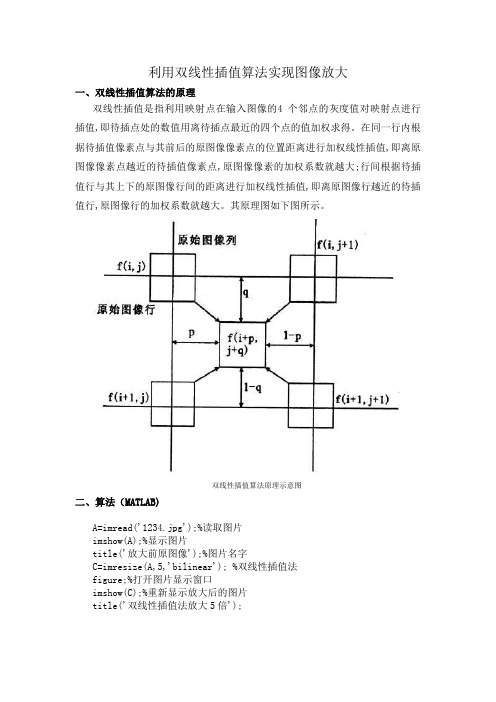
双线性插值是指利用映射点在输入图像的4 个邻点的灰度值对映射点进行插值,即待插点处的数值用离待插点最近的四个点的值加权求得。

在同一行内根据待插值像素点与其前后的原图像像素点的位置距离进行加权线性插值,即离原图像像素点越近的待插值像素点,原图像像素的加权系数就越大;行间根据待插值行与其上下的原图像行间的距离进行加权线性插值,即离原图像行越近的待插值行,原图像行的加权系数就越大。

其原理图如下图所示。

双线性插值算法原理示意图
二、算法（MATLAB)
A=imread('1234.jpg');%读取图片
imshow(A);%显示图片
title('放大前原图像');%图片名字
C=imresize(A,5,'bilinear'); %双线性插值法
figure;%打开图片显示窗口
imshow(C);%重新显示放大后的图片
title('双线性插值法放大5倍');
三、程序运行结果截图。

自适应Catmull-Rom样条图像放大

Ａｂｓｔｒａｃｔ：Ｂａｓｅｄｏｎａｇｅｏｍｅｔｒｉｃｃｌａｓｓｉｆｉｃａｔｉｏｎ，３ｎｅｗｉｍａｇｅａｍｐｌｉｆｉｃａｔｉｏｎｍｅｔｈｏｄｕｓｉｎｇａｄａｐｔｉｖｅＣａｔｍｕｌｌ — Ｒｏｍｉｎｔｅｒｐｏｌａｔｉｏｎｉｓｐｒｅｓｅｎｔｅｄｉｎｔｈｉｓｐａｐｅｒ．Ｃｏｍｐａｒｅｄｔｏｔｈｅｔｒａｄｉｔｉｏｎａｌｉｍａｇｅｒｅｃｏｎｓｔｒｕｃｔｉｏｎ
摘
要：针对Ｃａｔｍｕｌｌ — Ｒｏｍ样条图像插值放大不能保证图像内各物体之间边界清晰的问题，提出一种基于几何分类
的自适应Ｃａｔｍｕｌｌ — Ｒｏｍ样条图像插值放大算法．通过对原图像的边缘进行几何分类，根据原图像的边缘几何类型插值目标图像中的未知像素点；若未知像素点为原图像中的边缘，则调整Ｃａｔｍｕｌｌ — Ｒｏｍ样条的切向方向和切向长度来计算未知像素值，得到边缘保持的目标图像．实验结果表明，应用该算法得到的目标图像边界清晰、细节模糊减少，
ｍｅｔｈｏｄｕｓｉｎｇＣａｔｍｕｌｌ — Ｒｏｍｉｎｔｅｒｐｏｌａｔｉｏｎ，ｔｈｅｐｒｏｐｏｓｅｄｍｅｔｈｏｄｃａｎｐｒｅｓｅｒｖｅｇｅｏｍｅｔｒｉｃｆｅａｔｕｒｅｓｗｅｌ１．

使用双线性插值进行图像放大的实现

使用双线性插值进行图像放大的实现一、总体设计思路Step 1：实现图像的打开、显示、保存，在打开图片之后将图片读入内存并获得了该图像除文件头以外的部分在缓存内存储的句柄，以及该图的调色板，调色板颜色种类数等等参数。

Step 2：在显示的基础上，利用代码根据放大比例重新开辟一个缓存。

将原图的BITMAPINFOHEADER拷贝过来。

并修改biHeight、biWidth、biSizeImage等参数。

Step 3：利用双线性插值算法，以原图信息为基础生成新的像素信息。

原理：双线性插值维基百科，自由的百科全书跳转到：导航, 搜索双线性插值，又称为双线性内插。

在数学上，双线性插值是有两个变量的插值函数的线性插值扩展，其核心思想是在两个方向分别进行一次线性插值。

红色的数据点与待插值得到的绿色点假如我们想得到未知函数在点的值，假设我们已知函数在, , , 及四个点的值。

首先在x方向进行线性插值，得到然后在y方向进行线性插值，得到这样就得到所要的结果,如果选择一个坐标系统使得的四个已知点坐标分别为(0, 0)、(0, 1)、(1, 0) 和(1, 1)，那么插值公式就可以化简为或者用矩阵运算表示为与这种插值方法名称不同的是，这种插值方法并不是线性的，它的形式是它是两个线性函数的乘积。

另外，插值也可以表示为在这两种情况下，常数的数目都对应于给定的f的数据点数目。

线性插值的结果与插值的顺序无关。

首先进行y方向的插值，然后进行x方向的插值，所得到的结果是一样的。

双线性插值的一个显然的三维空间延伸是三线性插值。

二、具体实现方案及细节1、需要改变的项：①BITMAPINFOHEADER里的biHeight、biWidth、biSizeImage。

②所有像素点信息2、具体方案的设计：①对双线性插值的理解：放大图像时，插值就是根据比例得到一个坐标(x,y)。

该坐标可分为四种情况：(1)得到的x和y都是整数且落在原图中，则直接取出该像素点的颜色信息即可。

图像放大算法比较研究

2
1. 3
双三次插值算法双三次插值是高阶插值算法中常用的方法, 它对周
围邻近的 16 个像素点进行插值计算( 如图 3 所示 ) 。这种图像插值算法的优点是可以消除锯齿现象 , 插值质量高, 效果好, 与前面两种方法比较边缘阶梯失真现象得
( x - xi) ( x i+ 1 - x i ) ( x i+ 2 - x i ) B i, 3 = (x - xi)2 ( x i+ 2 - x i+ 1 ) ( x - x i+ 1 ) ( x i+ 1 - x i ) ( x i+ 2 - x i ( x i+ 2 - x i+ 1 ) ( x i+ 3 - x i+ 1 ) ( x i+ 3 - x ) ( x i+ 3 - x i+ 1 ) ( x i+ 3 - x i+ 2 ) 0, 利用它插值放大的图像较为平滑, 无明显的锯齿现象。同时可以通过快速算法极大地缩短运算时间。采用该方法对于彩色图象放大时 , 必须解决图像出现色偏差, 边缘细节保持不足够好的问题。基于三次 B 样条函数的插值算法 , 在插值过程中均表现为低通滤波器, 在不同程度上抑制了高频成分 , 34
灰度值, 所以又称为像素复写或零阶保持插值。如图 1 所示, 设 ( i, j ) , ( i, j + 1) , ( i + 1, j ) , ( i + 1, j + 1 ) 是灰度插值前的一个四点邻域 , 其灰度值分别为 g( i , j ) , g( i, j + 1) , g( i + 1, j ) , g( i + 1, j + 1) 。最近领域法是比较 ( u, v) 点和 ( i , j ) , ( i , j + 1) , ( i + 1, j ) , ( i + 1, j + 1) 四点之间的距离 , 然后以与 ( u, v) 点最近的那点的灰度值作为( u, v ) 点的灰度值[ 2] 。将两点之间的距离记为 D[ ( u, v ) , ( i , j ) ] , 则上述四点与( u, v) 点最近距离可由下式求得: D[ ( u, v) , ( i, j ) ] = m in { D[ ( u, v) , ( i, j ) ] , D[ ( u, v) , ( i, j + 1) ] , D[ ( u, v ) , ( i + 1, j ) ] , D[ ( u, v ) , ( i + 1, j + 1) ] } 求得与 ( u, v) 点距离最近的点( i , j ) 后, 由最近邻域法确定 ( u, v) 点的灰度为: g( u, v ) = g( i , j ) 最近邻插值运算简单快速, 能够保持插值图像边缘清晰 , 但边缘轮廓有显著的锯齿现象 , 图像背景产生马赛克 , 形成伪边缘, 视觉效果差, 重构误差较大。 1. 2 双线性插值算法作为对最近邻点法的一种改进, 双线性插值算法是利用周围 4 个邻点的灰度值在两个方向上做线性内插以得到待采样点的灰度值! , 即根据待采样点与相邻点 33

自适应Catmull-Rom样条图像放大

自适应Catmull-Rom样条图像放大陈利平【期刊名称】《计算机辅助设计与图形学学报》【年(卷),期】2013(025)002【摘要】Based on a geometric classification, a new image amplification method using adaptive Catmull-Rom interpolation is presented in this paper. Compared to the traditional image reconstruction method using Catmull-Rom interpolation, the proposed method can preserve geometric features well. First, the geometric edges of the original image are classified. Then for the edge pixels in the original image, the tangential direction and tangential length of the Catmull-Rom spline are adjusted accordingly. The experimental results show the feasibility of the method in which the edges in the target image are well preserved.%针对Catmull-Rom样条图像插值放大不能保证图像内各物体之间边界清晰的问题,提出一种基于几何分类的自适应Catmull-Rom样条图像插值放大算法.通过对原图像的边缘进行几何分类,根据原图像的边缘几何类型插值目标图像中的未知像素点；若未知像素点为原图像中的边缘,则调整Catmull-Rom样条的切向方向和切向长度来计算未知像素值,得到边缘保持的目标图像.实验结果表明,应用该算法得到的目标图像边界清晰、细节模糊减少,忠实地反映了原图像的面貌.【总页数】8页(P200-207)【作者】陈利平【作者单位】湖南工学院计算机与信息科学系衡阳421002【正文语种】中文【中图分类】TP391.4【相关文献】1.一种基于C2连续Catmull-Rom样条的图像放大方法 [J], 江巨浪;张佑生;胡连生;薛峰2.带形状因子的C 2连续五次Cardinal样条与Catmull-Rom样条 [J], 李军成;刘成志;易叶青3.基于Canny边缘检测的Catmull-Rom图像放大 [J], 陈利平;刘文华4.三次Catmull-Rom样条保广义凸插值的充要条件 [J], 王子睿;章仁江;金曼莎5.一种自适应Catmull-Rom样条图像缩放算法的设计实现 [J], 魏美荣;蒋林因版权原因，仅展示原文概要，查看原文内容请购买。

基于插值的图像放大技术-报告

西南科技大学专业方向设计报告课程名称：通信专业方向设计设计名称：基于插值的图像放大技术姓名：学号:班级：指导教师：起止日期：西南科技大学信息工程学院制方向设计任务书学生班级：学生姓名：学号：设计名称：基于插值的图像放大技术起止日期：指导教师：方向设计学生日志课程设计评语表基于插值的图像放大技术一、摘要对于位图的放大，提高放大图像的质量是图像放大算法追求的主要目标。

最邻近插值算法是一种最根本、最简单的图像缩放算法，效果也是最不好的，放大后的图像有很严重的马赛克，缩小后的图像有很严重的失真。

双线性插值算法就是一种比较好的图像缩放算法，它充分的利用了原图中待插点四周的四个真实存在的像素值来共同决定目标图中的新像素值，因此缩放效果比简单的最邻近插值要好很多。

二、设计目的和意义图像在计算机里主要有两种存储和表示方法。

矢量图是根据几何特性来绘制图形，矢量可以是一个点或一条线，矢量图只能靠软件生成，文件占用内存空间较小，因为这种类型的图像文件包含独立的分离图像，可以自由无限制的重新组合。

它的特点是放大后图像不会失真，和分辨率无关，适用于图形设计、文字设计和一些标志设计、版式设计等。

矢量图与位图的效果是天壤之别，矢量图无限放大不模糊，大部分位图都是由矢量导出来的，也可以说矢量图就是位图的源码，源码是可以编辑的。

位图图像, 亦称为点阵图像或绘制图像，是由称作像素（图片元素）的单个点组成的。

这些点可以进行不同的排列和染色以构成图样。

当放大位图时，可以看见赖以构成整个图像的无数单个方块。

扩大位图尺寸的效果是增大单个像素，从而使线条和形状显得参差不齐。

然而，如果从稍远的位置观看它，位图图像的颜色和形状又显得是连续的。

相对于缩小,图像放大的应用更加广泛和重要。

例如,目前高端的显示设备越来越普及,但是高分辨率的图像视频的生产远没有跟上显示设备的发展。

如果我们想要得到把原来的图像的高和宽各放大一倍,使用双线性插值技术，那么像素数会增加三倍。

IC芯片数字图像放大方法研究.

IC芯片数字图像放大方法研究引言在数字图像处理过程中，为对图像的细节部分更好进行观察与研究，常常需要对原图像进行清晰放大显示。图像的放大技术成为图像处理技术最基本而且是最重要的研究方向之一。本文在介绍目前数字图像插值放大技术的意义与主要方法之后，论述了图像放大技术在芯片检测中的重要性以及必要性，并通过对数字图像特征进行研究的基础上提出一种基于非均匀有理B样条（NURBS）的数字图像插值放大方法并运用于IC芯片图像检测工作中。此方法能

引言在数字图像处理过程中，为对图像的细节部分更好进行观察与研究，常常需要对原图像进行清晰放大显示。图像的放大技术成为图像处理技术最基本而且是最重要的研究方向之一。本文在介绍目前数字图像插值放大技术的意义与主要方法之后，论述了图像放大技术在芯片检测中的重要性以及必要性，并通过对数字图像特征进行研究的基础上提出一种基于非均匀有理B样条（NURBS）的数字图像插值放大方法并运用于IC芯片图像检测工作中。此方法能够获得稳定清晰的IC芯片放大数字图像，以便用于后续的图像研究处理工作。

1、图像放大在IC芯片检测中的重要性在目前的计算机芯片制造过程中，随着制造技术水平的不断提高，目前微型计算机芯片尺寸参数已经缩小为0.3mm×0.3mm以下，而芯片内部线宽已经达到0.13 以下，显然如此小的尺寸精度是无法采用通常的人眼识别和图像处理技术所能完成的。因此为了更加清楚地对计算机芯片微观表面图像进行检测处理，除了必须对芯片进行光学显微放大外，还需对采集到的图像进行数字图像放大处理。因此，目前计算机芯片的数字图像放大检测分析已经成为了芯片制造检测的重要环节之一。通过芯片整体微观形貌的图像放大，使得后续的图像分析与处理将变得更为简便和精确，而且其图像放大质量将直接影响到后续工作的正常开展以及进行。

2、基于NURBS曲面图像插值放大技术目前，对于一定分辨率的灰度值图像，在图像放大过程中，由于其受到图像信息（像素）数量的限定，不可避免地出现失真，方格化与马赛克化等一系列问题，从而导致失真，方格化与马赛克化等一系列问题，严重影响了后续图像处理工作的正常开展。本文结合自由曲面拟合方面的有关原理，提出一种新的基于NURBS自由曲面插值的图像像素插值放大的方法，应用于计算机芯片图像检测的实践当中[1]。理论研究与实践效果证明，此方法技术可行，结果清晰，实现起来具有一定的特点和优势。

基于非均匀B样条插值算法的图像放大

ｐｏｏｅ．Ｂｈｓｗｙｗｈｃｐｌｓａｎｎｕｉｒａａｔｒａｉｎｍｅｈｄｄｆｒｎｒｍｈｒｄｔｎｌａｇｒｍｓｔｅｒｐｓｄｙｔｉａｉｈａｐｉｏ — ｎｆｍｐｒｍｅｅｉｔｔｏｉｅｅｔｆｅｏｚｏｏｔｅｔｉｏａｏｔａｉｌｉｈ，ｈ
基于非均匀Ｂ样条插值算法的图像放大
冯杰飞，慧健韩
（．１山东经济学院计算机科学与技术学院，济南２０１；２山东省数字媒体技术重点实验室，５０４．济南２０１）５０４
（ｈ＠ｓｉ．ｄ．ｎｈｊｄｅｅｕｃ）
ｉａｅｅｇｓｈｅａｇｒｔｍｎｅｐｌｔｓｔｅｉａｅｅｇｓｗｉｈｔｉｃｂｉｌｏｉｈｗｈｎｉｅｐｏａｉｇ．Ｔｈ，ｔｅｖｉｕｌｅｅｔｍｇｄｅ，ｔｏｈｉｔｒｏａｅｈｍｇｄｅｔｈｅｂ — ｕｃａｇｒｔｍｅｎｔｒｌｔｎｌｉｕｓｈｓａｆｃｏｄｅａｅｏｔｍｉｅｎｅｇｓＣｎｂｐｉｚｄ．ＴｘｒｍｅｔｌｒｓｌｓｓｏｔａｈｍａｅｂｃｍｅｌａｅｄｓｏｈｒｂｙｔｅｎｅｗａＯｎｈｅｅｐｅｉｎａｅｕｔｈｗｈｔｔｅｉｇｅｏｓｃｅｒｒａｍｏｔｅｈｗｙ．ｎ
（．ｃｏｌｆＣｍｕｅＳｉｃｎｅｈｏｏｙｈｎｏｇＥｏｏｗＵｉｒｔｉａｈｎｏｇ２０１，Ｃｉ；１ＳｈｏｏｐｔｃｎｅａｄＴｃｎｌ，ＳａｄｎｃｎｍｎｖｓｙｎｎＳａｄｎ５０４ｈｎｏｒｅｇｅｉ，Ｊａ２ＫｙＬｂｒｔｒｉｉｌｄａＴｃｎｌｙｏＳａｏｇＰｏｉｃ，ＪｎｎＳａｄｎ５０４ｈｎ）．ｅａｏｏｙｏｇｔｉｅｈｏｏｈｎｎｒｖｅｉｈｎｏｇ２０１，ＣｉａｆＤａＭｅｇｆｄｎａａ