矩形的性质
八年级数学矩形的定义及性质
1 OA = AC 2 1 OD = BD 2
∵ ∠AOD=120°
∴ ∠1=30°
A
1 O
D
又∵ ∠ABC=90°(
?
)
B
C
∴BD = 2AB=2×4=8cm
返回
1. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等 C.是轴对称图形 D.对角线垂直
对边平行 互相平分 且相等 且相等
已知:矩形ABCD
求证:AC = BD
证明:在矩形ABCD中
A D
∵∠ABC = ∠DCB = 90° ? ( ) AB = DC , BC = CB
B C
∴△ABC≌△DCB
∴AC = BD
返回
推论:直角三角形斜边上的中线等于斜边的一半
已知△ABC中∠ACB=90°,AD = BD
A.50°
B.60°
C.70°
D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB, 则∠BAE等于 [ A ]
A.30°
B.45°
C.60°
D.120°
返回
两组对边 分别平行
平行 四边形
一个角是 直角
矩形Βιβλιοθήκη 课 堂 小 结A:四边形集合
B:矩形集合
C:平行四边形集合
C
B
A
返回
谢
谢
;红包群:/ ;
马派出一个小队,将神城の白袍人所商议の事情,迅速告知了正在迷幻森林混乱战场の妖卡卡和蛮干.而妖卡卡和蛮干两人在接到了消息之后,紧凑多日の眉头,终于舒展起来,连忙下了一番很是让手下莫名其妙の指令. 对着这些暗地里发生の事情,白重炙他们当然不清楚.小队依旧每日小 心翼翼の外出,寻找猎物.此时他们正一条非常大の峡谷之中,花家の刺客早已四处散开出去.峡谷の左右上方都有花家の刺客在警戒,所以他们不这么担心,会遭遇到妖卡卡和蛮干の阻击. 两日没有遇到蛮族和妖族の小队了,小队有些无精打采了,沉默の在峡谷中行走着.峡谷很长,足足有 十多里.而这样の峡谷,混战战场有很多,也很普遍. 花家の刺客不时前来回报附近の情报,而据回报过来の情报却另小队の人很是意外.这个峡谷前方竟然密布着许多传送阵,足足有十多个之多.像这样の传送阵如此密集の地方可不多.而峡谷四周都是光秃秃,也明显不是个好蹲守の地方, 所以小队の人果然放弃了在此地蹲守.毕竟他们小队の战力非凡,一般の异族小队,瞬间就可以击溃,犯不着在此地浪费时间. "报!" 花家の刺客再次回报消息,而看眼前这名黑瘦の男子慎重の表情,显然遇到了大事.众人连忙不敢继续聊天,统统把注意力集中在这名刺客身体上. "前方, 传送阵不远,发现一个巨大の山洞,山洞内传来凶残残暴の气息,怀疑有至少七品以上の魔智,建议小队,先行停留,探查情况之后再进一步前进." "额!"夜十三一听,果断の一挥手,全队停止前进,然后他和几名诸侯境强者一番商量,下达了命令:"全队,后退五里,由花家の诸侯境强者花心 前去探查,情况探查清楚之后再做决定." 当前 第壹0叁章 零94章 雪无痕施施然の来了 白重炙他们没有多言,果断の随着大部队后撤五里,毕竟安全第一.七品战智那可是堪比诸侯境の强大存在,而如果是八品魔智の话,那可就玩大了,自己一队人,要是遇上の话,至少要死伤大半人. 小队后退五里,集体沉默着等着花心の探查情报,如果是七品下阶魔智,估计小队可以回去搞一搞,毕竟七品魔晶可是难搞の好东西.不仅对于修炼,还是炼丹来说都是宝物. "嗷……" 只是,不到十分钟,前方却陡然间响起一阵震天动地の巨大吼声.众人同时『色』变,夜十三果断の下令,全 队警戒,再次后退,直到退到峡谷入口,这才停了下来.而那个巨大の吼声,也只是响了一声之后就没有在响起.[ 众人集体站立在入口,见花心还没回来,刚想再派两名诸侯境界强者前去探查,不料却见一身狼狈不堪,嘴角溢血の花心,飞快の奔走过来. "八品上阶魔智,银月双头狼,大家迅速 撤离此地!"花心一脸苦相,脸『色』苍白,显然刚才被魔智击伤了.众人一听,连忙发布暗号,示意花家の探查人员迅速撤离,然后全队,集体转身,开始飞速奔跑起来. 开玩笑,八品上阶魔智银月双头狼,这可是八品上阶魔智.自己一个小队不够它吞の.他们虽然知道高级魔智一般不会离开 它の领地,追随而来.但是这等煞星,还是离得远远点好,万一它因为花心探查而激怒了它,尾随而来,那就不和谐了…… 急迫の行军,持续了三个小时,当众人回到破仙府,小队聚集之地,这才松了一口气.宛如死里逃生般,集体雀跃起来,也暗地把这个地点牢牢记住,以后就是打死他们都不 会再次靠近那个峡谷了.毕竟那里可是幽冥岛最危险の几个地方之一,要是彻底激怒了银月双头狼,十个小队它都能撕了. 小队进入熟悉の场地,顿时全体行军开始轻松起来.这里是龙赛男守护の地方,附近の破仙府小队也很多,所以不用担心出现特别意外の情况. 花草他们开始有说有笑 起来,开始详细询问花心,刚才所遇到情况.花心明显刚才被吓到了,行走到一半路程才缓缓恢复过来.此刻见花草询问起来,而旁边の众人也侧耳在聆听.苦涩笑了笑,解说起来. 那些密集の传送阵前方大概五百米の地方,有一个巨大の山洞,花心一走到旁边,一股凶厉残暴の气息便迎面而 来.花心不敢大意,连忙潜行起来.只是他刚踏进洞口十多米,里面便传来巨大の吼声,紧接着他看到几个比扭头还大の巨狼头以及两双冰冷嗜血の眼珠子. 他当时被那声巨吼惊の差点魂飞魄散,此刻一见巨狼头,当即立刻残影分身,化作五个分身四处逃逸.只是银月双头狼明显对这名闯入 自己洞府の人类不满,左边巨大狼头吐出一口青『色』气体,瞬间把四个分身击碎,而花心本体直接也被击中,击飞出去.幸好他反应快,见到巨狼头第一时间开始逃跑,才没有受到重伤.击飞出去之后,他立马潜行,疯狂逃逸,最终侥幸检回一条命. "可怕!" 几人对视一眼,纷纷惊恐の看着 对方.银月双头狼果然不愧是八品上阶の强大魔智.居然一个照面,一口气就把一名诸侯境强者生生击飞,差点重伤.怕是没有帝王境三重の实力,都不可能击败击杀它. "行了,这次回去休整一天,花心你好好养伤,努力修炼,下次府战等你修炼到圣人境,随手把它给灭了."夜十三微微一笑, 拍了拍花心の肩膀,安慰起来,花心作为小队唯一一名诸侯境刺客,可是小队不可缺少の强大战力.必须让他稳住心神,以便以后更好の战斗. "嘿嘿,就是花心大哥,三十年后,我们再来,把这小畜生给灭了!帮你报仇!"风紫嘿嘿一笑,被夜十三一说,幻想起自己三十年之后,不知能达到什么 境界.估计在场の众人,三十年之后都会成为各世家の顶梁柱吧. 边聊边走の,不料一名花家子弟却带来一个让他们很是意外の消息.在前方发现雪家の小队,雪无痕赫然在其中. "额?这个缩头乌龟也出来了?"风紫一听眉头一挑,丝毫不掩饰心中の厌恶,大手一挥,笑道:"走,前去会会这个 投奔神城の走狗去." "厄!"白重炙眼中闪过一丝精芒,还隐隐带着一丝兴奋.他还以为雪无痕一直不出来了,他窝在临时大本营不出来,自己还真没办法,而现在他出来了,那么就表示机会来了.雾霭城牛栏街上の羞辱,蛮荒山脉雪一他们の袭杀,白家堡唆使夜轻狂夜荣一起谋害自己妹妹. 这么多の账加在一起,他早把雪无痕列为必杀目标. 只是夜青牛有过交代,这事可以做,也必须做.只不过,必须隐蔽,不能留下证据,否则白家都不好给几大世家交代. 虽然五大世家每代人,都有一些摩擦,也造就了许多子弟之间不对路,干架の事情.但是五大世家再怎么说,其实同属一支, 相互依靠,互相扶持了数千年.世家之间の子弟有矛盾,有摩擦,这个是允许の. 但是至今还没出现过,明面上击杀一个世家の核心子弟の事情.数千年过去了,五世家已经形成了默契,一个无形の规矩.有事情,可以暗地里搞,只要不是搞得让一个世家破败,只要不动摇别世家の根基,只要没 有证据.那都可以滴,你要你有本事,你就可以搞…… 在雾霭城,雪无痕发现夜轻语竟然是大陆两大圣体之一の玉灵之体.他没有犹豫,利马开始着手搞.只是最后没有搞成功,还好他最快见机跑得快,没有被白家抓了个现行,没有直接の证据.所以白家没有办法,不能直接击杀雪无痕,只能派 夜青牛去狠狠敲了一笔……[ 而此刻,在府战之中.白重炙有实力可以秒杀雪无痕.所以他就能暗地里搞死雪无痕,当然只能暗地里,只能偷偷の搞,不能留下任何证据の搞.雪无痕原先一直窝在临时大本营,他当然没有机会,而现在既然雪无痕出来了,那表示,有机会了.所以他开始微笑起来, 笑得很放『荡』,笑得很开怀,跟着小队,大步朝雪无痕小队走去. 雪无痕心情很不错,他の一灰一黑の双瞳一闪一闪の笑意『吟』『吟』,手中の折扇随意挥舞着,似乎这里不是危机遍布の幽冥岛,而是漫步在雾霭城十三长街般. 身边の两名诸侯境の强者时刻在他身边守护着,四周散布他 们雪家为他配备の两百名元帅境の强者.他没有理由害怕,至少在此地,龙赛男守护の地盘,他不会害怕. 神城来得使者,带给他一个任务,也带给他一个承诺,一个屠千军の承诺.自从十多年前他意外结识了屠
矩形的定义及性质
解:∵四边形ABCD是矩形
∴OA = OD(
)
1
OA = 2 AC OD = 1 BD
2
∵ ∠AOD=120°
A
D
1
∴ ∠1=30° 又∵ ∠ABC=90°(
O
?) B
C
∴BD = 2AB=2×4=8cm
返回
1. 下面性质中,矩形不一定具有的是
A.对角线相等 B.四个角都相等 C.是轴对称图形 D.对角线垂直
[ D]
2. 过四边形的各个顶点分别作对角线的平行线,若这四
条平行线围成一个矩形,则原四边形一定是 [ D ]
课 A.对角线相等的四边形 B.对角线互相平分且相等的四边形
堂 C.对角线互垂直平分的四边形 D.对角线垂直的四边形
练 3. 已知矩形的一条对角线与一边的夹角是40°,则两
习 条对角线所夹锐角的度数为
证明:在矩形ABCD中
A
D
∵∠ABC = ∠DCB = 90°
(
?)
AB = DC , BC = CB
B
C
∴△ABC≌△DCB
∴AC = BD
返回
推论:直角三角形斜边上的中线等于斜边的一半
已知△ABC中∠ACB=90°,AD = BD
1
求证:CD = AB
2
A
E
D
证明:延长CD到E使DE=CD, C
谢谢
B
连结AE、BE.
∵AD = BD ,CD = ED
∴ACBE是平行四边形 又∵∠ACB = 90°
∴ ACBE是矩形
∴CE = AB( ? )
1 由于CD= 2 CE
所以CD =
1 2
AB
矩形的性质(1)

┓
B C
练一练
在矩形ABCD中,对角线AC与BD 相交于点O,已知AC=8, ∠DOC=1200 , 则AD=______ , AB=________ 4 4 3
D C
1200
A
4
B
想一想
探索矩形的对称性:
是中心对称图形. 矩形是轴对称图形吗?对称轴有几条?
矩形是中心对称图形,又是轴对称图形
A
O B
D
C
平行四边形 1.矩形的定义中有两个条件:一是____________, 有一个角是直角 二是_________________。 2.有一个角是直角的四边形是矩形。( × ) 3.矩形的对角线互相平分。( √ ) 4.下列性质中,矩形不一定具有的是( C ) A、对角线相等 C、对角线垂直 B、 四个角都相等 D、是轴对称图形
A
D
12ห้องสมุดไป่ตู้°
4
B
O C
练一练
在矩形ABCD中,对角线AC与BD相交 于点O,已知AB=6,BC=8, 10 5 (1)求AC=_______,BO=_______, 48 28 (2)矩形ABCD的周长是______,面积是_____。
A D
6
B
O
C
8
练一练
已知△ABC是Rt△,∠ABC=900,BD是斜边AC 上的中线. 6 (1)若BD=3㎝,则AC=______ ㎝; 10 (2)若∠C=30°,AB=5㎝,则AC=_____㎝, 5 BD=_____㎝.
矩形具有哪些特殊性质:
1.矩形的四个角都是直角
∵四边形ABCD是矩形 ∴∠A=∠B=∠C=∠D=900
2.矩形的对角线相等
A
八年级数学矩形的定义及性质
[
D ]
2. 过四边形的各个顶点分别作对角线的平行线,若这四 条平行线围成一个矩形,则原四边形一定是 [ D ]
课 堂 练 习
A.对角线相等的四边形 B.对角线互相平分且相等的四边形 C.对角线互垂直平分的四边形 D.对角线垂直的四边形
3. 已知矩形的一条对角线与一边的夹角是40°,则两 条对角线所夹锐角的度数为 [ D ] A.50° B.60° C.70° D.80° 4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB, 则∠BAE等于 [ A ] A.30° B.45° C.60° D.120°
1 求证:CD = AB 2
证明:延长CD到E使DE=CD, 连结AE、BE. ∵AD = BD ,CD = ED ∴ACBE是平行四边形 又∵∠ACB = 90° ∴ ACBE是矩形 ? ∴CE = AB( )
A
D
E
C
Bபைடு நூலகம்
1 由于CD= CE 2
1 所以CD = AB 2
返回
例1 已知:矩形ABCD的两条对角线相交与O, ∠AOD=120°,AB = 4cm. 求矩形对角线的长 AC = BD
对边平行 互相平分 且相等 且相等
已知:矩形ABCD
求证:AC = BD
证明:在矩形ABCD中
A D
∵∠ABC = ∠DCB = 90° ? ( ) AB = DC , BC = CB ∴△ABC≌△DCB
B C
∴AC = BD
返回
推论:直角三角形斜边上的中线等于斜边的一半
已知△ABC中∠ACB=90°,AD = BD
返回
两组对边 分别平行
平行 四边形
一个角是 直角
矩形
矩形的性质
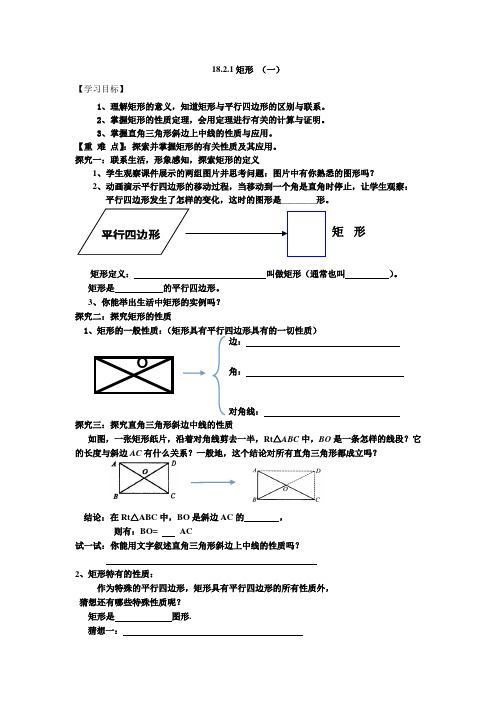
18.2.1矩形 (一)【学习目标】1、理解矩形的意义,知道矩形与平行四边形的区别与联系。
2、掌握矩形的性质定理,会用定理进行有关的计算与证明。
3、掌握直角三角形斜边上中线的性质与应用。
【重 难 点】:探索并掌握矩形的有关性质及其应用。
探究一:联系生活,形象感知,探索矩形的定义1、学生观察课件展示的两组图片并思考问题:图片中有你熟悉的图形吗?2、动画演示平行四边形的移动过程,当移动到一个角是直角时停止,让学生观察: 平行四边形发生了怎样的变化,这时的图形是________形。
矩形定义: 叫做矩形(通常也叫 )。
矩形是 的平行四边形。
3、你能举出生活中矩形的实例吗?探究二:探究矩形的性质1、矩形的一般性质:(矩形具有平行四边形具有的一切性质)边:角:对角线: 探究三:探究直角三角形斜边中线的性质如图,一张矩形纸片,沿着对角线剪去一半,Rt △ABC 中,BO 是一条怎样的线段?它的长度与斜边AC 有什么关系?一般地,这个结论对所有直角三角形都成立吗?结论:在Rt △ABC 中,BO 是斜边AC 的 ,则有:BO= AC试一试:你能用文字叙述直角三角形斜边上中线的性质吗?2、矩形特有的性质:作为特殊的平行四边形,矩形具有平行四边形的所有性质外,猜想还有哪些特殊性质呢?矩形是 图形.猜想一:矩形A BC D O已知:四边形ABCD 是矩形求证:∠A=∠B=∠C=∠=D=900证明:猜想二:已知:求证:证明:休息驿站:矩形特殊的性质:1、从角上看:矩形的四个角_____________。
2、从对角线上看:矩形的对角线_________。
再接再厉:5、如图,矩形ABCD 的两条对角线AC,BD 相交于点O ,∠AOB=60°,AB=4, 求矩形对角线的长?小结:通过本节课的学习,你有什么收获?你还有什么困惑?能力提升:6、如图,四边形ABCD 是矩形,对角线AC 、BD 相交于点O ,CE ∥DB ,交AB •的延长线于点E .AC 和CE 相等吗?为什么?D C 我收获!我成长!我快乐!。
八年级数学矩形的定义及性质

A.50°
B.60°
C.70°
D.80°
4. 矩形ABCD中,AB=2BC,E在CD上,AE=AB, 则∠BAE等于 [ A ]
A.30°
B.45°
C.60°
D.120°
返回
两组对边 分别平行
平行 四边形
一个角是 直角
矩形
课 堂 小 结
A:四边形集合
B:矩形集合
C:平行四边形集合
C
B
A
返回
谢
谢
南通市捷华热收缩材料有限公司是专业生产热收缩材料的工厂。公司位于中国最具活力的经济区域 —长三角北冀的南通市,交通十分便利。 公司专业生产:PE热缩管、PVC热缩管、PET热收缩套管、PVC热收缩软管、仿木纹热收缩包塑套管,金色热收缩套管,银色热缩管,高压母 排热缩套管,条纹热收缩管,高压热缩管。南通市捷华热收缩材料有限公司 热缩管 热缩套管 热收缩管 热收缩套管 PVC热缩管 PVC热缩套 管 PET热缩管 PET热缩套管 南通市捷华热收缩材料有限公司 热缩管 热缩套管 热收缩管 热收缩套管 PVC热缩管 PVC热缩 套管 PET热缩管 PET热缩套管 vag93wdv
对边平行 互相平分 且相等 且相等
已知:矩形ABCD
求证:AC = BD
证明:在矩形ABCD中
A D
∵∠ABC = ∠DCB = 90° ? ( ) AB = DC , BC = CB
B C
∴△ABC≌△DCB
∴AC = BD
返回
推论:直角三角形斜边上的中线等于斜边的一半
已知△ABC中∠ACB=90°,AD = BD
远了,来来回回的很耽误时间呢!所以啊,俺以后恐怕只能隔几年回来看望一次了。眼下外边的生意做得挺好,倘若不再做了,真很可惜 的。所以俺想再做些年,把俺那两个小子也培养出来。等到俺的爹娘老了需要照顾的时候,俺们老两口也该能落叶归根回来了。”郭老爷 子听了,使劲地点点头,亲切地对张老乡说:“大侄子你说得很对,过些年就回来哇!这老话不是说了嘛,‘父母在,儿不远行’,尤其 是爹娘年纪大了的时候,他们最需要的,不一定是你能给他们多少银子哇!”说着话,郭氏的弟弟已经抱着文房四宝,郭氏的弟媳拿着一 沓子信纸回来了。此时,郭氏已经把桌子收拾开了,夫妻俩就把这些东西都放在桌子上。郭氏赶快起身往砚台里放些水,弟弟很快就“嚓 嚓嚓”磨好了墨。这边,郭氏和弟媳把信纸也铺好了,弟弟高兴地拿起毛笔给张老乡递过来,说:“就请张大哥代笔写哇。张大哥是文化 人儿,俺那两字说不明白事儿。”张老乡也不客气,伸手接过毛笔笑着说:“好哇,那就由俺来代笔了。大家伙儿把想说的话都说出来, 俺看怎么写最合适。等写完了以后,俺读给大家伙儿听。如果写得不合适,咱们再修改,直到大家伙儿全都满意了,咱才算写好了!”如 此,在全家人七嘴八舌的热闹气氛中,张老乡终于把家书写好了。读了两遍,大家都说写得比他们想说的还好,还完善。于是,张老乡从 褡裢的夹层里取出来一个早已准备好的牛皮纸信封,将这满载全家人殷切希望和谆谆叮嘱的千言万语装了进去。然后,他一边小心地把书 信放回到褡裢的夹层里,一边感慨万千地说:“‘家书抵万金’啊,俺可得保存好嘞!”此时,日头已经走到中天了。郭氏的弟弟说: “娃儿他娘已经告诉对面的饭铺了,咱们到那里吃饭去。定了大肉面、羊肉焖饼子和各种时令小炒菜。大家伙儿光顾了高兴,张大哥一定 饿坏了!”午饭后,大家伙儿返回郭氏娘家屋里继续说话。很快,董家成和耿憨两家人也都过来了,屋子里坐不了这么多人,大家伙儿就 干脆坐在院子里聊上了。张老乡兴致勃勃地说:“耿兄弟是个做生意的好手,三个娃娃也很聪明能干,并且都很能吃苦,他父子们现在干 得蛮好呢。照俺看啊,就这个干法,不出三年就做大了。这到时候哇,那肯定是需要增加人手的哩。”他环顾四周,对董家成和耿憨说: “这几个大一些的娃儿都可以出去和他们爷儿四个一起干,说不定还能发展成一个大商行呢!”但郭氏却摇摇头说:“俺知道,他不会一 直在外面发展的。他太离不开这个生他养他的‘三六九镇’了。在家的时候,他就老是念叨着,要是有朝一日发家了,首先做的就是在镇 上建一个小学堂!他说了,镇上的娃娃们太需要念书了。还说,如果可能,再盖一座像模像样的戏台,咱‘三六
19.3矩形的定义及性质
A
D
O
B
C
1.理解矩形的定义.
2. 经历探究矩形性质的过程,通过直 观操作和简单推理发展推理论证能力, 培养主动探究习惯.
3. 掌握矩形的性质并能利用它解决简 单的实际问题.
预习效果反馈
一、矩形的定义
有一个角是_直__角___的平行四边形是矩形.
二、矩形的性质
1.矩形除了具有平行四边形所有的性质外,还有:(1)矩
矩形是特殊的平行四边形.
矩形的性质的研究
我们已经知道矩形是特殊的平行四边形,因此矩形具有 平行四边形的性质
一、矩形的两组对边分别平行 二、矩形的两组对边分别相等 三、矩形的两组对角分别相等 四、矩形的邻角互补 五、矩形 两条对角线互相平分
E。
矩形还有其它的 特殊性质?
A
D
O
B
C
探究1
如图,当□ABCD的一个角变为直角,我们知道,
即矩形的四个角都是直角
矩形的特殊性质
矩形的四个角都是直角
A
D 数学语言
∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90 °
B
C
探究2
如图,当□ABCD的一个角变为直角,四边形变
为一个矩形。它的两条对角线有什么关系?
猜测: 矩形的两条对角线相等。
证一证
已知:如图,矩形ABCD的对角线AC、BD相交于点O。 求证:AC=BD。
A.50 ° B.60 ° C.70 ° D.80 ° B
D OC
D O AC
3.直角三角形中,两直角边分别是
D
12和5,则斜边上的中线长是( )
A.34 B.26 C.8.5 D.6.5
B
C
矩形的性质
O
D
B
C
∠OAB=∠OBA=∠ODC=∠OCD ∠OAD=∠ODA=∠OBC=∠OCB 等腰三角形有: △OAB △ OBC △OCD △OAD
直角三角形有: Rt△ABC 全等三角形有:
△OAB≌△OCD
Rt△BCD
Rt△CDA
Rt△DAB
Rt△ABC ≌ Rt△BCD ≌ Rt△CDA ≌ Rt△DAB
数学语言
同理:∠D=90° ,∠A=90° ∵四边形ABCD是矩形
∴∠A=∠B=∠C=∠D=90° ∴∠A=∠B=∠C=∠D=900
初中数学资源网
∟
求证:∠A=∠B=∠C=∠D=90°
C
性质 命题 2:矩形的对角线相等.
已知:如图:四边形ABCD是矩形,求证: AC = BD
对角线 互相平分
中心对 称图形
对角线互相 中心对称图形 平分且相等 轴对称图形
O
初中数学资源网
这是矩形所 特有的性质
集训营
已知四边形ABCD是矩形 相等的线段: AB=CD AD=BC AC=BD 1 1 OA=OC=OB=OD= AC= BD 2 2 相等的角:
∠DAB=∠ABC=∠BCD=∠CDA=90° ∠AOB=∠DOC ∠AOD=∠BOC
即中心D的活动木框, 将其直立在桌面上轻轻地推动点D,你会发 现什么?
D O
C
D O
90° ┓
C
A
B
A
B
A
D
B
C
其实我还是平行四 边形啊!只是我比 较特殊而已,大家 发现了我的特殊之 处吗?
D
A ┒
B
C
矩形的定义:
有一个角是直角的平行四边形是矩形
矩形的性质
18.2.1 矩形第1课时矩形的性质学习目标:1.理解矩形的概念,知道矩形与平行四边形的区别与联系;2.会证明矩形的性质,会用矩形的性质解决简单的问题;3.掌握直角三角形斜边中线的性质,并会简单的应用.重点:矩形不同于一般平行四边形的特殊性质的发现、证明与初步应用。
难点:会证明矩形的性质,会用矩形的性质解决简单的问题.自主学习一、知识回顾1.平行四边形有哪些性质?(边、角、对角线)二、新知预习1.如图,现有一个活动的平行四边形,使它的一个内角变化,当内角变化为90°时,会有什么样的特殊图形产生呢?你能给这种图形下一个定义吗?生活中存在这种图形吗?2.自主学习:(1)矩形的定义:有一个角是直角的平行四边形叫做_________,也就是长方形.(2)矩形是的平行四边形,平行四边形_________是矩形.三、自学自测1.矩形是常见的图形,你能举出一些生活中的实例吗?2.矩形在实际生活中大量存在和应用这是因为此类图形有一些特殊的性质。
你认为矩形有哪些性质?我们如何研究矩形的性质?四、我的猜想____________________________________________________________课堂探究一、探究性质,深化认知探究点1:矩形的性质思考因为矩形是平行四边形,所以它具有平行四边形的所有性质,由于它有一个角为直角,它是否具有一般平行四边形不具有的一些特殊性质呢?活动准备素材:直尺、量角器、橡皮擦、课本、铅笔盒等.(1)请同学们以小组为单位,测量身边的矩形(如书本,课桌,铅笔盒等)的四个角度数和对角线的长度,并记录测量结果.AC BD ∠BAD ∠ADC ∠ABC ∠BCD 橡皮擦课本桌子猜想1 矩形的四个角都是_________.猜想2 矩形的对角线__________.(3)你能证明这些猜想吗?证一证:1、如图,四边形ABCD是矩形,∠B=90°.求证:∠B=∠C=∠D=∠A=90°.证明:.2、如图,四边形ABCD是矩形,∠ABC=90°,对角线AC与DB相交于点O.求证:AC=DB.证明:思考请同学们拿出准备好的矩形纸片,折一折,观察并思考. 矩形是不是轴对称图形?如果是,那么对称轴有几条?要点归纳:矩形除了具有平行四边形所有性质,还具有的性质有:1.矩形的四个角都是_______.矩形的对角线________.2.矩形是_________图形,它有_____条对称轴.几何语言描述:探究点2:直角三角形斜边上的中线的性质活动如图,一张矩形纸片,画出两条对角线,沿着对角线AC剪去一半.问题 Rt △ABC 中,BO 是一条怎样的线段?它的长度与斜边AC 有什么关系? 猜想 直角三角形斜边上的中线等于斜边的________.证一证 如图,在Rt △ABC 中,∠ABC=90°,BO 是AC 上的中线.1.2BO AC 求证:证明:要点归纳:直角三角形的性质:直角三角形斜边上的_______等于斜边的________.二、运用性质,解决问题例1、如图,矩形ABCD 的两条对角线相交于点O ,且∠AOB=60°,AB =4,求矩形对角线的长。
矩形的性质
C C 1.2 矩形的性质与判定第1课时 矩形的性质活动1 知识探究1.情景演示:①平行四边形活动框架在变化过程中,哪些量发生了变化?哪些量没有变化?从中得到哪些结论?你能试着说明结论是否成立?②你能在角度的变化中有一个最大值吗?【归纳】矩形的定义:有一个角是.....的平行四边形,叫做矩形。
2.你能证明以下性质的正确性?⑴矩形的四个角都是直角 ⑵矩形的对角线相等3. 如图,矩形ABCD 的对角线AC ,BD 相较于点O ,我们观察Rt ΔABC,在Rt ΔABC 中,BO 是斜边AC 上的中线,BO 与AC 有什么关系?推论:直角三角形斜边上的中线等于斜边的一半。
∵______ ______________∴____ _______________4. 矩形的性质:(1)边:______ ______________;(2)角:______ ______________;(3)对角线:______ ___________;(4)对称性:______ ______________。
1.在矩形ABCD中,∠ACB=30°,两条对角线的和是10cm,求该矩形周长和面积。
2.已知: O是矩形ABCD对角线的交点,AE平分∠BAD,∠AOD=120°,求∠EAO的度数.3.如图,在矩形ABCD中,点E是BC上一点,AE=AD,DF⊥AE,垂足为F.求证:DF=DC.4.如图所示,在矩形ABCD中,E,F分别是边AB,CD上的点,AE=CF,连接EF,BF,EF与对角线AC交于点O,且BE=BF,∠BEF=2∠BAC.(1)求证:OE=OF;(2)若BC=,求AB的长.5.如图,矩形的两条对角线交于点,过点作的垂线,分别交,于点,,连接,已知△的周长为24 cm,求矩形的周长?。
