log算子的基本原理
log算子计算公式

log算子计算公式Logarithmic Functions: Understanding and Applications。
Introduction。
Logarithmic functions, often denoted as log, are an important mathematical concept that is widely used in various fields such as science, engineering, finance, and computer science. In this article, we will explore the properties of logarithmic functions, their applications, and how they can be used to solve real-world problems.Properties of Logarithmic Functions。
The logarithmic function is the inverse of the exponential function. In other words, if y = b^x, then x = log_b(y), where b is the base of the logarithm. The most commonly used base for logarithms is 10 (denoted as log), and the natural logarithm with base e (denoted as ln). The logarithm of a number represents the exponent to which the base must be raised to produce that number. For example, log_10(100) = 2, because 10^2 = 100.Logarithmic functions have several important properties that make them useful in various applications. One of the key properties is the product rule, which states thatlog_b(xy) = log_b(x) + log_b(y). This property allows us to simplify complex expressions involving multiplication into simpler forms.Another important property is the quotient rule, which states that log_b(x/y) =log_b(x) log_b(y). This property allows us to simplify complex expressions involving division into simpler forms.Applications of Logarithmic Functions。
matlab数字图像处理实验报告

《数字图像处理实验报告》实验一图像的增强一.实验目的1.熟悉图像在MATLAB下的读写、输出;2.熟悉直方图;3.熟悉图像的线性指数等;4.熟悉图像的算术运算和几何变换。
二.实验仪器计算机、MATLAB软件三.实验原理图像增强是指根据特定的需要突出图像中的重要信息,同时减弱或去除不需要的信息。
从不同的途径获取的图像,通过进行适当的增强处理,可以将原本模糊不清甚至根本无法分辨的原始图像处理成清晰的富含大量有用信息的可使用图像。
其基本原理是:对一幅图像的灰度直方图,经过一定的变换之后,使其成为均匀或基本均匀的,即使得分布在每一个灰度等级上的像素个数.f=H等或基本相等。
此方法是典刑的图像空间域技术处理,但是由于灰度直方图只是近似的概率密度函数,因此,当用离散的灰度等级做变换时,很难得到完全平坦均匀的结果。
频率域增强技术频率域增强是首先将图像从空间与变换到频域,然后进行各种各样的处理,再将所得到的结果进行反变换,从而达到图像处理的目的。
常用的变换方法有傅里叶变换、DCT变换、沃尔什-哈达玛变换、小波变换等。
假定原图像为f(x,y),经傅立叶变换为F(u,v)。
频率域增强就是选择合适的滤波器H(u,v)对F(u,v)的频谱成分进行处理,然后经逆傅立叶变换得到增强的图像。
四.实验内容及步骤1.图像在MATLAB下的读写、输出;实验过程:>> I = imread('F:\image\');figure;imshow(I);title('Original Image');text(size(I,2),size(I,1)+15, ...'', ...'FontSize',7,'HorizontalAlignment','right');Warning: Image is too big to fit on screen; displaying at 25% > In imuitools\private\initSize at 86In imshow at 1962.给定函数的累积直方图。
一种改进的自适应各向异性LOG算子

如果 将 这个 椭 圆 以坐 标 原 点 为 中心 向逆 时针 方 向转 角度 , 据解 析 几何 的方 法 可计 算 出该 椭 根
再将 式 ( )的角 度信 息 量 带 人 式 ( )中 , 得 4 1 可
新 的 L G边缘检 测算 子公 式 : O
E:
oy
( ) ,) ,
() 6
式 ( ) , , ) 高斯 滤 波算 子 , ( ) 6 中 G( Y 为 l , 为 o
G ( Y = { [ XO / + yit oa) D , ) ( CSO s xs nc
2 1 各 向异性 L G算 子 . O 常用 的二 维 L G算 子 在 方 向与 Y方 向对 6 O
工 作 ,esbok等 提 出 了一 种 快 速 各 向异 性 高 斯 G uere
滤 波方 法 J这种 滤波 器 通过 在 两 个 不 同方 向上 选 ,
用 不 同的高 斯尺 度 , 而使 滤 波器 可 以在 去 噪 时较 从 好保 留图象边 缘 等重 要 信 息 , 利 用 高 斯 函数 的可 并
分解 性 将 滤 波器 沿 长 轴 和 短 轴 方 向分 解 为 两 个 一
取 不 同值 就 可 以得 到 各 向异 性 L G算 子 。L G O O
算 子变 为 :
维 滤波 算子 与 图像 卷 积 , 计 算 简 化 , 这 种 滤 波 使 但 器 的长 短 轴长 度 固定 , 能 自适 应 改 变 。文 献 [ ] 不 2
第 1 0卷
【国家自然科学基金】_log算子_基金支持热词逐年推荐_【万方软件创新助手】_20140802
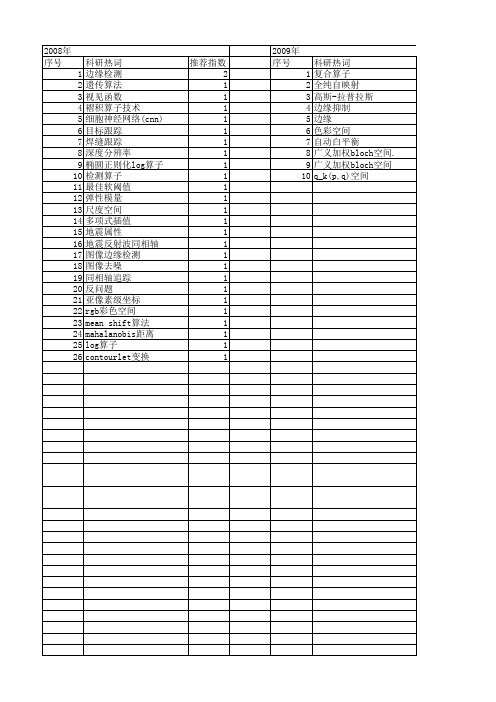
2012年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47
科研热词 推荐指数 图像处理 3 边缘检测 2 非采样contourlet变换 1 阈值法 1 错误注入 1 边缘提取 1 跟踪分组 1 贝尔面瘫 1 角点检测 1 红外图像 1 紧性 1 空间灰度矩 1 穴位定位 1 短间隙真空电弧 1 真空开关 1 直线提取 1 椭圆提取 1 树木年轮图像 1 有界性 1 最小二乘法 1 日志挖掘 1 形态学去噪 1 年轮识别 1 嵌入型钢坯字符 1 尺度空间 1 小波变换 1 安全性测试 1 多尺度边缘检测 1 复合算子 1 图像压缩 1 区域填充 1 加权bloch空间 1 关联规则挖掘 1 qk(p 1 q)空间 1 nonsubsampled contourlet transform 1 multiresolution edge detection1 log算子 1 log函数 1 log operator 1 k-carleson测度 1 image processing 1 ihs变换 1 ihs transform 1 hough变换 1 harris特征点 1 harris-laplace算子 1
推荐指数 2 2 2 2 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
2014年 序号 1 2 3 4 5 6 7 8 9 10 11 12 13 14
2014年 科研热词 高斯拉普拉斯算子 高斯型拉普拉斯变换 霍夫变换 阈值去噪 边缘信息 绝对角度 椭圆对称 最小生成树 文字笔画提取 小波系数能量 基于内容图像检索 偏振定标 一阶导阈值 log算子 推荐指数 1 1 1 1 1 1 1 1 1 1 1 1 1 1
二阶椭圆微分算子拉普拉斯算子

二阶椭圆微分算子拉普拉斯算子
二阶椭圆微分算子拉普拉斯算子(Laplace Operator)是一种广泛应用于图像处理和
偏微分方程领域的算子。
它既可以应用于欧几里得空间中的梯度(f)的散度(·f)运算,也可以推广到黎曼流形上的椭圆型算子,称为拉普拉斯-贝尔特拉米算子。
在图像处理领域,拉普拉斯算子常用于边缘检测。
其原理是利用拉普拉斯算子对图像进行滤波,从而锐化图像边缘。
拉普拉斯算子主要包括以下几种:
1. 二维拉普拉斯算子:应用于二维图像处理,可以检测图像中的边缘。
常见的二维拉普拉斯算子有Prewitt算子、Sobel算子和Roberts算子等。
2. 三维拉普拉斯算子:应用于三维图像处理,可以检测图像中的边缘。
常见的三维拉普拉斯算子有LoG算子和DoG算子等。
在偏微分方程领域,拉普拉斯算子主要用于求解椭圆型偏微分方程。
拉普拉斯算子对偏微分方程的解具有降维作用,可以将高维问题转化为低维问题求解。
此外,拉普拉斯算子还应用于偏微分方程的数值计算方法,如有限差分法、有限元法等。
总之,二阶椭圆微分算子拉普拉斯算子是一种重要的数学工具,在图像处理和偏微分方程领域具有广泛的应用价值。
1-边缘检测-sobel等解析

0 -4 8 -4 0
1 1 5 1 1
1 1 5 1 1
1 1 5 1 1
1 5 1 1
图像
拉普拉斯算子的分析: 缺点:对噪音的敏感;不能检测出边的方向
应用:拉普拉斯算子不直接用于边的检测,通常 只起辅助的角色;
检测一个像素是 在边的 亮的一边还是暗的一边 利用零跨越,确定边的位置
拉普拉斯高斯算法
0交叉点
理论曲线 实际曲线
一阶导数 二阶导数
(a)阶跃函数 (b)线条(屋顶)函数
两种常见的边缘一阶导数和二阶导数示意图
图像
水平方 向剖面
一阶导数
二阶导数
阶梯状-处于图像中 2个具有不同灰度值 的相邻区域之间
脉冲状-对应细 条状的灰度值突 变区域
屋顶状-上 升下降沿都 比较缓慢
一阶导数在图像由暗变明的 位置处有1个向上的阶跃,而 其它位置都为0,这表明可用 一阶导数的幅度值来检测边 缘的存在,幅度峰值一般对 应边缘位置 对(a、b) 而言
实现边缘检测有两种方法 一阶导数法:用梯度算子来计算 二阶导数法:用拉普拉斯算子来计算
边缘检测
一阶导数可以用于 检测图像中的一个 点是否在斜坡上. 二阶导数的符号可 以用于判断一个边 缘点.是在边缘亮的 一边还是暗的一边.
(1)对图像中的每条 边缘二阶导数生成 两个值 斜坡数字边缘模型 (2)一条连接二阶导 数正极值和负极值 斜坡部分与边缘的 的虚构直线将在边 模糊程度成正比. 缘中点附近穿过零 点.据此可以用于确 定粗边线的中心.
该算子没有把重点放在接近模板中心的 像素点. |Sx| 产生最强的响应是正交于x轴的边; |Sy| 则是正交于y轴的边。
边缘检测
给定图像中的一个 3*3区域,使用下面的边缘检测滤波 器进行检测,它们都使用一阶导数
特征提取

21
特征提取 –点特征提取算子
Förstner算子 (5) 选取极值点。
3)给定阈值Tq,若限制误差椭圆长短半轴之比不得大于3.2 - 2.4,则可求得Tq =0.32 – 0.5 若qc,r > Tq,则该像素为一备选点,按以下原则确定其权:
4)以权值为依据,选取一适当窗口中的极值点为特征点,即选 取窗口中权最大者为权值点。
2015年6月12日星期五
5
特征提取 – 影像信息量与特征
比特分割
比特分割是一种简单的方法。由于在影像数字化时,像元灰 度量化为256个灰度等级,即8个比特,比特分割就是用于确定 哪几位比特是信号,哪几位是噪声。 具体:比特分割就是将量化后的数据分成不同的比特位,依 次取出某一比特位上的值(0或1)形成二值图像。
2015年6月12日星期五
11
特征提取
影像信息量与特征
点特征提取算子
线特征提取算子
影像分割
定位算子
2015年6月12日星期五
12
特征提取 –点特征提取算子
点特征主要指明显点,如角点、圆点等。提取点特征的算子 称为兴趣算子(interest operator),即运用某种算法从影像中 提取我们所感兴趣的,即有利于某种目的的点。现在已提出了 一系列算法各异,且具有不同特色的兴趣算子,比较知名的有 Moravec算子、 Förstner算子与 Harris算子等。
若不考虑噪声,点特征与边缘特征的灰度分布均表现为从 小到大或从大到小的明显变化。
2015年6月12日星期五
10
特征提取 – 影像信息量与特征
特征
除了用局部信息量来检测特征之外,还可以利用各种梯度 或差分算子提取特征,其原理是对各个像素的邻域即窗口进 行一定的梯度或差分运算,选择其极值点(极大或极小)或超 过给定阈值的点作为特征点。
图像边缘检测各种算子MATLAB实现以及实际应用

《图像处理中的数学方法》实验报告学生姓名:***教师姓名:曾理学院:数学与统计学院专业:信息与计算科学学号:********联系方式:139****1645梯度和拉普拉斯算子在图像边缘检测中的应用一、数学方法边缘检测最通用的方法是检测灰度值的不连续性,这种不连续性用一阶和二阶导数来检测。
1.(1)一阶导数:一阶导数即为梯度,对于平面上的图像来说,我们只需用到二维函数的梯度,即:∇f=[g xg y]=[ðf ðxðfðy],该向量的幅值:∇f=mag(∇f)=[g x2+g y2]1/2= [(ðf/ðx)2+(ðf/ðy)2]1/2,为简化计算,省略上式平方根,得到近似值∇f≈g x2+g y2;或通过取绝对值来近似,得到:∇f≈|g x|+|g y|。
(2)二阶导数:二阶导数通常用拉普拉斯算子来计算,由二阶微分构成:∇2f(x,y)=ð2f(x,y)ðx2+ð2f(x,y)ðy22.边缘检测的基本思想:(1)寻找灰度的一阶导数的幅度大于某个指定阈值的位置;(2)寻找灰度的二阶导数有零交叉的位置。
3.几种方法简介(1)Sobel边缘检测器:以差分来代替一阶导数。
Sobel边缘检测器使用一个3×3邻域的行和列之间的离散差来计算梯度,其中,每行或每列的中心像素用2来加权,以提供平滑效果。
∇f=[g x2+g y2]1/2={[(z7+2z8+z9)−(z1+2z2+z3)]2+[(z3+2z6+z9)−(z1+2z4+z7)]2}1/2(2)Prewitt边缘检测器:使用下图所示模板来数字化地近似一阶导数。
与Sobel检测器相比,计算上简单一些,但产生的结果中噪声可能会稍微大一些。
g x=(z7+z8+z9)−(z1+z2+z3)g y=(z3+z6+z9)−(z1−z4−z7)(3)Roberts边缘检测器:使用下图所示模板来数字化地将一阶导数近似为相邻像素之间的差,它与前述检测器相比功能有限(非对称,且不能检测多种45°倍数的边缘)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于双边滤波的LOG边缘检测算法摘要:传统LOG边缘检测算法采用高斯函数滤波时,尽管抑制了噪声,但同时也损坏了部分低强度边缘。
针对这一问题,本文提出了结合双边滤波的LOG边缘检测算法,首先采用双边滤波来替代传统LOG算子中的高斯滤波,然后计算平滑后图像的拉普拉斯,最后提取运算后的零交叉点作为图像的边缘。
实验表明,改进后的LOG算法能有效抑制噪声,较好地保护边缘,提高了检测精度,减少伪边缘数,相对传统LOG算法具有更好的检测效果。
关键字:LOG算子;双边滤波;边缘保护;边缘检测1.引言边缘是指图像局部强度变化最显著的部分,反映了图像中物体最基本的特征,是对图像进行分割、理解以及检索的重要依据。
边缘检测一直是图像处理中的热点和难点[]1。
由于数字图像中可能包含不同程度的噪声,使得边缘检测在图像处理中比较困难。
经典的边缘检测算子,如Robert、Prewitt、Sobel等[]2,简单、易于实现,但对噪声敏感、抗干扰性能差。
Marr边缘检测算法[]3克服了一般微分运算对噪声敏感的缺点,利用能够反映人眼视觉特性的LOG算子对图像的边缘进行检测。
该方法在图像边缘检测中具有一定的优势,然而在实际应用中,边缘检测算法仍然存在着一定的问题。
比如尺度因子无法自适应调整、模板的尺寸对检测结果影响比较大、零穿越结果无法区分像素反差的大小等。
使得噪声对图像仍有较大的影响,众多学者对其进行了研究。
杨振亚等人[]4针对LOG算子的缺陷,提出了选择性平滑方式清除图像中的椒盐噪声;提出了依据图像灰度的一阶导数极大值和二阶导数零穿相结合的边缘检测方法,抑制了图像中的大部分其它噪声,并保持了边缘定位精度;还通过用图像灰度共生矩阵的惯性矩特征值,自适应调整高斯空间系数和边缘检测阈值,实现了图像边缘的自动提取。
李小红等人[]5分析LOG滤波器边缘检测方法及多尺度特性的理论基础上,提出了一种LOG边缘检测的改进算法。
该算法对滤波后的梯度图像选取一个阈值T以提高边缘检测的精度。
杨东华等人[6]根据实际应用中LOG模板的设计要求,提出了不等间隔采样和非均匀量化相结合的数字化方法。
该方法设计的模板能够获得更加丰富的图像边缘,并且边缘的连续性较好。
严国萍等人[]7对经典LOG 边缘检测算子引入了角度信息参量进行推导,使以圆为对称的经典的LOG 边缘检测算子变成为以椭圆对称,并且可以在坐标轴旋转任意角度时增强其边缘检测的能力,使之能对不同方向的边缘更加有效地进行检测。
但上述边缘检测方法实际操作都较为复杂,且大多不能很好的去除噪声且保留图像更多的细节信息。
双边滤波是一种非线性滤波方法,较一般的线性滤波方法(如高斯滤波)在去除噪声的同时也能避免边缘模糊,因此本文采用双边滤波来替代LOG 算子中原有的高斯滤波,能够有效地保护边缘,从而实现图像去噪和细节保留。
因此本文在分析基于零交叉的LOG 算子的基础上,针对图像噪声和边缘信息的特点,提出一种引入双边滤波的LOG 边缘检测算法。
2.传统的LOG 边缘检测算法LOG 算子来源于Marr 视觉理论中提出的边缘提取思想,即先对原始图像进行平滑处理,从而实现对噪声最大程度的抑制,再对平滑后的图像提取边缘。
LOG 算子被誉为最佳边缘检测算子之一[]8。
LOG 算子的基本步骤如下:(1) 采用二维高斯滤波器平滑滤波;(2) 采用二维拉普算子进行图像增强;(3) 依据二阶导数零交叉进行边缘检测。
二维高斯滤波器的函数(,)G x y )2ex p(21),(2222σπσy x y x G +-= (1)用(,)G x y 与原始图像),(y x f 进行卷积,得到平滑图像(),I x y()()(),,,I x y G x y f x y =* (2)其中*是卷积运算符,再用拉普拉斯算子()2∇来获取平滑图像(),I x y 的二阶方向导数图像(),M x y 。
由线性系统中卷积和微分的可交换性可得:()(){}222,,[(,)(,)][(,)](,)M x y I x y G x y f x y G x y f x y =∇=∇*=∇* (3)对图像的高斯平滑滤波与拉普拉斯微分运算可以结合成一个卷积算子: )2ex p()2(21),(22222242σσπσy x y x y x G +--+=∇ (4)式中),(2y x G ∇即为LOG 算子,又称为高斯拉普拉斯算子。
求取(),M x y 的零穿点轨迹即可得到图像),(y x f 的边缘。
以),(2y x G ∇对原始灰度图像进行卷积运算后提取的零交叉点作为边缘点。
然而在实际应用中,LOG 算子仍存在对噪声敏感,噪声平滑能力与边缘定位能力相矛盾等缺点。
这些问题影响了LOG 算子的应用效果,对此本文提出了这种改进方案。
3.改进的LOG 边缘检测算法3.1双边滤波Tomasi 和Manduchi 于1998年提出了双边滤波算法[]9。
该算法加权系数不仅考虑了像素间的距离,同时也考虑了灰度相似性[]10。
双边滤波方法可用如下公式表示:()()()()()(),,,,,,s i j s i j w i j I i j f x y w i j ∈Ω∈Ω=∑∑(5) 其中(),f x y 为去噪后图像,(),s w i j 为空间域权值,(),I i j 为原图像,Ω为像素(),x y 处的邻域范围。
同理,在灰度范围内进行滤波与空间范围内滤波的方法相似。
它可表示为:()()()()()(),,,,,,r i j r i j w i j I i j f x y w i j ∈Ω∈Ω=∑∑(6) 其中(),r w i j 为灰度域权值,将空间邻近度与灰度相似度相结合进行滤波,就得到双边滤波为:()()()()()(),,,,,,i j i j w i j I i j f x y w i j ∈Ω∈Ω=∑∑ (7)()()(),,,s r w i j w i j w i j = (8)在图像变化较为平缓的区域,其邻域内像素灰度值相差不大,双边滤波转化为高斯低通滤波器;在图像变化剧烈的区域,滤波器用边缘点邻域内灰度相似的像素点的灰度平均值代替原灰度值。
因此,双边滤波器既平滑了图像,又保护了图像边缘[]11。
3.2算法描述双边滤波既可以较好地去除图像噪声,又可以保护图像的边缘信息,解决了LOG 算子使用高斯滤波后图像模糊和边缘丢失问题。
()()()()()()()(),,,,,,,,s r i j p s r i j w i j w i j I i j f x y w w i j w i j ∈Ω==∑∑ (9)一般情况下,它的空间邻近度函数(),s w i j 和灰度相似度函数(),r w i j 都取为参数为欧几里得距离的高斯函数,通常定义为:()222,exp 2s s i x j y w i j σ⎡⎤-+-=-⎢⎥⎢⎥⎣⎦ (10)()22(,)(,),exp 2r r I i j I x y w i j σ⎡⎤-=-⎢⎥⎢⎥⎣⎦ (11)其中,s σ为基于高斯函数的空间标准差,r σ为基于高斯函数的灰度标准差。
将原始图像(,)f x y 与(),f x y 进行卷积运算,得出平滑后的图像(),I x y ,即:()()(),,,I x y f x y f x y =* (13)这样既平滑了图像又降低了噪声,孤立的噪声点和一些较小的结构组织将被滤除,同时保护了图像边缘。
图像增强仍采用二维拉普算子进行处理。
得出:()(){}()(){}22,,,,M x y I x y f x y f x y =∇=∇* (14) 拉普拉斯算子是一个二阶微分算子,它可在边缘处产生一个陡峭的零交叉,即一个由正到负的过零点,最后依据零交叉点进行边缘检测。
4.实验结果与比较本实验以MATLAB(R2010a)为实验平台,采用传统LOG 边缘检测算法和改进后的算法分别对Lena 图像和Cameraman 图像进行边缘检测。
(a)Lena图像(b)传统LOG算法(c)本文方法(d)Cameraman图像(e)传统LOG算法(f)本文方法图1实验结果图1中(b)与(c)对边可以发现,传统的LOG边缘检测算法对图像的边缘检测出很多漏检,图像边缘定位不够精确,轮廓不够清楚,提取的边缘信息过于冗杂,不能较好地显示图像的主要轮廓特征,不利于进一步的图像分析。
而改进后的LOG算法检测出了更多的边缘细节,可清楚的看出图像的轮廓边缘。
其精度要高于传统的LOG边缘检测算法。
从(e)与(f)对比同样可以发现,许多没有被传统LOG检测算法检测出来的真边缘出现在改进后的算法提取的边缘图像(f)中,从中可看出,图像去除了许多噪声,又避免丢失很多真边缘,而且边缘轮廓明显、清晰,连续性较好。
说明本文算法对图像的去噪和边缘检测效果均优于传统的LOG算法,能够获得更好的边缘检测图像。
5.结论本文对传统LOG边缘检测算法进行了分析,提出了结合双边滤波的LOG边缘检测算法。
实验表明,此算法能较好地滤除图像噪声,同时能很好的保持图像细节信息,简单实用,复杂度低,具备更好的推广应用价值。
参考文献[1]马娅丽,熊淑华,黑建业,一种改进的LOG边缘算法研究[J].计算机技术与发展,2013,23(9):7-9[2]Rafeal C G,Richard E W.数字图像处理[M].阮秋琦,阮宇智,译.第2版.北京:电子工业出版社,2003:581-584[3]Marr D,Hildreth E.Theory of edge detection [C]//Proceedings of the Royal Society of London.London,UK:[s.n.],1980:200-217[4]杨振亚,汪淑仙,王成道自适应图像边缘检测算法[J]计算机应用与软件,2003,23(5):15-17[5]李小红,基于LOG滤波器的图像边缘检测算法的研究[J]计算机应用应用与软件,2005,22(5):106-108[6]杨东华,李久贤,卞治国.Marr边缘检测算法的研究[J]中国图象图形学报,2006,11(6):823-826[7]严国萍,戴若愚,潘清基于LOG算子的自适应图像边缘检测方法[J]华中科技大学学报,2008,36(3):85-87[8]程东旭,杨艳,赵慧杰,一种改进的LOG边缘检测算法[J].中原工学院学报,2011,22(2):18-21[9]Tomasi C,Manduchi R. Bilateral Filtering for Gray and Color Images[C]//Proceedings of sixth international conference on computer vision(ICCV’98).Washington, DC, USA: IEEEComputer Society,1998. [10]胡伏原,姒绍辉,张艳宁等,自适应分数阶微分的复合双边滤波算法[J]中国图象图形学报,2013,18(10):1237-1246[11]张志强,王万玉,一种改进的双边滤波算法[J].中国图象图形学报,2009,14(3):443-447[12]李德军,赵文杰等,一种基于双边滤波的图像边缘检测方法[J].计算机技术与发展,2007,17(4):160-163。
