中考数学类比探究实战演练

合集下载

类比探究与动点问题专项训练(二)(含答案)

学生做题前请先回答以下问题问题1：想一想河南中考数学第22题常考类型有哪些？问题2：想一想河南中考数学第22题答题标准动作有哪些？问题3：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？类比探究与动点问题专项训练（二）一、单选题(共6道，每道16分)1.通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的．下面是一个案例，请补充完整．原题：如图1，点E，F分别在正方形ABCD的边BC，CD上，∠EAF=45°，连接EF，则EF=BE+DF，试说明理由．（1）思路梳理∵AB=AD，∴把△ADF绕点A顺时针旋转90°至△ABG，可使AD与AB重合．∵∠ABC=∠ABG=90°，∴∠EBG=180°，点E，B，G共线．根据___________，易证△AEF≌__________，得EF=BE+DF．（2）类比联想如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E，F分别在BC，CD边上，且∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足等量关系___________时，仍有EF=BE+DF．（3）引申拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在BC边上，且∠DAE=45°．猜想BD，DE，EC之间满足的数量关系，并写出推理过程．（建议学生打印做题，并在做完之后对比解题思路中的示范照片）（1）思路梳理∵AB=AD，∴把△ADF绕点A顺时针旋转90°至△ABG，可使AD与AB重合．∵∠ABC=∠ABG=90°，∴∠EBG=180°，点E，B，G共线．根据___________，易证△AEF≌__________，得EF=BE+DF．A.AAS，△AGEB.SAS，△AGEC.SAS，△AEGD.SSS，△AGE答案：C解题思路：见第3题中解析试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（2）类比联想如图2，在四边形ABCD中，AB=AD，∠BAD=90°，点E，F分别在BC，CD边上，且∠EAF=45°．若∠B，∠D都不是直角，则当∠B与∠D满足等量关系_________时，仍有EF=BE+DF．( )A.∠B=∠DB.∠B+∠D=180°C.∠B-∠D=90°D.∠B=2∠D答案：B解题思路：见第3题中解析试题难度：三颗星知识点：中考数学几何中的类比探究3.（上接第1，2题）（3）引申拓展如图3，在△ABC中，∠BAC=90°，AB=AC，点D，E均在BC边上，且∠DAE=45°，则BD，DE，EC之间满足的数量关系为( )A.DE=BD+ECB.C. D.答案：C解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究4.如图，在平行四边形ABCD中，AB=5，BC=10，F为AD的中点，CE⊥AB于点E，设．（1）当时，求CE的长；（2）当时，①设，能够得到，求k的值；②连接CF，当的值最大时，求BE的长．（建议学生打印做题，并在做完之后对比解题思路中的示范照片）（1）当α=60°时，EF的长为( )A.5B.C. D.答案：A解题思路：见第6题中解析试题难度：三颗星知识点：中点结构5.（上接第4题）（2）①当时，设，能够得到，则k的值为( )A. B.C. D.3答案：D解题思路：见第6题中解析试题难度：三颗星知识点：中点结构6.（上接第4，5题）（2）②连接CF，当的值最大时，BE的长为( )A. B.C. D.5答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半。

中考数学类比探究(二)——旋转、中点(习题及答案).

中考数学类比探究（二）——旋转、中点（习题）1.（1）如图1，菱形AEGH 的顶点E，H 在菱形ABCD 的边上，且∠BAD=60°，请直接写出HD:GC:EB 的结果（不必写出计算过程）．（2）将图1 中的菱形AEGH 绕点A 旋转一定角度，如图2，求HD:GC:EB．（3）把图2 中的菱形都换成矩形，如图3，且AD:AB=AH:AE=1:2，此时HD:GC:EB 的结果与（2）小题的结果相比有什么变化吗？如果有变化，直接写出变化后的结果（不必写出计算过程）；若无变化，请说明理由．2.（1）【问题发现】如图1，△ABC 和△CEF 都是等腰直角三角形，∠BAC=∠EFC=90°，点E 与点A 重合，则线段BE 与AF 的数量关系为；（2）【拓展研究】在（1）的条件下，将△CEF 绕点C 旋转，连接BE，AF，线段BE 与AF 的数量关系有无变化？仅就图2 的情形给出证明；（3）【问题发现】当AB=AC=2，△CEF 旋转到B，E，F 三点共线时，直接写出线段AF 的长．3.已知直线m∥n，点C 是直线m 上一点，点D 是直线n 上一点，CD 与直线m，n 不垂直，点P 为线段CD 的中点．（1）操作发现：直线l⊥m，l⊥n，垂足分别为A，B，当点A 与点C 重合时（如图1 所示），连接PB，请直接写出线段PA 与PB 的数量关系：．（2）猜想证明：在图1 的情况下，把直线l 向上平移到如图2 的位置，试问（1）中的PA 与PB 的关系式是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）延伸探究：在图2 的情况下，把直线l 绕点A 旋转，使得∠APB=90°（如图3 所示），若两平行线m，n 之间的距离为2k．求证：PA·PB=k·AB．4.已知正方形ABCD 与正方形CEFG，M 是AF 的中点，连接DM，EM．（1）如图1，点E 在CD 上，点G 在BC 的延长线上，请判断DM，EM 的数量关系与位置关系，并直接写出结论；（2）如图2，点E 在DC 的延长线上，点G 在BC 上，（1）中结论是否仍然成立？请证明你的结论；（3）将图1 中的正方形CEFG 绕点C 旋转，使D，E，F 三点在一条直线上，若AB=13，CE=5，请画出图形，并直接写出MF 的长．5 2 157 37 【参考答案】 1. （1）HD :GC :EB =1: （2） HD :GC :EB =1::1；:1；（3）有变化，HD :GC :EB =1: :2．2. （1）BE = AF ；（2）无变化，证明略；（3）线段 AF 的长为 3. （1）PA =PB ；-1或+1．（2）仍然成立，证明略；（3）证明略．4. （1）DM =EM ，DM ⊥EM ；（2）仍然成立，证明略；（3）图略，MF 的长为或．3 3 3 3。

中考数学----类比探究题练习(1)

中考数学----类比探究题练习（1）1.如图1，在四边形ABCD中，AB=CD，E，F分别是BC，AD的中点，连接EF并延长，与BA，CD的延长线分别交于点M，N，则∠BME=∠CNE（简要证明）．（1）如图2，在四边形ADBC中，AB与CD相交于点O，AB=CD，E，F分别是BC，AD的中点，连接EF，分别交CD，AB于点M，N，判断△OMN的形状，并说明理由．（2）如图3，在△ABC中，，点D在AC边上，且AB=CD．E，F分别是BC，AD的中点，连接EF并延长，与BA的延长线交于点G，连接DG，若∠EFC=60°，判断△AGD形状，并说明理由2、小明在一次数学兴趣小组活动中，对一个数学问题作如下探究：（1）问题情境：如图1，四边形ABCD中，AD∥BC，E为CD边的中点，连接AE并延长，交BC的延长线于点F，求证：（S表示面积）．（2）问题迁移：如图2，在已知锐角∠AOB内有一个定点P，过点P任意作一条直线，分别交射线OA，OB于点M，N．小明在直线MN绕着点P旋转的过程中发现，△MON的面积存在最小值，请问当直线MN在什么位置时，△MON的面积最小？并说明理由．（3）实际应用：如图3，若在道路OA，OB之间有一村庄Q发生疫情，防疫部门计划以公路OA，OB 和经过防疫站P的一条直线MN为隔离线，建立一个面积最小的三角形隔离区△MON．若测得∠AOB=66°，∠POB=30°，OP=4km，试求△MON的面积．（参考数据：sin66°≈0.91，tan66°≈2.25，）3、问题发现：如图1，在Rt△ABC中，AB＝AC＝2，∠BAC＝90°，点D为BC的中点，以CD为一边作正方形CDEF，点E恰好与点A重合，则线段BE与AF的数量关系为；(2)拓展探究：在(1)的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请仅就图2的情形给出证明；(3)问题解决：当正方形CDEF旋转到B，E，F三点共线时，直接写出线段AF的长．4、(1)问题发现：如图1，△ACB和△DCE均为等边三角形，点A，D，E在同一直线上，连接BE. 填空：①∠AEB的度数为；②线段AD，BE之间的数量关系为；(2)拓展探究：如图2，△ACB和△DCE均为等腰直角三角形，∠ACB＝∠DCE＝90°，点A，D，E在同一直线上，CM为△DCE中DE边上的高，连接BE，请判断∠AEB的度数及线段CM，AE，BE之间的数量关系，并说明理由；(3)解决问题：如图3，在正方形ABCD中，CD＝2，若点P满足PD＝1，且∠BPD＝90°，请直接写出点A到BP的距离．5、我们定义：如图1，在△ABC中，把AB绕点A顺时针旋转α(0°<α<180°)得到AB′，把AC 绕点A逆时针旋转β得到AC′，连接B′C′.当α＋β＝180°时，我们称△AB′C′是△ABC的“旋补三角形”，△AB′C′边B′C′上的中线AD叫做△ABC的“旋补中线”，点A叫做“旋补中心”．特例感知：(1)在图2，图3中，△AB′C′是△ABC的“旋补三角形”，AD是△ABC的“旋补中线”．①如图2，当△ABC为等边三角形时，AD与BC的数量关系为AD＝ BC；②如图3，当∠BAC＝90°，BC＝8时，则AD长为；猜想论证：(2)在图1中，当△ABC为任意三角形时，猜想AD与BC的数量关系，并给予证明；拓展应用：(3)如图4，在四边形ABCD中，∠C＝90°，∠D＝150°，BC＝12，CD＝23，DA＝6.在四边形内部是否存在点P，使△PDC是△PAB的“旋补三角形”？若存在，给予证明，并求△PAB的“旋补中线”长；若不存在，说明理由．图4中考数学----类比探究题练习（1）答案 1、解题思路2、解题思路3、解：（1）BE＝2AF；(2)无变化．理由如下：在Rt△ABC中，AB＝AC＝2，∴∠ABC＝∠ACB＝45°，∴sin∠ABC＝ACBC＝22. 在正方形CDEF中，∠FEC＝12∠FED＝45°，在Rt△CEF中，sin∠FEC＝CFCE＝22，∴CFCE＝ACBC. ∵∠FCE＝∠ACB＝45°，∴∠FCE－∠ACE＝∠ACB－∠ACE. ∴∠FCA＝∠ECB.∴△ACF∽△BCE.∴BEAF＝BCAC＝ 2.∴BE＝2AF. ∴线段BE与AF的数量关系无变化．(3)3－1或3＋1. 提示：分两种情况讨论：①当点E在线段BF上时，如图2由(1)知，CF＝EF＝CD＝ 2.在Rt△BCF中，CF＝2，BC＝22，根据勾股定理得BF＝6，∴BE＝BF－EF＝6－ 2. 由(2)知，BE＝2AF，∴AF＝3－1.②当点E在线段BF的延长线上时，如图3，∵△ABC，△CFE为等腰直角三角形．易证：△ACF∽△BCE.∴BEAF＝BCAC＝ 2.∴BE＝2AF.由(1)知，CF＝EF＝CD＝ 2.在Rt△BCF中，CF＝2，BC＝22，根据勾股定理得，BF＝6，∴BE＝BF＋EF＝6＋ 2.由(2)知，BE＝2AF，∴AF＝3＋1.即当正方形CDEF旋转到B，E，F三点共线时候，线段AF的长为3－1或3＋1. 4、解：（1） 60°；AD＝BE；(2)∠AEB＝90°，AE＝2CM＋BE.理由：∵△ACB和△CDE均为等腰直角三角形，∠ACB＝∠DCE＝90°，∴AC＝BC，CD＝CE，∠ACB－∠DCB＝∠DCE－∠DCB，即∠ACD＝∠BCE.∴△ACD≌△BCE(SAS)．∴AD＝BE，∠BEC＝∠ADC＝135°.∴∠AEB＝∠BEC－∠CED＝135°－45°＝90°.在等腰直角三形DCE中，CM为斜边DE上的高，∴CM＝DM＝ME，∴DE＝2CM.∴AE＝DE＋AD＝2CM＋BE；（3）3－12或3＋12.提示：∵PD ＝1，∠BPD ＝90°.∴BP 是以点D 为圆心，以1为半径的⊙D 的切线，点P 为切点．第一种情况：如图4，过点A 作AP 的垂线，交BP 于点P ′，可证△APD ≌△AP ′B ，PD ＝P ′B ＝1.∵CD ＝2，∴BD ＝2，BP ＝3，∴AM ＝12PP ′＝12(PB －BP ′)＝3－12. 第二种情况，如图5，可得AM ＝12PP ′＝12(PB ＋BP ′)＝3＋12.5、解：（1）12；4； (2)①猜想：AD ＝12BC.证明：如上图3，延长AD 至点E ，使DE ＝AD. ∵AD 是△ABC 的“旋补中线”，∴B ′D ＝C ′D.∴四边形AB ′EC ′是平行四边形．∴EC ′∥B ′A ，EC ′＝B ′A.∴∠AC ′E ＋∠B ′AC ′＝180°.由定义可知∠B ′AC ′＋∠BAC ＝180°，B ′A ＝BA ，AC ＝AC ′，∴∠AC ′E ＝∠BAC ，EC ′＝BA.∴△AC ′E ≌△CAB(SAS )．∴AE ＝BC.∵AD ＝12AE ，∴AD ＝12BC. (3)存在．以AD 为边向四边形ABCD 的内部作等边△PAD ，连接PB ，PC ，延长BP 交AD 于点F ，则有∠ADP ＝∠APD ＝60°，PA ＝PD ＝AD ＝6.∵∠CDA ＝150°，∴∠CDP ＝90°.过点P 作PE ⊥BC 于点E ，易知四边形PDCE 为矩形．∴CE ＝PD ＝6.∴tan ∠DPC ＝CD PD ＝236＝33.∴∠DPC ＝30°，∠EPC ＝60°.∴BE ＝12－6＝6＝CE. 又PE ⊥BC ，∴PC ＝PB ，∠BPE ＝∠CPE ＝60°.∴∠APD ＋∠BPC ＝60°＋120°＝180°.又PA ＝PD ，PB ＝PC ，∴△PDC 是△PAB 的“旋补三角形”．∵∠BPE ＝60°，∠DPE ＝90°，∴∠DPF ＝30°.∴BF ⊥AD ，AF ＝12AD ＝3，PF ＝3 3. 在Rt △PBE 中，PB ＝PE 2＋BE 2＝CD 2＋BE 2＝（23）2＋62＝43，∴BF ＝PB ＋PF ＝7 3.在Rt △ABF 中，AB ＝（73）2＋32＝239.∵△PDC 是△PAB 的“旋补三角形”，∴△PAB 的“旋补中线”长为12AB ＝39.。

江西省中考数学专题复习专题五类比探索型问题备考演练-人教版初中九年级全册数学试题

专题五类比探索型问题备考演练1．如图1，在△ABC中，AB＝AC，点D是直线BC上一点(不与B、C重合)，以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE.设∠BAC＝α，∠BCE＝β.(1)求证：△DAB≌△EAC；(2)当点D在线段BC上运动时，①若α＝50°，则β＝ __130__度；②猜想α与β之间的数量关系？并对你的结论给出证明；(3)当点D在线段BC的反向延长线上运动时，上题②中的结论是否仍然成立？若成立，试加以证明；若不成立，请你给出正确的数量关系，并说明理由．[解] (1)∵∠BAC＝∠DAE＝α，∴∠BAD＝∠CAE＝α－∠DAC.又AB＝AC，AD＝AE，∴△ABD≌△ACE.(2)②∵△ABD≌△ACE，∠BAC＝α.∴∠B＝∠ACE.∴∠B＋∠ACB＝β.∵∠BAC＋∠B＋∠ACB＝180°，∴α＋β＝180°.(3)当点D在线段BC的反向延长线上运动时，上题②中的结论不能成立，此时α＝β成立．其理由如下：类似(1)可证△DAB≌△EAC，∴∠DBA ＝∠ECA.又由三角形外角性质有∠DBA ＝α＋∠DCA， ∴∠ACE ＝α＋∠DCA，∴∠BCE ＝∠ACE－∠ACB＝α＋∠ACB－∠ACB＝β. ∴α＝β.2．如图所示，已知二次函数y ＝ax 2＋bx －1(a≠0)的图象过点A(2，0)和B(4，3)，l 为过点(0，－2)且与x 轴平行的直线，P(m ，n)是该二次函数图象上的任意一点，过P 作PH⊥l，H 为垂足．(1)求二次函数y ＝ax 2＋bx －1(a≠0)的解析式；【特例探究】(2)填空：当m ＝0时，OP ＝__1__，PH ＝__1__ ；当m ＝4时，OP ＝ __5__，PH ＝__5__；【证明】(3)对任意m ，n ，猜想OP 与PH 的大小关系，并证明你的猜想．[解] (1)∵二次函数y ＝ax 2＋bx －1(a≠0)的图象过点A(2，0)和B(4，3)，∴⎩⎪⎨⎪⎧4a ＋2b －1＝0，16a ＋4b －1＝3，解得⎩⎪⎨⎪⎧a ＝14，b ＝0，∴二次函数的解析式为y ＝14x 2－1.(3)猜想：OP ＝PH.证明：过点P 作PQ⊥x 轴于Q ， ∵P 在二次函数y ＝14x 2－1的图象上，∴设P ⎝ ⎛⎭⎪⎫m ，14m 2－1，则PQ ＝⎪⎪⎪⎪⎪⎪14m 2－1，OQ ＝|m|，∵△OPQ 为直角三角形， ∴OP ＝PQ 2＋OQ 2＝⎝ ⎛⎭⎪⎫14m 2－12＋m 2＝⎝ ⎛⎭⎪⎫14m 2＋12＝14m 2＋1，PH ＝y P －(－2)＝⎝ ⎛⎭⎪⎫14m 2－1－(－2)＝14m 2＋1，∴OP ＝PH.3．(2016·龙东)已知：点P 是平行四边形ABCD 对角线AC 所在直线上的一个动点(点P 不与点A 、C 重合)，分别过点A 、C 向直线BP 作垂线，垂足分别为点E 、F ，点O 为AC 的中点．(1)当点P 与点O 重合时如图1，易证OE ＝OF(不需证明)；(2)直线BP 绕点B 逆时针方向旋转，当∠OFE＝30°时，如图2、图3的位置，猜想线段CF 、AE 、OE 之间有怎样的数量关系？请写出你对图2、图3的猜想，并选择一种情况给予证明．[解] (1)∵AE⊥PB，CF ⊥BP ， ∴∠AEO ＝∠CFO＝90°，在△AEO 和△CFO 中， ⎩⎪⎨⎪⎧∠AEO＝∠CFO，∠AOE ＝∠COF，AO ＝CO ， ∴△AOE ≌△COF ， ∴OE ＝OF.(2)图2中的结论为：CF ＝OE ＋AE. 图3中的结论为：CF ＝OE －AE. 选图2中的结论证明如下：延长EO 交CF 于点G ， ∵AE ⊥BP ，CF ⊥BP ， ∴AE ∥CF ，∴∠EAO ＝∠G CO ，在△EOA 和△GOC 中， ⎩⎪⎨⎪⎧∠EAO＝∠GCO，AO ＝CO ，∠AOE ＝∠COG， ∴△EOA ≌△GOC ， ∴EO ＝GO ，AE ＝CG ，在Rt △EFG 中，∵EO ＝OG ， ∴OE ＝OF ＝GO ， ∵∠OFE ＝30°，∴∠OFG ＝90°－30°＝60°， ∴△OFG 是等边三角形， ∴OF ＝GF ， ∵OE ＝OF ， ∴OE ＝FG ， ∵CF ＝FG ＋CG ， ∴CF ＝OE ＋AE.选图3中的结论证明如下：延长EO 交FC 的延长线于点G ， ∵AE ⊥BP ，CF ⊥BP ， ∴AE ∥CF ， ∴∠AEO ＝∠G，在△AOE 和△COG 中， ⎩⎪⎨⎪⎧∠AEO＝∠G，∠AOE ＝∠COG，AO ＝CO ， ∴△AOE ≌△COG ， ∴OE ＝OG ，AE ＝CG ，在Rt △EFG 中，∵OE ＝OG ， ∴OE ＝OF ＝OG ， ∵∠OFE ＝30°，∴∠OFG ＝90°－30°＝60°，∴OF＝FG，∵OE＝OF，∴OE＝FG，∵CF＝FG－CG，∴CF＝OE－AE.1．(2015·某某)操作与证明：如图1，把一个含45°角的直角三角板ECF和一个正方形ABCD摆放在一起，使三角板的直角顶点和正方形的顶点C重合，点E、F分别在正方形的边CB、CD上，，EF的中点N，连接MD、MN.(1)连接AE，求证：△AEF是等腰三角形；猜想与发现：(2)在(1)的条件下，请判断MD、MN的数量关系和位置关系，得出结论．结论1：DM、MN的数量关系是__相等__；结论2：DM、MN的位置关系是__垂直__；拓展与探究：(3)如图2，将图1中的直角三角板ECF绕点C顺时针旋转180°，其他条件不变，则(2)中的两个结论还成立吗？若成立，请加以证明；若不成立，请说明理由．[解] (1)证明：∵四边形ABCD是正方形，∴AB＝AD＝BC＝CD，∠B＝∠ADF＝90°，∵△CEF是等腰直角三角形，∠C＝90°，∴CE＝CF，∴BC－CE＝CD－CF，即BE＝DF，∴△ABE≌△ADF，∴AE＝AF，△ABE≌△ADF，(3)(2)中的两个结论还成立，证明：连接AE ，交MD 于点G ，∵点M 为AF 的中点，点N 为EF 的中点， ∴MN ∥AE ，MN ＝12AE ，由(1)同理可得，AE ＝AF ，△ABE ≌△ADF ，在Rt △ADF 中，∵点M 为AF 的中点， ∴DM ＝12AF ，∴DM ＝MN ，∵△ABE ≌△ADF ，∴∠1＝∠2， ∵AB ∥DF ，∴∠1＝∠3，∵AD ∥BE ，∴∠2＝∠4，∴∠3＝∠4， ∵DM ＝AM ，∴∠MAD ＝∠5，∴∠DGE ＝∠5＋∠4＝∠MAD＋∠3＝90°， ∵MN ∥AE ，∴∠DMN ＝∠DGE＝90°， ∴DM ⊥MN. 2．情境观察将矩形ABCD 纸片沿对角线AC 剪开，得到△ABC 和△A′C′D，如图1所示，将△A′C′D 的顶点A′与点A 重合，并绕点A 按逆时针方向旋转，使点D 、A(A′)、B 在同一条直线上，如图2所示，观察图2可知：与BC 相等的线段是__AD(或A′D)__，∠CAC ′＝__90__°.问题探究如图3，在△ABC 中，AG ⊥BC 于点G ，以A 为直角顶点，分别以AB 、AC 为直角边，向△ABC 外作等腰Rt △ABE 和等腰Rt △ACF ，过点E 、F 作射线GA 的垂线，垂足分别为P 、Q ，试探究EP 与FQ 之间的数量关系，并证明你的结论．拓展延伸如图4，在△ABC 中，AG ⊥BC 于点G ，分别以AB 、AC 为一边向△ABC 外作矩形ABME 和矩形AF ，射线GA 交EF 于点H ，若AB ＝kAE ，AC ＝kAF ，试探究HE 与HF 之间的数量关系，并说明理由．[解] 问题探究结论：EP ＝FQ ，证明：∵△ABE 是等腰直角三角形，∴AB ＝AE ，∠BAE ＝90°，∴∠BAG ＋∠EAP＝90°， ∵AG ⊥BC ，∴∠BAG ＋∠ABG＝90°， ∴∠ABG ＝∠EAP，∵EP ⊥AG ，∴∠AGB ＝∠EPA＝90°， ∴Rt △ABG ≌Rt △EAP ，∴AG ＝EP ，同理AG ＝FQ ，∴EP ＝FQ ，拓展延伸结论：HE ＝HF ，理由：过点E 作EP⊥GA，FQ⊥GA，垂足分别为P 、Q ， ∵四边形ABME 是矩形，∴∠BAE ＝90°， ∴∠BAG ＋∠EAP＝90°，AG ⊥BC ， ∴∠BAG ＋∠ABG＝90°，∴∠ABG ＝∠EAP， ∵∠AGB ＝∠EPA＝90°，∴△ABG ∽△EAP ， ∴AG EP ＝AB EA，同理△ACG∽△FAQ，∴AG FQ ＝ACFA ，∵AB ＝kAE ，AC ＝kAF ，∴AB EA ＝ACFA ＝k ，∴AG EP ＝AGFQ，∴EP ＝FQ ， ∵∠EHP ＝∠FHQ，∴Rt △EPH ≌Rt △FQH ， ∴HE ＝HF.3．(2016·某某)在△ABC 中，AB ＝AC ，∠BAC ＝2∠DAE ＝2α.(1)如图1，若点D 关于直线AE 的对称点为F ，求证：△ADF∽△ABC； (2)如图2，在(1)的条件下，若α＝45°，求证：DE 2＝BD 2＋CE 2；(3)如图3，若α＝45°，点E 在BC 的延长线上，则等式DE 2＝BD 2＋CE 2还能成立吗？请说明理由．[解] (1)证明：∵点D 关于直线AE 的对称点为F ， ∴∠EAF ＝∠DAE，AD ＝AF ，又∵∠BAC＝2∠DAE， ∴∠BAC ＝∠DAF， ∵AB ＝AC ， ∴AB AD ＝AC AF ， ∴△ADF ∽△ABC.(2)证明：∵点D 关于直线AE 的对称点为F ， ∴EF ＝DE ，AF ＝AD ，∵α＝45°，∴∠BAD ＝90°－∠CAD，∠CAF ＝∠DAE＋∠EAF－∠CAD＝45°＋45°－∠CAD＝90°－∠C AD ， ∴∠BAD ＝∠CAF，在△ABD 和△ACF 中，⎩⎪⎨⎪⎧AB ＝AC ，∠BAD ＝∠CAF，AD ＝AF ，∴△ABD ≌△ACF(SAS)， ∴CF ＝BD ，∠ACF ＝∠B，∵AB ＝AC ，∠BAC ＝2α，α＝45°， ∴△ABC 是等腰直角三角形， ∴∠ACF ＝∠B＝∠ACB＝45°，∴∠ECF ＝∠ACB＋∠ACF＝45°＋45°＝90°，在Rt △CEF 中，由勾股定理得EF 2＝CF 2＋CE 2. ∴DE 2＝BD 2＋CE 2.(3)DE 2＝BD 2＋CE 2还能成立．理由如下：如图，作点D 关于AE 的对称点F ，连接EF 、CF ，由轴对称的性质得EF ＝DE ，AF ＝AD ， ∵α＝45°，∴∠BAD ＝90°－∠CAD，∠CAF ＝∠DAE＋∠EAF－∠CAD＝45°＋45°－∠CAD＝90°－∠CAD， ∴∠BAD ＝∠CAF，在△AB D 和△ACF 中，⎩⎪⎨⎪⎧AB ＝AC ，∠BAD ＝∠CAF，AD ＝AF ，∴△ABD ≌△ACF(SAS)， ∴CF ＝BD ，∠ACF ＝∠B，∵AB ＝AC ，∠BAC ＝2α，α＝45°， ∴△ABC 是等腰直角三角形， ∴∠B ＝∠ACB＝45°，∴∠ECF ＝∠ACB＋∠ACF＝45°＋45°＝90°，在Rt △CEF 中，由勾股定理得EF 2＝CF 2＋CE 2， ∴DE 2＝BD 2＋CE 2.。

中考数学类比探究(一)——直角、平行(习题及答案).

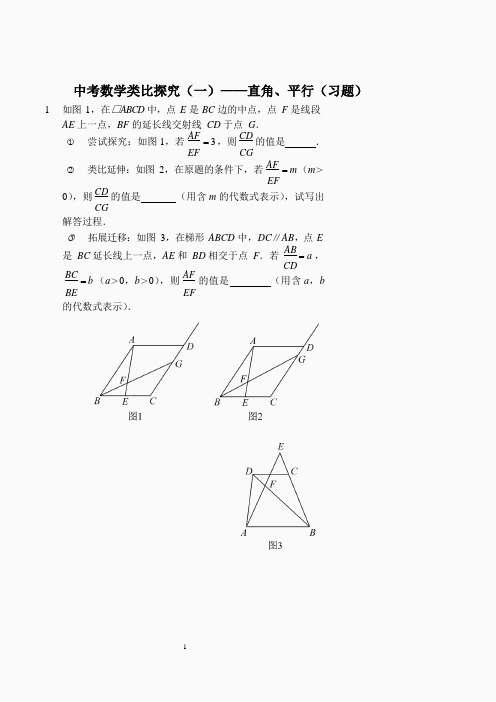
中考数学类比探究（一）——直角、平行（习题）1. 如图 1，在□ABCD 中，点 E 是 BC 边的中点，点 F 是线段AE 上一点，BF 的延长线交射线 CD 于点 G ．（1）尝试探究：如图 1，若 AF = 3 ，则 CD 的值是．EF CG（2）类比延伸：如图 2，在原题的条件下，若 AF = m （m ＞ EF0），则 CD 的值是（用含 m 的代数式表示），试写出CG解答过程．（3）拓展迁移：如图 3，在梯形 ABCD 中，DC ∥AB ，点 E是 BC 延长线上一点，AE 和 BD 相交于点 F ．若 AB = a ， CD BC = b （a ＞0，b ＞0），则 AF 的值是（用含 a ，bBE EF的代数式表示）．2.如图1，一副直角三角板满足AB=BC，AC=DE，∠ABC=∠DEF=90°，∠EDF=30°．【操作】将三角板DEF 的直角顶点E 放置于三角板ABC 的斜边AC 上，再将三角板DEF 绕点E 旋转，并使边DE 与边AB 交于点P，边EF 与边BC 交于点Q．【探究】在旋转过程中，（1）如图2，当CE=1时，EP 与EQ 满足怎样的数量关系？EA并给出证明．（2）如图3，当CE= 2 时，EP 与EQ 满足怎样的数量关系？EA并给出证明．（3）根据你对（1），（2）的探究结果，试写出当CE=m时，EAEP 与EQ 满足的数量关系式为．3.在△ABC 中，已知D 是BC 边的中点，G 是△ABC 的重心，过点G 的直线分别交AB，AC 于点E，F．（1）如图1，当点E 与点B 重合时，AG=GD（2）如图2，当EF∥BC 时，求证：BE+CF．= 1 ．AE AF（3）如图3，当EF 和BC 不平行，且点E，F 分别在线段AB，AC 上时，（2）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．提示：①过点 A 作AM∥BC，交EF 于点M，直线FE 交BC 于N；②NB+NC=2ND．（4）如图4，当点E 在AB 的延长线上或点F 在AC 的延长线上时，（2）中的结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．【参考答案】 1. 1 3 （）； 2（2） m ；2（3） a b ．2. （1）EP =EQ ，证明略；（2） EP = 1 2EQ ，证明略；（3） EP = 1 EQ ． m3. （1）2；（2）证明略；（3）（2）中的结论仍然成立，证明略；（4）（2）中的结论不成立，理由略．。

江西省中考数学专题复习专题五类比探索型问题备考演练

专题五类比探索型问题备考演练1．如图1，在△ABC中，AB＝AC,点D是直线BC上一点(不与B、C重合），以AD为一边在AD的右侧作△ADE，使AD＝AE，∠DAE＝∠BAC，连接CE。

设∠BAC＝α，∠BCE＝β。

(1)求证：△DAB≌△EAC;（2)当点D在线段BC上运动时，①若α＝50°,则β＝ __130__度；②猜想α与β之间的数量关系？并对你的结论给出证明；(3）当点D在线段BC的反向延长线上运动时，上题②中的结论是否仍然成立？若成立，试加以证明;若不成立，请你给出正确的数量关系，并说明理由．［解］（1）∵∠BAC＝∠DAE＝α,∴∠BAD＝∠CAE＝α－∠DAC.又AB＝AC,AD＝AE，∴△ABD≌△ACE.(2)②∵△ABD≌△ACE，∠BAC＝α。

∴∠B＝∠ACE.∴∠B＋∠ACB＝β.∵∠BAC＋∠B＋∠ACB＝180°，∴α＋β＝180°。

(3)当点D在线段BC的反向延长线上运动时，上题②中的结论不能成立,此时α＝β成立．其理由如下：类似(1）可证△DAB≌△EAC，∴∠DBA＝∠ECA.又由三角形外角性质有∠DBA＝α＋∠DCA，∴∠ACE＝α＋∠DCA，∴∠BCE＝∠ACE－∠ACB＝α＋∠ACB－∠ACB＝β。

∴α＝β。

2．如图所示，已知二次函数y＝ax2＋bx－1（a≠0）的图象过点A(2，0）和B(4，3）,l 为过点（0,－2）且与x轴平行的直线，P(m,n)是该二次函数图象上的任意一点,过P作PH⊥l,H为垂足．(1)求二次函数y＝ax2＋bx－1（a≠0)的解析式；【特例探究】(2)填空：当m＝0时,OP＝__1__，PH＝__1__ ;当m＝4时,OP＝ __5__，PH＝__5__；【证明】(3）对任意m，n，猜想OP与PH的大小关系，并证明你的猜想．[解] （1）∵二次函数y＝ax2＋bx－1（a≠0）的图象过点A(2，0）和B(4，3）,∴错误!解得错误!∴二次函数的解析式为y＝14x2－1。

2021年中考数学总复习直线形综合类比探究型专题训练(不用相似)(含答案与解析)

类比探究型几何综合题专题训练（不用相似）【类型1】通过位置变化（图形变换）进行类比探究〖例1〗已知：如图，等边△AOB的边长为4，点C为OA中点．（1）如图1，将OC绕点O顺时针旋转，使点C落到OB边的点D处，设旋转角为α（0°＜α≤360°）．则此时α＝；此时△COD是三角形（填特殊三角形的名称）．（2）如图2，固定等边△AOB不动，将（1）中得到的△OCD绕点O逆时针旋转，连接AC，BD，设旋转角为β（0°＜β≤360°）．①求证：AC＝BD；②当旋转角β为何值时，OC∥AB，并说明理由；③当A、C、D三点共线时，直接写出线段BD的长．〖例2〗现有与菱形有关的三幅图，如图：（1）（感知）如图①，AC是菱形ABCD的对角线，∠B＝60°，E、F分别是边BC、CD上的中点，连结AE、EF、AF．若AC＝2，则CE+CF的长为．（2）（探究）如图②，在菱形ABCD中，∠B＝60°．E是边BC上的点，连结AE，作∠EAF＝60°，边AF交边CD于点F，连结EF．若BC＝2，求CE+CF的长．（3）（应用）在菱形ABCD中，∠B＝60°．E是边BC延长线上的点，连结AE，作∠EAF＝60°，边AF交边CD延长线于点F，连结EF．若BC＝2，EF⊥BC时，借助图③求△AEF的周长．〖尝试练习〗1．如图1，等边△ABC与等边△BDE的顶点B重合，D、E分别在AB、BC上，AB＝2√2，BD＝2．现将等边△BDE从图1位置开始绕点B顺时针旋转，如图2，直线AD、CE相交于点P．（1）在等边△BDE旋转的过程中，试判断线段AD与CE的数量关系，并说明理由；（2）在等边△BDE顺时针旋转180°的过程中，当点B到直线AD的距离最大时，求PC的长；（3）在等边△BDE旋转一周的过程中，当A、D、E三点共线时，求CE的长．2．△ABC中，∠BAC＝90°，AB＝AC，点D为直线BC上一动点（点D不与B，C重合），以AD 为边在AD右侧作正方形ADEF，连接CF．（1）探究猜想如图1，当点D在线段BC上时，①BC与CF的位置关系为：；②BC、CD、CF之间的数量关系为：；（2）深入思考如图2，当点D在线段CB的延长线上时，结论①、②是否仍然成立？若成立，请给予证明；若不成立，请你写出正确结论再给予证明．（3）拓展延伸如图3，当点D在线段BC的延长线上时，正方形ADEF对角线交于点O．若已知AB＝2√2，CD＝14BC，请求出OC的长．3．如图1，正方形ABCD与正方形AEFG有公共的顶点A，且正方形AEFG的边AE，AG分别在正方形ABCD的边AB，AD上，显然BE＝DG，BE⊥DG．（1）将图1的正方形AEFG绕点A转动一定的角度到图2的位置．求证：①BE＝DG；②BE⊥DG；（2）如图3，若点D，G，E在同一条直线上，且正方形ABCD的边长是4√2，正方形AEFG的边长为3√2，求BE的长．【类型2】通过形状变化进行类比探究〖例3〗如图1，在△ABC中，AB＝AC，∠BAC＝α．D为BC边上一点（不与点B，C重合），将线段AD绕点A逆时针旋转α，得到AE，连接DE，CE．（1）求证：CE＝BD；（2）若α＝60°，其他条件不变，如图2．请猜测线段AC，CD，CE之间的数量关系，并说明理由；（3）若α＝90°，其他条件不变，如图3，请写出∠ACE的度数及线段AD，BD，CD之间的数量关系，并说明理由．〖例4〗如图1，在正方形ABCD中，点P是对角线BD上的一点，点E在AD的延长线上，且PC＝PE，PF交CD于点F．（1）求证：∠PCD＝∠PED；（2）连接EC，求证：EC＝√2AP；（3）如图2，把正方形ABCD改成菱形ABCD，其他条件不变，当∠DAB＝60°时，请直接写出线段EC和AP的数量关系．〖尝试练习〗4．已知菱形ABCD和菱形DEFG有公共的顶点D，C点在DE上，且∠ADC＝∠EDG，连接AE，CG，如图1．（1）试猜想AE与CG有怎样的数量关系（直接写出关系，不用证明）；（2）将菱形DEFG绕点D按顺时针方向旋转，使点E落在BC边上，如图2，连接AE和CG．你认为（1）中的结论是否还成立？若成立，请给出证明；若不成立，请说明理由；（3）在（2）的条件下，如果∠ADC＝∠EDG＝90°，如图3，你认为AE和CG是否垂直？若垂直，请给出证明；若不垂直，请说明理由．5．已知在平行四边形ABCD中，AB≠BC，将△ABC沿直线AC翻折，点B落在点E处，AD与CE相交于点O，联结DE．（1）如图1，求证：AC∥DE；（2）如图2，如果∠B＝90°，AB＝√3，BC＝√6，求△OAC的面积；（3）如果∠B＝30°，AB＝2√3，当△AED是直角三角形时，求BC的长．6．如图，在平行四边形ABCD中，∠BAD的平分线交BC于点E，交DC的延长线于F，以EC、CF为邻边作平行四边形ECFG．（1）求证：四边形ECFG是菱形；（2）连结BD、CG，若∠ABC＝120°，则△BDG是等边三角形吗？为什么？（3）若∠ABC＝90°，AB＝10，AD＝24，M是EF的中点，求DM的长．【自主反馈】7．如图1，△ABC是等边三角形，点D，E分别是BC，AB上的点，且BD＝AE，AD与CE交于点F．（1）求∠DFC的度数；（2）将CE绕着点C逆时针旋转120°，得到CP，连接AP，交BC于点Q．①补全图形（图2中完成）；②用等式表示线段BE与CQ的数量关系，并证明．8．已知△ABC是等腰三角形．（1）如图1，若△ABC，△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，求证：△ABD≌△ACE；（2）如图2，若△ABC为等边三角形，将线段AC绕点A逆时针旋转90°，得到AD，连接BD，∠BAC的平分线交BD于点E，连接CE．①求∠AED的度数；②试探究线段AE、CE、BD之间的数量关系，并证明．9．在Rt△ABC中，∠ABC＝90°，∠BAC＝30°，将△ABC绕点A顺时针旋转一定的角度α得到△AED，点B、C的对应点分别是E、D．（1）如图1，当点E恰好在AC上时，求∠CDE的度数；（2）如图2，若α＝60°时，点F是边AC中点，求证：DF＝BE；（3）如图3，点B、C的坐标分别是（0，0），（0，2），点Q是线段AC上的一个动点，点M是线段AO上的一个动点，是否存在这样的点Q、M使得△CQM为等腰三角形且△AQM为直角三角形？若存在，请直接写出满足条件的点M的坐标；若不存在，请说明理由．10．在等腰直角三角形纸片ABC中，点D是斜边AB的中点，AB＝10，点E为BC上一点，将纸片沿DE折叠，点B的对应点为点B'．（1）如图①，连接CD，则CD的长为；（2）如图②，B'E与AC交于点F，DB'∥BC．①求证：四边形BDB'E为菱形；②连接B'C，则△B'FC的形状为；（3）如图③，则△CEF的周长为．11．已知正方形ABCD，以CE为边在正方形ABCD外部作正方形CEFG，连AF，H是AF的中点，连接BH，HE．（1）如图1所示，点E在边CB上时，则BH，HE的关系为；（2）如图2所示，点E在BC延长线上，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请给出新的结论并证明．（3）如图3，点B，E，F在一条直线上，若AB＝13，CE＝5，直接写出BH的长．12．（1）操作发现：如图1，在矩形ABCD中，E是BC的中点，将△ABE沿AE折叠后得到△AFE，点F在矩形ABCD内部，延长AF交CD于点G．猜想线段GF与GC有何数量关系？并证明你的结论．（2）简单应用：在（1）中，如果AB＝4，AD＝6，求CG的长．（3）类比探究：如图2，将（1）中的矩形ABCD改为平行四边形，其它条件不变，（1）中的结论是否仍然成立？请说明理由．13．我们知道，平行四边形的对边平行且相等，利用这一性质，可以为证明线段之间的位置关系和数量关系提供帮助．重温定理，识别图形（1）如图①，我们在探究三角形中位线DE和第三边BC的关系时，所作的辅助线为“延长DE到点F，使EF＝DE，连接CF”，此时DE与DF在同一直线上且DE＝12DF，又可证图中的四边形为平行四边形，可得BC与DF的关系是，于是推导出了“DE∥BC，DE＝12BC”．寻找图形，完成证明（2）如图②，四边形ABCD和四边形AEFG都是正方形，△BEH是等腰直角三角形，∠EBH＝90°，连接CF、CH．求证CF＝√2BE．构造图形，解决问题（3）如图③，四边形ABCD和四边形AEFG都是菱形，∠ABC＝∠AEF＝120°，连接BE、CF．直接写出CF与BE的数量关系．类比探究型几何综合题专题训练（不用相似）答案与解析〖例1〗解：（1）如图1，∵△AOB是等边三角形，∴AO＝BO＝AB，∠AOB＝60°，∵将OC绕点O顺时针旋转，使点C落到OB边的点D处，∴OC＝OD，∠COD＝∠AOB＝60°＝α，∴△COD是等边三角形，答案为：60°，等边；（2）①∵△COD是等边三角形，∴OC＝OD，∠COD＝∠AOB＝60°，∴∠AOC＝∠BOD，又∵AO＝BO，∴△AOC≌△BOD（SAS），∴AC＝BD；②如图2，当点C在点O的上方时，若OC∥AB，∴∠AOC＝∠OAB＝60°＝β，如图2﹣1，当点C在点O的下方时，若OC∥AB，∴∠ABO＝∠BOC＝60°，∴β＝360°﹣60°﹣60＝240°，综上所述：β＝60°或240°；③如图3，当点D在线段AC上时，过点O作OE⊥AC于E，∵等边△AOB的边长为4，点C为OA 中点，∴AO＝AB＝OB＝4，OC＝OD＝CD＝2，∵∠AOB＝∠COD＝60°，∴∠AOC＝∠BOD，∴△AOC≌△BOD（SAS），∴AC＝BD，∵OE⊥CD，OC＝OD，∴CE＝DE＝1，∴OE＝√OC2−CE2＝√3，∴AE＝√OA2−OE2＝√13，∴AC＝AE+CE＝1+√13＝BD；如图4，当点C在线段AD上时，过点O作OF⊥AD于F，同理可求DF＝CF＝1，AF＝√13，∴AC＝BD＝√13﹣1，综上所述：BD＝√13+1或√13﹣1．〖例2〗解：（1）感知：∵四边形ABCD是菱形，∴BC＝CD＝AB＝2，∵E，F分别是边BC，CD的中点，∴CE＝12BC，CF＝12CD＝1，∴CE+CF＝2．故答案为：2．（2）探究：如图，连结AC．∵四边形ABCD是菱形，∴AB＝BC，AB∥CD．∴∠B+∠BCD＝180°．∵∠B＝60°，∴△ABC是等边三角形，∠BCD＝120°．∴∠BAC＝∠ACB＝60°，AB＝AC．∴∠ACF＝∠B＝60°．∵∠EAF＝60°，∴∠BAC﹣∠CAE＝∠EAF﹣∠CAE．∴∠BAE＝∠CAF．∴△ABE≌△ACF（ASA）．∴BE＝CF．∴CE+CF＝BC＝2．（3）应用：如图所示：∵四边形ABCD是菱形，∴AB＝BC，AB∥CD．∴∠B+∠BCD＝180°．∵∠B＝60°，∴△ABC是等边三角形，∠BCD＝120°．∴∠BAC＝∠ACB＝60°，AB＝AC．∴∠CAD＝∠B＝60°．∵∠EAF＝60°，∴∠CAD﹣∠DAE＝∠EAF﹣∠DAE．∴∠CAE＝∠DAF．∵∠ACE＝∠ADF，AC＝AD∴△ACE≌△ADF（ASA）．∴CE＝DF，AE＝AF，∵∠EAF＝60°，∴△AEF为等边三角形，∵EF⊥BC，∠ECF＝60°，∴CF＝2CE，∵CD＝BC＝2，∴CE＝2，∴EF=√CF2−CE2=2√3，∴△AEF的周长为6√3．〖尝试练习〗1．解：（1）AD＝CE，理由：∵△ABC与△BDE都是等边三角形，∴AB＝BC，BD＝BE，∠ABC＝∠DBE ＝60°，∴∠ABD ＝∠CBE ， ∴△ABD ≌△CBE （SAS ），∴AD ＝CE ；（2）如图2，过点B 作BH ⊥AD 于H ，在Rt △BHD 中，BD ＞BH ，∴当点D ，H 重合时，BD ＝BH ，∴BH ≤BD ，∴当BD ⊥AD 时，点B 到直线AD 的距离最大，∴∠EDP ＝90°﹣∠BDE ＝30°，同（1）的方法得，△ABD ≌△CBE （SAS ）， ∴∠BEC ＝∠BDA ＝90°，EC ＝AD ，在Rt △ABD 中，BD ＝2，AB ＝2√2，根据勾股定理得，AD ＝√AB 2−BD 2＝2， ∴CE ＝2，∵∠BEC ＝90°，∠BED ＝60°， ∴∠DEP ＝90°﹣60°＝30°＝∠EDP ，∴DP ＝EP ，如图2﹣1，过点P 作PQ ⊥DE 于Q ， ∴EQ ＝12DE ＝1，在Rt △EQP 中，∠PEQ ＝30°， ∴EP ＝EQcos ∠DEP ＝2√33， ∴PC ＝2−2√33；（3）①当点D 在AE 上时，如图3，∴∠ADB ＝180°﹣∠BDE ＝120°，∴∠BDE ＝60°，过点B 作BF ⊥AE 于F ，在Rt △BDF 中，∠DBF ＝30°，BD ＝2， ∴DF ＝1，BF ＝√3，在Rt △ABF 中，根据勾股定理得，AF ＝√AB 2−BF 2＝√5，AD ＝AF ﹣DF ＝√5﹣1，∴CE ＝AD ＝√5﹣1； ②当点D 在AE 的延长线上时，如图4，同①的方法得，AF ＝√5，DF ＝1，∴AD ＝AF +DF ＝√5+1，∴CE ＝AD ＝√5+1，即满足条件的CE 的长为√5+1和√5﹣1． 2．解：（1）①正方形ADEF 中，AD ＝AF ， ∵∠BAC ＝∠DAF ＝90°，∴∠BAD ＝∠CAF ，又∵AB=AC ，∴△DAB ≌△FAC （SAS ），∴∠ABC ＝∠ACF ，∵AB ＝AC ，∠BAC ＝90°，∴∠ABC ＝∠ACB ＝45°，∴∠ACB +∠ACF ═45°+45°＝90°，即BC ⊥CF ；②△DAB ≌△FAC ，∴CF ＝BD ，∵BC ＝BD +CD ， ∴BC ＝CF +CD ；故答案为：BC ＝CF +CD ；（2）CF ⊥BC 成立；BC ＝CD +CF 不成立，CD ＝CF +BC ．理由如下：∵正方形ADEF 中，AD ＝AF ，∵∠BAC ＝∠DAF ＝90°，∴∠BAD ＝∠CAF ，又∵AB=AC ， ∴△DAB ≌△FAC （SAS ），∴∠ABD ＝∠ACF ， ∵∠BAC ＝90°，AB ＝AC ，∴∠ACB ＝∠ABC ＝45°．∴∠ABD ＝180°﹣45°＝135°，∴∠BCF ＝∠ACF ﹣∠ACB ＝135°﹣45°＝90°，∴CF ⊥BC ．∵CD ＝DB +BC ，DB ＝CF ，∴CD ＝CF +BC ．（3）过点A 作AH ⊥BC 于点H ，过点E 作EM ⊥BD 于点M ，EN ⊥CF 于点N ， ∵∠BAC ＝90°，AB ＝AC ＝2√2， ∴BC ＝4，∴CD ＝14BC ＝1，∴BD ＝5，由（2）同理可证得△DAB ≌△FAC ，∴BC ⊥CF ，CF ＝BD ＝5，∵四边形ADEF 是正方形，∴OD ＝OF ，∵∠DCF ＝90°，∴DF ＝√CD 2+CF 2＝√26，∴OC ＝√262．3．证明：（1）如图2，延长DG交BE于H，∵四边形ABCD，四边形AEFG是正方形，∴AB＝AD，AG＝AE，∠DAB＝∠GAE＝90°，∴∠DAG＝∠BAE，∴△DAG≌△BAE（SAS），∴BE＝DG，∠ADG＝∠ABE，∵∠C+∠CBA+∠ABE+∠BHD+∠CDH＝360°，∴90°+90°+∠ADG+∠CDH+∠BHD＝360°，∴∠BHD＝90°，∴DG⊥BE；（2）如图3，连接BD，∵正方形ABCD的边长是4√2，正方形AEFG的边长为3√2，∴BD＝√2AD＝8，GE＝√2AE＝6，∵BD2＝DE2+BE2，∴64＝（6+BE）2+BE2，∴BE＝√23﹣3．〖例3〗证明：（1）∵将线段AD绕点A逆时针旋转α，∴AD＝AE，∠DAE＝α，∴∠BAC＝∠DAE，∴∠BAD＝∠CAE，又∵AB＝AC，AD＝AE，∴△BAD≌△CAE（SAS）∴BD＝CE；（2）AC＝CD+CE，理由如下：∵AB＝AC，∠BAC＝60°∴△ABC是等边三角形，∴AC＝BC，由（1）可知：BD＝CE，∴BC＝BD+CD＝CE+CD，∴AC＝CD+CE；（3）∠ACE＝45°，BD2+CD2＝2AD2，理由如下：∵AB＝AC，∠BAC＝90°，∴∠ABC＝∠ACB＝45°，∵△BAD≌△CAE∴∠ACE＝∠ABC＝45°，∴∠BCE＝∠ACE+∠ACB＝90°，∴CE2+CD2＝DE2，∵AD＝AE，∠DAE＝90°，∴DE2＝2AD2，∴CE2+CD2＝2AD2，∴BD2+CD2＝2AD2．〖例4〗（1）证明：∵四边形ABCD是正方形，∴AD＝DC，∠ADP＝∠CDP＝45°，又∵PD=PD，∴△ADP≌△CDP（SAS），∴∠PAD＝∠PCD，AP＝CP，∵PC＝PE，∴AP＝PE，∴∠PAD＝∠PED，∴∠PCD＝∠PED；（2）证明：∵四边形ABCD是正方形，∴∠ADC＝∠EDF＝90°，由（1）知，∠PCD＝∠PED，∵∠CFP＝∠EFD（对顶角相等），∴180°﹣∠CFP﹣∠PCD＝180°﹣∠EFD﹣∠PED，即∠CPF＝∠EDF＝90°，∵PC＝PE，∴△CPE是等腰直角三角形，∴EC＝√2CP，由（1）知，AP＝CP，∴EC＝√2AP；（3）解：AP＝CE；理由如下：∵四边形ABCD是菱形，∠DAB＝60°，∴AB＝BC，∠ABP＝∠CBP ＝60°，∠BAD＝∠BCD，∠EDC＝∠DAB＝60°，又∵PB=PB，∴△ABP≌△CBP（SAS），∴PA ＝PC，∠BAP＝∠BCP，∴∠DAP＝∠DCP，∵PC＝PE，∴PA＝PE，∴∠DAP＝∠AEP，∴∠DCP ＝∠AEP，∵∠CFP＝∠EFD，∴180°﹣∠CFP﹣∠PCF＝180°﹣∠EFD﹣∠AEP，即∠CPF＝∠EDF＝60°，∴△EPC是等边三角形，∴PC＝EC，∴EC＝AP，〖尝试练习〗4．解：（1）AE＝CG，理由如下：∵四边形ABCD和四边形DEFG都是菱形，∴DA＝DC，DE＝DG，又∵∠ADE=∠CDG，∴△DAE≌△DCG（SAS），∴AE＝CG；（2）成立，理由如下：∵∠ADC＝∠EDG，∴∠ADC﹣∠EDC＝∠EDG﹣∠EDC，即∠ADE＝∠CDG，又∵DA＝DC，DE＝DG，∴△DAE≌△DCG（SAS），∴AE＝CG；（3）AE⊥CG，理由如下：延长线段AE、GC交于点H，∵AD∥BC，∴∠CEH＝∠DAE，由（2）可知，△DAE ≌△DCG ，∴∠DAE ＝∠DCG ，∴∠CEH ＝∠DCG ， ∵四边形ABCD 是菱形，∠ADC ＝90°，∴四边形ABCD 是正方形，∴∠BCD ＝90°，∴∠ECH +∠DCG ＝90°，∴∠ECH +∠CEH ＝90°，∴∠CHE ＝90°，∴AE ⊥CG ． 5．（1）证明：由折叠的性质得：△ABC ≌△△ AEC ，∴∠ACB ＝∠ACE ，BC ＝EC ，∵四边形ABCD 是平行四边形，∴AD ＝BC ，AD ∥BC ．∴EC ＝AD ，∠ACB ＝∠CAD ，∴∠ACE ＝∠CAD ，∴OA ＝OC ，∴OD ＝OE ，∴∠ODE ＝∠OED ，∵∠AOC ＝∠DOE ，∴∠CAD ＝∠ACE ＝∠OED ＝∠ODE ，∴AC ∥DE ；（2）解：∵平行四边形ABCD 中，∠B ＝90°，∴四边形ABCD 是矩形，∴∠CDO ＝90°，CD ＝AB ＝√3，AD ＝BC ＝√6，由（1）得：OA ＝OC ，设OA ＝OC ＝x ，则OD ＝√6﹣x ，在Rt △OCD 中，由勾股定理得：（√3）2+（√6﹣x ）2＝x 2，解得：x ＝3√64，∴OA ＝3√64， ∴△OAC 的面积＝12OA ×CD ＝12×3√64×√3＝9√28；（3）解：分两种情况：①如图3，当∠EAD ＝90°时，延长EA 交BC 于G ，∵AD ＝BC ，BC ＝EC ，∴AD ＝EC ， ∵AD ∥BC ，∠EAD ＝90°，∴∠EGC ＝90°， ∵∠B ＝30°，AB ＝2√3，∴∠AEC ＝30°， ∴GC ＝12EC ＝12BC ，∴G 是BC 的中点，在Rt △ABG中，BG ＝√32AB ＝3，∴BC ＝2BG ＝6；②如图4，当∠AED ＝90°时∵AD ＝BC ，BC ＝EC ，∴AD ＝EC ，由折叠的性质得：AE ＝AB ，∴AE ＝CD ，又∵AC=AC ，∴△ACE ≌△CAD （SSS ）， ∴∠ECA ＝∠DAC ，∴OA ＝OC ，∴OE ＝OD ，∴∠OED ＝∠ODE ，∴∠AED ＝∠CDE ， ∵∠AED ＝90°，∴∠CDE ＝90°，∴AE ∥CD ，又∵AB ∥CD ，∴B ，A ，E 在同一直线上， ∴∠BAC ＝∠EAC ＝90°，∵Rt △ABC 中，∠B ＝30°，AB ＝2√3，∴AC ＝√33AB ＝2，BC ＝2AC ＝4；综上所述，当△AED 是直角三角形时，BC 的长为4或6．6．证明：（1）∵AF 平分∠BAD ，∴∠BAF ＝∠DAF ，∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ∥CD ，∴∠DAF ＝∠CEF ，∠BAF ＝∠CFE ，∴∠CEF ＝∠CFE ，∴CE ＝CF ，又∵四边形ECFG 是平行四边形， ∴四边形ECFG 为菱形；（2）△BDG 是等边三角形，理由如下：∵四边形ABCD 是平行四边形，∴AB ∥DC ，AB ＝DC ，AD ∥BC ，∵∠ABC ＝120°，∴∠BCD ＝60°，∠BCF ＝120°，由（1）知，四边形CEGF 是菱形，∴CE ＝GE ，∠BCG ＝12∠BCF ＝60°，∴CG ＝GE ＝CE ，∠DCG ＝120°，∵EG ∥DF ，∴∠BEG ＝120°＝∠DCG ，∵AE 是∠BAD 的平分线，∴∠DAE ＝∠BAE ，∵AD ∥BC ， ∴∠DAE ＝∠AEB ，∴∠BAE ＝∠AEB ，∴AB ＝BE ，∴BE ＝CD ，∴△BEG ≌△DCG （SAS ），∴BG ＝DG ，∠BGE ＝∠DGC ，∴∠BGD ＝∠CGE ，∵CG ＝GE ＝CE ，∴△CEG 是等边三角形， ∴∠CGE ＝60°，∴∠BGD ＝60°，∵BG ＝DG ， ∴△BDG 是等边三角形；（3）如图2中，连接BM ，MC ，∵∠ABC ＝90°，四边形ABCD 是平行四边形，∴四边形ABCD 是矩形，又由（1）可知四边形ECFG 为菱形，∠ECF＝90°，∴四边形ECFG为正方形．∵∠BAF＝∠DAF，∴BE＝AB＝DC，∵M为EF中点，∴∠CEM＝∠ECM＝45°，∴∠BEM＝∠DCM＝135°，∴△BME≌△DMC（SAS），∴MB＝MD，∠DMC＝∠BME．∴∠BMD＝∠BME+∠EMD＝∠DMC+∠EMD＝90°，∴△BMD是等腰直角三角形．∵AB＝10，AD＝24，∴BD＝√AB2+AD2＝26，∴DM＝√22BD＝13√2．【自主反馈】7．解：（1）∵△ABC是等边三角形，∴AB＝AC＝BC，∠BAC＝∠B＝∠ACB＝60°，又∵BD=AE，∴△ABD≌△CAE（SAS），∴∠BAD＝∠ACE，∵∠BAD+∠DAC＝60°，∴∠DFC＝∠ACE+∠DAC＝60°；（2）①根据题意补全图形如图2所示：②线段BE与CQ的数量关系为：CQ＝12BE；理由如下：∵CE绕着点C逆时针旋转120°，得到CP，∴CE＝CP，∠ECP＝120°，∵∠DFC＝60°，∴AD∥CP，∴∠ADC＝∠DCP，∵△ABD≌△CAE，∴CE＝AD，∴AD＝CP，∴△ADQ≌△PCQ（AAS），∴CQ＝DQ＝12CD，∵AB＝BC，BD＝AE，∴BE＝CD，∴CQ＝12BE．8．解：（1）∵△ABC，△ADE均是顶角为42°的等腰三角形，BC、DE分别是底边，∴AB＝AC，AD＝AE，∠BAC＝∠DAE，∴∠BAD＝∠CAE，∴△ABD≌△ACE（SAS）；（2）①∵△ABC是等边三角形，∴AB＝AC，∠BAC＝60°，由旋转知，AC＝AD，∠CAD＝90°，∴AB＝AD，∠BAD＝∠BAC+∠CAD＝150°，∴∠D＝12（180°﹣∠BAD）＝15°，∵AE是∠BAC的平分线，∴∠CAE＝12∠BAC＝30°，∴∠DAE＝∠CAD+∠CAE＝120°，∴∠AED＝180°﹣∠D﹣∠DAE＝45°；②BD＝2CE+√2AE；证明：如图，∵△ABC是等边三角形，∴AB＝AC，∵AE是∠BAC的角平分线，∴∠BAE＝∠CAE，∵AE＝AE，∴△BAE≌△CAE（SAS），∴BE＝CE，过点A作AF⊥AE交DE于F，∴∠EAF＝90°，由旋转知，∠CAD＝90°，∴∠CAE＝∠DAF，由①知，∠AED＝45°，∴∠AFE＝45°＝∠AEF，∴AE＝AF，∴EF＝√2AE，∵AC＝AD，∴△ACE≌△ADF（SAS），∴DF＝CE，∴BD＝BE+EF+DF＝CE+√2AE+CE ＝2CE+√2AE．9．解：（1）∵∠ABC＝90°，∠BAC＝30°，∴∠ACB＝60°，∵△ABC绕点A顺时针旋转α得到△AED，点E恰好在AC上，∴CA＝AD，∠EAD＝∠BAC＝30°，∴∠ACD＝∠ADC＝12（180°﹣30°）＝75°，∵∠EDA＝∠ACB＝60°，∴∠CDE＝∠ADC﹣∠EDA＝15°；（2）连接BF，∵点F是边AC中点，∴BF＝AF＝12AC，∵∠BAC＝30°，∴BC＝12AC，∴∠FBA＝∠BAC＝30°，∵△ABC绕点A顺时针旋转60°得到△AED，∴∠BAE＝∠CAD＝60°，CB＝DE，∠DEA＝∠ABC＝90°，∴DE ＝BF ，延长BF 交AE 于点G ，则∠BGE ＝∠GBA +∠BAG ＝90°， ∴∠BGE ＝∠DEA ，∴BF ∥ED ，∴四边形BFDE 是平行四边形，∴DF ＝BE ；（3）∵点B 、C 的坐标分别是（0，0），（0，2）， ∴BC ＝2，∵∠ABC ＝90°，∠BAC ＝30°， ∴AC ＝4，AB ＝2√3，若∠QMA ＝90°，CQ ＝MQ 时，如图3，设CQ ＝QM ＝x ，∠CAB ＝30°，∴AQ ＝2x ，AM ＝√3x ， ∴AC ＝x +2x ＝3x ＝4，∴x ＝43，∴AM ＝43√3，∴BM ＝AB ﹣AM ＝2√3﹣4√33＝2√33，∴点M （2√33，0）；若∠AQM ＝90°，CQ ＝QM 时，如图4，设CQ ＝QM ＝x ，∠CAB ＝30°， ∴AQ ＝√3x ，AM ＝2x ， ∴AC ＝x +√3x ＝4，∴x ＝2√3﹣2，∴AM ＝4√3﹣4， ∴BM ＝2√3﹣（4√3﹣4）＝4﹣2√3， ∴点M （4﹣2√3，0）；综上所述：M （2√33，0）或（4﹣2√3，0）．10．（1）解：∵△ABC 是等腰直角三角形，点D 是斜边AB 的中点，AB ＝10，∴CD ＝12AB ＝5（2）①证明：由折叠的性质得：B 'D ＝BD ，B 'E ＝BE ，∠B 'DE ＝∠BDE ，∵DB '∥BC ，∴∠B 'DE ＝∠BED ，∴∠BDE ＝∠BED ，∴BD ＝BE ，∴B 'D ＝BE ，∴四边形BDB 'E 是平行四边形，又∵B 'D ＝BD ，∴四边形BDB 'E 为菱形；②解：∵△ABC 是等腰直角三角形，点D 是斜边AB 的中点，∴CD ＝12AB ＝BD ，由折叠的性质得：B 'D ＝BD ，∴CD ＝B 'D ，∴∠DCB '＝∠DB 'C ，∵∠ACB ＝90°，∴AC ⊥BC ，∵DB '∥BC ，∴DB '⊥AC ，∴∠ACB '＝90°﹣∠DB 'C ，由①得：四边形BDB 'E 为菱形， ∴AB ∥B 'E ，∵CD ⊥AB ，∴CD ⊥B 'E ，∴∠EB 'C ＝90°﹣∠DCB '，∴∠ACB '＝∠EB 'C ， ∴FB '＝FC ，即△B 'FC 为等腰三角形；（3）解：连接B 'C ，如图③所示：∵△ABC 是等腰直角三角形，点D 是斜边AB 的中点，AB ＝10，∴BC ＝√22AB ＝5√2，∠B ＝45°，CD ＝12AB ＝BD ，∠ACD ＝12∠ACB ＝45°，由折叠的性质得：B 'D ＝BD ，∠B '＝∠B ＝45°，∴CD ＝B 'D ，∴∠DCB '＝∠DB 'C ，∴∠FCB '＝∠FB 'C ，∴CF ＝B 'F ，∴△CEF 的周长＝EF +CF +CE ＝EF +B 'F +CE ＝B 'E +CE ＝BE +CE ＝BC ＝5√2； 11．解：（1）BH ⊥HE ，BH ＝HE ；理由如下：延长EH 交AB 于M ，如图1所示： ∵四边形ABCD 和四边形CEFG 是正方形，∴AB ∥CD ∥EF ，AB ＝BC ，CE ＝FE ，∠ABC ＝90°，∴∠AMH ＝∠FEH ，∵H 是AF 的中点，∴AH ＝FH ，∴△AMH ≌△FEH （AAS ）， ∴AM ＝FE ＝CE ，MH ＝EH ，∴BM ＝BE ， ∵∠ABC ＝90°，∴BH ⊥HE ，BH ＝12ME ＝HE ；（2）结论仍然成立．BH ⊥HE ，BH ＝HE ．理由如下：延长EH 交BA 的延长线于点M ，如图2所示：∵四边形ABCD 是正方形，四边形EFGC 是正方形，∴∠ABE ＝∠BEF ＝90°，AB ＝BC ，AB ∥CD ∥EF ，CE ＝FE ，∴∠HAM ＝∠HFE ，∴△AHM ≌△FHE （ASA ），∴HM ＝HE ，AM ＝EF ＝CE ，∴BM ＝BE ，∵∠ABE ＝90°， ∴BH ⊥EH ，BH ＝12EM ＝EH ；（3）延长EH 到M ，使得MH ＝EH ，连接AH 、BH ，如图3所示：同（2）得：△AMH ≌△FEH （SAS ），∴AM ＝FE ＝CE ，∠MAH ＝∠EFH ， ∴AM ∥BF ，∴∠BAM +∠ABE ＝180°，∴∠BAM +∠CBE ＝90°，∵∠BCE +∠CBE ＝90°∴∠BAM ＝∠BCE ，∴△ABM ≌△CBE （SAS ），∴BM ＝BE ，∠ABM ＝∠CBE ，∴∠MBE ＝∠ABC ＝90°，∵MH ＝EH ，∴BH ⊥EH ，BH ＝12EM ＝MH ＝EH ，在Rt △CBE 中，BE ＝√CB 2−CE 2＝12，∵BH ＝EH ，BH ⊥EH ，∴BH ＝√22BE ＝6√2．12．解：（1）GF ＝GC ．理由如下：如图1，连接GE ， ∵E 是BC 的中点， ∴BE ＝EC ，∵△ABE 沿AE 折叠后得到△AFE ，∴BE ＝EF ，∴EF ＝EC ，∵四边形ABCD 是矩形，∴∠C ＝∠B ＝90°，∴∠EFG ＝90°，∴Rt △GFE ≌Rt △GCE （HL ），∴GF ＝GC ；（2）设GC ＝x ，则AG ＝4+x ，DG ＝4﹣x ，在Rt △ADG 中，62+（4﹣x ）2＝（4+x ）2，解得x ＝94．∴GC ＝94；（3）（1）中的结论仍然成立．证明：如图2，连接FC ，∵E 是BC 的中点，∴BE ＝CE ，∵将△ABE 沿AE 折叠后得到△AFE ，∴BE ＝EF ，∠B ＝∠AFE ，∴EF ＝EC ，∴∠EFC ＝∠ECF ，∵矩形ABCD 为平行四边形，∴∠B ＝∠D ， ∵∠ECD ＝180°﹣∠D ，∠EFG ＝180°﹣∠AFE ＝180°﹣∠B ＝180°﹣∠D ，∴∠ECD ＝∠EFG ，∴∠GFC ＝∠GFE ﹣∠EFC ＝∠ECG ﹣∠ECF ＝∠GCF ，∴∠GFC ＝∠GCF ，∴FG ＝CG ；即（1）中的结论仍然成立．13．解：（1）∵AE ＝CE ，DE ＝EF ，∠AED ＝∠CEF ，∴△AED ≌△CEF （SAS ）， ∴AD ＝CF ，∠ADE ＝∠F ，∴BD ∥CF ，∵AD ＝BD ，∴BD ＝CF ，∴四边形BCFD 是平行四边形，∴DF ＝BC ，DF ∥BC ，（2）证明：∵四边形ABCD 是正方形∴AB ＝BC ，∠ABC ＝90°，即∠ABE +∠CBE ＝90° ∵△BEH 是等腰直角三角形，∴EH ＝2BE ＝2BH ，∠BEH ＝∠BHE ＝45°， ∠EBH ＝90°，即∠CBH +∠CBE ＝90° ∴∠ABE ＝∠CBH ， ∴△ABE ≌△CBH （SAS ）， ∴AE ＝CH ，∠AEB ＝∠CHB ，∴∠CHE ＝∠CHB ﹣∠BHE ＝∠CHB ﹣45°＝∠AEB ﹣45°， ∵四边形AEFG 是正方形， ∴AE ＝EF ，∠AEF ＝90°，∴EF ＝HC ，∠FEH ＝360°﹣∠AEF ﹣∠AEB ﹣∠BEH ＝225°﹣∠AEB ， ∴∠CHE +∠FEH ＝∠AEB ﹣45°+225°﹣∠AEB ＝180°， ∴EF ∥HC 且 EF ＝HC ， ∴四边形EFCH 是平行四边形， ∴CF ＝EH ＝√2BE ；（3）CF＝√3BE，如图，过点B作BH，使∠EBH＝120°，且BH＝BE，连接EH、CH，则∠BHE＝∠BEH＝30°，∵∠ABC＝∠EBH＝120°，∴∠ABE＝∠CBH，∵AB＝BC，BE＝BH，∴△AEB≌△CHB（SAS），∴CH＝AE＝EF，∠CHB＝∠AEB，∵∠CHE＝∠CHB﹣∠BHE＝∠AEB﹣30°，∠FEH＝360°﹣∠AEF﹣∠AEB﹣∠BEH＝210°﹣∠AEB，∴∠CHE+∠FEH＝180°，∴CH∥EF且CH＝EF，∴四边形EFCH是平行四边形，∴CF＝EH，过B作BN⊥EH于N，在△EBH中，∠EBH＝120°，BH＝BE，∴∠BEN＝30°，EH＝2EN，BE，∴EN＝√32∴EH＝√3BE，∴CF＝EH＝√3BE．。

中考数学类比探究专项练习(二)(含答案)

学生做题前请先回答以下问题问题1：想一想类比探究问题常见的不变结构有哪些，处理方式是什么？问题2：类比探究问题在处理时若常见的结构不能解决问题，需要分析不变特征，如何分析不变特征？中考数学类比探究专项练习（二）一、单选题(共4道，每道7分)1.已知四边形ABCD中，E，F分别是边AB，AD上的点，DE与CF相交于点G．（1）如图1，若四边形ABCD是矩形，且DE⊥CF，求证：；（2）如图2，若四边形ABCD是平行四边形，试探究：当∠B与∠EGC满足什么关系时，成立？并证明你的结论；（3）如图3，若BA=BC=6，DA=DC=8，∠BAD＝90°，DE⊥CF，请直接写出的值．（2）中∠B与∠EGC应满足的关系是( )A.∠B=∠EGCB.∠B+∠EGC=90°C.∠B+∠EGC=120°D.∠B+∠EGC=180°答案：D解题思路：见第2题中解析试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（3）中的值为( )A. B.C. D.答案：B解题思路：试题难度：三颗星知识点：中考数学几何中的类比探究3.问题情境：张老师给爱好学习的小军和小俊提出这样一个问题：如图1，在△ABC中，AB=AC，P为BC 边上的任一点，过点P作PD⊥AB，PE⊥AC，垂足分别为D，E，过点C作CF⊥AB，垂足为F．求证：PD+PE=CF．小军的证明思路是：如图2，连接AP，由△ABP与△ACP的面积之和等于△ABC的面积可以证得：PD+PE=CF．小俊的证明思路是：如图2，过点P作PG⊥CF，垂足为G，可以证得：PD=GF，PE=CG，则PD+PE=CF．（1）变式探究：如图3，当点P在BC的延长线上时，其他条件不变，求证：PD-PE=CF；（2）结论运用：如图4，将矩形ABCD沿EF折叠，使点D落在点B上，点C落在点处，点P为折痕EF上的任一点，过点P作PG⊥BE，PH⊥BC，垂足分别为G，H，若AD=8，CF=3，求PG+PH的值；（3）迁移拓展：图5是一个航模的截面示意图，已知在四边形ABCD中，E为AB边上的一点，ED⊥AD，EC⊥CB，垂足分别为D，C，且，．M，N分别为AE，BE的中点，连接DM，CN，求△DEM与△CEN的周长之和．（2）中PG+PH的值为( )A.3B.4C.5D.答案：B解题思路：见第4题中解析试题难度：三颗星知识点：翻折变换（折叠问题）4.（上接第3题）（3）中△DEM与△CEN的周长之和为( )A.6B.C. D.答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边的一半。

类比探究专项训练(三)(含答案)

类比探究专项训练（三）一、单选题(共5道，每道20分)1.在等边三角形ABC中，点E在直线AB上，点D在直线BC上，且CE=DE．为判断AE和BD 之间的关系，小明准备分情况进行讨论．当E是AB中点时，如图1，小明发现，由于E是AB边的中点，利用三线合一可以得到AE=BE，∠ECB=30°，再由CE=DE可以得到∠D=30°，进而得到∠BED=30°，就可以得到BD=BE=AE．但是当E不是AB中点时，就不能照搬上述方式进行证明，此时小明想到了另外一种方式：过点E作EF∥BC，交AC于点F，也能证明AE=BD．（1）当E是线段AB上除端点和中点外的任一点时，如图2，按照上述辅助线证明AE=BD，证明过程中需要使用一对三角形全等，则证明此对三角形全等不能使用的条件是( )A.AASB.ASAC.SASD.SSS答案：D解题思路：1．解题要点①要在图2中照搬小明的思路，需要明白小明的思路在图1中是怎么证明的．考虑不能利用E是中点带来的结论，所以证明时，要避开中点带来的结论（AE=BE，∠ECB=30°），用其他条件来讨论．过点E作EF∥BC，交AC于点F，则△AEF是等边三角形，AE=EF=AF，能够证明△EFC≌△DBE，EF=BD，进而得到AE=BD．②在图2中，同样作出辅助线，如图所示，照搬①中的证明思路，先得到△AEF是等边三角形，AE=EF，再证明△EFC≌△DBE．关键在于判断三角形全等能够使用的条件有哪些．由题意得，BE=FC．∵∠ABC=∠AFE=60°，∴∠DBE=∠EFC=120°．∵∠D+∠DEB=60°，∠ECD+∠ECF=60°，∠D=∠ECD，∴∠DEB=∠ECF．同时∠D=∠ECD=∠CEF，即两个三角形中，三组内角分别对应相等，同时BE=CF，CE=DE，则证明△EFC≌△DBE可以使用AAS，ASA，SAS，不能使用的是SSS．③思考前面的证明过程，不变的特征是：△ABC是等边三角形，CE=DE．作平行线是为了得到等边三角形，进而得到全等三角形．④整个证明的路线图是：作辅助线；判断等边三角形（△AEF）；证明△EFC≌△DBE．2．解题过程我们利用SAS来证明AE=BD，具体过程如下：如图，过点E作EF∥BC，交AC于点F．则∠AEF=∠ABC=∠A=60°，∴△AEF是等边三角形，∴AE=EF=AF，∴BE=FC．∵CE=DE，∴∠D=∠ECD．∵∠ABC=∠ACB，∴∠D+∠DEB=∠ECD+∠ECF，∴∠DEB=∠ECF，∴△EFC≌△DBE（SAS），∴EF=BD，∴AE=BD．试题难度：三颗星知识点：中考数学几何中的类比探究2.（上接第1题）（2）当点E在BA的延长线上时，如图3，点D在BC边上，且CE=DE，按照下面的操作，能够证明AE=BD的是( )A.直接证明△EAC≌△BDEB.①过点A作AF∥BC，交EC于点F；②△AEF是等边三角形；③△AFC≌△BDEC.①过点E作EF∥BC，交CA的延长线于点F；②△AEF是等边三角形；③△EFC≌△DBED.①过点A作AF∥BC，交EC于点F，连接DF；②四边形FDBE是等腰梯形答案：C解题思路：1．解题要点此题中△ABC是等边三角形及CE=DE没有发生变化，所以可照搬（1）中的思路．作辅助线；判断等边三角形（△AEF）；证明△EFC≌△DBE．作出的辅助线是：过点E作EF∥BC，交CA的延长线于点F．2．解题过程完整的证明过程如下：如图，过点E作EF∥BC，交CA的延长线于点F．则∠AEF=∠B=∠EAF=∠BAC=60°，∴△AEF是等边三角形，∴AE=EF=AF，∴BE=FC．∵CE=DE，∴∠EDC=∠ECD，∴∠B+∠BED=∠ACB+∠FCE．∵∠B=∠ACB，∴∠BED=∠FCE，∴△EFC≌△DBE（SAS），∴EF=BD，∴AE=BD．试题难度：三颗星知识点：中考数学几何中的类比探究3.正方形ABCD中，O是对角线AC的中点，P是对角线AC上一动点，连接PB．（1）过点P作PF⊥CD于点F，PE⊥PB，交CD（或CD的延长线）于点E，如图1和图2所示，则DF和EF之间的数量关系是( )A. B.C.DF=EFD.答案：C解题思路：①题目当中的一个明显特征是，∠BPE是斜直角，通过补成弦图的方式来处理问题：如图，延长FP，交AB于点G．则四边形AGFD是矩形，△AGP是等腰直角三角形．此时能够证明△PFE≌△BGP，∴EF=PG=AG=DF．②由于在图1和图2中，PB⊥PE没有发生变化，PF⊥CD也没有发生变化，所以可以通过相同的思路分析（相同的辅助线，相同的证明思路）．2．解题过程以图1为例，如图，延长FP，交AB于点G．易知四边形AGFD是矩形，△AGP是等腰直角三角形，∴AG=DF=PG，AD=GF=AB，∴BG=PF．又∵∠EFP=∠PGB，∠EPF=90°-∠GPB=∠PBG，∴△PFE≌△BGP，∴EF=PG，∴DF=EF．试题难度：三颗星知识点：中考数学几何中的类比探究4.（上接第3题）（2）在（1）中，当点P在线段OA上时，如图所示，则线段PA，PC，CE 之间的数量关系为( )A. B.C. D.答案：D解题思路：①由于PA，PC都是斜放置的线段，所以考虑借助图形中出现的等腰直角三角形，将PA，PC转到正方形的边上，利用正方形和等腰直角三角形边长之间的关系对目标进行研究．②借助于（1）中作出的辅助线，能够得到．这样就把PA，PC，CE之间的关系转化为三条线段CF，EF，CE之间的关系．③整个思考过程：DF=EF；利用等腰直角三角形的线段关系：；CF=CE+EF．2．解题过程如图，由（1）可知DF=EF．在等腰直角三角形AGP中，，在等腰直角三角形PFC中，，而CF=CE+EF，∴，∴，即线段PA，PC，CE之间的数量关系为．试题难度：三颗星知识点：中考数学几何中的类比探究5.（上接第3，4题）（3）在（1）中，当点P在线段OC上时（不与点O，C重合），类比（2）中的做法，可以判断线段PA，PC，CE之间的数量关系为( )A. B.C. D.答案：C解题思路：1．解题要点（2）和（3）的区别仅在于点P在线段OA上和点P在线段OC上．PF⊥CD，PE⊥PB没有发生变化，所以可照搬（2）中的思路．2．解题过程如图，延长FP，交AB于点G，由（1）可知DF=EF．在等腰直角三角形AGP中，，在等腰直角三角形PFC中，，而CF=EF-CE，∴，∴，即线段PA，PC，CE之间的数量关系为．试题难度：三颗星知识点：中考数学几何中的类比探究。

中招考试几何类比探究题集锦一

中招考试几何类比探究题集锦一（附参考答案）一．解答题（共11小题）1．在△ABC中，AB=AC，∠BAC=2∠DAE=2α．（1）如图1，若点D关于直线AE的对称点为F，求证：△ABD≌△ACF；（2）如图2，在（1）的条件下，若α=45°，求证：DE2=BD2+CE2；（3）如图3，若α=45°，点E在BC的延长线上，请直接写出DE2，BD2，CE2三者之间的等量关系．2．（1）如图（1），已知：在△ABC中，∠BAC=90°，AB=AC，直线m经过点A，BD⊥直线m，CE⊥直线m，垂足分别为点D、E．猜测DE、BD、CE三条线段之间的数量关系（直接写出结果即可）．（2）如图（2），将（1）中的条件改为：在△ABC中，AB=AC，D、A、E三点都在直线m上，并且有∠BDA=∠AEC=∠BAC=α，其中α为任意锐角或钝角．请问第（1）题中DE、BD、CE之间的关系是否仍然成立？如成立，请你给出证明；若不成立，请说明理由．（3）拓展与应用：如图（3），D、E是D、A、E三点所在直线m上的两动点（D、A、E三点互不重合），点F为∠BAC平分线上的一点，且△ABF和△ACF均为等边三角形，连接BD、CE，若∠BDA=∠AEC=∠BAC，试判断线段DF、EF的数量关系，并说明理由．3．（1）问题发现如图1，△ABC和△ADE均为等边三角形，点D在边BC上，连接CE．请填空：①∠ACE的度数为；②线段AC、CD、CE之间的数量关系为．（2）拓展探究如图2，△ABC和△ADE均为等腰直角三角形，∠BAC=∠DAE=90°，点D在边BC 上，连接CE．请判断∠ACE的度数及线段AC、CD、CE之间的数量关系，并说明理由．（3）解决问题如图3，在四边形ABCD中，∠BAD=∠BCD=90°，AB=AD=2，CD=1，AC与BD交于点E，请直接写出线段AC的长度．4．【探究发现】如图1，△ABC是等边三角形，∠AEF=60°，EF交等边三角形外角平分线CF所在的直线于点F，当点E是BC的中点时，有AE=EF成立；【数学思考】某数学兴趣小组在探究AE、EF的关系时，运用“从特殊到一般”的数学思想，通过验证得出如下结论：当点E是直线BC上（B，C除外）任意一点时（其它条件不变），结论AE=EF仍然成立．假如你是该兴趣小组中的一员，请你从“点E是线段BC上的任意一点”；“点E是线段BC延长线上的任意一点”；“点E是线段BC反向延长线上的任意一点”三种情况中，任选一种情况，在备用图1中画出图形，并证明AE=EF．【拓展应用】当点E在线段BC的延长线上时，若CE=BC，在备用图2中画出图形，并运用上述结论求出S△ABC ：S△AEF的值．5．问题情境：在Rt△ABC中，AB=BC，∠B=90°，将一块等腰直角三角板的直角顶点O放在斜边AC上，将三角板绕点O旋转．（1）操作发现：当点O为AC中点时：①如图1，三角板的两直角边分别交AB，BC于E、F两点，连接EF，猜想线段AE、CF与EF之间存在的等量关系：（无需证明）；②如图2，三角板的两直角边分别交AB，BC延长线于E、F两点，连接EF，判断①中的结论是否成立．若成立，请证明；若不成立，请说明理由；（2）类比延伸：当点O不是AC中点时，如图3，三角板的两直角边分别交AB，BC于E、F两点，若=，请直接写出=．6．阅读发现：（1）如图①，在Rt△ABC和Rt△DBE中，∠ABC=∠DBE=90°，AB=BC=3，BD=BE=1，连结CD，AE．易证：△BCD≌△BAE．（不需要证明）提出问题：（2）在（1）的条件下，当BD∥AE时，延长CD交AE于点F，如图②，求AF的长．解决问题：（3）如图③，在Rt△ABC和Rt△DBE中，∠ABC=∠DBE=90°，∠BAC=∠DEB=30°，连结CD，AE．当∠BAE=45°时，点E到AB的距离EF的长为2，求线段CD的长为．7．如图1，两个完全相同的三角形纸片ABC和DEC重合放置，其中∠C=90°，∠B=∠E=30°．（1）操作发现：如图2，固定△ABC，使△DEC绕点C旋转，当点D恰好落在AB边上时，填空：①线段DE与AC的位置关系是；②设△BDC的面积为S1，△AEC的面积为S2，则S1与S2的数量关系是．（2）猜想论证当△DEC绕点C旋转到如图3所示的位置时，请猜想（1）中S1与S2的数量关系是否仍然成立？若成立，请证明；若不成立，请说明理由．（3）拓展探究已知∠ABC=60°，BD平分∠ABC，BD=CD，BC=9，DE∥AB交BC于点E（如图4）．若在射线BA上存在点F，使S△DCF=S△BDE，请求相应的BF的长．8．问题解决：如图（1），将正方形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN．当时，求的值．类比归纳：在图（1）中，若，则的值等于；若，则的值等于；若（n为整数），则的值等于．（用含n的式子表示）联系拓广：如图（2），将矩形纸片ABCD折叠，使点B落在CD边上一点E（不与点C，D 重合），压平后得到折痕MN，设，则的值等于．（用含m，n的式子表示）9．阅读理解：如图1，在直角梯形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，易证△ABP∽△PCD，从而得到BP•PC=AB•CD，解答下列问题．（1）模型探究：如图2，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD 时，结论BP•PC=AB•CD仍成立吗？试说明理由；（2）拓展应用：如图3，M为AB的中点，AE与BD交于点C，∠DME=∠A=∠B=45°且DM交AC于F，ME交BC于G．AB=，AF=3，求FG的长．10．基本模型如下图，点B、P、C在同一直线上，若∠B=∠1=∠C=90°，则△ABP∽△PCD成立，（1）模型拓展如图1，点B、P、C在同一直线上，若∠B=∠1=∠C，则△ABP∽△PCD成立吗？为什么？（2）模型应用①如图2，在等腰梯形ABCD中，AD∥BC，AD=1，AB=2，BC=4，在BC上截取BP=AD，作∠APQ=∠B，PQ交CD于点Q，求CQ的长；②如图3，正方形ABCD的边长为1，点P是线段BC上的动点，作∠APQ=90°，PQ交CD于Q，当P在何处时，线段CQ最长？最长是多少？。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1 图3ABC

EFP

ABCOEF

图2

图1FEOCB

图3ABC

EFP

ABCOEF

图2

图1

图3A

EFP

E图2

EDBAC

DBAC

EMD

CBA

中考数学类比探究在Rt△ABC中，AB=BC=5，∠ABC=90°．一块等腰直角三角板的直角顶点放在斜边AC的中点O处，将三角板绕点O旋转．

（1）如图1，三角板的两直角边分别交AB，BC于点E，F，此时，线段OE和OF之间有什么数量关系？请直接写出．（2）如图2，三角板的两直角边分别交AB，BC的延长线于点E，F，此时，（1）中的结论是否发生变化？写出你的猜想并加以证明．（3）如图3，若将三角板的直角顶点放在斜边上的点P处，当AP:AC=1:4 时，PE和PF有怎样的数量关系？证明你发现的结论．

已知：在△ABC中，∠BAC=90°，AB=AC，点D为直线BC上一动点（点D不与B，C重合），以AD为边作正方形ADEF，连接CF．（1）如图1，当点D在线段BC上时，求证：①BD⊥CF；②CF=BC-CD．（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出 CF，BC，CD三条线段之间的关系．

（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线 BC的两侧，其他条件不变．①请直接写出CF，BC，CD三条线段之间的关系；②若连接

正方形的对角线AE，DF，交点为O，连接OC，探究△AOC的形状，并说明理由．

如图1，在等腰Rt△ABC和等腰Rt△CDE（CD>BC）中，点C，B，D在同一直线上，点M是AE的中点，连接MD，MB．

（1）探究线段MD，MB的位置关系及数量关系，并证明．（2）将图1中的△CDE绕点C顺时针旋转45°，使△CDE的斜边CE恰好与△ABC的边BC垂直，如图2，原问题中的其他条件不变，则（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明．（3）若将图2中的△ABC绕点C逆时针旋转大于0°且小于45°的角，如图3，原问题中的其他条件不变，则（1）中得到的两个结论是否发生变化？写出你的猜想并加以证明． 2

图3BCQ

A图1

BCQ(P)E

CBD

AFE

CBD

图2BFD

OECA图1

COE

图3B

OECA

在△ABC中，∠A=90°，点D在线段BC上，∠EDB=12∠C，BE⊥DE，垂足为E，DE与AB相交于点F．（1）如图1，当AB=AC时，探究线段BE与FD的数量关系，并加以证明；

（2）如图2，当AB=kAC时，求BEFD的值（用含k的式子表示）．

已知点P是Rt△ABC斜边AB上一动点（不与点A，B重合），分别过点A，B向直线CP作垂线，垂足分别为E，F，Q是斜边AB的中点．（1）如图1，当点P与点Q重合时，AE与BF的位置关系是___________，QE与QF的数量关系是_____________ （2）如图2，当点P不与点Q重合时，试判断QE与QF的数量关系，并给予证明．（3）如图3，当点P在线段BA（或AB）的延长线上时，（2）中的结论是否仍然成立？请画出图形并给予证明．

在Rt△ABC中，∠BAC=90°，AD⊥BC于点D，点O是AC边上一点，连接BO，交AD于点F，OE⊥OB交BC于点E．（1）如图1，当O为边AC中点，2ACAB时，求OFOE的值；

（2）如图2，当O为边AC中点，ACnAB时，请直接写出OFOE的值；（3）如图3，当1AOOCm，ACnAB时，请直接写出OFOE的值．

AFEPQ

图2 3

CBDAFE

FECB

图3图2图1PDBC

AODCP

图3图2图1

PDBC

AODCP

图3图2

ABCE

DABCEFD

GABCEFD

（1）如图1，正方形ABCD与等腰Rt△AEF有公共顶点A，∠EAF=90°，连接BE，DF．将Rt△AEF绕点A旋转，在旋转过程中，BE，DF具有怎样的数量关系和位置关系？请给予证明．（2）如图2，将（1）中的正方形ABCD变为矩形ABCD，等腰Rt△AEF变为Rt△AEF（∠EAF=90°），且AD=kAB，AF=kAE，其他条件不变．（1）中的结论是否发生变化？请说明理由．（3）如图3，将（2）中的矩形ABCD变为平行四边形ABCD，将Rt△AEF变为△AEF，且∠BAD=∠EAF=，其他条件不变．（2）中的结论是否发生变化？如果不变，直接写出结论；如果变化，直接用k表示出线段BE，DF的数量关系，用表示出直线BE，DF形成的锐角．

已知：线段OA⊥OB，点C为OB中点，D为线段OA上一点，连接AC，BD交于点P．（1）如图1，当OA=OB，且D为OA中点时，求APPC的值；

（2）如图2，当OA=OB，且14ADOA时，求tan∠BPC的值；（3）如图3，当AD:OA:OB=1:n:2n时，直接写出tan∠BPC的值．

在□ABCD中，∠BAD的平分线交直线BC于点E，交直线DC于点F．（1）在图1中证明CE=CF；（2）如图2，若∠ABC=90°，G是EF的中点，连接DB，DG，直接写出∠BDG的度数；（3）如图3，若∠ABC=120°，FG∥CE，且FG=CE，连接DB，DG，求∠BDG的度数．

图2CBDAFEMN

图2图1

CBDAFEMN

mnAFCBEmnAFECBBCEFAnm

如图1，将正方形纸片ABCD折叠，使点B落在CD边上的点E处（不与点C，D重合），压平后得到折痕MN．当12CECD时，求AMBN的值．类比归纳

在图1中，若13CECD，则AMBN的值为__________；若14CECD，则AMBN的值为__________；若1CECDn（n为整数），则AMBN的值为__________．（用含n的式子表示）联系拓广如图2，将矩形纸片ABCD折叠，使点B落在CD边上的点E处（不与点CD，重合），压

平后得到折痕MN，设1ABBCm（1m），1CECDn，则AMBN的值为_______．（用含mn，的式子表示）

点A，B分别是两条平行线m，n上任意一点，在直线n上找一点C，使BC=kAB，连接AC，在直线AC上任取一点E，作∠BEF=∠ABC，EF交直线m于点F．（1）如图1，当∠ABC=90°，k=1时，判断线段EF和EB之间的数量关系，并证明．（2）如图2，当∠ABC=90°，k≠1时，（1）中的结论还成立吗？若成立，请证明；若不成立，请重新判断线段EF和EB之间的数量关系．（3）如图3，当0°<∠ABC<90°，k=1时，探究EF和EB之间的数量关系，并证明． 5

如图1，在梯形ABCD中，AD∥BC，∠ABC=2∠BCD=2α，点E在AD上，点F在DC上，且∠BEF=∠A．

（1）∠BEF=__________（用含α的代数式表示），并证明∠DEF=∠ABE；（2）当AB=AD时，猜想线段EB，EF的数量关系，并证明你的猜想；（3）如图2，当AB≠AD时，将“点E在AD上”改为“点E在AD的延长线上，且AE >AB，

AB=mDE，AD=nDE”，其他条件不变，求EBEF的值．（用含m，n的代数式表示）

图1BC

ADFE

图2ABCEDF