关于函数的不动点
不动点迭代法的原理

不动点迭代法的原理
不动点迭代法,也称不动点定理,是数学分析中一种重要的迭代方法。
它的原理基于不动点定理,该定理指出,对于某个给定的函数f(x),如果存在一个实数a,使得f(a) = a,那么a就是这个函数的一个不动点。
不动点迭代法的原理是,通过选取一个初始近似值x0,通过迭代公式xn+1=f(xn)来逐步逼近函数的不动点。
也就是说,我们从初始值开始,通过不断地将初始值代入函数f(x)中,然后再将得到的结果再次代入函数f(x)中,循环迭代,直到满足设定的精度要求或达到迭代次数限制。
不动点迭代法的关键在于选取合适的迭代函数f(x),使得迭代过程能够收敛到函数的不动点。
通常情况下,选择一个合适的迭代函数并不容易,需要依靠数学知识和经验进行判断。
不动点迭代法的优点是简单易实现,适用于求解非线性方程和优化问题。
但是它也存在一些限制,比如迭代过程可能会出现发散的情况,无法收敛到不动点,或者迭代过程非常缓慢等。
因此,在使用不动点迭代法时需要仔细选择迭代函数,并进行合理的调整和判断,以确保迭代过程的有效性和收敛性。
专题14 函数不动点问题(原卷版)

专题14函数不动点问题一、单选题1.(2020·广东海珠·高二期末)设函数()f x (a R e ∈,为自然对数的底数),若曲线y x x =上存在点00()x y ,使得00()f y y =,则a 的取值范围是 A .1e[1]e-, B .1e[e 1]e-+, C .[1e 1]+, D .[1,e]2.(2021·四川·高考真题(文))设函数(a ∈R ,e 为自然对数的底数).若存在b ∈[0,1]使f (f (b ))=b 成立,则a 的取值范围是( ) A .[1,e]B .[1,1+e]C .[e ,1+e]D .[0,1]3.(2021·山西省榆社中学高三月考(理))若存在一个实数t ,使得()F t t =成立,则称t 为函数()F x 的一个不动点.设函数()1(xg x e x a =+-(a R ∈,e 为自然对数的底数),定义在R 上的连续函数()f x 满足()()2f x f x x -+=,且当0x ≤时,()f x x '<.若存在01|()(1)2x x f x f x x ⎧⎫∈+-+⎨⎬⎩⎭,且0x 为函数()g x 的一个不动点,则实数a 的取值范围为( )A .⎛⎫-∞ ⎪ ⎪⎝⎭ B .⎡⎫+∞⎪⎢⎪⎣⎭ C .⎛⎤⎥ ⎝⎦ D .⎛⎫+∞⎪ ⎪⎝⎭4.(2021·四川自贡·高二期末(文))设函数()()1ln 2=+-∈f x x x a a R ,若存在[]1,b e ∈(e 为自然对数的底数),使得()()f f b b =,则实数a 的取值范围是( ) A .1,122⎡⎤--⎢⎥⎣⎦eB .e 1,ln 212⎡⎤--⎢⎥⎣⎦C .1,ln 212⎡⎤--⎢⎥⎣⎦D .1,02⎡⎤-⎢⎥⎣⎦5.(2021·重庆一中高一期中)设函数()2xf x e x a =+-(,a R e ∈为自然对数的底数),若存在实数[]0,1b ∈使()()f f b b =成立,则实数a 的取值范围是( ) A .[]0,eB .[]1,1e +C .[]1,2e +D .[]0,16.(2021·全国·高三专题练习)设函数()f x a ∈R ,e 为自然对数的底数),若曲线sin y x =上存在点()00x y ,使得()()00f f y y =,则a 的取值范围是( ).A .[]1e ,B .111e ⎡⎤-⎢⎥⎣⎦, C .[]1e 1+, D .11e 1e ⎡⎤-+⎢⎥⎣⎦,7.(2021·黑龙江·哈尔滨三中二模(理))设函数()2xf x e x a =+-(a R ∈),e 为自然对数的底数,若曲线sin y x =上存在点()00,x y ,使得()()00f f y y =,则a 的取值范围是( )A .11,1e e -⎡⎤-++⎣⎦B .[]1,1e +C .[],1e e +D .[]1,e8.(2016·江西南昌·高三专题练习)设函数()f x =a R ∈,e 为自然对数的底数),若曲线sin y x =上存在00(,)x y 使得00(())f f y y =,则a 的取值范围是 A .[]1,e B .1,1e -⎡⎤⎣⎦ C .[]1,1e +D .1,1e e -⎡⎤+⎣⎦9.(2016·海南·高三月考(理))设函数(),f x a R e =∈为自然对数的底数).若曲线sin y x =上存在 00,x y 使得()()00f f y y =,则a 的取值范围是 A .[]1,eB .11,1e -⎡⎤-⎣⎦C .[]1,1e +D .11,1e e -⎡⎤-+⎣⎦10.(2016·安徽合肥·高三期中(理))设函数,为自然对数的底数,若曲线上存在点,使得,则的取值范围是 A .B .C .D .11.(2014·重庆·高二期中(文))设函数()f x =a R ∈,e 为自然对数的底数).若存在[0,1]b ∈使(())f f b b =成立,则a 的取值范围是 A .[1,]eB .[1,1]e +C .[,1]e e +D .[0,1]12.(2021·全国·高一单元测试)设函数()f x =a ∈R ),若存在[]02,3x ∈,使得()00f f x x =⎡⎤⎣⎦,则a 的取值范围为( ) A .[]ln33,ln 22-- B .[]ln36,ln 22-- C .[]ln36,ln 24--D .[]ln 22,ln33++13.(2017·河北衡水中学二模(文))设函数()3(xg x e x a a =+-∈,R e 为自然对数的底数),定义在R 上的连续函数()f x 满足:()()2f x f x x -+=,且当0x <时,()'f x x <,若存在()(){}0|222x x f x f x x ∈+≥-+,使得()()00g g x x =,则实数a 的取值范围为A .12⎛⎤-∞ ⎥⎝⎦B .(],2e -∞+C .1,2e ⎛⎤-∞+ ⎥⎝⎦D .(2⎤-∞⎦14.(2021·云南大理·模拟预测(理))在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石.简单的讲就是对于满足一定条件的连续函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数,下列为“不动点”函数的是( )A .()ln 1f x x =-B .()e 1x f x =+C .1()f x x x=+D .2()21f x x x =+-15.(2021·河北·衡水中学实验学校一模(文))设函数()f x =e 1e 1sin 22y x -+=+上存在点0(x ,0)y 使得00(())f f y y =成立,则实数a 的取值范围为( ) A .[0,21]e e -+B .[0,21]e e +-C .[0,21]e e --D .[0,21]e e ++16.(2021·安徽省怀宁县第二中学高三月考(理))设D 是函数()y f x =定义域内的一个区间,若存在0x D ∈,使()00f x x =-,则称0x 是()f x 的一个“次不动点”,也称()f x 在区间D 上存在“次不动点”,若函数()2532f x ax x a =--+在区间[1,4]上存在“次不动点”,则实数a 的取值范围是( )A .[12,+∞)B .1(,]2-∞C .(-∞,0)D .(0,12)17.(2021·全国·高二课时练习)设函数()f x =若曲线sin y x =上存在点()00,x y ,使得()()00f f y y =,则实数a 的取值范围是( )A .[]1,2e +B .13,1e -⎡⎤-⎣⎦C .[]1,1e +D .13,1e e --⎡⎤+⎣⎦18.(2021·湖南·邵阳市第二中学模拟预测(理))设函数()f x 若曲线cos y x =上存在点()00,x y ,使得()()00f f y y =,则实数a 的取值范围是( ) A .[]1,eB .1e 3,1-⎡⎤-⎣⎦C .[]1,e 1+D .1e 3,e 1-⎡⎤-+⎣⎦19.(2021·江苏·南京田家炳高级中学高三月考)对于函数()f x ,把满足()00f x x =的实数0x 叫做函数()f x 的不动点.设()ln f x a x =,若()f x 有两个不动点,则实数a 的取值范围是( )A .()0,eB .(),e +∞C .()1,+∞D .()1,e20.(2021·浙江·高一期末)设函数35()22xx f x x a x +=+-++,若曲线cos y x =上存在点00(,)x y ,使得00(())f f y y =,则实数a 的取值范围是( )A .133[,]52-- B .35[,]22-C .314[,]23-D .514[,]23二、多选题21.(2021·吉林·梅河口市第五中学高一月考)在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可运用到有限维空间,并构成了一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L .E .J .Brouwer ).简单地讲就是对于满足一定条件的连续函数()f x ,存在实数0x ,使得()00f x x =,那么我们就称该函数为“不动点”函数.下列函数为“不动点”函数的是( ) A .()1f x x x =++B .()235f x x x =--C .4()3(0)f x x x x=->D .221,0()1,0x x x f x x x ⎧++>⎪=⎨-≤⎪⎩22.(2021·全国·高二单元测试)定义方程()()f x f x '=的实数根0x 为函数()f x 的“新不动点”,下列函数中只有一个“新不动点”的函数为( ) A .()212g x x =B .()e 2xg x x =--C .()ln g x x =D .()sin 2cos g x x x =+23.(2021·辽宁沈阳·高一期中)在数学中,布劳威尔不动点定理是拓扑学里一个非常重要的不动点定理,它可应用到有限维空间,并构成一般不动点定理的基石.布劳威尔不动点定理得名于荷兰数学家鲁伊兹·布劳威尔(L .E .J .Brouwer ),简单的讲就是对于满足一定条件的图象不间断的函数()f x ,存在一个点0x ,使得()00f x x =,那么我们称该函数为“不动点”函数.下列为“不动点”函数的是( )A .()3f x x +B .()23g x x x =-+C .()221,12,1x x f x x x ⎧-≤⎪=⎨->⎪⎩D .()1f x x x=-三、填空题24.(2021·云南师大附中高三月考(理))设函数()f x =e 1e 1sin 22y x -+=⋅+上存在点()00,x y ,使得()()00f f y y =成立,则实数a 的取值范围是___________.25.(2021·全国·高三专题练习(文))已知函数()2,xf x e x a a R =+-∈,若曲线sin y x =上存在点00,x y ,使得()()00f f y y =,则实数a 的取值范围是__________.26.(2017·江苏·常熟中学高三月考)已知函数()()ln R x f x x a a x =+-∈,若曲线122e e 1x x y +=+(e 为自然对数的底数)上存在点()00,x y 使得()()00f f y y =,则实数a 的取值范围为__________.27.(2021·黑龙江·铁人中学高二期末(文))对于函数()f x ,把满足()00f x x =的实数0x 叫做函数()f x 的不动点,设()ln f x a x =,若()f x 有两个不动点,则实数a 的取值范围是__________.。
不动点法原理

不动点法原理不动点法是一种数值计算方法,用于寻找方程$f(x)=x$ 的解,其中 $f(x)$ 是一个给定的函数。
它的原理是通过迭代的方式逼近不动点,即在每一次迭代中,将上一次迭代得到的结果作为输入,通过函数计算得到新的结果,直到满足某个终止条件为止。
具体来说,假设我们要解方程 $f(x)=x$,首先选择一个初始值$x_0$,然后迭代地计算 $x_1=f(x_0), x_2=f(x_1), x_3=f(x_2),\ldots$,直到达到满足终止条件的解。
终止条件可以是两次迭代之间的解的差值小于某个给定的阈值,或者设定一个最大迭代次数。
不动点法的关键是选择一个合适的函数 $f(x)$,使得方程$f(x)=x$ 的解也是 $f(x)$ 的不动点。
这通常可以通过对原方程进行变换得到。
一般来说,选择一个合适的初始值也对迭代的结果产生影响,过大或过小的初始值都可能导致迭代发散或者无法收敛到正确的解。
举个例子来说明不动点法的应用。
假设我们要解方程 $x^2-3x+2=0$,可以将这个方程变形为 $x=g(x)$ 的形式,其中$g(x)$ 是一个适当的函数。
我们可以令 $g(x)=x^2-3x+2$,这样原方程的解也就成了 $g(x)$ 的不动点。
选择一个初始值$x_0=0$,经过迭代计算,我们可以得到 $x_1=g(x_0)=-2,x_2=g(x_1)=0, x_3=g(x_2)=0, \ldots$,当迭代到 $x_2$ 时,解已经收敛,并且满足 $g(x_2)=x_2$,因此 $x_2$ 就是原方程的一个解。
总结来说,不动点法通过迭代计算来逼近方程$f(x)=x$ 的解,关键是选择适当的函数 $f(x)$ 和初始值 $x_0$,从而找到方程的不动点作为解。
不动点与稳定点

高考数学试题研究不动点:已知函数)(x f y =,I x ∈,若存在I x ∈0,使得00)(x x f =,则称0x 为函数)(x f y =的不动点。
不动点实际上是方程组⎩⎨⎧==x y x f y )(的解),(00y x 的横坐标,或两者图象的交点的横坐标 当然,这个方程组根据函数)(x f y =的不同,可能有多解。
例如1:⎩⎨⎧=-=x y x y 12的解只有一个)1,1(,故函数12-=x y 有一个不动点10=x 例如2:⎩⎨⎧=-=xy x y 122的解为)21,21(-,)1,1(,故函数122-=x y 有两个不动点1,21- 稳定点:已知函数)(x f y =,I x ∈,若存在I x ∈0,使得00))((x x f f =,则称0x 为函数)(x f y =的稳定点。
很显然,若0x 为函数)(x f y =的不动点,则0x 必为函数)(x f y =的稳定点。
证明是非常简单的!因为00)(x x f =,所以000)())((x x f x f f ==,即00))((x x f f =,故0x 也是函数)(x f y =的稳定点。
反之,有没有不是不动点的稳定点呢?答案是肯定的!例如3:设12)(-=x x f ,令x x =--1)12(2,解得1=x故函数12-=x y 有一个稳定点10=x例如4:12)(2-=x x f ,令x x =--1)12(222,因为不动点必为稳定点,所以该方程一定有两解1,21-=x ,由此因式分解,可得0)124)(12)(1(2=-++-x x x x 还有另外两解451±-=x ,故函数122-=x y 的稳定点有1,21-,451±- 其中451±-是稳定点,但不是不动点。
请看下面四个图形,分别对应例1、2、3、4.由此,清晰可见,不动点是函数图象与直线x y =的交点的横坐标,而稳定点是函数图象与它的反函数(可以是多值的)的图象的交点的横坐标.根据例1和例3,我们可以给出命题:若函数)(x f y =单调递增,则它的不动点与稳定点是完全等价的。
讲义1客观题提高题型3-不动点(蛛网算法)
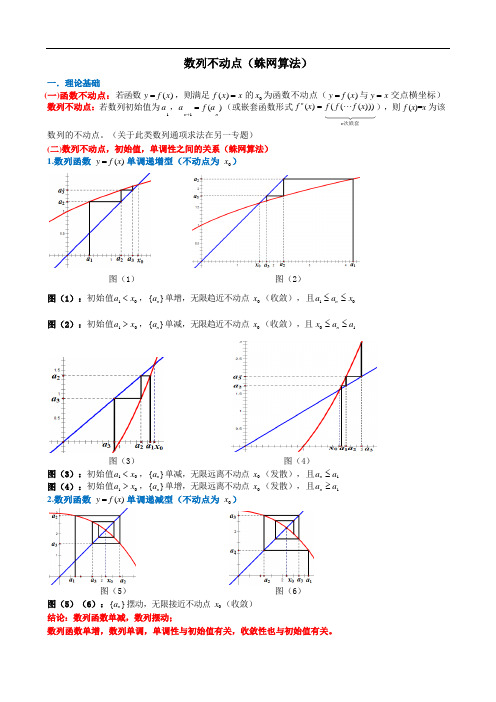
数列不动点(蛛网算法)一.理论基础(一)函数不动点:若函数 y = f (x ) ,则满足 f (x ) = x 的 x 0 为函数不动点( y = f (x ) 与 y = x 交点横坐标)数列不动点:若数列初始值为a ,a = f (a ) (或嵌套函数形式 f n(x ) = f ( f (⋅ ⋅ ⋅ f (x ))) ),则 f (x )=x 为该1n +1nn 次嵌套数列的不动点。
(关于此类数列通项求法在另一专题) (二)数列不动点,初始值,单调性之间的关系(蛛网算法) 1.数列函数 y = f (x ) 单调递增型(不动点为 x 0 )图(1)图(2)图(1):初始值a 1 < x 0 , {a n } 单增,无限趋近不动点 x 0 (收敛),且a 1 ≤ a n ≤ x 0图(2):初始值a 1 > x 0 , {a n } 单减,无限趋近不动点 x 0 (收敛),且 x 0 ≤ a n ≤ a 1图(3) 图(4) 图(3):初始值a 1 < x 0 , {a n } 单减,无限远离不动点 x 0 (发散),且a n ≤ a 1 图(4):初始值a 1 > x 0 , {a n } 单增,无限远离不动点 x 0 (发散),且a n ≥ a 1 2.数列函数 y = f (x ) 单调递减型(不动点为 x 0 )图(5)图(6)图(5)(6): {a n } 摆动,无限接近不动点 x 0 (收敛) 结论:数列函数单减,数列摆动;数列函数单增,数列单调,单调性与初始值有关,收敛性也与初始值有关。
n n n n n n 二.典型例题例1.数列{ a }满足a = 1 , a = a + sin a,对于 n ∈ N * ,下列选项错误的是( ) nA. a n +1 ≥ a n 1 n +1B. a n n n≤ 2n -1 C. a n ≤ πD. a n ≤ 2解析:令 f (x ) = x + sin x = x ,解得 x = k π ,如图(根据导函数可得), 初始值a 1 = 1 < π = x 0 ,{a n } 单增,无限趋近不动点 x 0 (收敛),且1 ≤ a n ≤ π 又因为在[0,π ] , sin x ≤ x ,则a= a + sin a ≤ 2a ,则a ≤ 2n -1 ,综上n +1nnnn所述,答案选 D.例 2.正项数列{a } 满足a = a 2 - 4a + 6 (n ≥ 1,n ∈ N * ) .若{a } 单调递增,则a 的取值范围是()nn +1nnn1A. a 1 > 3 B. a 1 > 3 或0 < a 1 < 1 C . a 1 > 3 或0 < a 1 < 2 D . a 1 > 2 或0 < a 1 < 1解析:a n +1 = a 2- 4a + 6 (n ≥1,n ∈ N * ) ,令 f (x ) =x 2 -4x +6 =x ,x = 2,3 ,所以 x = 2,3 为函数的不动点,由“蜘蛛网”迭代可知,当0 < a 1 < 1或 a 1 > 3 时,数列{a n } 单调递增;当1 < a 1 < 2 时,数列{a n } 单调递减; 故0 < a 1 < 1或a 1 > 3 ,选 B三、巩固强化1.已知数列{a n }满足a 1= a > 0, a n +1= -a 2+ ta (n ∈ N *),若存在实数t ,使{a n } 单调递增,则a 的取值范围是()AA .(0,1)B. (1,2)C.(2,3)D.(3,4)2. 已知数列{a } 满足a = 1, a = f (n ), (n ∈ N * ) ,若 S 是数列{a } 前 100 项和,且满足 S < 100 ,则n 1 2 n +1100 n 100f (x ) 不可能为( ) DA . f (x ) = x 2 B. f (x ) = x + 1+ 2 xC. f (x ) = e x - x -1D. f (x ) = ln x + x +13. 数列{a n } 满足a 1 = 1, a n +1 = -a 2+ ca -1 ,若{a n }单调递增,则实数c 的取值范围是 ( 3 , +14. 已知数列{x } 满足0 < x < x < π ,且 x= ⎧x n + sin x n , x n ≤ x n -1 (n ≥ 2) ,则( )An12n +1⎨x + cos x , x > x ⎩ n n n n -1A . x 3 < x 4 , x 2019 < π B. x 3 < x 4 , x 2019 > π C. x 3 > x 4 , x 2019 < πD. x 3 > x 4 , x 2019 > π。
函数迭代和不动点

函数迭代和不动点1 问题提出古代有一个善于经营的商人,他每天的银子都可以翻番,但是需要交税。
第一种交税方式是每天固定缴纳10两银子,第二种交税方式是每天缴纳总银两的三分之一。
假设商人星期一早上有12两银子,那么到了星期五生意结束后,他按哪种交税方式合算呢?先来看第一种方式,设每天开始时商人有银两x,那么当天结束时的银两为f(x)=2x-10.设第一天开始时银两为t, 那么结束时银两为f(t)=2t-10.第二天开始时银两为f(t),结束时的银两为f(f(t))=2f(t)-10=2(2t-10)-10=4t-30.第三天开始时银两为f(f(t)),结束时的银两为f(f(f(t)))=2f(f(t))-10=2(4t-30)-10=8t-70.同理第四天结束时的银两为f(f(f(f(t))))=2f(f(f(t)))-10=2(8t-70)-10=16t-150.第五天结束时的银两为f(f(f(f(f(t)))))=2f(f(f(f(t))))-10=2(16t-150)-10=32t-310.已知t=12,所以按照第一种缴税方式第五天结束后商人还剩银两为32x12-310=74,缴纳的税为50两.再看第二种缴税方式,设每天开始时商人有银两x,那么当天结束时的银两为f(x)=4x/3.设第一天开始时银两为t, 那么结束时银两为f(t)=4t/3.第二天开始时银两为f(t),结束时的银两为f(f(t))=4f(t)/3=16t/9 第三天开始时银两为f(f(t)),结束时的银两为f(f(f(t)))=4f(f(t))/3=64t/27第四天开始时银两为f(f(f(t))),结束时的银两为f(f(f(f(t))))=4f(f(f(t)))/3=256t/81第五天结束时的银两为f(f(f(f(f(t)))))=4f(f(f(f(t))))/3=1024t/243.已知t=12,所以按照第二种缴税方式第五天结束后商人还剩银两为1024x12/243=50.6,可以计算缴纳的税约为77.1两.这种同一个函数复合多次,我们叫做函数的迭代。
函数迭代与不动点
函数迭代与不动点——探析“如果f(x)有且仅有两个不动点,求证f[f(x)]不可能有且仅有3个不动点”问题定义:性质:若实数x 0为y=f(x)的不动点,则x 0也为y=f n (x)的不动点。
这个性质用数学归纳法是平凡的。
n=1时,结论平凡。
n=k 时,若有x 0为y=f k (x)的不动点n=k+1时,f k+1(x 0)=f(f k (x 0))=f(x 0)= x 0 ,故x 0为y=f k+1(x)的不动点 所以性质1是成立的。
而性质1,有广泛地使用,例如: f(x)=ax+b (a ≠1),则有f n (x)= ()11k b b a x a a-+--回到原题,用反证法,若f[f(x)]有且仅有3个不动点。
由性质,则f(x)有两个不动点,设为a、b。
F[f(x)]除了a、b的不动点设为c。
则f2(f(c))=f(f2(c))=f(c),因此f(c)为f[f(x)]的不动点。
则f(c)等于a、b、c中的一个。
若f(c)=c,则c为f(x)的不动点,这与f(x)恰有两个不动点,矛盾。
若f(c)=a或b,由对称性,不妨设f(c)=a,则f[f(c)]=f(a)=a,又f[f(x)]的不动点为c,则f[f(c)]=c,所以a=c,矛盾命题得证。
再次回到这个性质:若实数x0为y=f(x)的不动点,则x0也为y=f n(x)的不动点。
这个性质无论是在如本题,还是高考题中都有广泛运用,因此这个结论需要熟练牢记,并巧妙运用。
参考文献1 、中等数学 > 2003年3期 > 函数不动点在解题中的应用22、《中学数学教学》, 2014, 第6期(6):15-17。
用不动点法解函数数列等相关问题
4 5
2
( x + 4) -4 ,
……
f (5) ( x) =
4 5
5
( x + 4) -4 .
由于 f (5) ( x) 为正整数 ,则 55 | ( x + 4) .
因此 , x 的最小值为 55 - 4=3121 .
例 6 若 f ( x) = 19 x2 + 93 ,求 f ( n) ( x) .
所以 , f (α4 ) =α4 , …, f (α2 n ) =α2 n .
而这与 x →+ ∞, f ( x) →0 矛盾.
(2) 若 0< α<1 ,则由
1= f (1) = f α1 ·α
= f α1 f (α)
=αf
1 α
,
得f
1 α
=
1 α
,且由
0<
α<1
知α1 > 1.
类似 (1) 得出矛盾. 于是 , f ( x) 只有一个不动点.
a ≠- d ,则
1 an + 1 -
x0
=
2c a+ d
+
1 an -
x0 .
证明 : (1) 因为函数 f ( x) 有两个相异不
动点
x1 、x2
,所以 ,由
x=
ax + b得 cx + d
cx2 + ( d - a) x - b = 0.
变形得 cx2 - ax = b - dx ,即
b - dx = ( cx - a) x .
所以 , f ( x)
=
1 x
(x
∈R+ ) .
零点定理与不动点定理的应用
零点定理与不动点定理的应用数学是自然科学中一门极具理论性的学科,也是运用极广泛的一门学科。
在数学中,有两个非常重要的定理,它们分别是零点定理和不动点定理。
这两个定理在数学中的应用十分广泛,本文将主要从实际问题的角度出发,介绍它们的应用。
一、零点定理零点定理,顾名思义,就是寻找函数的零点。
一个函数f(x)的零点就是方程f(x)=0的根。
在应用中,我们通常会遇到这样一种情况:已知函数f(x),求它的零点。
这时,我们通常会通过函数图像来找到函数的零点。
在工程应用领域中,经常会需要求解复杂的方程组。
这时,我们可以将方程组转化为非线性方程f(x)=0的形式,然后利用零点定理来求解。
例如,在石化行业中,我们经常需要求解化学反应动力学方程,以预测反应过程中的各种参数。
而这些方程通常是非线性的,无法通过简单的代数方法来求解。
这时,我们可以通过建立反应动力学模型,然后通过计算机仿真来求解方程的零点,在工业上广泛应用。
另外一个实际应用是在机器人控制领域中。
在机器人的运动学分析中,往往需要解一些复杂的非线性方程,例如机械臂运动的角度计算问题。
这时,我们同样可以使用零点定理来寻找方程的零点,从而得到机器臂的所需运动角度。
二、不动点定理不动点定理是另一种重要的定理,它在数学中的应用远比零点定理广泛。
不动点定理的意思是寻找一个函数的不动点。
一个函数f(x)的不动点就是满足方程f(x)=x的点x。
在应用中,不动点定理通常用于解决优化问题。
例如,在经济学和金融学中,经常需要求解各类优化问题,例如成本最小化、利润最大化等。
而这些问题通常可以描述为一个函数的最优解,该函数的不动点就是最优解。
这时,我们可以利用不动点定理来找到函数的不动点,从而得到最优解。
再例如,在人工智能领域中,深度学习模型通常也可以被视为一个函数,模型的训练过程就是寻找这个函数的不动点。
在深度学习中,不动点定理被广泛应用于优化算法的设计和改进。
此外,不动点定理在随机过程中的应用也非常广泛。
不动点理论及其应用
不动点理论及其应用主要内容:●不动点理论—压缩映像原理●不动点理论在微分方程中的应用●不动点理论在中学数学中的应用目录:一、引言二、压缩映像原理三、在微分方程中的应用四、在中学数学中的应用五、其它一、 引言取一张照片,按比例缩小,然后把小照片随手放在大照片上,那么大小两张照片在同一个部位,一定有一个点是重合的。
这个重合点就是一个不动点。
函数的不动点, 在数学中是指被这个函数映射到其自身的一个点, 即函数)(x f 在取值过程中, 如果有一个点0x 使00)(x x f =,则 0x 就是一个不动点。
二、 压缩映像原理定理:(Banach 不动点定理—压缩映像原理)设 ),(ρX 是一个完备的距离空间, T 是),(ρX 到其自身的一个压缩映射,则T 在X 上存在唯一的不动点。
这里有三个概念:距离空间,完备的距离空间,压缩映射距离空间又称为度量空间。
定义:(距离空间)设 X 是一个非空集合。
X 称为距离空间,是指在X 上定义了一个双变量的实值函数 ),(y x ρ, 满足下面三个条件:(1)。
0),(≥y x ρ, 而且0),(=y x ρ, 当且仅当 y x =; (2)。
),(),(x y y x ρρ=;(3)。
),(),(),(z y y x z x ρρρ+≤, (X ,,∈∀z y x )。
这里 ρ 叫做 X 上的一个距离,以 ρ 为距离的距离空间 X 记作),(ρX 。
定义:(完备的距离空间)距离空间),(ρX 中的所有基本列都是收敛列,则称该空间是完备的。
定义:(压缩映射)称映射 ),(),(:ρρX X T → 是一个压缩映射,如果存在 10<<a , 使得 ),(),(y x a Ty Tx ρρ≤ ),(X y x ∈∀成立。
三、 在微分方程中的应用定理:(存在和唯一性)考虑如下初值问题⎪⎩⎪⎨⎧==.00)(),,(y x y y x f dx dy假设 ),(y x f 在矩形区域b y y a x x R ≤-≤-||,||:00内连续,而且对 y 满足Lipschitz 条件,则上述问题在区间],[00h x h x I +-= 上有且仅有一个解,其中.|),(|max },,min{),(y x f M Maa h R y x ∈>=(1)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
关于函数的不动点
在数学中,函数的不动点是指一个函数的输入和输出相等的点。
换句
话说,如果一个函数f在一些点x处的值等于x本身,那么x就是函数f
的不动点。
在形式化的表示中,可以用f(x)=x来表示。
不动点在很多数
学理论和应用中都有重要的意义,在探索函数的性质、解方程、优化问题
等方面都有广泛的应用。
首先,不动点理论是函数分析、拓扑学和离散动力系统等领域的重要
研究内容之一、在函数分析中,不动点定理是一个重要的工具,它可以帮
助我们证明函数的连续性、存在性和唯一性等性质。
其中,著名的
Banach不动点定理是函数分析中的一个重要结果,它指出了完备度量空
间中的压缩映射必然存在不动点。
通过不动点定理,我们可以解决一些方
程和优化问题,如求解方程f(x) = x的解、求解方程组、寻找最优解等。
其次,不动点还在离散动力系统的研究中起到重要的作用。
离散动力
系统是指在离散时间点上由函数迭代产生的动力学系统。
这些离散动力系
统可以通过不动点来描述。
例如,一个动力系统可以用差分方程f(x)来
表示,如果在x处的函数值等于x本身,那么x就是这个动力系统的不动点。
离散动力系统的稳定性、吸引子等性质可以通过不动点的性质来研究
和分析。
此外,在数值计算和优化问题中,不动点也起到关键的作用。
例如,
在迭代算法中,通过迭代产生的序列可以看作是函数的不动点的逼近值。
当迭代到一些值时,如果该值与下一次迭代产生的值相差很小,那么该值
可以近似地看作函数的不动点。
通过不动点的逼近,我们可以解决一些数
值计算问题,如求函数的根、求解方程组、求极值等。
除了在数学领域中的应用,不动点还在计算机科学和信息论等领域有
广泛的应用。
在计算机科学中,不动点理论被广泛应用于程序语言的语义
分析、类型推导、程序验证等方面。
通过不动点理论,我们可以定义各种
语言的语义,并进行形式化的推理和验证。
在信息论中,不动点也被用于
描述和分析数据压缩算法、信道编码等问题。
通过不动点的性质,我们可
以找到效率更高的数据压缩算法和信道编码方案。
综上所述,函数的不动点在数学和计算机科学等领域中有广泛的应用。
通过不动点的性质和定理,我们可以研究函数的性质、解方程、优化问题等。
不动点理论不仅在数学理论上有重要意义,也在实际应用中发挥着关
键的作用。
通过深入研究和应用不动点理论,我们可以更好地理解和分析
各种问题,并且提供更有效的解决方法。
