戴维南诺顿等效变换
电路定理——戴维南,诺顿,等效

P 20V (4A) 80W
产生功率 80W
例3.2.1 图(a)所示电路,已知i=1A;试求电压u
解用电流为1A电流源替换网络N 列节点方程: 解得:
4 3 1 1 1 u 1 2 3 2 6 3
u 2V
例3.2.2 图(a)所示电路,电路中仅电阻R可变,已知 R=R1时,测得电流i1=5A、i2=4A;当R=R2时,测得电流 i1=3.5A,i2=2A;当R=R3时,测得i2=8A,问此时测得的电 流i1等于多少?
u u u Ro i u oc
' "
例1、求图(a)所示单口网络的戴维南等效电路。 i
解:在端口标明开路电压uoc参考方向,注意到i=0,
u oc 1V (2) 2A 3V
将单口网络内电压源短路,电流源开路,得图(b)
Ro 1 2 3 6
(1 ) R2 u2 us R1 (1 ) R2
1 i1 us R1 (1 ) R2
例3.1.2 求电流 i1 与激励 u s 的函数关系
齐次定理: i1 Gus 设: i1 1A 节点1、2电压记1V 3V
电压源的电压等于该网络的开路电压uoc,这个 电阻等于从此单口网络两端看进去,当网络内部所有 独立源均置零(No)时的等效电阻R0 i =0 N
+
R0 戴维南等效电阻
3.3 等效电源定理
u _ oc
No
也称为输出电阻
例3.3.1 图(a)所示电路,求当RL分别等于2Ω、4Ω及16Ω时, 该电阻上电流i.
将已知条件代入得:
6 K U N 4 4 R U N 0 3 K 2 R U 2 N
电路定理(戴维宁和诺顿变换)

E
+ Is b a Is Is
a
b
与理想电流源串
联的元件可去掉
R
b
来列KCL方程。
例1
试求i1。
3 + 2 – 4A
6 I1 + 7V -
5 4
4A
解
用替代:
1 + 6V –
6 + 3V -
2
4 + 7V -
I1
7 2 4 15 I1 2.5 A 6 24 6
其余电源作用:
3A + 12V -
1 2A
i ( 2) (6 12) /( 6 3) 2 A ( 2) ( 2) u 6i 6 2 1 8V
画出分 电路图 6
+ ( 1) - u 1 3
3A
u u(1) u( 2 ) 9 8 17V (2) u (2) i
+ us –
解
则
i us ' i ' us
us 51 即 i ' i ' 1 1.5 A us 34
4-2 替 代 定 理 (置换定理)
Substitution theorem
4. 2
替代定理 (Substitution Theorem)
对于给定的任意一个电路,若某一支路电压为uk、
三、齐次定理 (homogeneity theorem)
齐次定理:在任何线性电阻、线性受控 源及独立源组成的电路中,当所有的激励 都同时增大或缩小K倍,响应也将同样增大 或缩小K倍。
1.
I1 R1
若 E1 增加 n 倍,各
R2
I2 R2
E1
+
戴维南等效电路和诺顿等效电路

戴维南等效电路和诺顿等效电路引言:在电路分析中,戴维南等效电路和诺顿等效电路是两个重要的概念。
它们是电路分析中常用的简化电路模型,可以帮助我们更好地理解和分析复杂电路的行为。
本文将详细介绍戴维南等效电路和诺顿等效电路的概念、原理以及应用。
一、戴维南等效电路1. 概念:戴维南等效电路是一种用电压源和电阻来代替电路中的电压源和电阻的方法,它能够将原电路和等效电路在外部电路特性上保持一致。
2. 原理:戴维南等效电路的原理是基于电压分压原理和电流合流原理。
根据电压分压原理,电路中的电压源可以用电压源和电阻串联组成的等效电路来代替。
而根据电流合流原理,电路中的电阻可以用电流源和电阻并联组成的等效电路来代替。
3. 应用:戴维南等效电路的应用非常广泛。
在电路分析和设计中,我们经常会遇到复杂的电路,使用戴维南等效电路可以将这些复杂电路简化为等效电路,从而更方便地进行分析和设计。
此外,戴维南等效电路还可以在电路模拟和电路实验中使用,用来代替实际电路进行仿真和测试。
二、诺顿等效电路1. 概念:诺顿等效电路也是一种用电流源和电阻来代替电路中的电流源和电阻的方法,它同样能够将原电路和等效电路在外部电路特性上保持一致。
2. 原理:诺顿等效电路的原理与戴维南等效电路类似,也是基于电压分压原理和电流合流原理。
根据电压分压原理,电路中的电流源可以用电流源和电阻并联组成的等效电路来代替。
而根据电流合流原理,电路中的电阻可以用电压源和电阻串联组成的等效电路来代替。
3. 应用:诺顿等效电路与戴维南等效电路一样,广泛应用于电路分析和设计中。
通过将复杂电路简化为等效电路,可以更方便地进行分析和设计工作。
此外,诺顿等效电路还可以用于电路仿真和测试,以替代实际电路进行模拟和实验。
三、戴维南等效电路和诺顿等效电路的区别戴维南等效电路和诺顿等效电路在原理和应用上有所不同。
戴维南等效电路是用电压源和电阻来代替电路中的电压源和电阻,而诺顿等效电路则是用电流源和电阻来代替电路中的电流源和电阻。
08戴维南和诺顿定理

4.3 戴维南定理和诺顿定理
(Thevenin’s Theorem and Norton’s Theorem)
一、 戴维南定理 二、 步骤 三、 求戴维南等效电路的方法 例题 四、诺顿定理 五、 最大功率传输定理
4.3 戴维南定理和诺顿定理
一、戴维南定理
对于任意一个线性含源二端网络NS,就其两个端钮a、b而 言,可以用一条实际电压源支路对外部进行等效,其中电压源
b
a +
NS
_uOC
b
a
N0
Req
b
戴维南等效电源的极性应与所求开路电压的 极性保持一致!
戴维南定理证明
4.3 戴维南定理和诺顿定理
Ia
a
+
替代
+
负
NS
U载
NS
U
_
I_
b
b4.3 戴维南定理和源自顿定理aIaa
+ 叠加
+
+
NS
U
I_
NS
U'=UOC +
N0
U"
_
I_
b
b
b
Req
U U U UOC ReqI
U '' OC
1 12 1 11
12
11
7 V
6
4.3 戴维南定理和诺顿定理
解
第一步:求开路电压Uoc。 方法:叠加定理 1、电压源单独作用,
1Ω
1Ω
a + 2Ω
1A 1Ω
+_ 1V 1Ω
Uoc
_
b
求U’oc。 UO' C
戴维南定理和诺顿定理实验报告

戴维南定理和诺顿定理实验报告戴维南定理实验总结戴维南定理和诺顿定理实验报告篇一:戴维南定理和诺顿定理实验报告实验一、戴维南定理一、实验目的:1、深刻理解和掌握戴维南定理。
2、初步掌握用Multisim软件绘制电路原理图。
3、初步掌握Multisim软件中的Multimeter、Voltmeter、Ammeter 等仪表的使用以及DC Operating Point、Parameter Sweep等SPICE仿真分析方法。
4、掌握电路板的焊接技术以及直流电源、万用表等仪表的使用。
二、实验内容:1、计算等效电压和等效电阻;2、用Multisim软件测量等效电压和等效电阻;3、用Multisim软件仿真验证戴维南定理;4、在实验板上测试等效电压和等效电阻;5、在实验板上验证戴维南定理;三、实验步骤1、计算等效电压V=US(R3//R33)/((R1//R11)+(R3//R33))=2.613 V ;等效电阻R=((R1//R3)+R2)//((R11//R33)+R22)=250 .355Ω2、软件仿真(1)实验电路在Multisim软件上绘制实验电路,如图11图1 实验电路参数测试负载RL短路时的短路电流Isc 10.42mA 负载RL开路时的开路电压Uoc 2.609V调节负载RL时的数据如表1所示。
(2)等效电路在Multisim软件上绘制等效电路,如图2图2 等效电路参数测试负载RL短路时的短路电流Isc 10.41mA 负载RL开路时的开路电压Uoc 2.60V调节负载RL时的数据如表1所示。
23、电路实测(1)实验电路负载RL短路时的短路电流Isc 10.01mA 负载RL开路时的开路电压Uoc 2.58V调节负载RL时的数据如表1所示。
(2)等效电路负载RL短路时的短路电流Isc 10.1mA 负载RL开路时的开路电压Uoc 2.58V调节负载RL时的数据如表1所示。
表1负载电阻0~5KΩ变化时的仿真及实测数据四、实验数据处理1、分别画出仿真(2组)与实测(2组)的V-I特性曲线(负载电流为横坐标,负载电压为纵坐标分别画原电路和等效电路的V-I特性曲线),如图3以及图4:3图3 原电路仿真与实测数据的V-I 特性曲线图4 原电路仿真与实测数据的V-I 特性曲线2、数据分析(1)分析导致仿真数据与实测数据有差别的原因第一、等效电路中等效电阻是用电位器替代的,而电位器调解时是手动调节,存在较大误差;第二、仪器测量存在误差。
(整理)戴维南定理和诺顿定理
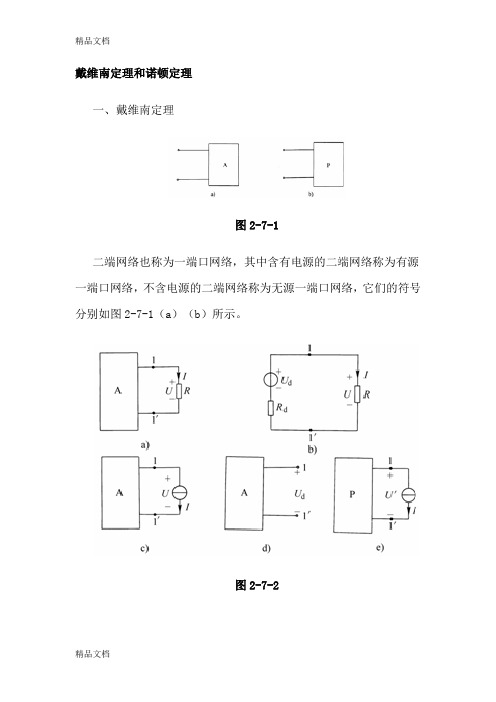
戴维南定理和诺顿定理一、戴维南定理图2-7-1二端网络也称为一端口网络,其中含有电源的二端网络称为有源一端口网络,不含电源的二端网络称为无源一端口网络,它们的符号分别如图2-7-1(a)(b)所示。
图2-7-2任一线性有源一端口网络(如图2-7-2(a)所示)对其余部分而言,可以等效为一个电压源和电阻相串联的电路(如图2-7-2(b)所示),其中的大小等于该有源一端口网络的开路电压,电压源的正极与开路端高电位点对应;等于令该有源一端口网络内所有独立源为零(即电压源短接、电流源开路)后所构成的无源一端口网络的等效电阻。
这就是戴维南定理,也称为等效电源定理;与串联的电路称为戴维南等效电路。
要计算一个线性有源一端口网络的戴维南等效电路,其步骤和方法为:1、计算:利有电路分析方法,计算相应端口的开路电压;2、计算:当线性有源一端口网络A中不含受控源时,令A内所有独立电源为零后得到的无源一端口网络P则为纯电阻网络,利用无源一端口网络的等效变换就可求出端口等效电阻;当线性一端口网络A中含有受控源时,令A内所有独立电源为零后得到的一端口网络P 中仍含有受控源,这时,可采用加压法和开路短路法求。
图2-7-3例2-7-1 利用戴维南定理求图2-7-4(a)所示电路中的电流I 为多少?图2-7-4 例2-7-1附图解:将A、B左边部分电路看作有源一端口网络,用戴维南等效电路替代后如图2-10-4(b)所示。
(1)求:将A、B端口开路,得到图2-10-4(c)所示电路。
由米尔曼公式得:(2)求等效电阻:令A、B以左的三个独立源为零,得到图2-10-4(d)所示电路,则A、B端口的等效电阻为:(3)从图2-10-4(b)中求I:图2-10-5 例2-7-2附图例2-7-2 在图2-7-5(a)所示电路中,已知,,求A、B端口的戴维南等效电路。
解:(1)求:图2-10-5(a)中A、B端口处于开路状态,列写KVL方程:(2)求等效电阻:下面分别用两种方法求解。
戴维南定理和诺顿定理
戴维南定理和诺顿定理§4-3 戴维南定理和诺顿定理戴维南定理(Thev enin’s theorem )是⼀个极其有⽤的定理,它是分析复杂⽹络响应的⼀个有⼒⼯具。
不管⽹络如何复杂,只要⽹络是线性的,戴维南定理提供了同⼀形式的等值电路。
在§2-4(输⼊电阻和等效电阻)⼀节中曾介绍过⼆端⽹络/也叫⼀端⼝⽹络的概念。
(⼀个⽹络具有两个引出端与外电路相联,不管其内部结构多么复杂,这样的⽹络叫⼀端⼝⽹络)。
含源单⼝(⼀端⼝)⽹络──内部含有电源的单⼝⽹络。
单⼝⽹络⼀般只分析端⼝特性。
这样⼀来,在分析单⼝⽹络时,除了两个连接端钮外,⽹络的其余部分就可以置于⼀个⿊盒⼦之中。
含源单⼝⽹络的电路符号:图中N ──⽹络⽅框──⿊盒⼦U单⼝松驰⽹络──含源单⼝⽹络中的全部独⽴电源置零,受控电源保留,(动态元件为零状态),这样的⽹络称为单⼝松驰⽹络。
电路符号:⼀、戴维南定理(⼀)定理:⼀含源线性单⼝⼀端⽹络N ,对外电路来说,可以⽤⼀个电压源和电阻的串联组合来等效置换,此电压源的电压等于端⼝的开路电压,电阻等于该单⼝⽹络对应的单⼝松驰⽹络的输⼊电阻。
(电阻等于该单⼝⽹络的全部独⽴电源置零后的输⼊电阻)。
上述电压源和电阻串联组成的电压源模型,称为戴维南等效电路。
该电阻称为戴维南等效电阻。
U任意负载任意负载U oc =U s求戴维南等效电路,对负载性质没有限定。
⽤戴维南等效电路置换单⼝⽹络后,对外电路的求解没有任何影响,即外电路中的电流和电压仍然等于置换前的值。
(⼆)戴维南定理的证明:1. 设⼀含源⼆端⽹络N 与任意负载相接,负载端电压为U ,端电流为I 。
2. 任意负载⽤电流源替代,取电流源的电流为I I S 。
⽅向与I 相同。
替代后,整个电路中的电流、电压保持不变。
下⾯⽤叠加定理分析端电压U 与端电流I 。
3. 设⽹络N 内的独⽴电源⼀起激励,受控源保留,电流源I S 置零,即ab 端开路。
这时端⼝电压、电流加上标(1),有4. I S 单独激励,⽹络N 内的独⽴电源均置零,受控电源保留,这时,含源⼆端⽹络N 转化成单⼝松驰⽹络N 0,图中端⼝电流、电压加上标(2),SU (1)=U ocI (1)=0有I R I R U eq S eq -=-=)2(I I I S ==)2( 应⽤叠加定理,得=+=-=+=I I I I I R U U U U eq oc )2()1()2()1( (1)可以看到,在戴维南等效电路中,关于ab 端的特性⽅程与(1)式相同。
课件:第2.2节 含源支路的等效变换
I
US
R
U
IS R I U
+ -
R US
I U
I
US U
I IS
U
IS US / R
US ISR
IS
I
R
U
2.2 含源支路的等效变换
电压源的正向,反向串联 电流源的正向,反向并联
US1
I
U
U S2
I
US U IS1IS2来自222
4V 2
I
2
2 I
I (A)
4V 2 2
I
2
1
4V 1
I
3
4V I
I (A)
I (V)
I (V)
4V
I
根据KVL
4V+3 I I (V) 0 I 1A
电路
刘洪臣 哈尔滨工业大学电气工程系
2.2 含源支路的等效变换
基本要求:掌握各种含源支路的等效化简方法和戴维 南、诺顿两种典型电路之间的等效变换规律,能熟练 运用这些等效规律化简电路。
1 戴维南与诺顿电路
U
US
I
US
U
Ri
端口特性方程
U US Ri I
I IS GiU
戴维南电路
IS
I
Gi U
2.5
2 I
6A
9V
2.5
I 9V 2A 2 2.5
3V I 2 2.5
2.2 含源支路的等效变换
【例题2.4】利用等效化简求电流I
6V
I
5A
3
6
2
2A
3 6V
线性电路分析:叠加、戴维宁、诺顿等效电路-目前我们已经探究出与
线性电路分析:叠加、戴维宁、诺顿等效电路目前我们已经探究出与时间无关的(阻性)器件也是线性的。
我们可以画出一个与时间无关的器件的电流/电压曲线。
电流作为电压的一个函数,它与电压的变化率无关。
而后面我们将要分析的电容和电感则不是与时间无关的器件。
与时间无关的器件经常被叫做阻性器件。
注意,我们经常将一个时序信号加在与时间无关的器件上。
我们只需对每个例子中电路特性逐一的进行分析。
我们将在后面的课程中进行更深入的探究。
线性如果对于任何两个输入x 1和x 2都满足 f(x 1+x 2)=f(x 1)+f(x 2),则函数f 是线性的。
阻性电路是线性的。
那就是说如果我们把集合{x i }作为电路的输入,并且f ({x i })作为电路的响应,则上述线性关系成立。
例如响应可以是在电路中任何节点的电压或通过任何器件的电流。
让我们一起来分析下面的例子。
由电路的KVL 可知Vs 1+Vs 2-iR =0 (1.1)或R Vs Vs i 21+=(1.2)由此我们可以看出电路的响应线性的取决于电压Vs 1和Vs 2。
观察线性的一个有效的方法是让电源分别作用。
不作用的电压源电压应设置为0:就是将电压源短路。
上面的这个简单电路。
我们可以把它看作是2个电路的叠加,每个电路里仅有一个电压源作用。
总电流是每个电路电流的总和。
R Vs Vs R Vs R Vs i i i 212121+=+=+= (1.3)这个结果和用 KVL 对原电路求解的结果一致。
独立源在不作用时的处理方法如下:电压源:电流源:例题1:思考下面的具有2个源的线性电路。
让我们一起用叠加来分析这个电路。
首先我们抑制电流源来分析这个只具有电压源作用的电路。
所以,电压源单独作用,流过电阻的电流是:i 1v =0 (1.4)22R Vsv i =(1.5)下面我们计算一下电流源单独作用下的响应注意到R 2被短路(R 2两端没有电压),所以没有电流通过它。
通过R 1的电流是I s ,所以R 1的电压降是,v 1=IsR 1 (1.6)因此,i 1=Is (1.7)22R Vsi =(1.8)通过电压源Vs 的电流是多少呢?另外一个例子:计算下面电路的节点电压v 。
戴维宁诺顿定理
戴维宁诺顿定理“戴维宁诺顿定理(David Norton Theorem)”,简称“Norton定理”,是电路理论中的一种重要方法。
Norton 定理是电路理论中的两类定理之一,另一类是Thevenin 定理。
这两个定理常常一起出现,并被称为是电路理论中的最重要定理之一。
Norton 定理是一个电源等效电路转换的方法,它将一个外部线路转化成一个等效的电源和内部电阻的并联组合。
在多种不同的电路分析情况下,它都可以非常有效地使用。
Norton 定理要求两个条件,第一个是原始电路必须是线性的且可以表示成一个网络。
,第二个条件是当将负载从联结点中分离出来后,必须要切断其电路,同时填入一个合适的短路。
这个定理可以用于求解启动电流、过度电流、故障电流等各种电路特性,可以缩减电路的供电元件数量,简化电路的设计和分析。
Norton 定理的核心在于等效电源的变换。
等效电源是指一个电源所具有的电流和电阻特性,而不是指它是一种电源。
将电路转化为一个电源和一个内部阻抗,就可以通过简单的计算和分析来得出等效电源。
Norton定理与Thevenin定理相比,明显而言,Thevenin定理更加适合电压源和电和电路进行计算,而Norton定理则适合采用电流源的电路进行计算,可以说Norton定理是Thevenin定理的对称定理。
在电路分析中,应该根据实际情况分析得出适用的定理,而在需要求解电流源的电路问题时,Norton定理是非常经济且实用的方法,它可以使得电路的分析和计算更加地直观和简单。
然而,在实际的生产和应用中,不同的问题和实际情况可能会导致不同的计算结果。
因此,我们必须在实际问题基础上,碰撞出适合的电路原理和方法。
总的来说,Norton 定理是电路分析和设计领域内的一种经典算法,它可以帮助我们在电路设计和分析过程中快速捕捉电路的特性,实现计算的效率提升。
此外,Norton 定理也是一项比较复杂且高级的计算技巧,它需要对电路基本原理和电路理论有一定的了解,并依据实际工作需要进行适当的更改和调整。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
戴维南诺顿等效变换
戴维南诺顿等效变换是电路分析中一种常用的技术,它可以将电路中的多个电阻、电流源和电压源等元件,转化为一个等效的电流源和电阻的组合。
这种变换使得电路分析更加简化和方便。
本文将详细介绍戴维南诺顿等效变换的原理和应用。
一、戴维南诺顿等效变换的原理
戴维南诺顿等效变换是基于戴维南定理提出的。
根据戴维南定理,任何一个线性电路都可以用一个电流源和一个电阻的组合来等效代替。
具体地,戴维南诺顿等效变换的原理如下:
1. 将电路中的电流源和电压源分别用等效的电阻和电流源替代;
2. 将电路中的电阻元件用导线连接,并通过测量电路两端的电压和电流,计算等效电流源和等效电阻。
二、戴维南诺顿等效变换的步骤
戴维南诺顿等效变换的具体步骤如下:
1. 找出电路中需要等效变换的部分,将其与电路其余部分分离;
2. 将电路中的电流源和电压源分别用等效的电阻和电流源替代;
3. 将电路中的电阻元件用导线连接,并通过测量电路两端的电压和电流,计算等效电流源和等效电阻;
4. 将等效电流源和等效电阻重新接入原电路中。
三、戴维南诺顿等效变换的应用
戴维南诺顿等效变换在电路分析中有着广泛的应用,主要体现在以下几个方面:
1. 简化电路分析:通过戴维南诺顿等效变换,可以将复杂的电路简化为等效电路,从而简化了电路分析的过程。
特别是在计算电路中,通过等效变换可以大大减少计算量。
2. 电路优化设计:在电路设计中,通过戴维南诺顿等效变换,可以将电路中的多个电阻元件合并为一个等效电阻,从而减少电路的复杂度和成本。
这对于电路优化设计具有重要意义。
3. 网络传输:在网络传输中,戴维南诺顿等效变换可以用于网络中的传输线建模。
通过等效变换,可以将传输线的复杂特性简化为等效电阻和电流源,使得网络传输的分析更加方便。
四、戴维南诺顿等效变换的注意事项
在进行戴维南诺顿等效变换时,需要注意以下几点:
1. 切断电路中的独立电源:在进行等效变换之前,需要将电路中的独立电源切断,以避免干扰等效电源的计算。
2. 考虑电路的边界条件:在计算等效电流源和等效电阻时,需要考虑电路的边界条件,如电路两端的电压和电流。
3. 确保等效电源的方向正确:在连接等效电流源和等效电阻时,需要确保电流的方向正确,以保证等效电源的正负极性一致。
4. 检查等效电阻的取值范围:在计算等效电阻时,需要检查其取值范围是否符合实际情况,以确保等效变换的准确性。
五、总结
戴维南诺顿等效变换是电路分析中一种常用的技术,通过将电路中的多个元件转化为一个等效电流源和电阻的组合,简化了电路分析的过程。
戴维南诺顿等效变换在电路分析、电路优化设计和网络传输等领域具有重要的应用价值。
在进行等效变换时,需要注意电路的边界条件、等效电源的方向和等效电阻的取值范围,以确保等效变换的准确性。
通过掌握戴维南诺顿等效变换的原理和应用,可以更加高效地进行电路分析和设计。
