2.4.1学案设计
人教版数学选修2-1抛物线及其标准方程教学案

2.4.1.1抛物线及其标准方程班级姓名小组号【学习目标】1.通过教材了解抛物线的定义,准线及焦点.2.通过教学案掌握焦点在两坐标轴上的抛物线的标准方程.3.通过教师讲解会求简单的抛物线的标准方程,解决相关题目.【重点难点】重点:掌握抛物线的定义、准线及在坐标轴上的标准方程;难点:根据标准方程判断抛物线的焦点、准线的位置,以及求抛物线的标准方程.【学情分析】初中我们学习过二次函数,知道二次函数是一条抛物线,本节课我们将继续研究抛物线及它的相关知识。
我们将先通过数形结合思想根据抛物线的定义来求解它的标准方程,进而引出准线方程。
以及在选择不同的坐标系我们得到不同形式的标准方程。
【导学流程】自主学习内容一、回顾旧知:二、基础知识感知1.抛物线定义:平面内与一个定点F和一条定直线l(l不经过点F)的距离相等的点的轨迹叫做抛物线,定点F叫做抛物线的焦点,定直线l叫做抛物线的准线.2.准线的方程:设点M(x,y)是抛物线上任意一点,点M到l的距离为d.抛物线就是集合.准线的标准方程为:22(0)y px p=>.它表示的抛物线的焦点在x轴的正半轴上,坐标是(,0)2p它的准线方程是2px=-.3抛物线标准方程的四种形式:根据抛物线焦点所在半轴的不同可得抛物线方程的的四种形式22y px=,22y px=-,22x py=,22x py=-(0)p>。
三、探究问题:【例1】已知抛物线的标准方程是y²=6x,求它的焦点坐标和准线方程。
【例2】2.以双曲线91622yx-=1的中心为顶点,左顶点为焦点的抛物线方程是()A.216y x=- B.216y x= C.28y x=- D.28y x=四、基础知识拓展与迁移抛物线还有哪些不同的形式?}|||{dMFMP==请及时记录自主学习过程中的疑难:小组讨论问题预设:已知抛物线关于y轴对称,它的顶点在坐标原点,并且经过点M-,求它的标准方程。
提问展示问题预设:-的抛物线的标准方程,并求对应抛物线的准线方程:求过点(3,2)课堂训练问题预设:1.抛物线y2=x上一点P到焦点的距离是2,则P点坐标为2.到点A(-1,0)和直线x=3距离相等的点的轨迹方程是________.整理内化:1.课堂小结2.本节课学习内容中的问题和疑难3.教学反思2.4.1.1抛物线及其标准方程【课后限时训练】时间50分钟第Ⅰ部分 本节知识总结第Ⅱ部分 基础知识达标一、选择题1.设抛物线的顶点在原点,准线方程为,则抛物线的方程是A .28y x =- B .28y x =C .24y x =-D .24y x =2.若抛物线2y ax =的准线与椭圆22143x y +=的右准线重合,则a 的值是( ) A.8 B.8- C.16 D.16- 3.抛物线21(0)y x m m=<的焦点坐标是( ) A.(0,)4m B. (0,)4m - C. 1(0,)4m D. 1(0,)4m- 4. 已知抛物线y 2=2px (p >0)的准线与圆(x -3)2+y 2=16相切,则p 的值为( )A.12B .1C .2D .45.以双曲线91622y x -=1的中心为顶点,右顶点为焦点的抛物线方程是( ) A.216y x =- B.216y x = C.28y x =- D.28y x =二、填空题6.以双曲线221169x y -=的中心为顶点,左焦点为焦点的抛物线方程是__________.7.抛物线y 2=16x 上到顶点和焦点距离相等的点的坐标是________. 8.焦点到准线的距离是2的准线方程是 .9.设抛物线的顶点在原点,其焦点F 在y 轴上,又抛物线上的点(k ,-2)与F 点的距离为4,则k 的值是 。
人教a版必修4学案:2.4.1平面向量数量积的物理背景及其含义(含答案)

2.4.1 平面向量数量积的物理背景及其含义自主学习知识梳理1.平面向量数量积(1)定义:已知两个非零向量a 与b ,我们把数量____________叫做a 与b 的数量积(或内积),记作a ·b ,即a ·b =|a ||b |cos θ,其中θ是a 与b 的夹角.(2)规定:零向量与任一向量的数量积为______.(3)投影:设两个非零向量a 、b 的夹角为θ,则向量a 在b 方向的投影是______________,向量b 在a 方向上的投影是__________.2.数量积的几何意义a ·b 的几何意义是数量积a ·b 等于a 的长度|a |与b 在a 的方向上的投影__________的乘积.3.向量数量积的运算律(1)a·b =________(交换律);(2)(λa )·b =________=__________(结合律);(3)(a +b )·c =__________(分配律).自主探究根据向量数量积的定义,补充完整数量积的性质.设a 与b 都是非零向量,θ为a 与b 的夹角.(1)a ⊥b ⇔__________;(2)当a 与b 同向时,a·b =________,当a 与b 反向时,a·b =________;(3)a·a =__________或|a |=a·a =a 2;(4)cos θ=__________;(5)|a·b |≤__________.对点讲练知识点一 求两向量的数量积例1 已知|a |=4,|b |=5,当(1)a ∥b ;(2)a ⊥b ;(3)a 与b 的夹角为30°时,分别求a 与b 的数量积.回顾归纳 求平面向量数量积的步骤是:①求a 与b 的夹角θ,θ∈[0°,180°];②分别求|a|和|b|;③求数量积,即a·b =|a|·|b|·cos θ,要特别注意书写时a 与b 之间用实心圆点“·”连结,而不能用“×”连结,也不能省去.变式训练1 已知正三角形ABC 的边长为1,求:(1)AB →·AC →;(2)AB →·BC →;(3)BC →·AC →.知识点二 求向量的模长例2 已知|a |=|b |=5,向量a 与b 的夹角为π3,求|a +b |,|a -b |.回顾归纳 此类求解模问题一般转化为求模平方,与向量数量积联系,要灵活应用a 2=|a |2,勿忘记开方.变式训练2 已知|a |=|b |=1,|3a -2b |=3,求|3a +b |.知识点三 向量的夹角或垂直问题例3 设n 和m 是两个单位向量,其夹角是60°,求向量a =2m +n 与b =2n -3m 的夹角.回顾归纳 求向量夹角时,应先根据公式把涉及到的量先计算出来再代入公式求角,注意向量夹角的范围是[0,π].变式训练3 已知|a |=5,|b |=4,且a 与b 的夹角为60°,则当k 为何值时,向量k a -b 与a +2b 垂直?1.两向量a 与b 的数量积是一个实数,不是一个向量,其值可以为正(当a ≠0,b ≠0,0°≤θ<90°时),也可以为负(当a ≠0,b ≠0,90°<θ≤180°时),还可以为0(当a =0或b =0或θ=90°时).2.数量积对结合律一般不成立,因为(a ·b )·c =|a ||b |·cos 〈a ,b 〉·c 是一个与c 共线的向量,而(a ·c )·b =|a |·|c |cos 〈a ,c 〉·b 是一个与b 共线的向量,两者一般不同.3.向量b 在a 上的投影不是向量而是数量,它的符号取决于θ角,注意a 在b 方向上的投影与b 在a 方向上的投影是不同的,应结合图形加以区分.课时作业一、选择题1.|a |=2,|b |=4,向量a 与向量b 的夹角为120°,则向量a 在向量b 方向上的投影等于( )A .-3B .-2C .2D .-12.已知a ⊥b ,|a |=2,|b |=3,且3a +2b 与λa -b 垂直,则λ等于( )A.32 B .-32 C .±32D .1 3.在边长为1的等边△ABC 中,设BC →=a ,CA →=b ,AB →=c ,则a·b +b·c +c·a 等于( )A .-32B .0 C.32D .3 4.设非零向量a 、b 、c 满足|a |=|b |=|c |,a +b =c ,则〈a ,b 〉等于( )A .150°B .120°C .60°D .30°5.若向量a 与b 的夹角为60°,|b |=4,(a +2b )·(a -3b )=-72,则向量a 的模为( )A .2B .4C .6D .12二、填空题6.已知向量a ,b 且|a |=5,|b |=3,|a -b |=7,则a·b =________.7.已知向量a 与b 的夹角为120°,且|a |=|b |=4,那么b ·(2a +b )的值为________.8.已知a 是平面内的单位向量,若向量b 满足b·(a -b )=0,则|b |的取值范围是________.三、解答题9.已知|a |=4,|b |=3,当(1)a ∥b ;(2)a ⊥b ;(3)a 与b 的夹角为60°时,分别求a 与b 的数量积.10.已知|a |=1,|b |=1,a ,b 的夹角为120°,计算向量2a -b 在向量a +b 方向上的投影.§2.4 平面向量的数量积2.4.1 平面向量数量积的物理背景及其含义答案知识梳理1.(1)|a ||b |·cos θ (2)0 (3)|a |cos θ |b |cos θ2.|b |cos θ3.(1)b·a (2)λ(a·b ) a ·(λb ) (3)a·c +b·c自主探究(1)a·b =0 (2)|a||b | -|a||b | (3)|a |2(4)a·b |a||b |(5)|a||b | 对点讲练例1 解 (1)a ∥b ,若a 与b 同向,则θ=0°,a ·b =|a |·|b |·cos 0°=4×5=20;若a 与b 反向,则θ=180°,∴a ·b =|a |·|b |cos 180°=4×5×(-1)=-20.(2)当a ⊥b 时,θ=90°,∴a ·b =|a |·|b |cos 90°=0.(3)当a 与b 的夹角为30°时,a ·b =|a |·|b |cos 30°=4×5×32=10 3. 变式训练1 解 (1)∵AB →与AC →的夹角为60°. ∴AB →·AC →=|AB →||AC →|cos 60°=1×1×12=12. (2)∵AB →与BC →的夹角为120°.∴AB →·BC →=|AB →||BC →|cos 120°=1×1×⎝⎛⎭⎫-12=-12. (3)∵BC →与AC →的夹角为60°,∴BC →·AC →=|BC →||AC →|cos 60°=1×1×12=12. 例2 解 a·b =|a||b |cos θ=5×5×12=252. |a +b |=(a +b )2=|a |2+2a·b +|b |2= 25+2×252+25=5 3. |a -b |=(a -b )2=|a |2-2a·b +|b |2= 25-2×252+25=5. 变式训练2 解 由|3a -2b |=3,得9|a |2-12a·b +4|b |2=9,∵|a |=|b |=1,∴a·b =13, ∴|3a +b |=(3a +b )2=9|a |2+6a·b +|b |2=2 3.例3 解 ∵|n |=|m |=1且m 与n 夹角是60°,∴m·n =|m||n |cos 60°=1×1×12=12. |a |=|2m +n |=(2m +n )2=4×1+1+4m·n= 4×1+1+4×12=7, |b |=|2n -3m |=(2n -3m )2=4×1+9×1-12m·n= 4×1+9×1-12×12=7, a·b =(2m +n )·(2n -3m )=m·n -6m 2+2n 2=12-6×1+2×1=-72. 设a 与b 的夹角为θ,则cos θ=a·b |a||b |=-727×7=-12. 又θ∈[0,π],∴θ=2π3,故a 与b 的夹角为2π3. 变式训练3 解 要想(k a -b )⊥(a +2b ),则需(k a -b )·(a +2b )=0,即k |a |2+(2k -1)a·b -2|b |2=0,∴52k +(2k -1)×5×4×cos 60°-2×42=0,解得k =1415,即当k =1415时,向量k a -b 与a +2b 垂直. 课时作业1.D [a 在b 方向上的投影是|a |cos θ=2×cos 120°=-1.]2.A [∵(3a +2b )·(λa -b )=3λa 2+(2λ-3)a·b -2b 2=3λa 2-2b 2=12λ-18=0.∴λ=32.] 3.A [a·b =BC →·CA →=-CB →·CA →=-|CB →||CA →|cos 60°=-12. 同理b·c =-12,c·a =-12, ∴a·b +b·c +c·a =-32.] 4.B [∵a +b =c ,∴|c |2=|a +b |2=a 2+2a ·b +b 2.又|a |=|b |=|c |,∴2a ·b =-b 2,即2|a ||b |cos 〈a ,b 〉=-|b |2.∴cos 〈a ,b 〉=-12,∴〈a ,b 〉=120°.] 5.C [∵a·b =|a|·|b |·cos 60°=2|a |,∴(a +2b )·(a -3b )=|a |2-6|b |2-a·b=|a |2-2|a |-96=-72.∴|a |=6.]6.-152解析 |a -b |2=|a |2-2a·b +|b |2=49,∴a·b =-152. 7.0解析 b ·(2a +b )=2a·b +|b |2=2×4×4×cos 120°+42=0.8.[0,1]解析 b·(a -b )=a·b -|b |2=|a|·|b |cos θ-|b |2=0,∵a 是单位向量,∴|a |=1,∴|b |=|a |cos θ=cos θ (θ为a 与b 的夹角),θ∈[0,π], ∴0≤|b |≤1.9.解 (1)当a ∥b 时,若a 与b 同向,则a 与b 的夹角θ=0°, ∴a·b =|a||b |·cos θ=4×3×cos 0°=12.若a 与b 反向,则a 与b 的夹角为θ=180°,∴a·b =|a||b |cos 180°=4×3×(-1)=-12.(2)当a ⊥b 时,向量a 与b 的夹角为90°,∴a·b =|a||b |·cos 90°=4×3×0=0.(3)当a 与b 的夹角为60°时,∴a·b =|a||b |·cos 60°=4×3×12=6. 10.解 (2a -b )·(a +b )=2a 2+2a ·b -a ·b -b 2=2a 2+a ·b -b 2=2×12+1×1×cos 120°-12=12. |a +b |=(a +b )2=a 2+2a ·b +b 2=1+2×1×1×cos120°+1=1.∴|2a -b |cos 〈2a -b ,a +b 〉 =|2a -b |·(2a -b )·(a +b )|2a -b |·|a +b |=(2a -b )·(a +b )|a +b |=12. ∴向量2a -b 在向量a +b 方向上的投影为12.。
2.4.1抛物线及其标准方程
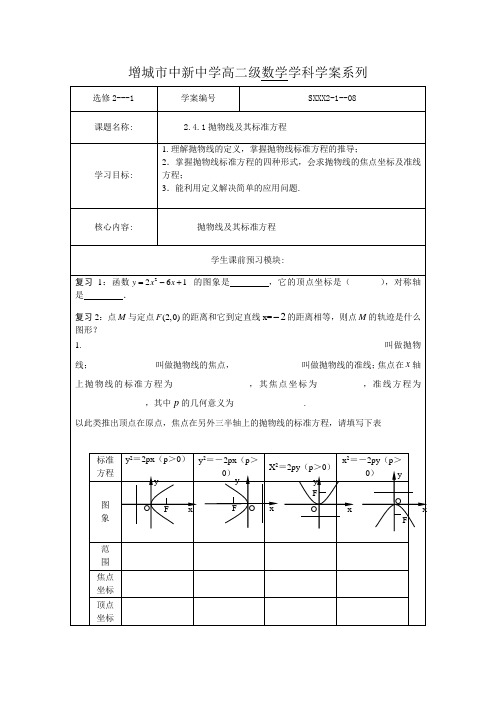
增城市中新中学高二级数学学科学案系列选修2---1 学案编号SXXX2-1--08 课题名称: 2.4.1抛物线及其标准方程学习目标: 1.理解抛物线的定义,掌握抛物线标准方程的推导;2.掌握抛物线标准方程的四种形式,会求抛物线的焦点坐标及准线方程;3.能利用定义解决简单的应用问题.核心内容: 抛物线及其标准方程学生课前预习模块:复习1:函数2261y x x=-+的图象是,它的顶点坐标是(),对称轴是.复习2:点M与定点(2,0)F的距离和它到定直线x=2-的距离相等,则点M的轨迹是什么图形?1. ____________________________________________________________________叫做抛物线;_______________叫做抛物线的焦点,________________叫做抛物线的准线;焦点在x轴上抛物线的标准方程为_________________,其焦点坐标为__________,准线方程为________________,其中p的几何意义为________________.以此类推出顶点在原点,焦点在另外三半轴上的抛物线的标准方程,请填写下表标准方程y2=2px(p>0)y2=-2px(p>0)X2=2py(p>0)x2=-2py(p>0)图象范围焦点坐标顶点坐标xyO F xyOF xyOFxyOF离心率对称轴焦|PF|=半径准线方程p的几何意义通径合作探究模块:例1:(1)已知抛物线标准方程是x y 62=,求它的焦点坐标和准线方程. (2)已知抛物线的焦点坐标是)2,0(-F ,求它的标准方程.例2:求满足下列条件的抛物线的标准方程: (1)焦点坐标是)0,5(-F (2)经过点)3,2(-A例3.已知抛物线关于x 轴对称,它的顶点在坐标原点,并且经过点)22,2(-M ,求它的标准方程,并用描点法画出图形.限时导练模块:1.求下列抛物线的焦点坐标和准线方程(1)x y 82= (2)y x 42=(3)0322=+x y (4)261x y -= (5))a (ax y 02≠=2.根据下列条件写出抛物线的标准方程(1)焦点是)0,2(-F(2)准线方程是31=y(3)焦点到准线的距离是4,焦点在y 轴上(4)经过点)2,6(-A(5)焦点在10x y --=上的抛物线的标准方程.3.抛物线y x 42=上的点P 到焦点的距离是10,求P 点坐标4.的轨迹方程相切,求动圆圆心)且与直线(过动圆M y ,P M 0220=+.5* .抛物线22y px = (0)p >上一点M 到焦点距离是a ()2pa >,则点M 到准线的距离是 ,点M 的横坐标是 .6*.设F 为抛物线y 2=ax (a >0)的焦点,点P 在抛物线上,且其到y 轴的距离与到点F 的距离之比为1∶2,则|PF |= .7*.已知点P 是抛物线y 2=2x 上的动点,点P 在y 轴上的射影是M ,点A 的坐标是⎪⎭⎫⎝⎛4,27,则|PA |+|PM |的最小值是 .学习感悟标准方程y2=2px(p>0)y2=-2px(p>0)X2=2py(p>0)x2=-2py(p>0)图象范围x≥0 x≤0 y≥0 y≤0焦点坐标F(p2,0)错误!未指定书签。
学案1:2.4 探究世界的本质

探究世界的本质【课前预习案】【目标导引】一、物质1.自然界的物质性自然界中的事物是按照形成和发展的,都有自己的,都是中的一部分。
2.物质的含义(1)含义:(2)唯一特性:知识拓展:对比客观实在与客观存在、物质与具体的物质形态联系①物质是对万事万物即具体的物质形态的概括抽象;物质依赖于具体的物质形态,离开具体的物质形态,就没有了物质。
②不能用物质代替具体的物质形态,否则就看不到世界的丰富多彩。
同样,也不能用具体的物质形态代替物质,否则又会抹杀世界的物质性。
③二者是共性与个性、普遍性与特殊性、抽象与具体的关系,而不是整体与部分、多数与少数的关系。
3.人类社会的物质性(1)人类社会是的产物。
在从猿到人的演化过程中,起了决定性的作用。
体现在:(2)人类社会在本质上是一个体系。
体现在:人的意识一开始就是因此,世界是的世界,世界的真正统一性就在于。
知识拓展:1.关于世界的物质性,有以下几种说法:世界的本质是物质;世界的本原是物质;世界的统一性在于它的物质性;世界统一于物质;世界是物质的。
2.深刻理解哲学上的物质概念二、运动1.含义:哲学上所讲的运动是指2.运动和物质(1),世界上不存在脱离运动的物质。
(2),脱离物质的运动是根本不存在的。
知识拓展:物质的“唯一特性”是客观实在性,这是从物质的本质上讲的,是相对于人的意识、精神而言的;运动是物质的“根本属性”(或固有属性),这是从物质存在的状态上讲的。
3.运动和静止运动静止区含义哲学上所讲的运动,是指宇宙间一一方面,事物在它发展的一定阶段和一定1.含义:知识拓展:不能把哲学上的规律混同于具体规律,二者是共性与个性、一般与个别的关系。
规律不等于现象,后者是前者的表现。
规律的客观性,说明规律无好坏之分。
规律一定是联系,但联系不一定都是规律。
规律并非永恒的,一切事物都是运动、变化和发展的。
因此,任何事物的规律也是随着事物存在的时间、地点和条件的变化而变化,也就是说规律也是变化发展的。
《2.4.1 基于解析算法的问题解决》作业设计方案-高中信息技术人教版必修1

《基于解析算法的问题解决》作业设计方案(第一课时)一、作业目标本作业旨在帮助学生掌握解析算法的基本概念和原理,提高他们的问题解决能力,同时培养他们的逻辑思维和计算思维能力。
二、作业内容1. 任务一:设计并实现一个简单的解析算法。
要求学生在规定时间内,使用计算机编程语言(如Python)编写程序,解决一个具体的问题,如求两个数的最大值。
学生需要详细描述算法的步骤和实现过程,并解释每个步骤的意义。
2. 任务二:阅读并理解解析算法的相关文献。
学生需要阅读一篇关于解析算法的文献,并回答以下问题:* 什么是解析算法?它与一般算法有何区别?* 解析算法的主要优点和缺点是什么?* 解析算法的应用场景有哪些?3. 任务三:分析一个实际问题的解析解法。
学生需要选择一个现实生活中的问题,如寻找最佳旅行路线,并尝试使用解析算法来解决。
学生需要讨论可能的算法类型,并解释如何使用计算机编程实现。
三、作业要求1. 作业应独立完成,不得抄袭。
2. 提交作业时,学生需要提供完整的代码或文字描述,并确保答案正确、逻辑清晰。
3. 作业应按照规定格式提交,格式包括题目、摘要、关键词、正文等部分。
4. 学生应尽可能使用图片、图表等方式,直观展示算法的实现过程和原理。
四、作业评价1. 评价标准:评价内容主要包括任务完成情况、逻辑清晰度、代码质量等几个方面。
2. 分值分配:任务一和任务二各占30分,任务三占40分。
3. 评价方式:教师评价与学生互评相结合,教师对每个学生的作业进行总体评价,同时鼓励学生之间互相学习和交流。
五、作业反馈1. 学生提交作业后,教师将对作业进行批改,并及时向学生反馈作业结果。
对于存在的问题,教师将给出具体的建议和指导。
2. 学生应根据教师的反馈,对作业进行修改和完善,以提高自己的学习效果。
同时,学生也可以在互评过程中获取其他同学的优点和经验,从而更好地提高自己的能力。
通过本次作业,学生将能够掌握解析算法的基本概念和原理,提高他们的问题解决能力,同时培养他们的逻辑思维和计算思维能力。
《2.4.1基于解析算法的问题解决》作业设计方案-高中信息技术人教版必修1

《基于解析算法的问题解决》作业设计方案(第一课时)一、作业目标本作业旨在通过实践操作,使学生掌握解析算法的基本概念和思想,能够运用解析算法解决实际问题,提高信息技术的实践应用能力。
二、作业内容1. 理论学习:学生需认真阅读教材中关于解析算法的相关内容,理解解析算法的基本原理和常见应用场景。
2. 实践操作:设计并实现一个简单的解析算法。
学生可选择生活中常见的问题,如字符串解析、数学问题解析等,运用所学知识设计出解决问题的算法。
3. 编程实践:学生需使用编程软件(如Python、Java等),将设计的解析算法编写成程序代码,并运行测试。
4. 记录与总结:学生需将设计算法的过程、编写代码的思路及运行结果详细记录,并总结自己在实践过程中的收获与不足。
三、作业要求1. 选题恰当:选择的题目应具有实际意义,能够通过解析算法进行有效解决。
2. 设计合理:设计的解析算法应符合问题需求,思路清晰,步骤明确。
3. 编程规范:编写的程序代码应符合编程规范,逻辑清晰,易于阅读和维护。
4. 及时完成:学生需在规定时间内完成作业,保证作业的质量和进度。
四、作业评价1. 教师评价:教师根据学生提交的作业内容、实践过程及总结进行综合评价,给出成绩及建议。
2. 同学互评:学生之间可进行互评,互相学习,共同进步。
3. 自我评价:学生需对自己的作业进行反思和评价,找出不足,为今后的学习提供借鉴。
五、作业反馈1. 教师反馈:教师需对学生的作业进行详细反馈,指出优点和不足,给出改进建议。
2. 学生反馈:学生需根据教师的反馈和同学的评价,及时调整学习方法和思路,提高学习效果。
3. 课堂讨论:在下一课时中,组织学生对作业过程中遇到的问题和收获进行课堂讨论,促进知识共享和经验交流。
六、附加建议1. 拓展学习:学生可利用课余时间,阅读相关书籍或网上资源,深入了解解析算法在其他领域的应用。
2. 实践应用:鼓励学生将所学知识应用到实际生活中,解决实际问题,提高信息技术的实际应用能力。
人教版高中数学必修第一册反函数的概念及求法教案
ξ2.4.1《反函数的概念及求法》学案[学习要求]:理解反函数的概念,会求简单函数的反函数,掌握互为反函数的三要素的之间的关系。
[重点难点]:重点为反函数的求法;难点为反函数概念的理解。
[互动课堂]:一、 反函数的概念:1. 定义:一般地,设函数))((A x x f y ∈=的值域是C ,根据这个函数中x ,y 的关系,用表示出,得到。
假设对于y 在C 中的任何一个值,通过 ,x 在A 中都有唯一的值和它对应,那么,x =ϕ(y )就表示,这样的函数x =ϕ(y ) (C y ∈),叫做函数))((A x x f y ∈=的反函数,记作.习惯上,我们一般用x 表示自变量,用y 表示函数,为此我们常常对调)(1y f x -=中字母x ,y ,把它改写成 。
2. 理解:〔1〕反函数是函数吗?为什么?〔2〕所有的函数都有反函数吗?什么样的两个函数才是反函数?〔3〕)(1x f y -=的反函数是谁?注意符号)(1x f -含义及读法?〔4〕函数本质上是映射。
那么在映射观点下,反函数是什么?从映射的定义可知,函数)(x f y =是定义域A 到值域C 的映射,而它的反函数)(1x f y -=是集合到集合的映射,因此,函数)(x f y =的定义域正好是它的反函数)(1x f y -=的;函数)(x f y =的值域是它的反函数)(1x f y -=的 . 〔如右表〕: 〔5〕反函数定义给出了反函数的求法。
二、求反函数:1. 例题精讲:①②略 ③)0(1≥+=x x y ④)1,(132≠∈-+=x R x x x y 且. 解: 解:总结归纳:求反函数的步骤:〔1〕〔2〕〔3〕例2.求函数⎩⎨⎧〈≤-〈≤-=)()()(0110122x x x x x f 的反函数。
解:总结归纳:求分段函数的反函数应:.例3.函数f 〔x 〕=x 2-1 〔x ≤-2〕,求f -1〔4〕的值。
解:思考:假设函数y=f 〔x 〕存在反函数,且f 〔a 〕=b ,那么f -1〔b 〕=?三.课堂练习: 〔A 〕1.函数y=-x 2+1〔x ≤0〕的反函数是〔 ) A .)(11-≥+-=x x y B. )(11≤--=x x y C. )()(11-≤+-=x x y D.)(11-≥+±=x x y2.如以下图表示的函数中,存在反函数的只能是〔 〕A B C D3.函数f 〔x 〕=x 2〔x ≥0〕的反函数为.4.函数y=355-≠∈+x R x x x ,(〕的反函数是. 〔B 〕1.假设函数)(22≥--=x x y ,那么它的反函数是〔 〕A .y=x 2+2 〔x ∈R 〕 B. y=x 2+2 〔x>0〕C. y=x 2+2 〔x≤0〕D. y= -x 2+2 〔x≤0〕2.设函数f 〔x 〕=),(433412-≠∈++x R x x x ,那么f -1〔2〕=〔 〕 A .65- B. 115 C. 52 D.52- 3.函数y=f 〔x 〕有反函数y=f -1〔x 〕,那么=-][1)(m f f . 4.函数5+=x x f )(.〔1〕求反函数)(x f 1- ;〔2〕试研究该函数与反函数的单调性。
§2.4 串联电路和并联电路1 学案
千淘万漉虽辛苦,吹尽狂沙始到金。
放弃时间的人,时间也放弃他。
——莎士比亚§2.4 串联电路和并联电路(一)同步导学案【学习目标】1、结合欧姆定律等知识分析、掌握串并联电路的电流、电压和电阻关系2、掌握简单的串并联的相关计算问题3、理解表头改装成常用电压表和电流表的原理,会求分压电阻和分流电阻的阻值。
【自主学习】1、电势差和电势的关系:_______。
2、恒定电流电路内各处的电荷分布___,任何位置的电荷都不可能_______。
3、如图1所示,把几个导体依次首尾相连,接入电路,这样的连接方式叫做联。
如图2所示,把几个导体的一端连在一起,另一端也连在一起,然后把这两端接入电路,这样的连接方式叫联。
如图3中,R2与R3是联,R1与R2、R3这部分电路是联,R4与R1、R2、R3这部分电路是联,整个电路应该叫做串、并联都有的混联电路。
【问题探究】1、串联电路:(1)串联电路中各处的电流____,即________。
(2)串联电路的总电压等于______________,即______________(3)串联电路的总电阻等于______________,即______________(4)串联电路中各个电阻两端电压跟它们的阻值成___比,即_________________。
2、并联电路:(1)并联电路各支路两端的电压_____,即______________。
(2)并联电路中总电流等于_________,即_________________(3)并联电路的总电阻的倒数等于___________,即____________________________(4)并联电路中通过各个电阻的电流跟它的阻值成_____比【归纳总结】①R1和R2并联后R= (若R1远大于R2,R≈ )②n个相同电阻(R1)串联,其总电阻R= .并联其总电阻R= .③不同阻值的电阻串联,总电阻与其中最大电阻有何关系?④不同阻值的电阻并联,总电阻与其中最小电阻有何关系?⑤在任何电路中,某一电阻增大,总电阻如何变?⑥在电路中, 电阻个数增多,总电阻如何变?【当堂训练】例1、甲、乙两个电阻的I-U图象如图所示则()A.甲、乙串联后的I-U图象位于图中的Ⅰ区B.甲、乙串联后的I-U图象位于图中的Ⅲ区C.甲、乙并联后的I-U图象位于Ⅱ区内D.甲、乙并联后的I-U图象位于Ⅲ区内【巩固提升】用最大阻值为28 Ω的滑动变阻器控制一只“6V,3W”灯泡的发光程度,分别把它们连成限流和分压电路接在9V的恒定电压上,求两种电路中灯泡的电流、电压调节范围.图2。
§2.4一元一次不等式学案1
§2.4.1一元一次不等式(一)一、相关知识链接 (1)一元一次方程的概念只含 未知数,并且 的最高次数是 ,这样的 方程叫做 。
(2)不等式的概念一般地,用符号 连接的式子叫不等式。
(3)一元一次方程的解法一元一次方程的解题过程一般可分为五步:① ② ③ ④ ⑤演练一:一元一次不等式的定义左右两边都是整式,只含有一个未知数,并且未知数的最高次数是1,像这样的不等式,叫做一元一次不等式。
例1 下列不等式,是一元一次不等式的是 ( )A 、2(1)42y y y -+>+B 、.2210x x --< C 、111236+> D 、2x y x +<+ 例2 已知22231kk x +->是关于x 的一元一次不等式,那么k =_______,练习: 若211852m x -->是关于x 的一元一次不等式,则m =_________. 演练二:一元一次不等式的解法 例3 解一元一次不等式652423-≤+-x x x ,并把解集在数轴上表示出来。
例4 关于x 的不等式3 a x ―2≤―a 的解集如图所示,则a 的值是 。
练习:1、不等式x 2≥2+x 的解集是 。
2、如果关于x 的不等式 (a+1) x>a+1的解集为x<1,那么a 的取值范围是 A 、a>0B 、a<0C 、 a>-1D 、a<-13、平面直角坐标系中的点P ⎪⎭⎫⎝⎛-m m 21,2关于x 轴的对称点在第四象限,则m 的取值范围在数轴上可表示为( )4、()()125134+<-x x5、22x +≥312-x6、求不等式x x 228)2(5-≤+的非负整数解拓展测试一、填空题(每空2分,共20分)1、若k kx -≤的解为1-≥x ,则k 。
若由x <y 得到y a x a 22<,则a 的取值范围是 。
2、一次函数2(3)y x b =+- 交y 轴于负半轴,则b 的取值范围是 。
《步步高 学案导学设计》2013-2014学年 高中数学 人教B版必修1【配套备课资源】2.4.1
研一研·问题探究、课堂更高效
2.4.1
探究点一 导引
函数零点的定义
考察下列一元二次方程与对应的二次函数:
(1)方程 x2-2x-3=0 与函数 y=x2-2x-3;
本 (2)方程 x2-2x+1=0 与函数 y=x2-2x+1; 课 时 (3)方程 x2-2x+3=0 与函数 y=x2-2x+3. 栏 目 问题 1 你能列表表示出方程的根,函数的图象及图象与 x 轴 开 关 的交点坐标吗?
个数有
本 课 时 栏 目 开 关
A.0
解析 因为 ac<0,所以 Δ=b2-4ac>0,
所以函数 y=ax2+bx+c 的图象与 x 轴有两个交点,
即函数 f(x)的零点个数为 2.
小结
求函数的零点或判断零点的个数除了利用零点的定
义外,还经常利用其等价结论.
研一研·问题探究、课堂更高效
2.4.1
跟踪训练 1 C.(4,0)
解析
令 x2-4=0,得 x=± 2,
故交点坐标为(± 2,0),所以函数的零点为± 2.
练一练·当堂检测、目标达成落实处
2.4.1
2.若函数 f(x)在定义域 R 上的图象是连续的,图象穿过区间 (0,4),且方程 f(x)=0 在(0,4)内仅有一个实数根,则 f(0)· f(4) 的值
本 课 时 栏 目 开 关
问题 5 函数的零点与函数图象上的点有什么区别? 答 函数的零点不是点, 是函数值为 0 时对应的自变量的值,
也是函数图象与 x 轴交点的横坐标;函数图象上的点可用有 序实数对表示,而函数的零点只用一个实数表示.
研一研·问题探究、课堂更高效
2.4.1
例1
已知函数 y=ax2+bx+c,若 ac<0,则函数 f(x)的零点 ( C ) B.1 C.2 D.不确定
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学案设计 第二单元 4 《诗经》两首 氓
学习目标 1.学习赋、比、兴的艺术表现手法,体会其表达效果。 2.品味诗中情景交融的片段,把握抒情女主人公的思想感情的变化。 3.探究悲剧产生的原因,树立正确的爱情观。 自主认知 一、整体感知 1.阅读诗歌,把握诗歌的感情基调。 2.思考诗歌表现的主题。 二、自练自测 1.对下列各句的解释,有误的一项是( ) A.将子无怒,秋以为期——请你不要生气,把秋天订为婚期吧。 B.既见复关,载笑载言——终于又看到了你,就又说又笑。 C.女之耽兮,不可说也——姑娘沉溺在爱情里,就无法劝说了。 D.三岁为妇,靡室劳矣——多年来做你的妻子,家里的劳苦活儿没有不干的。 2. 填空。 (1)《 》是我国古代最早的一部诗歌总集。收录了从西周到春秋时期的诗歌共 篇,包括“ ”“ ”“ ”三部分。 (2)《诗经》的句式以四言为主。根据不同内容的表达需要,分别采用“ ”“ ”“ ”的艺术手法。 三、质疑问难 将预习过程中的疑问写在下面,并在小组内部讨论解决。
合作探究 1.《氓》中的女主人公是一个什么样的人?
2.分析一下“氓”是个什么样的人?(结合诗句) 3.从全诗看,女子内心的情感经历了怎样的变化过程? 4.《氓》运用了哪些表现手法? 学案设计 5.女主人公的痛苦是不是仅仅来自变心的丈夫? 课堂练习 一、基础知识 1.下列加点字的注音有误的一项是( ) A.氓.之蚩蚩(ménɡ) 靡.室劳矣(mí) 犹可说.也(shuō)
B.匪.来贸丝(fēi) 乘彼垝.垣(ɡuǐ) 自我徂.尔(cú) C.夙.兴夜寐(sù) 隰则有泮.(pàn) 无食桑葚.(shèn) D.载.笑载言(zài) 无与士耽.(dān) 渐车帏裳.(chánɡ) 2.下列加点词的用法和意义相同的一项是( )
A. ①将子无怒,秋以为期②剩彼垝垣,以望复关
B. ①士也罔极,二三其德②信誓旦旦,不思其反 C. ①送子涉淇,至于顿丘②于嗟女兮,无与士耽 D. ①氓之蚩蚩,抱布贸丝②静言思之,躬自悼矣 3.下列加点词解释不正确的一项是( ) A.以尔车来,以我贿.迁 贿:财物。
B.于嗟女兮,无与士耽. 耽:耽搁。 C.女也不爽.,士贰其行 爽:过错。 D.言既遂.矣,至于暴矣 遂:顺心、满足。 4.下列运用借代手法的一句是( ) A.桑之落矣,其黄而陨。 B.桑之未落,其叶沃若。 C.不见复关,泣涕涟涟。 D.及尔偕老,老使我怨。 5.补写出下列诗句的空缺部分。 (1)三岁为妇, 。 ,靡有朝矣。 (2) , 。女也不爽,士贰其行。 (3)淇则有岸, 。总角之宴, 。 (4)信誓旦旦,不思其反。 , ! 二、课内阅读 阅读下面的诗歌,回答6~8题。 学案设计 氓 氓之蚩蚩,抱布贸丝。匪来贸丝,来即我谋。送子涉淇,至于顿丘。匪我愆期,子无良媒。将子无怒,秋以为期。 乘彼垝垣,以望复关。不见复关,泣涕涟涟。既见复关,载笑载言。尔卜尔筮,体无咎言。以尔车来,以我贿迁。 桑之未落,其叶沃若。于嗟鸠兮,无食桑葚!于嗟女兮,无与士耽!士之耽兮,犹可说也。女之耽兮,不可说也! 桑之落矣,其黄而陨。自我徂尔,三岁食贫。淇水汤汤,渐车帷裳。女也不爽,士贰其行。士也罔极,二三其德。 三岁为妇,靡室劳矣。夙兴夜寐,靡有朝矣。言既遂矣,至于暴矣。兄弟不知,咥其笑矣。静言思之,躬自悼矣。 及尔偕老,老使我怨。淇则有岸,隰则有泮。总角之宴,言笑晏晏。信誓旦旦,不思其反。反是不思,亦已焉哉! 6.《氓》三处写到“淇水”,任选一处所写“淇水”,赏析其作用。
7. 简要分析《氓》中女子的形象。 8.对诗歌中第1、4章内容和手法的说明错误的一项是( ) A.第1章写的是古代青年男女的求婚经过:氓诚恳求婚,“我”热情相送。 B.从第1章看,古代青年男女恋爱是讲究媒妁之言的,没有媒人的婚恋是不被社会认可的。 C.第4章写婚后“我”遭遗弃的情况:氓家庭贫寒,遭受水灾,“我”被遗弃。 D.第4章在表现手法上运用了托物起兴的方式,由桑叶变黄引起并比喻“氓”的变心。 三、拓展阅读 阅读下面的诗歌,完成第9~10题。
桃 夭
桃之夭夭,灼灼其华。之子于归①,宜其室家。 学案设计 桃之夭夭,有②其实。之子于归,宜其家室。 桃之夭夭,其叶蓁蓁③。之子于归,宜其家人。 注:①归:出嫁。②(fén):草木果实翻身硕大的样子。③蓁蓁(zhēn):草木茂盛的样子。 9.本诗在章法结构上采用了 的形式。 10.请从比兴手法运用的角度赏析全诗。
阅读下面两首诗,完成第11~12题。 相 鼠
相鼠有皮,人而无仪。 人而无仪,不死何为! 相鼠有齿,人而无止。 人而无止,不死何俟! 相鼠有体,人而无礼。 人而无礼,胡不遄死? (选自《诗经·鄘风》) 河 广 谁谓河广?一苇杭①之。谁谓宋远?跂予②望之。 谁谓河广?曾不容刀。谁谓宋远?曾不崇朝③。 (选自《诗经·卫风》) 注:①杭:通“航”,渡过。②予:而。③崇朝(zhōnɡ zhāo):即“终朝”,从黎明到早饭这段时间。 11.《相鼠》一诗表达了什么思想感情?
12.《相鼠》与《河广》这两首诗在章法结构上有什么共同之处?试分析这样写的好处。 学案设计 四、精彩语言运用 13.对下面一段话中画线部分进行改写。 要求:①以“儒家学者”为开头。②不改变句子的原意,但语序可变动。 《诗经》从一开始,尽管还没有赋予它以儒家经典的意义,人们还习惯地称它为“诗三百”,但它的本来面目就逐步被儒家学者掩盖、断章取义、歪曲篡改,被拿去附会剥削阶级所需要的道德伦理观念。 参考答案 【自主认知】
自练自测
1.C 解析:“无法劝说”应为“无法脱身”。 2.(1)诗经 305 风 雅 颂 (2)赋 比 兴 【合作探究】 1.婚前:温柔、纯真、热情。婚后:勤劳、任劳任怨;面对男人的无情,不再抱有幻想。 2.婚前:氓之蚩蚩、信誓旦旦——表面憨厚、急躁、任性。婚后:二三其德、至于暴——暴躁、用情不专。 3.恋爱时的温柔痴情——婚变中的怨恨沉痛——觉醒后的清醒刚烈。 4.比兴手法:“桑之未落,其叶沃若”比喻暗示女子容颜润泽美丽,她和男子的爱情也十分滋润。“桑之落矣,其黄而陨”比喻暗示女子容颜憔悴衰老,她和男子的爱情也逐渐枯竭。用“于嗟鸠兮,无食桑葚”比兴,劝诫女孩子不要和男子沉溺爱情。因为“士之耽兮,犹可说也。女之耽兮,不可说也!”对比手法:婚前婚后女子的处境和男子的态度形成鲜明对比。 5.不是。这一婚姻悲剧有一定的必然性和普遍性。在男权社会中,女性在经济上、政治上都处于附属地位,她们生活天地狭小,生活的幸福与否全寄托在丈夫身上。如果遇上一个对感情、对家庭不负责任的丈夫,那她的悲剧是不可避免的。再者,娘家人的不理解,更能反映出那个时代人的爱情观、婚姻观和女子在爱情和社会中的弱势地位,更能反映出这场婚姻不仅是个人的悲剧,更是时代的悲剧。 【课堂练习】
1.A 解析:“说”应读“tuō”。
2.B 解析:A项,①个词,把,②连词,来。B项,①②都代词,他。C项,①介词,②感叹词。D项,①用于主谓之间,取消句子独立性,②代词。 3.B 解析:“耽”是“沉溺”的意思。 4.C 解析:A、B两项是“比”的手法,D项是顶真的手法。“复关”是借代。 5.(1)靡室劳矣 夙兴夜寐 (2)淇水汤汤 渐车帷裳 (3)隰则有泮 言笑晏晏 (4)反是不思 亦已焉哉 6.谈婚论嫁时,送子涉淇,淇水喻示了爱情的缠绵。(遭弃归途中,淇水湿帷,淇水暗合了婚 学案设计 姻的变故。归家静思时,淇水有岸,淇水反衬了悲剧的宽广。) 7.《氓》中女子是一场悲剧婚姻中的弃妇。她美丽多情,敢于追求美好的婚姻生活;她勤劳坚强,勇敢地面对婚变而和不专一的爱情诀别。
8.C 解析:第4章用桑树、淇水起兴,写弃妇婚后多年忍受贫苦生活,没有什么差错,而男
人却变了心。 9. 重章叠句 10.答案:以“桃之夭夭”起兴,通过铺垫和渲染,热烈而真挚地表达了对新娘的赞美和祝福。以桃设计,通过对桃花、桃实、桃叶的描写,在赞美新娘美丽贤淑的同时,从不同的角度祝福新娘婚后夫妻和睦、子孙繁衍、家族兴旺。联想巧妙,形象鲜明,意趣盎然。
解析:“比兴”是《诗经》常见的表现手法,解答该题要指出用来作比、起兴之物,理解其深
层的含义。 参考译文: 桃树长得多么壮盛,花儿朵朵正鲜美。
这位女子出嫁后,定能使家庭和顺。 桃树长得多么壮盛,果实累累结满枝。 这位女子出嫁后,定能使家庭美满。 桃树长得多么壮盛,绿叶茂盛展生机。 这位女子出嫁后,定能使家人幸福。 11.这首诗讽刺胡作非为、荒淫无耻之徒,表达了人们的憎恨和诅咒。诗人以老鼠作比,指斥无耻之徒连老鼠都不如。 12.两首诗从行文方式来看,都运用了重章叠句的表现手法,只更换个别的字眼,增强了诗歌的音乐性和节奏感,更能充分地抒发情怀。 参考译文: 相 鼠
看那老鼠有张皮,却见有人没威仪。
却见有人没威仪,为何还活不倒毙! 看那老鼠有牙齿,却见有人无廉耻。 却见有人无廉耻,活着不死等何时? 看那老鼠有肢体,却见有人不懂礼。
