2019-2020学年度下学期线上教学六月自主测试八年级数学试题(手写答案)
2019~2020学年度第二学期期末考试八年级数学答案
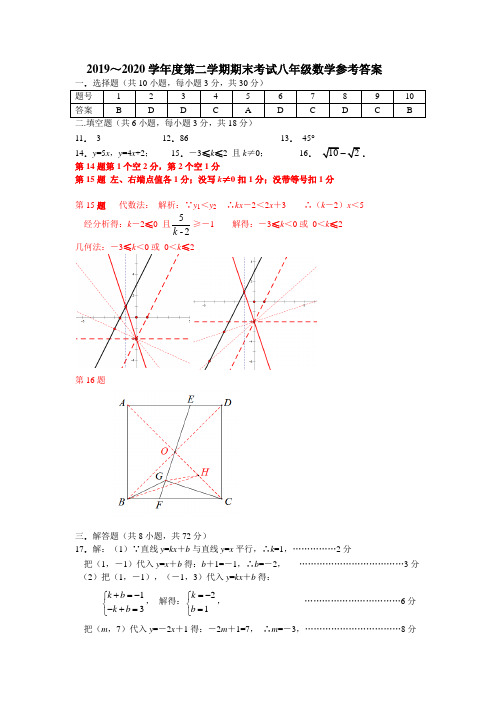
2019~2020学年度第二学期期末考试八年级数学参考答案一.选择题(共10小题,每小题3分,共30分) 题号 1 2 3 4 5 6 7 8 9 10 答案BDDCADCDCB二.填空题(共6小题,每小题3分,共18分)11. 3 12.86 13. 45°14.y =5x ,y =4x +2; 15.-3≤k ≤2 且k ≠0; 16. 102-. 第14题第1个空2分,第2个空1分第15题 左、右端点值各1分;没写k ≠0扣1分;没带等号扣1分第15题 代数法: 解析:∵y 1<y 2 ∴kx -2<2x +3 ∴(k -2)x <5 经分析得:k -2≤0 且2-5k ≥-1 解得:-3≤k <0或 0<k ≤2 几何法:-3≤k <0或 0<k ≤2第16题三.解答题(共8小题,共72分)17.解:(1)∵直线y =kx +b 与直线y =x 平行,∴k =1,……………2分把(1,-1)代入y =x +b 得:b +1=-1,∴b =-2, ………………………………3分 (2)把(1,-1),(-1,3)代入y =kx +b 得:13k b k b +=-⎧⎨-+=⎩, 解得:21k b =-⎧⎨=⎩, ……………………………6分 把(m ,7)代入y =-2x +1得:-2m +1=7, ∴m =-3,……………………………8分18.证明:(1)∵E 是CD 的中点,∴DE =CE , …………………1分∵CF //OD ,∴∠ODE =∠FCE , ………………………………………3分在△EDO 和△ECF 中,,,,ODE FCE DE O E CE DE B F ⎧⎪⎨⎪∠=∠∠∠=⎩= ∴△EDO ≌△ECF ,…………………4分 (2)∵△EDO ≌△ECF ∴OD=CF , ……………………………………5分 ∵CF //OD ,∴四边形OCFD 是平行四边形形, ……………………………………6分 ∵四边形ABCD 是菱形,∴AC ⊥BD ,∴∠COD =90°, ……………………………7分 ∴四边形OCFD 是矩形. ……………………………………8分19. (1)a =20,b =28, ………………………………2分 (2)72°, ………………………………3分 (3)814181088714618510+++×+×+×+×=6.4, ………………………………5分答:所有被调查学生课外阅读的平均本数为6.4本.………………………………6分 (4)12008141810814×++++=528, ……………………………7分答:估计该校八年级学生课外阅读7本及以上的人数约有528人.………………8分 20.解:(1)画图如图:………3分 (2)画图如图:………6分 (3)画图如图:………8分21.解:(1)把D (3,m )代入y =x -2得:m =3-2=1, ………1分 ∴点D 的坐标为(3,1)把D (3,1)代入y =kx +7得:3k +7=1,∴k = -2, …………………………3分 (2)由(1)得:直线AB 的解析式为y = -2x +7,当y =n 时,x -2=n ,x = n +2 ∴点M 的坐标为(n +2,n )当x =n 时,y = -2n +7 ∴点N 的坐标为(n ,-2n +7) …………………………5分 ∵点P (n ,n ), ∴PM = 2,PN =7-3n , ∵PN =2PM , ∴47-3=n , ∴n = 1或311, …………………………8分22.(A B 总计(t)C x-60300-x240D 260-x x260总计(t)200 300 500(2)①y1 = -5x+5300;y2 = 20x+4500;………………………………5分②由题意得:60030002600xxxx⎧≥≥≥⎪≥⎪⎪⎨⎪⎩---,解得60≤x≤260,………………………………6分∴y1-y2= -25x+800<0,∴y1<y2,∴A城总运费比B城总运费少………………………………7分(3)设两城总运费为W元,则W= -5x+5300+15(300﹣x)+(35﹣a)x=(15﹣a)x+9800;若0<a<15时15﹣a>0,W随x的增大而增大,∴当x=60时y取最小值,∴60(15﹣a)+9800≥10160,解得a≤9,∴0<a≤9 ………………8分若a=15时W=9800,不符合题意;若a>15时15﹣a<0,W随x的增大而减少,∴当x=260时y取最小值,∴260(15﹣a)+9800≥10160,解得a≤13813,不符合题意;………………9分综合可得:0<a≤9.……………………………………………10分23.(1)①证明:连接AG,∵四边形ABCD是矩形,∴∠ABC=∠BAD=90°,AD=BC,∵∠BAD=90°,BG=GF,∴AG=BG,……………………………………1分∴∠BAG=∠ABG,∴∠GAD=∠GBC,………………………2分在△GAD和△GBC中,AD BCDAG CBGAG BG=⎧⎪∠=∠⎨⎪=⎩∴△GAD≌△GBC,∴DG=CG;…………………………………………………………………………3分②解:连接FC 交DG 于点Q ,取FC 的中点H ,连接DH , ∵CE 垂直平分BF , ∴FC =BC ,∵四边形ABCD 是矩形, ∴AD =BC ,AB =DC , ∵BC =2AB , ∴FC =2CD ,∵∠FDC =90°,FH =HC , ∴FH =HC =DH ,∴CD =HC =DH , ∴△CDH 是等边三角形,∴∠FCD =60°,∴∠DFC =90°-∠FCD =30°, ………………5分 ∵FC =BC ,BG =GF , ∴∠FCG =∠BCG ,∵△GAD ≌△GBC ,∴∠ADG =∠BCG , ∴∠ADG =∠FCG ,∴∠FQG -∠ADG =∠FQG -∠FCG , ∴∠DGC =∠DFC =30°; ………………7分 (2)34; …………………………………………………………………………10分 24.解:(1)∵y =k (x -3)+4 ……………………………………2分∴当x =3时,y =4 ∴点P 的坐标为(3,4). ……………………………………3分 (2)延长AB 交x 轴于点E ,直线y =kx -3k +4交y 轴于点G ,∵当x =0时,y =4-3k , ∴G (0,4-3k ), ∴OG =4-3k .……………………4分 ∵BP 平分∠OBA , ∴∠ABP=∠OBP ,∵AB //y 轴, ∴∠ABP=∠OGB , ……………5分 ∴∠OBG=∠OGB , ∴OB =OG =4-3k . ……………6分 在Rt △OBE 中,222OB BE OE =+, ∴222)3-4()34(6k k =++,∴43-=k . …………………………………………7分(3)作PS ⊥x 轴于点S ,NT ⊥x 轴于点T , 在Rt △OPS 中,522=+=PS OS OP ,设M (m ,0) 当m =3时,PM =NM =4, ∴N (7,0) 当0<m <3时,可证△PMS ≌△MNT ,PS =MT =4,MS =NT =3-m , ∴N (4+m ,m -3) 当m >3时,可证△PMS ≌△MNT ,PS =MT =4,MS =NT =m -3, ∴N (4+m ,m -3) ∴点N 在直线y =x -7上 ………………………9分若直线y =x -7与y 轴交于点Q (0,7),则∠OQN =45°,作点O 关于直线y =x -7的对称点O '(7,-7),当点P 、N 、O '三点共线时,ON+PN 最小为PO ',此时,△OPN 的周长最小为OP+PO ',在Rt △O 'PR 中,137''22=+=PR RO PO ,………………10分 设直线PO '的解析式为y =kx +b , 把(3,4),(7,-7)代入得:3477k b k b +=⎧⎨+=-⎩, 解得:11-4494k b ⎧=⎪⎪⎨⎪=⎪⎩………11分 ∴直线PO '的解析式为449411-+=x y , 71149-44y x y x =-⎧⎪⎨=+⎪⎩, 解得:771528-15x y ⎧=⎪⎪⎨⎪=⎪⎩∴点N 的坐标为(1577,1528-).………12分。
青岛版2020八年级数学下册第六章平行四边形自主学习能力达标测试题4(附答案详解)

青岛版2020八年级数学下册第六章平行四边形自主学习能力达标测试题4(附答案详解)1.如图,平行四边形ABCD 中,对角线AC 和BD 相交于点O ,如果AC=12,BD=10,AB=m ,那么m 的取值范围是( )A .1<m <11B .2<m <22C .10<m <12D .2<m <62.如图,点P (3,4),⊙P 半径为2,A (2.8,0),B (5.6,0),点M 是⊙P 上的动点,点C 是MB 的中点,则AC 的最小值是( )A .1.4B .32C .52D .2.63.如图,在△ABC 中,点D 、E 分别是边AB 、AC 的中点,已知DE=6cm ,则BC 的长是( )A .3cmB .12cmC .18cmD .9cm 4.如图所示,DE 为△ABC 的中位线,点F 在DE 上,且∠AFB=90°,若AB=6,BC=10,则EF 的长为( )A .1B .2C .3D .55.如图,矩形ABCD 的对角线AC 与BD 相交于点O ,304ADB AB ∠︒=,=,则OC 等于()A.5 B.4 C.3.5 D.36.如图,在▱ABCD中,EF∥BC,GH∥AB,EF,GH相交于点O,则图中共有平行四边形()A.6个B.7个C.8个D.9个7.下列命题中,假命题是()A.两组对角分别相等的四边形是平行四边形B.有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形C.一组邻边互相垂直,两组对边分别平行的四边形是矩形D.有一组邻边相等且互相垂直的平行四边形是正方形8.在Rt△ABC中,∠ACB=90°,D是AB的中点,若AB=8,则CD的长为()A.6 B.5 C.4 D.39.能够判别一个四边形是菱形的条件是()A.一组对角相等且一条对角线平分这组对角B.对角线互相平分C.对角线互相垂直且相等D.对角线相等且互相平分10.平行四边形的对角线分别为,一边长为12,则的值可能是下列各组数中的()A.8与14 B.10与14 C.18与20 D.10与28 11.在□ABCD中,∠A:∠B=2:3,则∠B=____,∠C=_____,∠D=____.12.如图,已知小正方形ABCD的面积为1,把它的各边延长一倍得到新正方形A1B1C1D1,则正方形A1B1C1D1的面积为______;把正方形A1B1C1D1边长按原法延长一倍得到正方形A2B2C2D2;……以此下去,则正方形A n B n C n D n的面积为______.13.如图,已知矩形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC 上.若BE =3,EC =5,则AB 的长为_____.14.如图,正方形ABCD 中,AB=2,对角线AC ,BD 相交于点O ,将△OBC 绕点B 逆时针旋转得到△O′BC′,当射线O′C′经过点D 时,线段DC′的长为_____.15.在面积为15的平行四边形ABCD 中,过点A 作AE ⊥直线BC 于点E ,作AF ⊥直线CD 于点F .若5AB =,6BC =,则CE CF +的值为__________.16.如图,在Y ABCD 中,AM=13AD ,BD 与MC 相交于点O ,则S △MOD ∶S △BOC =_____.17.用边长为10 cm 的正方形,做了一套七巧板.拼成如图所示的一座“桥”,则“桥”中涂色部分的面积为______cm.18.如图,正方形ABCD 的顶点D 在正方形ECGF 的边EC 上,顶点B 在GC 的延长线上,连接EG 、BE ,EGC ∠的平分线GH 过点D 交BE 于H ,连接HF 交EG 于M ,则MG ME的值为________.19.如图,正方形ABCD 的边长为12,点E 在边AB 上,BE=8,过点E 作EF ∥BC ,分别交BD 、CD 于G 、F 两点.若点P 、Q 分别为DG 、CE 的中点,则PQ 的长为_____.20.正方形ABCD 中,F 是AB 上一点,H 是BC 延长线上一点,连接FH ,将△FBH 沿FH 翻折,使点B 的对应点E 落在AD 上,EH 与CD 交于点G ,连接BG 交FH 于点M ,当GB 平分∠CGE 时,BM=226,AE=8,则ED=_____.21.如图,在□ABCD 中,点E ,F 分别在边AB ,DC 上,且AE =CF ,连接DE ,BF . 求证:DE =BF .22.已知,如图,在Rt ABC V 中,E 是两锐角平分线的交点,ED BC ⊥,EF AC ⊥,垂足分别为D ,F ,求证:四边形CDEF 是正方形.23.在一个平行四边形中若一个角的平分线把一条边分成长是2cm 和3cm•的两条线段,求该平行四边形的周长是多少?24.如图1,若四边形ABCD 、四边形GFED 都是正方形,显然图中有AG CE =,AG CE ⊥;()1当正方形GFED 绕D 旋转到如图2的位置时,AG CE =是否成立?若成立,请给出证明;若不成立,请说明理由;()2当正方形GFED 绕D 旋转到如图3的位置时,延长CE 交AG 于H ,交AD 于M . ①求证:AG CH ⊥;②当4AD =,2DG =时,求CH 的长.25.如图所示,O 为矩形ABCD 的对角线的交点,//DE AC ,//CE BD .()1试判断四边形OCED 的形状,并说明理由;()2若10AB =,12BC =,求四边形OCED 的面积.26.如图:在矩形ABCD 中,E 、F 分别是AB 、AD 边上的点,且BE=AF ,∠1=∠2. (1)Rt △AEF 与Rt △BCE 全等吗?说明理由; (2)△CEF 是不是直角三角形?说明理由.27.如图,在△ABC 中,∠C =2∠B ,D 是BC 上的一点,且AD ⊥AB ,点E 是BD 的中点,连结AE.(1)求证:∠AEC =∠C ;(2)若AE =6.5,AD =5,则△ABE 的周长是多少?28.如图,矩形OABC 的边OA ,OC 分别与坐标轴重合,并且点B 的坐标为OBE ∆.将该矩形沿OB 折叠,使得点A 落在点E 处,OE 与BC 的交点为D .(1)求证:△OBD 为等腰三角形;(2)求点E 的坐标;(3)坐标平面内是否存在一点F ,使得以点B ,E ,F ,O 为顶点的四边形是平行四边形,若存在,请直接写出点F的坐标;若不存在,请说明理由.参考答案1.A【解析】∵四边形ABCD是平行四边形,AC=12,BD=10,∴OA=OC=6,OD=OB=5,在△OAB中,OA﹣OB<m<OA+OB,∴6﹣5<m<6+5,∴1<m<11.故选A.2.B【解析】【分析】如图,连接OP交⊙P于M′,连接OM.因为OA=AB,CM=CB,所以AC=12OM,所以当OM最小时,AC最小,可知当M运动到M′时,OM最小,由此即可解决问题.【详解】如图,连接OP交⊙P于M′,连接OM,由勾股定理得:,∵OA=AB,CM=CB,∴AC=12 OM,∴当OM最小时,AC最小,∴当M运动到M′时,OM最小,此时AC的最小值=12OM′=12(OP﹣PM′)=12×(5-2)=32,故选B.【点睛】本题考查了点与圆的位置关系、坐标与图形的性质、三角形中位线定理、最小值问题等知识,解题的关键是理解圆外一点到圆的最小距离以及最大距离,学会用转化的思想思考问题.3.B【解析】∵点D、E分别是边AB、AC的中点,∴BC=2DE=2×6=12cm,故选B.4.B【解析】∵DE为△ABC的中位线,∴DE=12BC=5,∵∠AFB=90°,D是AB 的中点,∴DF=12AB=3,∴EF=DE﹣DF=2,故选B.5.B【解析】试题解析:∵四边形ABCD是矩形,,,90 AC BD OA OC BAD∴==∠=o,30ADB∠=oQ,∴AC=BD=2AB=8,142OC AC ∴==; 故选B. 点睛:平行四边形的对角线互相平分.6.D【解析】解:∵四边形ABCD 是平行四边形,∴AB ∥CD ,AD ∥BC .∵AD ∥EF ,CD ∥GH ,∴AB ∥GH ∥CD ,AD ∥EF ∥BC ,∴平行四边形有:▱ABCD ,▱ABHG ,▱CDGH ,▱BCFE ,▱ADFE ,▱AGOE ,▱BEOH ,▱OFCH ,▱OGDF 共9个.即共有9个平行四边形.故选D .7.B【解析】选项A , 两组对角分别相等的四边形是平行四边形,命题正确;选项B ,有一条对角线与一组邻边构成等腰三角形的平行四边形是菱形,命题错误;选项C ,一组邻边互相垂直,两组对边分别平行的四边形是矩形,命题正确;选项D ,有一组邻边相等且互相垂直的平行四边形是正方形,命题正确.故选A.8.C【解析】解:∵∠ACB =90°,D 是AB 的中点,∴CD =12AB =12×8=4.故选C . 9.A【解析】【分析】求出四边形是平行四边形和一组邻边相等,再根据菱形的判定推出,即可判断A ;对角线垂直的平行四边形是菱形,根据以上内容即可判断B 、C 、D .【详解】A 、∵AC 平分∠BAD 和∠BCD , ∴∠BAC=∠DAC=12∠BAD ,∠BCA=∠DCA=12∠BCD , ∵∠BAD=∠BCD , ∴∠BAC=∠DAC=∠BCA=∠DCA , ∴AB=BC ,AB ∥CD ,AD ∥BC , ∴四边形ABCD 是平行四边形, ∵AB=BC , ∴平行四边形ABCD 是菱形,故本选项正确; B 、对角线互相平分的四边形是平行四边形,不一定是菱形,故本选项错误;C 、只有在平行四边形的基础上,添加条件对角线互相垂直的四边形才是菱形,故本选项错误;D、对角线相等且平分的四边形是矩形,不是菱形,故本选项错误;【点睛】本题主要考查了对菱形、平行四边形、矩形的判定的应用,属于基础题型.注意:有一组邻边相等的平行四边形是菱形,对角线互相垂直的平行四边形是菱形.10.C【解析】根据三角形的两边之和大于第三边,两边之差小于第三边,若x y>,则12221222x yx y⎧+>⎪⎪⎨⎪-<⎪⎩,所以符合条件的,x y可能是18与20;所以选C.11.108º,72º,108º【解析】解:∵平行四边形ABCD中,∠A+∠B=180°,又∵∠A:∠B=2:3,∴∠A=72°,∠B=108°,∴∠D=∠B=108°,∠C=∠A=72°.故答案为108º,72º,108º.12.5 5n【解析】已知小正方形ABCD的面积为1,则把它的各边延长一倍后,三角形AA1D1的面积=×2AB×AB=AB2=1,新正方形A1B1C1D1的面积是4×1+1=5,从而正方形A2B2C2D2的面积为5×5=25,以此进行下去…,则正方形A n B n C n D n的面积为5n,故答案为:5, 5n.13.6.【解析】分析:根据折叠的性质得出AF=AB,EF=BE=3,在Rt△EFC中根据勾股定理求出CF=4,设AF=AB=x,则AC=x+4,在Rt△ABC中根据勾股定理列方程即可求出AB的长.详解:由△ABE沿着AE折叠至△AEF的位置可得:AF=AB,EF=BE=3,∠AFE=∠B=90°,在Rt△EFC中根据勾股定理得CF=4,设AF=AB=x,则AC=x+4,在Rt△ABC中根据勾股定理得:AB2+BC2=AC2,即x2+(3+5)2=(x+4)2,解得:x=6,即AB=6.点睛:本题主要考查了矩形中的折叠问题,根据勾股定理列出方程是解决此题的关键.14【解析】【分析】根据正方形与旋转的性质可得,设DC′=x,然后在Rt△BDO′中,根据勾股定理即可求得答案.【详解】∵四边形ABCD是正方形,∴AB=BC=CD=AD=2,∴∵△OBC绕点B逆时针旋转得到△O′BC′,∴,设DC′=x,在Rt△BDO′中,∵BD2=BO′2+O′D2,∴()2=2+)2,∴..【点睛】本题主要考查正方形的性质,旋转的性质,勾股定理.解此题的关键在于熟练掌握其知识点. 15.31+ 【解析】如下图,过A 作AE BC ⊥,AF CD ⊥,∴615AE ⋅=,解得:52AE =, 在Rt AEB V 中,∵90AEB =︒∠,12AE AB =, ∴30ABE ∠=︒,∴532BE =, ∴536CE =-, ∵平行四边形ABCD ,∴30ABE D ∠=∠=︒,∴132AF AD ==, 33DF =,∴335CF =-,∴536335CE CF +=-+-, 31=+. 故答案为:312+.16.4:9【解析】∵四边形ABCD 是平行四边形,∴AD =BC ,AD ∥BC ,∵AM =13AD , ∴==23, ∵AD ∥BC ,∴△DOM ∽△BOC ,∴=()2=,故答案为4:9.17.50【解析】【分析】读图分析阴影部分与整体的位置关系;易得阴影部分的面积即为△ABC 的面积,是原正方形的面积的一半.【详解】观察得到阴影部分为正方形的一半,即为2110=502⨯. 故答案为50.【点睛】本题目考查了七巧板;正方形的性质.主要考查正方形对角线相互垂直平分相等的性质,读图也很关键.根据图形之间的关系得出面积关系是解题关键. 1821【解析】【分析】取EG 中点O, 连接OH, 先证明ΔBCE ≌ΔDCG 推出HG ⊥BE, 再证明ΔBGH ≌ΔEGH, 推出OH 是三角形中位线, 设HN=a, 则BC=2a, 设正方形ECGF 的边长是2b, 则NC=b, CD=2a, 利用ΔDHN ∽ΔDGC, 得到DN HN DC CG=, 求出a 、b 之间的关系,最后由ΔEFM ∽ΔOMH,得2b a+b EM EF OM OH ==,可得EM MG的值可得答案. 【详解】解:取EG 中点O,连接OHQ 四边形ABCD 是正方形,∴BC=DC,∠BCE=o 90,同理可得CE=CG, ∠DCG=o 90,在ΔBCE 和ΔDCG 中,BC=DC ,∠BCE=∠DCG=o 90,CE=CG∴ΔBCE ≌ΔDCG,∴∠BEC=∠DGC ,Q ∠EDH=∠CDG, ∠DGC+∠CDG=o 90,∴∠EDH+∠BEC=o 90,∴∠EHD=o 90,∴HG ⊥BE,在ΔBGH 和ΔEGH 中, ∠EHG=∠BHG ,HG=HG ,∠EGH=∠BGH∴ΔBGH ≌ΔEGH,∴BH=EH,Q EH=HB , EO=OG ,∴HO //BG,HO=12BG=12EF, 设EC 和OH 相交于点N.设HN=a,则BC=2a,设正方形ECGF 的边长是2b,则NC=b, CD=2a,Q OH//BC,∴ΔDHN ∽ΔDGC,∴DN HN DC CG =,即:b-2a a =2a 2b, 即:22a +2ab-b =0解得2或2) b (舍去),则a b-1, Q EF//OH,∴ΔEFM~ΔOMH, ∴2b a+bEM EF OM OH == ∴2b a+3b EM OE =,b a+3bEM EG =,∴b 1a a+2b +2bEM MG ==,∴1MG ME =1.【点睛】本题主要考查正方形的性质及三角形相似.19.【解析】【分析】根据题意作出合适的辅助线,利用三角形中位线定理、三角形的相似可以求得PH 和QH 的长,然后根据勾股定理即可求得PQ 的长.【详解】作QM ⊥EF 于点M ,作PN ⊥EF 于点N ,作QH ⊥PN 交PN 的延长线于点H ,如图所示,∵正方形ABCD 的边长为12,BE=8,EF ∥BC ,点P 、Q 分别为DG 、CE 的中点, ∴DF=4,CF=8,EF=12,∴MQ=4,PN=2,MF=6,∵QM ⊥EF ,PN ⊥EF ,BE=8,DF=4,∴△EGB ∽△FGD , ∴EG BE FG DF=, 即1284FG FG -=, 解得,FG=4,∴FN=2,∴MN=6﹣2=4,∴QH=4,∵PH=PN+QM,∴PH=6,∴PQ=22PH QH+=213,故答案为:213.【点睛】本题考查了三角形中位线定理、正方形的性质、勾股定理、相似三角形的判定与性质,正确添加辅助线、结合图形熟练应用相关性质和定理进行解题是关键. 20.4【解析】解:如图,过B作BP⊥EH于P,连接BE,交FH于N,则∠BPG=90°.∵四边形ABCD 是正方形,∴∠BCD=∠ABC=∠BAD=90°,AB=BC,∴∠BCD=∠BPG=90°.∵GB平分∠CGE,∴∠EGB=∠CGB.又∵BG=BG,∴△BPG≌△BCG,∴∠PBG=∠CBG,BP=BC,∴AB=BP.∵∠BAE=∠BPE=90°,BE=BE,∴Rt△ABE≌Rt△PBE(HL),∴∠ABE=∠PBE,∴∠EBG=∠EBP+∠GBP=12∠ABC=45°,由折叠得:BF=EF,BH=EH,∴FH垂直平分BE,∴△BNM是等腰直角三角形.∵BM=226,∴BN=NM=213,∴BE=413.∵AE=8,∴Rt△ABE中,AB=22BE AE-=12,∴AD=12,∴DE=12﹣8=4.故答案为4.点睛:本题考查了翻折变换、正方形的性质、全等三角形的判定和性质、角平分线的定义、勾股定理、线段垂直平分线的性质等知识,解题的关键是学会添加辅助线,构造全等三角形解决问题.21.详见解析【解析】【分析】欲证明DE BF=,只要证明DAEV≌BCFV即可.由四边形ABCD是平行四边形,可证A C∠=∠,AD CB=,从而根据“SAS”可证明DAEV≌BCFV.【详解】证明:Q四边形ABCD是平行四边形,A C∴∠=∠,AD CB=,在DAEV和BCFV中,AD CBA CAE CF=⎧⎪∠=∠⎨⎪=⎩,DAEV∴≌()SASBCFV,DE BF∴=.【点睛】本题考查平行四边形的性质、全等三角形的判定和性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.22.见解析【解析】【分析】过E作EM⊥AB,根据角平分线的性质可得EF=ED=EM.再证明四边形EFDC是矩形,可根据邻边相等的矩形是正方形得到四边形CDEF是正方形.【详解】证明:过E作EM AB⊥,∵AE平分CAB∠,∴EF EM=,∵EB平分CBA∠,∴EM ED=,∴EF ED=,∵ED BC ⊥,EF AC ⊥,ABC V 是直角三角形,∴90CFE CDE C ∠=∠=∠=o ,∴四边形EFDC 是矩形,∵EF ED =,∴四边形CDEF 是正方形.【点睛】考查角平分线的性质,正方形的判定,作出辅助线,熟练掌握角平分线上的点到角两边的距离相等是解题的关键.23.14cm 或16cm【解析】如图,因为AE 平分∠DAB ,所以∠DAE=∠BAE ;因为CD ∥AB ,所以∠DEA=∠BAE ,所以∠DAE=∠DEA ,则△ADE 是等腰三角形,DA=DE.①当DE=2时,AD=DE=2,EC=3,所以CD=5,则平行四边形的周长为5+5+2+2=14; ②当DE=3时,AD=DE=3,EC=2,所以CD=5,则平行四边形的周长为5+5+3+3=16. 答:该平行四边形的周长是14cm 或16cm.24.()1AG CE =成立.证明见解析;(2)①证明见解析,②810CH =. 【解析】【分析】(1)利用SAS 证△ADG ≌△CDE 即可; (2)①同样先证明△ADG ≌△CDE ,得出∠DAG=∠DCE ,而∠DCM+∠DMC=90°,从而∠DAG+∠AMH=90°,结论显然;②连接AC 、CG ,注意到DG ∥AC ,△GAC 与△DAC 的面积相等,于是考虑用等积变换,求出AG 即可求出CH .【详解】()1AG CE =成立.证明:∵四边形ABCD 、四边形DEFG 是正方形,∴GD DE =,AD DC =,90GDE ADC ∠=∠=o . ∴90GDA ADE EDC ∠=-∠=∠o .∴AGD CED ≅V V .∴AG CE =.()2①类似()1可得AGD CED ≅V V ,∴12∠=∠.又∵HMA DMC ∠=∠,∴90AHM ADC ∠=∠=o ,即AG CH ⊥.②连接GE ,交AD 于P ,连接CG ,由题意有2sin451GP PD ==︒=,∴3AP =,10AG =∵EG AD ⊥,CD AD ⊥,∴//EG CD ,∴以CD 为底边的CDG V 的高为1PD =,(延长CD 画高) AGD ACD ACG CGD ACDG S S S S S +==+V V V V 四边形∴41441041CH ⨯+⨯=+⨯∴810CH = 【点睛】本题考查了的四边形的相关知识点,解题的关键是熟练的掌握四边形的性质与应用.25.()1四边形OCED 是菱形,理由见解析;(2)60.【解析】【分析】(1)由条件可先证得四边形OCED 为平行四边形,结合矩形的性质可得OC OD =,可证得结论;(2)连接OE ,可证明四边形BCEO 为平行四边形,可求得OE 的长,结合条件可求得菱形OCED 的面积.【详解】()1四边形OCED 是菱形,理由如下:∵//DE AC ,//CE BD ,∴四边形OCED 是平行四边形,又∵在矩形ABCD 中,OC OD =,∴四边形OCED 是菱形;()2连接OE ,由菱形OCED 得CD OE ⊥,又∵BC CD ⊥,∴//OE BC ,又∵//CE BD ,∴四边形BCEO 是平行四边形,∴12OE BC ==,∴1110126022OCED S OE CD =⋅=⨯⨯=菱形. 【点睛】本题主要考查菱形、矩形的判定和性质,掌握菱形的判定和性质、矩形的对角线相等且平分是解题的关键,即①有一组邻边相等的平行四边形是菱形,②对角线互相垂直的平行四边形是菱形,③四边形都相等的四边形是菱形.26.(1)结论:Rt △AEF 与Rt △BCE 全等(2)结论:△CEF 是直角三角形.【解析】试题分析:(1)根据HL,由BE=AF、EC=EF,即可证明;(2)只要证明∠4+∠5=90°,即可解决问题;试题解析:(1)结论:Rt△AEF与Rt△BCE全等.理由:在矩形ABCD中,∠A=∠B=90°∵BE=AF,∵∠1=∠2,∴CE=EF∴Rt△AEF≌Rt△BCE.(2)结论:△CEF是直角三角形.理由:∵Rt△AEF≌Rt△BCE.∴∠3=∠5,∵∠3+∠4=90°,∠5+∠4=90°,∴∠CEF=180°﹣(∠4+∠5)=180°﹣90°=90°,所以△CEF是直角三角形.27.(1)见解析;(2)25【解析】试题分析:(1)在Rt△ADB中,点E是BD的中点,根据直角三角形的性质,可得BE=AE,故∠AEC=2∠B=∠C;(2)根据直角三角形的性质可得BD=2AE,根据勾股定理可得AB的长,可得答案.试题解析:(1)∵AD⊥AB,∴△ABD为直角三角形,又∵点E是BD的中点,∴AE =12BD =BE , ∴∠B =∠BAE ,∠AEC =∠B +∠BAE =2∠B ,又∵∠C =2∠B ,∴∠AEC =∠C ;(2)在Rt △ABD 中,AD =5,BD =2AE =2×6.5=13,∴AB 2=BD 2-AD 2=132-52=122,∴AB =12,∴△ABE 的周长为AB +BE +AE =12+6.5+6.5=25.28.(1)证明见解析;(2)点E 的坐标为2432(,)55;(3)F 点坐标为1612(,)55-,1612(,)55-,6452(,)55. 【解析】【分析】(1)根据折叠的性质,得到△OBE ≌△OBA ,由此得到∠EOB=∠AOB ,然后根据矩形的性质和平行线的性质得到OD=BD ,即△OBD 是等腰三角形;(2)过点E 作EF x ⊥轴于F 交BC 于G ,设CD 的长为x ,则8BD BC CD x =-=-,由(1)值OD=8-x ,然后根据勾股定理求出CD 、OB 、BD 的长,再根据AAS 证得△OCD ≌△BED ,得到3,4DE CD BE OC ====,最后根据三角形的面积求出EG 的长,进而利用矩形的性质和勾股定理求出E 点的坐标;(3)根据平行四边形的判定与性质,分类讨论F 点的坐标即可.【详解】(1)∵OBE ∆是由OBA ∆折叠所得∴OBE ∆≌OBA ∆.,∴12∠=∠,又∵四边形OABC 是矩形∴//OA BC .,∴13∠=∠∴OD BD =,∴OBD ∆为等腰三角形;(2)过点E 作EF x ⊥轴于F 交BC 于G设CD 的长为x ,则8BD BC CD x =-=-由(1)知8OD BD x ==-∵四边形OABC 是矩形∴90,OCD OAB OC AB ∠=∠=︒=∴在Rt OCD ∆中222OC CD OD +=即()22238x x +=-解得3x =即3,8835CD OD BD x ===-=-=由(1)知OBE ∆≌OBA ∆∴90OEB OAB ∠=∠=︒∴90OCD BED ∠=∠=︒∴ 在△OCD 和△BED 中 OCD BED ODC BDE OD BD ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△OCD ≌△BED∴3,4DE CD BE OC ====∵EF x ⊥轴∴90OFB ∠=︒∵//OA BC∴90CGE OFB ∠=∠=︒∴CG BD ⊥∴1122BDE S DE BE BD EG ∆=⋅=⋅ 即1134522BDE S EG ∆=⨯⨯=⨯ ∴125EG =.∴在Rt DGE ∆中95DG === ∵90OCG OFE CGF ∠=∠=∠=︒∴四边形OFGC 是矩形 ∴924355OF CG CD DG ==+=+= 1232455EF EG GF =+=+=. ∴点E 的坐标为2432,55⎛⎫ ⎪⎝⎭; (3)11612,55F ⎛⎫-⎪⎝⎭ 21612,55F ⎛⎫- ⎪⎝⎭ 36452,55F ⎛⎫ ⎪⎝⎭. 【点睛】 此题主要考查了坐标系与四边形的综合,主要用到全等三角形的判定与性质,矩形的性质,平行四边形的判定与性质,勾股定理等知识,综合性比较强,难度较大.。
2019-2020初中数学八年级下册《频数分布及其图形》专项测试(含答案) (566)

八年级数学下册《频数分布及其图形》测试卷学校:__________一、选择题1.(2分)有l0个数据的平均数为7,另有20个数据的平均数为l3,那么这30个数据的平均数是()A.7 B. 10 C.1l D.132.(2分)样本频数分布反映了()A.样本数据的多少 B.样本数据的平均水平C.样本数据的离散程度 D.样本数据在各个小范围内数量的多少3.(2分)大课间活动在我市各校蓬勃开展.某班大课间活动抽查了20名学生每分钟跳绳次数,获得如下数据(单位:次):50,63,77,83,87,88,89,91,93,100,102,111,117,121, 130, 133,146, 158, 177,188.则跳绳次数在90~110这一组的频率是()A.0.1 B.0.2 C.0.3 D.0.74.(2分)样本容量为140,最大、最小值的差为23,确定组距为4,某小组的频数为42,则组数和这个小组的频率是()A.6,3 B.6,0.3 C.6,0.5 D.5.5,0.25.(2分) 在 =3.141 592 653 589 7中,频数最大的数字是()A.1 B.3 C.5 D.96.(2分)将100个数据分成8个组,如下表:则第六组的频数为()A.12 B.13 C.14 D.157.(2分)观察重庆市统计局公布的“十五”时期重庆市农村居民人均收入每年相对于上一年的增长率的统计图,下列说法正确的是()A.2003年农村居民人均收入低于2002年B.农村居民人均收入相对于上年增长率低于9%的有2年C.农村居民人均收入最多是2004年D.农村居民人均收入每年相对于上一年的增长率有大有小,但农村居民人均收入在持续增加8.(2分)某班有48位同学,在一次数学测验中,分数只取整数,统计其成绩,绘制出频数分布直方图(横半轴表示分数,把50.5分到100.5分之间的分数分成5组,组距是10分,纵半轴表示频数)如图所示,从左到右的小矩形的高度比是1:3:6:4:2,则由图可知,其中分数在70.5~80.5之间的人数是()A.9 B.18 C.12 D.69.(2分)在10,20,40,30,80,90,50,40,40,50这10个数据中,极差是()A.40 B.70 C.80 D.90评卷人得分二、填空题10.(3分)在前100个正整数中,3的倍数出现的频数是,其频率是,4的倍数出现的频率是 .11.(3分)抽取某校学生一个容量为150的样本,测得学生身高后,得到身高频数分布直方图如图,已知该校有学生1500人,则可以估计出该校身高位于160cm至165cm之间的学生大约有人.12.(3分)现抽查甲,乙丙三种不同型号的产品,出现次品的频率分别是0.1,0.3,0.2,则三种产品中合格率最高的是产品.13.(3分)已知一个40个数据的样本,把它分成六组,第一组到第四组的频数分别为10,5,7,6,第五组的频率是0.10,则第六组的频率为 .14.(3分)某村共有银行储户110户,存款在2~3万元之间的银行储户的频率是0.2,则该村存款在2~3万元的银行储户有户.15.(3分)数据1,2,3,4,10的极差为.16.(3分)某中学今年“五一”长假期问要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中,随机调查了50个家庭在新工资制度实施后的收人情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).分组频数频率1000~120030.0601200~1400120.2401400~1600180.3601600~l8000.2001800~200052000~220020.040合计50 1.000请你根据以上提供的信息,解答下列问题:(1)补全频数分布表和频数分布直方图;(2)这50个家庭收入的中位数落在第小组内;(3)请你估算该小区600个家庭中收入较低(不足l400元)的家庭个数大约有个.17.(3分)抽取某校学生一个容量为l50的样本,测得学生身高后,得到身高频数分布直方图如图,已知该校有学生l500人,则可以估计出该校身高位于160 cm至165 cm之间的学生大约有.人.18.(3分)某研究性学习小组,为了了解本校八年级学生一天中做家庭作业所用的大致时间(时间以整数记,单位:min),对本校的八年级学生做了抽样调查,并把调查得到的所有数据(时间)进行整理,分成五个时间段,绘制成统计图(如图所示).请结合统计图中提供的信息,回答下列问题:(1)这个研究性学习小组所抽取样本的容量是人.(2)在被调查的学生中,一天做家庭作业所用的大致时问超过l20 min(不包括120 min)的人数占被调查学生总人数的%.(3)这次调查得到的所有数据的中位数落在了五个时间段中 min内.19.(3分)一次体检,七(1)班24名男生有2人是1.48 m,7人身高在1.50 m到1.60 m 之间,ll人身高在1.60 m至1.70 m之问,有4人身高超过1.70 m,最高的身高已达1.79 m,则七(1)班男生身高的极差是.20.(3分)从某厂生产的各种规格的电阻中,抽取l00 只进行测量,得到一组数据,其中最大值为 11.58Ω,最小值为10.72Ω,对这组数据进行整理时,确定它的组距为0.10Ω,则应分成组.21.(3分)将l00个数据分成8个组,如下表:组号l234b678频数1114121313x1210则第6组的频数为.评卷人得分三、解答题22.(6分)为了促进长三角区域的便捷沟通,实现节时、节能,杭州湾跨海大桥于2008年5线路弯路(宁波一杭州一上海)直路(宁波跨海大桥一上海)路程316 km196 km过路费140元180元(1)若小车的平均速度为80 km/h,则小车走直路比走弯路节省多少时间?(2)若小车每公里的油耗为x(L),汽油价格为5.80元/升,问x为何值时,走哪条线路的总费用较少(总费用=过路费+油耗费)?(3)据杭州湾跨海大桥管理部门统计:从宁波经跨海大桥到上海的小车中,其中五类不同油耗的小车平均每小时通过的车辆数,得到如图所示的频数分布直方图,请你估算1天内这五类小车走直路比走弯路共节省多少升汽油?23.(6分)国家规定“中小学生每天在校体育活动的时间不低于1 h”.为此,某市就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图(部分)如图所示,其中分组情况是:A组:0.5t≥ h t<h; B组:0.51h t h≤< D组: 1.5h t h≤< C组:1 1.5请根据上述信息解答下列问题:(1)C组的人数是;(2)本次调查数据的中位数落在组内;(3)若该辖区约有24000名初中孚至确估计其中达到国家规定体育活动时间的人约有多少?24.(6分)某生产车间40名工人的日加工零件数(件)如下:30,26,42,41,36,44,40,37,43,35,37,25,45,29,43,31,36,49,34,47, 33,43,48,42,32,25,30,4奄,29,34,38,46,43,39,35,40,48,33,27,28.(1)根据以上数据分成如下5组:25~30,30~35,35~40,40~45,45~50,绘制频数分布表、频数分布直方图和折线图;(2)求工人的平均日加工零件数(取整数).25.(6分)某面粉批发商通过统计前48个星期的面粉销售量(单位:吨),对数据适当分组后,列出了如下频数分布表:(1)在图1、图2中分别画出频数分布直方图和频数折线图;(2)试说明这位面粉批发商每星期进面粉多少吨比较合适(精确到0.1吨)?26.(6分)推动信息技术的发展,举行了电脑设计作品比赛,各班派学生代表参加,现将所有比赛成绩(得分取整数,满分为100分)进行处理然后分成五组,并绘制了频数分布直方图,请结合图中提供的信息,解答下列问题:(1)参加比赛学生的总人数是多少?(2)80.5~90.5这一分数段的频数、频率是多少?(3) 根据统计图,请你也提出一个问题,并做出回答.27.(6分)今青少年视力水平的下降已引起全社会的关注,为了了解某中学毕业年级300名学生的视力情况,从中抽取了一部分学生的视力,进行数据整理后如下表: (1)在这个问题中总体是 ; (2)填写频数分布表中未完成的部分;(3)若视力为4.9,5.0,5.1均属正常,不需矫正,试估计该校毕业年级学生视力正常的人数约为多少?28.(6分)将某雷达测速区监测到的一组汽车的时速数据整理,得到其频数及频率如下表(未完 成):注:30~40为时速大于等于30 km 而小于40 km ,其他类同. (1)请你把表中的数据填写完整; (2)补全频数分布直方图;(3)如果此地汽车时速不低于60 km 即为违章,则违章车辆共有多少辆?29.(6分)为增强学生的身体素质,某校坚持长年的全员体育锻炼,并定期进行体育测试,如图是将某班学生的立定跳远成绩(精确到0.01米)进行整理后,分成五组,画出的频数分布直方图的一部分,已知从左到右四个小组的频率分别是0.05、0.15、0.30、0.35,第五小组的频数是9.(1)请将频数分布直方图补充完整;(2)该班参加这次测试的学生有多少人?(3)若成绩在2.00米以上(含2.00米)的为合格,问该班成绩的合格率是多少?(4)这次测验中你能肯定该班学生成绩的众数和中位数各落在哪一小组内吗?(只须写出能或不能,不必说明理由)30.(6分) 某中学为了培养学生的社会实践能力,今年“五一”长假期间要求学生参加一项社会调查活动.为此,小明在他所居住小区的600个家庭中,随机调查了50个家庭在新工资制度实施后的收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).请你根据以上提供的信息,解答下列问题:(1)补全频数分布表和频数分布直方图;(2)这50个家庭收入的中位数落在小组;(3)请你估算该小区600个家庭中收入较低(不足1400元)的家庭个数大约有多少?【参考答案】***试卷处理标记,请不要删除一、选择题1.C2.D3.B4.B5.C6.D7.D8.B9.C二、填空题10.33,0.33, 0.2511.30012.甲13.0.2 14.22 15.916.(1)略;(2)三;(3)180 17.30018.(1)30;(2)70%;(3)120.5~150.5 19.0.31 m 20.9 21.15 评卷人 得分三、解答题22.(1)32h (2)①当587x =时,小车走直路的总费用与走弯路的总费用相等;③当587x <时,小车走弯路的总费用较少;③当587x >时,小车走直路的总费用较少 (3) (316-196)×(100×0.06+200×0.08+500×0.10+500×0.12+100×0.18)×24=432000 L23.(1)120人 (2)C (3)14400人 24.(1)略 (2)37件 25.(1)(2)由频数折线图,得(19×6 + 20×7 + 21×9 + 22×12 + 23×8 + 24×6)÷ 48 = 1035 ÷ 48 =21.6吨 26.⑴52人;(2)80.5~90.5这一分数段的频数为10,频率是265;(3)答案不唯一,提问题举例: 90.5~100.5分数段内的学生与50.5~60.5分数段内的学生哪一个多?答:在90.5~100.5分数段内的学生多.27.⑴某中学毕业年级300名学生视力的全体情况;⑵频率分布表的第一列应填4.25~4.55;第二列从上到下依次为:18,50;第三列从上到下依次为:0.46,0.36;⑶108名. 28.(1)略;(2)略;(3)76辆29.⑴第五小组的频率为0.15,与第二小组的频率相同,因此表示第五小组频率的长方形与第二小组的相同,图略. (2)60人;(3)80%;(4)不能肯定众数和中位数落在哪一小组内.30.⑴10, 0.100;(2)第三小组 1400~1600;⑶ 180.。
青岛版2020八年级数学下册第六章平行四边形自主学习能力达标测试题(附答案详解)
青岛版2020八年级数学下册第六章平行四边形自主学习能力达标测试题(附答案详解)1.如图,将矩形纸片ABCD 折叠,使点A 与点C 重合,折痕为EF ,若AB =4,BC =2,那么线段EB 的长为( )A . 25B . 23C . 45D . 43 2.如图,有一矩形纸片ABCD ,AB=10,AD=6,将纸片折叠,使AD 边落在AB 边上,折痕为AE ,再将AED ∆以DE 为折痕向右折叠,AE 与BC 交于点F ,则CEF ∆的面积为( )A .4B .6C .8D .103.如图,菱形ABCD 中,AB ∥y 轴,且B (﹣10,1)、C (2,6),则点A 的坐标为( )A .(﹣10,12)B .(﹣10,13)C .(﹣10,14)D .(2,12)4.能判断一个四边形是平行四边形的为( )A .一组对边平行,另一组对边相等B .一组对边平行,一组对角相等C .一组对边平行,一组对角互补D .一组对边平行,两条对角线相等5.两条对角线互相垂直平分且相等的四边形是( )A .矩形B .菱形C .正方形D .都有可能6.如图,在正方形ABCD 中,△ABE 和△CDF 为直角三角形,∠AEB =∠CFD =90°,AE =CF =5,BE =DF =12,则EF 的长是( )A .72B .8C .7D .737.如图所示,在□ABCD 中,AD =5,AB =3,AE 平分∠BAD 交BC 边于点E ,则线段BE 、CE 的长分别是( )A .2和3B .3和2C .4和1D .1和48.如图,已知平行四边形ABCD 的两条对角线AC 与BD 交于平面直角坐标系的原点,点D 的坐标为(3,2),则点B 的坐标为( )A .(-2,-3)B .(-3,2)C .(3,-2)D .(-3,-2) 9.如图所示,在△ABC 中,已知点D 、E 、F 分别是BC 、AD 、CE 的中点,且ABC S V =4,则BEF S V 的值是( )A .1B .1.5C .2D .2.510.如图,菱形ABCD 的对角线相交于点O ,若AC=12,AB=7,则菱形ABCD 的面积是( )A .13B .36C .13D .6011.如图,在三角形ABC中,∠A=90°,AB=AC=2,将△ABC折叠,使点B落在边AC上点D (不与点A重合)处,折痕为PQ,当重叠部分△PQD为等腰三角形时,则AD的长为_____.12.已知菱形ABCD的两条对角线长分别为12和16,则这个菱形ABCD的面积S=.13.如图,矩形ABCD的对角线AC,BD相交于点O,若AB=3,OC=2.5,则BC长为______________.14.如图:正方形ABCD中,以AB为边,在正方形内作等边△ABE,△ABE周长为15,点P为对角线AC上一动点,则PD+PE最小值为____.15.如图,在菱形ABCD中,DE⊥AB,cos A=45,BE=2,则tan∠DBE=________.16.如图,在 ABCD中,E为BC边上一点,且AB=AE,若AE平分∠DAB,∠EAC=25°,则∠AED的度数是______度.17.如图,四边形ABCD中,AD∥BC,E是DC上一点,连接BE并延长交AD延长线于点F,请你只添加一个条件:使得四边形BDFC为平行四边形.18.如图,在平行四边形ABCD中,DB=DC,∠A=70°,CE⊥BD于E,则∠BCE=▲ °.19.如图,在平行四边形ABCD中,对角线交于点0,点E、F在直线AC上(不同于A、C),当E、F的位置满足_______的条件时,四边形DEBF是平行四边形.20.已知在□ABCD中,AB=4,BC=7,则这个平行四边形的周长为_____.21.已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,且BE=DF.求证:∠AEF=∠AFE.22.如图,在□ABCD中,∠A+∠C =160°,求∠A、∠B、∠C、∠D的度数.23.如图,在等腰三角形ABC中,AB=AC,AH⊥BC,点E是AH上一点,延长AH至点F,使FH=EH.(1)求证:四边形EBFC是菱形;(2)如果∠BAC=∠ECF,求证:AC⊥CF.24.如图,在矩形ABCD中,点E是BC边上的一个动点,沿着AE翻折矩形,使点B落在点F 处若AB =3,BC =3AB ,解答下列问题:(1)在点E 从点B 运动到点C 的过程中,求点F 运动的路径长;(2)当点E 是BC 的中点时,试判断FC 与AE 的位置关系,并说明你的理由;(3)当点F 在矩形ABCD 内部且DF =CD 时,求BE 的长.25.如图,在矩形ABCD 中,AB 2cm =,BC 4cm.=点P 从点D 出发向点A 运动,运动到点A 即停止;同时,点Q 从点B 出发向点C 运动,运动到点C 即停止,点P 、Q 的速度都是1cm/s ,连接PQ 、AQ 、CP.设点P 、Q 运动的时间为ts .()1当t 为何值时,四边形ABQP 是矩形;()2当t 为何值时,四边形AQCP 是菱形.26.如图,在□ABCD 中,对角线AC 、BD 相交于点O ,AF ⊥BD ,CE ⊥BD ,垂足分别为E 、F ;连结AE 、CF ,求证:四边形AFCE 是平行四边形.27.如图,四边形ABCD 为正方形,O 为正方形ABCD 对角线的交点,M 是CA 延长线上的一个动点(点M 与点C 、A 都不重合),过点A 、C 分别向直线BM 作垂线段,垂足分别为E ,F ,连接OE .(1)若AM AB =,求证:AME BCF ∠=∠;(2)用等式直接写出线段CF ,AE ,OE 之间的数量关系,并证明.28.如图,将矩形ABCD(纸片)折叠,使点B与AD边上的点K重合,EG为折痕;点C与AD边上的点K重合,FH为折痕.已知∠1=67.5°,∠2=75°,EF=3+1,求BC的长.参考答案1.B【解析】试题分析:连接CE ,设BE=x ,则AE=4-x ,根据折叠图形的性质可得:CE=AE=4-x ,根据Rt △BCE 的勾股定理可得:222)4(2x x -=+,解得:x=23. 考点:折叠图形的性质2.C【解析】【分析】根据折叠易得BD ,AB 长,利用相似可得BF 长,也就求得了CF 的长度,△CEF 的面积=12CF•CE . 【详解】解:由折叠的性质知,第二个图中BD=AB-AD=4,第三个图中AB=AD-BD=2,因为BC ∥DE ,所以BF :DE=AB :AD ,所以BF=2,CF=BC-BF=4,所以△CEF 的面积=12CF•CE=8; 故选:C .点睛:本题利用了:①折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等;②矩形的性质,平行线的性质,三角形的面积公式等知识点.3.C【解析】【分析】根据两点间距离公式求出BC ,再根据菱形的性质即可解决问题.【详解】∵B (﹣10,1)、C (2,6),∴BC =13.∵四边形ABCD是菱形,∴AB=BC=13,∴点A坐标为(﹣10,14).故选C.【点睛】本题考查了菱形的性质、两点间距离公式、坐标与图形性质等知识,解题的关键是灵活应用这些知识解决问题.4.B【解析】试题分析:因为平行四边形的五种判定方法分别是:(1)两组对边分别平行的四边形是平行四边形;(2)两组对边分别相等的四边形是平行四边形;(3)一组对边平行且相等的四边形是平行四边形;(4)两组对角分别相等的四边形是平行四边形;(5)对角线互相平分的四边形是平行四边形,B.一组对边平行,一组对角相等,利用平行线的性质,结合条件一组对角相等可证得:另一组对边平行或另一组对角相等,所以可证明四边形是平行四边形,故选:B.考点:平行四边形的判定.5.C【解析】【分析】根据菱形,矩形,正方形的判定进行分析即可.【详解】两条对角线互相垂直平分的四边形是菱形,两条对角线相等的四边形是矩形,所以两条对角线互相垂直平分且相等的四边形是正方形.故选:C【点睛】掌握菱形,矩形,正方形的判定.6.A【解析】【分析】由正方形的性质得出∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,由SSS证明△ABE≌△CDF,得出∠ABE=∠CDF,证出∠ABE=∠DAG=∠CDF=∠BCH,由AAS证明△ABE≌△ADG,得出AE=DG,BE=AG,同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,得出EG=GF=FH=EF=7,证出四边形EGFH是正方形,即可得出结果.【详解】如图所示:∵四边形ABCD是正方形,∴∠BAD=∠ABC=∠BCD=∠ADC=90°,AB=BC=CD=AD,∴∠BAE+∠DAG=90°,在△ABE和△CDF中,{?AB CDAE CFBE DF===,∴△ABE≌△CDF(SSS),∴∠ABE=∠CDF,∵∠AEB=∠CFD=90°,∴∠ABE+∠BAE=90°,∴∠ABE=∠DAG=∠CDF,同理:∠ABE=∠DAG=∠CDF=∠BCH,∴∠DAG+∠ADG=∠CDF+∠ADG=90°,即∠DGA=90°,同理:∠CHB=90°,在△ABE和△ADG中,{90ABE DAGAEB DGA AB DA∠=∠∠=∠=︒= ,∴△ABE ≌△ADG (AAS ),∴AE=DG ,BE=AG ,同理:AE=DG=CF=BH=5,BE=AG=DF=CH=12,∴EG=GF=FH=EF=12-5=7,∵∠GEH=180°-90°=90°,∴四边形EGFH 是正方形,∴;故选:A .【点睛】本题考查了正方形的判定与性质、全等三角形的判定与性质;熟练掌握正方形的判定与性质,证明三角形全等是解决问题的关键.7.B【解析】【分析】根据平行四边形的性质和角平分线,可推出AB=BE ,再由已知条件即可求解.【详解】∵AE 平分∠BAD∴∠BAE=∠DAE∵▱ABCD∴AD ∥BC∴∠DAE=∠AEB∴∠BAE=∠BEA∴AB=BE=3∴EC=AD-BE=2故选B .【点睛】此题主要考查了平行四边形性质及等腰三角形的性质.8.D【解析】【分析】由平行四边形的性质得出B与D关于原点O对称,即可得出点B的坐标.【详解】∵四边形ABCD是平行四边形,O为角线AC与BD的交点,∴B与D关于原点O对称,∵点D的坐标为(3,2),∴点B的坐标为(−3,−2).故答案选:D.【点睛】本题考查了平行四边形的性质,解题的关键是熟练的掌握坐标与图形的性质. 9.A【解析】∵点D是BC的中点,∴BD=CD,∴S△ABD=S△ACD=12S△ABC=12×4=2,同理,S△BDE=S△ABE=12S△ABD=12×2=1,S△CDE=S△ACE=12S△ACD=12×2=1,∴S△BCE=S△BDE+S△CDE=1+1=2,∵F是CE的中点,∴S△BEF=12S△BCE=12×2=1.10.A 【解析】由菱形的性质得出AC⊥BD,OA=OC=12AC=6,OB=OD=12BD,由勾股定理求出OB,得出BD的长,菱形ABCD的面积=12AC×BD,即可得出结果.解:∵四边形ABCD 是平行四边形,∴AC ⊥BD ,OA =OC =12AC =6,OB =OD =12BD ,∴OB =∴BD∴菱形ABCD 的面积=12AC ×BD =12×12×故选A.11.2或﹣2.【解析】分析:分①PD=DQ ;②DQ=PQ ;③PD=PQ 三种情况结合已知条件分析解答即可.详解:若△PDQ 为等腰三角形,则存在以下三种情况:(1)当PD=DQ 时,由折叠的性质可知,PD=PB ,DQ=BQ ,∴PD=PB=BQ=DQ ,∴四边形BQDP 是菱形,∴PD ∥BC ,BP ∥DQ ,∵∠A=90°,AB=AC ,∴△ABC 是等腰直角三角形,∴△APD 和△CDQ 都是等腰直角三角形,设AD=x ,则AP=x ,PD=PB=2-x ,在Rt △APD 中,由勾股定理可得:222(2)x x x +=-,解得:1222x x ==-,(不合题意,舍去),∴此时AD=2;(2)DQ=PQ 时,由折叠的性质可知:BQ=DQ=PQ,又∵在△ABC中,∠B=45°,∴∠BPQ=∠B=45°,∴∠PQB=90°,∴PQ⊥BC,∵将点B沿PQ折叠后点B落在AC上,∴点B与点C重合,∴x=AD=AC=2;(3)当PD=PQ时,由折叠的性质考点:PQ=PD=BP,∴∠BQP=∠B=45°,∴∠QPB=90°,∵将点B沿PQ折叠后点B落在AC上,∴点B与点A重合,∵B与点A重合,不符合题意,舍去;∴此种情况不成立;综上所述,AD的长为2或2.故答案为:2或2.点睛:解答本题时需注意存在三种可能情况,需根据已知条件分三种情况讨论计算,不要忽略了其中任何一种情况.12.96.【解析】【分析】根据菱形的性质,菱形的面积=对角线乘积的一半.【详解】菱形的面积是:1121696 2⨯⨯=.故答案为:96【点睛】本题考核知识点:菱形面积. 解题关键点:记住根据对角线求菱形面积的公式.13.4【解析】∵四边形ABCD是矩形,∴AC=2OC=5.由勾股定理得2222534BC AC AB=-=-=.14.5.【解析】【分析】由于点B与D关于AC对称,所以连接BD,与AC的交点即为P点.此时PD+PE=BE最小,而BE是等边△ABE的边,BE=AB,从而得出结果.【详解】解:连接BD,与AC交于点F,BE与AC交点为P,连接PD,∵点B与D关于AC对称,∴PD=PB,∴PD+PE=PB+PE=BE最小.又∵△ABE是等边三角形,周长为15,∴BE=AB=5,即PD+PE的最小值为5.故答案是:5.【点睛】题本考查轴对称--最短路线问题,难点主要是确定点P的位置.凡是涉及最短距离的问题,一般要考虑线段的性质定理,结合轴对称变换来解决,多数情况要作点关于某直线的对称点.15.3【解析】试题解析:设菱形的边长为a,在RT△ADE中,∵∠DEA=90°,AD=a,AE=a-2,∴cosA=45 AEAD=,∴245aa-=,∴a=10,∴AD=10,AE=8,,∴tan∠DBE=632DEEB==.考点:1.菱形的性质;2.三角函数的定义.16.85【解析】【分析】先证明∠B=∠EAD,然后利用SAS证明△ABC≌△EAD,得出∠AED=∠BAC.再证明△ABE 为等边三角形,可得∠BAE=60°,求出∠BAC的度数,即可得∠AED的度数.【详解】∵在平行四边形ABCD中,AD∥BC,BC=AD,∴∠EAD=∠AEB.又∵AB=AE,∴∠B=∠AEB,∴∠B=∠EAD.在△ABC和△EAD中,∵AB=AE,∠ABC=∠EAD,BC=AD,∴△ABC≌△EAD(SAS),∴∠AED=∠BAC.∵AE平分∠DAB,∴∠BAE=∠DAE,∴∠BAE=∠AEB=∠B,∴△ABE为等边三角形,∴∠BAE=60°,∴∠BAC=∠BAE+∠EAC=85°,∴∠AED=∠BAC=85°.故答案为85.【点睛】本题考查了平行四边形的性质、全等三角形的判定与性质,等边三角形的判定与性质;熟记平行四边形的性质,证明三角形全等和等边三角形是解决问题的关键.17.BD∥FC.【解析】试题解析:∵AD∥BC,当BD∥FC时,四边形BDFC为平行四边形.考点:平行四边形的判定.18.20【解析】由平行四边形ABCD中,易得∠BCD=∠A=70°,又因为DB=DC,所以∠DBC=∠DCB=70°;再根据CE⊥BD,可得∠BCE=20°.解答:解:∵四边形ABCD是平行四边形,∴∠BCD=∠A=70°,∵DB=DC,∴∠DBC=∠DBC=70°,∵CE⊥BD,∴∠CEB=90°,∴∠BCE=20°.故答案为20°.19.AE=CF(答案不唯一)【解析】试题分析:根据平行四边形的性质可得OA=OC,OB=OD,,只要满足OE=OF,根据对角线互相平分的四边形是平行四边形即可判定四边形DEBF是平行四边形,所以添加的条件只要能推出OE=OF即可.考点:平行四边形的性质及判定.20.22【解析】【分析】根据平行四边形的性质可知,平行四边形的对边相等,所以平行四边形的周长等于两邻边和的二倍,直接求解即可.【详解】解:C平行四边形=2(AB+BC)=2×(4+7)=2×11=22.故答案为22.【点睛】考查了平行四边形的性质,在应用平行四边形的性质解题时,要根据具体问题,有选择的使用,避免混淆性质,以致错用性质.21.证明见解析【解析】试题分析:在菱形中,由SAS求得△ABE≌△ADF,再由等边对等角得到∠AEF=∠AFE.试题解析:证明:∵ABCD是菱形,∴AB=AD,∠B=∠D.又∵EB=DF,∴△ABE≌△ADF,∴AE=AF,∴∠AEF=∠AFE.22.∠A=∠C=80°,∠D=∠B=100°.【解析】试题分析:由ABCD是平行四边形,得到∠A=∠C.再由∠A+∠C =160°,得到∠A,∠C的度数,再利用邻角互补求∠B,∠D的度数.试题解析:解:∵四边形ABCD是平行四边形,∴∠A=∠C,∠B=∠D.又∵∠A+∠C =160°,∴∠A=∠C=80°.在平行四边形ABCD中,∵AD∥BC,∴∠D=∠B=100°.23.(1)证明见解析;(2)证明见解析.【解析】试题分析:(1)根据题意可证得△BCE为等腰三角形,由AH⊥CB,则BH=HC,从而得出四边形EBFC是菱形;(2)由(1)得∠2=∠3,再根据∠BAC=∠ECF,得∠4=∠3,由AH⊥CB,得∠3+∠1+∠2=90°,从而得出AC⊥CF.试题解析:证明:(1)∵AB=AC,AH⊥CB,∴BH=HC.∵FH=EH,∴四边形EBFC是平行四边形.又∵AH⊥CB,∴四边形EBFC是菱形.(2)证明:如图,∵四边形EBFC是菱形.∴∠2=∠3=12∠ECF.∵AB=AC,AH⊥CB,∴∠4=12∠BAC.∵∠BAC=∠ECF∴∠4=∠3.∵AH⊥CB∴∠4+∠1+∠2=90°.∴∠3+∠1+∠2=90°.即:AC⊥CF.24.(1)2π;(2)FC与AE的位置关系为:FC∥AE;(33【解析】【分析】(1)根据翻折的性质可得AF=AB,∠BAE=∠EAF,当当点E运动到点C时利用三角函数求出∠BAF的度数,最后再根据弧长公式,求出点F的运动路径长.(2)根据题意知道BE =EF=EC,再利用三角形内角和∠BFE+∠CFE=90°,最后根据翻折的性质求出∠BHE=90°,即可证出FC与AE的位置关系.(3) 过点F作FM⊥AD于点M,延长MF交BC于点N,根据题意求出AM的值,然后利用勾股定理求出MF,根据矩形的性质得到FN, 设BE=x,则EN 33﹣x,利用勾股定理求出BE的长.【详解】解:(1)由翻折的性质得:AF =AB ,∠BAE =∠EAF ,∴点F 运动的路径是以A 为圆心,AB 为半径,∠BAF 为圆心角的弧长,如图1所示:当点E 运动到点C 时,tan ∠BAE =BC AB ∴∠BAE =60°,∠BAF =120°,∴点F 的运动路径长为:1203π 180⨯=2π; (2)FC 与AE 的位置关系为:FC ∥AE ;理由如下:连接BF 交AE 于点H ,如图2所示:由折叠性质得:BE =EF ,∵BE =CE ,∴BE =EF =EC ,∴∠FBE =∠BFE ,∠CFE =∠FCE ,∵∠FBE+∠BFE+∠CFE+∠FCE =180°,∴∠BFE+∠CFE =90°,即∠BFC =90°,由折叠的性质得:BF ⊥AE ,∴∠BHE =90°,∴FC ∥AE ;(3)过点F 作FM ⊥AD 于点M ,延长MF 交BC 于点N ,如图3所示:∵AB =3,BC ,∴BC =∵四边形ABCD 是矩形,∴AB =CD =3,DF =DC =3,∴AF =DF ,∵MF ⊥AD ,∴AM =12AD在Rt △MAF 中,MF 32, ∵∠BAD =∠B =90°,MF ⊥AD ,∴四边形ABNM是矩形,∴BN=AM=332,MN=AB=3,∴FN=MN﹣MF=3﹣32=32,设BE=x,则EN=332﹣x,由折叠的性质得:FE=BE=x,在Rt△EFN中,EF2﹣EN2=FN2,即:x2﹣(33﹣x)2=(32)2,解得:x=3,∴BE的长为3.【点睛】本题考查矩形的性质和翻折的性质综合题,学生们熟练掌握弧长公式、勾股定理,等腰三角形的性质是解题的关键.25.()1当t 2s =时,四边形ABQP 为矩形;()2 当t 1.5s =时,四边形AQCP 为菱形.【解析】【分析】()1当四边形ABQP 是矩形时,BQ AP =,据此求得t 的值;()2当四边形AQCP 是菱形时,AQ AC =,列方程求得运动的时间t ;【详解】()1由已知可得,BQ DP t ==,AP CQ 4t ==-在矩形ABCD 中,B 90∠=o ,AD//BC ,当BQ AP =时,四边形ABQP 为矩形,t 4t ∴=-,得t 2=故当t 2s =时,四边形ABQP 为矩形.()2由()1可知,四边形AQCP 为平行四边形∴当AQ CQ =时,四边形AQCP 为菱形4t =-时,四边形AQCP 为菱形,解得t 1.5=,故当t 1.5s =时,四边形AQCP 为菱形.【点睛】本题考查了菱形、矩形的判定与性质.解决此题注意结合方程的思想解题.26.见解析【解析】整体分析:用SAS 证明△AOF ≌△COE ,得到OF=OE ,由对角线互相平分的四边形是平行四边形求证. 证明:连接AE ,CF.∵四边形ABCD 是平行四边形,∴AO =OC.∵AF ⊥BD ,CE ⊥BD ,∴∠AFO =∠CEO =90°.在△AOF 与△COE 中∠AFO =∠CFO =90°,AO =OC ,∠AOF =∠COE ,∴△AOF ≌△COE(AAS),∴OF =OE ,∴四边形AECF 是平行四边形.27.(1)见解析;(2))22OE AE CF =+,证明见解析 【解析】【分析】 (1)由等边对等角得到AME ABE ∠=∠,由正方形的性质和同角的余角相等,得到FCB ABE ∠=∠,即可得到结论成立;(2)延长EO 交FC 的延长线于点N ,连接OF ,找到证明全等的条件,得到AOE CON ∆∆≌,得到12OE ON EN ==,AE CN =,从而得到OE OF =,同理可得BE CF =,然后证明OBE OCF ∆∆≌,得到BOE COF ∠=∠,然后得到OEF ∆是等腰直角三角形,即可得到答案.【详解】(1)证明:∵AM AB =,∴AME ABE ∠=∠.∵四边形ABCD 是正方形,CF EF ⊥,∴90CBA ∠=︒,90CFB ∠=︒.即90BCF FBC ∠+∠=︒,90CBF ABE ∠+∠=︒.∴FCB ABE ∠=∠,∴AME BCF ∠=∠;(2)解:()2OE AE CF=+.证明:如图,延长EO交FC的延长线于点N,连接OF,∵四边形ABCD是正方形,∴AO CO=.∵AE BM⊥,CF BM⊥,∴AE CFP.∴AEO CNO∠=∠.又∵AOE CON∠=∠,∴AOE CON∆∆≌.∴12OE ON EN==,AE CN=.在Rt EFN∆中,点O是斜边EN的中点,∴12OE OF EN==.∵四边形ABCD是正方形,∴90ABC∠=︒,AB BC=.易证ABE BCF△△≌,∴BE CF=.在OBE△和OCF∆中,∵OB OCOE OFBE CF=⎧⎪=⎨⎪=⎩,∴()SSSOBE OCF∆∆≌.∴BOE COF ∠=∠. ∵90COF FOB ∠+∠=︒,∴90BOE FOB ∠+∠=︒.∴OEF V 是等腰直角三角形.∴45OEB ∠=︒.∴()2NC CF EN +=.∴()()122222OE EN NC CF AE CF ==+=+. 【点睛】此题是四边形的综合题,主要考查了正方形的性质,全等三角形的判定和性质,直角三角形的性质性质,解(2)的关键是构造全等三角形,判断出△OEF 是等腰直角三角形,是一道中考常考题.本题难度较大,学生需要熟练掌握数形结合的思想和正确做出辅助线进行解题. 错因分析:(1)不能由AM AB =得到AME ABE ∠=∠,不能由等角代换得到AME BCF ∠=∠;(2)不能正确作出辅助线;不能熟练运用全等三角形的判定和性质;不能正确求出45FEN ∠=︒28.BC 的长为3+2+3.【解析】分析:由题意知∠3=180°﹣2∠1=45°、∠4=180°﹣2∠2=30°、BE=KE 、KF=FC ,作KM ⊥BC ,设KM=x ,知EM=x 、MF=3x ,根据EF 的长求得x=1,再进一步求解可得.详解:由题意,得:∠3=180°﹣2∠1=45°,∠4=180°﹣2∠2=30°,BE=KE 、KF=FC , 如图,过点K 作KM ⊥BC 于点M ,设KM=x ,则EM=x 、3,∴33+1,解得:x=1,∴KF=2,∴∴BC的长为点睛:本题主要考查翻折变换,解题的关键是掌握翻折变换的性质:折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.。
(完整版)2019-2020初中数学八年级下册《二次根式》专项测试(含答案)(815),推荐文档

x - 2 ⋅y - 2 x + 5 333(6 - x )2 (x - 2)(3 - x ) 3 - x 3 112 25八年级数学下册《二次根式》测试卷学校:姓名: 班级: 考号:题号 一二三总分得分一、选择题1.(2分)若 = 成立,则x 的取值范围为( )A .x ≥2B .x ≤3C .2≤x ≤3D .2<x <32.(2分)若 x - 2 y + = 0 ,则(-xy )2 的值为( ) A .64B . -64C .16D . -163.(2分)若式子 在实数范围内有意义,则x 的取值范围是( ) A .x>-5B .x<-5C .x ≠-5D .x ≥-54.(2分)下列各数中,与2 的积为有理数的是()A . 2 +B . 2 -C . -2 +D . 5.(2分)在Rt ΔABC 中,∠C =Rt ∠,BC:AC =1:2,AB =5,则斜边上的高长为( ) 153B.2 C . 1 D .2 1536.(2分)- 5<x < 5的非正整数x 是( ) A .-1B .0C .-2,-1,0D .1,-1,0x +47.(2分)式 x -2中,x 的取值范围是( ) A .x≥-4B .x >2C .x≥-4且x≠2D .x>-4且x≠28.(2分) 使 = x - 6 成立的条件是( ) A. x < 6B. x > 6C. x ≤ 6D. x ≥ 69.(2分) 计算 (-11)2 + | -11 | - ,正确的结果是( )A .-11B .11C . 22D .-2210.(2分)化简: 5的结果正确是( ) 3A. 评卷人得分2a -1 (1-a)21-aabx - 38 -xx -533 -2a-2a-3 +x1038 -xx -5A.1105B.25 C.D.11.(2分)下列二次根式中,字母a < 1 的根式是()A.B.C.D.12.(2分)若是二次根式,则应满足的条件是()A. a , b 均为非负数B.a ≥ 0 且b > 0二、填空题C.a> 0bD.a≥ 0b13.(3分)长方形的面积是24,其中一边长是2 ,则另一边长是.1 1 1 1,,……,,14.(3分)用计算器探索:已知按一定规律的一组数:1,从中选出若干个数,使它们的和大于3,那么至少要选个数.19 20,如果15.(3分)若1<x < 2 ,则化简2+ 2x - 1 = .16.(3分)自由下落物体的高度h (米)与下落的时间t (秒)的关系为h = 4.9t 2 .现有一铁球从离地面19米高的建筑物的顶部作自由下落,到达地面需要的时间是秒.(精确到0.1秒)17.(3分)若代数式1有意义,则实数x的取值范围是.18.(3分) 若=成立,则x 的取值范围是.19.(3分) 若一个正三角形的路标的面积为2 ,则它的边长为.20.(3分) 二次根式中,a 的取值范围是.21.(3分)数a在数轴上的位置如图所示:化简a2 - | 1-a | = .22.(3分)当a 满足时,有意义.23.(3分)当x 满足时,有意义.三、解答题31011-a2(x - 2)2评卷人得分评卷人得分45 8 321 3 5 5 3 1824.(6分)用电器的电阻R ,功率P 与它两端的电压U 之间有关系式 R =U 2P,有两个外观完全相同的用电器,甲的电阻为 14.4Ω,乙的电阻为 22.5Ω,现测得某用电器的功率为1000 W ,两端电压在110V 至130V 之间,请你通过计算说明该用电器是甲还是乙.25.(6分)化简:(1) ⨯ 2 3 ⨯(- 1 210) ;(2) 4 + + 4(3) ( -1)2 - (2 3)2 ;(4) (2 - 2)(3 + 2 2)26.(6分)计算(3 +150 - 4 1) ÷ .5 227.(6分)如图,已知盒子的长,宽,高分别是30m , 24 m ,18 m ,则盒内最多可放多长的棍子?28.(6分)阅读下面解题过程,并回答问题:2化简:)2 - | 1-x | .解:由隐含条件1- 3x ≥ 0 ,得 x ≤ 1,∴1- x > 03∴原式= (1- 3x )- (1- x ) = 1- 3x -1+ x = -2x2 .29.(6分)有意义,化简| x - 4 | - | 7 - x | .30.(6分)1 ≤ x ≤ 2x 的取值范围是什么?【参考答案】***试卷处理标记,请不要删除一、选择题1.C 2.A 3.D 4.D 5.B 6.C 7.B 8.D 9.B5 2 2 2 2 3 2 3 2 2 10.D 11.D 12.D评卷人得分13. 414.5 15. x +1 16.2.0 17. x > 318. 5 < x ≤ 8 19. 2 20. a ≤ 32二、填空题21.-122. a < 0 23. x ≥ 3三、解答题24.甲25.(1) -4 (2)7 + 2 (3) -8 - 2 (4)2 +26.解:原式= (9 + - 2 2) ÷ 4 =8 ÷4 =227. 30 m 28.1 29.-330.1 ≤ x ≤ 232 2 评卷人得分“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。
2019-2020年八年级下学期期末考试数学试卷含答案(人教版)

2018-2019学年度八年级下学期期末考试数学试卷第Ⅰ卷 选择题(共30分)一、选择题:本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.“垃圾分类,从我做起”,以下四幅图案分别代表四类可回收垃圾,其中是中心对称图形的是( )A .B .C .D .2.下列各式由左边到右边的变形中,属于分解因式的是( )A .()a x y ax ay -=-B .22()()a b a b a b -=+-C .243(4)3x x x x -+=-+D .211()a a a a +=+3. 下列实数中,能够满足不等式30x -<的正整数是( )A .-2B .3C .4D .24. 小颖一家自驾某地旅行,手机导航系统推荐了两条线路,线路一全程75km ,线路二全程90km ,汽车在线路二上行驶的平均车速是线路一上平均车速的1.8倍,且线路二的用时比线路一的用时少半小时,若汽车在线路一上行驶的平均速度为/xkm h ,则下面所列方程正确的是( )A .759011.82x x =+B .759011.82x x =-C .759011.82x x =+D .759011.82x x =- 5. 小贤的爸爸在钉制平行四边形框架时,采用了一种方法:如图,将两根木条AC BD 、的中点重叠,并用钉子固定,则四边形ABCD 就是平行四边形,这种方法的依据是( )A .两组对边分别平行的四边形是平行四边形B .两组对角分别相等的四边形是平行四边形C .两组对边分别相等的四边形是平行四边形D .对角线互相平分的四边形是平行四边形6. 如图,在ABC ∆中,ABC ∠和ACB ∠的平分线相交于点O ,过点O 作//EF BC 交AB 于点E ,交AC 于点F ,过点O 作OD AC ⊥于点D ,某班学生在一次数学活动课中,探索出如下结论,其中错误的是( )A .EF BE CF =+B .点O 到ABC ∆各边的距离相等C .90BOC A ∠=+∠oD .设OD m =,AE AF n +=,则12AEFS mn ∆= 7. 已知不等式组122123x a x x -≥⎧⎪+-⎨>⎪⎩的解集如图所示(原点未标出,数轴的单位长度为1),则 a 的值为( )A .4B .3C .2D .18. 已知21x y -=,2xy =,则322344x y x y xy -+的值为( )A .-2B .1C .-1D .29. 某n 边形的每个外角都等于与它相邻内角的14,则n 的值为( ) A .7 B .8 C .10 D .910. 如图,点C 是线段BE 的中点,分别以BC CE 、为边作等腰ABC ∆和等腰CDE ∆,90BAC CDE ∠=∠=o ,连接AD BD AE 、、,且BD AE 、相交于点G ,CG 交AD 于点F ,则下列说法中,不正确的是( )A .CF 是ACD ∆的中线B .四边形ABCD 是平行四边形C .AE BD = D .AG 平分CAD ∠第Ⅱ卷 非选择题(共90分)二、填空题(共5个小题,每题3分,满分15分,将答案填在答题纸上)11. 分式a a b +与22b a b-的最简公分母是 . 12. 因式分解:252x x -= .13.如图,已知一块直角三角板的直角顶点与原点O 重合,另两个顶点A ,B 的坐标分别为(1,0)-,(0,3),现将该三角板向右平移使点A 与点O 重合,得到'OCB ∆,则点B 的对应点'B 的坐标为 .14. 如图,两个完全相同的正五边形ABCDE ,AFGHM 的边DE ,MH 在同一直线上,且有一个公共顶点A ,若正五边形ABCDE 绕点A 旋转x 度与正五边形AFGHM 重合,则x 的最小值为 .15. 如图,在平行四边形ABCD 中,8AB =,12BC =,120B ∠=o ,E 是BC 的中点,点P 在平行四边形ABCD 的边上,若PBE ∆为等腰三角形,则EP 的长为 .三、解答题:本大题共8个小题,共75分.解答应写出文字说明、证明过程或演算步骤. 16.(1)解不等式:922x x +>(2)解方程:11293331x x =+--17. 如图,在ABCD 中,点E ,F 分别在边BC ,AD 上,且DF BE =.求证:四边形AECF 是平行四边形.18. 如图,在ABC ∆中,AB AC =,36A ∠=o ,DE 是AC 的垂直平分线.(1)求证:BCD ∆是等腰三角形.(2)若BCD ∆的周长是a ,BC b =,求ACD ∆的周长.(用含a ,b 的代数式表示)19. 在如图所示的网格上按要求画出图形,并回答问题.(1)将ABC ∆平移,使得点A 平移到图中点D 的位置,点B 、点C 的对应点分别为点E 、点F ,请画出DEF ∆.(2)画出ABC ∆关于点D 成中心对称的111A B C ∆.(3)DEF ∆与111A B C ∆是否关于某个点成中心对称?如果是,请在图中画出这个对称中心,并记作点O .20. 数学课后,小玲和同桌小娟各自拿出自己的漂亮的正方形手帕,她们俩各有一条方格手帕和一条绣花手帕,如图,小玲说:“我的方格手帕的边长比你的方格手帕的边长大0.6cm .”小娟说:“我的绣花手帕的边长比你的绣花手帕的边长大0.6cm .”设小玲的两块手帕的面积和为1S ,小娟的两块手帕的面积和为2S ,请同学们运用因式分解的方法算一算2S 与1S 的差.21. 如图1,将线段AB 平移至DC ,使点A 与点D 对应,点B 与点C 对应,连接AD 、BC .(1)填空:AB 与CD 的位置关系为 ,BC 与AD 的位置关系为 .(2)如图2,若G 、E 为射线DC 上的点,AGE GAE ∠=∠,AF 平分DAE ∠交直线CD 于F ,且30FAG ∠=o ,求B ∠的度数.22. 学校广播站要招聘一名播音员,擅长诵读的小龙想去应聘,但是不知道是否符合应聘条件,于是在微信上向好朋友亮亮倾诉,如图所示的是他们的部分对话内容,面对小龙的问题,亮亮也犯了难.(1)请聪明的你用所学的方程知识帮小龙计算一下,他是否符合学校广播站的应聘条件?(2)小龙和奶奶各读一篇文章,已知奶奶所读文章比小龙所读文章至少多了3200个字,但奶奶所用的时间是小龙的2倍,则小龙至少读了多少分钟?23. 定义:既相等又垂直的两条线段称为“等垂线段”,如图1,在Rt ABC ∆中,90A ∠=o ,AB AC =,点D 、E 分别在边AB 、AC 上,AD AE =,连接DE 、DC ,点M 、P 、N 分别为DE 、DC 、BC 的中点,且连接PM 、PN .观察猜想(1)线段PM 与PN “等垂线段”(填“是”或“不是”)猜想论证(2)ADE ∆绕点A 按逆时针方向旋转到图2所示的位置,连接BD ,CE ,试判断PM 与PN 是否为“等垂线段”,并说明理由.拓展延伸(3)把ADE ∆绕点A 在平面内自由旋转,若4AD =,10AB =,请直接写出PM 与PN 的积的最大值.试卷答案一、选择题1-5: CBDAD 6-10:CADCD二、填空题11. 2()()a b a b +- 12. (52)x x - 13. 14. 14415. 6、、三、解答题16.(1)解:去分母得94x x +>移项、合并得39x ->-解得3x <所以不等式的解集为3x <(2)解:去分母得1316x =-+ 解得43x =- 经检验,43x =-是分式方程的解.17.证明:∵四边形ABCD 是平行四边形∴//AF EC ,AD BC =∵DF BE =∴AD DF BC BE -=-∴AF EC =∴四边形AECF 是平行四边形18.解:(1)∵AB AC =,36A ∠=o ∴180722AB ACB -∠∠=∠==oo∵DE 是AC 的垂直平分线∴AD DC =∴36ACD A ∠=∠=o∵CDB ∠是ADC ∆的外角∴72CDB ACD A ∠=∠+∠=o∴B CDB ∠=∠∴CB CD =∴BCD ∆是等腰三角形.(2)∵AD CD CB b ===,BCD ∆的周长是a∴AB a b =-∵AB AC =∴AC a b =-∴ACD ∆的周长AC AD CD a b b b a b =++=-++=+19.解:(1)如图,DEF ∆即为所求.(2)如图,111A B C ∆即为所求.(3)是,如图,点O 即为所求.20.解:222221(29.821.2)(29.221.8)S S -=+-+ 2222(29.821.8)(29.221.2)=---(29.821.8)(29.821.8)(29.221.2)(29.221.2)=+--+-51.6850.48=⨯-⨯(51.650.4)8=-⨯9.6=(2cm )21.解:(1)//AB CD ,//AD BC(2)∵//AB CD∴BAG G ∠=∠∵G EAG ∠=∠∴EAG BAG ∠=∠∵AF 平分DAE ∠∴FAE FAD ∠=∠∴2BAD FAG ∠=∠∵30FAG ∠=o∴60BAD ∠=o∵//BC AD∴180B BAD ∠+∠=o∴120B ∠=o22.解:(1)设小龙每分钟读x 个字,则小龙奶奶每分钟读(50)x -个字 根据题意,得1050130050x x=- 解得260x =经检验,260x =是所列方程的解,并且符合实际问题的意义. ∵学校广播站招聘的条件是每分钟250-270字∴小龙符合学校广播站的应聘条件.(2)设小龙读了y 分钟,则小龙奶奶读了2y 分钟, 由题意知(26050)22603200y y -⨯-≥解得20y ≥∴小龙至少读了20分钟.23.解:(1)是(2)由旋转知BAD CAE ∠=∠∵AB AC =,AD AE =∴ABD ∆≌ACE ∆(SAS )∴ABD ACE ∠=∠,BD CE = 利用三角形的中位线得12PN BD =,12PM CE =, ∴PM PN =由中位线定理可得//PM CE ,//PN BD∴DPM DCE ∠=∠,PNC DBC ∠=∠∵DPN DCB PNC DCB DBC ∠=∠+∠=∠+∠∴MPN DPM DPN DCE DCB DBC ∠=∠+∠=∠+∠+∠ BCE DBC ACB ACE DBC =∠+∠=∠+∠+∠ACB ABD DBC ACB ABC =∠+∠+∠=∠+∠∵90BAC ∠=o∴90ACB ABC ∠+∠=o∴90MPN ∠=o∴PM 与PN 为“等垂线段”(3)PM 与PN 的积的最大值为49. 提示:12PM PN BD ==∴BD 最大时,PM 与PN 的积最大 ∴点D 在BA 的延长线上∴14BD AB AD =+=∴7PM =∴249PM PN PM •==。
中山市2019---2020学年下学期期末水平测试试卷及答案---八年级数学
中山帀2019-2020学年下学期期末水平测试试卷八年级数学(测比时Wh 90分忡•満分:120分)ilfK<fc:请悔A ■筠AFM *上•不∙IJ▲攵故■β6M7. tUH> n^AM D中∙Z4O/J-60* •L b∏.次根代∙⅛M∣β∣:次權式的址(A. JiB. √4)c. TSD. √32∙<ιb h∣IWil*th 人的日林Ftt分别丸33、30. 3U31、29(单値6这侃敬竭的众散毗< >A. 2'>B. 30C. 31D. 333∙F列IHH钱段不備构成fit角加形的她<)A・ 2. 3. 4 B. 3∙ 4. 5C・ 1. I, J 2 D・6∙ 8, 104.F列运WιL<A的址()A. >^ + √3-√5B. √2×√8≡4C. (√3)1≡6D. √iδ+2=√5一、单项选择& (n IO个小ML旬小H3分•満分30分)5. ML乙、R 个Neh lti的游客人Il(IMfi專且毎个团游專的平均年龄都是35岁.这三个Ill游卅I的的方片分别MS/ 28∙ SJF8.6∙ S R2≡1.7∙导游小李凤韓欢带游客年IHn近的团臥•若在二个团中选择个•则他虑选()⅛∏τC・丙团 D.三个团■一样卜列式子不一定王确的是()C. ZBAD=ZB(JDD. AOCoA•叩团 B.乙团6.切Nt OABcDn对角钱Ifl交「点O∙A・AC-BD B. AB^CDC∙疝D∙ 6R.二29.柿"…尹l ・E 妣仲” C栗*间S 名I 人日ΛJ ΛTfl β<ft 次为6. 9. 5. 5. 4. 的中位■若二次根式有童义・則X 的取值范国足 一_.IEOABCD 中.Z^-IO5% MZD≡ ________ ・正方形的边长为近•则这个正方形的对角&长为 _________ • 妁图・IIHybr∙3经过点4 (1∙ 2),划它与=输的交Q8的峑标为17∙如Hb αTΛf(Λ)ψ^<中∙ rttt^≡^χ・|耳他忌0初ClW0ac∙ OC 分剧交于A E' F∙已ΛO∕f -3t oc∙4∙ W∆C1L Λ 的仙|«是 __________________ .三■解£%(-> <Λj 个小■. W ΦB6分.J ■分I ■分)18. RWi G 75 Λ)÷Λ÷√3(∣-√∣2)八■■■■・■ ■;・ <**«)A ・O A ・它»R*不泾违■四象IV C・它的K*^βilA (0. |)10. F 畀•&的楚命RiAiZ 的是( A・对Il 角柏9G to*α-b,那么a 2 ^b 2B. D.D. 二填空JK (*7个小■得小*4分.Fln 備∙κ的■人««x y>0 Λfltt*ff ・ M4>⅜ιβW 止方电的四満分2«分)16.如阳・^^ABCD 中.ZC=≡<0∙ . £.存分别是*乩 应)的中九!?£/"• Ift 形磁D 的用K 为_∙e.已*ιKIX的8tMtty∙te÷2A-)(ħΛ9^tt»A. ■■的■力(-俎需;黠器常器<≈l≈≈ r94,求*欣这学制的散7总W成城・20. »1«.議个小止方形的边K沟为∣∙求叭角形.四、解答建(二)(共3个小BL甜小m分•満分24分)21.集中学为了WX対四人的阖读情况•飲"四大古負和你漩* 了几■■ 的何題对全校学切H"抽样HtMM朋険制的朋折示的■个不丸蹄鏡itffi.讹饰合用中倍JMf决卜咒何Bh22.荣通讯公<W出①<2)曲种收応方式供川户选恂则,…M><∣nfM费.M轉无JIHIW. HjMl种收"力兀皿诂时Mx <5>H)I JIlk(Tt)ZMMrfI∙IIiBW l⅜《I)分别求∣uωa>rt 种收W 力Λ∙l1∕t∣f∣*∙xzw,rj<2)何IH购种收列方式"用用鼻?W ∙ft∙M ・■ 3 Ol (IUJh(1)(2)情通过计养佔计全校学牛平均甸人畑債渎妙跡人"名儿Ml 4l ∣IO U‰√M. MB∣t(*m24・如阳・止方» ABlD中.^EJt血BC上一点∙^LAC TA F.点P是的中克・(1) 求证:BPX FP:(2) IIItDA 泉证。
鲁教版2019-2020八年级数学下册第六章特殊的平行四边形自主学习能力达标测试题C(附答案)
鲁教版2019-2020八年级数学下册第六章特殊的平行四边形自主学习能力达标测试题C (附答案)1.如图,30EOF ∠=︒,A ,B 为射线OE 上两点,点P 为射线OF 上一点,且10OP =,90APB ∠=︒,则线段AB 的最小值为( ).A .10B .52C .53D .82.如图,将矩形ABCD 沿对角线AC 剪开,再把△ACD 沿CA 方向平移得到△A 1C 1D 1,连结AD 1,BC 1.若∠ACB =30°,AB =1,CC 1=x ,△ACD 与△A 1C 1D 1重叠部分的面积为s ,则下列结论:①△A 1AD 1≌△CC 1B ②当x =1时,四边形ABC 1D 1是菱形 ③当x =2时,△BDD 1为等边三角形 ④s =32(x ﹣2)2(0<x <2),其中正确的有( )A .1 个B .2 个C .3 个D .4 个3.如图,四边形ABCD 是正方形,AB =1,点F 是对角线AC 延长线上一点,以BC 、CF 为邻边作菱形BEFC ,连接DE ,则DE 的长是( ).A .2B .21+C .3D .24.如图,矩形ABCD 中, AB=8,BC=4,P ,Q 分别是直线AB ,AD 上的两个动点,点E 在边CD 上,2DE =,将DEQ ∆沿EQ 翻折得到FEQ ∆,连接PF ,PC ,则PF PC +的最小值为( )A .622-B .8C .10D .822-5.下列命题是真命题的是( )A .对角线互相平分且相等的四边形是菱形B .对角线互相平分且垂直的四边形是矩形C .对角线互相垂直且相等的四边形是正方形D .对角线互相平分的四边形是平行四边形6.矩形、菱形、正方形都具有的性质是( )A .一组邻边相等,对角线互相垂直平分B .一组邻角相等,对角线也相等C .一组对边平行且相等,对角线互相平分D .对角线相等,且互相垂直平分 7.如图,已知某菱形花坛ABCD 的周长是24m ,120BAD ∠=o ,则花坛对角线AC 的长是( )A .63mB .6mC .33mD .3m8.如图,延长矩形ABCD 的边BC 至点E ,使CE =BD ,连结AE ,如果∠ABD =60°,那么∠BAE 的度数是( )A .40°B .55°C .75°D .80°9.如图,下列结论:①四边形ABCD 是平行四边形,且AB BC ⊥;②四边形ABCD是平行四边形,且AC BD ⊥;③四边形ABCD 是矩形,且AC BD ⊥;④四边形ABCD 是菱形,且AC BD =.其中能推出四边形ABCD 为正方形的有( )A .①②B .②③C .③④D .①②③④10.在四边形ABCD 中,两对角线交于点O ,若OA =OB =OC =OD ,则这个四边形( )A .可能不是平行四边形 B .一定是菱形C .一定是正方形D .一定是矩形11.如图,点O是菱形ABCD两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为8和10时,则阴影部分的面积为_____.12.如图,在矩形ABCD中,对角线AC、BD相交于点O,点E、F分别是AO、AD 的中点,若AB=2cm,BC=16cm,则EF=_________cm.13.如图,正方形ABCD的边长为8,点E是BC上的一点,连接AE并延长交射线DC 于点F,将△ABE沿直线AE翻折,点B落在点N处,AN的延长线交DC于点M,当AB=2CF时,则NM的长为_____.14.如图,在正方形ABCD和正方形DEFG中,点G在CD上,DE=2,将正方形DEFG 绕点D顺时针旋转60°,得到正方形DE'F'G',此时点G'在AC上,连接CE',则CE'+CG'=_____.15.如图,已知正方形ABCD,点E在边DC上,DE=4,EC=2,则AE的长为___ .16.如图,等边△BCP在正方形ABCD内,则∠APD=_____度.17.有一个角是直角的平行四边形是_______;有一组邻边相等的平行四边形是______________;四条边都相等,四个角都是直角的四边形是___________.18.如图,菱形ABCD 的一个内角是60∘,将它绕对角线的交点O 顺时针旋转90∘后得到菱形A′B′C′D′.旋转前后两菱形重叠部分多边形的周长为2431=+S S ,则菱形ABCD 的边长为_________.19.如图,一根木棍斜靠在与地面(OM )垂直的墙(ON )上,设木棍中点为P ,若木棍A 端沿墙下滑,且B 沿地面向右滑行.在此滑动过程中,点P 到点O 的距离_______(填 不变.变小 或变大 ).20.如图,矩形ABCD 中,6AB =,8BC =,E 是BC 边上一点,将ABE △沿AE 翻折,点B 恰好落在对角线AC 上的点F 处,则BE 的长为________.21.如图,正方形ABCD 的对角线AC ,BD 交于点O ,DE 平分ODA ∠交OA 于点E ,若2AB =,则线段OE 的长为________.22.长方形OABC绕顶点C(0,5)逆时针方向旋转,当旋转到CO′A′B′位置时,边O′A′交边AB于D,且A′D=2,AD=4.(1)求BC长;(2)求阴影部分的面积.23.如图,在四边形ABCD中,AC平分∠BAD,∠ABC=90°,AC=AD=2,M、N分别为AC、CD的中点,连接BM、MN、BN.(1)求证:BM=MA;(2)若∠BAD=60°,求BN的长;(3)当∠BAD=°时,BN=1.(直接填空)24.如图,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.(1)在图1中画出以线段AB为一边的矩形ABCD(不是正方形),且点C和点D均在小正方形的顶点上;(2)在图2中画出以线段AB为一腰,底边长为22的等腰三角形ABE,点E在小正方形的项点上.25.如图,在△ABC 中,AD 是高,E 、F 分别是AB 、AC 的中点。
北师大版2020八年级数学下册第三章图形的平移与旋转自主学习能力达标测试题2(附答案)
北师大版2020八年级数学下册第三章图形的平移与旋转自主学习能力达标测试题2(附答案)1.下列图形可由平移得到的是( )A .B .C .D .2.如图,在平面直角坐标系中,△ABC 和△DEF 为等边三角形,AB =DE ,点B ,C ,D 在x 轴上,点A ,E ,F 在y 轴上,下面判断正确的是( )A .△DEF 是△ABC 绕点O 顺时针旋转90°得到的B .△DEF 是△ABC 绕点O 逆时针旋转90°得到的 C .△DEF 是△ABC 绕点O 顺时针旋转60°得到的D .△DEF 是△ABC 绕点O 顺时针旋转120°得到的3.如图,P 是等边三角形ABC 内一点,且PA=4,PB=23,PC=2,以下五个结论:①∠ BPC=120°;②∠APC=120°;③143ABC S =V ;④AB=28;⑤点P 到△ABC 三边的距离分别为PE,PF,PG ,则有3PE PF PG AB ++=其中正确的有( )A .4个B .3个C .2个D .1个4.如图,在等腰直角△ABC 中,∠BAC =90°,点D 是△ABC 所在平面上一点,且满足DB =3,DA =5,则CD 的最小值为( )A.523-C.2 D.1-B.5325.下面的图形中,既是中心对称又是轴对称的图形是()A.B.C.D.6.将点P(﹣1,4)向左平移3个单位后得到点P′,则点P′的坐标为()A.(﹣1,7)B.(﹣1,1)C.(2,4)D.(﹣4,4)7.如图图形中,既是轴对称图形,又是中心对称图形的是()A.B.C.D.8.下列图形中既是轴对称又是中心对称的是()A.B.C.D.9.在线段、角、等腰三角形、平行四边形、矩形、菱形、正方形这几个图形中,既是轴称图形又是中心对称图形的个数是()A.3个B.4个C.5个D.6个10.在平面直角坐标系中,把点A(﹣10,1)向上平移4个单位,得到点A′,则A′的坐标是_____.11.如图,箭头ABCD在网格中做平行移动,当点A移到点P位置时,点C移到的位置为点_______12.如图,△ABC是等边三角形,点A(-3,0),点B(3,0),点D是y轴上的一个动点,连接BD,将线段BD绕点B逆时针旋转60°,得到线段BE,连接DE,得到△BDE,则OE的最小值为______.13.如图,在Rt△ABC中,∠BAC=90°,将△ABC绕点A顺时针旋转90°得到△AB′C′,连接CC′,若AC=4,AB=1,则△B′C′C的面积为_____.14.若△ABC与△DEF关于点O成中心对称,且A、B、C的对称点分别为D、E、F,若AB=5,AC=3,则EF的范围是______.15.在平面直角坐标系中,点A(﹣4,2)关于原点对称的点的坐标为____.16.如图,在扇形OAB中,∠AOB=90°,OA=3,将扇形OAB绕点A逆时针旋转n°(0<n<180)后得到扇形O′AB′,当点O在弧AB'上时,n为__°.17.在如图所示的方格纸(1格长为1个单位长度)中,△ABC的顶点都在格点上,将△ABC绕点O按顺时针方向旋转得到△A'B'C',使各顶点仍在格点上,则其旋转角的度数是____________..18.如下图所示的四个图形中,是中心对称图形的是__________,是轴对称图形的__________. (填序号)19.若线段AB、CD关于点P成中心对称,则线段AB、CD的关系是______.20.如图,方格纸中每个小正方形的边长都为l.,在方格纸内将经过一次平移后得到,图中标出了点B的对应点.(1)在给定的方格纸中画出平移后的;(2)画出边上的中线;(3)画出边上的高线;(4)若连接,则线段与的关系为_______.(直接写出结果)21.如图1,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C、D,连接AC,BD,CD.(1)点C的坐标是,点D的坐标是.(2)在坐标轴上是否存在一点P,S△P AC=14S四边形ABDC,若存在这样一点,请求出点P的坐标,若不存在,试说明理由.(3)如图2,在线段CO上取一点G,使OG=3CG在线段OB上取一点F,使OF=2BF,CF与BG交于点H,求四边形OGHF的面积.22.利用直尺画图()1利用图()1中的网格,过P点画直线AB的平行线和垂线.()2把图()2网格中的三条线段通过平移使三条线段AB、CD、EF首尾顺次相接组成一个三角形.()3如果每个方格的边长是单位1,那么图()2中组成的三角形的面积等于______.23.如图,将△ABC沿着从B到D的方向平移后得到△EDF,若AB=16cm,AE=12cm,CE=4cm.(1)指出△ABC平移的距离是多少?(2)求线段BD、DE、EF的长.24.已知O为直线AB上一点,∠COE为直角,OF平分∠AOE.(1)如图1,若∠COF=30°,则∠BOE=_______;若∠COF=m°,则∠BOE=_______,∠BOE 和∠COF的数量关系为___________;(2)当射线OE绕点O逆时针旋转到图2的位置时,(1)中∠BOE和∠COF的数量关系是否仍成立?请说明理由.25.如图,在边长为1个单位长度的小正方形组成的网格中,点A,B都是格点,将△ABO 向左平移6个单位长度得到△A1B1O1;将△A1B1O1绕点B1按逆时针方向旋转90°后,得到△A2B2O2,请画出△A1B1O1和△A2B2O2,并直接写出点O2的坐标.26.在长方形ABCD中,AB=a,BC=b(a<b),在图中将线段A1A2向右平移1个单位长度得到线段B 1B 2,得到封闭图形A 1A 2B 2B 1在图②中,将折线A 1A 2--A 2A 3向右平移1个单位长度到折线B 1B 2--B 2B 3得到封闭图形A 1A 2A 3B 3B 2B 1.(1)在图①中,封闭图形A 1A 2B 2B 1的面积为______(用含a 的式子表示).(2)在图②中,除去封闭图形A 1A 2A 3B 3B 2B 1后剩余图形的面积和为______(用含a 、b 的式子表示).(3)如图③,在一块长方形草地ABCD 中,有两条互相垂直且宽度相同的长方形小路.若AB=a(m),BC=b(m)(a <b),小路的宽度为1m ,用两种不同的方法表示草地的面积(用含a 、b 的式子表示);27.如图,平面直角坐标系xoy 中(4,6)A -,(1,2)B -,(4,1)C -.(1)作出ABC ∆关于直线1x =对称的图形△111A B C 并写出△111A B C 各顶点的坐标; (2)将△111A B C 向左平移2个单位,作出平移后的△222A B C ,并写出△222A B C 各顶点的坐标;(3)观察ABC ∆和△222A B C ,它们是否关于某直线对称?若是,请指出对称轴,并求ABC ∆的面积.参考答案1.A【解析】【分析】根据平移、中心对称、旋转、轴对称逐一判断可得.【详解】A.此图案可以由平移得到,符合题意;B.此图案可以由中心对称得到,不符合题意;C.此图案可以由旋转得到,不符合题意;D.此图案可以由轴对称得到,不符合题意.故选A.【点睛】本题考查了利用平移设计图案,掌握平移、中心对称、旋转、轴对称的定义是解题的关键.2.A【解析】【分析】根据△ABC和△DEF为等边三角形,AB=DE,得出△ABC≌△DEF,由点B,C,D在x 轴上,点A,E,F在y轴上得出A与D是对应点,进而得出△DEF与△ABC位置关系.【详解】解:∵△ABC和△DEF为等边三角形,AB=DE,∴△ABC≌△DEF,∵点B,C,D在x轴上,点A,E,F在y轴上得出A与D是对应点,∴△DEF是△ABC绕点O顺时针旋转90°得到的,故选:A.【点睛】此题主要考查了旋转的性质,熟练掌握旋转的性质是解题关键.旋转只改变图形的位置,不改变图形的形状和大小,即旋转前后两个图形全等,对应顶点到旋转中心的距离相等,对应点与旋转中心的夹角等于旋转角.3.B【解析】【分析】作BH⊥PC于H,根据等边三角形的性质得:BA=BC,∠ABC=60°,把△ABP绕点B顺时针旋转60°得到△CBD,证明出△PBD为等边三角形和△PCD为直角三角形即可求出①;根据平角性质,可得∠BPH=30°,证明△ABP为直角三角形,即可求出②和④;根据面积公式求出③;根据等面积法即可求出④.【详解】作BH⊥PC于H根据等边三角形的性质得:BA=BC,∠ABC=60°把△ABP绕点B顺时针旋转60°得到△CBD,连接PD得到上图根据旋转的性质可得CD=AP=4,BD=BP=3∠PBD=60°∴△PBD为等边三角形∴PD=PB=23∠BPD=60°在三角形PDC中,PC=2,PD= 23CD=4∴PC2+PD2=CD2∴△PCD为直角三角形,∠CPD=90°∴∠BPC=∠BPD+∠CPB=150°,故①错误;根据平角性质,可得∠BPH=30°在直角三角形PBH中,∵∠BPH=30°∴PB=23∴BH=132PB PH=3CH=PC+PH=2+3=5 在直角三角形BCH中22228BC BH CH =+=,则228AB =,故④正确;又∵222BP AP AB +=∴△ABP 为直角三角形,∠APB=90°∴∠APC=360°-∠APB-∠BPC=120°,故选项②正确;2ABC S BC ==V ③错误; 111111222222ABC S PE AB PF BC PG AC PE AB PF AB PG AB =++=++V g g g g g g2AB =∴2PE PF PG AB ++=,故选项⑤正确 故答案选择:B. 【点睛】本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等边三角形的性质与勾股定理的逆定理. 4.A 【解析】 【分析】将△ADC 绕点A 顺时针旋转90°,得到△ABE ,CD 转化为BE ,由于AE 、AD 、BD 都是定值,所以当E 、B 、D 三点共线时,BE 最小,即CD 最小. 【详解】将△ADC 绕点A 顺时针旋转90°,得到△ABE .则CD =BE ,△ADE 是等腰直角三角形,ED = ∵AE 、AD 、BD 都是定值,所以当E 、B 、D 三点共线时,BE 最小,即CD 最小.此时BE 最小值为DE ﹣BD =3.故选:A.【点睛】本题主要考查了旋转的性质、全等三角形的判定和性质,解题的关键是通过旋转转化线段,利用两点之间线段最短求最值.5.D【解析】【分析】根据轴对称图形与中心对称图形的概念进行判断即可.【详解】A、是轴对称图形,不是中心对称图形.故错误;B、不是轴对称图形,是中心对称图形.故错误;C、不是轴对称图形,是中心对称图形.故错误;D、既是轴对称图形,也是中心对称图形.故正确.故选D.【点睛】本题考查的是中心对称图形与轴对称图形的概念:轴对称图形的关键是寻找对称轴,图形两部分沿对称轴折叠后可重合;中心对称图形是要寻找对称中心,旋转180度后与原图重合.6.D【解析】【分析】根据横坐标,右移加,左移减;纵坐标,上移加,下移减进行计算即可.【详解】解:将点P(−1,4)向左平移3个单位后得到点P′,则点P′的坐标为(−4,4),【点睛】此题主要考查了坐标与图形的变化−−平移,关键是掌握点的坐标的变化规律.7.A【解析】【分析】判断轴对称的关键是寻找对称轴,两边图像折叠后可重合,判断中心对称的关键是要寻找对称中心,旋转180°后与原图重合.【详解】A项,既是轴对称图形,也是中心对称图形,符合题意.B项,是轴对称图形,不是中心对称图形,不符合题意.C项,不是轴对称图形,是中心对称图形,不符合题意.D项,是轴对称图形,不是中心对称图形,不符合题意.故答案选A.【点睛】本题主要是要根据轴对称图形与中心对称图形的概念进行求解.8.A【解析】【分析】根据轴对称和中心对称的定义,对选项进行判断,即可得到答案.【详解】解:A、是轴对称图形,也是中心对称图形,故此选项正确;B、是轴对称图形,不是中心对称图形,故此选项错误;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误;故选:A.【点睛】本题考查轴对称和中心对称的定义,解题的关键是熟练掌握轴对称和中心对称的定义. 9.B【解析】【分析】根据轴对称图形与中心对称图形的概念求解.既是轴对称图形又是中心对称图形的是:线段、矩形、菱形、正方形,共4个,故选B.【点睛】此题主要考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.10.(﹣10,5)【解析】【分析】利用平移中点的变化规律:横坐标右移加,左移减;纵坐标上移加,下移减求解即可.【详解】解:把点A(﹣10,1)向上平移4个单位,得到点A′,则A′的坐标是(−10,5),故答案为:(−10,5).【点睛】本题考查坐标的平移变化,解题的关键是熟练掌握平移规律.11.R【解析】【分析】根据平移的基本性质,C在A左边1个单位处,经过平移,对应点位置关系不变.【详解】当点A移到点P位置时,点C移到的位置为点R.故答案为:R.【点睛】本题考查平移的基本性质:①平移不改变图形的形状和大小;②经过平移,对应点所连的线段平行且相等,对应线段平行且相等,对应角相等.12.3 2【解析】【分析】取BC中点G,连接DG,由“SAS”可证△BGD≌△BOE,可得OE=DG,当DG⊥OC时,DG的值最小,由含30°角的直角三角形的性质即可求出DG的值,即OE最小值.【详解】如图,取BC中点G,连接DG,OE,∵△ABC是等边三角形,点A(-3,0),点B(3,0),∴AO=BO=3,∠BCO=30°,∠ABC=60°,∴BC=AB=6,∵点G是BC中点,∴CG=BG=OA=OB=3,∵将线段BD绕点B逆时针旋转60°,∴∠DBE=60°,BD=BE,∴∠ABC=∠DBE,∴∠CBD=∠ABE,且BE=BD,BG=OB=3,∴△BGD≌△BOE(SAS),∴OE=DG,∴当DG⊥OC时,DG的值最小,即OE的值最小.∵∠BCO=30°,DG⊥OC∴DG=12CG=32,∴OE的最小值为3 2 .故答案为3 2【点睛】本题考查了全等三角形的判定和性质,等边三角形的性质,旋转的性质,添加恰当的辅助线构造全等三角形是本题的关键.13.6【分析】根据旋转的性质可得AC=AC′=4,AB′=AB=1,∠CAC′=90°,然后利用S△B′C′C=S△ACC′﹣S△AB′C′进行求解.【详解】解:∵△ABC绕点A顺时针旋转90°后得到的△AB′C′,∴AC=AC′=4,AB′=AB=1,∠CAC′=90°,∴△ACC′为等腰直角三角形,∴S△B′C′C=S△ACC′﹣S△AB′C′=12×4×4﹣12×4×1=6.故答案为6.【点睛】本题主要考查了旋转的性质和三角形面积计算,熟知旋转不改变图形的大小与形状是解题关键.14.2<EF<8【解析】【分析】根据成中心对称的两个图形对应线段长相等可知EF的取值范围等于BC的取值范围;【详解】解:∵△ABC与△DEF关于点O成中心对称,且A、B、C的对称点分别为D、E、F,AB=5,AC=3,∴DE=5,DF=3∴EF的取值范围为:2<EF<8故答案为:2<EF<8【点睛】本题考查关于某点对称的图形之间的关系,解题关键是熟练掌握关于某点对称的图形性质.15.(4,﹣2).【解析】【分析】直接利用关于原点对称点的性质得出答案.解:点A(﹣4,2)关于原点对称的点的坐标是:(4,﹣2).故答案为:(4,﹣2).【点睛】此题主要考查了关于原点对称点的性质,正确记忆横纵坐标的符号是解题关键.16.60【解析】【分析】连接OO′,可知△OO′A为等边三角形,可求得n.【详解】解:连接OO′,由旋转的性质可知OA=O′A,又OO′=O′A,∴△OO′A为等边三角形,∴n=60.【点睛】本题主要考查旋转的性质,由旋转得到△OO′A为等边三角形是解题的关键17.90°【解析】【分析】根据旋转角的概念找到∠BOB′是旋转角,从图形中可求出其度数即可.【详解】根据旋转角的概念:对应点与旋转中心连线的夹角,可知∠BOB′是旋转角,且∠BOB′=90°,故答案为:90°.【点睛】本题主要考查了旋转角的概念,解题的关键是根据旋转角的概念找到旋转角.18.①②③④【解析】【分析】中心对称图形的定义:在平面内,把一个图形绕着某个点旋转180°,如果旋转后的图形能与原来的图形重合,那么这个图形叫做中心对称图形,这个点叫做它的对称中心,如果一个图形沿一条直线折叠,直线两旁的部分能够互相重合,这个图形叫做轴对称图形,这条直线叫做对称轴;然后根据中心对称图形的定义和轴对称图形的概念对各图形分析判断即可得解.【详解】是中心对称图形的是①,是轴对称图形的②③④.故答案为:①,②③④.【点睛】此题考查中心对称图形,轴对称图形,解题关键在于对图形的识别.19.平行且相等.【解析】【分析】根据线段AB、CD关于点P成中心对称,再根据中心对称的性质得出对应边之间的关系即可.【详解】解:∵线段AB、CD关于点P成中心对称,∴线段AB、CD的关系是:平行且相等.故答案为:平行且相等.【点睛】此题主要考查了中心对称的性质,正确记忆中心对称的对应边关系是解决问题的关键.20.(1)如答图中所示.见解析;(2)如答图中所示,见解析;(3)如答图中所示,见解析;(4).【解析】【分析】(1)结合的位置,绘制出的图像,即可.(2)结合中线为顶点到底中点的连线,即可.(3)过A点做BC的垂线,即可.(4)结合平行四边形的判定和性质,得出,即可.【详解】(1)如答图中所示.(2)如答图中所示(3)如答图中所示(4)【点睛】本题考查图形的平移,平行四边形的判定,高的绘制,中线的绘制,熟练掌握作图步骤是解题的关键.21.(1)(0,2),(4,2);(2)存在,点P的坐标为(﹣3,0)或(1,0)或(0,6)或(0,﹣2);(3)74.【解析】【分析】(1)根据向右平移横坐标加,向上平移纵坐标加写出点C、D的坐标即可;(2)先根据平行四边形的面积公式求出S四边形ABDC=8,然后分点P在x轴上时求出AP的长度,分两种情况写出点P的坐标;点P在y轴上时,求出CP的长,分两种情况写出点P 的坐标;(3)求出点G、F的坐标,利用待定系数法求出直线CF、BG的解析式,联立求出点H的坐标,再根据S四边形OGHF=S△OBG﹣S△HBF列式计算即可得出结果.【详解】解:(1)∵点A(﹣1,0),B(3,0)分别向上平移2个单位,再向右平移1个单位,∴点C、D的坐标分别为(0,2),(4,2),故答案为:(0,2),(4,2);(2)∵点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A、B分别向上平移2个单位,再向右平移1个单位,分别得到对应点C、D,∴四边形ABCD是平行四边形,AB=4,∵C(0,2),∴OC=2,∴S四边形ABDC=4×2=8,点P在x轴上时,∵S△PAC=14S四边形ABDC,∴12AP×2=14×8,解得AP=2,当点P在点A的左边时,﹣1﹣2=﹣3,点P的坐标为(﹣3,0),点P在点A的右边时,﹣1+2=1,点P的坐标为(1,0);点P在y轴上时,∵S△PAC=14S四边形ABDC,∴12CP×1=14×8,解得CP=4,点P在点C的上方时,2+4=6,点P的坐标为(0,6),点P在点C的下方时,2﹣4=﹣2,点P的坐标为(0,﹣2),综上所述,点P的坐标为(﹣3,0)或(1,0)或(0,6)或(0,﹣2);(3))∵OG=3CG,∴OG=313OC=34×2=32,∴点G的坐标为(0,32),∵B(3,0),∴OB=3,∵OF=2BF,∴OF=212+OB=23×3=2,∴点F的坐标为(2,0),设直线CF的解析式为:y=kx+a,则202ak a=⎧⎨=+⎩,解得:12ka=-⎧⎨=⎩,∴直线CF的解析式为:y=﹣x+2,设直线BG的解析式为:y=mx+n,则0332m nn=+⎧⎪⎨=⎪⎩,解得:1232mn⎧=-⎪⎪⎨⎪=⎪⎩,∴直线BG的解析式为:y=﹣12x+32联立21322y xy x=-+⎧⎪⎨=-+⎪⎩,解得:11 xy=⎧⎨=⎩,∴点H的坐标为(1,1),∴S四边形OGHF=S△OBG﹣S△HBF=12×3×32﹣12×(3﹣2)×1=94﹣12=74. 【点睛】本题是四边形综合题,主要考查了坐标与图形性质、平行四边形面积的计算、三角形面积的计算、平移的性质、用待定系数法求直线的解析式、分类讨论等知识;熟练掌握平移的性质,进行分类讨论是解题的关键.22.(1)见解析(2)见解析(3)3.5【解析】【分析】()1根据网格结构的特点,利用直线与网格的夹角的关系找出与AB 平行的格点以及垂直的格点作出即可;()2根据网格结构的特点,过点E 找出与AB 、CD 位置相同的线段,过点F 找出与AB 、CD 位置相同的线段,作出即可;()3根据S S =-V 正方形三个角上的三角形的面积即可得出结论.【详解】()1如图所示、()2如图所示;()111333122313222EFH S =⨯-⨯⨯-⨯⨯-⨯⨯V 39132=--- 3.5=.故答案为:3.5.【点睛】本题考查的是作图-平移变换,熟知图形平移不变性的性质是解答此题的关键.23.(1)12cm ;(2)BD =12cm ,DE =16cm ,EF =8cm .【解析】【分析】(1)找准平移前后的对应点即可确定平移的距离;(2)根据平移的性质分别求得相应的线段的长即可.【详解】(1)∵AE=12cm,∴平移的距离=AE=12cm;(2)∵三角形ABC沿着从B到D的方向平移后得到三角形EDF,∴BD=AE=12cm,DE=AB=16cm,EF=AC=AE﹣CE=16﹣4=8(cm).【点睛】本题考查了平移的性质,熟练掌握平移的性质,数形结合,准确识图是解题的关键.24.(1)60°;2m°;∠BOE=2∠COF;(2)∠BOE=2∠COF仍成立.理由见解析.【解析】【分析】(1)当∠COF= m°,根据弧余得到∠EOF=90°- m°,再由OF平分∠AOE,得到∠AOE=2∠EOF=180°-2 m°,然后根据邻补角的定义得到∠BOE=180°-(180°-2 m°)=2 m°,所以有∠BOE=2∠COF.并且当n=34°时,可求出对应的∠BOE;(2)和(1)推论得方法一样,可得到∠BOE=2∠COF.【详解】(1) ∵∠COE是直角,∠COF=30°,∴∠EOF=90°-30°=60°,由∵OF平分∠AOE.∴∠AOE=2∠EOF=120°,∴∠BOE=180°-120°=60°;当∠COF= m°,∴∠EOF=90°- m°,∴∠AOE=2∠EOF=180°-2 m°,∴∠BOE=180°-(180°-2 m°)=2 m°,所以有∠BOE=2∠COF,故答案为:60°;2m°;∠BOE=2∠COF;(2)∠BOE=2∠COF仍成立,设∠COF=n°,∵∠COE是直角,∴∠EOF=90°-n°,又∵OF平分∠AOE,∴∠AOE=2∠EOF=180°-2n°,∴∠BOE=180°-(180°-2n°)=2n°,即∠BOE=2∠COF.【点睛】本题考查了旋转的性质、角平分线的定义、互余互补的含义等知识,熟练掌握相关知识是解题的关键.25.作图见解析;(﹣3,﹣3)【解析】【分析】分别作出平移变换和旋转变换后的对应点,再顺次连接即可得.【详解】解:如图所示,△A1B1O1、△A2B2O2即为所求:其中点O2的坐标为(﹣3,﹣3).【点睛】本题主要考查作图﹣旋转变换、平移变换,解题的关键是熟练掌握旋转变换和平移变换的定义、性质.26.(1)a;(2)ab-a;(3)(a-1)(b-1),ab-a-b+1.【解析】【分析】(1)利用平行四边形的面积计算封闭图形A1A2B2B1的面积即可;(2)结合图形,根据平移的性质可知,图②中剩余图形的面积都可看作是以(b-1)为长,为a 宽的矩形的面积;(3)结合图形可知,草地的面积可看作长度减小1,宽度小1的矩形面积,也可用原长方形面积减去两条长方形小路的面积计算.【详解】解:(1)在图①中,根据平移的性质可知,封闭图形A 1A 2B 2B 1为平行四边形,∴封闭图形A 1A 2B 2B 1的面积=AB∙1=a ;(2)在图②中,根据平移的性质可知,图②中剩余图形的面积都可看作是以(b-1)为长,为a 宽的矩形的面积,∴除去封闭图形A 1A 2A 3B 3B 2B 1后剩余图形的面积和为:a(b-1)=ab-a ;(3)方法一,草地的面积=(a-1)(b-1),方法二,草地的面积=ab-a-1(b-1)=ab-a-b+1.故答案为(1)a ;(2)ab-a ;(3)(a-1)(b-1),ab-a-b+1.【点睛】本题是四边形综合题,考查了作图--应用与设计作图,平移的性质,以及数形结合思想,熟练掌握平移的性质和长方形的面积公式是解题的关键.27.(1)图形见解析,1(6,6)A ,1(3,2)B ,1(6,1)C ;(2)图形见解析,2(4,6)A ,2(1,2)B ,2(4,1)C ;(3)ABC ∆和△222A B C 关于y 轴对称,ABC ∆的面积为7.5【解析】【分析】(1)分别作出三顶点关于直线x =1的对称点,再顺次连接即可得;(2)将△A 1B 1C 1的三个顶点分别向左平移,再顺次连接即可得;(3)观察图形即可得:再利用三角形的面积公式求解可得.【详解】(1)如图所示,△A 1B 1C 1即为所求,A 1(6,6),B 1(3,2),C 1(6,1).(2)如图所示,△A2B2C2即为所求,A2(4,6),B2(1,2),C2(4,1);(3)△ABC和△A2B2C2关于y轴对称,△ABC的面积为125×3=7.5.【点睛】本题考查了作图﹣轴对称变换,掌握轴对称的性质是解答本题的关键.。
2019-2020学年八年级下学期开学分班测试及答案17
2019-2020学年八年级下学期开学分班测试数学试卷(时间:90分钟 满分100分)一.选择题(每题2分,共16分)1.如果函数y =x ﹣b (b 为常数)与函数y =﹣2x +4的图象的交点坐标是(2,0),那么关于x 、y 的二元一次方程组24x y bx y -=⎧⎨+=⎩的解是( )A. 20x y =⎧⎨=⎩B. 02x y =⎧⎨=⎩C. 20x y =-⎧⎨=⎩D. 02x y =⎧⎨=-⎩2.如图,在△ABC 中,∠ACB =90°,D 是AB 中点,连接CD .若AB =10,则CD 的长为( )A. 5B. 6C. 7D. 83.已知图中的两个三角形全等,则∠α的度数是( )A 72°B. 60°C. 58°D. 50°4.如图,数轴上点A 对应的数是0,点B 对应的数是1,BC ⊥AB ,垂足为B ,且BC=1,以A 为圆心,AC 为半径画弧,交数轴于点D ,则点D 表示的数为( )A 1.4C. 1.5D. 25.下面四个艺术字中,是轴对称图形的个数是( ) A. 1个B. 2个C. 3个D. 4个.6.在平面直角坐标系中,点M(﹣2,1)在()A. 第一象限B. 第二象限C. 第三象限D. 第四象限7.如图,直线y=﹣x+c与直线y=ax+b的交点坐标为(3,﹣1),关于x的不等式﹣x+c≥ax+b的解集为()A. x≥﹣1B. x≤﹣1C. x≥3 D. x≤38.均匀地向一个容器注水,最后将容器注满.在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是()A. B. C. D.二.填空题(每题2分,共16分)9.17、0.303003…(相邻两个3之间依次多一个0)中,无理数有_____个.10.平面直角坐标系中,将点A(1,﹣2)向上平移1个单位长度后与点B重合,则点B的坐标是().11.用四舍五入法对9.2345取近似数为_____.(精确到0.01)12.在平面直角坐标系中,点P(2,3)关于y轴对称的点的坐标是_____.13.如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是______.(填写一个即可,不得添加辅助线和字母)14.如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=_____°.15.如图,在△ABC 中,AB =AC =13,BC =10,D 为BC 上一点,若BD =5,则AD 的长为_____.16.如图,在Rt △ABC 中,∠A=90°,∠ABC 的平分线B D 交AC 于点D ,DE 是BC 的垂直平分线,点E 是垂足.若DC=2,AD=1,则BE 的长为______.17.已知y 是x 的一次函数,函数y 与自变量x 的部分对应值如表,点(x 1,y 1),(x 2,y 2)在该函数的图象上.若x 1>x 2,则y 1_____y 2.18.老师让同学们举一个y 是x 的函数的例子,同学们分别用表格、图象、函数表达式列举了如下4个x 、y 之间的关系: ②其中y 一定是x 的函数的是_____.(填写所有正确的序号)三.解答题(共9题,满分68分)19.(本题满分4分)计算:|π﹣3|+2+﹣1)0.20.(本题满分8分)求下面各式中的x : (1)x 2=4; (2)(x ﹣1)3=8.21.(本题满分6分)如图,在△ABC 与△FDE 中,点D 在AB 上,点B 在DF 上,∠C =∠E ,AC ∥FE ,AD =FB .求证:△ABC ≌△FDE .22.(本题满分8分)如图,在7×7网格中,每个小正方形的边长都为1.(1)建立适当平面直角坐标系后,若点A (3,4)、C (4,2),则点B 的坐标为 ;(2)图中格点△ABC 的面积为 ;(3)判断格点△ABC 的形状,并说明理由.23.(本题满分8分)已知一次函数24y x =-+,完成下列问题: (1)求此函数图像与x 轴、y 轴交点坐标;(2)画出此函数的图像;观察图像,当04y ≤≤时,x 的取值范围是 ;(3)平移一次函数24y x =-+的图像后经过点(-3,1),求平移后的函数表达式.24.(本题满分8分)小红驾车从甲地到乙地,她出发第xh 时距离乙地ykm ,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y 与x 之间的函数关系. (1)B 点坐标为( , );(2)求线段AB 所表示的y 与x 之间的函数表达式;(3)小红休息结束后,以60km/h 的速度行驶,则点D 表示的实际意义是 .25.(本题满分8分)如图,已知△ABC 与△ADE 为等边三角形,D 为BC 延长线上的一点.(1)求证:△ABD ≌△ACE ; (2)求证:CE 平分∠ACD .的的26.(本题满分8分)建立一次函数关系解决问题:甲、乙两校为了绿化校园,甲校计划购买A种树苗,A 种树苗每棵24元;乙校计划购买B种树苗,B种树苗每棵18元.两校共购买了35棵树苗.若购进B种树苗的数量少于A种树苗的数量,请给出一种两校总费用最少的方案,并求出该方案所需的总费用.27.(本题满分10分)如图①,四边形OACB为长方形,A(﹣6,0),B(0,4),直线l为函数y=﹣2x﹣5的图象.(1)点C的坐标为;(2)若点P在直线l上,△APB为等腰直角三角形,∠APB=90°,求点P的坐标;小明的思考过程如下:第一步:添加辅助线,如图②,过点P作MN∥x轴,与y轴交于点N,与AC的延长线交于点M;第二步:证明△MPA≌△NBP;第三步:设NB=m,列出关于m的方程,进而求得点P的坐标.请你根据小明的思考过程,写出第二步和第三步的完整解答过程;(3)若点P在直线l上,点Q在线段AC上(不与点A重合),△QPB为等腰直角三角形,直接写出点P的坐标.2019-2020学年八年级下学期开学分班测试数学试卷答案与分析一.选择题1.如果函数y =x ﹣b (b 为常数)与函数y =﹣2x +4的图象的交点坐标是(2,0),那么关于x 、y 的二元一次方程组24x y bx y -=⎧⎨+=⎩的解是( )A. 20x y =⎧⎨=⎩B. 02x y =⎧⎨=⎩C. 20x y =-⎧⎨=⎩D. 02x y =⎧⎨=-⎩2.如图,在△ABC 中,∠ACB =90°,D 是AB 中点,连接CD .若AB =10,则CD 的长为( )A. 5B. 6C. 7D. 83.已知图中的两个三角形全等,则∠α的度数是( )A 72°B. 60°C. 58°D. 50°4.如图,数轴上点A 对应的数是0,点B 对应的数是1,BC ⊥AB ,垂足为B ,且BC=1,以A 为圆心,AC 为半径画弧,交数轴于点D ,则点D 表示的数为( )A 1.4C. 1.5D. 25.下面四个艺术字中,是轴对称图形的个数是( ) A. 1个B. 2个C. 3个D. 4个6.在平面直角坐标系中,点M (﹣2,1)在( ).A. 第一象限B. 第二象限C. 第三象限D. 第四象限7.如图,直线y=﹣x+c与直线y=ax+b的交点坐标为(3,﹣1),关于x的不等式﹣x+c≥ax+b的解集为()A. x≥﹣1B. x≤﹣1C. x≥3 D. x≤38.均匀地向一个容器注水,最后将容器注满.在注水过程中,水的高度h随时间t的变化规律如图所示,这个容器的形状可能是()A. B. C. D.二.填空题9.17、0.303003…(相邻两个3之间依次多一个0)中,无理数有_____个.10.平面直角坐标系中,将点A(1,﹣2)向上平移1个单位长度后与点B重合,则点B的坐标是().11.用四舍五入法对9.2345取近似数为_____.(精确到0.01)12.在平面直角坐标系中,点P(2,3)关于y轴对称的点的坐标是_____.13.如图,已知∠ACD=∠BCE,AC=DC,如果要得到△ACB≌△DCE,那么还需要添加的条件是______.(填写一个即可,不得添加辅助线和字母)14.如图,在△ABC中,AB=AC,D为AB上一点,AD=CD,若∠ACD=40°,则∠B=_____°.15.如图,在△ABC 中,AB =AC =13,BC =10,D 为BC 上一点,若BD =5,则AD 的长为_____.16.如图,在Rt △ABC 中,∠A=90°,∠ABC 的平分线B D 交AC 于点D ,DE 是BC 的垂直平分线,点E 是垂足.若DC=2,AD=1,则BE 的长为______.17.已知y 是x 的一次函数,函数y 与自变量x 的部分对应值如表,点(x 1,y 1),(x 2,y 2)在该函数的图象上.若x 1>x 2,则y 1_____y 2.18.老师让同学们举一个y 是x 的函数的例子,同学们分别用表格、图象、函数表达式列举了如下4个x 、y 之间的关系: ②其中y一定是x的函数的是_____.(填写所有正确的序号)三.解答题19.计算:|π﹣3|+2+﹣1)0.20.求下面各式中的x:(1)x2=4;(2)(x﹣1)3=8.21.如图,在△ABC与△FDE中,点D在AB上,点B在DF上,∠C=∠E,AC∥FE,AD=FB.求证:△ABC≌△FDE.22.如图,在7×7网格中,每个小正方形的边长都为1.(1)建立适当平面直角坐标系后,若点A(3,4)、C(4,2),则点B的坐标为;(2)图中格点△ABC的面积为;(3)判断格点△ABC的形状,并说明理由.23.已知一次函数24y x=-+,完成下列问题:(1)求此函数图像与x轴、y轴交点坐标;(2)画出此函数的图像;观察图像,当04y≤≤时,x的取值范围是;的(3)平移一次函数24y x =-+的图像后经过点(-3,1),求平移后的函数表达式.24.小红驾车从甲地到乙地,她出发第xh 时距离乙地ykm ,已知小红驾车中途休息了1小时,图中的折线表示她在整个驾车过程中y 与x 之间的函数关系.(1)B 点坐标为( , );(2)求线段AB 所表示的y 与x 之间的函数表达式;(3)小红休息结束后,以60km/h 的速度行驶,则点D 表示的实际意义是 .25.如图,已知△ABC 与△ADE 为等边三角形,D 为BC 延长线上的一点.(1)求证:△ABD ≌△ACE ;(2)求证:CE 平分∠ACD .26.建立一次函数关系解决问题:甲、乙两校为了绿化校园,甲校计划购买A 种树苗,A 种树苗每棵24元;乙校计划购买B 种树苗,B 种树苗每棵18元.两校共购买了35棵树苗.若购进B 种树苗的数量少于A种树的苗的数量,请给出一种两校总费用最少的方案,并求出该方案所需的总费用.27.如图①,四边形OACB为长方形,A(﹣6,0),B(0,4),直线l为函数y=﹣2x﹣5的图象.(1)点C的坐标为;(2)若点P在直线l上,△APB为等腰直角三角形,∠APB=90°,求点P的坐标;小明的思考过程如下:第一步:添加辅助线,如图②,过点P作MN∥x轴,与y轴交于点N,与AC的延长线交于点M;第二步:证明△MPA≌△NBP;第三步:设NB=m,列出关于m的方程,进而求得点P的坐标.请你根据小明的思考过程,写出第二步和第三步的完整解答过程;(3)若点P在直线l上,点Q在线段AC上(不与点A重合),△QPB为等腰直角三角形,直接写出点P的坐标.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七一中学2019~2020学年度下学期线上教学六月自主测试八年级
数学试题
一、选择题(共10小题,每小题3分,共30分)
1.使1-a 有意义的a 的取值范围是( )
A .a >1
B .a ≥1
C .a <1
D .a ≤1
2.下列二次根式中,不是最简二次根式的是( )
A .5
B .10
C .15
D .20
3.若A (-2,a )、B (-3,b )是函数y =-x +3的图象上的两点,则a 与b 的大小关系为( )
A .a <b
B .a >b
C .a =b
D .无法判断
4.一个四边形的三个相邻内角度数依次如下,那么其中是平行四边形的是( ) A .88°、108°、88° B .88°、114°、108° C .88°、92°、92°
D .88°、92°、88° 5.下列计算错误的是( )
A .252223=+
B .228=÷
C .532=+
D .228=-
6.已知三角形三边的长分别为3、4、6,则该三角形的形状是( )
A .锐角三角形
B .直角三角形
C .钝角三角形
D .无法确定
7.如图,四个一次函数y =ax ,y =bx ,y =cx +1,y =dx -3的图象如图所示,则a 、b 、c 、d 的大小关系是( )
A .b >a >d >c
B .a >b >c >d
C .a >b >d >c
D .b >a >c >d
8.菱形的周长等于高的8倍,则次菱形的较大内角是( )
A .60°
B .90°
C .120°
D .150° 9.如图,点C 、D 分别在两条直线y =kx 和x y 27=
上,点A (0,2),B 点在x 轴正半轴上.已知四边形ABCD 是正方形,则k =( )
A .25
B .52
C .75
D .5
7 10.已知正方形ABCD 和等边△CDE 如图摆放,F 是DE 的中点,且FB 2-F A 2=16,则正方形ABCD 的边长为( )
A .24
B .34
C .4
D .32
二、填空题(本大题共6个小题,每小题3分,共18分)
11.计算:12=__________
12.一次函数y =kx +b 的图象不经过第一象限,则k 、b 的取值范围分别是_____________
13.如图,直线y =-0.5x +m 与y =x +5的交点的横坐标为-2,则关于x 的不等式-0.5x +m
>x +5>0的整数解为__________________
14.如图,在△ABC 中,D 是BC 上的点,AD =AB ,E 、F 分别是AC 、BD 的中点,AC =6,则EF =__________
15.某天早晨,小童从家跑步去体育场锻炼,同时小郑从体育场晨练结束回家,途中两人相遇.小童跑到体育场后发现要下雨,立即按原路返回,遇到小郑后两人一起回到家(小童和小郑始终在同一条笔直的公路上行走).如图是两人离家的距离y (米)与小童出发的时间x (分)之间的函数图象.当x =_______________时,小童与小郑相距600米
16.把a 、b 、c 三个数按照从小到大排列,中间的数记作MID {a ,b ,c },直线y =kx +2k (k >0)与函数y =MID {32
1+x ,2x +1,-x +2}的图象有且只有1个交点,则k 的取值范围是________ 三、解答题(共8题,共72分)
17.(本题8分)计算:(1)
32131312+- (2) 183)63482(+÷-
18.(本题8分)如图,点E 、F 是□ABCD 的对角线BD 上两点,BF =DE ,求证:四边形AECF 为平行四边形
19.(本题8分)如图,在所给的正方形网格中,每个小正方形的边长均为1个单位,每个小正方形的顶点称为格点.格点△ABD 中,A (-3,5)、B (-7,2)、D (0,2)
(1) 作出□ABCD ,并直接写出C 点坐标为_____________
(2) 作出BD 的中点M
(3) 在y 轴上作出点N (不与点D 重合),使得∠NAD =∠NBD
20.(本题8分)如图,已知直线l:y=2x+4交x轴于A,交y轴于B
(1) 直接写出直线l向右平移2个单位得到的直线l1的解析式_______________
(2) 直接写出直线l关于y=-x对称的直线l2的解析式______________
(3) 点P在直线l上,若S△OAP=2S△OBP,求P点坐标
21.(本题8分)如图,已知矩形ABCD中,AB=1,E是BC上一点,将△DCE沿DE翻折得到△DC′E
(1) 如图1,若点B恰好在DC′的延长线上,且C′B=C′D,求CE的长
(2) 如图2,若点A恰好在EC′的延长线上,且C′A=2C′E,求BE的长
22.(本题10分)我国南方某省A、B两市遭受严重洪涝灾害,临近县市C、D决定调运物资支援.已知C市有救灾物资240吨,D市有救灾物资260吨.现将这些救灾物资全部调往A、B 两市,A市需要的物资比B市需要的物资少100吨.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B 市的救灾物资为x吨
(1)A市需救灾物资___________吨,B市需救灾物资___________吨
(2) 设调运这些物资的总运费为w元,求w与x之间的函数关系式并写出自变量x的取值范围
(3) 经过抢修,从D市到B市的路况得到了改善,缩短了运输时间,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围
23.(本题10分)在四边形ABCD 中,AB ∥CD ,AB +CD =BD ,AC 与BD 交于点E
(1) 如图1,求证:判断△CDE 的形状并证明你的结论
(2) 如图2,若∠DAC =45°,且AE CE 2 ,猜想:∠BDC 和∠BDA 的数量关系并证明
(3) 如图3,若∠DAC =60°,点F 在AB 上,∠ACF =∠ADB ,AB =2,CF =6,则BD =_____
24.(本题12分)在平面直角坐标系中,已知动点P (t -6,t 2
1)在定直线l 1上运动 (1) 求直线l 1的函数解析式
(2) 如图1,l 1与x 轴交于点A ,与y 轴交于点B ,点C 与点A 关于y 轴对称,过点P 作y 轴的平行线,交x 轴于点M ,交直线BC 于点Q
① 若△PQB 的面积为3,求点M 的坐标
② 如图2,连接BM .若∠BMP =∠BAC ,求点P 的坐标
七一中学下学期线上教学六月自主测试八年级数学试题答案。
