(完整word版)离散数学习题解+代数系统
离散数学习题解答 习题-
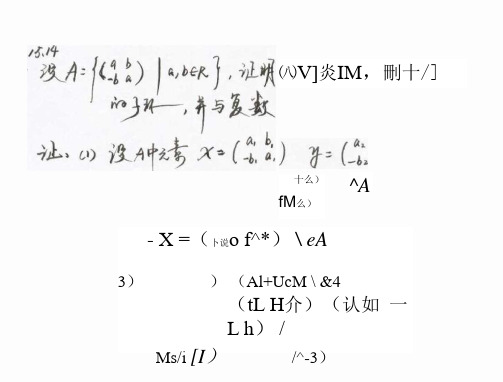
今 fft'P 乂'二b,(“勺广,反私
少: = wo 今什</吵£
人根推6》峰_,a ^JLx/
由o相吻什f(t-5V’一么H .祕毕件
- 氏 I b , l/ b^b f O ,
6 h =江扒
乡 fen 6 6^ 令 Cb)Q
4= V <6)26认) 茗t g^Jzst^ b - fv^ -^r 以rz
W JL 二 / A,n / H e£
j -铋卜< 以二⑽化
、b吾⑷ f, 故卑或喊象, 香屮,
^i>? C O)
^3 -、'。:、 C f ^'(C* - I
㈧V]炎IM,刪十/]
十么) ^A
fM么)
- X =(卜说o f^*) \ eA
3)
) (Al+UcM \ &4
(tL H介)(认如 一
L h) /
Ms/i [I)
/^-3)
? 9 (f 叫 )二广久 + L)f 认 t“八二(^.i)tt^b^i) 二 ifc< )+仍) j -曲(H-hD C ^b^tb^\\ 二(A4*-U “〉十 f A.bx + hiAa)^ -(fti+ t>i t ) “▲ + “€)-和, 艸) 屮為圬态_寺才 1斧x切厂叫卜U“年“十b“二仲 二枝呼'?uc敝碱宇.#
⑷今州pi咧~ ■/>城解峥和吨呼仗W4象均i > it ^^4. 件 中、£4; ®, 幻一* Go也多]
仆d)二竹叫-I。],卿)二於睁Z4J
A* 今
令X/十十/ 一/二Xt/十扣
:)c^D 十 xcxV/> 二
《离散数学》题库及答案解析

《离散数学》题库与答案一、选择或填空(数理逻辑部分)1、下列哪些公式为永真蕴含式?( A )(1)⌝Q=>Q→P (2)⌝Q=>P→Q (3)P=>P→Q (4)⌝P∧(P∨Q)=>⌝P答:在第三章里面有公式(1)是附加律,(4)可以由第二章的蕴含等值式求出(注意与吸收律区别)2、下列公式中哪些是永真式?( )(1)(┐P∧Q)→(Q→⌝R) (2)P→(Q→Q) (3)(P∧Q)→P (4)P→(P∨Q)答:(2),(3),(4)可用蕴含等值式证明3、设有下列公式,请问哪几个是永真蕴涵式?( )(1)P=>P∧Q (2) P∧Q=>P (3) P∧Q=>P∨Q(4)P∧(P→Q)=>Q (5) ⌝(P→Q)=>P (6) ⌝P∧(P∨Q)=>⌝P答:(2)是第三章的化简律,(3)类似附加律,(4)是假言推理,(3),(5),(6)都可以用蕴含等值式来证明出是永真蕴含式4、公式∀x((A(x)→B(y,x))∧∃z C(y,z))→D(x)中,自由变元是( ),约束变元是( )。
答:x,y, x,z(考察定义在公式∀x A和∃x A中,称x为指导变元,A为量词的辖域。
在∀x A和∃x A的辖域中,x的所有出现都称为约束出现,即称x为约束变元,A中不是约束出现的其他变项则称为自由变元。
于是A(x)、B(y,x)和∃z C(y,z)中y为自由变元,x和z为约束变元,在D(x)中x为自由变元)5、判断下列语句是不是命题。
若是,给出命题的真值。
( )(1)北京是中华人民共和国的首都。
(2) 陕西师大是一座工厂。
(3) 你喜欢唱歌吗? (4) 若7+8>18,则三角形有4条边。
(5) 前进! (6) 给我一杯水吧!答:(1) 是,T (2) 是,F (3) 不是 (4) 是,T (5) 不是 (6) 不是 (命题必须满足是陈述句,不能是疑问句或者祈使句。
全版离散数学 练习题及答案.ppt

课件
例3 对任意两个集合A, B,试证 A (A B) A B
证明 对于任意的x
x A (A B)
x {x x A x ( A B)} x {x x A (x A B)} x {x x A (x A x B)} x {x x A (x A x B)} x {x x A x B}
课件
例10 求图的最小生成树
A 1B34 Nhomakorabea5
2 E
6
1A 2
B
E
4
6
C7 D
C
D
课件
例11
• 无向树T有7片树叶, 3个3度顶点,其余的 都是4度顶点,则T有几个4度顶点?
• 解:设T有x个4度顶点 顶点度数之和: 7+3*3+4x 由树的性质可得总边数: 7+3+x-1 由握手原理可得: 7+3*3+4x=2(7+3+x-1)
求g f
g f { 1,b , 2,b , 3,b }
课件
例12 求复合函数
X {1,2,3}, Y {p, q}, Z {a,b} f { 1, p , 2, p , 3, q } g { p,b , q,b }
求g f
g f { 1,b , 2,b , 3,b }
课件
例: 求幺元、零元、逆元
x A B 因为 x 是任意的,所以有
x ((x A (A B)) (x A B)) 的真值为T,
因此 A ( A B)课件 A B
例4 判断关系的性质
R1 { a, a , a,b , b,b , c,c }
a
1 1 0
M R 1 0 1 0
0 0 1
离散数学(第五版)清华大学出版社第6章习题解答

离散数学(第五版)清华大学出版社第6章习题解答6.1 A:⑨; B:⑨; C:④; D:⑥; E:③分析对于给定的集合和运算判别它们是否构成代数系统的关键是检查集合对给定运算的封闭性,具体方法已在5.3节做过说明. 下面分别讨论对各种不同代数系纺的判别方法.1°给定集合S和二元运算°,判定<S, °>是否构成关群、独导点和群.根据定义,判别时要涉及到以下条件的验证:条件1 S关于°运算封闭:条件2 °运算满足结合集条件3 °运算有幺元,条件4 °∀x∈S,x−1∈S.其中关群判定只涉及条件1和2;独导点判定涉及条件1、2、和3;而群的判定则涉及到所有的四个条件。
2 ° 给定集合S和二元运算°和*,判定<S, °, *>是否构成环,交换环,含幺环,整环,域.根据有关定义需要检验的条件有:条件1 <S, °>S构成交换群,条件2 <S, *> 构成关群,条件3 * 对°运算的分配律,条件4 * 对运算满足交换律,条件5 * 运算有幺元,条件6 * 运算不含零因子——消去律,条件7 |S|≥2,∀x∈S,x≠0,有x−1∈S(对*运算).其中环的判定涉及条件1,2和3;交换环的判定涉及条件1,2,3和4;含幺环的判定涉及条件1,2,3和5;整环的判定涉及条件1-6;而域的判定则涉及全部7个条件. 3° 判定偏序集<S,≤>或代数系统<S,o,*>是否构成格、分本配格、有补格和布尔格. 73若<S,≤>为偏序集,首先验证∀x,y∧y和x∨y是否属于S.若满足条件则S为格,且<S,∨,∧>构成代数系统.若<S,o,*>是代数系统且°和*运算满足交换律、结合律和吸收律,则<S,o,*>构成格。
离散数学必备知识点总结(word文档物超所值)

总结离散数学知识点第2章命题逻辑1.→.前键为真.后键为假才为假;<—>.相同为真.不同为假;2.主析取范式:极小项(m)之和;主合取范式:极大项(M)之积;3.求极小项时.命题变元的肯定为1.否定为0.求极大项时相反;4.求极大极小项时.每个变元或变元的否定只能出现一次.求极小项时变元不够合取真.求极大项时变元不够析取假;5.求范式时.为保证编码不错.命题变元最好按P,Q,R的顺序依次写;6.真值表中值为1的项为极小项.值为0的项为极大项;7.n个变元共有个极小项或极大项.这为(0~-1)刚好为化简完n2n2n2后的主析取加主合取;8.永真式没有主合取范式.永假式没有主析取范式;9.推证蕴含式的方法(=>):真值表法;分析法(假定前键为真推出后键为真.假定前键为假推出后键也为假)10.命题逻辑的推理演算方法:P规则.T规则①真值表法;②直接证法;③归谬法;④附加前提法;第3章谓词逻辑1.一元谓词:谓词只有一个个体.一元谓词描述命题的性质;多元谓词:谓词有n个个体.多元谓词描述个体之间的关系;2.全称量词用蕴含→.存在量词用合取^;3.既有存在又有全称量词时.先消存在量词.再消全称量词;第4章 集合1.N.表示自然数集.1,2,3…….不包括0;2.基:集合A 中不同元素的个数.|A|;3.幂集:给定集合A.以集合A 的所有子集为元素组成的集合.P(A);4.若集合A 有n 个元素.幂集P(A)有个元素.|P(A)|==;n 2||2A n25.集合的分划:(等价关系)①每一个分划都是由集合A 的几个子集构成的集合;②这几个子集相交为空.相并为全(A);6.集合的分划与覆盖的比较:分划:每个元素均应出现且仅出现一次在子集中;覆盖:只要求每个元素都出现.没有要求只出现一次;第5章 关系1.若集合A 有m 个元素.集合B 有n 个元素.则笛卡尔A×B 的基数为mn.A 到B 上可以定义种不同的关系;mn22.若集合A 有n 个元素.则|A×A|=.A 上有个不同的关系;2n 22n3.全关系的性质:自反性.对称性.传递性;空关系的性质:反自反性.反对称性.传递性;全封闭环的性质:自反性.对称性.反对称性.传递性;4.前域(domR):所有元素x 组成的集合;后域(ranR):所有元素y 组成的集合;5.自反闭包:r(R)=RU ;x I 对称闭包:s(R)=RU ;1-R 传递闭包:t(R)=RU U U……2R 3R 6.等价关系:集合A 上的二元关系R 满足自反性.对称性和传递性.则R 称为等价关系;7.偏序关系:集合A 上的关系R 满足自反性.反对称性和传递性.则称R 是A 上的一个偏序关系;8.covA={<x,y>|x,y 属于A.y 盖住x};9.极小元:集合A 中没有比它更小的元素(若存在可能不唯一); 极大元:集合A 中没有比它更大的元素(若存在可能不唯一); 最小元:比集合A 中任何其他元素都小(若存在就一定唯一); 最大元:比集合A 中任何其他元素都大(若存在就一定唯一);10.前提:B 是A 的子集上界:A 中的某个元素比B 中任意元素都大.称这个元素是B 的上界(若存在.可能不唯一);下界:A 中的某个元素比B 中任意元素都小.称这个元素是B 的下界(若存在.可能不唯一);上确界:最小的上界(若存在就一定唯一);下确界:最大的下界(若存在就一定唯一);第6章 函数1.若|X|=m,|Y|=n,则从X 到Y 有种不同的关系.有种不同的函mn 2mn 数;2.在一个有n 个元素的集合上.可以有种不同的关系.有种不同22n n n 的函数.有n!种不同的双射;3.若|X|=m,|Y|=n.且m<=n.则从X 到Y 有种不同的单射;A m n4.单射:f:X-Y.对任意,属于X,且≠.若f()≠f();1x 2x 1x 2x 1x 2x 满射:f:X-Y.对值域中任意一个元素y 在前域中都有一个或多个元素对应;双射:f:X-Y.若f 既是单射又是满射.则f 是双射;5.复合函数:f ºg=g(f(x));6.设函数f:A-B.g:B-C.那么①如果f,g 都是单射.则f ºg 也是单射;②如果f,g 都是满射.则f ºg 也是满射;③如果f,g 都是双射.则f ºg 也是双射;④如果f ºg 是双射.则f 是单射.g 是满射;第7章 代数系统1.二元运算:集合A上的二元运算就是到A的映射;2A2. 集合A上可定义的二元运算个数就是从A×A到A上的映射的个数.即从从A×A到A上函数的个数.若|A|=2,则集合A上的二元运算的个数为==16种;2*22423. 判断二元运算的性质方法:①封闭性:运算表内只有所给元素;②交换律:主对角线两边元素对称相等;③幂等律:主对角线上每个元素与所在行列表头元素相同;④有幺元:元素所对应的行和列的元素依次与运算表的行和列相同;⑤有零元:元素所对应的行和列的元素都与该元素相同;4.同态映射:<A,*>,<B,^>,满足f(a*b)=f(a)^f(b),则f为由<A,*>到<B,^>的同态映射;若f是双射.则称为同构;第8章群1.广群的性质:封闭性;半群的性质:封闭性.结合律;含幺半群(独异点):封闭性.结合律.有幺元;群的性质:封闭性.结合律.有幺元.有逆元;2.群没有零元;3.阿贝尔群(交换群):封闭性.结合律.有幺元.有逆元.交换律;4.循环群中幺元不能是生成元;5.任何一个循环群必定是阿贝尔群;第10章格与布尔代数1.格:偏序集合A中任意两个元素都有上、下确界;2.格的基本性质:1) 自反性a≤a对偶: a≥a2) 反对称性a≤b ^ b≥a => a=b对偶:a≥b ^ b≤a => a=b3) 传递性a≤b ^ b≤c => a≤c对偶:a≥b ^ b≥c => a≥c4) 最大下界描述之一a^b≤a对偶avb≥aA^b≤b对偶avb≥b5)最大下界描述之二c≤a,c≤b => c≤a^b对偶c≥a,c≥b=> c≥avb6) 结合律a^(b^c)=(a^b)^c对偶 av(bvc)=(avb)vc7) 等幂律a^a=a 对偶 ava=a8) 吸收律a^(avb)=a 对偶 av(a^b)=a9) a≤b <=> a^b=a avb=b10) a≤c,b≤d => a^b≤c^d avb≤cvd11) 保序性b≤c => a^b≤a^c avb≤avc12)分配不等式av(b^c)≤(avb)^(avc)对偶a^(bvc)≥(a^b)v(a^c)13)模不等式a≤c<=> av(b^c)≤(avb)^c3.分配格:满足a^(bvc)=(a^b)v(a^c)和av(b^c)=(avb)^(avc);4.分配格的充要条件:该格没有任何子格与钻石格或五环格同构;5.链格一定是分配格.分配格必定是模格;6.全上界:集合A中的某个元素a大于等于该集合中的任何元素.则称a为格<A,<=>的全上界.记为1;(若存在则唯一)全下界:集合A中的某个元素b小于等于该集合中的任何元素.则称b为格<A,<=>的全下界.记为0;(若存在则唯一)7.有界格:有全上界和全下界的格称为有界格.即有0和1的格;8.补元:在有界格内.如果a^b=0,avb=1.则a和b互为补元;9.有补格:在有界格内.每个元素都至少有一个补元;10.有补分配格(布尔格):既是有补格.又是分配格;11.布尔代数:一个有补分配格称为布尔代数;第11章图论1.邻接:两点之间有边连接.则点与点邻接;2.关联:两点之间有边连接.则这两点与边关联;3.平凡图:只有一个孤立点构成的图;4.简单图:不含平行边和环的图;5.无向完全图:n个节点任意两个节点之间都有边相连的简单无向图;有向完全图:n个节点任意两个节点之间都有边相连的简单有向图;6.无向完全图有n(n-1)/2条边.有向完全图有n(n-1)条边;7.r-正则图:每个节点度数均为r的图;8.握手定理:节点度数的总和等于边的两倍;9.任何图中.度数为奇数的节点个数必定是偶数个;10.任何有向图中.所有节点入度之和等于所有节点的出度之和;11.每个节点的度数至少为2的图必定包含一条回路;12.可达:对于图中的两个节点,.若存在连接到的路.则称i v j v i v j v 与相互可达.也称与是连通的;在有向图中.若存在到的i v j v i v j v i v j v 路.则称到可达;i v j v 13.强连通:有向图章任意两节点相互可达;单向连通:图中两节点至少有一个方向可达;弱连通:无向图的连通;(弱连通必定是单向连通)14.点割集:删去图中的某些点后所得的子图不连通了.如果删去其他几个点后子图之间仍是连通的.则这些点组成的集合称为点割集; 割点:如果一个点构成点割集.即删去图中的一个点后所得子图是不连通的.则该点称为割点;15.关联矩阵:M(G).是与关联的次数.节点为行.边为列;ij m i v j e 无向图:点与边无关系关联数为0.有关系为1.有环为2; 有向图:点与边无关系关联数为0.有关系起点为1终点为-1. 关联矩阵的特点:无向图:①行:每个节点关联的边.即节点的度;②列:每条边关联的节点;有向图:③所有的入度(1)=所有的出度(0);16.邻接矩阵:A(G).是邻接到的边的数目.点为行.点为列;ij a i v j v 17.可达矩阵:P(G).至少存在一条回路的矩阵.点为行.点为列;P(G)=A(G)+(G)+(G)+(G)2A 3A 4A 可达矩阵的特点:表明图中任意两节点之间是否至少存在一条路.以及在任何节点上是否存在回路;A(G)中所有数的和:表示图中路径长度为1的通路条数; (G)中所有数的和:表示图中路径长度为2的通路条数;2A (G)中所有数的和:表示图中路径长度为3的通路条数;3A (G)中所有数的和:表示图中路径长度为4的通路条数;4A P(G)中主对角线所有数的和:表示图中的回路条数;18.布尔矩阵:B(G).到有路为1.无路则为0.点为行.点为列;i v j v 19.代价矩阵:邻接矩阵元素为1的用权值表示.为0的用无穷大表示.节点自身到自身的权值为0;20.生成树:只访问每个节点一次.经过的节点和边构成的子图;21.构造生成树的两种方法:深度优先;广度优先;深度优先:①选定起始点;0v ②选择一个与邻接且未被访问过的节点;0v 1v ③从出发按邻接方向继续访问.当遇到一个节点所1v 有邻接点均已被访问时.回到该节点的前一个点.再寻求未被访问过的邻接点.直到所有节点都被访问过一次;广度优先:①选定起始点;0v ②访问与邻接的所有节点,,……,,这些作为0v 1v 2v k v第一层节点;③在第一层节点中选定一个节点为起点;1v ④重复②③.直到所有节点都被访问过一次;22.最小生成树:具有最小权值(T)的生成树;23.构造最小生成树的三种方法:克鲁斯卡尔方法;管梅谷算法;普利姆算法;(1)克鲁斯卡尔方法①将所有权值按从小到大排列;②先画权值最小的边.然后去掉其边值;重新按小到大排序; ③再画权值最小的边.若最小的边有几条相同的.选择时要满足不能出现回路.然后去掉其边值;重新按小到大排序;④重复③.直到所有节点都被访问过一次;(2)管梅谷算法(破圈法)①在图中取一回路.去掉回路中最大权值的边得一子图;②在子图中再取一回路.去掉回路中最大权值的边再得一子图; ③重复②.直到所有节点都被访问过一次;(3)普利姆算法①在图中任取一点为起点.连接边值最小的邻接点;1v 2v ②以邻接点为起点.找到邻接的最小边值.如果最小边值比2v 2v 邻接的所有边值都小(除已连接的边值).直接连接.否则退回.连1v 1v 接现在的最小边值(除已连接的边值);1v③重复操作.直到所有节点都被访问过一次;24.关键路径例2 求PERT图中各顶点的最早完成时间, 最晚完成时间, 缓冲时间及关键路径.解:最早完成时间TE(v1)=0TE(v2)=max{0+1}=1TE(v3)=max{0+2,1+0}=2TE(v4)=max{0+3,2+2}=4TE(v5)=max{1+3,4+4}=8TE(v6)=max{2+4,8+1}=9TE(v7)=max{1+4,2+4}=6TE(v8)=max{9+1,6+6}=12最晚完成时间TL(v8)=12TL(v7)=min{12-6}=6TL(v6)=min{12-1}=11TL(v5)=min{11-1}=10TL(v4)=min{10-4}=6TL(v3)=min{6-2,11-4,6-4}=2TL(v2)=min{2-0,10-3,6-4}=2TL(v1)=min{2-1,2-2,6-3}=0缓冲时间TS(v1)=0-0=0TS(v2)=2-1=1TS(v3)=2-2=0TS(v4)=6-4=2TS(v5=10-8=2TS(v6)=11-9=2TS(v7)=6-6=0TS(v8)=12-12=0关键路径: v1-v3-v7-v825.欧拉路:经过图中每条边一次且仅一次的通路;欧拉回路:经过图中每条边一次且仅一次的回路;欧拉图:具有欧拉回路的图;单向欧拉路:经过有向图中每条边一次且仅一次的单向路;欧拉单向回路:经过有向图中每条边一次且仅一次的单向回路;26.(1)无向图中存在欧拉路的充要条件:①连通图;②有0个或2个奇数度节点;(2)无向图中存在欧拉回路的充要条件:①连通图;②所有节点度数均为偶数;(3)连通有向图含有单向欧拉路的充要条件:①除两个节点外.每个节点入度=出度;②这两个节点中.一个节点的入度比出度多1.另一个节点的入;度比出度少1;(4)连通有向图含有单向欧拉回路的充要条件:图中每个节点的出度=入度;27.哈密顿路:经过图中每个节点一次且仅一次的通路;哈密顿回路:经过图中每个节点一次且仅一次的回路;哈密顿图:具有哈密顿回路的图;28.判定哈密顿图(没有充要条件)必要条件:任意去掉图中n个节点及关联的边后.得到的分图数目小于等于n;充分条件:图中每一对节点的度数之和都大于等于图中的总节点数;29.哈密顿图的应用:安排圆桌会议;方法:将每一个人看做一个节点.将每个人与和他能交流的人连接.找到一条经过每个节点一次且仅一次的回路(哈密顿图).即可;30.平面图:将图形的交叉边进行改造后.不会出现边的交叉.则是平面图;31.面次:面的边界回路长度称为该面的次;32.一个有限平面图.面的次数之和等于其边数的两倍;33.欧拉定理:假设一个连通平面图有v个节点.e条边.r个面.则 v-e+r=2;34.判断是平面图的必要条件:(若不满足.就一定不是平面图)设图G是v个节点.e条边的简单连通平面图.若v>=3.则e<=3v-6;35.同胚:对于两个图G1,G2.如果它们是同构的.或者通过反复插入和除去2度节点可以变成同构的图.则称G1.G2是同胚的;36.判断G是平面图的充要条件:图G不含同胚于K3.3或K5的子图;37.二部图:①无向图的节点集合可以划分为两个子集V1.V2;②图中每条边的一个端点在V1.另一个则在V2中;完全二部图:二部图中V1的每个节点都与V2的每个节点邻接;判定无向图G为二部图的充要条件:图中每条回路经过边的条数均为偶数;38.树:具有n个顶点n-1条边的无回路连通无向图;39.节点的层数:从树根到该节点经过的边的条数;40.树高:层数最大的顶点的层数;41.二叉树:①二叉树额基本结构状态有5种;②二叉树内节点的度数只考虑出度.不考虑入度;③二叉树内树叶的节点度数为0.而树内树叶节点度数为1; ④二叉树内节点的度数=边的总数(只算出度);握手定理“节点数=边的两倍”是在同时计算入度和出度的时成立;⑤二叉树内节点的总数=边的总数+1;⑥位于二叉树第k 层上的节点.最多有个(k>=1);12 k ⑦深度为k 的二叉树的节点总数最多为-1个.最少k 个(k>=1);k 2 ⑧如果有个叶子.个2度节点.则=+1;0n 2n 0n 2n 42.二叉树的节点遍历方法:先根顺序(DLR );中根顺序(LDR );后根顺序(LRD );43.哈夫曼树:用哈夫曼算法构造的最优二叉树;44.最优二叉树的构造方法:①将给定的权值按从小到大排序;②取两个最小值分支点的左右子树(左小右大).去掉已选的这两个权值.并将这两个最小值加起来作为下一轮排序的权值; ③重复②.直达所有权值构造完毕;45.哈夫曼编码:在最优二叉树上.按照左0右1的规则.用0和1代替所有边的权值;每个节点的编码:从根到该节点经过的0和1组成的一排编码;。
《离散数学》word版

第七章图在自然界和人类社会的实际生活中,用图形来描述和表示某些事物之间的关系既方便又直观。
例如用工艺流程图来描述某项工程中各工序之间的先后关系,用网络图来描述某通讯系统中各通讯站之间信息传递关系,用开关电路图来描述IC中各元件电路导线连接关系等等。
图论起源于18世纪,它是研究由线连成的点集的理论。
一个图中的结点表示对象,两点之间的连线表示两对象之间具有某种特定关系(先后关系、胜负关系、传递关系和连接关系等)。
事实上,任何一个包含了某种二元关系的系统都可以用图形来模拟。
由于我们感兴趣的是两对象之间是否有某种特定关系,所以图形中两点之间连接与否最重要,而连接线的曲直长短则无关紧要。
由此经数学抽象产生了图的概念。
研究图的基本概念和性质、图的理论及其应用构成了图论的主要内容。
7.1 图的基本概念7.1.1图的定义7.1.1.1无向图定义7.1.1 设A,B是任意集合。
集合{(a,b)|aA且bB}称为A和B的无序积,记为A&B。
在无序积中,两个元素间的顺序是无关紧要的,即(a,b)=(b,a)。
定义7.1.2 无向图G是一个二元组<V,E>,记作G=<V,E>,其中V是一个非空有限集合,其元素称为结点(顶点)。
E是一个V&V的多重子集,其元素称为边(无向边)。
我们可用平面上的点来表示顶点,两点间的连线表示边,从而将任一个无向图用图形表示出来。
[例7.1.1]无向图G=<V,E>,其中V={a,b,c,d,e,f},E={(a,b),(a,c),(a,d),(b,b),(b,c),(b,c),(b,d),(c,d)}。
7.1.1.2有向图定义7.1.3 有向图G是一个二元组<V,E>,记作G=<V,E>,其中V是一个非空有限集合,其元素称为顶点,E是一个V V的多重子集,其元素称为有向边或弧,简称为边。
注:1)在有向图G=<V,E>中,若e=〈u,v〉,则称u和v为e的起点和终点;2)自回路既可看成是有向边又可看成是无向边;3)去掉有向图中边的方向得到的图称为该有向图的基图。
离散数学第三版-屈婉玲-课后习题答案
离散数学习题答案习题一及答案:(P14-15)14、将下列命题符号化:(5)李辛与李末是兄弟解:设p:李辛与李末是兄弟,则命题符号化的结果是p(6)王强与刘威都学过法语p q解:设p:王强学过法语;q:刘威学过法语;则命题符号化的结果是(9)只有天下大雨,他才乘班车上班q p解:设p:天下大雨;q:他乘班车上班;则命题符号化的结果是(11)下雪路滑,他迟到了解:设p:下雪;q:路滑;r:他迟到了;则命题符号化的结果是(p q)r15、设p:2+3=5.q:大熊猫产在中国.r:太阳从西方升起.求下列复合命题的真值:(p q r)((p q)r)(4)解:p=1,q=1,r=0,(p q r)(110)1,((p q)r)((11)0)(00)1 (p q r)((p q)r)111 19、用真值表判断下列公式的类型:(p p)q(2)解:列出公式的真值表,如下所示:p p qq(p p)(p p)q0 0 1 1 1 10 1 1 0 1 01 0 0 1 0 11 1 0 0 0 1由真值表可以看出公式有3个成真赋值,故公式是非重言式的可满足式。
20、求下列公式的成真赋值:(4)(p q)q解:因为该公式是一个蕴含式,所以首先分析它的成假赋值,成假赋值的条件是:p0(p q) 1q0q0成真赋值有:01,10,11。
所以公式的习题二及答案:(P38)5、求下列公式的主析取范式,并求成真赋值:(2)(p q)(q r)解:原式(p q)q r(p p)q rq r,此即公式的主析取范式,m m(p q r)(p q r)37所以成真赋值为011,111。
*6、求下列公式的主合取范式,并求成假赋值:(2)(p q)(p r)解:原式,此即公式的主合取范式,M(p p r)(p q r)(p q r)4所以成假赋值为100。
7、求下列公式的主析取范式,再用主析取范式求主合取范式:(1)(p q)r解:原式p q(r r)((p p)(q q)r)(p q r)(p q)r(p q)r(p q)r(p q)r(pq r(p q r)(p q)r(p q)r(p q)r(pq r,此即主析取范式。
离散数学讲解第五章
2018/12/20
20
例5 *
e a b c
设G= {a,b,c,e}, * 是G上的二元运算, e
e a b c
a
a e c b
b
b c e a
c
c b a e
a*=b*a=c,
b*c=c*b=a, a*c=c*a=b <G;*>是一阿贝尔群,但它不
是循环群,一般称这个群为
2018/12/20 2
例3 设S={|是集合A上的关系},对于关系的复合运 算可构成代数系统 <S; >,<S;>是半群。
若F={f |f :AA},则对于函数的复合运算,代
数系统<F;>也是半群。 对任意 a∈S ,定义 an+1=an*a a1=a (n=1,2,……) (* )
例7 对于半群 <S;*>的任一元素a S ,令集合 T={a,a2,a3,…}
<T;*>是<S;*>的子半群。
2018/12/20 6
定义5-6 设<S;*>是一独异点,若<T;* >是<S;*>的子代
数,且单位元 e T,则称<T;*>是<S;*>的子独 异点。 例8 对于独异点<Z;+ > , 子集N2, N3, N4, … ,它们均不 能构成<Z;+>的子独异点, 令Z2={2n|nZ}, Z3={3n|nZ}, Z4={4n|nZ} 则<Z2 ;+ >, <Z3 ;+ >, <Z4 ;+ >都是 <Z ;+>的子独异点。
离散数学代数系统中的群与域知识梳理
离散数学代数系统中的群与域知识梳理离散数学是研究不连续量的数学分支,而代数系统是离散数学的基础概念之一。
在代数系统中,群与域是两个重要的概念。
本文将对离散数学代数系统中的群与域的相关知识进行梳理。
一、群的定义及性质群是代数系统中一种基本的代数结构,它是一个集合与一个二元运算的组合,满足四个条件:封闭性、结合律、单位元和逆元。
1.1 封闭性在群中的任意两个元素进行运算后,结果仍然属于这个群。
即对于群 G 中任意的 a、b,有 a * b ∈ G。
1.2 结合律在群中进行运算的结果不受运算元素的顺序影响。
即对于群 G 中任意的 a、b、c,有 (a * b) * c = a * (b * c)。
1.3 单位元群中存在一个特殊元素,称为单位元,它与群中的任意元素进行运算后得到这个元素本身。
即对于群 G 中任意的 a,有 a * e = e * a = a,其中 e 是群 G 的单位元。
1.4 逆元对于群 G 中的每个元素 a,群中存在一个元素 b,使得 a * b = b * a = e,其中 e 是群 G 的单位元,并且称元素 b 是元素 a 的逆元,记作 b = a^(-1)。
二、群的例子2.1 整数环(Z,+)整数环是一个群,其中的运算为加法。
整数环满足群的四个条件:封闭性、结合律、单位元和逆元。
例如,对于整数环中的任意两个整数 a、b,其和仍然为整数,满足封闭性;整数的加法满足结合律;0 是整数环的单位元,对于任意整数 a,有 a + 0 = 0 + a = a;对于任意整数 a,存在一个整数 -a,使得 a + (-a) = (-a) + a = 0。
2.2 二进制群(Zn,⊕)二进制群是一个有限集合,其中的运算为模 n 的加法(⊕)。
二进制群也满足群的四个条件:封闭性、结合律、单位元和逆元。
例如,对于二进制群中的任意两个元素 a、b,其模 n 的和仍然在这个群中,满足封闭性;模 n 的加法满足结合律;0 是二进制群的单位元,对于任意元素 a,有 a ⊕ 0 = 0 ⊕ a = a;对于任意元素 a,存在一个元素 b,使得 a ⊕ b = b ⊕ a = 0。
(完整word版)离散数学第二版 屈婉玲 1-5章(答案)
《离散数学1-5章》练习题答案第2,3章(数理逻辑)1.答:(2),(3),(4)2.答:(2),(3),(4),(5),(6)3.答:(1)是,T (2)是,F (3)不是(4)是,T (5)不是(6)不是4.答:(4)5.答:⌝P ,Q→P6.答:P(x)∨∃yR(y)7.答:⌝∀x(R(x)→Q(x))8、c、P→(P∧(Q→P))解:P→(P∧(Q→P))⇔⌝P∨(P∧(⌝Q∨P))⇔⌝P∨P⇔ 1 (主合取范式)⇔ m0∨ m1∨m2∨ m3 (主析取范式)d、P∨(⌝P→(Q∨(⌝Q→R)))解:P∨(⌝P→(Q∨(⌝Q→R)))⇔ P∨(P∨(Q∨(Q∨R)))⇔ P∨Q∨R⇔ M0 (主合取范式)⇔ m1∨ m2∨m3∨ m4∨ m5∨m6 ∨m7 (主析取范式) 9、b、P→(Q→R),R→(Q→S) => P→(Q→S)证明:(1) P 附加前提(2) Q 附加前提(3) P→(Q→R) 前提(4) Q→R (1),(3)假言推理(5) R (2),(4)假言推理(6) R→(Q→S) 前提(7) Q→S (5),(6)假言推理(8) S (2),(7)假言推理d、P→⌝Q,Q∨⌝R,R∧⌝S⇒⌝P证明、(1) P 附加前提(2) P→⌝Q 前提(3)⌝Q (1),(2)假言推理(4) Q∨⌝R 前提(5) ⌝R (3),(4)析取三段论(6 ) R∧⌝S 前提(7) R (6)化简(8) R∧⌝R 矛盾(5),(7)合取所以该推理正确10.写出∀x(F(x)→G(x))→(∃xF(x) →∃xG(x))的前束范式。
解:原式⇔∀x(⌝F(x)∨G(x))→(⌝(∃x)F(x) ∨ (∃x)G(x))⇔⌝(∀x)(⌝F(x)∨G(x)) ∨(⌝(∃x)F(x) ∨ (∃x)G(x))⇔ (∃x)((F(x)∧⌝ G(x)) ∨G(x)) ∨ (∀x) ⌝F(x)⇔ (∃x)((F(x) ∨G(x)) ∨ (∀x) ⌝F(x)⇔ (∃x)((F(x) ∨G(x)) ∨ (∀y) ⌝F(y)⇔ (∃x) (∀y) (F(x) ∨G(x) ∨⌝F(y))(集合论部分)1、答:(4)2.答:323.答:(3)4. 答:(4)5.答:(2),(4)6、设A,B,C是三个集合,证明:a、A⋂ (B-C)=(A⋂B)-(A⋂C)证明:(A⋂B)-(A⋂C)= (A⋂B)⋂~(A⋂C)=(A⋂B) ⋂(~A⋃~C)=(A⋂B⋂~A)⋃(A⋂B⋂~C)= A⋂B⋂~C=A⋂(B⋂~C)=A⋂(B-C)b、(A-B)⋃(A-C)=A-(B⋂C)证明:(A-B)⋃(A-C)=(A⋂~B)⋃(A⋂⋂~C) =A⋂ (~B ⋃~C)=A⋂~(B⋂C)= A-(B⋂C)(二元关系部分)1、答:(1)R={<1,1>,<4,2>} (2) R1-={<1,1>,<2,4>}2.答:RοR ={〈1,1〉,〈1,3〉,〈2,2〉,〈2,4〉}R-1 ={〈2,1〉,〈1,2〉,〈3,2〉,〈4,3〉}3.答:R={<1,1>,<2,2>,<3,3>,<4,4>,<5,5>,<6,6>,<1,2>,<1,3>,<1,4>,<1,5>,<1,6>,<2,4>,<2,6>,<3,6>}4.答:R 的关系矩阵=⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡000000001000000001 R 1-的关系矩阵=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡0000000100000000015、解:(1)R={<2,1>,<3,1>,<2,3>};M R =⎪⎪⎪⎭⎫ ⎝⎛001101000;它是反自反的、反对称的、传递的;(2)R={<1,2>,<2,1>,<1,3>,<3,1>,<2,3>,<3,2>};M R =⎪⎪⎪⎭⎫⎝⎛011101110;它是反自反的、对称的;(3)R={<1,2>,<2,1>,<1,3>,<3,3>};M R =⎪⎪⎪⎭⎫⎝⎛100001110;它既不是自反的、也不是反自反的、也不是对称的、也不是反对称的、也不是传递的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(完整word版)离散数学习题解+代数系统 1 离散数学习题解
代数系统 习题四 第四章代数系统
1.设I为整数集合。判断下面的二元关系是否是I上的二元运算 a)+={(x,y),z|x,y,zI且z=x+y} b)-={((x,y),z)|x,y,zI且z=x-y} c)×={((x,y),z)|x,y,zI且z=x×y} d)/={((x,y),z)|x,y,zI且z=x/y} e)R={((x,y),z)|x,y,zI且z=xy}
f)={((x,y),z)|x,y,zI且z=yx } g)min = {((x,y),z)|x,y,zI且z=max(x,y)} h)min = {((x,y),z)|x,y,zI且z=min(x,y)} i)GCD = {((x,y),z)|x,y,zI且z= GCD(x,y)} j)LCM={((x,y),z)|x,y,z∈I且z= LCM(x,y)} [解] a)是。由于两个整数之和仍为整数,且结果唯一,故知+:I2→I是I上的一个二元运算. b)是。由于两个整数之差仍为整数,且结果唯一,故知一:I2→I是I上的一个二元运算。 c)是.由于两个整数这积仍为整数,且结果唯一,故知x:I2→I是I上的一个二元运算。 d)不是:例如若x=5,y=6,则z=x/y=5/6I;当y=0时z=x|y=x/0无定义.
e)不是。例如若x=2,y= —2,则z=xy=2 –2=221=I41;若x=y=0,则z=xy=0,则z=I2x; g)是。由于两个整数中最大者仍为整数,且结果唯一。故知max:I2→I是I上的一个二元运算。 h)是。由于两个整数中最小者仍为整数,且结果唯一。故知min:I2→I是I上的一个二元运算。 i)是。由于两个整数的最大公约数仍为整数,且结果唯一。故知GCD:I2→I是I上的一个二元运算。 j)是.由于两个整数的最小公倍数仍为整数,且结果唯一.故知LCD:I2→I是I上的一个二元运算。 注:两个整数a和b的最大公约数GCD(a,b)定义为同时除尽a和b的正整数中最大的一个;两个数a数b的最小公倍数LCM(a,b)定义为同时是a和b的正倍数中最小的一个. 2.设X={x | x=2n,n∈N}问普通数的加法是否是X上的二元运算?普通数的乘法呢? [答] 普通的加法运算不是X是X上的二元运算,因为存在着x1=2∈X,x2=22∈X,使x1+x2=2+22=6X. 普通的乘法运算是X上的二元运算,因为对于任意的x1=1n2X,x2=2n2X,这里n1,n2N,都有x1·x2=1n2·2n2=21nn2X(因为n1+n2∈N)。 3.设〈X,* 〉是代数系统,*是X上的二元运算,若有元素el∈X,使Xx,有el*x=x,则称el是关于*的左幺元。若有元素erX,使Xx,有x * el=x,则称er是关于*的右幺元。 a) 试举出公含有左幺的代数系统的例子。 b) 试举出仅含有左幺的代数系统的例子。 c) 证明:在代数系统中,若关于*有左幺元和右幺元,则左幺元等于右幺元。 [解] :a) 构造代数系统(完整word版)离散数学习题解+代数系统 2 令X={a,b,c,d},*:X×→X→X,其运算表如下:
* a b c d a d a b c b a b c d c a b c c d a b c d
则此代数系统含有左幺元b,d,但不含右幺元。 b) 构造代数系统〈X,* >如下: 令X={1,2,3,4} *: X×→X→X,其运算表如下:
* 1 2 3 4 1 1 2 4 3 2 2 1 3 4 3 3 4 1 2 4 4 4 2 3
则此代数系统含有右幺元1,但不含左幺元。 c) [证] 因为代数系统〈X,*>关于*运算存在着左、右幺元,ei,er∈X 则 el = el * er = er∈ 4.设〈X,*〉是代数系统,*是X上的二元运算.若有元素Ol∈X,使x∈X,有Ol*x=Ol是关于*的左零元。若有元素Or∈X,使x∈X,有x*Or=Or,则称Or是关于*的右零元。 a) 试举出公含有左零元的代数系统的例子。 b) 试举出仅含有左零元的代数系统的例子。 c) 证明:在代数系统中,若关于*有左零元和右右零元,则左零元等于右零元. [解] a) 构造代数系统〈X,*〉如下: 令X={a,b,c},*:X×X→X,其运算表如下:
* a b c a a a a b b b b c b c a
则a和b都是左零元,但没有右零元。 b) 构造代数系统〈X,*〉如下: (完整word版)离散数学习题解+代数系统 3 令X={1,2,3},*:X×→X→X,其运算表如下:
* 1 2 3 1 2 3 3 2 3 1 3 3 1 2 3
则3是右零元,但没有左零元。 c) [证] 因为代数系统Ol=Ol*Or=Or
5.当给出一个代数系统的二元运算表时,如何从表上判断这个二元运算是否满足结合律,是否满足交换律,
是否有幺元,是否有零元,每个元素是否有逆元。 [答] 在一个代数系统〈X,*〉中, 1) 运算*满足结合律,当且仅当在运算表中,对任何x,y∈X,x行每个元素与y的*积对应的等于x与y列每个元素的*积。 2) 运算*满足交换律,当且仅当运算表关于主对角线是对称的. 3) 运算*有幺元,当且仅当存在一元素,它所对应的行和列依次与运算表的行和列相一致. 4) 运算*有零元,当且仅存在一元素,它所对应的行和列中每个元素都是蛇自己。 5) 若运算*有幺元,X中每个元素x有逆元,当且仅当存在一元素y∈Y,使得x所在行,y所在列的元素以及y所在行,x所在列的元素都是幺元。 6.设y*x=e,则称y是x的左逆元。若存在z∈X,使得x*z=e,则称z是x的右逆元。指出下表中各元素的左、右逆元的情况。
* a b c d e a a b c d e b b d a c d
c c a b a b d d a c d c e e d a c e
[解] a是幺元;b的左逆元和右逆元都是c;即b和c互为逆元;d的左逆元是c而左 逆元是b;b有两个左逆元c和d;e的右逆元是c,但e没有左逆元;c有两个左逆元b和e有两个右逆元b,d. 7.设是代数系统,*是X上的二元运算.x,y∈X,有x*y=x.问*是否满足结合律,是否满足交换律,是否有幺元,是否有零元,每个元素是否有逆元。 [解] a) *运算满足结合律 因为对任何x,y,z∈X,都有 (完整word版)离散数学习题解+代数系统 4 x*(y*z)=x*y=x=x*y=(x*y)*z b) *运算不满足交换律 因为对于二个元素x,y∈X,有x*y=x,而y*x=y。所以当X包含多于一个元素时,能使x≠y,从而x*y≠y * x。 c) 没有幺元 因为若有幺元e∈X存在,则对任何x∈X,应有e * x * e,但是e * x= e,x * e=x,于是推得x=e,当X中包含多于一个元素时,就会有x ≠ e,矛盾。 d) 没有零元,仿c) 保证。 e) 对于每个元素都没有逆元。因为没有幺元存在。 并且若存在一个元素a∈X,使得对每个元素x∈X,都有一个元素y∈X,使y * x=x * y=a,则有y=x=a,当X中包含多一个元素时,这将不总是成立的(只在x=a,且a具有幂等性时才成立) 8.设〈N,*〉是代数系统,*是N上的二元运算,x,y∈N,x * y=LCM(x,y).问*是否满足结合律,是否满足交换律,是否有幺元,是否有零元,每个元素是否有逆元. [解] a) *运算满足结合律 因为,对于任何x,y,z∈N, (x*y)* z =LCM ((x * y),z) = LCM (LCM(x,y),z) = LCM ((x,y,z) = LCM ((x,(y * z) = LCM ((x * y),z) = x * (y * z) 注:关于LCM(LCM(x,y),z)= LCM(x,y,z)我们可证明如下: 设C1=LCM(x,y,z),d= LCM(x,y),从而C1=LCM(d,z), C2= LCM(x,y,z),因此只需证C1=C2即可,为此 由于C2= LCM(x,y,z),故此x | C2,y |C2,z | C2,因此由d= LCM(x,y)及x | C2,y |C2,从d2
的最小性有d≤C2于是d |C2(否则C2=kd+r,0<r<d,由于x |d,y | d及x | C2,y | C2,故有x | r,
y | r,这与d=LCM(x,y)的最小性矛盾).即d|C2且z|C2故此由C1=LCM(d,z)的最小性,可知C1≤C2。 另一方面,由C1= LCM(d,z)知d |C1,z|C1,又由d=LCM(x,y)知x |d,y | d,y | d,因此有x|C1,y|C1,并且z | C1。因而C2=LCM(x,y,z)的最小性可 知C2≤C1。 所以,C1=C2.同理可证LCM(x,LCM(y,z))=LCM(x,y,z)。 b) *运算满足交换律 因为 对于任何x,y∈N, x * y=LCM(x,y) = LCM(y,x) =y * x (c)*运算有幺元1∈N。 因为,对于任何x∈N, x * 1=LCM(x,1) =x =LCM(1,x)
