1003届高三第一次联考质量分析-数学总结 (2)
高三数学第次考质量分析
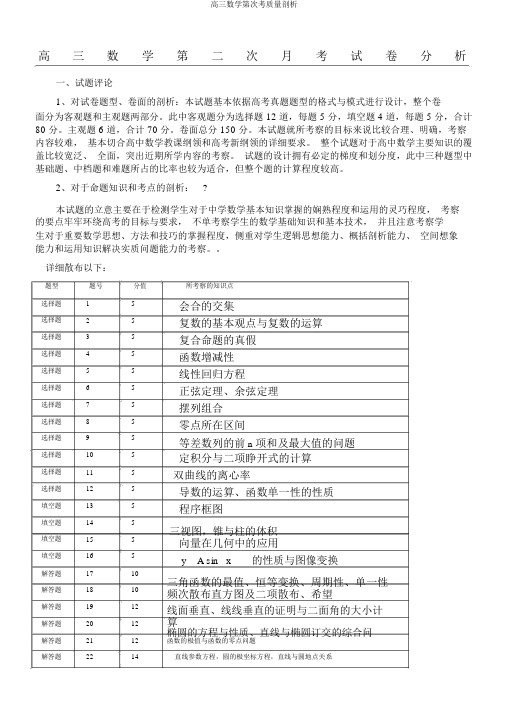
高三数学第二次月考试卷分析一、试题评论1、对试卷题型、卷面的剖析:本试题基本依据高考真题题型的格式与模式进行设计,整个卷面分为客观题和主观题两部分。
此中客观题分为选择题 12 道,每题 5 分,填空题 4 道,每题 5 分,合计80 分。
主观题 6 道,合计 70 分。
卷面总分 150 分。
本试题就所考察的目标来说比较合理、明确,考察内容较难,基本切合高中数学教课纲领和高考新纲领的详细要求。
整个试题对于高中数学主要知识的覆盖比较宽泛、全面,突出近期所学内容的考察。
试题的设计拥有必定的梯度和划分度,此中三种题型中基础题、中档题和难题所占的比率也较为适合,但整个题的计算程度较高。
2、对于命题知识和考点的剖析:?本试题的立意主要在于检测学生对于中学数学基本知识掌握的娴熟程度和运用的灵巧程度,考察的要点牢牢环绕高考的目标与要求,不单考察学生的数学基础知识和基本技术,并且注意考察学生对于重要数学思想、方法和技巧的掌握程度,侧重对学生逻辑思想能力、概括剖析能力、空间想象能力和运用知识解决实质问题能力的考察。
详细散布以下:题型题号分值选择题15选择题25选择题35选择题45选择题55选择题65选择题75选择题85选择题95选择题105选择题115选择题125填空题135填空题145填空题155填空题165解答题1710解答题1810解答题1912解答题2012解答题2112解答题2214所考察的知识点会合的交集复数的基本观点与复数的运算复合命题的真假函数增减性线性回归方程正弦定理、余弦定理摆列组合零点所在区间等差数列的前 n 项和及最大值的问题定积分与二项睁开式的计算双曲线的离心率导数的运算、函数单一性的性质程序框图三视图,锥与柱的体积向量在几何中的应用y A sin x的性质与图像变换三角函数的最值、恒等变换、周期性、单一性频次散布直方图及二项散布、希望线面垂直、线线垂直的证明与二面角的大小计算椭圆的方程与性质、直线与椭圆订交的综合问函数的极值与函数的零点问题直线参数方程,圆的极坐标方程,直线与圆地点关系二、答卷剖析1.数据剖析题1234567891011号均 4.6 3.73 2.0 4.1 2.3 2.6 2.1 3.1 2.98 3.11 2.26分846261875367905556题1213—171819202122客观主观总均号—16题题分均 1.310.5 5.1 4.97.5 2.8 2.5 2.234.535.770.3分187790625523203428427此中选择题第3、 5、 6、 7、9、11、12 题得分较低,填空题得分适中,解答题18、20、 21、22得分较低。
2024届高三第一次学业水平质量评价数学

2024届高三第一次学业水平质量评价数学随着2024届高三学生迈入高中生涯的第一次学业水平质量评价,数学作为一门重要的学科,也是其中不可忽视的一部分。
今天我将从数学学科的内容、教学方法和学生的自主学习能力三个方面,对2024届高三第一次学业水平质量评价中的数学进行评价。
首先,根据国家课程标准,高中数学的内容包括代数、几何、函数、数与数量关系、数据与统计等多个部分。
在这次评价中,我们可以考察学生在这些知识点上的掌握情况。
数学作为一门纯粹的学科,对于学生的逻辑思维能力、抽象思维能力和数学运算能力都有一定的要求。
评价中可以通过选择题、填空题和解答题等形式来考察学生的基础知识和解题能力。
对于代数和几何部分,可以通过计算题、证明题等来考察学生的运算能力和逻辑推理能力。
对于函数、数与数量关系和数据与统计等部分,可以通过实际问题的应用题来考察学生的综合运用能力。
这种以多样化的考题形式来评价学生的数学水平,可以全面了解学生的知识掌握情况和解题能力。
其次,对于数学学科的教学方法,评价也需要关注。
数学是一门需要理论结合实践的学科,因此教师在课堂上的教学方法非常重要。
在课堂上,教师应该采用启发式教学方法,引导学生进行自主探究和自主学习。
通过学生自主提问、小组讨论和实际问题解决等方式,培养学生的探究精神和解决问题的能力。
评价中可以对教师的教学方法进行观察和评估,以了解教师是否能够有效引导学生进行自主学习。
最后,学生的自主学习能力也是评价数学水平的一个重要方面。
高中数学涉及的知识点较多,学生需要有较强的自主学习能力,能够快速理解和掌握新的数学知识。
在学习过程中,学生应该形成良好的学习方法和习惯,主动查阅教材、参考资料和网络资源,提高自己的问题解决能力。
在评价中,可以通过对学生的第一次学业水平质量评价成绩进行分析,了解学生的自主学习水平和学习效果。
综上所述,2024届高三第一次学业水平质量评价数学对学生的数学知识掌握情况、教学方法和自主学习能力进行评价。
高三第一次联考数学试题及答案

高三第一次联考数学试题及答案一、选择题(每题4分,共40分)1. 若函数\( f(x) = x^2 - 4x + 3 \)的零点为\( x_1 \)和\( x_2 \),则\( x_1 + x_2 \)的值为:A. 1B. 2C. 3D. 4答案:B2. 已知双曲线的方程为\( \frac{x^2}{a^2} - \frac{y^2}{b^2} = 1 \),其中\( a > 0 \),\( b > 0 \),若该双曲线的渐近线方程为\( y = \pm \frac{b}{a}x \),则下列哪个选项是正确的?A. \( a = b \)B. \( a > b \)C. \( a < b \)D. \( a \)和\( b \)的大小关系无法确定答案:C3. 已知向量\( \vec{a} = (3, -1) \),\( \vec{b} = (2, 2) \),则\( \vec{a} \cdot \vec{b} \)的值为:A. 4B. 2C. 0D. -2答案:B4. 函数\( y = \sin(2x + \frac{\pi}{6}) \)的周期为:A. \( \pi \)B. \( \frac{\pi}{2} \)C. \( \frac{\pi}{3} \)D. \( 2\pi \)答案:A5. 已知等差数列\( \{a_n\} \)的前三项分别为\( a_1 = 1 \),\( a_2 = 3 \),\( a_3 = 5 \),则该数列的通项公式为:A. \( a_n = 2n - 1 \)B. \( a_n = 2n + 1 \)C. \( a_n = 2n - 3 \)D. \( a_n = 2n + 3 \)答案:A6. 已知\( \log_2 3 = a \),则\( \log_2 27 \)的值为:A. \( 3a \)B. \( 2a \)C. \( 4a \)D. \( 5a \)答案:C7. 已知\( \tan \theta = \frac{1}{2} \),求\( \sin \theta \)的值:A. \( \frac{\sqrt{5}}{5} \)B. \( \frac{2\sqrt{5}}{5} \)C. \( \frac{\sqrt{5}}{3} \)D. \( \frac{2\sqrt{5}}{3} \)答案:B8. 已知\( \cos \alpha = \frac{3}{5} \),且\( \alpha \)在第二象限,则\( \sin \alpha \)的值为:A. \( \frac{4}{5} \)B. \( -\frac{4}{5} \)C. \( \frac{3}{5} \)D. \( -\frac{3}{5} \)答案:B9. 已知\( \sin \beta = \frac{1}{2} \),且\( \beta \)在第一象限,则\( \cos \beta \)的值为:A. \( \frac{\sqrt{3}}{2} \)B. \( -\frac{\sqrt{3}}{2} \)C. \( \frac{1}{2} \)D. \( -\frac{1}{2} \)答案:A10. 已知\( \tan \gamma = \frac{4}{3} \),且\( \gamma \)在第三象限,则\( \cos \gamma \)的值为:A. \( \frac{3}{5} \)B. \( -\frac{3}{5} \)C. \( \frac{4}{5} \)D. \( -\frac{4}{5} \)答案:B。
庆阳市高三第一次质量检测数学试卷分析
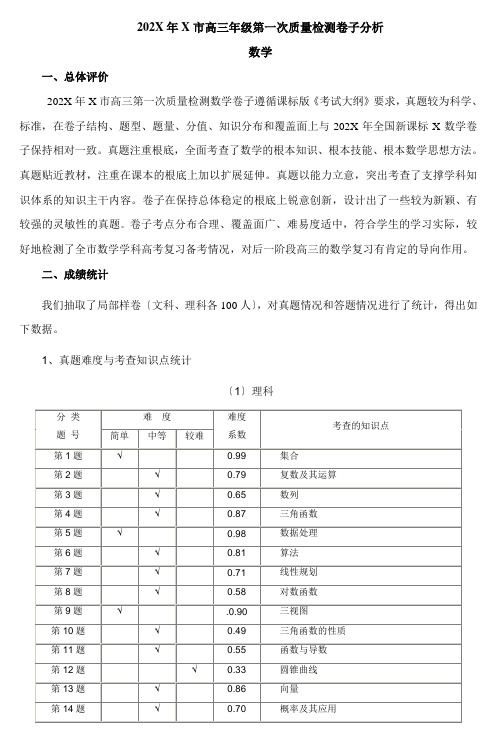
202X年X市高三年级第一次质量检测卷子分析数学一、总体评价202X年X市高三第一次质量检测数学卷子遵循课标版《考试大纲》要求,真题较为科学、标准,在卷子结构、题型、题量、分值、知识分布和覆盖面上与202X年全国新课标X数学卷子保持相对一致。
真题注重根底,全面考查了数学的根本知识、根本技能、根本数学思想方法。
真题贴近教材,注重在课本的根底上加以扩展延伸。
真题以能力立意,突出考查了支撑学科知识体系的知识主干内容。
卷子在保持总体稳定的根底上锐意创新,设计出了一些较为新颖、有较强的灵敏性的真题。
卷子考点分布合理、覆盖面广、难易度适中,符合学生的学习实际,较好地检测了全市数学学科高考复习备考情况,对后一阶段高三的数学复习有肯定的导向作用。
二、成绩统计我们抽取了局部样卷〔文科、理科各100人〕,对真题情况和答题情况进行了统计,得出如下数据。
1、真题难度与考查知识点统计〔1〕理科2、各段成绩分布情况统计〔1〕理科〔2〕文科其中理科全卷最高分133分,最低分53分;人均83.3分,难度为0.56;优秀率12.0%〔110分及以上〕;及格率42.0%〔90分及以上〕。
文科全卷最高分138分,最低分42分;人均82.6分,难度为0.55;优秀率8.0%〔110分及以上〕,及格率38.0%〔90分及以上〕。
三、答卷情况分析选择题主要考查集合、复数运算、程序框图、函数性质、三视图、三角函数、圆锥曲线、导数等知识点;第9题以三视图为载体考查学生空间想象能力,要求考生有肯定的分析推理能力;第11题以导数为背景考查学生阅读理解及解决问题的能力;第12题属于圆椭曲线题目,要求考生有较强对思维能力和运算能力。
填空题主要考查了平面向量、概率、立体几何、数列、解三角形、不等式等内容。
填空题13题考查了平面向量的有关问题,得分率很高。
14题涉及概率问题,学生经验缺少,得分一般。
15题〔理〕涉及立体几何的知识,学生分析能力的欠缺,找不到解题的切入点而丢分,得分率极低;〔文〕涉数列知识,比拟简单得分。
高三第一次联考质量分析

理性分析寻求突破——宁远县20XX届高三第一次联考质量分析月20-21日,我市举行了20XX届全市高三第一次联考,我县一、二、三中和舜德学校的高三年级共2707人参考,其中文科考生776人,占28.67%,理科考生1931人,占71.33%。
为保证此次考试的可信度,各校都成立了专门的领导小组,作了周密的准备和安排,在高三部分教师赴长沙出席“20XX年新课程全国卷高考备考复习研讨会”的情况下,各校考试秩序井然。
市教科院巡视组对我县各校的考纪考风给予了充分肯定。
、亮点分析、一中文科学生陈兰姣以559分的优异成绩列全市文科第9名,谢望望同学以556分的成绩列第13名,这是我县近些年来文科的最好名次。
、一中理科学生谢永林同学以628.5分排全市第15名,此外,一中还有欧徐利等4名理科尖子生因赴长沙参考全国物理竞赛而未参加此次联考。
、我县应届生模拟二本上线人数比上届第一次联考增加158人,其中一中增加139人、二中增加17人、三中增加7人。
、学生质量明显提升,全县一本总数为188人,比上届第一次联考增加77人,特别是一中一本总数由上届的83人,上升到本次的161人。
、位置分析次联考因部分县(区)的补习学校未参考,难以通过有限的数据对各县(区)所处的位置作出准确的评判。
将我县的四所高中与全市同类学校作对比,可看出各校所处的位置,明确今后的努力方向。
中通过三年的不懈努力,以538人的上线人数昂首进入省示范性学校的第一方阵,因被过大的学生基数所拖累,上线率仍未达到全市同类学校的平均水平。
提高招生门坎,严格控制招生人数是提高上线率的正道。
与祁阳一中相比,宁远一中文科的提质增效显得格外迫切。
二中在11所市示范性学校中处于中上水平,其17.23%的上线率居第三位。
三中无论是上线人数还是上线率,都处于市示范性学校的中下水平,特别是其文科上线人数有迅速“归零”的危险,文科教学急待加强。
3:舜德学校与普通高中上线人数比较在参考的6所普通高中中,舜德学校应届生以14.01%的上线率处在第一的位置。
高三年级第一次月考诊断考试数学试卷分析

高三年级第一次月考诊断考试数学试卷分析数学石自明对于高三年级第一次月考诊断考试数学试卷分析如下:第一次高三月考诊断考试立足于检测学生复习备考中的知识漏洞和知识盲点,为下一步开展好二轮重点复习提供有一定价值的参考信息,便于我们及时调整复习策略。
试题立足考查学生在第一轮复习阶段的基础知识、基本技能、基本数学思想与方法的应用,一方面力争试题有一定的基础性、层次性,发挥了试卷的诊断功能。
试题突出以能力考查为主线,没有怪题、偏题,比较有利于推进下阶段高三数学复习工作。
文理科数学考试试卷大致相似,题目难易适中,情境绝大多数源于教材,或是教材中几个试题的简单组合,其目的都是让考生感到亲切、熟悉,只要概念清晰,基础扎实,就能较好地作答.试题选用何种素材呈现,认真仔细思考每个问题的测试难度.兼顾考试性质和学科发展的实际,跳出题海,站到一定高度突出展示其学科主干,让考生感觉到“熟悉中有新意,模拟中有信度”。
主要失分点有:第14题,其数形结合的典型性;学生主要失分原因:没有很好的养成数形结合思想。
第18题,本题为立体几何证明题,共两问,满分12分。
学生失分原因如下:(1)线面垂直的性质定理没有掌握好;(2)证明时条件没有写全面;(3)空间图形当作平面图形;(4)数学符号使用错误等。
第20题,第一问变相考查圆锥曲线的概念和性质,第二问“和积代换”是关键;主要考察椭圆的标准方程,椭圆的定义,正余弦定理的应用,本题第一问是容易题,得分主要在此体现,第二问较难,由于本班学生基础知识比较薄弱,所以第二问基本都不会做。
在此题,要求全体学生要会做第一问,第二问因人而异,能者做之。
第21题,设计的两个函数在其定义域内都是单调的,导数应用点到为止,同时结合逻辑知识进行考查,这种形式虽比较出乎意料,但却能较真实检测学生的基础知识和基本解题能力.学生主要失分原因:(1)导数计算不正确;(2)参数的方程和不等式不会处理;(3)知道参数在方程和不等式中的作用,但不会分类讨论;(4)不会利用已知条件对根进行估值。
2024届高三第一次学业质量评价(t8联考)数学试题
1、设集合A = {x | x是小于5的正整数},B = {x | x是奇数},则A ∩ B =A、{1, 2, 3}B、{1, 3, 5}C、{1, 3}D、{3, 5}解析:集合A中小于5的正整数为{1, 2, 3, 4},集合B中的奇数为所有奇数。
取交集即取两个集合中共有的元素,故A ∩ B = {1, 3}。
(答案:C)2、已知等差数列{an}的前n项和为Sn,若a1 = 2,S3 = 12,则a4 =A、6B、8C、10D、12解析:等差数列前n项和公式为Sn = n/2 * (2a1 + (n-1)d),其中d为公差。
由S3 = 12,代入a1 = 2,n = 3,可得d = 4。
因此,a4 = a1 + 3d = 2 + 3*4 = 14 - 2 = 12。
(答案:D)3、若复数z满足(1 + i)z = 2i,则z =A、1 + iB、1 - iC、-1 + iD、-1 - i解析:由(1 + i)z = 2i,得z = 2i / (1 + i)。
为了消去分母中的虚部,同时乘以共轭复数(1 - i),得z = (2i(1 - i)) / ((1 + i)(1 - i)) = 2(i - i2) / (1 - i2) = 2(i + 1) / 2 = 1 + i。
(答案:A)4、已知向量a = (1, 2),b = (3, 4),则a · b =A、5B、7C、11D、13解析:向量点积公式为a · b = a1b1 + a2b2。
代入向量a = (1, 2),b = (3, 4),得a · b = 13 + 24 = 3 + 8 = 11。
(答案:C)5、一个圆锥的底面半径为2,高为3,则其体积为A、4πB、8πC、12πD、16π解析:圆锥体积公式为V = (1/3)πr2h,其中r为底面半径,h为高。
代入r = 2,h = 3,得V = (1/3)π223 = 4π。
高三第一次月考总结(3篇)
计划:
禹城市迎宾路北首路西
机电一体化
数控技术应用
计算机技术应用
汽车制造与检修
物流服务与管理
电子技术应用
机械装配与维修
德州市华忆
职业技术学校
计划:
电话:
临邑县城宏泰大街号
机电技术应用
免学费
会计
免学费
航空服务
免学费
学前教育
免学费
建筑工程施工
免学费
德州市年技工院校招生计划
学校
专业
学制
招生计划
建筑工程技术(高中起点高技)
数控技术(高中起点高技)
电子商务(高中起点高技)
数控技术(高中起点技师)
(前两年)(第三年后)
汽车检测与维修技术(高中起点技师)
(前两年)(第三年后)
机电一体化技术(高中起点技师)
(前两年)(第三年后)
制冷与空调技术(高中起点技师)
(前两年)(第三年后)
模具设计与制造技术(高中起点技师)
(前两年)(第三年后)
电子商务(高中起点技师)
(前两年)(第三年后)
电气自动化技术(高中起点技师)
(前两年)(第三年后)
合计
注:“收费标准”栏中标注“免学费”“”或空的均为免学费。
志愿代码
收费标准
备注
德州交通技工学校
计划:
德州经济开发区三八东路汽摩学院
电话:、
汽车维修
汽车钣金与涂装
汽车制造与装配
汽车营销
农业机械使用与维护
数控加工(数控车工)
机电设备安装与维修
制冷设备运用与维修
农村电气技术
计算机应ቤተ መጻሕፍቲ ባይዱ与维修
高三数学第一次月考质量分析讲课讲稿
高三数学第一次月考质量分析一.命题的思路1、命题尽量依据高考数学的内容和要求。
贴近现行高中数学课程的知识内容、思想方法和能力要求。
加强基础概念,基本题型,基本方法的考查;突出已复习过的高中数学的重点内容。
2. 通过考试,让更多的学生打上比较好的分数,以此来提高学生一轮复习的信心。
3考查的内容,集合,简易逻辑,函数与导数。
4。
内容设置集合题占15。
逻辑占15 函数导数70这是理科, 考虑文科学生特点及学生的实际情况,集合题占25。
逻辑占15 函数导数605、控制试题难度,以中低档试题为主。
命题注重通法通解的考查力度,对重点知识,重要考点重复考查。
二,试卷分析(见附表)三、成绩统计与分析:人数 120分以上 100分以上 90分以上 80分以上 50分以下补习班 28 3 6 3 3 3213班 40 0 1 2 5 14214班 48 0 0 1 4 33216班 46 0 0 0 2 29215班 45 1 5 4 2 5217班 32 0 0 0 0 28218班 44 0 1 1 0 28四,问题及原因1,基本的计算能力普遍较差(表现在不少学生在会做的题中没有得满分甚至一分不得)。
比如,因式分解应用,用算需要稍作变形的就没法进行,基础知识、基本方法掌握不牢固,基本公式记忆不牢固, 21题求函数的导数出错。
通性通法不知道。
这一点文科较严重,比如,集合的运算不会。
理科的分类讨论,数学题中几乎每一道题都要经过灵活、严密的变形和计算。
在高考数学考试中可以毫不夸张的说,计算和变形基本功占到所有数学基本功的60%——70%。
变形是解题的生命,没有变形也就没有解题思路的发现和产生。
知道思路,但不能作对2.是数学基础差的学生对数学学习没有兴趣,导致大多数学生平时上课不用心,课后练习少,咱要考大学,但学生做的题远远没有考高中做的多,好多学生不做,做题少大概高一就开始了,考试中拿到试卷后就无事可做,到时随意做做选择题、填空题了事。
高三第一次月考总结(4篇)
高三第一次月考总结“决定做事行为,做事行为决定习惯,习惯决定性格,性格决定命运。
”比尔·盖茨的一席话令我对人生又有了新的感悟。
一次次的失败,一次次的总结,但每次结果却没什么大的变化。
成绩的不见好转,说明我自己在思想上存在问题,所以当务之急并不是解决成绩,而是思想上的问题,因为这将关系到我一生的命运。
成绩问题的确很让人头疼,不过路是自己选的,问题也应由自己来承担,针对单科存在的问题还是应该系统的分析。
这次考试语文试卷得了____分,放在高三高三的确是个高分,但对于高三来说,语文____分以下的成绩都是低分。
汉语作为母语,每个人在思想中都已形成了一种固定的模式,所以要人为的改变这种模式确实有点困难。
语文卷总的来看,影响成绩的还是选择和作文,这就涉及到一些基础知识,基础知识丢分,我个人认为还是比较好弥补的。
我还是很有信心在第一次月考中突破____分的~数学自古以来就是文科生的弱科,但这个社会又是一个弱肉强食的社会,如果你不强,就注定被人吃掉。
所以我还是选择无条件的提升数学成绩,针对此次考试,数学卷子综合来说还是比较简单,但因马虎未审清题意,所以丢了许多不该丢的分。
此次数学考试,就我个人看来____分是正常分数,因为这____分都是基础分,最次也得过____分。
上高三以来我的数学成绩一直是班级里的,但这次的失误令我十分懊悔,希望没有令数学老师失望,下次月考,我会拿回本属于我的东西。
英语常被中国人看作第一种语言,但在经济发达、国际交流日益频繁的今天,英语早已成为了中国的第一种母语。
汉语、英语不过关,很难在社会上生存,此外还必须掌握日语或法语第一门语言。
香港大学的更是以英语为交流方式,由此可见,英语对于我们这些90后来说非常重要,必须无条件的学好英语。
政史地一直被人们视为小科,但自分文理以来,政史地就已占据了半片江山,想要考高分,政史地绝不能缺腿。
可我现在还仅仅是拘泥于及格…首先在基础上我就很不过关,所以受题的难易程度影响很大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1003届高三第一次联考质量分析-数学总结
考试情况分析
近年来,高考的竞争越来越激烈,各地的高考质量评估也越来越
高。为了提高学生的应试水平,许多学校都会组织一些模拟考试或联
考。1003届高三的第一次联考是其中一次。我们将针对数学科目的考
试情况进行分析和总结。
题型及分值分布
本次数学考试共分为两部分,一部分是选择题,另一部分是主观
题。
• 选择题:共30道,每题分值为3分,总分为90分。
• 主观题:共6道大题,每题分值为16分,总分为96分。
其中,选择题的知识点涵盖了整个高中数学的范围,题目难度较
为平均。主观题则主要集中在高中数学的重点知识,难度逐步增加。
具体情况分析
选择题
选择题的分数最高为90分,本次考试的平均分数为60.5分,最
高分为89分。值得注意的是,选择题中其中的第19题次分数出现了
较大的波动,成为了本次数学联考的难点之一。但总体来说,选择题
比较公平,并且题目的难度没有太大的起伏。
主观题
在主观题方面,所有题目中最高分数为90分,平均分数为54.3
分。最高分数为86.5分,中位数为55分。
整体来说,主观题的难度明显高于选择题,尤其是第3题和第4
题的难度较大,因此在这两道题目上学生普遍得分不高。但也有一些
学生在第2题中表现出色,得到了高分。
此外,习惯性思维和计算错误也是影响学生考试成绩的主要障碍。
学生情况分析
通过对多位学生的考试成绩进行统计和分析,我们可以发现不同
学生的成绩差异很大,在一定程度上反映了他们的学习水平和学生态
度。
优秀学生
优秀学生在本次考试中的表现基本上没有什么问题。他们能够快
速准确地做出题目,没有犯太多的错误。同时,在运用所学知识的同
时,也能够创新思考并进行自己的总结和归纳,最终拿到高分。
普通学生
普通学生在本次考试中的情况比较令人关注。这类学生在题目思
考和解答过程中,存在一些基本错误和求助错误的现象,提升学生思
考能力和技巧就显得尤为重要。
较差学生
较差学生的情况最为令人担忧。他们在本次考试中的表现不够出
色,越来越容易因为在平时学习过程中积压的问题而导致学习顶不住,
考试发挥不佳的情况。加强对这部分学生的辅导和指导,就显得尤为
必要了。
解决方案
对于数学联考的成绩和学生学习状况,学校可以采取一下几种措
施:
做好诊断反馈
学校可以通过针对性的测试和调查,了解学生们在不同知识点上
的实际理解情况,分析不同年级和同班学生的优势和不足,将数据分
析、解读和反馈机制制度化。
加强学习态度
学习成绩的高低不仅仅取决于学生的能力,也取决于学习态度和
学科热爱程度。学校应该引导学生看到学科的美好,并创造良好的环
境和氛围,从而增强学生对学科的兴趣和热爱程度。
精准辅导学生
学校应当根据学生的基础情况和实际需求,提供个性化、差异化
的辅导服务,使学生在学习过程中能够得到更好的帮助和支持,并取
得优秀的成绩。此外,老师们还应该及时地分析学生的错误,并帮助
学生克服错误。
总结
本次数学联考,选择题难度较小,主观题难度较大。学生的考试
表现各有不同,需要加强诊断反馈、加强学习态度和精准辅导学生等
方面,以提高学生的成绩。
