电源等效变换的条件
知识点:独立电源的等效变换-教学文稿

二、知识准备 ,
(一)独立电压源与独立电流源的等效变换
例11 试求图1-57(a)所示电流源的等效电压源和图1-57(c)所示电压源的等效电 流源。
解:图1-57(a)所示为电流源变为电压源时,根据等效变换的原则,电压源的电动
(五)电源其它特殊联接的等效
1理想电压源与任何二端网络(包括元件)并联,对外电路而言,这部 分 电路可以等效为相同的恒压源; 2理想电流源与任何二端元件串联,对外电路而言,这部分电路可以等 效 为相同的理想电流源; 3恒压源与恒流源串联,串联电路的电流等于恒流源的电流,端口电压 由 外电路决定; 4恒压源与恒流源并联,并联电路的端口电压等于恒压源的电动势,输 出 电流由外电路决定。
图1-61 实际电压源并联的等效
I
/ S
I
S1
IS2
IS3
RS/ RS1//RS2 // RS3
四、知识深化
(四)实际电流源串联的等效
当几个实际电流源串联时,可先将电流源等效为电压源,然后再进行电压 源合并,化简为一个电压源,若需要时再将电压源等效为电流源。
图1-62 实际电流源串联的等效
四、知识深化
图1-65 例12图
五、归纳总结
1.将一个电动势为US、内阻为RS的实际电压源等效变换为一个实际电 流源时,该实际电流源的内阻依然为RS,但其电流为IS=US/RS。恒流
源方向与电压源的电动势方向一致。 2.将一个实际电流源等效为一个实际电压源时,该实际电压源的内阻依
然为RS,但电动势为US=ISRS。电压源电动势的方向与电流源电流方向
讲授内容
项目一: 电路分析基本定律与分析方法知识点ຫໍສະໝຸດ 独立电源的等效变换目录
常见几种电路的等效变换
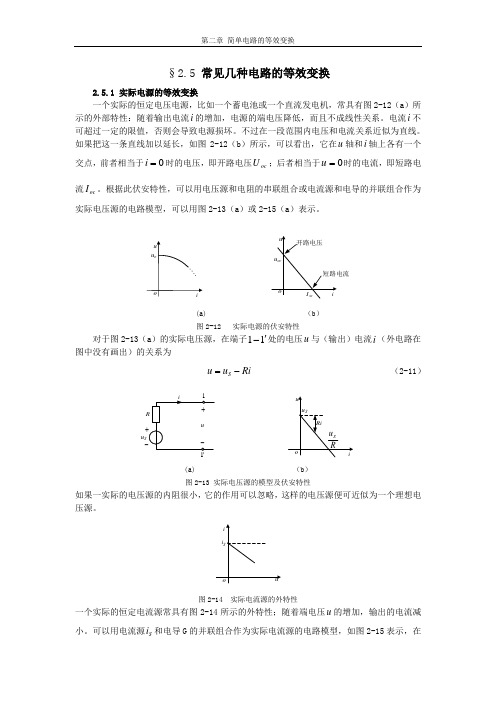
§2.5 常见几种电路的等效变换2.5.1 实际电源的等效变换一个实际的恒定电压电源,比如一个蓄电池或一个直流发电机,常具有图2-12(a )所示的外部特性:随着输出电流i 的增加,电源的端电压降低,而且不成线性关系。
电流i 不可超过一定的限值,否则会导致电源损坏。
不过在一段范围内电压和电流关系近似为直线。
如果把这一条直线加以延长,如图2-12(b )所示,可以看出,它在u 轴和i 轴上各有一个交点,前者相当于0=i 时的电压,即开路电压oc U ;后者相当于0=u 时的电流,即短路电流oc I 。
根据此伏安特性,可以用电压源和电阻的串联组合或电流源和电导的并联组合作为实际电压源的电路模型,可以用图2-13(a )或2-15(a )表示。
(a) (b ) 图2-12 实际电源的伏安特性对于图2-13(a )的实际电压源,在端子11'-处的电压u 与(输出)电流i (外电路在图中没有画出)的关系为Ri u u S -= (2-11)Su(a) (b ) 图2-13 实际电压源的模型及伏安特性如果一实际的电压源的内阻很小,它的作用可以忽略,这样的电压源便可近似为一个理想电压源。
图2-14 实际电流源的外特性一个实际的恒定电流源常具有图2-14所示的外特性;随着端电压u 的增加,输出的电流减小。
可以用电流源S i 和电导G 的并联组合作为实际电流源的电路模型,如图2-15表示,在端子11'-处的电压u 与(输出)电流i 的关系为(a) (b ) 图2-15 实际电流源的电路模型及伏安特性Gu i i S -= (2-12) 如果一实际的电流源的并联电导很小,它的作用可以忽略,这电源便可近似为一个理想电流源。
如果令RG 1=S S Gu i = (2-13)式(2-11)和(2-12)所示的两个方程将完全相同,也就是在端子11'-处的电压u 与电流i 的关系将完全相同。
电压源与电流源的等效变换讲解

V
COM
RL(W) 0 U(V)
I(mA)
200
400
600
800
1000 2000 3000
8
4.测定实际电流源的外特性
万用表直流毫安挡
mA
COM
IS 10mA
测流孔
Ro
RL
1KW
万用表直流电压挡
V
COM
RL(W) 0 U(V)
I(mA)
200
400
600
800
1000 2000 3000
9
5.测定电源等效变换的条件
Us为+12V直流稳压电源。
RL为可调电阻箱,调节RL, 令其阻值由大至小变化,记
录
两
表
的
读
数
。+ US
12V -
测流孔
R1
200W
RL
万用表直流电压挡
V
COM
RL(W) U(V)
I(mA)
2000 1500 1000 800 500 300 200
6
2.测定实际电压源的外特性
Us与R0组成实际电压源。 RL为可调电阻箱,调节RL, 令其阻值由大至小变化,记
使两表的读数与(a)时的数值相等,记录Is之值,验证等效变换条
件的正确性。
10
五、实验注意事项
1. 在测电压源外特性时,不要忘记测空载时的电压值, 测电流 源外特性时,不要忘记测短路时的电流值,注意恒流源负载电 压不可超过20伏,负载更不可开路。
2. 换接线路时,必须关闭电源开关。 3. 直流仪表的接入应注意极性与量程。
联)来摸拟一个实际的电压源(或电流源)。
3. 一个实际的电源,就其外部特性而言,既可以看成是一个电
实际电流源和实际电压源的等效变换条件

实际电流源和实际电压源的等效变换条件一、引言在电路中,实际电流源和实际电压源是两个常见的电源类型,它们在电路设计和分析中起着重要的作用。
实际电流源是指能够输出稳定电流的电源,而实际电压源则是能够输出稳定电压的电源。
在一些情况下,我们需要将一个实际电流源转化为一个等效的电压源,或者将一个实际电压源转化为一个等效的电流源。
本文将探讨实际电流源和实际电压源之间的等效变换条件。
二、实际电流源和实际电压源的定义2.1 实际电流源实际电流源是一种能够提供稳定电流的电源,它的输出电流不受外部负载的影响。
实际电流源的符号为I,单位为安培(A)。
实际电流源可以被表示为一个理想电流源和一个内部电阻的串联组合。
2.2 实际电压源实际电压源是一种能够提供稳定电压的电源,它的输出电压不受外部负载的影响。
实际电压源的符号为V,单位为伏特(V)。
实际电压源可以被表示为一个理想电压源和一个内部电阻的并联组合。
三、实际电流源和实际电压源的等效变换3.1 将实际电流源转化为实际电压源的条件将一个实际电流源转化为一个等效的电压源需要满足以下条件:1.内部电阻为零:需要假设实际电流源的内部电阻为零,这样才能保证等效电压源的输出电压与实际电流源的输出电压一致。
2.稳定电流输出:需要保证等效电压源的输出电流稳定,不受外部负载的影响。
3.输出电压与负载之间的关系:需要建立实际电流源输出电流和等效电压源输出电压之间的关系,一般通过Ohm’s Law来描述。
3.2 将实际电压源转化为实际电流源的条件将一个实际电压源转化为一个等效的电流源需要满足以下条件:1.内部电阻趋于无穷大:需要假设实际电压源的内部电阻趋于无穷大,这样才能保证等效电流源的输出电流与实际电压源的输出电流一致。
2.稳定电压输出:需要保证等效电流源的输出电压稳定,不受外部负载的影响。
3.输出电流与负载之间的关系:需要建立实际电压源输出电压和等效电流源输出电流之间的关系,一般通过Ohm’s Law来描述。
第2章(1) 电路分析的等效变换法

p=Gequ2 = (G1+ G2+ …+Gn ) u2
=G1u2+G2u2+ +Gnu2
=p1+ p2++ pn 表明
(1) 电阻并连时,各电阻消耗的功率与电阻大小成反比 (2) 等效电阻消耗的功率等于各并联电阻消耗功率的总和
三. 电阻的串并联 电路中有电阻的串联,又有电阻的并联,
这种连接方式称电阻的串并联。
:电流放大倍数
(2) 电压控制电流源 ( VCCS )
i1 +
u1 _ gu 1
i2 +
u2 _
i2 gu1
g: 转移电导
(3) 电压控制电压源 ( VCVS )
i1 + u1 _ + -
i2 +
u2 u1
: 电压放大倍数
u1 u2
_
(4) 电流控制电压源 ( CCVS )
变Y
由三式两两相乘后再相加,再分别除以三式中的每一个, 可得Y型型的变换条件:
简记方法:
RΔ
Y电阻两两乘积之和 Y不相邻电阻
Y变
特例:若三个电阻相等(对称),则有
R = 3R Y
外大内小
R12 R1
R31
R2 R23
R3
例
桥 T 电路 1k 1k 1k 1k R
1/3k
B
i
+ u -
等效 C
i
+ u -
对A电路中的电流、电压和功率而言,满足
B A C A
(1)电路等效变换的条件
两电路具有相同的VCR 未变化的外电路A中 的电压、电流和功率 化简电路,方便计算
有伴电源的等效变换
-
+
6A 2Ω
3A 5Ω
I
电路原理
§2−5 有伴电源的等效变换 −
R
ik Rk
i + u u i u = αik – R i i = αik / R–u/R
αik
-
+
受控电流源的方向是受 受控电流源的方向是受 控电压源电位升的方向。 控电压源电位升的方向。
ik Rk
+ R
αik /R
u -
电路原理
电路原理
Rs1 = Rs 2 = Rs
§2−5 有伴电源的等效变换 −
有伴电压源
R i(t) + u(t) 等效
有伴电流源
i(t) + R u(t) -
us(t)
+ -
is(t)
等效条件: 等效件: 相同; ① R相同; 相同
② is = us/R; ;
电路原理
③电流源的方向为电压源电位升的方向。 电流源的方向为电压源电位升的方向。
8/4=2A
i 4Ω
+ u -
?
i + u 电路原理
例题分析
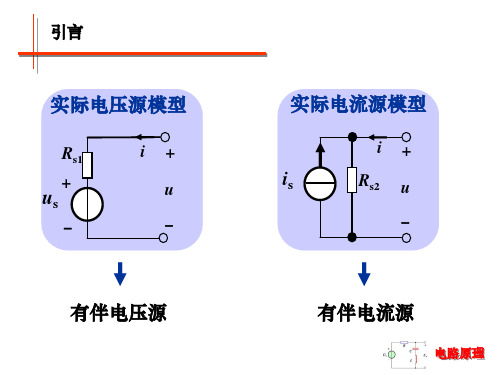
例1 试用有伴电源等效变 换求图示电路中的电流I。
4Ω + 8V 4A 4Ω
3Ω
3A 5Ω
I
3Ω
2A 4Ω
4A 4Ω
3A 5Ω
I
电路原理
例题分析
3Ω
2A 4Ω
4A 4Ω
3A 5Ω
I
I =3/10=0.3A
9V
3Ω 2Ω + 12V -
3Ω I 5Ω
引言
实际电压源模型
Rs1 i + u -
电路等效变换的条件
电路等效变换的条件
嘿,咱今天就来聊聊电路等效变换的条件。
你知道吗,就像我上次修家里那盏老是一闪一闪的台灯一样。
我看着它那奇怪的闪烁,就想着得把它修好啊。
我把台灯拆开,里面那复杂的电路就展现在我眼前。
这就好像是一个大迷宫,我得找到正确的路才行。
我开始研究那些电线、电阻啥的,就想着怎么能让它恢复正常。
这不就和电路等效变换有点像嘛。
要实现电路等效变换,首先各个元件之间的关系得搞清楚呀,就像我得清楚台灯里每个零件的作用一样。
然后呢,还得保证变换前后电路的功能不能变,就好比我修好台灯后,它得还是能正常亮起来,不能说修完了反而出问题了。
而且啊,在这个过程中,还得特别细心,不能弄错一点,不然就全乱套了。
就像我修台灯时,要是不小心把哪根线接错了,那可能不但没修好,还会搞出更大的麻烦。
这和电路等效变换是一个道理,得精确无误才行。
还有啊,要考虑整体的情况,不能只盯着一个地方看。
修台灯也得从整体去思考,不能光想着解决一个小问题而忽略了其他潜在的问题。
只有这样,才能真正实现有效的变换,就像我最终让台灯重新稳稳地亮起来一样。
总之呢,电路等效变换的条件其实就和我们生活中的很多事情一样,要细心、要全面考虑、要保证前后的一致性。
下次再看到那些复杂的电路,我就会想起修台灯的经历,哈哈,这就是生活中的小智慧和电路知识的奇妙结合呀!所以呀,记住这些条件,让我们在电路的世界里也能游刃有余,就像我搞定那盏台灯一样!。
电路原理 有伴电源的等效变换
电路原理
§25 有伴电源的等效变换
有伴电压源
R i(t)
有伴电流源
i(t)
us(t)
+ -
+
u(t) 等效
is(t)
R
+ u(t) -
等效条件: ① R相同;
② is = us/R;
电路原理
③电流源的方向为电压源电位升的方向。
§25 有伴电源的等效变换
(1)无伴电压源和无伴电流源不能进行等效变换; (2) 这种变换对外电路是等效的。若要计算被变换电路内部的 相关量,则返回原电路进行计算。 uR = 8 - u 4Ω + 8V + uR - i
+
u -
+ 8V -
i
+ u= 8V -
8/4=2A
i 4Ω
+ u
?
i + u
-
-
电路原理
例题分析
例1 试用有伴电源等效变 换求图示电路中的电流I。
4Ω + 8V 4A 4Ω
3Ω
3A 5ΩI3Ω Nhomakorabea2A
4A
3A 4Ω
I
4Ω
5Ω
电路原理
例题分析
3Ω
2A 4Ω
4A 4Ω
3A
5Ω
I
I =3/10=0.3A
4a例题分析电路原理电路原理例题分析6a31003a电路原理电路原理受控电流源的方向是受控电压源电位升的方向
**放在戴维宁前面讲 Req + i + u 等效 戴维宁 等效电路
a
i
uoc
Na
+ u -
b isc
电路实验报告-电压源和电流源的等效变换-20210221
电路实验报告-电压源和电流源的等效变换-20210221 《电路与模电》实验报告实验题目:电压源与电流源的等效变换姓名:学号:实验时间:实验地点:指导老师:班级:装订线一、实验目的1. 掌握电源外特性的测试方法。
2. 验证电压源与电流源等效变换的条件。
二、实验原理1. 一个直流稳压电源在一定的电流范围内,其内阻很小。
故在实用中,常将它视为一个理想的电压源,即认为输出电压不随负载电流而变,其伏安特性V=f(I)是一条平行于I轴的直线。
同样,一个实际的恒流源在实用中,在一定的电压范围内,可视为一个理想的电流源。
2. 一个实际的电压源(或电流源),其端电压(或输出电流)不可能不随负载而变,因它具有一定的内阻值。
故在实验中,用一个小阻值的电阻与稳压源相串联来摸拟一个实际的电压源,用一个大电阻与恒流源并联来模拟实际的电流源。
3. 一个实际的电源,就其外部特性而言,即可以看成是一个电压源,又可以看成是一个电流源。
若视为电压源,则可用一个理想的电压源ES与一个电阻R0相串联的组合来表示;若视为电流源,则可用一个理想电流源IS与一电导g0相并联的组合来表示。
若它们能向同样的负载提供出同样大小的电流和端电压,则称这两个电源是等效的,它们具有相同的外特性。
一个电压源与一个电流源等效变换的条件为: 图3-1 电压源与电流源的等效变换IS?USR0,g0?1R0,或US?ISR0,R0?1g0IIS=US/R0,g0=1/R0IRLUS=ISR0,R0=1/g0+US_R0 U+IS_g0URL三、实验内容1. 测定直流稳压电源与电压源的外特性(1) 按图3-2接线,US为+6V直流稳压电源,R1=200Ω,R2=470Ω。
调节R2,令其阻值由大至小变化,记录两表的读数于表3-1。
图3-2 直流稳压电源的外特性测量表3-1 直流稳压电源的外特性测量数据R2 U I ∞ 500 400 300 200 100 0 I+mA_+US_6VR1V200ΩR2470Ω电流单位:电压单位:电阻单位:Ω(2) 按图3-3接线,虚线框可模拟为一个实际的电压源,调节电位器R2,令其阻值由大至小变化,记录两表的数据于3-2。
两种实际电源模型的等效变换ppt课件
精选ppt
3
第2章 直流电阻电路的分析计算
1 .实际电压源模型(一)
电压源 U S 和电阻R的串联组合
I U
+
R
+ Us
-
Us U
ห้องสมุดไป่ตู้
-
0
Us / R I
(a )
(b )
图2.12 电压源和电阻串联组合
精选ppt
4
第2章 直流电阻电路的分析计算
1 .实际电压源模型(二)
其外特性方程为
UUs RI (2.12)
精选ppt
13
第2章 直流电阻电路的分析计算
思考题
用一个等效电源替代下列各有源二端网络。
+ -
4V
+
10V
-
(a)
20A
4A
(b)
精选ppt
14
感谢亲观看此幻灯片,此课件部分内容来源于网络, 如有侵权请及时联系我们删除,谢谢配合!
第2章 直流电阻电路的分析计算
2.3 两种实际电源模型的 等效变换
精选ppt
1
第2章 直流电阻电路的分析计算
目的与要求
1.理解实际电压源、实际电流源的模型 2.会对两种电源模型进行等效变换
精选ppt
2
第2章 直流电阻电路的分析计算
重点与难点
重点 两种电源模型等效变换的条件 难点 用电源模型等效变换法分析电路
精选ppt
7
第2章 直流电阻电路的分析计算
3.两种实际电源模型的等效变换
比较式(2.12)和式(2.13), 只要满足
1
G
, R
Is
GUs
实际电压源和实际电流源间就可以等效变换。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电源等效变换的条件
电源等效变换指的是将某一电路的电源替换为另一种电源,达到相同电路效果的方法。
在实际生产中,这种方法可用于简化电路分析与设计,提高生产效率。
然而,电源等效变换并不是任何时候都是可行的,需要满足一定的条件。
一、等效源的性质相同首先,等效变换需要满足等效源的性质相同,即能量输出和电压与电流的波形相同。
在实际电路中,能量输出代表了电路功能的实现方式,而电压、电流波形代表了电路的基本形式。
因此,等效源的性质相同是电源等效变换的必要前提。
二、电路连接相同与引出端相同其次,电源等效变换需要满足电路连接相同与引出端相同。
电路连接相同指的是等效源连接到电路中的方式相同,如继电器电源连接的方式就有串联和并联两种;引出端相同指的是等效源与电路连接的接口相同。
三、等效源输出电压和电流相同再次,等效源输出电压和电流需要相同。
因为输出电压和电流是表征电路性能和运行状态的重要参数,直接关系到电路的实际工作效果和安全性能。
如果等效源的电压和电流输出不同,那么电路的运行状态和效果也必然有所不同。
四、内阻值相同最后,等效变换需要满足内阻值相同。
内阻是电源内部电路中电流和电压之间的关系,是影响功率输出和转换效率的重要因素。
因此,等效源内部的电阻值需要与原电源内部电阻值相同,才能保证等效变换有效。
综上所述,电源等效变换需要满足等效源的性质相同、电路连接相同与引出端相同、等效源输出电压和电流相同、内阻值相同等条件。
只有满足这些条件,才能实现等效变换,简化电路分析和设计,提高生产效率。
因此,在实际应用中,需要严格遵守这些条件,确保电路运行和效果的稳定和可靠。
