2014挑战中考数学压轴题(第七版精选)
中考数学压轴题100题精选含答案

中考数学压轴题100题精选【含答案】【001】如图,已知抛物线2(1)y a x=-+a≠0)经过点(2)A-,0,抛物线的顶点为D,过O作射线OM AD∥.过顶点D平行于x轴的直线交射线OM于点C,B在x轴正半轴上,连结BC.(1)求该抛物线的解析式;(2)若动点P从点O出发,以每秒1个长度单位的速度沿射线OM运动,设点P运动的时间为()t s.问当t为何值时,四边形DAOP分别为平行四边形?直角梯形?等腰梯形?(3)若O C O B=,动点P和动点Q分别从点O和点B同时出发,分别以每秒1个长度单位和2个长度单位的速度沿OC和BO运动,当其中一个点停止运动时另一个点也随之停止运动.设它们的运动的时间为t()s,连接PQ,当t为何值时,四边形BCPQ的面积最小?并求出最小值及此时PQ的长.【002】如图16,在Rt△ABC中,∠C=90°,AC = 3,AB = 5.点P从点C出发沿CA以每秒1个单位长的速度向点A匀速运动,到达点A后立刻以原来的速度沿AC返回;点Q从点A出发沿AB以每秒1个单位长的速度向点B匀速运动.伴随着P、Q的运动,DE保持垂直平分PQ,且交PQ于点D,交折线QB-BC-CP于点E.点P、Q同时出发,当点Q到达点B时停止运动,点P也随之停止.设点P、Q运动的时间是t秒(t>0).(1)当t = 2时,AP = ,点Q到AC的距离是;(2)在点P从C向A运动的过程中,求△APQ的面积S与t的函数关系式;(不必写出t的取值范围)(3)在点E从B向C运动的过程中,四边形QBED能否成为直角梯形?若能,求t的值.若不能,请说明理由;(4)当DE经过点C 时,请直接写出t的值.AP 图16【003】如图,在平面直角坐标系中,已知矩形ABCD 的三个顶点B (4,0)、C (8,0)、D (8,8).抛物线y=ax2+bx 过A 、C 两点.(1)直接写出点A 的坐标,并求出抛物线的解析式;(2)动点P 从点A 出发.沿线段AB 向终点B 运动,同时点Q 从点C 出发,沿线段CD向终点D 运动.速度均为每秒1个单位长度,运动时间为t 秒.过点P 作PE ⊥AB 交AC 于点E ,①过点E 作EF ⊥AD 于点F ,交抛物线于点G.当t 为何值时,线段EG 最长?②连接EQ .在点P 、Q 运动的过程中,判断有几个时刻使得△CEQ 是等腰三角形? 请直接写出相应的t 值。
九年级数学中考压轴题2014年全国各地中考数学真题分类解析汇编:12 反比例函数

反比例函数一、选择题1. (2014•福建泉州,第7题3分)在同一平面直角坐标系中,函数y=mx+m与y =(m≠0)的图象可能是()B C D的图象可知=2. (2014•广西贺州,第10题3分)已知二次函数y=ax2+bx+c(a,b,c是常数,且a≠0)的图象如图所示,则一次函数y=cx+与反比例函数y=在同一坐标系内的大致图象是()A.B.C.D.考点:二次函数的图象;一次函数的图象;反比例函数的图象.分析:先根据二次函数的图象得到a>0,b<0,c<0,再根据一次函数图象与系数的关系和反比例函数图象与系数的关系判断它们的位置.解答:解:∵抛物线开口向上,∴a>0,∵抛物线的对称轴为直线x=﹣>0,∴b<0,∵抛物线与y轴的交点在x轴下方,∴c<0,∴一次函数y=cx +的图象过第二、三、四象限,反比例函数y =分布在第二、四象限.故选B.点评:本题考查了二次函数的图象:二次函数y=ax2+bx+c(a、b、c为常数,a≠0)的图象为抛物线,当a>0,抛物线开口向上;当a<0,抛物线开口向下.对称轴为直线x=﹣;与y轴的交点坐标为(0,c).也考查了一次函数图象和反比例函数的图象.3.(2014年天津市,第9 题3分)已知反比例函数y =,当1<x<2时,y的取值范围是()A.0<y<5 B.1<y<2 C.5<y<10 D.y>10考点:反比例函数的性质.分析:将x=1和x=2分别代入反比例函数即可确定函数值的取值范围.解答:解:∵反比例函数y=中当x=1时y=10,当x=2时,y=5,∴当1<x<2时,y的取值范围是5<y<10,故选C.点评:本题考查了反比例函数的性质:(1)反比例函数y=(k≠0)的图象是双曲线;(2)当k>0,双曲线的两支分别位于第一、第三象限,在每一象限内y随x的增大而减小;(3)当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大.4.(2014•新疆,第11题5分)若点A(1,y1)和点B(2,y2)在反比例函数y=图象上,则y1与y2的大小关系是:y1y2(填“>”、“<”或“=”).的图象上,=1>5.(2014•温州,第10题4分)如图,矩形ABCD的顶点A在第一象限,AB∥x轴,AD∥y 轴,且对角线的交点与原点O重合.在边AB从小于AD到大于AD的变化过程中,若矩形ABCD的周长始终保持不变,则经过动点A的反比例函数y=(k≠0)中k的值的变化情况是()AB•AB•ADAB•AD6.(2014•四川自贡,第9题4分)关于x的函数y=k(x+1)和y=(k≠0)在同一坐标系中的图象大致是()B关于x的函数y=k(x+1)和y=(k≠0)在同一坐标系中的图象大致是()B7.(2014·云南昆明,第8题3分)左下图是反比例函数)0(≠=k k xk y 为常数,的图像,则一次函数k kx y -=的图像大致是( )8. (2014•湘潭,第8题,3分)如图,A 、B 两点在双曲线y =上,分别经过A 、B 两点向轴作垂线段,已知S 阴影=1,则S 1+S 2=( )(第1题图)C B A9. (2014•益阳,第6题,4分)正比例函数y=6x的图象与反比例函数y=的图象的交点位于()根据反比例函数与一次函数的交点问题解方程组得或的图象的交点坐标为(10. (2014•株洲,第4题,3分)已知反比例函数y=的图象经过点(2,3),那么下列四个点中,也在这个函数图象上的是()11. (2014•扬州,第3题,3分)若反比例函数y=(k≠0)的图象经过点P(﹣2,3),则该函数的图象的点是()(二.填空题1. (2014•广西玉林市、防城港市,第18题3分)如图,OABC是平行四边形,对角线OB 在轴正半轴上,位于第一象限的点A和第二象限的点C分别在双曲线y=和y=的一支上,分别过点A、C作x轴的垂线,垂足分别为M和N,则有以下的结论:①=;②阴影部分面积是(k1+k2);③当∠AOC=90°时,|k1|=|k2|;④若OABC是菱形,则两双曲线既关于x轴对称,也关于y轴对称.其中正确的结论是①④(把所有正确的结论的序号都填上).||=OM||=ON,所以有=||=(||=OM||=ON =||((2.(2014年天津市,第14题3分)已知反比例函数y=(k为常数,k≠0)的图象位于第一、第三象限,写出一个符合条件的k的值为1.考点:反比例函数的性质.专题:开放型.分析:反比例函数y=(k为常数,k≠0)的图象在第一,三象限,则k>0,符合上述条件的k的一个值可以是1.(正数即可,答案不唯一)解答:解:∵反比例函数的图象在一、三象限,∴k>0,只要是大于0的所有实数都可以.例如:1.故答案为:1.点评:此题主要考查反比例函数图象的性质:(1)k>0时,图象是位于一、三象限;(2)k<0时,图象是位于二、四象限.3.(2014•武汉,第15题3分)如图,若双曲线y=与边长为5的等边△AOB的边OA,AB分别相交于C,D两点,且OC=3BD,则实数k的值为.x=坐标为(xx=x x=x﹣故答案为:4.(2014•邵阳,第13题3分)若反比例函数的图象经过点(﹣1,2),则k的值是﹣2 .5.(2014•孝感,第17题3分)如图,Rt△AOB的一条直角边OB在x轴上,双曲线y=经过斜边OA的中点C,与另一直角边交于点D.若S△OCD=9,则S△OBD的值为6.|=.,kkk三角形的面积是6.(2014•浙江湖州,第15题4分)如图,已知在Rt△OAC中,O为坐标原点,直角顶点C在x轴的正半轴上,反比例函数y=(k≠0)在第一象限的图象经过OA的中点B,交AC于点D,连接OD.若△OCD∽△ACO,则直线OA的解析式为.分析:设OC=a,根据点D在反比例函数图象上表示出CD,再根据相似三角形对应边成比例列式求出AC,然后根据中点的定义表示出点B的坐标,再根据点B在反比例函数图象上表示出a、k的关系,然后用a表示出点B的坐标,再利用待定系数法求一次函数解析式解答.解:设OC=a,∵点D在y=上,∴CD=,∵△OCD∽△ACO,∴=,∴AC==,∴点A(a,),∵点B是OA的中点,∴点B的坐标为(,),∵点B在反比例函数图象上,∴=,解得,a2=2k,∴点B的坐标为(,a),设直线OA的解析式为y=mx,则m•=a,解得m=2,所以,直线OA的解析式为y=2x.故答案为:y=2x.点评:本题考查了相似三角形的性质,反比例函数图象上点的坐标特征,用OC的长度表示出点B的坐标是解题的关键,也是本题的难点.7.(2014年江苏南京,第11题,2分)已知反比例函数y=的图象经过点A(﹣2,3),则当x=﹣3时,y=.考点:反比例函数分析:先把点A(﹣2,3)代入y=求得k的值,然后将x=﹣3代入,即可求出y的值.解答:∵反比例函数y=的图象经过点A(﹣2,3),∴k=﹣2×3=﹣6,∴反比例函数解析式为y=﹣,∴当x=﹣3时,y=﹣=2.故答案是:2.点评:本题考查了反比例函数图象上点的坐标特征.利用待定系数法求得反比例函数解析式是解题的关键.8.(2014•滨州,第17题4分)如图,菱形OABC的顶点O是原点,顶点B在y轴上,菱形的两条对角线的长分别是6和4,反比例函数的图象经过点C,则k的值为﹣6 .的图象上,,解得9.(2014•菏泽,第13题3分)如图,Rt△ABO中,∠AOB=90°,点A在第一象限、点B在第四象限,且AO:BO=1:,若点A(x0,y0)的坐标x0,y0满足y0=,则点B(x,y)的坐标x,y所满足的关系式为y=﹣2x.)(,10.(2014•济宁,第14题3分)如图,四边形OABC是矩形,ADEF是正方形,点A、D在x 轴的正半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=的图象上,OA=1,OC=6,则正方形ADEF的边长为2.,设==(三.解答题1. (2014•福建泉州,第26题14分)如图,直线y=﹣x+3与x,y轴分别交于点A,B,与反比例函数的图象交于点P(2,1).(1)求该反比例函数的关系式;(2)设PC⊥y轴于点C,点A关于y轴的对称点为A′;①求△A′BC的周长和sin∠BA′C的值;②对大于1的常数m,求x轴上的点M的坐标,使得sin∠BMC=.,然后把点===的图象上,=,.3+=BC=3=3.=3+的值为==.,=.,的坐标为(﹣═==+(﹣)和(﹣(﹣﹣联想到点2. (2014•广东,第23题9分)如图,已知A(﹣4,),B(﹣1,2)是一次函数y=kx+b 与反比例函数y=(m≠0,m<0)图象的两个交点,AC⊥x轴于C,BD⊥y轴于D.(1)根据图象直接回答:在第二象限内,当x取何值时,一次函数大于反比例函数的值?(2)求一次函数解析式及m的值;(3)P是线段AB上的一点,连接PC,PD,若△PCA和△PDB面积相等,求点P坐标.考点:反比例函数与一次函数的交点问题.分析:(1)根据一次函数图象在上方的部分是不等式的解,观察图象,可得答案;(2)根据待定系数法,可得函数解析式;(3)根据三角形面积相等,可得答案.解答:解:(1)由图象得一次函数图象在上的部分,﹣4<x<﹣1,当﹣4<x<﹣1时,一次函数大于反比例函数的值;(2)设一次函数的解析式为y=kx+b,y=kx+b的图象过点(﹣4,),(﹣1,2),则,解得一次函数的解析式为y=x+,反比例函数y=图象过点(﹣1,2),m=﹣1×2=﹣2;(3)连接PC、PD,如图,设P(x,x+)由△PCA和△PDB面积相等得(x+4)=|﹣1|×(2﹣x﹣),x=﹣,y=x+=,∴P点坐标是(﹣,).点评:本题考查了反比例函数与一次函数的交点问题,利用了函数与不等式的关系,待定系数法求解析式.3. (2014•珠海,第19题7分)如图,在平面直角坐标系中,边长为2的正方形ABCD关于y轴对称,边在AD在x轴上,点B在第四象限,直线BD与反比例函数y=的图象交于点B、E.(1)求反比例函数及直线BD的解析式;(2)求点E的坐标.=,﹣,解得.=,解得4.(2014年四川资阳,第20题8分)如图,一次函数y=kx+b(k≠0)的图象过点P(﹣,0),且与反比例函数y=(m≠0)的图象相交于点A(﹣2,1)和点B.(1)求一次函数和反比例函数的解析式;(2)求点B的坐标,并根据图象回答:当x在什么范围内取值时,一次函数的函数值小于反比例函数的函数值?考点:反比例函数与一次函数的交点问题.分析:(1)根据待定系数法,可得函数解析式;(2)根据二元一次方程组,可得函数图象的交点,根据一次函数图象位于反比例函数图象的下方,可得答案.解答:解:(1)一次函数y=kx+b(k≠0)的图象过点P(﹣,0)和A(﹣2,1),∴,解得,∴一次函数的解析式为y=﹣2x﹣3,反比例函数y=(m≠0)的图象过点A(﹣2,1),∴,解得m=﹣2,∴反比例函数的解析式为y=﹣;(2),解得,或,∴B(,﹣4)由图象可知,当﹣2<x<0或x>时,一次函数的函数值小于反比例函数的函数值.点评:本题考查了反比例函数与一次函数的交点问题,待定系数法是求函数解析式的关键.5.(2014年云南省,第17题6分)将油箱注满k升油后,轿车科行驶的总路程S(单位:千米)与平均耗油量a(单位:升/千米)之间是反比例函数关系S=(k是常数,k≠0).已知某轿车油箱注满油后,以平均耗油量为每千米耗油0.1升的速度行驶,可行驶700千米.(1)求该轿车可行驶的总路程S与平均耗油量a之间的函数解析式(关系式);(2)当平均耗油量为0.08升/千米时,该轿车可以行驶多少千米?考点:反比例函数的应用.分析:(1)将a=0.1,s=700代入到函数的关系S=中即可求得k的值,从而确定解析式;(2)将a=0.08代入求得的函数的解析式即可求得s的值.解答:解:(1)由题意得:a=0.1,s=700,代入反比例函数关系S=中,解得:k=sa=70,所以函数关系式为:s=;(2)将a=0.08代入s=得:s===875千米,故该轿车可以行驶多875米;点评:本题考查了反比例函数的应用,解题的关键是从实际问题中抽象出反比例函数模型.6.(2014•舟山,第22题10分)实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(时)的关系可近似地用二次函数y=﹣200x2+400x 刻画;1.5小时后(包括1.5小时)y与x可近似地用反比例函数y=(k>0)刻画(如图所示).(1)根据上述数学模型计算:①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?②当x=5时,y=45,求k的值.(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.=>7.(2014•襄阳,第22题6分)如图,一次函数y1=﹣x+2的图象与反比例函数y2=的图象相交于A,B两点,与x轴相交于点C.已知tan∠BOC=,点B的坐标为(m,n).(1)求反比例函数的解析式;(2)请直接写出当x<m时,y2的取值范围.= =,;==,即得;8.(2014•四川自贡,第22题12分)如图,一次函数y=kx+b与反比例函数的图象交于A(m,6),B(3,n)两点.(1)求一次函数的解析式;(2)根据图象直接写出的x的取值范围;(3)求△AOB的面积.)代入得,时,9.(2014•浙江湖州,第20题分)如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=的图象上,过点A的直线y=x+b交x轴于点B.(1)求k和b的值;(2)求△OAB的面积.分析:(1)根据待定系数法,可得答案;(2)根据三角形的面积公式,可得答案.解:(1)把A(2,5)分别代入y=和y=x+b,得,解得k=10b=3;(2)作AC⊥x轴与点C,,由(1)得直线AB的解析式为y=x+3,∴点B的坐标为(﹣3,0),OB=3,点A的坐标是(2,5),∴AC=5,∴=5=.点评:本题考查了反比例函数与一次函数的交点问题,利用了待定系数法,三角形的面积公式.10.(2014•浙江宁波,第22题10分)如图,点A、B分别在x,y轴上,点D在第一象限内,DC⊥x轴于点C,AO=CD=2,AB=DA=,反比例函数y=(k>0)的图象过CD的中点E.(1)求证:△AOB≌△DCA;(2)求k的值;(3)△BFG和△DCA关于某点成中心对称,其中点F在y轴上,是判断点G是否在反比例函数的图象上,并说明理由.=的图象上.,=,==1=的图象上.11. (2014•泰州,第26题,14分)平面直角坐标系xOy中,点A、B分别在函数y1=(x >0)与y2=﹣(x<0)的图象上,A、B的横坐标分别为a、b.(第1题图)(1)若AB∥x轴,求△OAB的面积;(2)若△OAB是以AB为底边的等腰三角形,且a+b≠0,求ab的值;(3)作边长为3的正方形ACDE,使AC∥x轴,点D在点A的左上方,那么,对大于或等于4的任意实数a,CD边与函数y1=(x>0)的图象都有交点,请说明理由.的纵坐标分别为、﹣,根据两点())(﹣)﹣(=,),,)=﹣,(),而×=的纵坐标分别为、﹣,()(﹣)))))﹣﹣=(,,)﹣,﹣(﹣),(12.(2014•呼和浩特,第23题8分)如图,已知反比例函数y=(x>0,k是常数)的图象经过点A(1,4),点B(m,n),其中m>1,AM⊥x轴,垂足为M,BN⊥y轴,垂足为N,AM与BN的交点为C.(1)写出反比例函数解析式;(2)求证:△ACB∽△NOM;(3)若△ACB与△NOM的相似比为2,求出B点的坐标及AB所在直线的解析式.可得,则=,再根据反比例函数解析式可得=,则==,可得=(===﹣上,==,而,=,),﹣+.13.(2014•德州,第21题10分)如图,双曲线y=(x>0)经过△OAB的顶点A和OB的中点C,AB∥x轴,点A的坐标为(2,3).(1)确定k的值;(2)若点D(3,m)在双曲线上,求直线AD的解析式;(3)计算△OAB的面积.===2)代入得:,的中点,即=,=)==,得到14.(2014•菏泽,第17题7分)(2)如图,在平面直角坐标系xOy中,已知一次函数y=kx+b的图象经过点A(1,0),与反比例函数y=(x>0)的图象相交于点B(2,1).①求m的值和一次函数的解析式;②结合图象直接写出:当x>0时,不等式kx+b>的解集.,15.(2014年山东泰安,第26题)如图①,△OAB中,A(0,2),B(4,0),将△AOB向右平移m个单位,得到△O′A′B′.(1)当m=4时,如图②.若反比例函数y=的图象经过点A′,一次函数y=ax+b的图象经过A′、B′两点.求反比例函数及一次函数的表达式;(2)若反比例函数y=的图象经过点A′及A′B′的中点M,求m的值.分析:(1)根据题意得出:A′点的坐标为:(4,2),B′点的坐标为:(8,0),进而利用待定系数法求一次函数解析式即可;(2)首先得出A′B′的中点M的坐标为:(m+4﹣2,1)则2m=m+2,求出m的值即可.解:(1)由图②值:A′点的坐标为:(4,2),B′点的坐标为:(8,0),∴k=4×2=8,∴y=,把(4,2),(8,0)代入y=ax+b得:,解得:,∴经过A′、B′两点的一次函数表达式为:y=﹣x+4;(2)当△AOB向右平移m个单位时,A′点的坐标为:(m,2),B′点的坐标为:(m+4,0)则A′B′的中点M的坐标为:(m+4﹣2,1)∴2m=m+2,解得:m=2,∴当m=2时,反比例函数y=的图象经过点A′及A′B′的中点M.点评:此题主要考查了待定系数法求一次函数解析式以及坐标的平移等知识,得出A′,B′点坐标是解题关键.。
2014年广东中考数学专项复习:压轴题

2014年广东中考数学专项复习:压轴题1.设都是实数,且.我们规定:满足不等式的实数的所有取值的全体叫做闭区间,表示为.对于一个函数,如果它的自变量与函数值满足:当时,有,我们就称此函数是闭区间上的“闭函数”.(1)反比例函数是闭区间上的“闭函数”吗?请判断并说明理由;(2)若一次函数是闭区间上的“闭函数”,求此函数的解析式;(3)若实数c,d满足,且,当二次函数是闭区间上的“闭函数”时,求的值答案:解:(1)是;由函数的图象可知,当时,函数值随着自变量的增大而减少,而当时,;时,,故也有,所以,函数是闭区间上的“闭函数”.(2)因为一次函数是闭区间上的“闭函数”,所以根据一次函数的图象与性质,必有:①当时,,解之得.∴一次函数的解析式为.②当时,,解之得.∴一次函数的解析式为.…故一次函数的解析式为或.(3)由于函数的图象开口向上,且对称轴为,顶点为,由题意根据图象,分以下两种情况讨论:①当时,必有时,且时,,即方程必有两个不等实数根,解得,.而0,6分布在2的两边,这与矛盾,舍去;②当时,必有函数值的最小值为,由于此二次函数是闭区间上的“闭函数”,故必有,从而有,而当时,,即得点;又点关于对称轴的对称点为,由“闭函数”的定义可知必有时,,即,解得,.故可得,符合题意.综上所述,为所求的实数.2.如图1所示,将一个边长为2的正方形和一个长为2、宽为1的长方形拼在一起,构成一个大的长方形.现将小长方形绕点顺时针旋转至,旋转角为. (1)当点恰好落在边上时,求旋转角的值;(2)如图2,为中点,且0°<<90°,求证:;(3)小长方形绕点顺时针旋转一周的过程中,与能否全等?若能,直接写出旋转角的值;若不能,说明理由.答案:3.如图,在平面直角坐标系中,直线与抛物线y=ax2+bx-3(a≠0)交于A、B两点,点A在x轴上,点B的纵坐标为5.点P是直线AB下方的抛物线上的一动点(不与点A、B重合),过点P作x轴的垂线交直线AB于点C,作PD⊥AB于点D.(1)求抛物线的解析式;(2)设点P的横坐标为m.①用含m的代数式表示线段PD的长,并求出线段PD长的最大值;②连结PB,线段PC把△PDB分成两个三角形,是否存在适合的m的值,使这两个三角形的面积比为1:2.若存在,直接写出m的值;若不存在,请说明理由.答案:(1)在中,当y=0时,x=-1;当y=5时,x=4.A(-1,0)、B(4,5)将A(-1,0)、B(4,5)分别代入y=ax2+bx-3中,得解得,.∴所求解析式为y=x2-2x-3(2)①设直线AB交y轴于点E,求得E(0,1),∴OA=OE,∠AEO=45°,∠ACP=∠AEO=45°, ∴.设,则,∴.∴.∴PD的最大值为.②当m=0或m=3时,PC把△PDB分成两个三角形的面积比为1:2.4.在平面直角坐标系中,已知抛物线y=-x2+bx+c(b,c为常数)的顶点为P,等腰直角三角形ABC的顶点A的坐标为(0,–1),C的坐标为(4,3),直角顶点B在第四象限.(1)如图,若该抛物线过A,B两点,求b,c的值;(2)平移(1)中的抛物线,使顶点P在直线AC上滑动,且与直线AC交于另一点Q.①点M在直线AC下方,且为平移前(1)中的抛物线上的点,当以M,P,Q三点为顶点的三角形是以PQ为腰的等腰直角三角形时,求点M的坐标;②取BC的中点N,连接NP,BQ.当取最大值时,点Q的坐标为________.答案:解:(1)∵等腰直角三角形ABC的顶点A的坐标为(0,-1),C的坐标为(4,3)∴点B的坐标为(4,-1).∵抛物线过A(0,-1),B(4,-1)两点,∴抛物线的函数表达式为:(2)∵A(0,-1),C(4,3),∴直线AC的解析式为:y=x-1.设平移前抛物线的顶点为P0,则由(1)可得P的坐标为(2,1),且P在直线AC上.∵点P在直线AC上滑动,∴可设P的坐标为(m,m-1),则平移后抛物线的函数表达式为:∴P(m,m-1),Q(m-2,m-3).过点P作PE∥x轴,过点Q作QF∥y轴,则PE=m-(m-2)=2,QF=(m-1)-(m-3)=2①当PQ为直角边时:点M到PQ的距离为(即为PQ的长).由A(0,-1),B(4,-1),P(2,1)可知,△ABP0为等腰直角三角形,且BP⊥AC,BP=如答图1,过点B作直线l1∥AC,交抛物线y=∴可设直线l1的解析式为:y=x+b1,∵B(4,-1),∴-1=4+b1,解得b1=-5,∴直线l1的解析式为:y=x-5.②当PQ为斜边时:MP=MQ=2,可求得点M到PQ的距离为如答图2,取AB的中点F,则点F的坐标为(2,-1).由A(0,-1),F(2,-1),P0(2,1)可知:△AFP为等腰直角三角形,且点F到直线AC的距离为过点F作直线l2∥AC,交抛物线y=∴可设直线l2的解析式为:y=x+b2,∵F(2,-1),∴-1=2+b2,解得b2=-3,∴直线l2的解析式为:y=x-3.②5.如图1,已知直线y=x+3与x轴交于点A,与y轴交于点B,抛物线y=-x2+bx+c经过A、B两点,与x轴交于另一个点C,对称轴与直线AB交于点E,抛物线顶点为D.(1)求抛物线的解析式;(2)在第三象限内,F为抛物线上一点,以A、E、F为顶点的三角形面积为3,求点F 的坐标;(3)点P从点D出发,沿对称轴向下以每秒1个单位长度的速度匀速运动,设运动的时间为t秒,当t为何值时,以P、B、C为顶点的三角形是直角三角形?直接写出所有符合条件的t值.(4)连接B、C,点G是线段AB上一点,作GQ平行于x轴交线段BC与点Q,过G作GM ⊥x轴与M,过Q作QN⊥x轴与N,求矩形GQNM面积的最大值和G点的坐标.答案:解:(1)∵y=x+3与x轴交于点A,与y轴交于点B,∴当y=0时,x=-3,即A点坐标为(-3,0),当x=0时,y=3,即B点坐标为(0,3),将A(-3,0),B(0,3)代入y=-x2+bx+c,∴抛物线的解析式为y=-x2-2x+3;(2)如图1,设第三象限内的点F的坐标为(m,-m2-2m+3),则m<0,-m2-2m+3<0.∵y=-x2-2x+3=-(x+1)2+4,∴对称轴为直线x=-1,顶点D的坐标为(-1,4),设抛物线的对称轴与x轴交于点G,连接FG,则G(-1,0),AG=2.∵直线AB的解析式为y=x+3,∴当x=-1时,y=-1+3=2,∴E点坐标为(-1,2).(3)设P点坐标为(-1,n).∵B(0,3),C(1,0),∴BC2=12+32=10.分三种情况:①如图2,如果∠PBC=90°,那么PB2+BC2=PC2,即(0+1)2+(n-3)2+10=(1+1)2+(n-0)2,化简整理得6n=16,解得n=②如图3,如果∠BPC=90°,那么PB2+PC2=BC2,2222化简整理得n2-3n+2=0,解得n=2或1,∴P点坐标为(-1,2)或(-1,1),∵顶点D的坐标为(-1,4),∴PD=4-2=2或PD=4-1=3,∵点P的速度为每秒1个单位长度,∴t2=2,t3=3;③如图4,如果∠BCP=90°,那么BC2+PC2=PB2,即10+(1+1)2+(n-0)2=(0+1)2+(n-3)2,化简整理得6n=-4,解得n=(4)略6.如图,在Rt△ABC中,AB=AC=24,一动点P从点B出发,沿BC方向以每秒1个单位长度的速度匀速运动,到达点C即停止.在整个运动过程中,过点P作PD⊥BC与Rt△ABC的直角边相交于点D,延长PD至点Q,使得PD=QD,以PQ为斜边在PQ左侧作等腰直角三角形PQE.设运动时间为t秒(1)在整个运动过程中,设△ABC与△PQE重叠部分的面积为S,请直接写出.....S与t之间的函数关系式以及相应的自变量t的取值范围;(2)当点D在线段AB上时,连接AQ、AP,是否存在这样的t,使得△APQ成为等腰三角形?若存在,求出对应的t的值;若不存在,请说明理由;(3)当t=4秒时,以PQ为斜边在PQ右侧作等腰直角三角形PQF,将四边形PEQF绕点P 旋转,PE与线段AB相交于点M,PF与线段AC相交于点N.试判断在这一旋转过程中,四边形PMAN的面积是否发生变化?若发生变化,求出四边形PMAN的面积y与PM的长x之间的函数关系式以及相应的自变量x的取值范围;若不发生变化,求出此定值.答案:。
2014年全国各地中考数学压轴题及答案解析(一)

A
F
B
BE8 tBF (8 t)10 t
BP5(t4)PFBFBP10 t5(t4)30 t
C
POFBEF90�POBEOPFB
l
QE O
A
FP B
Rt POF sinB t t t PEQF 4S S
5 ABCD ABCDAB10CD6ADBC4 P
B BA A 2 P BC
ACCBBA P ACCBBA 345
l AC CB
lAC CBAB EF P l t
P A P l
1 t
P E t
P F
2 P AC PEF E P P
EF F F EFAB t 3 P EF Q PEQF t 4PEF S S t S
3DPB90� BPB60�DPA30�
B
A
B
D
A D
C B
E
P
B
B
FC E
A
P
B
B
DG
D K
AP
A
H
E C
C
B EB
PB
A60�ADP90�
AP2AD102t8t1
PDB90�
DMAB MDNBB N ቤተ መጻሕፍቲ ባይዱAM2DM2NC3DN3
PE E P t
1A
�
2PBE PE PBEPBE ABCD S
S t S
3 DPB
t
D
C
B
D
C
E
A
P
160� 2AB60�PBPB PBB PBPBBB2tBEBEtPEt 0t2 SSPBE BE�PE t�t t2 2t4 SSPBESFBC t2 (2t4)2 t 24t4 4t5 PBPE DC GH GKPH K PBB BPB60�A PGAD DGAP APGD PGAD4 ABCDGHPBPH GPHBPH BPB30� GHPGPH30�PGGH4 GK PG2PKKHPG�cos30�2 PH2PK4 SSPGH PH�GK �4�24 S t S
最新挑战中考数学压轴题(第七版精选)
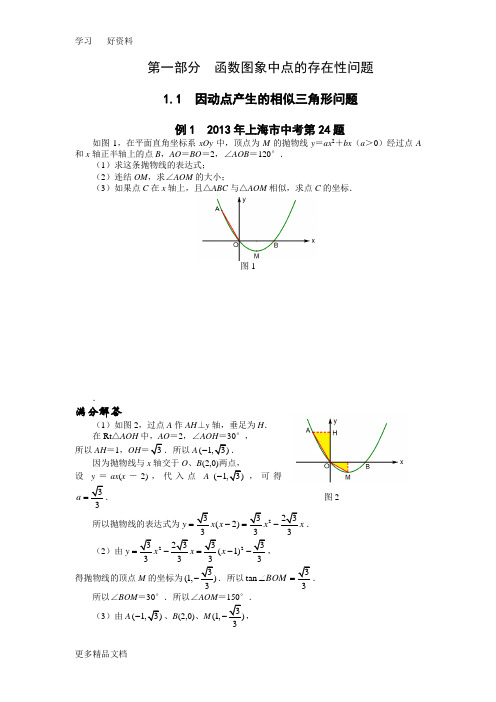
第一部分 函数图象中点的存在性问题1.1 因动点产生的相似三角形问题例1 2013年上海市中考第24题如图1,在平面直角坐标系xOy 中,顶点为M 的抛物线y =ax 2+bx (a >0)经过点A 和x 轴正半轴上的点B ,AO =BO =2,∠AOB =120°.(1)求这条抛物线的表达式;(2)连结OM ,求∠AOM 的大小;(3)如果点C 在x 轴上,且△ABC 与△AOM 相似,求点C 的坐标.图1.满分解答(1)如图2,过点A 作AH ⊥y 轴,垂足为H . 在Rt △AOH 中,AO =2,∠AOH =30°, 所以AH =1,OH =3.所以A (1,3)-.因为抛物线与x 轴交于O 、B (2,0)两点, 设y =ax (x -2),代入点A (1,3)-,可得33a =. 图2 所以抛物线的表达式为23323(2)333y x x x x =-=-.(2)由2232333(1)3333y x x x =-=--, 得抛物线的顶点M 的坐标为3(1,)3-.所以3tan 3BOM ∠=. 所以∠BOM =30°.所以∠AOM =150°. (3)由A (1,3)-、B (2,0)、M 3(1,)3-,得3tan 3ABO ∠=,23AB =,233OM =. 所以∠ABO =30°,3OAOM=.因此当点C 在点B 右侧时,∠ABC =∠AOM =150°. △ABC 与△AOM 相似,存在两种情况:①如图3,当3BA OA BC OM ==时,23233BA BC ===.此时C (4,0). ②如图4,当3BC OABA OM==时,33236BC BA ==⨯=.此时C (8,0).图3 图4考点伸展在本题情境下,如果△ABC 与△BOM 相似,求点C 的坐标.如图5,因为△BOM 是30°底角的等腰三角形,∠ABO =30°,因此△ABC 也是底角为30°的等腰三角形,AB =AC ,根据对称性,点C 的坐标为(-4,0).图5例2 2012年苏州市中考第29题如图1,已知抛物线211(1)444by x b x =-++(b 是实数且b >2)与x 轴的正半轴分别交于点A 、B (点A 位于点B 是左侧),与y 轴的正半轴交于点C .(1)点B 的坐标为______,点C 的坐标为__________(用含b 的代数式表示); (2)请你探索在第一象限内是否存在点P ,使得四边形PCOB 的面积等于2b ,且△PBC 是以点P 为直角顶点的等腰直角三角形?如果存在,求出点P 的坐标;如果不存在,请说明理由;(3)请你进一步探索在第一象限内是否存在点Q ,使得△QCO 、△QOA 和△QAB 中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q 的坐标;如果不存在,请说明理由.图1.满分解答(1)B 的坐标为(b , 0),点C 的坐标为(0,4b ). (2)如图2,过点P 作PD ⊥x 轴,PE ⊥y 轴,垂足分别为D 、E ,那么△PDB ≌△PEC . 因此PD =PE .设点P 的坐标为(x, x). 如图3,联结OP .所以S 四边形PCOB =S △PCO +S △PBO =1152428b x b x bx ⨯⋅+⨯⋅==2b .解得165x =.所以点P 的坐标为(1616,55).图2 图3 (3)由2111(1)(1)()4444b y x b x x x b =-++=--,得A (1, 0),OA =1.①如图4,以OA 、OC 为邻边构造矩形OAQC ,那么△OQC ≌△QOA . 当BA QA QA OA =,即2QA BA OA =⋅时,△BQA ∽△QOA . 所以2()14bb =-.解得843b =±Q 为(1,23+.②如图5,以OC 为直径的圆与直线x =1交于点Q ,那么∠OQC =90°。
2014年中考数学压轴题专题讲义

2014年中考数学压轴题专题讲义1. 如图,在△ABC 中,D 、E 分别是AB 、AC 的中点。
BE =2DE ,延长DE 到点F ,使得EF =BE ,连接CF .(1)求证:四边形BCFE 是菱形;(2)若CE =4,∠BCF =120°,求菱形BCFE 的面积.2. 如图,在△ABC 中,AD 是BC 边上的中线,E 是AD 的中点,过点A 作BC 的平行线交BE 的延长线于点F ,连接CF .(1)求证:AF =DC ;(2)若AB ⊥AC ,试判断四边形ADCF 的形状,并证明你的结论.3. 为创建“国家卫生城市”,进一步优化市中心城区的环境,永州市政府拟对部分路段的人行道地砖、花池、排水管道等公用设施全面更新改造,根据市政建设的需要,须在60天内完成工程.现在甲、乙两个工程队有能力承包这个工程.经调查知道:乙队单独完成此项工程的时间比甲队单独完成多用25天,甲、乙两队合作完成工程需要30天,甲队每天的工程费用2500元,乙队每天的工程费用2000元.(1)甲、乙两个工程队单独完成各需多少天?(2)请你设计一种符合要求的施工方案,并求出所需的工程费用.CD E F4.某商品的进价为每件40元,如果售价为每件50元,每个月可卖出210件;如果售价超过50元但不超过80元,每件商品的售价每上涨1元,则每月少卖1件;如果售价超过80元后,若再涨价,则每涨1元每月少卖3件,设每件商品的售价为x元,每月的销售量为y件.(1)求y与x的函数关系式并写出自变量x的取值范围;(2)设每月的销售利润为W,请写出W与x的函数关系式;(3)每件商品的售价定为多少元时,每个月可获得最大利润?最大的月利润是多少元?5. 如图,对称轴为直线72x=的抛物线经过点A(6,0)和B(0,4).(1)求抛物线解析式及顶点坐标;(2)设点E(x,y)是抛物线上一动点,且位于第四象限,四边形OEAF是以OA为对角线的平行四边形.求平行四边形OEAF的面积S与x之间的函数关系式,并写出自变量x的取值范围;①当平行四边形OEAF的面积为24时,请判断平行四边形OEAF是否为菱形?②是否存在点E,使平行四边形OEAF为正方形?若存在,求出点E的坐标;若不存在,请说明理由.图1 图26. 如图,抛物线254y ax ax =-+经过ABC △的三个顶点,已知BC x ∥轴,点A 在x 轴上,点C 在y 轴上,且AC BC =.(1)求抛物线的对称轴;(2)写出A B C ,,三点的坐标并求抛物线的解析式;(3)探究:若点P 是抛物线对称轴上且在x 轴下方的动点,是否存在PAB △是等腰三角形.若存在,求出所有符合条件的点P 坐标;不存在,请说明理由.7. 如图10,已知点A (3,0),以A 为圆心作⊙A 与Y 轴切于原点,与x 轴的另一个交点为B ,过B 作⊙A 的切线l.(1)以直线l 为对称轴的抛物线过点A 及点C (0,9),求此抛物线的解析式;(2)抛物线与x 轴的另一个交点为D ,过D 作⊙A 的切线DE ,E 为切点,求此切线长;(3)点F 是切线DE上的一个动点,当△BFD 与EAD△相似时,求出BF 的长 .8.如图AB是⊙O的直径,AP是⊙O的切线,A是切点,BP与⊙O交于点C.(1)若AB=2,∠P=30°,求AP的长;(2)若D为AP的中点,求证:直线CD是⊙O的切线.9.如图,AB是⊙O的直径,AM,BN分别切⊙O于点A,B,CD交AM,BN于点D,C,DO平分∠ADC.(1)求证:CD是⊙O的切线;(2)若AD=4,BC=9,求⊙O的半径R.10.(2013•宁波)若一个四边形的一条对角线把四边形分成两个等腰三角形,我们把这条对角线叫这个四边形的和谐线,这个四边形叫做和谐四边形.如菱形就是和谐四边形.(1)如图1,在梯形ABCD中,AD∥BC,∠BAD=120°,∠C=75°,BD平分∠ABC.求证:BD是梯形ABCD的和谐线;(2)如图2,在12×16的格图上(每个小正方形的边长为1)有一个扇形BAC,点A.B.C均在格点上,请在答题卷给出的两个格图上各找一个点D,使得以A、B、C、D为顶点的四边形的两条对角线都是和谐线,并画出相应的和谐四边形;(3)四边形ABCD中,AB=AD=BC,∠BAD=90°,AC是四边形ABCD的和谐线,求∠BCD的度数.11.(1)如图①,在正方形ABCD中,△AEF的顶点E,F分别在BC,CD边上,高AG与正方形的边长相等,求∠EAF的度数.(2)如图②,在Rt△ABD中,∠BAD=90°,AB=AD,点M,N是BD边上的任意两点,且∠MAN=45°,将△ABM绕点A逆时针旋转90°至△ADH位置,连接NH,试判断MN,ND,DH之间的数量关系,并说明理由.(3)在图①中,连接BD分别交AE,AF于点M,N,若EG=4,GF=6,BM=32,求AG,MN的长.12.如图,已知Rt△ABC中,∠B=90°,∠A=60°,AB=2cm。
中考数学压轴题集锦精选100题(含答案)
中考数学压轴题集锦精选100题(含答案)一、中考压轴题1.如图,在△ABC中,∠BAC=30°,以AB为直径的⊙O经过点C.过点C作⊙O的切线交AB的延长线于点P.点D为圆上一点,且=,弦AD的延长线交切线PC于点E,连接BC.(1)判断OB和BP的数量关系,并说明理由;(2)若⊙O的半径为2,求AE的长.【分析】(1)首先连接OC,由PC切⊙O于点C,可得∠OCP=90°,又由∠BAC=30°,即可求得∠COP=60°,∠P=30°,然后根据直角三角形中30°角所对的直角边等于斜边的一半,证得OB=BP;(2)由(1)可得OB=OP,即可求得AP的长,又由=,即可得∠CAD=∠BAC=30°,继而求得∠E=90°,继而在Rt△AEP中求得答案.【解答】解:(1)OB=BP.理由:连接OC,∵PC切⊙O于点C,∴∠OCP=90°,∵OA=OC,∠OAC=30°,∴∠OAC=∠OCA=30°,∴∠COP=60°,∴∠P=30°,在Rt△OCP中,OC=OP=OB=BP;(2)由(1)得OB=OP,∵⊙O的半径是2,∴AP=3OB=3×2=6,∵=,∴∠CAD=∠BAC=30°,∴∠BAD=60°,∵∠P=30°,∴∠E=90°,在Rt△AEP中,AE=AP=×6=3.【点评】此题考查了切线的性质、直角三角形的性质以及圆周角定理.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.2.如图,在矩形ABCD中,AB=8,AD=6,点P、Q分别是AB边和CD边上的动点,点P从点A向点B运动,点Q从点C向点D运动,且保持AP=CQ.设AP=x.(1)当PQ∥AD时,求x的值;(2)当线段PQ的垂直平分线与BC边相交时,求x的取值范围;(3)当线段PQ的垂直平分线与BC相交时,设交点为E,连接EP、EQ,设△EPQ的面积为S,求S关于x的函数关系式,并写出S的取值范围.【分析】(1)根据已知条件,证明四边形APQD是矩形,再根据矩形的性质和AP=CQ 求x即可;(2)连接EP、EQ,则EP=EQ,设BE=y,列出等式(8﹣x)2+y2=(6﹣y)2+x2然后根据函数的性质来求x的取值范围;(3)由图形的等量关系列出方程,再根据函数的性质来求最值.【解答】解:(1)当PQ∥AD时,则∠A=∠APQ=90°,∠D=∠DQP=90°,又∵AB∥CD,∴四边形APQD是矩形,∴AP=QD,∵AP=CQ,AP=CD=,∴x=4.(2)如图,连接EP、EQ,则EP=EQ,设BE=y.∴(8﹣x)2+y2=(6﹣y)2+x2,∴y=.∵0≤y≤6,∴0≤≤6,∴≤x≤.(3)S△BPE=•BE•BP=••(8﹣x)=,S△ECQ==•(6﹣)•x=,∵AP=CQ,∴S BPQC=,∴S=S BPQC﹣S△BPE﹣S△ECQ=24﹣﹣,整理得:S==(x﹣4)2+12(),∴当x=4时,S有最小值12,当x=或x=时,S有最大值.∴12≤S≤.【点评】解答本题时,涉及到了矩形的判定、矩形的性质、勾股定理以及二次函数的最值等知识点,这是一道综合性比较强的题目,所以在解答题目时,一定要把各个知识点融会贯通,这样解题时才会少走弯路.3.汽车产业的发展,有效促进我国现代化建设.某汽车销售公司2005年盈利1500万元,到2007年盈利2160万元,且从2005年到2007年,每年盈利的年增长率相同.(1)该公司2006年盈利多少万元?(2)若该公司盈利的年增长率继续保持不变,预计2008年盈利多少万元?【分析】(1)需先算出从2005年到2007年,每年盈利的年增长率,然后根据2005年的盈利,算出2006年的利润;(2)相等关系是:2008年盈利=2007年盈利×每年盈利的年增长率.【解答】解:(1)设每年盈利的年增长率为x,根据题意得1500(1+x)2=2160解得x1=0.2,x2=﹣2.2(不合题意,舍去)∴1500(1+x)=1500(1+0.2)=1800答:2006年该公司盈利1800万元.(2)2160(1+0.2)=2592答:预计2008年该公司盈利2592万元.【点评】本题的关键是需求出从2005年到2007年,每年盈利的年增长率.等量关系为:2005年盈利×(1+年增长率)2=2160.4.如图,已知直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,连接PC并延长PC交y轴于点D(0,3).(1)求证:△POD≌△ABO;(2)若直线l:y=kx+b经过圆心P和D,求直线l的解析式.【分析】(1)首先连接PB,由直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,可求得∠APB=∠DPO=60°,∠ABO=∠POD=90°,即可得△P AB是等边三角形,可得AB=OP,然后由ASA,即可判定:△POD≌△ABO;(2)易求得∠PDO=30°,由OP=OD•tan30°,即可求得点P的坐标,然后利用待定系数法,即可求得直线l的解析式.【解答】(1)证明:连接PB,∵直径为OA的⊙P与x轴交于O、A两点,点B、C把三等分,∴∠APB=∠DPO=×180°=60°,∠ABO=∠POD=90°,∵P A=PB,∴△P AB是等边三角形,∴AB=P A,∠BAO=60°,∴AB=OP,∠BAO=∠OPD,在△POD和△ABO中,∴△POD≌△ABO(ASA);(2)解:由(1)得△POD≌△ABO,∴∠PDO=∠AOB,∵∠AOB=∠APB=×60°=30°,∴∠PDO=30°,∴OP=OD•tan30°=3×=,∴点P的坐标为:(﹣,0)∴,解得:,∴直线l的解析式为:y=x+3.【点评】此题考查了圆周角定理、全等三角形的判定与性质、直角三角形的性质、等边三角形的判定与性质以及待定系数法求一次函数的解析式.此题综合性较强,难度适中,注意准确作出辅助线,注意数形结合思想的应用.5.广安市某楼盘准备以每平方米6000元的均价对外销售,由于国务院有关房地产的新政策出台后,购房者持币观望,房地产开发商为了加快资金周转,对价格经过两次下调后,决定以每平方米4860元的均价开盘销售.(1)求平均每次下调的百分率.(2)某人准备以开盘价均价购买一套100平方米的住房,开发商给予以下两种优惠方案以供选择:①打9.8折销售;②不打折,一次性送装修费每平方米80元,试问哪种方案更优惠?【分析】(1)根据题意设平均每次下调的百分率为x,列出一元二次方程,解方程即可得出答案;(2)分别计算两种方案的优惠价格,比较后发现方案①更优惠.【解答】解:(1)设平均每次下调的百分率为x,则6000(1﹣x)2=4860,解得:x1=0.1=10%,x2=1.9(舍去),故平均每次下调的百分率为10%;(2)方案①购房优惠:4860×100×(1﹣0.98)=9720(元);方案②可优惠:80×100=8000(元).故选择方案①更优惠.【点评】本题主要考查一元二次方程的实际应用,解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系,列出方程,再求解,属于中档题.6.用两种方法解答:已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,求代数式(m2+mp+1)(n2+np+1)的值.【分析】本题主要是利用韦达定理来计算.已知m、n是关于x的方程x2+(p﹣2)x+1=0两个实数根,有四个等式可供使用:m+n=2﹣p①,mn=1②,m2+(p﹣2)m+1=0③,n2+(p﹣2)n+1=0④.通过变形方法,合理地选择解题方法.【解答】解:∵m、n是x2+(p﹣2)x+1=0的根,∴m+n=2﹣p,mn=1.方法一:m2+(p﹣2)m+1=0,n2+(p﹣2)n+1=0.即m2+pm+1=2m,n2+pn+1=2n.原式=2m×2n=4mn=4.方法二:(m2+mp+1)(n2+np+1)=(m2+mp)(n2+np)+m2+mp+n2+np+1=m2n2+m2np+mpn2+mnp2+m2+mp+n2+np+1=1+mp+np+p2+m2+n2+mp+np+1=2+p2+m2+n2+2(m+n)p=2+p2+m2+n2+2(2﹣p)p=2+p2+m2+n2+4p﹣2p2=2+(m+n)2﹣2mn+4p﹣2p2+p2=2+(2﹣p)2﹣2+4p﹣2p2+p2=4﹣4p+p2+4p﹣p2=4.【点评】本题主要是通过根与系数的关系来求值.注意把所求的代数式转化成m+n=2﹣p,mn=1的形式,正确对所求式子进行变形是解题的关键.7.如图,⊙O是等边△ABC的外接圆,AB=2,M、N分别是边AB、AC的中点,直线MN交⊙O于E、F两点,BD∥AC交直线MN于点D.求出图中线段DM上已有的一条线段的长.【分析】连接OA交MN于点G,则OA⊥BC,由三角形的中位线的性质可得MN的长,易证得△BMD≌△AMN,有DM=MN,由相交弦定理得ME•MF=MA•MB,就可求得EM,DE的值.【解答】解:∵M,N分别是边AB,AC的中点∴MN∥BC,MN=BC=1又∵BD∥AC∴∠DBA=∠A=60°∵BM=AM,∠BMD=∠AMN∴△BMD≌△AMN∴DM=MN=1连接OA交MN于点G,则OA⊥BC∴OA⊥EF∴EG=FG,MG=FN由相交弦定理得:ME•MF=MA•MB∴EM(EM+1)=1解得EM=(EM=不合题意,舍去)∴DE=DM﹣EM=∴DE(3﹣DE)=1解得DE=(DE=不合题意,舍去).【点评】本题利用了三角形的中位线的性质,等边三角形的性质,全等三角形的判定和性质,一元二次方程的解法求解.8.如图,已知△BEC是等边三角形,∠AEB=∠DEC=90°,AE=DE,AC,BD的交点为O.(1)求证:△AEC≌△DEB;(2)若∠ABC=∠DCB=90°,AB=2 cm,求图中阴影部分的面积.【分析】(1)在△AEC和△DEB中,已知AE=DE,BE=CE,且夹角相等,根据边角边可证全等.(2)由图可知,在连接EO并延长EO交BC于点F,连接AD之后,整个图形是一个以EF所在直线对称的图形.即△AEO和△DEO面积相等,只要求出其中一个即可,而三角形AEO面积=•OE•FB,所以解题中心即为求出OE和FB,有(1)中结论和已知条件即可求解.【解答】(1)证明:∵∠AEB=∠DEC=90°,∴∠AEB+∠BEC=∠DEC+∠BEC,即∠AEC=∠DEB,∵△BEC是等边三角形,∴CE=BE,又AE=DE,∴△AEC≌△DEB.(2)解:连接EO并延长EO交BC于点F,连接AD.由(1)知AC=BD.∵∠ABC=∠DCB=90°,∴∠ABC+∠DCB=180°,∴AB∥DC,AB==CD,∴四边形ABCD为平行四边形且是矩形,∴OA=OB=OC=OD,又∵BE=CE,∴OE所在直线垂直平分线段BC,∴BF=FC,∠EFB=90°.∴OF=AB=×2=1,∵△BEC是等边三角形,∴∠EBC=60°.在Rt△AEB中,∠AEB=90°,∠ABE=∠ABC﹣∠EBC=90°﹣60°=30°,∴BE=AB•cos30°=,在Rt△BFE中,∠BFE=90°,∠EBF=60°,∴BF=BE•cos60°=,EF=BE•sin60°=,∴OE=EF﹣OF==,∵AE=ED,OE=OE,AO=DO,∴△AOE≌△DOE.∴S△AOE=S△DOE∴S阴影=2S△AOE=2וEO•BF=2×××=(cm2).【点评】考查综合应用等边三角形、等腰三角形、解直角三角形、直角三角形性质,进行逻辑推理能力和运算能力.9.如图,有一直径MN=4的半圆形纸片,其圆心为点P,从初始位置Ⅰ开始,在无滑动的情况下沿数轴向右翻滚至位置Ⅴ,其中,位置Ⅰ中的MN平行于数轴,且半⊙P与数轴相切于原点O;位置Ⅱ和位置Ⅳ中的MN垂直于数轴;位置Ⅲ中的MN在数轴上;位置Ⅴ中的点N到数轴的距离为3,且半⊙P与数轴相切于点A.解答下列问题:(1)位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;(2)求位置Ⅲ中的圆心P在数轴上表示的数;(3)纸片半⊙P从位置Ⅲ翻滚到位置Ⅳ时,求点N所经过路径长及该纸片所扫过图形的面积;(4)求OA的长.[(2),(3),(4)中的结果保留π].【分析】(1)先求出圆的半径,再根据切线的性质进行解答;(2)根据位置Ⅰ中的长与数轴上线段ON相等求出的长,再根据弧长公式求出的长,进而可得出结论;(3)作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形,在Rt△NPH中,根据sin∠NPH==即可∠NPH、∠MP A的度数,进而可得出的长,【解答】解:(1)∵⊙P的直径=4,∴⊙P的半径=2,∵⊙P与直线有一个交点,∴位置Ⅰ中的MN与数轴之间的距离为2;位置Ⅱ中的半⊙P与数轴的位置关系是相切;故答案为:2,相切;(2)位置Ⅰ中的长与数轴上线段ON相等,∵的长为=π,NP=2,∴位置Ⅲ中的圆心P在数轴上表示的数为π+2.(3)点N所经过路径长为=2π,S半圆==2π,S扇形==4π,半⊙P所扫过图形的面积为2π+4π=6π.(4)如图,作NC垂直数轴于点C,作PH⊥NC于点H,连接P A,则四边形PHCA为矩形.在Rt△NPH中,PN=2,NH=NC﹣HC=NC﹣P A=1,于是sin∠NPH==,∴∠NPH=30°.∴∠MP A=60°.从而的长为=,于是OA的长为π+4+π=π+4.【点评】本题考查的是直线与圆的关系、弧长的计算、扇形的面积公式,在解答此题时要注意Ⅰ中的长与数轴上线段ON相等的数量关系.10.如图,△ABC内接于⊙O,AB=6,AC=4,D是AB边上一点,P是优弧BAC的中点,连接P A、PB、PC、PD.(1)当BD的长度为多少时,△P AD是以AD为底边的等腰三角形?并证明;(2)在(1)的条件下,若cos∠PCB=,求P A的长.【分析】(1)根据等弧对等弦以及全等三角形的判定和性质进行求解;(2)过点P作PE⊥AD于E.根据锐角三角函数的知识和垂径定理进行求解.【解答】解:(1)当BD=AC=4时,△P AD是以AD为底边的等腰三角形.∵P是优弧BAC的中点,∴=.∴PB=PC.又∵∠PBD=∠PCA(圆周角定理),∴当BD=AC=4,△PBD≌△PCA.∴P A=PD,即△P AD是以AD为底边的等腰三角形.(2)过点P作PE⊥AD于E,由(1)可知,当BD=4时,PD=P A,AD=AB﹣BD=6﹣4=2,则AE=AD=1.∵∠PCB=∠P AD(在同圆或等圆中,同弧所对的圆周角相等),∴cos∠P AD=cos∠PCB=,∴P A=.【点评】综合运用了等弧对等弦的性质、全等三角形的判定和性质、锐角三角函数的知识以及垂径定理.11.在△ABC中,AB=BC,将△ABC绕点A沿顺时针方向旋转得△A1B1C1,使点C1落在直线BC上(点C1与点C不重合),(1)如图,当∠C>60°时,写出边AB1与边CB的位置关系,并加以证明;(2)当∠C=60°时,写出边AB1与边CB的位置关系(不要求证明);(3)当∠C<60°时,请你在如图中用尺规作图法作出△AB1C1(保留作图痕迹,不写作法),再猜想你在(1)、(2)中得出的结论是否还成立并说明理由.【分析】(1)AB1∥BC.因为等腰三角形,两底角相等,再根据平行线的判定,内错角相等两直线平行,可证明两直线平行.(2)当∠C=60°时,写出边AB1与边CB的位置关系也是平行,证明方法同(1)题.(3)成立,根据旋转变换的性质画出图形.利用三角形全等即可证明.【解答】解:(1)AB1∥BC.证明:由已知得△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(5分)(2)如图1,∠C=60°时,AB1∥BC.(7分)(3)如图,当∠C<60°时,(1)、(2)中的结论还成立.证明:显然△ABC≌△AB1C1,∴∠BAC=∠B1AC1,∴∠B1AB=∠C1AC,∵AC1=AC,∴∠AC1C=∠ACC1,∵∠C1AC+∠AC1C+∠ACC1=180°,∴∠C1AC=180°﹣2∠ACC1,同理,在△ABC中,∵BA=BC,∴∠ABC=180°﹣2∠ACC1,∴∠ABC=∠C1AC=∠B1AB,∴AB1∥BC.(13分)【点评】考查图形的旋转,等腰三角形的性质,平行线的判定.本题实质是考查对图形旋转特征的理解,旋转前后的图形是全等的.12.九年级(1)班课外活动小组利用标杆测量学校旗杆的高度,已知标杆高度CD=3m,标杆与旗杆的水平距离BD=15m,人的眼睛与地面的高度EF=1.6m,人与标杆CD的水平距离DF=2m,求旗杆AB的高度.【分析】利用三角形相似中的比例关系,首先由题目和图形可看出,求AB的长度分成了2个部分,AH和HB部分,其中HB=EF=1.6m,剩下的问题就是求AH的长度,利用△CGE∽△AHE,得出,把相关条件代入即可求得AH=11.9,所以AB=AH+HB=AH+EF=13.5m.【解答】解:∵CD⊥FB,AB⊥FB,∴CD∥AB∴△CGE∽△AHE∴即:∴∴AH=11.9∴AB=AH+HB=AH+EF=11.9+1.6=13.5(m).【点评】主要用到的解题思想是把梯形问题转化成三角形问题,利用三角形相似比列方程来求未知线段的长度.13.一个不透明的口袋里有红、黄、绿三种颜色的球(除颜色外其余都相同),其中红球有2个,黄球有1个,任意摸出一个黄球的概率为.(1)试求口袋里绿球的个数;(2)若第一次从口袋中任意摸出一球(不放回),第二次任意摸出一球,请你用树状图或列表法,求出两次都摸到红球的概率.【分析】(1)根据概率的求解方法,利用方程求得绿球个数;(2)此题需要两步完成,所以采用树状图法或者列表法都比较简单,解题时要注意是放回实验还是不放回实验,此题为不放回实验.【解答】解:(1)设口袋里绿球有x个,则,解得x=1.故口袋里绿球有1个.(2)红一红二黄绿红一红二,红一黄,红一绿,红一红二红一,红二黄,红一绿,红二黄红一,黄红二,黄绿,黄绿红一,绿红二,绿黄,绿故,P(两次都摸到红球)=.【点评】(1)解题时要注意应用方程思想;(2)列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件.用到的知识点为:概率=所求情况数与总情况数之比.14.已知:y关于x的函数y=(k﹣1)x2﹣2kx+k+2的图象与x轴有交点.(1)求k的取值范围;(2)若x1,x2是函数图象与x轴两个交点的横坐标,且满足(k﹣1)x12+2kx2+k+2=4x1x2.①求k的值;②当k≤x≤k+2时,请结合函数图象确定y的最大值和最小值.【分析】(1)分两种情况讨论,当k=1时,可求出函数为一次函数,必与x轴有一交点;当k≠1时,函数为二次函数,若与x轴有交点,则△≥0.(2)①根据(k﹣1)x12+2kx2+k+2=4x1x2及根与系数的关系,建立关于k的方程,求出k 的值;②充分利用图象,直接得出y的最大值和最小值.【解答】解:(1)当k=1时,函数为一次函数y=﹣2x+3,其图象与x轴有一个交点.当k≠1时,函数为二次函数,其图象与x轴有一个或两个交点,令y=0得(k﹣1)x2﹣2kx+k+2=0.△=(﹣2k)2﹣4(k﹣1)(k+2)≥0,解得k≤2.即k≤2且k≠1.综上所述,k的取值范围是k≤2.(2)①∵x1≠x2,由(1)知k<2且k≠1,函数图象与x轴两个交点,∴k<2,且k≠1.由题意得(k﹣1)x12+(k+2)=2kx1①,将①代入(k﹣1)x12+2kx2+k+2=4x1x2中得:2k(x1+x2)=4x1x2.又∵x1+x2=,x1x2=,∴2k•=4•.解得:k1=﹣1,k2=2(不合题意,舍去).∴所求k值为﹣1.②如图,∵k1=﹣1,y=﹣2x2+2x+1=﹣2(x﹣)2+.且﹣1≤x≤1.由图象知:当x=﹣1时,y最小=﹣3;当x=时,y最大=.∴y的最大值为,最小值为﹣3.【点评】本题考查了抛物线与x轴的交点、一次函数的定义、二次函数的最值,充分利用图象是解题的关键.15.如图①,有四张编号为1、2、3、4的卡片,卡片的背面完全相同.现将它们搅匀并正面朝下放置在桌面上.(1)从中随机抽取一张,抽到的卡片是眼睛的概率是多少?(2)从四张卡片中随机抽取一张贴在如图②所示的大头娃娃的左眼处,然后再随机抽取一张贴在大头娃娃的右眼处,用树状图或列表法求贴法正确的概率.【分析】根据概率的求法,找准两点:①全部情况的总数;②符合条件的情况数目;二者的比值就是其发生的概率.【解答】解:(1)所求概率为;(2)方法①(树状图法)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3)∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为,方法②(列表法)1 2 3 4第一次抽取第二次抽取1(2,1)(3,1)(4,1)2(1,2)(3,2)(4,2)3(1,3)(2,3)(4,3)4(1,4)(2,4)(3,4)共有12种可能的结果:(1,2),(1,3),(1,4),(2,1),(2,3),(2,4),(3,1),(3,2),(3,4),(4,1),(4,2),(4,3),∵其中有两种结果(1,2),(2,1)是符合条件的,∴贴法正确的概率为.【点评】此题考查概率的求法:如果一个事件有n种可能,而且这些事件的可能性相同,其中事件A出现m种结果,那么事件A的概率P(A)=.16.经统计分析,某市跨河大桥上的车流速度v(千米/小时)是车流密度x(辆/千米)的函数,当桥上的车流密度达到220辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为80千米/小时,研究表明:当20≤x≤220时,车流速度v是车流密度x的一次函数.(1)求大桥上车流密度为100辆/千米时的车流速度;(2)在交通高峰时段,为使大桥上的车流速度大于40千米/小时且小于60千米/小时,应控制大桥上的车流密度在什么范围内?(3)车流量(辆/小时)是单位时间内通过桥上某观测点的车辆数,即:车流量=车流速度×车流密度.求大桥上车流量y的最大值.【分析】(1)当20≤x≤220时,设车流速度v与车流密度x的函数关系式为v=kx+b,根据题意的数量关系建立方程组求出其解即可;(2)由(1)的解析式建立不等式组求出其解即可;(3)设车流量y与x之间的关系式为y=vx,当x<20和20≤x≤220时分别表示出函数关系由函数的性质就可以求出结论.【解答】解:(1)设车流速度v与车流密度x的函数关系式为v=kx+b,由题意,得,解得:,∴当20≤x≤220时,v=﹣x+88,当x=100时,v=﹣×100+88=48(千米/小时);(2)由题意,得,解得:70<x<120.∴应控制大桥上的车流密度在70<x<120范围内;(3)设车流量y与x之间的关系式为y=vx,当0≤x≤20时y=80x,∴k=80>0,∴y随x的增大而增大,∴x=20时,y最大=1600;当20≤x≤220时y=(﹣x+88)x=﹣(x﹣110)2+4840,∴当x=110时,y最大=4840.∵4840>1600,∴当车流密度是110辆/千米,车流量y取得最大值是每小时4840辆.【点评】本题考查了车流量=车流速度×车流密度的运用,一次函数的解析式的运用,一元一次不等式组的运用,二次函数的性质的运用,解答时求出函数的解析式是关键.17.如图,反比例函数的图象经过点A(4,b),过点A作AB⊥x轴于点B,△AOB 的面积为2.(1)求k和b的值;(2)若一次函数y=ax﹣3的图象经过点A,求这个一次函数的解析式.【分析】(1)由△AOB的面积为2,根据反比例函数的比例系数k的几何意义,可知k的值,得出反比例函数的解析式,然后把x=4代入,即可求出b的值;(2)把点A的坐标代入y=ax﹣3,即可求出这个一次函数的解析式.【解答】解:(1)∵反比例函数的图象经过点A,AB⊥x轴于点B,△AOB的面积为2,A(4,b),∴OB×AB=2,×4×b=2,∴AB=b=1,∴A(4,1),∴k=xy=4,∴反比例函数的解析式为y=,即k=4,b=1.(2)∵A(4,1)在一次函数y=ax﹣3的图象上,∴1=4a﹣3,∴a=1.∴这个一次函数的解析式为y=x﹣3.【点评】本题主要考查了待定系数法求一次函数的解析式和反比例函数中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.18.图(1)是一个10×10格点正方形组成的网格.△ABC是格点三角形(顶点在网格交点处),请你完成下面的两个问题:(1)在图(1)中画出与△ABC相似的格点△A1B1C1和△A2B2C2,且△A1B1C1与△ABC的相似比是2,△A2B2C2与△ABC的相似比是;(2)在图(2)中用与△ABC,△A1B1C1,△A2B2C2全等的格点三角形(每个三角形至少使用一次),拼出一个你熟悉的图案,并为你设计的图案配一句贴切的解说词.【分析】(1)△A1B1C1与△ABC的相似比是2,则让△ABC的各边都扩大2倍就可.△A2B2C2与△ABC的相似比是;△ABC的直角边是2,所以△A2B2C2与的直角边是即一个对角线的长度.斜边为2.依此画图即可;(2)拼图有审美意义即可,答案不唯一.【解答】解:【点评】本题主要考查了相似图形的画法,做这类题时根据的是相似图形的性质,即相似比相等.对应角相等.19.如图,矩形ABCD的边AD、AB分别与⊙O相切于点E、F,(1)求的长;(2)若,直线MN分别交射线DA、DC于点M、N,∠DMN=60°,将直线MN沿射线DA方向平移,设点D到直线的距离为d,当时1≤d≤4,请判断直线MN与⊙O的位置关系,并说明理由.【分析】(1)连接OE、OF,利用相切证明四边形AFOE是正方形,再根据弧长公式求弧长;(2)先求出直线M1N1与圆相切时d的值,结合1≤d≤4,划分d的范围,分类讨论.【解答】解:(1)连接OE、OF,∵矩形ABCD的边AD、AB分别与⊙O相切于点E、F,∴∠A=90°,∠OEA=∠OF A=90°∴四边形AFOE是正方形∴∠EOF=90°,OE=AE=∴的长==π.(2)如图,将直线MN沿射线DA方向平移,当其与⊙O相切时,记为M1N1,切点为R,交AD于M1,交BC于N1,连接OM1、OR,∵M1N1∥MN∴∠DM1N1=∠DMN=60°∴∠EM1N1=120°∵MA、M1N1切⊙O于点E、R∴∠EM1O=∠EM1N1=60°在Rt△EM1O中,EM1===1∴DM1=AD﹣AE﹣EM1=+5﹣﹣1=4.过点D作DK⊥M1N1于K在Rt△DM1K中DK=DM1×sin∠DM1K=4×sin∠60°=2即d=2,∴当d=2时,直线MN与⊙O相切,当1≤d<2时,直线MN与⊙O相离,当直线MN平移到过圆心O时,记为M2N2,点D到M2N2的距离d=DK+OR=2+=3>4,∴当2<d≤4时,MN直线与⊙O相交.【点评】本题考查的是直线与圆的位置关系,解决此类问题可通过比较圆心到直线距离d 与圆半径大小关系完成判定.20.如图所示,AB=AC,AB为⊙O的直径,AC、BC分别交⊙O于E、D,连接ED、BE.(1)试判断DE与BD是否相等,并说明理由;(2)如果BC=6,AB=5,求BE的长.【分析】(1)可通过连接AD,AD就是等腰三角形ABC底边上的高,根据等腰三角形三线合一的特点,可得出∠CAD=∠BAD,根据圆周角定理即可得出∠DEB=∠DBE,便可证得DE=DB.(2)本题中由于BE⊥AC,那么BE就是三角形ABC中AC边上的高,可用面积的不同表示方法得出AC•BE=CB•AD.进而求出BE的长.【解答】解:(1)DE=BD证明:连接AD,则AD⊥BC,在等腰三角形ABC中,AD⊥BC,∴∠CAD=∠BAD(等腰三角形三线合一),∴=,∴DE=BD;(2)∵AB=5,BD=BC=3,∴AD=4,∴S△ABC=•AC•BE=•CB•AD,∴BE=4.8.【点评】本题主要考查了等腰三角形的性质,圆周角定理等知识点的运用,用等腰三角形三线合一的特点得出圆周角相等是解题的关键.21.如图,在Rt△ABC中,∠C=90°,Rt△BAP中,∠BAP=90°,已知∠CBO=∠ABP,BP交AC于点O,E为AC上一点,且AE=OC.(1)求证:AP=AO;(2)求证:PE⊥AO;(3)当AE=AC,AB=10时,求线段BO的长度.【分析】(1)根据等角的余角相等证明即可;(2)过点O作OD⊥AB于D,根据角平分线上的点到角的两边的距离相等可得CO=DO,利用“SAS”证明△APE和△OAD全等,根据全等三角形对应角相等可得∠AEP=∠ADO=90°,从而得证;(3)设C0=3k,AC=8k,表示出AE=CO=3k,AO=AP=5k,然后利用勾股定理列式求出PE=4k,BC=BD=10﹣4k,再根据相似三角形对应边成比例列式求出k=1然后在Rt △BDO中,利用勾股定理列式求解即可.【解答】(1)证明:∵∠C=90°,∠BAP=90°∴∠CBO+∠BOC=90°,∠ABP+∠APB=90°,又∵∠CBO=∠ABP,∴∠BOC=∠APB,∵∠BOC=∠AOP,∴∠AOP=∠APB,∴AP=AO;(2)证明:如图,过点O作OD⊥AB于D,∵∠CBO=∠ABP,∵AE=OC,∴AE=OD,∵∠AOD+∠OAD=90°,∠P AE+∠OAD=90°,∴∠AOD=∠P AE,在△AOD和△P AE中,,∴△AOD≌△P AE(SAS),∴∠AEP=∠ADO=90°∴PE⊥AO;(3)解:设AE=OC=3k,∵AE=AC,∴AC=8k,∴OE=AC﹣AE﹣OC=2k,∴OA=OE+AE=5k.由(1)可知,AP=AO=5k.如图,过点O作OD⊥AB于点D,∵∠CBO=∠ABP,∴OD=OC=3k.在Rt△AOD中,AD===4k.∴BD=AB﹣AD=10﹣4k.∵OD∥AP,∴,即解得k=1,∵AB=10,PE=AD,∴PE=AD=4K,BD=AB﹣AD=10﹣4k=6,OD=3在Rt△BDO中,由勾股定理得:BO===3.【点评】本题考查了全等三角形的判定与性质,角平分线上的点到角的两边的距离相等的性质,勾股定理,相似三角形的判定与性质,(2)作辅助线构造出过渡线段DO并得到全等三角形是解题的关键,(3)利用相似三角形对应边成比例求出k=1是解题的关键.22.如图,AD是⊙O的直径.(1)如图①,垂直于AD的两条弦B1C1,B2C2把圆周4等分,则∠B1的度数是22.5°,∠B2的度数是67.5°;(2)如图②,垂直于AD的三条弦B1C1,B2C2,B3C3把圆周6等分,分别求∠B1,∠B2,∠B3的度数;(3)如图③,垂直于AD的n条弦B1C1,B2C2,B3C3,…,B n∁n把圆周2n等分,请你用含n的代数式表示∠B n的度数(只需直接写出答案).【分析】根据条件可以先求出圆的各段弧的度数,根据圆周角等于所对弧的度数的一半,就可以求出圆周角的度数.【解答】解:(1)垂直于AD的两条弦B1C1,B2C2把圆周4等分,则是圆的,因而度数是45°,因而∠B1的度数是22.5°,同理的度数是135度,因而,∠B2的度数是67.5°;(2)∵圆周被6等分∴===360°÷6=60°∵直径AD⊥B1C1∴==30°,∴∠B1==15°∠B2==×(30°+60°)=45°∠B3==×(30°+60°+60°)=75°;(3)B n∁n把圆周2n等分,则弧BnD的度数是:,则∠B n AD=,在直角△AB n D中,.【点评】本题是把求圆周角的度数的问题转化为求弧的度数的问题,依据是圆周角等于所对弧的度数的一半.23.今年,我国政府为减轻农民负担,决定在5年内免去农业税.某乡今年人均上缴农业税25元,若两年后人均上缴农业税为16元,假设这两年降低的百分率相同.(1)求降低的百分率;(2)若小红家有4人,明年小红家减少多少农业税?(3)小红所在的乡约有16000农民,问该乡农民明年减少多少农业税?【分析】(1)设降低的百分率为x,则降低一次后的数额是25(1﹣x),再在这个数的基础上降低x,则变成25(1﹣x)(1﹣x)即25(1﹣x)2,据此即可列方程求解;(2)每人减少的税额是25x,则4个人的就是4×25x,代入(1)中求得的x的值,即可求解;(3)每个人减少的税额是25x,乘以总人数16000即可求解.【解答】解:(1)设降低的百分率为x,依题意有,25(1﹣x)2=16,解得,x1=0.2=20%,x2=1.8(舍去);(2)小红全家少上缴税25×20%×4=20(元);(3)全乡少上缴税16000×25×20%=80 000(元).答:降低的增长率是20%,明年小红家减少的农业税是20元,该乡农民明年减少的农业税是80 000元.【点评】本题考查求平均变化率的方法.若设变化前的量为a,变化后的量为b,平均变化率为x,则经过两次变化后的数量关系为a(1±x)2=b.24.在△ABC中,AB=AC,D为BC上一点,由D分别作DE⊥AB于E,DF⊥AC于F.设DE=a,DF=b,且实数a,b满足9a2﹣24ab+16b2=0,并有=2566,∠A使得方程x2﹣x•sin A+sin A﹣=0有两个相等的实数根.(1)试求实数a,b的值;(2)试求线段BC的长.【分析】(1)由题意可知:2a2b=2566,则2a2b=248,则a2b=48.化简9a2﹣24ab+16b2=0得:(3a﹣4b)2=0,则3a﹣4b=0,即3a=4b,则根据,可求得a与b的值;(2)要求BC的长需求出BD和CD的长,知BD、CD分别是直角三角形BDE和直角三角形CDF中的斜边.又知在△ABC中,AB=AC,则∠B=∠C,则根据三角函数只要知道∠B或∠C的读数即可,要求∠B或∠C的读数需求的∠A的读数,根据判别式可以求得∠A的读数.【解答】解:(1)由条件有,解得;(2)又由关于x的方程的判别式△=sin2A﹣sin A+=(sin A﹣)2=0,则sin A=,而∠A为三角形的一个内角,所以∠A1=60°或∠A2=120° 2分当∠A=60°时,△ABC为正三角形,∠B=∠C=60°于是分别在Rt△BDE和Rt△CDF中有BD=,CD=所以BC=BD+DC=.当∠A=120°时,△ABC为等腰三角形,∠B=∠C=30°同上方法可得BC=14. 3分所以线段BC的长应为或14.【点评】考查了解直角三角形以及判别式的应用.25.某市城建部门经过长期市场调查发现,该市年新建商品房面积P(万平方米)与市场新房均价x(千元/平方米)存在函数关系P=25x;年新房销售面积Q(万平方米)与市场新房均价x(千元/平方米)的函数关系为Q=﹣10;(1)如果年新建商品房的面积与年新房销售面积相等,求市场新房均价和年新房销售总额;(2)在(1)的基础上,如果市场新房均价上涨1千元,那么该市年新房销售总额是增加还是减少?变化了多少?结合年新房销售总额和积压面积的变化情况,请你提出一条合理。
2014年全国各地中考数学压轴题集锦答案(三)
2014年全国各地中考数学压轴题集锦答案(三)41.(哈尔滨模拟)如图,直线y=-kx+6k(k>0)与x轴、y轴分别相交于点A、B,且△AOB的面积是24.(1)求直线AB的解析式;(2)点P从点O出发,以每秒2个单位的速度沿折线OA-AB运动;同时点E从点O出发,以每秒1个单位的速度沿y轴正半轴运动,过点E作与x轴平行的直线l,与线段AB 相交于点F,当点P与点F重合时,点P、E均停止运动.连接PE、PF,设△PEF的面积为S,点P运动的时间为t秒,求S与t的函数关系式,并直接写出自变量t的取值范围;(3)在(2)的条件下,过P作x轴的垂线,与直线l相交于点M,连接AM,当tan∠MAB=12时,求t的值.解:(1)∵y=-kx+6k,当x=0时,y=6k;当y=0时,x=6 ∴OA=6,OB=6k∵S△AOB=24,∴12×6×6k=24,∴k=43∴直线AB的解析式为y=-43x+8(2)根据题意,OE=t,EF∥OA,∴△BEF∽△BOA∴EFOA=BEBO,即EF6=8-t8,∴EF=34(8-t)①当0<t≤3时,点P在OA上运动过点P作PH⊥EF于H,则PH=OE=t∴S=12EF²PH=12²34(8-t)²t=-38t2+3t②当点P在AB上运动时过点P作PG⊥OA于G,设直线PG与EF相交于点M,则MG=OE=t易知△APG∽△ABO,∴PGBO=APAB∵OA=6,OB=8,∴AB=62+82=10∴PG8=2t-610,∴PG=45(2t-6)当点P与点F重合时,有PG=OE∴45(2t-6)=t,解得t=8,即PG=8点P 与点F 重合前,MP =MG -PG =t -4 5 (2t -6)=-3 5 t +245∴S =12EF ²MP =1 2 ²3 4 (8-t)(-3 5 t + 245 )= 9 40 t 2- 18 5 t +725综上,S =⎩⎨⎧-38t2+3t (0<t≤3)9 40 t 2- 18 5 t + 725(3<t<8)(3)①当点P 在OA 上,点M 在点F 左侧时 作MC ⊥AB 于C ,FD ⊥OA 于D则FD =OE =t ,EM =OP =2t ,MF =EF -EM =34(8-t)-2t在Rt △CMF 中,CMCF=tan ∠MFC =tan ∠BAO =OBOA=43设CM =4k ,则CF =3k ,MF =(4k)2+(3k)2=5k在Rt △MAC 中,CMAC=tan ∠MAC =tan ∠MAB =12∴AC =2CM =8k ,∴AF =5k ,∴MF =AF 在Rt △AFD 中, FDAF=tAF=sin ∠F AD =sin ∠BAO =4 5∴AF =54t ,∴3 4 (8-t)-2t =5 4 t ,解得t =32当点P 在OA 上,点M 在点F 右侧时,可求得t =114②当点P 在AB 上时,过点M 作MK ⊥AB 于K 在Rt △PMK 中,MKPK=tan ∠MPK =tan ∠ABO =34设MK =3m ,则PK =4m ,MP =5m ,AK =6m∴AP =AK -PK =2m ,∴2t -6=2m ∵MP =t -4 5 (2t -6),∴t -45(2t -6)=5m∴t -4 5 (2t -6)=5 2 (2t -6),解得t =9928综上所述,满足条件的t 值是32或 114或992842.(哈尔滨模拟)如图,在平面直角坐标系中,O 为坐标原点,点A 在x 轴的正半轴上,△AOB 为等腰三角形,且OA =OB =10,过点B 作y 轴的垂线,垂足为D ,直线AB 的解析式为y =-3x +30,点C 在线段BD 上,点D 关于直线OC 的对称点在腰OB 上. (1)求点B 坐标;(2)点P 从点B 出发,以每秒1个单位的速度沿折线BC -CO 运动;同时点Q 从点O 出发,以每秒1个单位的速度沿对角线OB 向终点B 运动,当一点停止运动时,另一点也随之停止运动.设△PQC 的面积为S ,运动时间为t ,求S 与t 的函数关系式,并写出自变量t 的取值范围;(3)在(2)的条件下,连接PQ,设PQ与OB所成的锐角为α,当α=90°-∠AOB时,求t的值.解:(1)过点B作BF⊥OA于F,设B(a,-3a+30)在Rt△OBF中,a2+(-3a+30)2=102解得a1=10(舍去),a2=8当a=8时,-3a+30=6∴B(8,6)(2)设点D关于直线OC的对称点为D′,连接CD′∵D′在腰OB上,∴OD=OD′,∠DOC=∠D′OC又OC=OC,∴△DOC≌△D′OC∴CD′=CD,∠CDO′=∠CDO=90°∴S△POQ=12OD²BD=12OD²CD+12OB²CD′∴CD=OD²BDOD+OB=6×86+10=3,∴BC=5①当0≤t<5时,点P在线段BC上过点Q作QE⊥BD于E,则△BQE∽△BOD∴QEOD=BQBO,即QE6=10-t10,∴QE=6-35t∴S=12PC²QE=12(5-t)(6-35t)即S=310t2-92t+15②当5<t≤10时,点P在线段CO上过点Q作QF⊥OC于F∵COQ=∠COD,∠QFO=∠CDO=90°∴△QFO∽△CDO,∴QFCD=OQOC即QF3=t35,∴QF=55t∴S=12PC²QF=12(t-5)²55t即S=510t2-52t(3)①当0≤t<5时 ∵α=90°-∠AOB =∠BOD ,即∠PQB =∠DOB ∴PQ ∥DO ,∴△BPQ ∽△BDO∴BPBD=BQBO,即 t8 =10-t10 ,∴t =409②当5<t≤10时,过点P 作PH ⊥OB 于H∵∠PQO =∠BOD ,∴tan ∠PQO =∠BOD =4 3设PH =4k ,则QH =3k ,OH =8k ,OP =45k ∴OQ =11k ,∴11k =t ,∴k =t11∴OP =45k =4511t 又∵OP =35-(t -5)=35+5-t ∴4511t =35+5-t ,∴t =1435-55 41∴当α=90°-∠AOB 时,t 的值为409或 1435-554143.(哈尔滨模拟)如图,在平面直角坐标系中,点A (256,0),点B (3,4),将△OAB沿直线OB 翻折,点A 落在第二象限内的点C 处. (1)求点C 的坐标;(2)动点P 从点O 出发,以每秒5个单位的速度沿OB 向终点B 运动,连接AP ,将射线AP 绕着点A 逆时针旋转与y 轴交于一点Q ,且旋转角α=12∠OAB .设线段OQ 的长为d ,点P 运动的时间为t 秒,求d 与t 的函数关系式(直接写出时间t 的取值范围);(3)在(2)的条件下,连接CP .点P 在运动的过程中,是否存在CP ∥AQ ,若存在,求此时t 的值,并辨断点B 与以点P 为圆心,OQ 长为半径的⊙P 的位置关系;若不存在,请说明理由.解:(1)过点B 作BG ⊥x 轴于G ,过点C 作CH ⊥x 轴于H ∵A (256,0),B (3,4),∴OA =256,OG =3,BG =4∴AG=76,∴AB=AG2+BG2=256,∴AB=OA∵△OAB沿直线OB翻折得到△OCB∴△OAB≌△OCB,∴AB=OA=BC=CO ∴四边形ABCO是菱形∴CO∥AB,∴∠COH=∠BAG∴Rt△CHO≌Rt△BGA,∴CH=BG=4,OH=AG=7 6∴C(-76,4)(2)连接AC交BO于点E∵菱形ABCO,∴AC⊥BO,∠OAE=12∠OAB∵α=12∠OAB,∴∠OAP=∠OAE,∴∠OAQ=∠EAP∵∠AOQ=∠AEP=90°,∴△AOQ≌△AEP∴PEOQ=AEAO由(1)知,CH=4,AH=16 3∴AC=AH2+CH2=203,∴AE=103,同理OE=52①当0≤t<12时∵OP=5t,∴PE=52-5t,∴52-5td=103256∴d=-254t+258②当12<t≤1时,同理可求d=254t-258(3)过点P作PK⊥AB于K∵AQ∥CP,∴∠PCE=∠QAE ∵AE=CE,AC⊥BO,∴PC=P A∴∠P AE=∠PCE=∠QAE=12∠P AQ∴∠P AB=∠QAE,∴∠P AE=∠P AB,∴PE=PK ∵菱形ABCO,∴∠PBK=∠OBF∴sin∠PBK=sin∠OBF=OFOB=PKPB=45∵OP=5t,OB=5,∴PE=5t-52,PB=5-5t∴5t -52 5-5t=4 5 ,解得t =13 18∴存在CP ∥AQ ,此时t =1318∵1 2<13 18<1,∴当t =13 18 时,OQ =d = 25 4 t - 25 8 =25 18BP =OB -OP =5-5t =2518∴BP =OQ ,即点B 与圆心P 的距离等于⊙P 的半径,点B 在⊙P 上 ∴存在CP ∥AQ ,此时t =1318,且点B 在⊙P 上 44.(黑龙江大庆)已知等边△ABC 的边长为3个单位,若点P 由A 出发,以每秒1个单位的速度在三角形的边上沿A →B →C →A 方向运动,第一次回到点A 处停止运动,设AP =S ,用t 表示运动时间.(1)当点P 由B 到C 运动的过程中,用t 表示S ;(2)当t 取何值时,S 等于7(求出所有的t 值);(3)根据(2)中t 的取值,直接写出在哪些时段AP <7? 解:(1)当点P 在BC 上时,有3≤t≤6作PM ⊥AB ,垂足为M由PB =t -3,∠B =60°,得PM =32 (t -3 ),BM = 12( t -3) ∴AM =3-12(t -3)于是S =AP =AM 2+BM 2=(t -3 )2-3( t -3 )+9(3≤t≤6)(2)当S =7时(i )当点P 在AB 上时,有t =7 (ii )当点P 在CA 上时,有t =9-7(iii )当点P 在BC 上时,S =(t -3 )2-3( t -3 )+9=7解得t =4或t =5综上t =7或t =9-7或t =4或t =5(3)根据(2)可知0<t<7,4<t<5,9-7<t≤9 这三个时间段内AP <7 45.(黑龙江大兴安岭、鸡西、齐齐哈尔、黑河、七台河)如图,在平面直角坐标系中,已知Rt △AOB 的两条直角边OA 、OB 分别在y 轴和x 轴上,并且OA 、OB 的长分别是方程x2-7x +12=0的两根(OA <OB ),动点P 从点A 开始在线段AO 上以每秒1个单位长度的速度向点O 运动;同时,动点Q 从点B 开始在线段BA 上以每秒2个单位长度的速度向点AA CB运动,设点P 、Q 运动的时间为t 秒. (1)求A 、B 两点的坐标.(2)求当t 为何值时,△APQ 与△AOB 相似,并直接写出此时点Q 的坐标.(3)当t =2时,在坐标平面内找一点M ,使以A 、P 、Q 、M 为顶点的四边形是平行四边形,求M 点的坐标;(4)在P 、Q 运动过程中,在坐标平面内是否存在点N ,使以A 、P 、Q 、N 为顶点的四边形是菱形?若存在,请直接写出N解:(1)解方程x2-7x +12=0,得x 1=3,x 2=4∵OA <OB ,∴OA =3,OB =4∴A (0,3),B (4,0)(2)由题意得,AP =t ,AQ =5-2t 可分两种情况讨论:①当∠APQ =∠AOB 时,△APQ ∽△AOB如图1, t3=5-2t5,解得t =1511∴Q (2011,1811) ②当∠AQP =∠AOB 时,△APQ ∽△ABO 如图2, t5=5-2t3,解得t =2513∴Q (1213,3013)(3)当t =2时,AP =2,AQ =5-2t =1 ∴PO =1,∴P (0,1), 点Q 的横坐标为:1×cos ∠ABO = 45,纵坐标为:3-1×sin ∠ABO = 125∴Q (45,125)若AP 是平行四边形的边,则MQ ∥AP ,MQ =AP =2,如图3、图4 ∴点M 的横坐标为45,纵坐标为:125+2=225或 125-2=25∴M 1(45,225),M 2(45,25)若AP 是平行四边形的对角线,则△AMP ≌PQA ,如图5∵点Q的横坐标为45,∴点M的横坐标为-45∵点A的纵坐标比点Q的纵坐标大3 5∴点M的纵坐标比点P的纵坐标大3 5即点M的纵坐标为:1+35=85∴M3(-45,85)(4)存在.N1(43,13),N2(32,5516),N3(-2017,3617)提示:有三种情况若AP=AQ,则在坐标平面内存在点N,使四边形APNQ是菱形,如图6∴t=5-2t,解得t=53,∴AQ=53∴Q(43,2),∴N1(43,13)若AP=PQ,则在坐标平面内存在点N,使四边形APQN是菱形,如图7由题意,P(0,3-t),Q(4-85t,65t)∴PQ2=(4-85t)2+(3-t-65t)2∴t2=(4-85t)2+(3-t-65t)2,解得t=2516或t=52当t=52时,点Q与点A重合,不合题意,舍去∴t=2516,∴Q(32,158)∴N2(32,5516)若AQ=PQ,则在坐标平面内存在点N,使四边形ANPQ是菱形,如图8连接NQ交AP于O′,则NQ⊥AP,AO′=O′P∴AP=2AO′,∴t=65(5-2t)解得t=3017,∴Q(2017,3617)∴N3(-2017,3617)46.(吉林)如图,在△ABC 中,∠A =90°,AB =2cm ,AC =4cm .动点P 从点A 出发,沿AB 方向以1cm /s 的速度向点B 运动,动点Q 从点B 同时出发,沿BA 方向以1cm /s 的速度向点A 运动.当点P 到达点B 时,P ,Q 两点同时停止运动.以AP 为一边向上作正方形APDE ,过点Q 作QF ∥BC ,交AC 于点F .设点P 的运动时间为t s ,正方形APDE 和梯形BCFQ 重合部分的面积为S cm 2.(1)当t =_________s 时,点P 与点Q 重合; (2)当t =_________s 时,点D 在QF 上;(3)当点P 在Q ,B 两点之间(不包括Q ,B 两点)时,求S 与t 之间的函数关系式.解:(1)1 (2)45提示:点D 在QF 上时∵QF ∥BC ,∠DPQ =CAB =90° ∴△PQD ∽△ABC ,∴ PDPQ=ACAB即t2-2t=42,解得t =45B Q D PC A EF BCA (备用图)47.(吉林模拟)如图,梯形OABC中,OA在x轴上,CB∥OA,∠OAB=90°,B(4,4),BC=2.动点E从点O出发,以每秒1个单位的速度沿线段OA运动,到点A停止,过点E 作ED⊥x轴交折线O-C-B于点D,以DE为一边向右作正方形DEFG.设运动时间为t (秒),正方形DEFG与梯形OABC重叠面积为S(平方单位).(1)求tan∠AOC的值;(2)求S与t的函数关系式,并求出S的最大值;(3)连接AC,AC的中点为M,t为何值时,△DMG为等腰三角形?解:(1)过C 作CD ⊥x 轴于H∵B (4,4),BC =2,∴OH =2,CH =4 ∴tan ∠AOC =CHOH=42=2,(2)当点F 与点A 重合时,OE =t ,AE =DE =4-t∴tan ∠AOC =DEOE=4-t t=2,解得t =43当0<t≤4 3时,S =DE 2=( 2OE )2=( 2t)2=4t 2当4 3≤t ≤2时,S =DE ²AE =2t ²( 4-t)=-2t 2+8t 当2≤t ≤4时,S =4AE =4( 4-t)=-4t +16当0<t ≤4 3 时,t = 4 3 时,S 最大=64 9当43≤t≤2时,t =2时,S 最大=8 当2≤t≤4时,t =2时,S 最大=8 综上,t =2时,S 的最大值为8(3)t 1= 13-213 9 ,t 2= 32,t 3=23-1提示:由题意,A (4,0),C (2,4) ∴M (3,2)当0<t≤2时,D (t ,2t ),G (3t ,2t )∴DM 2=( t -3 )2+( 2t -2)2,DG 2=4t 2MG 2=( 3t -3 )2+( 2t -2)2若DG =MG ,则4t 2=( 3t -3 )2+( 2t -2)2解得t = 13+2 13 9 >2(舍去)或t =13-2139若MD =MG ,则( t -3 )2+( 2t -2 )2=( 3t -3 )2+( 2t -2)解得t =0(舍去)或t =32若DM =DG ,则(t -3 )2+( 2t -2)2=4t2,无实数解 当2<t≤4时,D (t ,4),G (t +4,4)∴DM 2=(t -3 )2+ 2 2,DG 2=42MG 2=( t +1 )2+ 22 若DG =MG ,则4 2=( t +1 )2+ 22解得t =23-1或t =-23-1(舍去)若MD =MG ,则( t -3 )2+ 2 2=( t +1 )2+ 22备用图解得t=1(舍去)若DM=DG,则(t-3)2+22=42解得t=3±23(舍去)48.(吉林长春)如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=4cm.D、E分别为边AB、BC的中点,连接DE.点P从点A出发,沿折线AD-DE-EB运动,到点B停止.点P在线段AD上以5cm/s的速度运动,在折线DE-EB上以1cm/s的速度运动.当点P与点A不重合时,过点P作PQ⊥AC于点Q,以PQ为边作正方形PQMN,使点M落在线段AQ上.设点P的运动时间为t(s).(1)当点P在线段DE上运动时,线段DP的长为______________cm(用含t的代数式表示).(2)当点N落在AB边上时,求t的值.(3)当正方形PQMN与△ABC重叠部分图形为五边形时,设五边形的面积为S(cm2),求S与t的函数关系式.(4)连接CD.当点N与点D重合时,有一点H从点M出发,在线段MN上以2.5cm/s 的速度沿M-N-M连续做往返运动,直至点P与点E重合时,点H停止往返运动;当点P 在线段EB上运动时,点H始终在线段MN的中心处.直接写出在点P的整个运动过程中,点H落在线段CD上时t的取值范围.(1)(t-2)(2)①当点P在线段DE上时,如图①PD=PN=PQ=2,∴t-2=2∴t=4②当点P在线段EB上时,如图②PN=2PB∵PN=PC=(t-6)+2=t-4PB=2-(t-6)=8-t∴t-4=2(8-t),解得t=20 3∴当点N落在AB边上时,t的值为4或20 3(3)①当2<t<4时,如图③S=22-14(4-t)2即S=-14t2+2t②当203<t<8时,如图④图①图②(Q)图③S =(t -4)2-1 4(3t -20)2即S =-54t2+22t -84 (4)t =143或t =5或6≤t≤8提示:当点H 第一次落在线段CD 上时 2.5(t -4)+1 2 ( t -4 )=2,解得t =143当点H 第二次落在线段CD 上时 2.5(t -4)-2= 12( t -4),解得t =5当点H 第三次落在线段CD 上时 6-2.5(t -4)= 12( t -4),解得t =6当6≤t≤8时,点H 恒在线段CD 上 49.(长春模拟)如图,在△AOB 中,∠AOB =90°,OA =OB =6,C 为OB 上一点,射线CD ⊥OB 交AB 于点D ,OC =2.点P 从点A 出发以每秒 2个单位长度的速度沿AB 方向运动,点Q 从点C 出发以每秒2个单位长度的速度沿CD 方向运动,P ,Q 两点同时出发,当点P 到达点B 时停止运动,点Q 也随之停止.过点P 作PE ⊥OA 于点E ,PF ⊥OB 于点F ,得到矩形PEOF ,以点Q 为直角顶点向下作等腰直角三角形QMN ,斜边MN ∥OB ,且MN=QC .设运动时间为t (秒).(1)求t =1时FC 的长度. (2)求MN =PF 时t 的值.(3)当△QMN 和矩形PEOF 有重叠部分时,求重叠(阴影)部分图形面积S 与t 的函数关系式.(4)直接写出△QMN 和矩形PEO F 的边有三个公共点时t 的值.解:(1)根据题意,△AOB 、△AEP 都是等腰直角三角形∵AP =2t ,∴OF =EP =t ∵OC =2,∴FC =|2-t| ∴当t =1时,FC =1(2)∵AP =2t ,∴AE =t ,PF =OE =6-t ∵MN =QC =2t ,MN =PF ∴2t =6-t ,∴t =2(3)当点F 在点C 左侧时,设MQ 、MN 分别与PF 交于点G 、H 当△QMN 和矩形PEOF 有重叠部分时则MH =GH =t -(2-t )=2t -2≥0,得t≥1当点F 与点C 重合时,t =2当1≤t≤2时,重叠部分为△MGH ,如图①图④(Q )B图①B图③图②∵MH =GH =t -(2-t)=2t -2∴S=1 2(2t -2)2=2t 2-4t +2当点E 落在MQ 上时,如图②∵AE =t ,EK =MK =t -2,AK =6-t ,AE +EK =AK ∴t +(t -2 )=6-t ,∴t =83当2<t≤83时,重叠部分为五边形IJKLP ,如图③ ∵JK =MK =t -2,AK =6-t ,∴AJ =6-t -(t -2)=8-∴EK =6-t -t =6-2t ,EI =EJ =8-2t -t =8-3t∴S=S 矩形EKLP-S △EJI =t (6-2t )- 1 2 ( 8-3t )2=- 13 2t 2+当MN 与EP 重合时,t =3 当83<t≤3时,重叠部分为矩形EKLP ,如图④ ∴S=t (6-2t)=-2t 2+6t(4)t =2或t =83提示:如图⑤、图②50.(长春模拟)如图,在平面直角坐标系中,梯形ABCD 的顶点A 、B 、D 的坐标分别为A (-3,0),B (15,0),D (0,4),且CD =10.一条抛物线经过C 、D 两点,其顶点M 在x 轴上.点P 从点A 出发以每秒5个单位的速度沿AD 向点D 运动,到点D 后又以每秒3个单位的速度沿DC 向点C 运动,到点C 停止;同时,点E 从点B 出发以每秒5个单位的速度沿BO 运动,到点O 停止.过点E 作y 轴的平行线,交边BC 或CD 于点R .设P 、E 两点运动的时间为t (秒).(1)写出点M 的坐标,并求这条抛物线的解析式; (2)当点Q 和点R 之间的距离为8时,求t 的值;(3)直接写出使△MPQ 成为直角三角形时t 值的个数;(4)设P 、Q 两点直径的距离为d ,当2≤d ≤7时,求t 的取值范围.解:(1)M (5,0)设抛物线的解析式为y =a (x -5)2∵抛物线经过点D (0,4),∴25a =4,∴a =425∴抛物线的解析式为y = 4 25 ( x -5 )2或y = 4 25 x 2- 8 5x +4 (2)作CN ⊥AB 于N ,则CN =4,BN =5①当0≤t ≤1时,由△BQE ∽△BCN 得: BE QE = BN CN =54图⑤∵BE =5t ,∴QE =4t ∵RQ =8,∴RE =4t +8 ∴R (15-5t ,4t +8)∵点R 在抛物线y =4 25 (x -5)2上,∴4 25(15-5t -5)2=4t +8解得t 1= 5+ 17 2 >1(舍去) ,t 2=5-172②当1≤t≤3时,QR ≤CN =4∴当t = 5-172时,点Q 和点R 之间的距离为8(3)4 提示:当0≤t ≤1时,P 在线段AD 上,Q 在线段BC 上,∠PMQ ≥∠DMC>90°当1<t ≤ 13 3 时(P 到达C 时,t =1+ 10 3=133),P 、Q 均在CD 上若∠PMQ =90°,则由射影定理得:(8-3t )(10-5t )=42解得t 1= 35- 265 15 ,t 2=35+26515若∠PQM =90°,则Q 到达M 的正上方,t = 105=2若∠QPM =90°,则P 到达M 的正上方,t =1+ 5 3=83所以使△MPQ 成为直角三角形时的t 值有4个(4)∵当t =1时,P 、Q 分别到达D 、C 两点,CD =10 ∴当2≤d≤7时,P 、Q 均在CD 上当点P 和点Q 相遇前,d =PQ =3+15-( 3t +5t)=18-8t∴2≤18-8t ≤7,解得 118≤t≤2当点P 和点Q 相遇后,d =PQ =8t -18∴2≤8t -18≤7,解得 5 2 ≤t ≤258∵25 8 >3,而3t -3=7时,t =10 3∴5 2 ≤t ≤10 3综上所述,当2≤d ≤7时,t 的取值范围为 11 8 ≤t ≤2或 5 2 ≤t ≤10351.(辽宁大连)如图,△ABC 中,∠C =90°,AC =8cm ,BC =6cm ,点P 、Q 同时从点C 出发,以1cm /s 的速度分别沿CA 、CB 匀速运动,当点Q 到达点B 时,点P 、Q 同时停止运动.过点P 作AC 的垂线l 交AB 于点R ,连接PQ 、RQ ,并作△PQR 关于直线l 对称的图形,得到△PQ ′R .设点Q 的运动时间为t (s ),△PQ ′R 与△P AR 重叠部分的面积为S (cm 2). (1)t 为何值时,点Q ′ 恰好落在AB 上?(2)求S 与t 的函数关系式,并写出t 的取值范围;(3)S 能否为98cm 2?若能,求出此时的t 值,若不能,说明理由.B lACQ PRQ ′BA 备用图CBA备用图C解:(1)过点Q ′ 作Q ′H ⊥AC ,垂足为H (如图1) ∴∠Q ′HA =90°=∠C ,Q ′H ∥BC ∴AQ ′H △∽△ABC ,∴Q ′HBC=AHAC由题意知QC =CP =PH =Q ′H =t ∴ t6=AH8 ,即AH =43t ∵CP +PH +HA =CA ,即t +t +43t =8∴t =12 5,即t 为125s 时,点Q ′ 恰好落在AB 上 (2)①当0<t≤125时(如图2) 同理RPBC=APAC,即RP6 =8-t8∴RP =34(8-t)∴S =S △PQ ′R=S △PQR=12RP ²CP =1 2 ×3 4 (8-t )×t =- 3 8t 2+3t ②当125<t≤6时(如图3) 设PQ ′ 与AB 相交于点M ,过点M 作MH ⊥AC ,垂足为H 设MH =a ,由对称性知,∠MPH =∠QPC =45°,则PH =MH =a 同理MHBC =AHAC,即a6 =AH8 ,∴AH = 4 3a∵CP +PH +HA =CA ,即t +a +43a =8∴a =37(8-t)∴S =12RP ²PH =1 2 ×3 4 (8-t )×3 7 ( 8-t )= 9 56 ( 8-t )2=- 9 56 t 2- 18 7 t +72 7综上,S =⎩⎨⎧-3 8t2+3t (0<t ≤125)- 9 56t2- 18 7 t + 72 7 (125<t≤6)(3)若S = 98,则 ①当0<t≤125时,-38t 2+3t =98,解得t 1=4+13(舍去),t 2=4-13 ②当125<t≤6时,956(8-t)2=98,解得t 1=8+7(舍去),t 2=8-7 Bl ACQ PRQ ′图1HBl ACQ PRQ ′图2B l ACQP RQ ′图3MH即S 能为98cm 2,此时t 为(4-13 )s 或( 8-7)s 52.(辽宁葫芦岛)△ABC 中,BC =AC =5,AB =8,CD 为AB 边的高,如图1,A 在原点处,点B 在y 轴正半轴上,点C 在第一象限.若A 从原点出发,沿x 轴向右以每秒1个单位长的速度运动,则点B 随之沿y 轴下滑,并带动△ABC 在平面内滑动,如图2.设运动时间为t 秒,当B 到达原点时停止运动. (1)当t =0时,求点C 的坐标;(2)当t =4时,求OD 的长及∠BAO 的大小;(3)求从t =0到t =4这一时段点D 运动路线的长;(4)当以点C 为圆心,CA 为半径的圆与坐标轴相切时,求t 的值.解:(1)∵BC =AC ,CD ⊥AB∴D 为AB 的中点,∴AD =12AB =4在Rt △CAD 中,CD =5 2-42=3∴点C 的坐标为(3,4)(2)如图2,当t =4时,AO =4 在Rt △ABO 中,D 为AB 的中点∴OD =12AB =4∴△AOD 为等边三角形,∴∠BAO =60°(3)如图3,从t =0到t =4这一时段点D 的运动路线是DD ′︵其中OD =OD ′=4,又∠D ′OD =90°-60°=30° ∴DD ′︵的长为 30π×4 180 =2π 3(4)由题意,AO =t当⊙C 与x 轴相切时,A 为切点,如图4 ∴CA ⊥OA ,∴CA ∥y 轴∴∠CAD =∠ABO ,∴Rt △CAD ∽Rt △ABO ∴ABCA=AOCD,即85=t3∴t =245当⊙C 与y 轴相切时,B 为切点,如图5图2图1 图2图3图5图4同理可得t =325∴t 的值为245或32553.(辽宁丹东)已知抛物线y =ax2-2ax +c 与y 轴交于C 点,与x 轴交于A 、B 两点,点A的坐标是(-1,0),O 是坐标原点,且|OC |=3|OA |. (1)求抛物线的函数表达式;(2)直接写出直线BC 的函数表达式;(3)如图1,D 为y 轴负半轴上的一点,且OD =2,以OD 为边向左作正方形ODEF .将正方形ODEF 以每秒1个单位的速度沿x 轴的正方向移动,当点F 与点B 重合时停止移动.在移动过程中,设正方形O ′DEF 与△OBC 重叠部分的面积为S ,运动时间为t 秒. ①求S 与t 之间的函数关系式;②在运动过程中,S 是否存在最大值?如果存在,直接写出这个最大值;如果不存在,请说明理由;(4)如图2,点P (1,k )在直线BC 上,点M 在x 轴上,点N 在抛物线上,是否存在以A 、M 、N 、P 为顶点的平行四边形?若存在,请直接写出M 点坐标;若不存在,请说明理由.解:(1)∵A (-1,0),|OC |=3|OA |,∴C (0,-3) ∵抛物线y =ax2-2ax +c 经过A 、C 两点∴⎩⎪⎨⎪⎧a +2a +c =0c =-3 解得⎩⎪⎨⎪⎧a =1b =-3 ∴抛物线的函数表达式为y =x2-2x -3 (2)直线BC 的函数表达式为y =x -3 (3)①设D (m ,-2),则E (m -2,-2) 当正方形ODEF 的顶点D 运动到直线BC 上时 有-2=m -3,∴m =1正方形ODEF 的边EF 运动到与OC 重合时 m =2当正方形ODEF 的顶点E 运动到直线BC 上时 有-2=(m -2)-3,∴m =3图2图1在y =x -3中,当y =0时,x =3,∴B (3,0) 当正方形ODEF 的顶点F 运动到与点B 重合时 有m =3+2=5当0<t ≤1时,重叠部分为矩形OGDO ′ S =2t当1<t≤2时,重叠部分为五边形OGHIO ′ HD =ID =t -1S =S 矩形OGDO ′-S △HID=2t -1 2 (t -1)2=-1 2 t 2当2<t≤3时,重叠部分为五边形FEHIO ′S =S 正方形O ′DEF-S △HID=22-1 2 (t -1)2=-1 2 当3<t≤5时,重叠部分为△FKBFB =FK =2-(t -3)=5-tS =1 2 (5-t)2=1 2 t 2-5t +25 2②当t =2秒时,S 有最大值,最大值为 72(4)存在.M 1(-2-1,0),M 2(2-1,0) M 3(3-6,0),M 4(3+6,0) 提示:如图54.(辽宁本溪)如图,已知抛物线y =ax2+bx +3经过点B (-1,0)、C (3,0),交y 轴于点A ,将线段OB 绕点O 顺时针旋转90°,点B 的对应点为点M ,过点A 的直线与x 轴交于点D (4,0).直角梯形EFGH 的上底EF 与线段CD 重合,∠FEH =90°,EF ∥HG ,EF =EH =1.直角梯形EFGH 从点D 开始,沿射线DA 方向匀速运动,运动的速度为1个长度单位/秒,在运动过程中腰FG 与直线AD 始终..重合,设运动时间为t 秒. (1)求此抛物线的解析式;(2)当t 为何值时,以M 、O 、H 、E 为顶点的四边形是特殊的平行四边形;(3)作点A 关于抛物线对称轴的对称点A ′,直线HG 与对称轴交于点K .当t 为何值时,以A 、A ′、G 、K 为顶点的四边形为平行四边形,请直接写出符合条件的t 值.解:(1)∵抛物线y =ax2+bx +3经过点B (-1,0)、C (3,0)∴⎩⎪⎨⎪⎧a -b +3=09a +3b +3=0 解得⎩⎪⎨⎪⎧a =-1b =2 ∴抛物线的解析式为y =-x2+2x +3(2)过点F ′ 作F ′N ⊥OD 轴于点N ,延长E ′H ′ 交x 轴于点P ∵点M 是点B 绕O 点顺时针旋转90°后得到的 ∴点M 的坐标为(0,1) ∵点A 是抛物线与y 轴的交点 ∴A 点坐标为(0,3),∴OA =3 ∵D (4,0),∴OD =4∴AD =3 2+42=5∵E ′H ′∥OM ,E ′H ′=OM =1∴四边形MOH ′E ′ 是平行四边形(当EH 不与y 轴重合时)∵F ′N ∥OA ,∴△F ′ND ∽△AOD ,∴F ′NAO=NDOD=F ′DAD∵直角梯形E ′F ′G ′H ′ 是直角梯形EFGH 沿射线DA 方向平移得到的 ∴F ′D =t ,∴F ′N3=ND4=t5,∴F ′N =35t ,ND =45t ∵E ′F ′=PN =1,∴OP =OD -ND -PN =4- 45t -1=3-45t ∵E ′P =F ′N =35t ,E ′H ′=1,∴H ′P =35t -1 若平行四边形MOH ′E ′ 是矩形,则∠MOH ′=90°此时H ′G ′ 与x 轴重合,∴F ′N =1 ∵35t =1,∴t =53即当t =53秒时平行四边形MOH ′E ′ 是矩形若平行四边形MOH ′E ′ 是菱形,则OH ′=E ′H ′=1 在Rt △H ′OP 中,(3-45 t)2+(35t -1 )2=12备用图解得t =3即当t =3秒时平行四边形MOH ′E ′ 是菱形 综上:当t =53秒时平行四边形MOH ′E ′ 是矩形; 当t =3秒时平行四边形MOH ′E ′ 是菱形 (3)t 1=3512 秒,t 2=9512秒提示:∵KG ∥AA ′,∴当KG =AA ′=2时,以A 、A ′、G 、K 为顶点的四边形为平行四边形 当点E 与点C 重合、点F 与点D 重合时KG =KH +HG =KH +CD +CHtan ∠ADO=2+1+43 =133∴移动t 秒时,KG =13 3-45t (直线HG 在AA ′ 下方)或KG = 45t -133(直线HG 在AA ′上方) 由 13 3-45 t =2,得t =3512由45t -13 3 =2,得t =951255.(辽宁模拟)将Rt △ABC 和Rt △DEF 按图1摆放(点F 与点A 重合),点A 、E 、F 、B 在同一直线上。
中考数学压轴题100题精选及答案(全)
(1)求点 的坐标(用 表示);
(2)求抛物线的解析式;
(3)设点 为抛物线上点 至点 之间的一动点,连结 并延长交 于点 ,连结 并延长交 于点 ,试证明: 为定值.
【008】如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD。
(1) 求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由。
【009】一次函数 的图象分别与 轴、 轴交于点 ,与反比例函数 的图象相交于点 .过点 分别作 轴, 轴,垂足分别为 ;过点 分别作 轴, 轴,垂足分别为 与 交于点 ,连接 .
(1)求证:梯形 是等腰梯形;
(2)动点 、 分别在线段 和 上运动,且 保持不变.设 求 与 的函数关系式;
(3)在(2)中:①当动点 、 运动到何处时,以点 、 和点 、 、 、 中的两个点为顶点的四边形是平行四边形?并指出符合条件的平行四边形的个数;②当 取最小值时,判断 的形状,并说明理由.
(3)在该二次函数的图象上是否存在点D,使四边形ABCD为直角梯形?若存在,求出点D的坐标;若不存在,请说明理由。
【007】如图1,在平面直角坐标系中,点O是坐标原点,四边形ABCO是菱形,点A的坐标为(-3,4),
点C在x轴的正半轴上,直线AC交y轴于点M,AB边交y轴于点H.
(1)求直线AC的解析式;
【020】如图甲,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连结AD,以AD为一边且在AD的右侧作正方形ADEF。
济南创佳教育2014中考压轴题4
2014济南创佳教育挑战中考9.(2011盐城,28,12分)如图,已知一次函数y =-x +7与正比例函数y =x 34的图象交于点A ,且与x 轴交于点B . (1)求点A 和点B 的坐标;(2)过点A 作AC ⊥y 轴于点C ,过点B 作直线l ∥y 轴.动点P 从点O 出发,以每秒1个单位长的速度,沿O ﹣C ﹣A 的路线向点A 运动;同时直线l 从点B 出发,以相同速度向左平移,在平移过程中,直线l 交x 轴于点R ,交线段BA 或线段AO 于点Q .当点P 到达点A 时,点P 和直线l 都停止运动.在运动过程中,设动点P 运动的时间为t 秒.①当t 为何值时,以A 、P 、R 为顶点的三角形的面积为8?②是否存在以A 、P 、Q 为顶点的三角形是等腰三角形?若存在,求t 的值;若不存在,请说明理由.10. 28.(2011江苏无锡,28,10分)十一届全国人大常委会第二十次会议审议的个人所得税法修正案草案(简称“个税法草案”),拟将现行个人所得税的起征点由每月2000元提高注:“月应纳税额”为个人每月收入中超出起征点应该纳税部分的金额.“速算扣除数”是为快捷简便计算个人所得税而设定的一个数.例如:按现行个人所得税法的规定,某人今年3月的应纳税额为2600元,他应缴税款可以用下面两种方法之一来计算:方法一:按1~3级超额累进税率计算,即500×5%+1500×10%+600×15%=265(元).方法二:用“月应纳税额x适用税率﹣速算扣除数”计算,即2600×15%﹣l25=265(元).(1)请把表中空缺的“速算扣除数”填写完整;(2)甲今年3月缴了个人所得税1060元,若按“个税法草案”计算,则他应缴税款多少元?(3)乙今年3月缴了个人所得税3千多元,若按“个税法草案”计算,他应缴的税款恰好不变,那么乙今年3月所缴税款的具体数额为多少元?11.(2011江苏扬州,28,12分)如图,在Rt△ABC中,∠BAC=90º,AB<AC,M是BC边的中点,MN⊥BC交AC于点N,动点P从点B出发沿射线BA以每秒3厘米的速度运动。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一部分 函数图象中点的存在性问题 1.1 因动点产生的相似三角形问题
1.如图1,在平面直角坐标系xOy中,顶点为M的抛物线y=ax2+bx(a>0)经过点A和x 轴正半轴上的点B,AO=BO=2,∠AOB=120°. (1)求这条抛物线的表达式; (2)连结OM,求∠AOM的大小; (3)如果点C在x轴上,且△ABC与△AOM相似,求点C的坐标.
图1
2.如图1,已知抛物线211(1)444byxbx(b是实数且b>2)与x轴的正半轴分别交于点A、B(点A位于点B是左侧),与y轴的正半轴交于点C. (1)点B的坐标为______,点C的坐标为__________(用含b的代数式表示); (2)请你探索在第一象限内是否存在点P,使得四边形PCOB的面积等于2b,且△PBC是以点P为直角顶点的等腰直角三角形?如果存在,求出点P的坐标;如果不存在,请说 明理由; (3)请你进一步探索在第一象限内是否存在点Q,使得△QCO、△QOA和△QAB中的任意两个三角形均相似(全等可看作相似的特殊情况)?如果存在,求出点Q的坐标;如果不存在,请说明理由.
图1 3.如图1,已知抛物线的方程C1:1(2)()yxxmm (m>0)与x轴交于点B、C,与y轴交于点E,且点B在点C的左侧. (1)若抛物线C1过点M(2, 2),求实数m的值; (2)在(1)的条件下,求△BCE的面积; (3)在(1)的条件下,在抛物线的对称轴上找一点H,使得BH+EH最小,求出点H的坐标; (4)在第四象限内,抛物线C1上是否存在点F,使得以点B、C、F为顶点的三角形与△BCE相似?若存在,求m的值;若不存在,请说明理由.
图1 4.如图1,已知梯形OABC,抛物线分别过点O(0,0)、A(2,0)、B(6,3). (1)直接写出抛物线的对称轴、解析式及顶点M的坐标; (2)将图1中梯形OABC的上下底边所在的直线OA、CB以相同的速度同时向上平移,分别交抛物线于点O1、A1、C1、B1,得到如图2的梯形O1A1B1C1.设梯形O1A1B1C1的面积为S,A1、 B1的坐标分别为 (x1,y1)、(x2,y2).用含S的代数式表示x2-x1,并求出当S=36时点A1的坐标; (3)在图1中,设点D的坐标为(1,3),动点P从点B出发,以每秒1个单位长度的速度沿着线段BC运动,动点Q从点D出发,以与点P相同的速度沿着线段DM运动.P、Q两点同时出发,当点Q到达点M时,P、Q两点同时停止运动.设P、Q两点的运动时间为t,是否存在某一时刻t,使得直线PQ、直线AB、x轴围成的三角形与直线PQ、直线AB、抛物线的对称轴围成的三角形相似?若存在,请求出t的值;若不存在,请说明理由.
图1 图2 5.如图1,抛物线经过点A(4,0)、B(1,0)、C(0,-2)三点. (1)求此抛物线的解析式; (2)P是抛物线上的一个动点,过P作PM⊥x轴,垂足为M,是否存在点P,使得以A、P、M为顶点的三角形与△OAC相似?若存在,请求出符合条件的 点P的坐标;若不存在,请说明理由; (3)在直线AC上方的抛物线是有一点D,使得△DCA的面积最大,求出点D的坐标.
, 图1 1.2 因动点产生的等腰三角形问题 6.如图1,在Rt△ABC中,∠A=90°,AB=6,AC=8,点D为边BC的中点,DE⊥BC交边AC于点E,点P为射线AB上的一动点,点Q为边AC上的一动点,且∠PDQ=90 (1)求ED、EC的长; (2)若BP=2,求CQ的长; (3)记线段PQ与线段DE的交点为F,若△PDF为等腰三角形,求BP的长.
图1 备用图
7.如图1,抛物线y=ax2+bx+c经过A(-1,0)、B(3, 0)、C(0 ,3)三点,直线l是抛物线的对称轴. (1)求抛物线的函数关系式; (2)设点P是直线l上的一个动点,当△PAC的周长最小时,求点P的坐标; (3)在直线l上是否存在点M,使△MAC为等腰三角形,若存在,直接写出所有符合条件的点M的坐标;若不存在,请说明理由.
图1 8.如图1,点A在x轴上,OA=4,将线段OA绕点O顺时针旋转120°至OB的位置. (1)求点B的坐标; (2)求经过A、O、B的抛物线的解析式; (3)在此抛物线的对称轴上,是否存在点P,使得以点P、O、B为顶点的三角形是等腰三角形?若存在,求点P的坐标;若不存在,请说明理由.
图1 9.如图1,已知一次函数y=-x+7与正比例函数43yx的图象交于点A,且与x轴交于点B. (1)求点A和点B的坐标; (2)过点A作AC⊥y轴于点C,过点B作直线l//y轴.动点P从点O出发,以每秒1个单位长的速度,沿O—C—A的路线向点A运动;同时直线l从点B出发,以相同速度向左平移,在平移过程中,直线l交x轴于点R,交线段BA或线段AO于点Q.当点P到达点A时,点P和直线l都停止运动.在运动过程中,设动点P运动的时间为t秒. ①当t为何值时,以A、P、R为顶点的三角形的面积为8? ②是否存在以A、P、Q为顶点的三角形是等腰三角形?若存在,求t的值;若不存在,请说明理由.
10.如图1,在矩形ABCD中,AB=m(m是大于0的常数),BC=8,E为线段BC上的动点(不与B、C重合).连结DE,作EF⊥DE,EF与射线BA交于点F,设CE=x,BF=y. (1)求y关于x的函数关系式; (2)若m=8,求x为何值时,y的值最大,最大值是多少?
(3)若12ym,要使△DEF为等腰三角形,m的值应为多少?
图1
11.如图1,在等腰梯形ABCD中,AD//BC,E是AB的中点,过点E作EF//BC交CD于点F,AB=4,BC=6,∠B=60°. (1)求点E到BC的距离; (2)点P为线段EF上的一个动点,过点P作PM⊥EF交BC于M,过M作MN//AB交折线ADC于N,连结PN,设EP=x. ①当点N在线段AD上时(如图2),△PMN的形状是否发生改变?若不变,求出△PMN的周长;若改变,请说明理由; ②当点N在线段DC上时(如图3),是否存在点P,使△PMN为等腰三角形?若存在,请求出所有满足条件的x的值;若不存在,请说明理由.
图1 图2 图3
1.3 因动点产生的直角三角形问题 12.如图1,抛物线213442yxx与x轴交于A、B两点(点B在点A的右侧),与y轴交于点C,连结BC,以BC为一边,点O为对称中心作菱形BDEC,点P是x轴上的一个动点,设点P的坐标为(m, 0),过点P作x轴的垂线l交抛物线于点Q. (1)求点A、B、C的坐标; (2)当点P在线段OB上运动时,直线l分别交BD、BC于点M、N.试探究m为何值时,四边形CQMD是平行四边形,此时,请判断四边形CQBM的形状,并说明理由; (3)当点P在线段EB上运动时,是否存在点Q,使△BDQ为直角三角形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.
图1 13.如图1,抛物线233384yxx与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C. (1)求点A、B的坐标; (2)设D为已知抛物线的对称轴上的任意一点,当△ACD的面积等于△ACB的面积时,求点D的坐标; (3)若直线l过点E(4, 0),M为直线l上的动点,当以A、B、M为顶点所作的直角三角形有且只有....三个时,求直线l的解析式.
图1 14.平面直角坐标系中,反比例函数与二次函数y=k(x2+x-1)的图象交于点A(1,k)和点B(-1,-k). (1)当k=-2时,求反比例函数的解析式; (2)要使反比例函数与二次函数都是y随x增大而增大,求k应满足的条件以及x的取值范围; (3)设二次函数的图象的顶点为Q,当△ABQ是以AB为斜边的直角三角形时,求k的值.
16.直角坐标系xOy中,抛物线22153244mmyxxmm与x轴的交点分别为原点O和点A,点B(2,n)在这条抛物线上. (1)求点B的坐标; (2)点P在线段OA上,从点O出发向点A运动,过点P作x轴的垂线,与直线OB交于点E,延长PE到点D,使得ED=PE,以PD为斜边,在PD右侧作等腰直角三角形PCD(当点P运动时,点C、D也随之运动). ①当等腰直角三角形PCD的顶点C落在此抛物线上时,求OP的长; ②若点P从点O出发向点A作匀速运动,速度为每秒1个单位,同时线段OA上另一个点Q从点A出发向点O作匀速运动,速度为每秒2个单位(当点Q到达点O时停止运动,点P也停止运动).过Q作x轴的垂线,与直线AB交于点F,延长QF到点M,使得FM=QF,以QM为斜边,在QM的左侧作等腰直角三角形QMN(当点Q运动时,点M、N也随之运动).若点P运动到t秒时,两个等腰直角三角形分别有一条边恰好落在同一条直线上,求此刻t的值.
图1 17.已知A、B是线段MN上的两点,4MN,1MA,1MB.以A为中心顺时针旋转点M,以B为中心逆时针旋转点N,使M、N两点重合成一点C,构成△ABC,设xAB. (1)求x的取值范围; (2)若△ABC为直角三角形,求x的值; (3)探究:△ABC的最大面积?
图1
18.直线434xy和x轴、y轴的交点分别为B、C,点A的坐标是(-2,0). (1)试说明△ABC是等腰三角形; (2)动点M从A出发沿x轴向点B运动,同时动点N从点B出发沿线段BC向点C运动,运动的速度均为每秒1个单位长度.当其中一个动点到达终点时,他们都停止运动.设M运动t秒时,△MON的面积为S. ① 求S与t的函数关系式; ② 设点M在线段OB上运动时,是否存在S=4的情形?若存在,求出对应的t值;若不存在请说明理由; ③在运动过程中,当△MON为直角三角形时,求t的值.
图1
19.直线434xy和x轴、y轴的交点分别为B、C,点A的坐标是(-2,0).
