2018年高中数学_第三章 圆锥曲线与方程 3.1.1 椭圆及其标准方程课件3 北师大版选修2-1
合集下载
选择必修 第三章 3.3.1 抛物线及其标准方程 课件(共24张PPT)

知新探究
利用信息技术作图.如图,F是定点,是不经
过点的定直线,是直线上任意一点,我们先
连接,再作的垂直平分线,过作定直
线的垂线,交直线于点.你能发现点满足
的几何条件吗?拖动点,观察点的轨迹,它
的轨迹是什么形状呢?你是否接触过类似的图
形呢?
可以发现,在点M随着点H运动的过程中,始终有ǀMFǀ=ǀMHǀ,即点M与定点F的
并能解决简单的求抛物线标准方程问题.
3.数学抽象素养和数学运算素
养.
知新引入
通过前面的学习可以发现点M到定点F的
距离与M到定直线l(不过点F)的距离之比
为k,当0<k<1时,点M的轨迹为椭圆;当
k>1时,点M的轨迹为双曲线;当k=1时,即
动点M到定点F的距离与它到定直线l的距离
相等时,点M的轨迹会是什么形状?
∴4=-2p×(-3)或9=2p×2.
∴ =
2
或
3
=
9
.
4
4
3
9
2
∴所求抛物线方程为 2 = − 或 2 = .
初试身手
1.⑴已知抛物线的方程是y=-2x2,求它的焦点坐标和准线方程;
1
2
⑵已知抛物线的准线为y=- ,求它的标准方程;
解: ⑴因为y=-2x2可化为x2 =-1y,抛物线焦点在y轴负半轴上,所以焦点
2
2
向向右.
p的几何意义是焦点到准线的距离(焦准距).
在建立椭圆、双曲线的标准方程时,选取不同的坐标系我们得到了不同形式的
标准方程.抛物线的标准方程有哪些不同的形式?请探究之后填写下表.
新知探究
图形
标准方程
y2=2px(p>0)
高中数学选择性必修一(人教版)《3.1.1椭圆及其标准方程》课件

2.已知椭圆xa22+by22=1(a>b>0),F1,F2 是它的焦点.过 F1 的直 线 AB 与椭圆交于 A,B 两点,求△ABF2 的周长.
解:如图,∵|AF1|+|AF2|=2a,|BF1|+|BF2|=2a, ∴△ABF2 的周长=|AB|+|BF2|+|AF2|=|AF1|+|BF1|+ |AF2|+|BF2|=4a.
即 25=|PF1|2+|PF2|2-|PF1|·|PF2|.
①
由椭圆的定义得 10=|PF1|+|PF2|,
所以 100=|PF1|2+|PF2|2+2|PF1|·|PF2|.2|=75,
所以|PF1|·|PF2|=25,
所以
S△F1PF2=12|PF1|·|PF2|·sin
()
A.10
B.8
C.5
D.4
解析:∵a=5,∴|PF1|+|PF2|=2a=10. 答案:A 3.已知椭圆中 a=5, c= 5, 焦点在 x 轴上,则椭圆的标准方 程为_________.
答案:2x52+2y02 =1
题型一 椭圆的定义及应用
[学透用活]
[典例 1] (1)下列说法正确的是
()
[解] (1)由于椭圆的焦点在 x 轴上, ∴设它的标准方程为xa22+by22=1(a>b>0). ∴a=5,c=4,∴b2=a2-c2=25-16=9. 故所求椭圆的标准方程为2x52 +y92=1. (2)由于椭圆的焦点在 y 轴上, ∴设它的标准方程为ay22+xb22=1(a>b>0). ∴a=2,b=1. 故所求椭圆的标准方程为y42+x2=1.
()
A.(5,0),(-5,0)
B.(0,5),(0,-5)
C.(0,12),(0,-12)
北师版高中数学选择性必修第一册精品课件 第2章 圆锥曲线 1.1 椭圆及其标准方程

从而|F1F2|=2c=6.
在△PF1F2 中,由勾股定理可得|PF2|2=|PF1|2+|F1F2|2,即|PF2|2=|PF1|2+36,
又由椭圆定义知|PF1|+|PF2|=2×2√3=4√3,
所以|PF2|=4√3-|PF1|.
从而有(4√3-|PF1|)2=|PF1|2+36,
√3
解得|PF1|= 2 .所以△F1PF2 的面积
之和恰好等于定圆半径,即|PA|+|PB|=|PM|+|PB|=|BM|=8>|AB|,所以动圆
圆心P的轨迹是以A,B为左、右焦点的椭圆,其中c=3,a=4,b2=a2-c2=
2
42-32=7,其轨迹方程为16
+
2
=1.
7
规律方法
1.利用椭圆定义求动点轨迹方程的三个步骤
2.椭圆定义的应用要注意其适用条件,涉及与几何图形有关的轨迹问题要
= 4.
2
2
4
5
标准方程为 1 + 1 =1.
规律方法 求椭圆标准方程的方法
(1)定义法:根据椭圆定义,确定a2,b2的值,结合焦点位置写出椭圆的标准
方程.
(2)待定系数法:先判断焦点位置,设出标准方程形式,最后由条件确定待定
系数即可.即“先定位,后定量”.
当所求椭圆的焦点位置不能确定时,应按焦点在x轴上和焦点在y轴上进行
椭圆的中心在坐标原点,椭圆的对称轴为坐标轴.
2
2.两种椭圆 2
+
2
2
=1, 2
2
+
2
=1 (a>b>0)的相同点是:它们的形状、大小都
在△PF1F2 中,由勾股定理可得|PF2|2=|PF1|2+|F1F2|2,即|PF2|2=|PF1|2+36,
又由椭圆定义知|PF1|+|PF2|=2×2√3=4√3,
所以|PF2|=4√3-|PF1|.
从而有(4√3-|PF1|)2=|PF1|2+36,
√3
解得|PF1|= 2 .所以△F1PF2 的面积
之和恰好等于定圆半径,即|PA|+|PB|=|PM|+|PB|=|BM|=8>|AB|,所以动圆
圆心P的轨迹是以A,B为左、右焦点的椭圆,其中c=3,a=4,b2=a2-c2=
2
42-32=7,其轨迹方程为16
+
2
=1.
7
规律方法
1.利用椭圆定义求动点轨迹方程的三个步骤
2.椭圆定义的应用要注意其适用条件,涉及与几何图形有关的轨迹问题要
= 4.
2
2
4
5
标准方程为 1 + 1 =1.
规律方法 求椭圆标准方程的方法
(1)定义法:根据椭圆定义,确定a2,b2的值,结合焦点位置写出椭圆的标准
方程.
(2)待定系数法:先判断焦点位置,设出标准方程形式,最后由条件确定待定
系数即可.即“先定位,后定量”.
当所求椭圆的焦点位置不能确定时,应按焦点在x轴上和焦点在y轴上进行
椭圆的中心在坐标原点,椭圆的对称轴为坐标轴.
2
2.两种椭圆 2
+
2
2
=1, 2
2
+
2
=1 (a>b>0)的相同点是:它们的形状、大小都
2018年高中数学 第三章 圆锥曲线与方程 3.3.1 双曲线及其标准方程课件6 北师大版选修2-1
y
y
M
M
F2
F1 o F2 x
x
F1
方程
焦点 a.b.c
x2 y2 1 a2 b2
y2 x2 a2 b2 1
F ( ±c, 0)
F(0, ± c)
c2a2b2
c2 a 2 b 2a 0 ,b 0
练习:写出以下双曲线的a,b,c及焦点坐标
1. x2 y2 1 16 9 y2 x2
3.会求双曲线的标准方程。
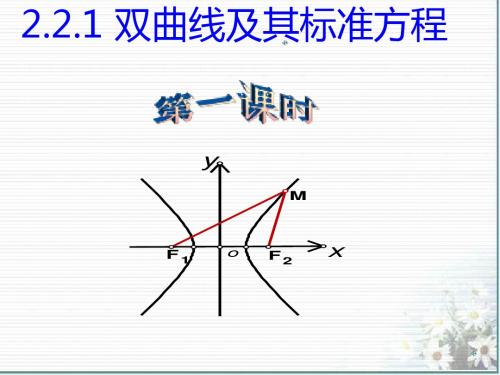
定义:
平面内与两个定点F1,F2的距离的差的绝对值
动 等于常数(小于︱F1F2︱)的点的轨迹叫做双曲线.
画
① 两个定点F1、F2——双曲线的焦点;
② |F1F2|=2c ——焦距.
M
注意
(1)差的绝对值等于常数 ;F1 o F2 (2)常数小于︱F1F2︱
1、|MF1 | - |MF2 | =2a (2a< |F1F2| )
y2 b
1
(ab0) 有相同的
焦点 F1 、F 2 。点 P为椭圆与双曲线的
公共点,则 |PF 1||PF 2| 等于( )
A. ma
B. 1 (m a )
2
C. m2 a2
D. m a
小结
定义 图象
| |MF1|-|MF2| | =2a(0 < 2a<|F1F2|)
y
y
M
M
F2
∴ b2 = 52-32 =16
所以点P的轨迹方程为: x2 y2 1 (x>0) 9 16
变式2 已知两定点F1(-5,0),F2(5,0),平面上一动点P, 满足||PF1|-|PF2| |= 10,求点P的轨迹方程.
