07磁场对运动电荷及载流导线的作用
全国优质课大赛一等奖高中物理新课标教材选修三《磁场对运动电荷的作用力》教学设计+教学反思

问题引领,自主导学——《磁场对运动电荷的作用力》教学设计摘要:近年来,为了提高课堂效率,培养学生提出问题、解决问题、自主学习、合作学习能力,以问题为引领的自主导学模式悄然兴起。
教师通过课堂问题引领学生积极思考,让学生在自主学习、合作交流中加深对知识的理解、应用,并主动建构。
关键词:问题引领、自主导学、合作交流一、教学设计思路教材分析:本节课是人教版选修3-1第三章第5节《磁场对运动电荷的作用》的内容。
涉及到的知识点有“洛伦兹力的方向和大小”、“电视显像管的工作原理”。
在前一节学生学习了磁场对通电导线的作用——安培力,会用左手定则判断安培力的方向并计算大小,这为本节课进一步研究磁现象的电本质——洛伦兹力打下了基础。
对洛伦兹力的方向和大小的探究过程能很好的培养学生的合作交流能力,让学生体验科学探究的一般过程,是本节课的重点。
另一方面,由于时代在进步,电视机向薄发展,所以电视机显像管原理可以简单带过或用其他实例替代。
教学思路:为激发学生学习兴趣,本节课以自然现象(极光)为切入口引入新课,结合实验探究,采用问题引领,启发学生对洛伦兹力的方向和大小进行探究。
让学生在科学探究体验过程中,合作学习、深入讨论、总结提升。
二、教学目标1.知识与技能(1)知道磁场对电流作用(安培力)实质是磁场对运动电荷作用(洛仑兹力)的宏观表现。
(2)知道洛仑兹力的方向由左手定则判定,并会熟练地应用。
(3)能根据安培力的表达式F=BIL推导洛仑兹力表达式f=qvB,并能够进行简单计算。
2.过程与方法(1)通过实验探究让学生总结洛伦兹力的方向的判断方法;(2)通过理论探究让学生总结洛伦兹力的大小的计算方法。
3.情感、态度与价值观(1)提高学生透过现象认清本质的认知能力;(2)培养学生主动探索、善于分析的科学态度。
三、教学重难点1.利用左手定则会判断洛伦兹力的方向;2.掌握垂直进入磁场方向的带电粒子受到洛伦兹力大小的计算。
六、板书设计3.5磁场对运动电荷的作用微观宏观七、课后作业1.上网查阅资料:极光的形成2.课第2、3、4题教学反思有幸上了一节《磁场对运动电荷的作用》,在设计教学流程、改进实验装置、思考问题导学的学案、课堂教学、课后观摩及专家点评过程中学习到不少新的理念、新的知识。
大学物理知识点(磁学与电磁感应)

y
Idl B
B
dF
dF
I
Idl
x L 任意闭合平面载流导线在均匀磁场中所受的力为零 。 F3 P 注:载流线圈在均匀磁 F2 M 场中所受力矩不一定为 零 B I O F 1 M Npm B en N F4
在均匀磁场中
F BIL
o
P
**应用介质中安培环路定理解题方法**
I 0 Bo
2R
2 IR 0 pm B 0 3 3
2x
2πx
注意:在一定的x处,磁场强弱随载流环的半径变 化,故可用求极值的方法讨论轴线某一定点处磁 场随载流环半径变化的趋势。
无限长柱面电流的磁场
无限长柱体电流的磁场
L1
r
R
I
L2
r
B
0 I
2π R
o R
r
二、磁场的基本性质
1、 感生电动势
S定
B dS i s t
方向由楞次定律判断
o
B变
2、 感生电场
B Ei dl s t dS
感生电场是涡旋场,其电场线与磁感 应强度增大的方向成左手螺旋关系。
3、 感生电场与感生电动势的计算 感生电场 : 当变化的磁场的分布具有特殊对称性时: 1 dB Ei r (r R) 2 dt
五、磁场的能量
1、通电线圈的自感磁能 2、磁场的磁能
1 2 Wm LI 2
目前范畴内:
1 1 2 1 2 w m H B BH 2 2 2
W m V w m dV
电磁学基本物理图象
运动
电荷
激 发
电流
激 发
载流导体的磁场

载流导体的磁场磁场是物理学中一种重要的概念,它是由电荷运动所产生的。
而载流导体就是指电流通过的导体,当电流通过导体时,会产生磁场。
本文将从载流导体的特性、磁场的产生和磁场的应用等方面进行探讨。
一、载流导体的特性载流导体是指电流通过的导体,可以是直线导线、螺线管等。
在导体中,电流的流动是由电荷的迁移所引起的。
导体中的电荷载流会产生磁场,磁场的强弱与导体中的电流有关。
二、磁场的产生1. 法拉第定律法拉第定律是描述电流通过导体时产生磁场的基本规律。
根据法拉第定律,电流通过载流导体时,会在其周围产生一个闭合的磁力线圈。
磁力线的方向可以用拇指右手法则来确定,即将右手握住导线,大拇指指向电流的方向,其他四指所指的方向就是磁力线圈的方向。
2. 磁场的强度载流导体所产生的磁场强度与导线形状、电流大小等参数有关。
当电流通过一段直线导线时,磁场的强度与导线到导线距离的平方成反比,与电流的大小成正比。
当电流通过螺线管等环形导线时,磁场的强度与导线的圈数及电流大小有关。
三、磁场的应用1. 电动机电动机是利用磁场与电流作用产生转动力的装置。
电动机中,通过电流通入导体产生磁场,然后与外部磁场相互作用,产生力矩使电机转动。
电动机的工作原理基于洛伦兹力和电流在磁场中的相互作用。
2. 电磁铁电磁铁是通过电流激励磁铁产生磁场的一种设备。
电磁铁是由一段载流导线绕制而成,通电时产生磁场,使铁芯具有吸力。
电磁铁的应用广泛,如电磁吸盘、电磁制动器等。
3. 传感器磁场的强度可以通过传感器进行检测和测量。
例如,利用霍尔元件可以测量磁场的强度和方向。
传感器在工业控制、导航、测量等领域有着广泛的应用。
4. 磁共振成像磁共振成像是一种利用强大的磁场和无线电波产生图像的医学技术。
人体组织中的原子核受到磁场的激励后会发出信号,通过接收和分析这些信号可以产生高分辨率的图像,用于诊断和研究。
总结:载流导体通过电流产生磁场是物理学中的基本现象,载流导体的磁场强度与电流的大小、导线的形状等参数有关。
14.1 磁场对运动电荷的作用力 洛仑兹力

3. 形成机制
以载流子为正电荷为例说明, 以载流子为正电荷为例说明 受力分析: 受力分析 洛伦兹力
v。 设载流子速度为
υ
f = qυB
v v v fL = q × B v
(方向向上 方向向上) 方向向上 VH fL Fe
v B
B
洛仑兹力使载流子横向漂移, 洛仑兹力使载流子横向漂移 出现电荷积累。 出现电荷积累。 上端积累了正电荷, 上端积累了正电荷, 下端积累了负电荷。 下端积累了负电荷。 v v 横向电场力: fe = qE 横向电场力: 上下两端形成电势差 VH 。
14
第14章 磁力
绚丽多彩的极光
在地磁两极附近, 在地磁两极附近,由于磁 感线与地面近似垂直, 感线与地面近似垂直,外层空 间入射的带电粒子可直接射入 高空大气层内。 高空大气层内。它们和空气分 子的碰撞产生的辐射就形成 了极光。 了极光。
15 第14章 磁力
3)磁流体船 )
进水
发动机
出水
B
电流
第14章 磁力
讨论
1)霍尔效应的应用 )
IB 由式 V H = υ Bb = nqd
区分半导体材料类型
可测载流子的正负和浓度; 可测载流子的正负和浓度; 可测磁感强度 B 。
研究半导体材料 性质( 性质(浓度随杂 温度等变化) 质、温度等变化)
v
—— 霍尔系数的正负与 载流子电荷性质有关
2)量子霍尔效应 ) 1980年 德国物理学家克里青发现:霍尔电阻与磁场成非 年 德国物理学家克里青发现: 线性关系,这一效应叫量子霍尔效应。 线性关系,这一效应叫量子霍尔效应。 在极低温、 在极低温、强磁场下
h RK = 2 = 25812.80Ω e
磁场强度毕奥萨伐尔定律及运动电荷产生的磁场大学物理电子教案

R sin r
B
讨论:
2 x R
2
0 IR
2 2 3/ 2
R
I
x = 0;
B
xP x
o
1.载流圆环环心处
Bo 有:
0 I
2R
R B
o
I
2.圆弧电流中心处
0 I 0 I 有: Bo 2 R 2 4R
R
B
O
14
例4:一根无限长导线通有电流I,中部弯成圆弧形, 如图所示。求圆心o点的磁感应强度B。
4
二、磁场
磁铁和运动电荷(电流)会在周围空间激发场 ---磁场。 磁场的基本性质:对运动电荷(电流)有力的作用。 磁场是一种物质, 其物质性体现在: 1)磁场对磁铁、对电流、对运动电荷均有作用力; 2)载流导体在磁场中移动时,磁场的作用力对它作功。 3)变化的磁场在空间传播,表明磁场具有动量。 恒定磁场—在空间的分布不随时间变化的磁场。 注意:无论电荷是运动还是静止,它们之间都存在库仑 相互作用,但只有运动着的电荷才存在着磁相互作用。
0 I B cos 1 cos 2 4a
讨论: 1.无限长载流直导线的磁场:
l 2
Idl
l o
r
I 0 1 0, 2 ; B 2a
1
dB P x
a
I
2.半无限长载流直导线的磁场:
1 , 2 ; B
例2:一宽为 a 无限长载流平面,通 有电流 I , 求距平面左侧为 b 与电流 共面的 P 点磁感应强度 B 的大小。 解:以 P 点为坐标原点,向右为坐 标正向; 分割电流元为无限多宽为 dx P 的无限长载流直导线; B
磁场对载流导体的作用
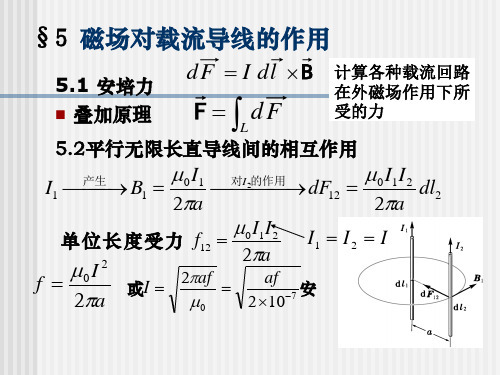
dF1 = dF2 = IBdh
F1 + F2 = 0
力矩 : dL = IBdh( x1 + x2 ) = IBdS
总力矩
L = ∑ dL = ∑ IBdS = IBS
若线圈平面与磁场成任意角度,则可将B 若线圈平面与磁场成任意角度,则可将B分解成
B = B⊥ + B||
L = IS (n × B) = m × B
B
o
d
2πmv // 2πmv ≈ 螺距 d = qB qB
荷质比的测定: 荷质比的B 2
磁聚焦法测荷质比
e 8π 2 ∆U = 2 2 ℓB m
回旋加速器: 回旋加速器:回旋加速器的基本原理就是利用回旋
频率与粒子速度无关的性质 回旋半径 R = mv qB
2πR 2π m = 回旋周期 T = v⊥ qB 2π mv // 螺距 d = v //T == qB
从磁场中某点 o 发射一束很窄的带电粒子 都很相近, 流,它们的速率 v 都很相近,且与 B 的夹角 θ 都很小, 都很小,尽管 v ⊥ = v sinθ ≈ vθ 会使各个粒子沿 不同半径的螺旋线运动, 不同半径的螺旋线运动,但是 v // = v cosθ ≈ v 却近似相等, 也近似相等, 却近似相等,因此的螺距 d 也近似相等,所以 后又会重新会聚在一起, 各个粒子经过距离 d 后又会重新会聚在一起, 称之为磁聚焦. 称之为磁聚焦.
交变电场的周期 T = 2π m qB qBR 离子的最终速率 v = m 1 2 q2 B 2 R2 离子的动能 Ek = mv = 2 2m
霍耳效应
原理:带电粒子在磁场中运动 原理: 样品:导体或半导体长方形样品 样品:导体或半导体长方形样品 载流子:带正电如图a 载流子:带正电如图a 载流子:带负电如图b 载流子:带负电如图b 实验表明: 实验表明: IB U AA' = K d E
大学物理-磁力Magnetic Force
13
1998年诺贝尔物理学奖获得者之一——崔琦
美籍华人 Daniel C. Tsui 1939 生于河南 分数量子霍尔效应 崔琦和施特默1982 1998’Nobel Prize
14
§5.5 安培力 Ampere Force ——磁场对载流导线的作用力
dF Idl B
1.均匀磁场中
Idl B
带电粒子在均匀磁场中的运动:
① v // B ②v B ③一般情形
18
⒊霍尔效应 ——在磁场中,载流导体上会出现横向(与 电流方向垂直)电势差
产生机制:
B
b +Q
Fm
q v UH
Fe
Q
I
19
⒋安培力:dF Idl B
⑴均匀磁场中: ①载流导线
Idl
B
L
b lab
I
B
a
F Ilab B
——匀速圆周 运动半径
——与速度大 小无关
——螺旋运动
5
2.带电粒子在非均匀磁场中的运动
q
F
F 有指向磁场较弱方向 B 的分量, q 将被反射。
——磁镜效应
v B F 三者空间关系要想象
应用:磁约束 I
(人工核聚变)
6
~
B
7
天然磁约束——Van Allen辐射带:
p 地球
第一辐射带:质子 (h~几千km)
与 I 方向成右手螺旋关系
I
n0
S 面积 16
N匝载流线圈的磁矩: pm NISn 0
2.非均匀磁场中的安培力:F Idl B L
Note: 在非均匀磁场中,载流线圈所受磁力 一般不为零
2024年大学物理磁场试题库含答案
第八章 磁场填空题 (简单)1、将通有电流为I的无限长直导线折成1/4圆环形状,已知半圆环的半径为R,则圆心O点的磁感应强度大小为 。
08IRμ2、磁场的高斯定理表白磁场是 无源场 。
3、只要有运动电荷,其周围就有 磁场 产生;4、(如图)无限长直导线载有电流I 1,矩形回路载有电流I 2,I 2回路的AB 边与长直导线平行。
电流I1产生的磁场作用在I 2回路上的合力F 的大小为,F的方向 水平向左 。
(综01201222()I I L I I La ab μμππ-+合) 5、有一圆形线圈,通有电流I,放在均匀磁场B 中,线圈平面与B垂直,则线圈上P点将受到 安培 力的作用,其方向为 指向圆心 ,线圈所受合力大小为 0 。
(综合)6、 是 磁场中的安培环路定理 ,它所反应的物理意义∑⎰==⋅n i i lI l d B 00μ是 在真空的稳恒磁场中,磁感强度沿任一闭合途径的积分等于乘以该闭合途径所包围的各电流的代数B 0μ和。
7、磁场的高斯定理表白通过任意闭合曲面的磁通量必等于 0 。
4题图5题图8、电荷在磁场中 不一定 (填一定或不一定)受磁场力的作用。
9、磁场最基本的性质是对 运动电荷、载流导线 有力的作用。
10、如图所示,在磁感强度为B 的均匀磁场中,有二分之一径为R的半球面,B 与半球面轴线的夹角为。
求通过该半球面的磁通量为。
(综合)α2cos B R πα- 12、一电荷以速度v 运动,它既 产生 电场,又 产生 磁场。
(填“产生”或“不产生”)13、一电荷为+q,质量为m ,初速度为的粒子垂直进入磁感应强度为B 的均匀磁场中,粒子将作 匀速圆0υ周 运动,其盘旋半径R=,盘旋周期T= 。
0m Bq υ2mBqπ14、把长直导线与半径为R 的半圆形铁环与圆形铁环相连接(如图a、b 所示),若通以电流为,则 a圆心I O的磁感应强度为___0__________;图b圆心O 的磁感应强度为。
大学物理第九章磁场
第九章磁场Stationary Magnetic Field磁铁和电流周围存在着磁场,磁现象的本质就是电荷的运动, 磁场的基本特性是对位于其中的运动电荷有力的作用.1、磁感应强度的定义;2、毕奥-萨伐尔定律,安培环路定理;3、几种电流产生的磁感应强度的计算;4、磁场对运动电荷、载流导线、载流线圈的作用;5、磁场和磁介质之间的相互作用.第一节磁场磁感应强度磁现象永磁体——磁铁的性质S N(1)具有磁性(magnetism),能吸引铁、钴、镍等物质;(2)永磁体具有磁极(magnetic pole),磁北极和磁南极;(3)磁极之间存在相互作用,同性相斥,异性相吸;(4)磁极不能单独存在.奥斯特实验(1819年)NS I在载流导线附近的小磁针会发生偏转Hans ChristianOersted,1777~1851年丹麦物理学家1820年安培的发现SN F I 放在磁体附近的载流导线或线圈会受到力的作用而发生运动.安培分子电流假说(1822年)一切磁现象的根源是电流!磁性物质的分子中存在着“分子电流”,磁性取定于物质中分子电流的磁效应之和.一、磁场(Magnetic Field)电流~~~磁铁、电流~~~电流运动电荷~~~运动电荷、运动电荷~~~磁铁通过一种特殊物质的形式——磁场来传递的.磁铁周围存在磁场,运动电荷和载流导线周围也存在磁场.磁场对其中的运动电荷和载流导线有力的作用;磁力也能做功,具有能量.电流与电流之间的相互作用I I ++--II ++--磁场对运动电荷的作用S +电子束N运动电荷磁场运动电荷从运动的点电荷在磁场中所受的磁力来定义磁感应强度的大小和方向!B 方向:小磁针在磁场中,其磁北极N 的指向B 二、磁感应强度(Magnetic Induction)磁感应强度:描述磁场性质的物理量B点电荷在磁场中运动的实验+B v F max c 、电荷q 沿磁场方向运动时,F = 0;b 、F 大小随v 变化;d 、电荷q 沿垂直磁场方向运动时,F max .(2)在垂直磁场方向改变速率v ,改变点电荷电量q在磁场中同一点,F max /qv 为一恒量,而在不同的点上,F max /qv 的量值不同.(1)点电荷q 以不同运动v a 、受磁力,;F v磁感应强度的大小:qv F B m ax =单位:T 特斯拉(Tesla)G 高斯(Gauss)T10G 14-=磁感应强度的方向:max F vB a.由小磁针的N 极指向定,b.由到的右手螺旋法则定max F v三、磁感应线用磁感应线来形象地描写磁感应强度这一矢量场在空间的分布:曲线上某点处的切向表示该点的方向;曲线在某处的疏密表示该点的大小.B B 磁感应线的特点★任一条磁感应线是闭合的,或两端伸向无穷远;★磁感应线与载流回路互相套联;★任两条磁感应线不能相交.IB四、磁通量(Magnetic Flux)通过磁场中某给定面的磁感应线的总数.θcos d d m S B Φ=⎰⎰=⋅=S S m S B S B Φd cos d θ 单位:Wb ,1Wb=1T ﹒m 2磁通量:穿过磁场中任意闭合曲面的磁通量为零.磁场是无源场:其磁感应线闭合成环,无头无尾;同时也表示不存在磁单极,无单个的N 或S 极.The total magnetic flux through a closed surface is always zero.d 0S B S ⋅=⎰ 五、磁场的高斯定理(Gauss’s law for magnetism)寻找磁单极子1975 年:美国加州大学,休斯敦大学联合小组报告,用装有宇宙射线探测器气球在40 km 高空记录到电离性特强离子踪迹,认为是磁单极. 为一次虚报.1982年,美国斯坦福大学报告,用d = 5 cm 的超导线圈放入D =20 cm 超导铅筒. 由于迈斯纳效应屏蔽外磁场干扰,只有磁单极进入会引起磁通变化,运行151天,记录到一次磁通突变, 改变量与狄拉克理论相符. 但未能重复,为一悬案.人类对磁单极的探寻从未停止,一旦发现磁单极,将改写电磁理论.1820年实验得到:长直载流导线周围的磁感应强度与距离成反比与电流强度成正比. r I B Laplace 对此结果作了分析整理,得出了电流元产生的磁场的磁感应强度表达式.一、毕奥—萨伐尔定律(Law of Biot and Savart)I B r 第二节毕奥—萨伐尔定律d I l IBd l r d I l02d sin d 4I l B r μθπ=002d d 4I l r B r μπ⨯= μo 为真空中的磁导率:μo = 4 π⨯10-7 T·m·A -1. 整个载流导线在P 点产生的磁感应强度为:002d d 4L LI l r B B r μπ⨯==⎰⎰ P d I l θr d Bnqvs I =0024qv r B r μπ⨯= ++++++I S v d I l 导体中带电粒子的定向运动形成电流I ,并由此可分析得到运动电荷产生的磁场.+v r B ×-v r B·二、运动电荷的磁场圆电流轴线上的磁感应强度02d sin d 4I l B r μθπ=02d sin 90cos d cos 4x I l B B B r μααπ︒===⎰⎰22xR r +=22cos R R x α=+x x P R αr d B d I ld B x d B y 毕奥—萨伐尔定律的应用d I l r ⊥ 注意到,通过对称性分析,可知B y = 0,因此:()()2200323222220d 42RR l IR B R x R x πμμπ==++⎰方向:沿轴线与电流成右手螺旋关系.()2032222IRB R x μ=+定义圆电流磁矩:mp IS ISn == 在圆心处x = 0,B 大小:R IB 20μ=IS m p ()2322m 02x R P B += πμ圆电流轴线上磁场的另一种表达式:例:亥姆霍兹圈:两个完全相同的N 匝共轴密绕短线圈,其中心间距与半径R 相等,通有同向平行等大电流I . 求轴线上O 1、O 2之间的磁场.x I P1o 匝N R ⋅⋅R R 匝N o 2o I x o1o 2B 1B 2o 实验室用近似均匀磁场解20322222P NIR B R R x μ=+⎡⎤⎛⎫++ ⎪⎢⎥⎝⎭⎣⎦20322222NIRR R x μ⎡⎤⎛⎫+- ⎪⎢⎥⎝⎭⎣⎦00.72O NIB Rμ=0120.68O O NIB B Rμ==θ2Oθ1Pa d xx载流长直导线的磁感应强度02d sin d 4I x B rμθπ=tan x a θ=-2d d sin a x θθ=θsin a r =2022sin d sin d 4sin I aB B aμθθθπθ==⎰⎰Iθrd B 210sin d 4I B a θθμθθπ=⎰()012cos cos 4I a μθθπ=-方向:对图中所在的P 点,磁感应强度垂直纸面向外.()012cos cos 4I B aμθθπ=-对无限长载流导线θ1= 0 , θ2= π:02I B aμπ=半无限长载流导线θ1= π/2 , θ2 = π:04I B aμπ=若P 点在导线延长线上:B =导线密绕,且长度远大于直径:=外B 实验可知:内部的磁感应强度只有平行于轴线的分量;并且平行于轴的任一直线上各点大小相等.︒⋅⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅BI单位长度上的匝数n载流长直螺线管内部的磁场︒⋅⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅BInIB 0μ=内部为均匀磁场,在长直螺线管的两端点处的磁场为中间的一半:012S B nIμ=0nIμ012nI μ通过对圆电流的磁感应强度的叠加积分,可以求得螺线管中间的磁感应强度大小为:方向由右手螺旋法则确定.恒定磁场是无源场,静电场是有源场;静电场是保守场,是无旋场;对静电场和恒定磁场作类比分析:1d SE S q ε⋅=∑⎰d 0LE l ⋅=⎰d 0SB S ⋅=⎰d ?LB l ⋅=⎰表达了恒定磁场的什么性质?第三节安培环路定理安培环路定理:0d LB l Iμ⋅=∑⎰L 磁场中任一闭合曲线—具有一定绕向的环路是环路上各点的磁感应强度,为空间所有电流产生,包括穿过L 的和不穿过的电流.:B:穿过以L 为边界的任意曲面的电流的代数和.I ∑------对L 包围的电流求代数和,并且规定:与L 绕向成右旋关系的电流I i >0,否则I i <0.以长直电流的磁场为例验证1) 路径选在垂直于长直载流导线的平面内,以导线与平面交点O 为圆心,半径为r 的圆周路径L ,其指向与电流成右手螺旋关系.BIr oL00200cos 0d d =d 22rL L I I B l l l r rIπμμππμ⋅=⋅=⎰⎰⎰BIr oL若电流反向:02000d d 2 =d 2cos L L rI I B l l r I l rππμπμμπ⋅=⋅-=-⎰⎰⎰2) 在垂直于导线平面内围绕电流的任意闭合路径Bθϕd ld rLI 02020000d 2 =d 2 d cos 2d L L I B l r I r r I I l ππμπμϕπμϕπμθ⋅=⋅==⎰⎰⎰⎰同理,在电流反向时------积分结果取负.3) 闭合路径不包围电流ϕ1L 2L I()()[]121200d d d =d d 2 02LL L L L B l B l B l I Iμϕϕπμϕϕπ⋅=⋅+⋅+=+-=⎰⎰⎰⎰⎰4) 空间存在多个长直电流时()12110in d d d d =L LLLiLB l B B l B l B l I μ⋅=++⋅=⋅+⋅+⎰⎰⎰⎰∑安培环路定理揭示磁场是非保守场,是涡旋场.l B L d ⋅⎰穿过的电流:对和均有贡献BL 不穿过的电流:对上各点有贡献;对无贡献BL l B Ld ⋅⎰L 0d LB l Iμ⋅=∑⎰可证对任意的稳恒电流和任意形式的闭合环路均成立.注意:练习:如图,流出纸面的电流为2I ,流进纸面的电流为I ,则下述各式中那一个是正确的?⊗∙I 21L 2L 3L 4L I10 ( d )2A L B l I μ⋅=⎰ 20(B) d L B l I μ⋅=⎰30 d (C)L B l I μ⋅=-⎰40(D) d L B l I μ⋅=-⎰Br RB RrP IQ 长直圆柱形载流导线内外的磁场圆柱截面半径为R ,电流I 沿轴流动.过P 点(或Q 点)取半径为r 的磁感应线为积分回路,求出B 矢量的环流:0d 2LB l B r I πμ⋅=⋅=∑⎰r ≥R012I I I B r r μπ==∝∑,r< R20222I r IrI B r R Rπμππ==∝∑,方向沿圆周与电流成右手关系!or LL BoRrr1∝B r∝思考:无限长均匀载流直圆筒,B ~r 曲线?BoRr管外磁场为零.无限长直载流螺线管内磁场︒⋅⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗⊗︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅︒⋅BI单位长度上的匝数n解密绕长螺线管,已知I , n ,计算管内的磁感应强度.dc ab 作矩形安培环路abcd 如图,绕行方向为逆时针.00d d 000=b c d a LabcdB l B l B dl B dl B dlBcd I ncdIμμ⋅=⋅+⋅+⋅+⋅=+++=⎰⎰⎰⎰⎰∑0B nIμ=无限长螺线管磁场为均匀.求螺线环内的磁感应强度I l B L∑=⋅⎰0d μ 02B r NIπμ⋅=rNI B πμ20=2N n rπ=nIB 0μ=Or 1r 2Pr 为平均半径, 考虑到对称性,环内磁场的磁感应线都是同心圆,选择通过管内某点P 的磁感应线L 作为积分环路:方向由电流方向通过右手法则判断.第四节磁场对运动电荷的作用一. 洛仑兹力磁场对运动电荷的作用f qv B=⨯ 大小:θsin qvB F =特点:不改变大小,只改变方向,不对做功.vq v vBf运动正电荷受力方向垂直于和构成的平面,成右手螺旋.v B1、运动方向与磁场方向平行sin F qvB θ=θ= 0 , F = 0带电粒子在均匀磁场中的运动匀速直线运动θBvq+f⊗θBvq-fB+v⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯B 2、运动方向与磁场方向垂直RvmqvB 2=qBmv R =v B f qvB⊥⇒=R22R m T v qBππ==匀速圆周运动周期f+v半径托克马克装置3、沿任意方向方向运动匀速圆周运动与匀速直线运动的合成——轨迹为螺旋线qBmv R θsin =qBm T π2=螺距//2cos m h v T v qBπθ==h +B ⊥v //v θv例有一均匀磁场,B = 1.5 T ,水平方向由南向北. 有一5.0 兆电子伏特的质子沿竖直向下的方向通过磁场,求作用在质子上的力?(m = 1.67⨯10-27 kg )) J (100.8) eV (100.5211362k -⨯=⨯==mv E ) s m (101.31067.1100.822172713k ---⋅⨯=⨯⨯⨯==m E v ︒⨯⨯⨯⨯⨯==-90sin 5.1101.3106.1sin 719θqvB F )N (104.712-⨯=解方向向东F q v 下B 北二、质谱仪(mass spectrograph)R +-⋅⋅⋅P ⋅⋅⋅⋅⋅⋅⋅⋅⋅N ⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅B N :粒子源,P :速度选择器 qE qvB v E B ''=⇒=质谱分析:qB mv R x 22==E x B qB m 2'=谱线位置:同位素质量;谱线黑度:相对含量.B’三、霍尔效应(Hall effect)现象:通电流I ,磁场垂直于I ,在既垂直于I ,又垂直于的方向出现电势差∆U. B B m e F qv B F qE =⨯= H I IB U Bb R nqbd d∆==霍尔电势差:解释:载流子q 以漂移,受到磁场力,正负电荷上下两侧积累,形成电场,受力平衡时,有稳定的霍尔电场.v x y zB I b d P 型半导体v q +++++++-+------e F m F I nqvbd =霍尔系数R H 与载流子浓度n 成反比. 在金属中,由于载流子浓度很大,因此霍尔系数很小,相应地霍尔效应也很弱; 而在半导体中,载流子浓度较小,因此霍尔效应也较明显. 霍尔效应是半导体研究的重要手段. 问题:对n 型半导体,霍尔电势差的方向如何?应用:测载流子浓度测载流子电性—半导体类型B 测磁场(霍耳元件)H 1R nq霍尔系数(Hall coefficient):一、安培定律(Ampère Law )磁场对电流元的作用Bl I F ⨯=d d 载流导线所受磁场力d d L L F F I l B ==⨯⎰⎰ 第五节磁场对电流的作用磁矩L I B d I l Fm F qv B =⨯ d F qv BdN qv BnSdl =⨯=⨯载流直导线在均匀磁场中所受的力d L F I l B =⨯⎰ sin d L F IB l θ=⎰θsin ILB F =sin d L IB l θ=⎰安培力的方向由右手螺旋法则可知为垂直纸面向里×IBθFB θd I lLA B C D I 1I 21d I l 2d I l 1B 2B 1d F 2d F 平行长直载流导线间的相互作用力距a 的两无限长直导线,I 1、I 2,导线CD 上的电流元受力:2222d d sin F B I l θ=012 ,22I B a μπθπ==CD 单位长度受力:2012121d d d 2d F I I F l a l μπ==安培:真空中相距为1m 的无限长直细导线,载有相等的电流,若每米导线上受力正好为2⨯10-7N ,则导线内电流定义为1A.例:如图,均匀磁场垂直纸面向外,半径为R 的半圆导线通有电流I ,求作用在导线上的安培力.解R y x Bd θθd I l d F d x F d y F d F =IB d l =IBR d θd d F I l B =⨯ 0d (d )sin 2y y L F F F IBR IBR πθθ====⎰⎰方向为y 轴正向.推广:起点终点相同的载流直导线所受的力?对称性-----各电流元受力水平分量之和为零。
大学物理稳恒磁场理论及习题解读
250 0 方向垂直A面
B
BC
0 N C I C
2 RC
0 20 5
2 0.10
O BA
5000 方向垂直C面
B
2 BA
2 BC
7.02 10 T 方向 : tan
4
1
BC 63.4 BA
NIZQ
第14页
大学物理学
恒定磁场
NIZQ
问题: 磁现象产生的原因是什么?
第 2页
大学物理学
恒定磁场
• 电流的磁效应 1820年奥斯特实验表明: 电流对磁极有 力的作用. 1820年 9月 11日在法国科学院演示的奥 斯特的实验 ,引起了安培的兴趣 .一周之后 安培发现了电流间也存在着相互作用力.
此后安培又提出了著名的安 培定律 : 磁体附近的载流导线 会受到力的作用而发生运动.
NIZQ
第 3页
大学物理学
恒定磁场
结论: 磁现象与电荷的运动有着密切的关系 . 运动电荷既能产 生磁效应,也受到磁力的作用. 安培把磁性归结为电流之间的相互作用 . 1822年安培提 出了分子电流假说:
• 一切磁现象起源于电荷的运动.
• 磁性物质的分子中存在分子电流, 每个分子电流相当于一基元磁体。
写成矢量表示:
0 Idl sin
2 4π r 0 Idl r dB 4π r 3
真空中的磁导率: 0= 410-7亨利· 米-1 (H· m-1)
NIZQ
第 8页
大学物理学
恒定磁场
• 毕奥—萨伐尔定律的应用 恒定磁场的计算: 1.选取电流元或某些典型电流分布为积分元. 2.由毕-萨定律写出积分元的磁场dB .
